Allgemeine Lösung der Differentialgleichung online. Lösen der einfachsten Differentialgleichungen erster Ordnung
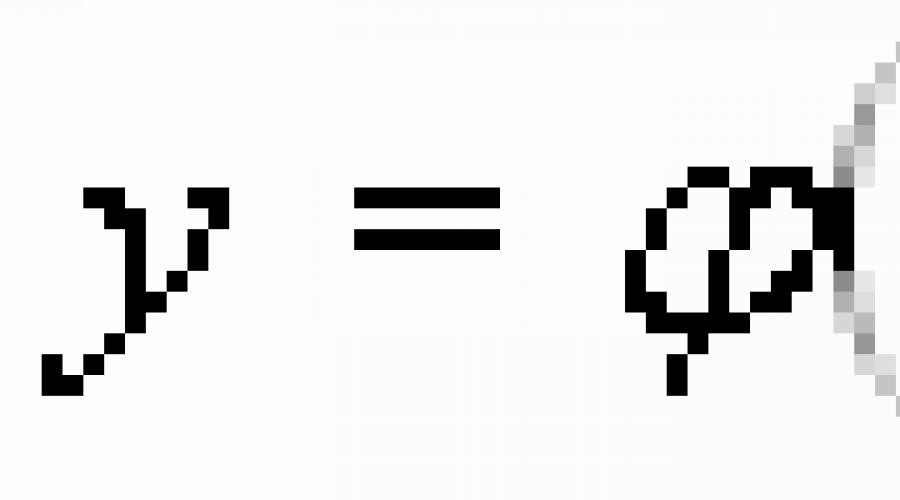
Lesen Sie auch
I. Gewöhnliche Differentialgleichungen
1.1. Grundlegende Konzepte und Definitionen
Eine Differentialgleichung ist eine Gleichung, die eine unabhängige Variable in Beziehung setzt X, die erforderliche Funktion j und seine Ableitungen oder Differentiale.
Symbolisch wird die Differentialgleichung wie folgt geschrieben:
F(x,y,y")=0, F(x,y,y")=0, F(x,y,y",y",.., y (n))=0
Eine Differentialgleichung heißt gewöhnlich, wenn die gesuchte Funktion von einer unabhängigen Variablen abhängt.
Lösen einer Differentialgleichung heißt eine Funktion, die diese Gleichung in eine Identität umwandelt.
Die Ordnung der Differentialgleichung ist die Ordnung der höchsten in dieser Gleichung enthaltenen Ableitung
Beispiele.
1. Betrachten Sie eine Differentialgleichung erster Ordnung
Die Lösung dieser Gleichung ist die Funktion y = 5 ln x. In der Tat, ersetzen y" In die Gleichung erhalten wir die Identität.
Und das bedeutet, dass die Funktion y = 5 ln x– eine Lösung dieser Differentialgleichung ist.
2. Betrachten Sie die Differentialgleichung zweiter Ordnung y" - 5y" +6y = 0. Die Funktion ist die Lösung dieser Gleichung.
Wirklich, .
Wenn wir diese Ausdrücke in die Gleichung einsetzen, erhalten wir: , – Identität.
Und das bedeutet, dass die Funktion die Lösung dieser Differentialgleichung ist.
Integrieren von Differentialgleichungen ist der Prozess, Lösungen für Differentialgleichungen zu finden.
Allgemeine Lösung der Differentialgleichung eine Funktion der Form genannt ![]() , die so viele unabhängige beliebige Konstanten enthält, wie die Ordnung der Gleichung.
, die so viele unabhängige beliebige Konstanten enthält, wie die Ordnung der Gleichung.
Teillösung der Differentialgleichung ist eine Lösung, die aus einer allgemeinen Lösung für verschiedene numerische Werte beliebiger Konstanten erhalten wird. Die Werte beliebiger Konstanten liegen bei bestimmten Anfangswerten des Arguments und der Funktion.
Der Graph einer bestimmten Lösung einer Differentialgleichung heißt Integralkurve.
Beispiele
1. Finden Sie eine bestimmte Lösung für eine Differentialgleichung erster Ordnung
xdx + ydy = 0, Wenn j= 4 bei X = 3.
Lösung. Wenn wir beide Seiten der Gleichung integrieren, erhalten wir
Kommentar. Eine durch Integration erhaltene beliebige Konstante C kann in jeder für weitere Transformationen geeigneten Form dargestellt werden. In diesem Fall ist es unter Berücksichtigung der kanonischen Kreisgleichung zweckmäßig, eine beliebige Konstante C in der Form darzustellen.
![]() - allgemeine Lösung der Differentialgleichung.
- allgemeine Lösung der Differentialgleichung.
Bestimmte Lösung der Gleichung, die die Anfangsbedingungen erfüllt j = 4 bei X = 3 ergibt sich aus der allgemeinen Lösung durch Einsetzen der Anfangsbedingungen in die allgemeine Lösung: 3 2 + 4 2 = C 2 ; C=5.
Wenn wir C=5 in die allgemeine Lösung einsetzen, erhalten wir x 2 +y 2 = 5 2 .
Dies ist eine spezielle Lösung einer Differentialgleichung, die aus einer allgemeinen Lösung unter gegebenen Anfangsbedingungen erhalten wird.
2. Finden Sie die allgemeine Lösung der Differentialgleichung
Die Lösung dieser Gleichung ist eine beliebige Funktion der Form, wobei C eine beliebige Konstante ist. Tatsächlich erhalten wir beim Einsetzen in die Gleichungen: , .
Folglich hat diese Differentialgleichung unendlich viele Lösungen, da für unterschiedliche Werte der Konstante C die Gleichheit unterschiedliche Lösungen der Gleichung bestimmt.
Durch direkte Substitution können Sie beispielsweise überprüfen, ob die Funktionen funktionieren ![]() sind Lösungen der Gleichung.
sind Lösungen der Gleichung.
Ein Problem, bei dem Sie eine bestimmte Lösung für die Gleichung finden müssen y" = f(x,y) Erfüllung der Anfangsbedingung y(x 0) = y 0, wird Cauchy-Problem genannt.
Lösung der Gleichung y" = f(x,y), die Anfangsbedingung erfüllend, y(x 0) = y 0, wird als Lösung des Cauchy-Problems bezeichnet.
Die Lösung des Cauchy-Problems hat eine einfache geometrische Bedeutung. Tatsächlich, nach diesen Definitionen, um das Cauchy-Problem zu lösen y" = f(x,y) angesichts dessen y(x 0) = y 0 bedeutet, die Integralkurve der Gleichung zu finden y" = f(x,y) die durch einen gegebenen Punkt geht M 0 (x 0,y 0).
II. Differentialgleichungen erster Ordnung
2.1. Grundlegendes Konzept
Eine Differentialgleichung erster Ordnung ist eine Gleichung der Form F(x,y,y") = 0.
Eine Differentialgleichung erster Ordnung umfasst die erste Ableitung und keine Ableitungen höherer Ordnung.
Die gleichung y" = f(x,y) heißt eine nach der Ableitung gelöste Gleichung erster Ordnung.
Die allgemeine Lösung einer Differentialgleichung erster Ordnung ist eine Funktion der Form, die eine beliebige Konstante enthält.
Beispiel. Betrachten Sie eine Differentialgleichung erster Ordnung.
Die Lösung dieser Gleichung ist die Funktion.
Tatsächlich erhalten wir, wenn wir diese Gleichung durch ihren Wert ersetzen

![]() also 3x=3x
also 3x=3x
Daher ist die Funktion eine allgemeine Lösung der Gleichung für jede Konstante C.
Finden Sie eine bestimmte Lösung gegebene Gleichung, die die Anfangsbedingung erfüllt y(1)=1 Anfangsbedingungen ersetzen x = 1, y =1 In die allgemeine Lösung der Gleichung kommen wir von wo C=0.
Somit erhalten wir eine bestimmte Lösung aus der allgemeinen Lösung, indem wir den resultierenden Wert in diese Gleichung einsetzen C=0– private Lösung.
2.2. Differentialgleichungen mit separierbaren Variablen
Eine Differentialgleichung mit separierbaren Variablen ist eine Gleichung der Form: y"=f(x)g(y) oder durch Differentiale, wo f(x) Und g(y)– spezifizierte Funktionen.
Für diejenigen j, für die die Gleichung y"=f(x)g(y) ist äquivalent zur Gleichung, ![]() in dem die Variable j ist nur auf der linken Seite vorhanden und die Variable x ist nur auf der rechten Seite vorhanden. Sie sagen: „In Gl. y"=f(x)g(y Trennen wir die Variablen.“
in dem die Variable j ist nur auf der linken Seite vorhanden und die Variable x ist nur auf der rechten Seite vorhanden. Sie sagen: „In Gl. y"=f(x)g(y Trennen wir die Variablen.“
Gleichung des Formulars ![]() wird als Gleichung mit getrennten Variablen bezeichnet.
wird als Gleichung mit getrennten Variablen bezeichnet.
Integration beider Seiten der Gleichung ![]() Von X, wir bekommen G(y) = F(x) + C ist die allgemeine Lösung der Gleichung, wobei G(y) Und F(x)– einige Stammfunktionen jeweils von Funktionen und f(x), C Willkürliche Konstante.
Von X, wir bekommen G(y) = F(x) + C ist die allgemeine Lösung der Gleichung, wobei G(y) Und F(x)– einige Stammfunktionen jeweils von Funktionen und f(x), C Willkürliche Konstante.
Algorithmus zur Lösung einer Differentialgleichung erster Ordnung mit separierbaren Variablen
Beispiel 1
Löse die Gleichung y" = xy
Lösung. Ableitung einer Funktion y" Ersetzen Sie es durch
Trennen wir die Variablen
Integrieren wir beide Seiten der Gleichheit:

Beispiel 2
2yy" = 1- 3x 2, Wenn y 0 = 3 bei x 0 = 1
Dies ist eine Gleichung mit getrennten Variablen. Stellen wir es uns in Differentialen vor. Dazu schreiben wir diese Gleichung in der Form um ![]() Von hier
Von hier ![]()
Wir finden, dass wir beide Seiten der letzten Gleichheit integrieren
Ersetzen der Anfangswerte x 0 = 1, y 0 = 3 wir werden finden MIT 9=1-1+C, d.h. C = 9.
Daher wird das erforderliche Teilintegral sein ![]() oder
oder ![]()
Beispiel 3
Schreiben Sie eine Gleichung für eine Kurve, die durch einen Punkt verläuft M(2;-3) und eine Tangente mit einem Winkelkoeffizienten haben
Lösung. Je nach Zustand
Dies ist eine Gleichung mit trennbaren Variablen. Durch Division der Variablen erhalten wir: ![]()
Wenn wir beide Seiten der Gleichung integrieren, erhalten wir: 
Unter Verwendung der Anfangsbedingungen x = 2 Und y = - 3 wir werden finden C:

Daher hat die erforderliche Gleichung die Form ![]()
2.3. Linear Differentialgleichung erste Bestellung
Eine lineare Differentialgleichung erster Ordnung ist eine Gleichung der Form y" = f(x)y + g(x)
Wo f(x) Und g(x)- einige spezifizierte Funktionen.
Wenn g(x)=0 dann heißt die lineare Differentialgleichung homogen und hat die Form: y" = f(x)y
Wenn dann die Gleichung y" = f(x)y + g(x) als heterogen bezeichnet.
Gemeinsame Entscheidung lineare homogene Differentialgleichung y" = f(x)y wird durch die Formel gegeben: wo MIT- Willkürliche Konstante.
Insbesondere, wenn C = 0, dann ist die Lösung y = 0 Wenn eine lineare homogene Gleichung die Form hat y" = ky Wo k eine Konstante ist, dann hat ihre allgemeine Lösung die Form: .
Allgemeine Lösung einer linearen inhomogenen Differentialgleichung y" = f(x)y + g(x) ergibt sich aus der Formel ![]() ,
,
diese. ist gleich der Summe der allgemeinen Lösung der entsprechenden linearen homogenen Gleichung und der besonderen Lösung dieser Gleichung.
Für eine lineare inhomogene Gleichung der Form y" = kx + b,
Wo k Und B- Einige Zahlen und eine bestimmte Lösung sind eine konstante Funktion. Daher hat die allgemeine Lösung die Form.
Beispiel. Löse die Gleichung y" + 2y +3 = 0
Lösung. Stellen wir die Gleichung im Formular dar y" = -2y - 3 Wo k = -2, b= -3 Die allgemeine Lösung ergibt sich aus der Formel.
Daher ist C eine beliebige Konstante.
2.4. Lösung linearer Differentialgleichungen erster Ordnung nach der Bernoulli-Methode
Finden einer allgemeinen Lösung für eine lineare Differentialgleichung erster Ordnung y" = f(x)y + g(x) reduziert sich auf die Lösung zweier Differentialgleichungen mit getrennten Variablen mittels Substitution y=uv, Wo u Und v- unbekannte Funktionen von X. Diese Lösungsmethode wird Bernoulli-Methode genannt.
Algorithmus zur Lösung einer linearen Differentialgleichung erster Ordnung
y" = f(x)y + g(x)
1. Geben Sie die Vertretung ein y=uv.
2. Differenzieren Sie diese Gleichheit y" = u"v + uv"
3. Ersatz j Und y" in diese Gleichung: u"v + uv" =f(x)uv + g(x) oder u"v + uv" + f(x)uv = g(x).
4. Gruppieren Sie die Terme der Gleichung so u nimm es aus der Klammer:
5. Suchen Sie aus der Klammer, indem Sie sie mit Null gleichsetzen, die Funktion
Dies ist eine trennbare Gleichung: ![]()
Teilen wir die Variablen und erhalten: ![]()
Wo ![]() .
.
.
.
6. Ersetzen Sie den resultierenden Wert v in die Gleichung ein (aus Schritt 4):
![]()
und finden Sie die Funktion Dies ist eine Gleichung mit trennbaren Variablen:
![]()
7. Schreiben Sie die allgemeine Lösung in das Formular: ![]() , d.h. .
, d.h. .
Beispiel 1
Finden Sie eine bestimmte Lösung der Gleichung y" = -2y +3 = 0 Wenn y =1 bei x = 0
Lösung. Lassen Sie es uns durch Substitution lösen y=uv,.y" = u"v + uv"
Ersetzen j Und y" in diese Gleichung erhalten wir
Indem wir den zweiten und dritten Term auf der linken Seite der Gleichung gruppieren, entfernen wir den gemeinsamen Faktor u außerhalb der Klammern
Wir setzen den Ausdruck in Klammern mit Null gleich und finden nach Lösung der resultierenden Gleichung die Funktion v = v(x)
Wir erhalten eine Gleichung mit getrennten Variablen. Integrieren wir beide Seiten dieser Gleichung: Finden Sie die Funktion v:
![]()
Ersetzen wir den resultierenden Wert v in die Gleichung erhalten wir:
Dies ist eine Gleichung mit getrennten Variablen. Integrieren wir beide Seiten der Gleichung: ![]() Finden wir die Funktion u = u(x,c)
Finden wir die Funktion u = u(x,c) ![]() Lassen Sie uns eine allgemeine Lösung finden:
Lassen Sie uns eine allgemeine Lösung finden: ![]() Lassen Sie uns eine bestimmte Lösung der Gleichung finden, die die Anfangsbedingungen erfüllt y = 1 bei x = 0:
Lassen Sie uns eine bestimmte Lösung der Gleichung finden, die die Anfangsbedingungen erfüllt y = 1 bei x = 0:

III. Differentialgleichungen höherer Ordnung
3.1. Grundlegende Konzepte und Definitionen
Eine Differentialgleichung zweiter Ordnung ist eine Gleichung, die Ableitungen nicht höherer als zweiter Ordnung enthält. Im allgemeinen Fall wird eine Differentialgleichung zweiter Ordnung wie folgt geschrieben: F(x,y,y",y") = 0
Die allgemeine Lösung einer Differentialgleichung zweiter Ordnung ist eine Funktion der Form, die zwei beliebige Konstanten enthält C 1 Und C 2.
Eine besondere Lösung einer Differentialgleichung zweiter Ordnung ist eine Lösung, die aus einer allgemeinen Lösung für bestimmte Werte beliebiger Konstanten erhalten wird C 1 Und C 2.
3.2. Lineare homogene Differentialgleichungen zweiter Ordnung mit konstante Koeffizienten.
Lineare homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten wird als Gleichung der Form bezeichnet y" + py" +qy = 0, Wo P Und Q- konstante Werte.
Algorithmus zur Lösung homogener Differentialgleichungen zweiter Ordnung mit konstanten Koeffizienten
1. Schreiben Sie die Differentialgleichung in der Form: y" + py" +qy = 0.
2. Erstellen Sie die charakteristische Gleichung und bezeichnen Sie sie y" durch r 2, y" durch R, j in 1: r 2 + pr +q = 0
6.1. GRUNDLEGENDE KONZEPTE UND DEFINITIONEN
Bei der Entscheidung mehrere Aufgaben In Mathematik und Physik, Biologie und Medizin ist es oft nicht möglich, sofort einen funktionalen Zusammenhang in Form einer Formel herzustellen, die die Variablen verbindet, die den untersuchten Prozess beschreiben. Normalerweise müssen Sie Gleichungen verwenden, die neben der unabhängigen Variablen und der unbekannten Funktion auch deren Ableitungen enthalten.
Definition. Eine Gleichung, die eine unabhängige Variable, eine unbekannte Funktion und ihre Ableitungen verschiedener Ordnungen verbindet, wird aufgerufen Differential.
Normalerweise wird eine unbekannte Funktion bezeichnet y(x) oder einfach ja, und seine Derivate - y", y" usw.
Auch andere Bezeichnungen sind möglich, zum Beispiel: if j= x(t), dann x"(t), x""(t)- seine Derivate und T- unabhängige Variable.
Definition. Wenn eine Funktion von einer Variablen abhängt, heißt die Differentialgleichung gewöhnlich. Generelle Form gewöhnliche Differentialgleichung:
oder
Funktionen F Und F Möglicherweise sind einige Argumente nicht enthalten, aber damit die Gleichungen Differentialgleichungen sind, ist das Vorhandensein einer Ableitung unerlässlich.
Definition.Die Ordnung der Differentialgleichung heißt die Ordnung der höchsten darin enthaltenen Ableitung.
Zum Beispiel, x 2 y"- j= 0, y" + sin X= 0 sind Gleichungen erster Ordnung und y"+ 2 y"+ 5 j= X- Gleichung zweiter Ordnung.
Bei der Lösung von Differentialgleichungen wird die Integrationsoperation verwendet, die mit dem Auftreten einer beliebigen Konstante verbunden ist. Wenn die Integrationsaktion angewendet wird N mal, dann wird die Lösung natürlich enthalten N beliebige Konstanten.
6.2. DIFFERENZGLEICHUNGEN ERSTER ORDNUNG
Generelle Form Differentialgleichung erster Ordnung wird durch den Ausdruck bestimmt
Die Gleichung darf nicht explizit enthalten X Und ja, enthält aber notwendigerweise y".
Wenn die Gleichung geschrieben werden kann als
dann erhalten wir eine nach der Ableitung aufgelöste Differentialgleichung erster Ordnung.
Definition. Die allgemeine Lösung der Differentialgleichung erster Ordnung (6.3) (oder (6.4)) ist die Menge der Lösungen  , Wo MIT- Willkürliche Konstante.
, Wo MIT- Willkürliche Konstante.
Der Graph der Lösung einer Differentialgleichung heißt Integralkurve.
Angabe einer beliebigen Konstante MIT Bei unterschiedlichen Werten können Teillösungen erhalten werden. Auf der Oberfläche xOy Die allgemeine Lösung ist eine Familie von Integralkurven, die jeder einzelnen Lösung entsprechen.
Wenn Sie einen Punkt setzen A (x 0 , y 0), durch die die Integralkurve verlaufen muss, also in der Regel aus einer Menge von Funktionen ![]() Eines kann man herausgreifen – eine private Lösung.
Eines kann man herausgreifen – eine private Lösung.
Definition.Private Entscheidung einer Differentialgleichung ist ihre Lösung, die keine beliebigen Konstanten enthält.
Wenn ![]() ist eine allgemeine Lösung, dann aus der Bedingung
ist eine allgemeine Lösung, dann aus der Bedingung
 Sie können eine Konstante finden MIT. Die Bedingung wird aufgerufen ausgangsbedingung.
Sie können eine Konstante finden MIT. Die Bedingung wird aufgerufen ausgangsbedingung.
Das Problem, eine bestimmte Lösung für die Differentialgleichung (6.3) oder (6.4) zu finden, die die Anfangsbedingung erfüllt  bei
bei ![]() angerufen Cauchy-Problem. Gibt es für dieses Problem immer eine Lösung? Die Antwort ist im folgenden Satz enthalten.
angerufen Cauchy-Problem. Gibt es für dieses Problem immer eine Lösung? Die Antwort ist im folgenden Satz enthalten.
Satz von Cauchy(Theorem der Existenz und Einzigartigkeit einer Lösung). Lassen Sie die Differentialgleichung ein y"= f(x,y) Funktion f(x,y) und sie
partielle Ableitung  in einigen Fällen definiert und kontinuierlich
in einigen Fällen definiert und kontinuierlich
Region D, einen Punkt enthalten  Dann in der Gegend D existiert
Dann in der Gegend D existiert
einzige Entscheidung Gleichung, die die Anfangsbedingung erfüllt ![]() bei
bei 
Der Satz von Cauchy besagt, dass es unter bestimmten Bedingungen eine eindeutige Integralkurve gibt j= f(x), durch einen Punkt gehen  Punkte, an denen die Bedingungen des Satzes nicht erfüllt sind
Punkte, an denen die Bedingungen des Satzes nicht erfüllt sind
Cauchies werden genannt besonders. An diesen Stellen bricht es F(x, y) oder.
Entweder verlaufen mehrere Integralkurven oder keine durch einen singulären Punkt.
Definition. Wenn die Lösung (6.3), (6.4) in der Form gefunden wird F(x, y, C)= 0, relativ zu y nicht erlaubt, dann heißt es allgemeines Integral Differentialgleichung.
Der Satz von Cauchy garantiert nur, dass eine Lösung existiert. Da es keine einheitliche Methode zum Finden einer Lösung gibt, betrachten wir nur einige Arten von Differentialgleichungen erster Ordnung, in die integriert werden kann Quadraturen
Definition. Die Differentialgleichung heißt in Quadraturen integrierbar, wenn es bei der Lösungsfindung auf die Integration von Funktionen ankommt.
6.2.1. Differentialgleichungen erster Ordnung mit separierbaren Variablen
Definition. Eine Differentialgleichung erster Ordnung heißt Gleichung mit trennbare Variablen,
Die rechte Seite der Gleichung (6.5) ist das Produkt zweier Funktionen, die jeweils nur von einer Variablen abhängen.
Zum Beispiel die Gleichung  ist eine Gleichung mit Trennfunktion
ist eine Gleichung mit Trennfunktion
gemischt mit Variablen  und die Gleichung
und die Gleichung 
kann nicht in der Form (6.5) dargestellt werden.
Bedenkt, dass  , schreiben wir (6.5) in der Form um
, schreiben wir (6.5) in der Form um 
Aus dieser Gleichung erhalten wir eine Differentialgleichung mit getrennten Variablen, in der die Differentiale Funktionen sind, die nur von der entsprechenden Variablen abhängen:

Wir haben Begriff für Begriff integriert

wobei C = C 2 - C 1 - beliebige Konstante. Ausdruck (6.6) ist allgemeines Integral Gleichung (6.5).
Indem wir beide Seiten der Gleichung (6.5) durch dividieren, können wir diejenigen Lösungen verlieren, für die  In der Tat, wenn
In der Tat, wenn  bei
bei 
Das  ist offensichtlich eine Lösung für Gleichung (6.5).
ist offensichtlich eine Lösung für Gleichung (6.5).
Beispiel 1. Finden Sie eine Lösung der Gleichung, die erfüllt
Zustand: j= 6 at X= 2 (j(2) = 6).
Lösung. Wir werden ersetzen y" Dann  . Multiplizieren Sie beide Seiten mit
. Multiplizieren Sie beide Seiten mit
dx, denn während der weiteren Integration ist ein Weggehen nicht möglich dx im Nenner:

und dann beide Teile durch dividieren  wir erhalten die Gleichung,
wir erhalten die Gleichung,
die integriert werden können. Integrieren wir: 

Dann  ; Potenzierend erhalten wir y = C. (x + 1) - ob-
; Potenzierend erhalten wir y = C. (x + 1) - ob-
Allgemeine Lösung.
Anhand der Ausgangsdaten bestimmen wir eine beliebige Konstante und setzen sie in die allgemeine Lösung ein
Endlich bekommen wir j= 2(x + 1) ist eine bestimmte Lösung. Schauen wir uns noch ein paar Beispiele für die Lösung von Gleichungen mit trennbaren Variablen an.
Beispiel 2. Finden Sie die Lösung der Gleichung 
Lösung. Bedenkt, dass  , wir bekommen
, wir bekommen  .
.
Wenn wir beide Seiten der Gleichung integrieren, haben wir

Wo 
Beispiel 3. Finden Sie die Lösung der Gleichung Lösung. Wir unterteilen beide Seiten der Gleichung in diejenigen Faktoren, die von einer Variablen abhängen, die nicht mit der Variablen unter dem Differentialvorzeichen übereinstimmt, d.h. ![]() und integrieren. Dann bekommen wir
und integrieren. Dann bekommen wir

und endlich,

Beispiel 4. Finden Sie die Lösung der Gleichung
Lösung. Wissen, was wir bekommen werden. Abschnitt
Lim-Variablen. Dann 

Integrieren, verstehen wir

Kommentar. In den Beispielen 1 und 2 lautet die erforderliche Funktion j explizit ausgedrückt (allgemeine Lösung). In den Beispielen 3 und 4 - implizit (allgemeines Integral). Die Form der Entscheidung wird künftig nicht präzisiert.
Beispiel 5. Finden Sie die Lösung der Gleichung Lösung.

Beispiel 6. Finden Sie die Lösung der Gleichung  , befriedigend
, befriedigend
Zustand Ihr)= 1.
Lösung. Schreiben wir die Gleichung in das Formular 
Beide Seiten der Gleichung mit multiplizieren dx und weiter, wir bekommen

Wenn wir beide Seiten der Gleichung integrieren (das Integral auf der rechten Seite wird in Teile genommen), erhalten wir 
Aber je nach Zustand j= 1 bei X= e. Dann
Ersetzen wir die gefundenen Werte MIT zur allgemeinen Lösung:

Der resultierende Ausdruck wird Teillösung der Differentialgleichung genannt.
6.2.2. Homogene Differentialgleichungen erster Ordnung
Definition. Die Differentialgleichung erster Ordnung heißt homogen, wenn es in der Form dargestellt werden kann

Stellen wir einen Algorithmus zur Lösung einer homogenen Gleichung vor.
1.Stattdessen j Lassen Sie uns eine neue Funktion einführenDann ![]() und deshalb
und deshalb 

2. In Bezug auf die Funktion u Gleichung (6.7) nimmt die Form an
das heißt, die Ersetzung reduziert eine homogene Gleichung auf eine Gleichung mit trennbaren Variablen.
3. Wenn wir Gleichung (6.8) lösen, finden wir zuerst u und dann j= ux.
Beispiel 1. Löse die Gleichung  Lösung. Schreiben wir die Gleichung in das Formular
Lösung. Schreiben wir die Gleichung in das Formular
Wir führen die Substitution durch:  Dann
Dann 
Wir werden ersetzen 
Mit dx multiplizieren:  Teilen durch X und weiter
Teilen durch X und weiter  Dann
Dann

Nachdem wir beide Seiten der Gleichung über die entsprechenden Variablen integriert haben, haben wir

oder wenn wir zu den alten Variablen zurückkehren, erhalten wir endlich

Beispiel 2.Löse die Gleichung  Lösung.Lassen
Lösung.Lassen  Dann
Dann

Teilen wir beide Seiten der Gleichung durch x2:  Öffnen wir die Klammern und ordnen wir die Begriffe neu an:
Öffnen wir die Klammern und ordnen wir die Begriffe neu an:


Wenn wir zu den alten Variablen übergehen, kommen wir zum Endergebnis:

Beispiel 3.Finden Sie die Lösung der Gleichung  angesichts dessen
angesichts dessen

Lösung.Durchführen eines Standardaustauschs  wir bekommen
wir bekommen

oder 

oder

Dies bedeutet, dass die jeweilige Lösung die Form hat  Beispiel 4. Finden Sie die Lösung der Gleichung
Beispiel 4. Finden Sie die Lösung der Gleichung
Lösung.

Beispiel 5.Finden Sie die Lösung der Gleichung  Lösung.
Lösung.

Selbstständige Arbeit
Finden Sie Lösungen für Differentialgleichungen mit separierbaren Variablen (1-9).

Finden Sie eine Lösung für homogene Differentialgleichungen (9-18).

6.2.3. Einige Anwendungen von Differentialgleichungen erster Ordnung
Problem des radioaktiven Zerfalls
Die Zerfallsrate von Ra (Radium) ist zu jedem Zeitpunkt proportional zu seiner verfügbaren Masse. Finden Sie das Gesetz des radioaktiven Zerfalls von Ra, wenn bekannt ist, dass es im ersten Moment Ra gab und die Halbwertszeit von Ra 1590 Jahre beträgt.
Lösung. Sei im Moment die Masse Ra X= x(t) g, und  Dann ist die Abklingrate Ra gleich
Dann ist die Abklingrate Ra gleich

Je nach den Bedingungen des Problems 
Wo k
Wenn wir die Variablen in der letzten Gleichung trennen und integrieren, erhalten wir
Wo 
Zur Bestimmung C Wir verwenden die Anfangsbedingung: wann ![]() .
.
Dann ![]() und deshalb,
und deshalb, 
Proportionalitätsfaktor k ermittelt aus der Zusatzbedingung:
Wir haben
Von hier  und die erforderliche Formel
und die erforderliche Formel

Problem mit der bakteriellen Reproduktionsrate
Die Vermehrungsrate der Bakterien ist proportional zu ihrer Anzahl. Am Anfang waren es 100 Bakterien. Innerhalb von 3 Stunden verdoppelte sich ihre Zahl. Finden Sie die Abhängigkeit der Bakterienzahl von der Zeit. Wie oft wird die Anzahl der Bakterien innerhalb von 9 Stunden ansteigen?
Lösung. Lassen X- Anzahl der Bakterien gleichzeitig T. Dann, je nach Bedingung, 
Wo k- Proportionalitätskoeffizient.
Von hier  Aus der Bedingung ist das bekannt
Aus der Bedingung ist das bekannt  . Bedeutet,
. Bedeutet,
Aus der Zusatzbedingung  . Dann
. Dann
Die Funktion, die Sie suchen: 
Also, wann T= 9 X= 800, d.h. innerhalb von 9 Stunden erhöhte sich die Bakterienzahl um das 8-fache.
Das Problem der Erhöhung der Enzymmenge
In einer Bierhefekultur ist die Wachstumsrate des aktiven Enzyms proportional zu seiner Anfangsmenge X. Anfangsmenge an Enzym A innerhalb einer Stunde verdoppelt. Abhängigkeit finden
x(t).
Lösung. Unter der Bedingung hat die Differentialgleichung des Prozesses die Form 
von hier

Aber  . Bedeutet, C= A und dann
. Bedeutet, C= A und dann ![]()
Das ist auch bekannt 
Somit,
6.3. DIFFERENZGLEICHUNGEN ZWEITER ORDNUNG
6.3.1. Grundlegendes Konzept
Definition.Differentialgleichung zweiter Ordnung wird eine Beziehung genannt, die die unabhängige Variable, die gewünschte Funktion und ihre ersten und zweiten Ableitungen verbindet.
In besonderen Fällen kann x in der Gleichung fehlen, bei oder y". Allerdings muss eine Gleichung zweiter Ordnung notwendigerweise y enthalten." Im allgemeinen Fall wird eine Differentialgleichung zweiter Ordnung wie folgt geschrieben:
oder, wenn möglich, in der bezüglich der zweiten Ableitung aufgelösten Form:
Wie bei einer Gleichung erster Ordnung kann es auch bei einer Gleichung zweiter Ordnung allgemeine und besondere Lösungen geben. Die allgemeine Lösung lautet:
Eine bestimmte Lösung finden
unter Anfangsbedingungen - gegeben
Zahlen) aufgerufen wird Cauchy-Problem. Geometrisch bedeutet das, dass wir die Integralkurve finden müssen bei= y(x), Durchqueren eines bestimmten Punktes  und an diesem Punkt eine Tangente haben, die ist
und an diesem Punkt eine Tangente haben, die ist
richtet sich nach der positiven Achsenrichtung Ochse angegebenen Winkel. e.  (Abb. 6.1). Das Cauchy-Problem hat eine eindeutige Lösung, wenn die rechte Seite der Gleichung (6.10)
(Abb. 6.1). Das Cauchy-Problem hat eine eindeutige Lösung, wenn die rechte Seite der Gleichung (6.10)  unaufhörlich
unaufhörlich
ist diskontinuierlich und hat stetige partielle Ableitungen nach äh, äh" in einer Gegend des Ausgangspunkts

Konstanten finden  In einer privaten Lösung enthalten, muss das System aufgelöst werden
In einer privaten Lösung enthalten, muss das System aufgelöst werden

Reis. 6.1. Integralkurve

Differentialgleichungen lösen. Dank unseres Online-Dienstes können Sie Differentialgleichungen jeder Art und Komplexität lösen: inhomogen, homogen, nichtlinear, linear, erster, zweiter Ordnung, mit trennbaren oder nicht trennbaren Variablen usw. Eine Lösung von Differentialgleichungen erhalten Sie in analytischer Form mit detaillierte Beschreibung. Viele Menschen interessieren sich für die Frage: Warum ist es notwendig, Differentialgleichungen online zu lösen? Diese Art von Gleichung ist in der Mathematik und Physik weit verbreitet, wo es unmöglich sein wird, viele Probleme zu lösen, ohne die Differentialgleichung zu berechnen. Differentialgleichungen sind auch in den Wirtschaftswissenschaften, der Medizin, der Biologie, der Chemie und anderen Wissenschaften weit verbreitet. Das Online-Lösen einer solchen Gleichung vereinfacht Ihre Aufgaben erheblich und gibt Ihnen die Möglichkeit, den Stoff besser zu verstehen und sich selbst zu testen. Vorteile der Online-Lösung von Differentialgleichungen. Eine moderne mathematische Serviceseite ermöglicht Ihnen die Lösung von Differentialgleichungen online irgendwelche Schwierigkeiten. Wie Sie wissen, gibt es das große Menge Arten von Differentialgleichungen und jede von ihnen hat ihre eigenen Lösungsmethoden. Auf unserem Service können Sie online Lösungen für Differentialgleichungen jeglicher Ordnung und Art finden. Um eine Lösung zu erhalten, empfehlen wir Ihnen, die Ausgangsdaten einzugeben und auf die Schaltfläche „Lösung“ zu klicken. Fehler bei der Bedienung des Dienstes sind ausgeschlossen, sodass Sie zu 100 % sicher sein können, dass Sie die richtige Antwort erhalten haben. Lösen Sie Differentialgleichungen mit unserem Service. Differentialgleichungen online lösen. Standardmäßig ist in einer solchen Gleichung die Funktion y eine Funktion der x-Variablen. Sie können aber auch eine eigene Variablenbezeichnung angeben. Wenn Sie beispielsweise y(t) in einer Differentialgleichung angeben, ermittelt unser Dienst automatisch, dass y eine Funktion der Variablen t ist. Die Ordnung der gesamten Differentialgleichung hängt von der maximalen Ordnung der Ableitung der in der Gleichung vorhandenen Funktion ab. Das Lösen einer solchen Gleichung bedeutet, die gewünschte Funktion zu finden. Unser Service hilft Ihnen, Differentialgleichungen online zu lösen. Es erfordert von Ihrer Seite keinen großen Aufwand, die Gleichung zu lösen. Sie müssen lediglich die linke und rechte Seite Ihrer Gleichung in die erforderlichen Felder eingeben und auf die Schaltfläche „Lösung“ klicken. Bei der Eingabe muss die Ableitung einer Funktion durch einen Apostroph gekennzeichnet werden. In Sekundenschnelle erhalten Sie das fertige Produkt detaillierte Lösung Differentialgleichung. Unser Service ist absolut kostenlos. Differentialgleichungen mit separierbaren Variablen. Wenn in einer Differentialgleichung auf der linken Seite ein Ausdruck steht, der von y abhängt, und auf der rechten Seite ein Ausdruck, der von x abhängt, dann heißt eine solche Differentialgleichung mit separierbaren Variablen. Die linke Seite kann eine Ableitung von y enthalten; die Lösung für Differentialgleichungen dieser Art wird in Form einer Funktion von y vorliegen, ausgedrückt durch das Integral der rechten Seite der Gleichung. Liegt auf der linken Seite ein Differential der Funktion von y vor, so werden in diesem Fall beide Seiten der Gleichung integriert. Wenn die Variablen in einer Differentialgleichung nicht getrennt sind, müssen sie getrennt werden, um eine getrennte Differentialgleichung zu erhalten. Lineare Differentialgleichung. Eine Differentialgleichung, deren Funktion und alle ihre Ableitungen ersten Grades sind, heißt linear. Allgemeine Form der Gleichung: y’+a1(x)y=f(x). f(x) und a1(x) sind kontinuierliche Funktionen von x. Die Lösung derartiger Differentialgleichungen reduziert sich auf die Integration zweier Differentialgleichungen mit getrennten Variablen. Ordnung der Differentialgleichung. Eine Differentialgleichung kann erster, zweiter und n-ter Ordnung sein. Die Ordnung einer Differentialgleichung bestimmt die Ordnung der höchsten darin enthaltenen Ableitung. In unserem Service können Sie Differentialgleichungen lösen zuerst online, zweiter, dritter usw. Befehl. Die Lösung der Gleichung ist eine beliebige Funktion y=f(x). Wenn Sie sie in die Gleichung einsetzen, erhalten Sie eine Identität. Der Prozess, eine Lösung für eine Differentialgleichung zu finden, wird Integration genannt. Cauchy-Problem. Ist zusätzlich zur Differentialgleichung selbst die Anfangsbedingung y(x0)=y0 gegeben, so spricht man vom Cauchy-Problem. Die Indikatoren y0 und x0 werden zur Lösung der Gleichung addiert und der Wert einer beliebigen Konstante C bestimmt, und dann wird eine bestimmte Lösung der Gleichung bei diesem Wert von C bestimmt. Dies ist die Lösung des Cauchy-Problems. Das Cauchy-Problem wird auch als Problem mit Randbedingungen bezeichnet, was in der Physik und Mechanik sehr verbreitet ist. Sie haben auch die Möglichkeit, das Cauchy-Problem zu stellen, das heißt, aus allen möglichen Lösungen der Gleichung einen Quotienten auszuwählen, der die gegebenen Anfangsbedingungen erfüllt.
Eine Differentialgleichung ist eine Gleichung, die eine Funktion und eine oder mehrere ihrer Ableitungen umfasst. Bei den meisten praktischen Problemen handelt es sich um Funktionen physikalische Quantitäten, die Ableitungen entsprechen den Änderungsraten dieser Größen und die Gleichung bestimmt die Beziehung zwischen ihnen.
In diesem Artikel werden Methoden zur Lösung bestimmter Arten gewöhnlicher Differentialgleichungen beschrieben, deren Lösungen in der Form geschrieben werden können elementare Funktionen, also polynomial, exponentiell, logarithmisch und trigonometrisch, sowie deren Umkehrfunktionen. Viele dieser Gleichungen erscheinen in wahres Leben, obwohl die meisten anderen Differentialgleichungen mit diesen Methoden nicht gelöst werden können und für sie die Antwort in Form spezieller Funktionen oder Potenzreihen geschrieben oder durch numerische Methoden gefunden wird.
Um diesen Artikel zu verstehen, müssen Sie sich mit Differential- und Integralrechnung auskennen und über ein gewisses Verständnis für partielle Ableitungen verfügen. Es wird außerdem empfohlen, die Grundlagen der linearen Algebra in ihrer Anwendung auf Differentialgleichungen, insbesondere Differentialgleichungen zweiter Ordnung, zu kennen, obwohl Kenntnisse der Differential- und Integralrechnung zur Lösung dieser Gleichungen ausreichen.
Vorabinformationen
- Differentialgleichungen haben eine umfangreiche Klassifizierung. In diesem Artikel geht es um gewöhnliche Differentialgleichungen, das heißt über Gleichungen, die eine Funktion einer Variablen und ihrer Ableitungen enthalten. Gewöhnliche Differentialgleichungen sind viel einfacher zu verstehen und zu lösen als partielle Differentialgleichungen, die Funktionen mehrerer Variablen umfassen. In diesem Artikel werden partielle Differentialgleichungen nicht behandelt, da die Methoden zur Lösung dieser Gleichungen normalerweise durch ihre besondere Form bestimmt werden.
- Nachfolgend finden Sie einige Beispiele für gewöhnliche Differentialgleichungen.
- d y d x = k y (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=ky)
- d 2 x d t 2 + k x = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)x)((\mathrm (d) )t^(2)))+kx=0)
- Nachfolgend finden Sie einige Beispiele für partielle Differentialgleichungen.
- ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = 0 (\displaystyle (\frac (\partial ^(2)f)(\partial x^(2)))+(\frac (\partial ^(2 )f)(\partial y^(2)))=0)
- ∂ u ∂ t − α ∂ 2 u ∂ x 2 = 0 (\displaystyle (\frac (\partial u)(\partial t))-\alpha (\frac (\partial ^(2)u)(\partial x ^(2)))=0)
- Nachfolgend finden Sie einige Beispiele für gewöhnliche Differentialgleichungen.
- Befehl einer Differentialgleichung wird durch die Ordnung der höchsten in dieser Gleichung enthaltenen Ableitung bestimmt. Die erste der oben genannten gewöhnlichen Differentialgleichungen ist erster Ordnung, während die zweite eine Gleichung zweiter Ordnung ist. Grad Differentialgleichung heißt Höchster Abschluss, auf den einer der Terme dieser Gleichung angehoben wird.
- Die folgende Gleichung ist beispielsweise dritter Ordnung und zweiten Grades.
- (d 3 y d x 3) 2 + d y d x = 0 (\displaystyle \left((\frac ((\mathrm (d) )^(3)y)((\mathrm (d) )x^(3)))\ rechts)^(2)+(\frac ((\mathrm (d) )y)((\mathrm (d) )x))=0)
- Die folgende Gleichung ist beispielsweise dritter Ordnung und zweiten Grades.
- Die Differentialgleichung lautet lineare Differentialgleichung für den Fall, dass die Funktion und alle ihre Ableitungen ersten Grades sind. Ansonsten lautet die Gleichung nichtlineare Differentialgleichung. Das Besondere an linearen Differentialgleichungen ist, dass ihre Lösungen zur Bildung von Linearkombinationen verwendet werden können, die auch Lösungen der gegebenen Gleichung sind.
- Nachfolgend finden Sie einige Beispiele für lineare Differentialgleichungen.
- Nachfolgend finden Sie einige Beispiele für nichtlineare Differentialgleichungen. Die erste Gleichung ist aufgrund des Sinusterms nichtlinear.
- d 2 θ d t 2 + g l sin θ = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)\theta )((\mathrm (d) )t^(2)))+( \frac (g)(l))\sin \theta =0)
- d 2 x d t 2 + (d x d t) 2 + t x 2 = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)x)((\mathrm (d) )t^(2)))+ \left((\frac ((\mathrm (d) )x)((\mathrm (d) )t))\right)^(2)+tx^(2)=0)
- Gemeinsame Entscheidung Eine gewöhnliche Differentialgleichung ist nicht eindeutig, sie beinhaltet beliebige Integrationskonstanten. In den meisten Fällen entspricht die Anzahl der willkürlichen Konstanten der Ordnung der Gleichung. In der Praxis werden die Werte dieser Konstanten anhand der Gegebenheiten ermittelt Anfangsbedingungen, also entsprechend den Werten der Funktion und ihrer Ableitungen bei x = 0. (\displaystyle x=0.) Die Anzahl der Anfangsbedingungen, die gefunden werden müssen private Lösung Differentialgleichung ist in den meisten Fällen auch gleich der Ordnung der gegebenen Gleichung.
- In diesem Artikel geht es beispielsweise um die Lösung der folgenden Gleichung. Dies ist eine lineare Differentialgleichung zweiter Ordnung. Seine allgemeine Lösung enthält zwei beliebige Konstanten. Um diese Konstanten zu finden, ist es notwendig, die Anfangsbedingungen zu kennen x (0) (\displaystyle x(0)) Und x ′ (0) . (\displaystyle x"(0).) Normalerweise werden an dieser Stelle die Anfangsbedingungen angegeben x = 0 , (\displaystyle x=0,), obwohl dies nicht notwendig ist. In diesem Artikel wird auch erläutert, wie bestimmte Lösungen für gegebene Anfangsbedingungen gefunden werden können.
- d 2 x d t 2 + k 2 x = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)x)((\mathrm (d) )t^(2)))+k^(2 )x=0)
- x (t) = c 1 cos k x + c 2 sin k x (\displaystyle x(t)=c_(1)\cos kx+c_(2)\sin kx)
- In diesem Artikel geht es beispielsweise um die Lösung der folgenden Gleichung. Dies ist eine lineare Differentialgleichung zweiter Ordnung. Seine allgemeine Lösung enthält zwei beliebige Konstanten. Um diese Konstanten zu finden, ist es notwendig, die Anfangsbedingungen zu kennen x (0) (\displaystyle x(0)) Und x ′ (0) . (\displaystyle x"(0).) Normalerweise werden an dieser Stelle die Anfangsbedingungen angegeben x = 0 , (\displaystyle x=0,), obwohl dies nicht notwendig ist. In diesem Artikel wird auch erläutert, wie bestimmte Lösungen für gegebene Anfangsbedingungen gefunden werden können.
Schritte
Teil 1
Gleichungen erster OrdnungBei der Nutzung dieses Dienstes können einige Informationen an YouTube übertragen werden.
-
Lineare Gleichungen erster Ordnung. In diesem Abschnitt werden Methoden zur Lösung linearer Differentialgleichungen erster Ordnung im Allgemeinen und in Sonderfällen erläutert, in denen einige Terme gleich Null sind. Tun wir mal so y = y (x) , (\displaystyle y=y(x),) p (x) (\displaystyle p(x)) Und q (x) (\displaystyle q(x)) sind Funktionen X. (\displaystyle x.)
D y d x + p (x) y = q (x) (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))+p(x)y=q(x ))
P (x) = 0. (\displaystyle p(x)=0.) Nach einem der Hauptsätze mathematische Analyse, das Integral der Ableitung einer Funktion ist auch eine Funktion. Daher reicht es aus, die Gleichung einfach zu integrieren, um ihre Lösung zu finden. Dies sollte bei der Berechnung berücksichtigt werden unbestimmtes Integral Es erscheint eine beliebige Konstante.
- y (x) = ∫ q (x) d x (\displaystyle y(x)=\int q(x)(\mathrm (d) )x)
Q (x) = 0. (\displaystyle q(x)=0.) Wir verwenden die Methode Trennung von Variablen. Dadurch werden verschiedene Variablen auf unterschiedliche Seiten der Gleichung verschoben. Sie können beispielsweise alle Mitglieder aus verschieben y (\displaystyle y) in eins, und alle Mitglieder mit x (\displaystyle x) auf die andere Seite der Gleichung. Mitglieder können auch übertragen werden d x (\displaystyle (\mathrm (d) )x) Und d y (\displaystyle (\mathrm (d) )y), die in abgeleiteten Ausdrücken enthalten sind, es sollte jedoch beachtet werden, dass diese gerecht sind Symbol, was beim Differenzieren einer komplexen Funktion praktisch ist. Diskussion dieser Mitglieder, die aufgerufen werden Differentiale, würde den Rahmen dieses Artikels sprengen.
- Zuerst müssen Sie die Variablen auf die gegenüberliegenden Seiten des Gleichheitszeichens verschieben.
- 1 y d y = − p (x) d x (\displaystyle (\frac (1)(y))(\mathrm (d) )y=-p(x)(\mathrm (d) )x)
- Lassen Sie uns beide Seiten der Gleichung integrieren. Nach der Integration erscheinen auf beiden Seiten beliebige Konstanten, die auf die rechte Seite der Gleichung übertragen werden können.
- ln y = ∫ − p (x) d x (\displaystyle \ln y=\int -p(x)(\mathrm (d) )x)
- y (x) = e − ∫ p (x) d x (\displaystyle y(x)=e^(-\int p(x)(\mathrm (d) )x))
- Beispiel 1.1. Im letzten Schritt haben wir die Regel verwendet e a + b = e a e b (\displaystyle e^(a+b)=e^(a)e^(b)) und ersetzt e C (\displaystyle e^(C)) An C (\displaystyle C), da dies ebenfalls eine beliebige Integrationskonstante ist.
- d y d x − 2 y sin x = 0 (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))-2y\sin x=0)
- 1 2 y d y = sin x d x 1 2 ln y = − cos x + C ln y = − 2 cos x + C y (x) = C e − 2 cos x (\displaystyle (\begin(aligned )(\frac (1)(2y))(\mathrm (d) )y&=\sin x(\mathrm (d) )x\\(\frac (1)(2))\ln y&=-\cos x+C\\\ln y&=-2\cos x+C\\y(x)&=Ce^(-2\cos x)\end(aligned)))
P (x) ≠ 0 , q (x) ≠ 0. (\displaystyle p(x)\neq 0,\ q(x)\neq 0.) Um eine allgemeine Lösung zu finden, haben wir eingeführt integrierender Faktor als Funktion von x (\displaystyle x) um die linke Seite auf eine gemeinsame Ableitung zu reduzieren und so die Gleichung zu lösen.
- Multiplizieren Sie beide Seiten mit μ (x) (\displaystyle \mu (x))
- μ d y d x + μ p y = μ q (\displaystyle \mu (\frac ((\mathrm (d) )y)((\mathrm (d) )x))+\mu py=\mu q)
- Um die linke Seite auf die allgemeine Ableitung zu reduzieren, müssen folgende Transformationen durchgeführt werden:
- d d x (μ y) = d μ d x y + μ d y d x = μ d y d x + μ p y (\displaystyle (\frac (\mathrm (d) )((\mathrm (d) )x))(\mu y)=(\ frac ((\mathrm (d) )\mu )((\mathrm (d) )x))y+\mu (\frac ((\mathrm (d) )y)((\mathrm (d) )x)) =\mu (\frac ((\mathrm (d) )y)((\mathrm (d) )x))+\mu py)
- Die letzte Gleichheit bedeutet das d μ d x = μ p (\displaystyle (\frac ((\mathrm (d) )\mu )((\mathrm (d) )x))=\mu p). Dies ist ein integrierender Faktor, der ausreicht, um jede lineare Gleichung erster Ordnung zu lösen. Jetzt können wir die Formel zur Lösung dieser Gleichung bezüglich ableiten μ , (\displaystyle \mu ,) obwohl es für das Training nützlich ist, alle Zwischenberechnungen durchzuführen.
- μ (x) = e ∫ p (x) d x (\displaystyle \mu (x)=e^(\int p(x)(\mathrm (d) )x))
- Beispiel 1.2. Dieses Beispiel zeigt, wie man eine bestimmte Lösung für eine Differentialgleichung mit gegebenen Anfangsbedingungen findet.
- t d y d t + 2 y = t 2 , y (2) = 3 (\displaystyle t(\frac ((\mathrm (d) )y)((\mathrm (d) )t))+2y=t^(2) ,\quad y(2)=3)
- d y d t + 2 t y = t (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )t))+(\frac (2)(t))y=t)
- μ (x) = e ∫ p (t) d t = e 2 ln t = t 2 (\displaystyle \mu (x)=e^(\int p(t)(\mathrm (d) )t)=e ^(2\ln t)=t^(2))
- d d t (t 2 y) = t 3 t 2 y = 1 4 t 4 + C y (t) = 1 4 t 2 + C t 2 (\displaystyle (\begin(aligned)(\frac (\mathrm (d) )((\mathrm (d) )t))(t^(2)y)&=t^(3)\\t^(2)y&=(\frac (1)(4))t^(4 )+C\\y(t)&=(\frac (1)(4))t^(2)+(\frac (C)(t^(2)))\end(aligned)))
- 3 = y (2) = 1 + C 4 , C = 8 (\displaystyle 3=y(2)=1+(\frac (C)(4)),\quad C=8)
- y (t) = 1 4 t 2 + 8 t 2 (\displaystyle y(t)=(\frac (1)(4))t^(2)+(\frac (8)(t^(2)) ))
Lösen linearer Gleichungen erster Ordnung (aufgezeichnet von Intuit – National Open University). -
Nichtlineare Gleichungen erster Ordnung. In diesem Abschnitt werden Methoden zur Lösung einiger nichtlinearer Differentialgleichungen erster Ordnung erläutert. Obwohl es keine allgemeine Methode zum Lösen solcher Gleichungen gibt, können einige davon mit den folgenden Methoden gelöst werden.
D y d x = f (x , y) (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=f(x,y))
d y d x = h (x) g (y) . (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=h(x)g(y).) Wenn die Funktion f (x , y) = h (x) g (y) (\displaystyle f(x,y)=h(x)g(y)) kann in Funktionen einer Variablen zerlegt werden, eine solche Gleichung heißt Differentialgleichung mit separierbaren Variablen. In diesem Fall können Sie die oben beschriebene Methode verwenden:- ∫ d y h (y) = ∫ g (x) d x (\displaystyle \int (\frac ((\mathrm (d) )y)(h(y)))=\int g(x)(\mathrm (d) )X)
- Beispiel 1.3.
- d y d x = x 3 y (1 + x 4) (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac (x^(3))( y(1+x^(4)))))
- ∫ y d y = ∫ x 3 1 + x 4 d x 1 2 y 2 = 1 4 ln (1 + x 4) + C y (x) = 1 2 ln (1 + x 4) + C (\displaystyle (\ begin(aligned)\int y(\mathrm (d) )y&=\int (\frac (x^(3))(1+x^(4)))(\mathrm (d) )x\\(\ frac (1)(2))y^(2)&=(\frac (1)(4))\ln(1+x^(4))+C\\y(x)&=(\frac ( 1)(2))\ln(1+x^(4))+C\end(aligned)))
D y d x = g (x , y) h (x , y) . (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac (g(x,y))(h(x,y))).) Tun wir mal so g (x , y) (\displaystyle g(x,y)) Und h (x, y) (\displaystyle h(x,y)) sind Funktionen x (\displaystyle x) Und j. (\displaystyle y.) Dann homogene Differentialgleichung ist eine Gleichung, in der g (\displaystyle g) Und h (\displaystyle h) Sind homogene Funktionen im gleichen Maße. Das heißt, die Funktionen müssen die Bedingung erfüllen g (α x , α y) = α k g (x , y) , (\displaystyle g(\alpha x,\alpha y)=\alpha ^(k)g(x,y),) Wo k (\displaystyle k) wird als Homogenitätsgrad bezeichnet. Jede homogene Differentialgleichung kann geeignet verwendet werden Ersetzungen von Variablen (v = y / x (\displaystyle v=y/x) oder v = x / y (\displaystyle v=x/y)) in eine separierbare Gleichung umwandeln.
- Beispiel 1.4. Die obige Beschreibung der Homogenität mag unklar erscheinen. Schauen wir uns dieses Konzept anhand eines Beispiels an.
- d y d x = y 3 − x 3 y 2 x (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac (y^(3)-x^ (3))(y^(2)x)))
- Zunächst ist zu beachten, dass diese Gleichung in Bezug auf nichtlinear ist j. (\displaystyle y.) Wir sehen auch, dass es in diesem Fall unmöglich ist, die Variablen zu trennen. Gleichzeitig ist diese Differentialgleichung homogen, da sowohl der Zähler als auch der Nenner mit einer Potenz von 3 homogen sind. Daher können wir Variablen ändern v = y/x. (\displaystyle v=y/x.)
- d y d x = y x − x 2 y 2 = v − 1 v 2 (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac (y)(x ))-(\frac (x^(2))(y^(2)))=v-(\frac (1)(v^(2))))
- y = v x , d y d x = d v d x x + v (\displaystyle y=vx,\quad (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac ((\mathrm (d) )v)((\mathrm (d) )x))x+v)
- d v d x x = − 1 v 2 . (\displaystyle (\frac ((\mathrm (d) )v)((\mathrm (d) )x))x=-(\frac (1)(v^(2))).) Als Ergebnis haben wir die Gleichung für v (\displaystyle v) mit trennbaren Variablen.
- v (x) = − 3 ln x + C 3 (\displaystyle v(x)=(\sqrt[(3)](-3\ln x+C)))
- y (x) = x − 3 ln x + C 3 (\displaystyle y(x)=x(\sqrt[(3)](-3\ln x+C)))
D y d x = p (x) y + q (x) y n . (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=p(x)y+q(x)y^(n).) Das Bernoulli-Differentialgleichung- eine spezielle Art nichtlinearer Gleichung ersten Grades, deren Lösung mit Elementarfunktionen geschrieben werden kann.
- Multiplizieren Sie beide Seiten der Gleichung mit (1 − n) y − n (\displaystyle (1-n)y^(-n)):
- (1 − n) y − n d y d x = p (x) (1 − n) y 1 − n + (1 − n) q (x) (\displaystyle (1-n)y^(-n)(\frac ( (\mathrm (d) )y)((\mathrm (d) )x))=p(x)(1-n)y^(1-n)+(1-n)q(x))
- Wir verwenden die Regel zum Ableiten einer komplexen Funktion auf der linken Seite und transformieren die Gleichung in eine lineare Gleichung bezüglich y 1 − n , (\displaystyle y^(1-n),) welches mit den oben genannten Methoden gelöst werden kann.
- d y 1 − n d x = p (x) (1 − n) y 1 − n + (1 − n) q (x) (\displaystyle (\frac ((\mathrm (d) )y^(1-n)) ((\mathrm (d) )x))=p(x)(1-n)y^(1-n)+(1-n)q(x))
M (x, y) + N (x, y) d y d x = 0. (\displaystyle M(x,y)+N(x,y)(\frac ((\mathrm (d) )y)((\mathrm (d) )x))=0.) Das Gleichung in totalen Differentialen. Es ist notwendig, das sogenannte zu finden potentielle Funktion φ (x , y) , (\displaystyle \varphi (x,y),), was die Bedingung erfüllt d φ d x = 0. (\displaystyle (\frac ((\mathrm (d) )\varphi )((\mathrm (d) )x))=0.)
- Um diese Bedingung zu erfüllen, ist es notwendig, Folgendes zu haben Gesamtableitung. Die Gesamtableitung berücksichtigt die Abhängigkeit von anderen Variablen. Um die Gesamtableitung zu berechnen φ (\displaystyle \varphi ) Von x , (\displaystyle x,) Wir nehmen an, dass y (\displaystyle y) kann auch davon abhängen X. (\displaystyle x.)
- d φ d x = ∂ φ ∂ x + ∂ φ ∂ y d y d x (\displaystyle (\frac ((\mathrm (d) )\varphi )((\mathrm (d) )x))=(\frac (\partial \varphi )(\partial x))+(\frac (\partial \varphi )(\partial y))(\frac ((\mathrm (d) )y)((\mathrm (d) )x)))
- Der Vergleich der Begriffe gibt uns Auskunft M (x , y) = ∂ φ ∂ x (\displaystyle M(x,y)=(\frac (\partial \varphi )(\partial x))) Und N (x, y) = ∂ φ ∂ y. (\displaystyle N(x,y)=(\frac (\partial \varphi )(\partial y)).) Dies ist ein typisches Ergebnis für Gleichungen in mehreren Variablen, bei denen die gemischten Ableitungen glatter Funktionen einander gleich sind. Manchmal wird dieser Fall aufgerufen Satz von Clairaut. In diesem Fall ist die Differentialgleichung eine totale Differentialgleichung, wenn die folgende Bedingung erfüllt ist:
- ∂ M ∂ y = ∂ N ∂ x (\displaystyle (\frac (\partial M)(\partial y))=(\frac (\partial N)(\partial x)))
- Die Methode zum Lösen von Gleichungen in Totaldifferentialen ähnelt der Suche nach potentiellen Funktionen in Gegenwart mehrerer Ableitungen, auf die wir kurz eingehen werden. Lassen Sie uns zunächst integrieren M (\displaystyle M) Von X. (\displaystyle x.) Weil das M (\displaystyle M) ist eine Funktion und x (\displaystyle x), Und y, (\displaystyle y,) Bei der Integration erhalten wir eine unvollständige Funktion φ , (\displaystyle \varphi ,) bezeichnet als φ ~ (\displaystyle (\tilde (\varphi ))). Das Ergebnis hängt auch davon ab y (\displaystyle y) Integrationskonstante.
- φ (x , y) = ∫ M (x , y) d x = φ ~ (x , y) + c (y) (\displaystyle \varphi (x,y)=\int M(x,y)(\mathrm (d) )x=(\tilde (\varphi ))(x,y)+c(y))
- Danach, um zu bekommen c (y) (\displaystyle c(y)) Wir können die partielle Ableitung der resultierenden Funktion nach bilden y, (\displaystyle y,) das Ergebnis gleichsetzen N (x, y) (\displaystyle N(x,y)) und integrieren. Sie können auch zunächst integrieren N (\displaystyle N), und bilden Sie dann die partielle Ableitung nach x (\displaystyle x), mit dem Sie eine beliebige Funktion finden können d(x). (\displaystyle d(x).) Beide Methoden sind geeignet und in der Regel wird für die Integration die einfachere Funktion gewählt.
- N (x , y) = ∂ φ ∂ y = ∂ φ ~ ∂ y + d c d y (\displaystyle N(x,y)=(\frac (\partial \varphi )(\partial y))=(\frac (\ partiell (\tilde (\varphi )))(\partial y))+(\frac ((\mathrm (d) )c)((\mathrm (d) )y)))
- Beispiel 1.5. Sie können partielle Ableitungen vornehmen und sehen, dass die folgende Gleichung eine totale Differentialgleichung ist.
- 3 x 2 + y 2 + 2 x y d y d x = 0 (\displaystyle 3x^(2)+y^(2)+2xy(\frac ((\mathrm (d) )y)((\mathrm (d) )x) )=0)
- φ = ∫ (3 x 2 + y 2) d x = x 3 + x y 2 + c (y) ∂ φ ∂ y = N (x , y) = 2 x y + d c d y (\displaystyle (\begin(aligned)\varphi &=\int (3x^(2)+y^(2))(\mathrm (d) )x=x^(3)+xy^(2)+c(y)\\(\frac (\partial \varphi )(\partial y))&=N(x,y)=2xy+(\frac ((\mathrm (d) )c)((\mathrm (d) )y))\end(aligned)))
- d c d y = 0 , c (y) = C (\displaystyle (\frac ((\mathrm (d) )c)((\mathrm (d) )y))=0,\quad c(y)=C)
- x 3 + x y 2 = C (\displaystyle x^(3)+xy^(2)=C)
- Wenn die Differentialgleichung keine totale Differentialgleichung ist, können Sie in manchen Fällen einen integrierenden Faktor finden, der es Ihnen ermöglicht, sie in eine totale Differentialgleichung umzuwandeln. Allerdings werden solche Gleichungen in der Praxis selten verwendet, und obwohl der integrierende Faktor existiert, es findet es zufällig nicht einfach Daher werden diese Gleichungen in diesem Artikel nicht berücksichtigt.
Teil 2
Gleichungen zweiter Ordnung-
Homogene lineare Differentialgleichungen mit konstanten Koeffizienten. Diese Gleichungen werden in der Praxis häufig verwendet, daher ist ihre Lösung von größter Bedeutung. In diesem Fall geht es nicht um homogene Funktionen, sondern um die Tatsache, dass auf der rechten Seite der Gleichung eine 0 steht. Im nächsten Abschnitt wird gezeigt, wie man das entsprechende löst heterogen Differentialgleichung. Unten ein (\displaystyle a) Und b (\displaystyle b) sind Konstanten.
D 2 y d x 2 + a d y d x + b y = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )x^(2)))+a(\frac ((\mathrm (d) )y)((\mathrm (d) )x))+by=0)
Charakteristische Gleichung. Das Besondere an dieser Differentialgleichung ist, dass sie sehr einfach gelöst werden kann, wenn man darauf achtet, welche Eigenschaften ihre Lösungen haben sollten. Aus der Gleichung geht das klar hervor y (\displaystyle y) und seine Ableitungen sind proportional zueinander. Aus früheren Beispielen, die im Abschnitt über Gleichungen erster Ordnung besprochen wurden, wissen wir, dass nur eine Exponentialfunktion diese Eigenschaft besitzt. Daher ist es möglich, einen Antrag zu stellen Ansatz(eine fundierte Vermutung) darüber, wie die Lösung einer bestimmten Gleichung aussehen wird.
- Die Lösung hat die Form einer Exponentialfunktion e r x , (\displaystyle e^(rx),) Wo r (\displaystyle r) ist eine Konstante, deren Wert gefunden werden soll. Setzen Sie diese Funktion in die Gleichung ein und erhalten Sie den folgenden Ausdruck
- e r x (r 2 + a r + b) = 0 (\displaystyle e^(rx)(r^(2)+ar+b)=0)
- Diese Gleichung besagt, dass das Produkt einer Exponentialfunktion und eines Polynoms gleich Null sein muss. Es ist bekannt, dass der Exponent für keinen Gradwert gleich Null sein kann. Daraus schließen wir, dass das Polynom gleich Null ist. Somit haben wir das Problem der Lösung einer Differentialgleichung auf das viel einfachere Problem der Lösung einer algebraischen Gleichung reduziert, die als charakteristische Gleichung für eine gegebene Differentialgleichung bezeichnet wird.
- r 2 + a r + b = 0 (\displaystyle r^(2)+ar+b=0)
- r ± = − a ± a 2 − 4 b 2 (\displaystyle r_(\pm )=(\frac (-a\pm (\sqrt (a^(2)-4b)))(2)))
- Wir haben zwei Wurzeln. Da diese Differentialgleichung linear ist, ist ihre allgemeine Lösung eine Linearkombination von Teillösungen. Da es sich um eine Gleichung zweiter Ordnung handelt, wissen wir, dass dies der Fall ist Wirklich allgemeine Lösung, und es gibt keine anderen. Eine strengere Begründung dafür finden sich in Lehrbüchern mit Theoremen über die Existenz und Einzigartigkeit einer Lösung.
- Eine nützliche Methode zur Überprüfung, ob zwei Lösungen linear unabhängig sind, ist die Berechnung Wronskiana. Wronskian W (\displaystyle W) ist die Determinante einer Matrix, deren Spalten Funktionen und ihre aufeinanderfolgenden Ableitungen enthalten. Der Satz der linearen Algebra besagt, dass die in der Wronski-Funktion enthaltenen Funktionen linear abhängig sind, wenn die Wronski-Funktion gleich Null ist. In diesem Abschnitt können wir prüfen, ob zwei Lösungen linear unabhängig sind – dazu müssen wir sicherstellen, dass der Wronski-Operator nicht Null ist. Der Wronski-Ansatz ist wichtig bei der Lösung inhomogener Differentialgleichungen mit konstanten Koeffizienten durch die Methode der Variation von Parametern.
- W = | y 1 y 2 y 1 ′ y 2 ′ | (\displaystyle W=(\begin(vmatrix)y_(1)&y_(2)\\y_(1)"&y_(2)"\end(vmatrix)))
- In Bezug auf die lineare Algebra bildet die Menge aller Lösungen einer gegebenen Differentialgleichung einen Vektorraum, dessen Dimension der Ordnung der Differentialgleichung entspricht. In diesem Bereich kann man eine Basis auswählen linear unabhängig Entscheidungen voneinander. Dies ist möglich, da die Funktion y (x) (\displaystyle y(x)) gültig linearer Operator. Derivat Ist linearer Operator, da er den Raum differenzierbarer Funktionen in den Raum aller Funktionen umwandelt. Gleichungen werden in den Fällen als homogen bezeichnet, in denen für jeden linearen Operator gilt L (\displaystyle L) Wir müssen eine Lösung für die Gleichung finden L [ y ] = 0. (\displaystyle L[y]=0.)
Betrachten wir nun einige konkrete Beispiele. Wir werden den Fall mehrerer Wurzeln der charakteristischen Gleichung etwas später im Abschnitt über die Reduzierung der Ordnung betrachten.
Wenn die Wurzeln r ± (\displaystyle r_(\pm )) Sind verschiedene reelle Zahlen, hat die Differentialgleichung nächste Lösung
- y (x) = c 1 e r + x + c 2 e r − x (\displaystyle y(x)=c_(1)e^(r_(+)x)+c_(2)e^(r_(-)x ))
Zwei komplexe Wurzeln. Aus dem Grundsatz der Algebra folgt, dass Lösungen von Polynomgleichungen mit reellen Koeffizienten Wurzeln haben, die reell sind oder konjugierte Paare bilden. Deshalb, wenn komplexe Zahl r = α + i β (\displaystyle r=\alpha +i\beta ) ist dann die Wurzel der charakteristischen Gleichung r ∗ = α − i β (\displaystyle r^(*)=\alpha -i\beta ) ist auch die Wurzel dieser Gleichung. Somit können wir die Lösung in das Formular schreiben c 1 e (α + i β) x + c 2 e (α − i β) x , (\displaystyle c_(1)e^((\alpha +i\beta)x)+c_(2)e^( (\alpha -i\beta)x),) Es handelt sich jedoch um eine komplexe Zahl, die zur Lösung praktischer Probleme nicht geeignet ist.
- Stattdessen können Sie verwenden Eulers Formel e i x = cos x + i sin x (\displaystyle e^(ix)=\cos x+i\sin x), wodurch Sie die Lösung in Form trigonometrischer Funktionen schreiben können:
- e α x (c 1 cos β x + i c 1 sin β x + c 2 cos β x − i c 2 sin β x) (\displaystyle e^(\alpha x)(c_(1)\cos \ beta x+ic_(1)\sin \beta x+c_(2)\cos \beta x-ic_(2)\sin \beta x))
- Jetzt können Sie anstelle einer Konstante c 1 + c 2 (\displaystyle c_(1)+c_(2)) aufschreiben c 1 (\displaystyle c_(1)), und der Ausdruck i (c 1 − c 2) (\displaystyle i(c_(1)-c_(2))) ersetzt durch c 2 . (\displaystyle c_(2).) Danach erhalten wir folgende Lösung:
- y (x) = e α x (c 1 cos β x + c 2 sin β x) (\displaystyle y(x)=e^(\alpha x)(c_(1)\cos \beta x+c_ (2)\sin\beta x))
- Es gibt eine andere Möglichkeit, die Lösung in Form von Amplitude und Phase zu schreiben, die für physikalische Probleme besser geeignet ist.
- Beispiel 2.1. Finden wir eine Lösung für die unten angegebene Differentialgleichung mit den angegebenen Anfangsbedingungen. Dazu müssen Sie die resultierende Lösung nehmen, sowie seine Ableitung, und setzen Sie sie in die Anfangsbedingungen ein, was es uns ermöglicht, beliebige Konstanten zu bestimmen.
- d 2 x d t 2 + 3 d x d t + 10 x = 0 , x (0) = 1 , x ′ (0) = − 1 (\displaystyle (\frac ((\mathrm (d) )^(2)x)(( \mathrm (d) )t^(2)))+3(\frac ((\mathrm (d) )x)((\mathrm (d) )t))+10x=0,\quad x(0) =1,\x"(0)=-1)
- r 2 + 3 r + 10 = 0 , r ± = − 3 ± 9 − 40 2 = − 3 2 ± 31 2 i (\displaystyle r^(2)+3r+10=0,\quad r_(\pm ) =(\frac (-3\pm (\sqrt (9-40)))(2))=-(\frac (3)(2))\pm (\frac (\sqrt (31))(2) )ich)
- x (t) = e − 3 t / 2 (c 1 cos 31 2 t + c 2 sin 31 2 t) (\displaystyle x(t)=e^(-3t/2)\left(c_(1 )\cos (\frac (\sqrt (31))(2))t+c_(2)\sin (\frac (\sqrt (31))(2))t\right))
- x (0) = 1 = c 1 (\displaystyle x(0)=1=c_(1))
- x ′ (t) = − 3 2 e − 3 t / 2 (c 1 cos 31 2 t + c 2 sin 31 2 t) + e − 3 t / 2 (− 31 2 c 1 sin 31 2 t + 31 2 c 2 cos 31 2 t) (\displaystyle (\begin(aligned)x"(t)&=-(\frac (3)(2))e^(-3t/2)\left(c_ (1)\cos (\frac (\sqrt (31))(2))t+c_(2)\sin (\frac (\sqrt (31))(2))t\right)\\&+e ^(-3t/2)\left(-(\frac (\sqrt (31))(2))c_(1)\sin (\frac (\sqrt (31))(2))t+(\frac ( \sqrt (31))(2))c_(2)\cos (\frac (\sqrt (31))(2))t\right)\end(aligned)))
- x ′ (0) = − 1 = − 3 2 c 1 + 31 2 c 2 , c 2 = 1 31 (\displaystyle x"(0)=-1=-(\frac (3)(2))c_( 1)+(\frac (\sqrt (31))(2))c_(2),\quad c_(2)=(\frac (1)(\sqrt (31))))
- x (t) = e − 3 t / 2 (cos 31 2 t + 1 31 sin 31 2 t) (\displaystyle x(t)=e^(-3t/2)\left(\cos (\frac (\sqrt (31))(2))t+(\frac (1)(\sqrt (31)))\sin (\frac (\sqrt (31))(2))t\right))
Lösen von Differentialgleichungen n-ter Ordnung mit konstanten Koeffizienten (aufgezeichnet von Intuit – National Open University). - Die Lösung hat die Form einer Exponentialfunktion e r x , (\displaystyle e^(rx),) Wo r (\displaystyle r) ist eine Konstante, deren Wert gefunden werden soll. Setzen Sie diese Funktion in die Gleichung ein und erhalten Sie den folgenden Ausdruck
-
Absteigende Reihenfolge. Ordnungsreduktion ist eine Methode zur Lösung von Differentialgleichungen, wenn eine linear unabhängige Lösung bekannt ist. Diese Methode besteht darin, die Ordnung der Gleichung um eins zu verringern, wodurch Sie die Gleichung mit den im vorherigen Abschnitt beschriebenen Methoden lösen können. Lassen Sie die Lösung bekannt sein. Die Hauptidee der Ordnungsreduktion besteht darin, eine Lösung in der folgenden Form zu finden, in der die Funktion definiert werden muss v (x) (\displaystyle v(x)), es in die Differentialgleichung einsetzen und finden v(x). (\displaystyle v(x).) Schauen wir uns an, wie Ordnungsreduktion verwendet werden kann, um eine Differentialgleichung mit konstanten Koeffizienten und mehreren Wurzeln zu lösen.
Mehrere Wurzeln homogene Differentialgleichung mit konstanten Koeffizienten. Denken Sie daran, dass eine Gleichung zweiter Ordnung zwei linear unabhängige Lösungen haben muss. Wenn die charakteristische Gleichung mehrere Wurzeln hat, ist die Menge der Lösungen Nicht bildet einen Raum, da diese Lösungen linear abhängig sind. In diesem Fall ist es notwendig, mithilfe der Ordnungsreduktion eine zweite linear unabhängige Lösung zu finden.
- Die charakteristische Gleichung soll mehrere Wurzeln haben r (\displaystyle r). Nehmen wir an, dass die zweite Lösung in der Form geschrieben werden kann y (x) = e r x v (x) (\displaystyle y(x)=e^(rx)v(x)) und setze es in die Differentialgleichung ein. In diesem Fall die meisten Terme, mit Ausnahme des Termes mit der zweiten Ableitung der Funktion v , (\displaystyle v,) wird reduziert.
- v ″ (x) e r x = 0 (\displaystyle v""(x)e^(rx)=0)
- Beispiel 2.2. Gegeben sei die folgende Gleichung mit mehreren Wurzeln r = − 4. (\displaystyle r=-4.) Bei der Substitution werden die meisten Begriffe gekürzt.
- d 2 y d x 2 + 8 d y d x + 16 y = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )x^(2)))+8( \frac ((\mathrm (d) )y)((\mathrm (d) )x))+16y=0)
- y = v (x) e − 4 x y ′ = v ′ (x) e − 4 x − 4 v (x) e − 4 x y ″ = v ″ (x) e − 4 x − 8 v ′ (x) e − 4 x + 16 v (x) e − 4 x (\displaystyle (\begin(aligned)y&=v(x)e^(-4x)\\y"&=v"(x)e^(-4x )-4v(x)e^(-4x)\\y""&=v""(x)e^(-4x)-8v"(x)e^(-4x)+16v(x)e^ (-4x)\end(ausgerichtet)))
- v ″ e − 4 x − 8 v ′ e − 4 x + 16 v e − 4 x + 8 v ′ e − 4 x − 32 v e − 4 x + 16 v e − 4 x = 0 (\displaystyle (\begin(aligned )v""e^(-4x)&-(\cancel (8v"e^(-4x)))+(\cancel (16ve^(-4x)))\\&+(\cancel (8v"e ^(-4x)))-(\cancel (32ve^(-4x)))+(\cancel (16ve^(-4x)))=0\end(aligned)))
- Ähnlich wie bei unserem Ansatz für eine Differentialgleichung mit konstanten Koeffizienten kann in diesem Fall nur die zweite Ableitung gleich Null sein. Wir integrieren zweimal und erhalten den gewünschten Ausdruck für v (\displaystyle v):
- v (x) = c 1 + c 2 x (\displaystyle v(x)=c_(1)+c_(2)x)
- Dann kann die allgemeine Lösung einer Differentialgleichung mit konstanten Koeffizienten für den Fall, dass die charakteristische Gleichung mehrere Wurzeln hat, in der folgenden Form geschrieben werden. Der Einfachheit halber können Sie sich daran erinnern, dass es ausreicht, einfach den zweiten Term mit zu multiplizieren, um eine lineare Unabhängigkeit zu erhalten x (\displaystyle x). Diese Lösungsmenge ist linear unabhängig und somit haben wir alle Lösungen dieser Gleichung gefunden.
- y (x) = (c 1 + c 2 x) e r x (\displaystyle y(x)=(c_(1)+c_(2)x)e^(rx))
D 2 y d x 2 + p (x) d y d x + q (x) y = 0. (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )x^( 2)))+p(x)(\frac ((\mathrm (d) )y)((\mathrm (d) )x))+q(x)y=0.) Eine Bestellreduzierung ist möglich, wenn die Lösung bekannt ist y 1 (x) (\displaystyle y_(1)(x)), die in der Problemstellung gefunden oder angegeben werden kann.
- Wir suchen nach einer Lösung im Formular y (x) = v (x) y 1 (x) (\displaystyle y(x)=v(x)y_(1)(x)) und setze es in diese Gleichung ein:
- v ″ y 1 + 2 v ′ y 1 ′ + p (x) v ′ y 1 + v (y 1 ″ + p (x) y 1 ′ + q (x)) = 0 (\displaystyle v""y_( 1)+2v"y_(1)"+p(x)v"y_(1)+v(y_(1)""+p(x)y_(1)"+q(x))=0)
- Weil das y 1 (\displaystyle y_(1)) ist eine Lösung einer Differentialgleichung, alle Terme mit v (\displaystyle v) werden reduziert. Am Ende bleibt es dabei lineare Gleichung erster Ordnung. Um dies klarer zu sehen, nehmen wir eine Änderung der Variablen vor w (x) = v ′ (x) (\displaystyle w(x)=v"(x)):
- y 1 w ′ + (2 y 1 ′ + p (x) y 1) w = 0 (\displaystyle y_(1)w"+(2y_(1)"+p(x)y_(1))w=0 )
- w (x) = exp (∫ (2 y 1 ′ (x) y 1 (x) + p (x)) d x) (\displaystyle w(x)=\exp \left(\int \left((\ frac (2y_(1)"(x))(y_(1)(x)))+p(x)\right)(\mathrm (d) )x\right))
- v (x) = ∫ w (x) d x (\displaystyle v(x)=\int w(x)(\mathrm (d) )x)
- Wenn die Integrale berechnet werden können, erhalten wir die allgemeine Lösung als Kombination von Elementarfunktionen. Andernfalls kann die Lösung in integraler Form belassen werden.
- Die charakteristische Gleichung soll mehrere Wurzeln haben r (\displaystyle r). Nehmen wir an, dass die zweite Lösung in der Form geschrieben werden kann y (x) = e r x v (x) (\displaystyle y(x)=e^(rx)v(x)) und setze es in die Differentialgleichung ein. In diesem Fall die meisten Terme, mit Ausnahme des Termes mit der zweiten Ableitung der Funktion v , (\displaystyle v,) wird reduziert.
-
Cauchy-Euler-Gleichung. Die Cauchy-Euler-Gleichung ist ein Beispiel für eine Differentialgleichung zweiter Ordnung mit Variablen Koeffizienten, die exakte Lösungen haben. Diese Gleichung wird in der Praxis beispielsweise zur Lösung der Laplace-Gleichung in Kugelkoordinaten verwendet.
X 2 d 2 y d x 2 + a x d y d x + b y = 0 (\displaystyle ))+ax(\frac ((\mathrm (d) )y)((\mathrm (d) )x))+by=0)
Charakteristische Gleichung. Wie Sie sehen können, enthält in dieser Differentialgleichung jeder Term einen Leistungsfaktor, dessen Grad der Ordnung der entsprechenden Ableitung entspricht.
- So können Sie versuchen, im Formular nach einer Lösung zu suchen y (x) = x n , (\displaystyle y(x)=x^(n),) wo es notwendig ist, zu bestimmen n (\displaystyle n), genauso wie wir nach einer Lösung in Form einer Exponentialfunktion für eine lineare Differentialgleichung mit konstanten Koeffizienten suchten. Nach Differenzierung und Substitution erhalten wir
- x n (n 2 + (a − 1) n + b) = 0 (\displaystyle x^(n)(n^(2)+(a-1)n+b)=0)
- Um die charakteristische Gleichung verwenden zu können, müssen wir davon ausgehen x ≠ 0 (\displaystyle x\neq 0). Punkt x = 0 (\displaystyle x=0) angerufen regelmäßiger Singularpunkt Differentialgleichung. Solche Punkte sind wichtig, wenn Differentialgleichungen mithilfe von Potenzreihen gelöst werden. Diese Gleichung hat zwei Wurzeln, die unterschiedlich und reell, mehrfach oder komplex konjugiert sein können.
- n ± = 1 − a ± (a − 1) 2 − 4 b 2 (\displaystyle n_(\pm )=(\frac (1-a\pm (\sqrt ((a-1)^(2)-4b )))(2)))
Zwei verschiedene echte Wurzeln. Wenn die Wurzeln n ± (\displaystyle n_(\pm )) real und unterschiedlich sind, dann hat die Lösung der Differentialgleichung die folgende Form:
- y (x) = c 1 x n + + c 2 x n − (\displaystyle y(x)=c_(1)x^(n_(+))+c_(2)x^(n_(-)))
Zwei komplexe Wurzeln. Wenn die charakteristische Gleichung Wurzeln hat n ± = α ± β i (\displaystyle n_(\pm )=\alpha \pm \beta i), die Lösung ist eine komplexe Funktion.
- Um die Lösung in eine reale Funktion umzuwandeln, nehmen wir eine Änderung der Variablen vor x = e t , (\displaystyle x=e^(t),) also t = ln x , (\displaystyle t=\ln x,) und verwenden Sie die Eulersche Formel. Ähnliche Aktionen wurden früher bei der Bestimmung beliebiger Konstanten durchgeführt.
- y (t) = e α t (c 1 e β i t + c 2 e − β i t) (\displaystyle y(t)=e^(\alpha t)(c_(1)e^(\beta it)+ c_(2)e^(-\beta it)))
- Dann kann die allgemeine Lösung geschrieben werden als
- y (x) = x α (c 1 cos (β ln x) + c 2 sin (β ln x)) (\displaystyle y(x)=x^(\alpha )(c_(1)\ cos(\beta \ln x)+c_(2)\sin(\beta \ln x)))
Mehrere Wurzeln. Um eine zweite linear unabhängige Lösung zu erhalten, ist es notwendig, die Ordnung erneut zu reduzieren.
- Es sind ziemlich viele Berechnungen erforderlich, aber das Prinzip bleibt dasselbe: Wir ersetzen y = v (x) y 1 (\displaystyle y=v(x)y_(1)) in eine Gleichung, deren erste Lösung ist y 1 (\displaystyle y_(1)). Nach Reduktionen erhält man die folgende Gleichung:
- v ″ + 1 x v ′ = 0 (\displaystyle v""+(\frac (1)(x))v"=0)
- Dies ist eine lineare Gleichung erster Ordnung bzgl v ′ (x) . (\displaystyle v"(x).) Seine Lösung ist v (x) = c 1 + c 2 ln x . (\displaystyle v(x)=c_(1)+c_(2)\ln x.) Somit kann die Lösung in der folgenden Form geschrieben werden. Das kann man sich leicht merken – um die zweite linear unabhängige Lösung zu erhalten, ist lediglich ein zusätzlicher Term mit erforderlich ln x (\displaystyle \ln x).
- y (x) = x n (c 1 + c 2 ln x) (\displaystyle y(x)=x^(n)(c_(1)+c_(2)\ln x))
- So können Sie versuchen, im Formular nach einer Lösung zu suchen y (x) = x n , (\displaystyle y(x)=x^(n),) wo es notwendig ist, zu bestimmen n (\displaystyle n), genauso wie wir nach einer Lösung in Form einer Exponentialfunktion für eine lineare Differentialgleichung mit konstanten Koeffizienten suchten. Nach Differenzierung und Substitution erhalten wir
-
Inhomogene lineare Differentialgleichungen mit konstanten Koeffizienten. Inhomogene Gleichungen haben die Form L [ y (x) ] = f (x), (\displaystyle L=f(x),) Wo f (x) (\displaystyle f(x))- sogenannt Freies Mitglied. Nach der Theorie der Differentialgleichungen ist die allgemeine Lösung dieser Gleichung eine Superposition private Lösung y p (x) (\displaystyle y_(p)(x)) Und zusätzliche Lösung y c (x) . (\displaystyle y_(c)(x).) Allerdings bedeutet eine bestimmte Lösung in diesem Fall nicht eine Lösung, die durch die Anfangsbedingungen gegeben ist, sondern vielmehr eine Lösung, die durch das Vorhandensein von Heterogenität (ein freier Begriff) bestimmt wird. Eine zusätzliche Lösung ist eine Lösung der entsprechenden homogenen Gleichung, in der f (x) = 0. (\displaystyle f(x)=0.) Die Gesamtlösung ist eine Überlagerung dieser beiden Lösungen, da L [ y p + y c ] = L [ y p ] + L [ y c ] = f (x) (\displaystyle L=L+L=f(x)), und da L [ y c ] = 0 , (\displaystyle L=0,) Eine solche Überlagerung ist tatsächlich eine allgemeine Lösung.
D 2 y d x 2 + a d y d x + b y = f (x) (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )x^(2)))+a (\frac ((\mathrm (d) )y)((\mathrm (d) )x))+by=f(x))
Methode unbestimmter Koeffizienten. Die Methode der unbestimmten Koeffizienten wird in Fällen verwendet, in denen der Dummy-Term eine Kombination aus exponentiellem, trigonometrischem, hyperbolischem oder ist Potenzfunktionen. Nur diese Funktionen haben garantiert eine endliche Anzahl linear unabhängiger Ableitungen. In diesem Abschnitt werden wir eine bestimmte Lösung der Gleichung finden.
- Vergleichen wir die Begriffe in f (x) (\displaystyle f(x)) mit Begriffen in, ohne auf konstante Faktoren zu achten. Es gibt drei mögliche Fälle.
- Keine zwei Mitglieder sind gleich. In diesem Fall eine besondere Lösung y p (\displaystyle y_(p)) wird eine lineare Kombination von Begriffen aus sein y p (\displaystyle y_(p))
- f (x) (\displaystyle f(x)) enthält Mitglied x n (\displaystyle x^(n)) und Mitglied aus y c , (\displaystyle y_(c),) Wo n (\displaystyle n) ist Null oder eine positive ganze Zahl, und dieser Term entspricht einer separaten Wurzel der charakteristischen Gleichung. In diesem Fall y p (\displaystyle y_(p)) wird aus einer Kombination der Funktion bestehen x n + 1 h (x) , (\displaystyle x^(n+1)h(x),) seine linear unabhängigen Ableitungen sowie andere Terme f (x) (\displaystyle f(x)) und ihre linear unabhängigen Ableitungen.
- f (x) (\displaystyle f(x)) enthält Mitglied h (x), (\displaystyle h(x),) Das ist eine Arbeit x n (\displaystyle x^(n)) und Mitglied aus y c , (\displaystyle y_(c),) Wo n (\displaystyle n) ist gleich 0 oder eine positive ganze Zahl, und dieser Begriff entspricht mehrere Wurzel der charakteristischen Gleichung. In diesem Fall y p (\displaystyle y_(p)) ist eine Linearkombination der Funktion x n + s h (x) (\displaystyle x^(n+s)h(x))(Wo s (\displaystyle s)- Multiplizität der Wurzel) und ihre linear unabhängigen Ableitungen sowie andere Mitglieder der Funktion f (x) (\displaystyle f(x)) und seine linear unabhängigen Ableitungen.
- Schreiben wir es auf y p (\displaystyle y_(p)) als Linearkombination der oben aufgeführten Begriffe. Dank dieser Koeffizienten in einer linearen Kombination diese Methode wird als „Methode der unbestimmten Koeffizienten“ bezeichnet. Wenn darin enthalten y c (\displaystyle y_(c)) Mitglieder können aufgrund des Vorhandenseins beliebiger Konstanten verworfen werden y c . (\displaystyle y_(c).) Danach ersetzen wir y p (\displaystyle y_(p)) in die Gleichung ein und setzen ähnliche Begriffe gleich.
- Wir bestimmen die Koeffizienten. In diesem Stadium entsteht ein System algebraischer Gleichungen, das in der Regel problemlos gelöst werden kann. Die Lösung dieses Systems ermöglicht es uns, zu erhalten y p (\displaystyle y_(p)) und damit die Gleichung lösen.
- Beispiel 2.3. Betrachten wir eine inhomogene Differentialgleichung, deren freier Term eine endliche Anzahl linear unabhängiger Ableitungen enthält. Eine besondere Lösung einer solchen Gleichung kann mit der Methode der unbestimmten Koeffizienten gefunden werden.
- d 2 y d t 2 + 6 y = 2 e 3 t − cos 5 t (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )t^(2) ))+6y=2e^(3t)-\cos 5t)
- y c (t) = c 1 cos 6 t + c 2 sin 6 t (\displaystyle y_(c)(t)=c_(1)\cos (\sqrt (6))t+c_(2)\sin (\sqrt (6))t)
- y p (t) = A e 3 t + B cos 5 t + C sin 5 t (\displaystyle y_(p)(t)=Ae^(3t)+B\cos 5t+C\sin 5t)
- 9 A e 3 t − 25 B cos 5 t − 25 C sin 5 t + 6 A e 3 t + 6 B cos 5 t + 6 C sin 5 t = 2 e 3 t − cos 5 t ( \displaystyle (\begin(aligned)9Ae^(3t)-25B\cos 5t&-25C\sin 5t+6Ae^(3t)\\&+6B\cos 5t+6C\sin 5t=2e^(3t)-\ cos 5t\end(ausgerichtet)))
- ( 9 A + 6 A = 2 , A = 2 15 − 25 B + 6 B = − 1 , B = 1 19 − 25 C + 6 C = 0 , C = 0 (\displaystyle (\begin(cases)9A+ 6A =2,&A=(\dfrac (2)(15))\\-25B+6B=-1,&B=(\dfrac (1)(19))\\-25C+6C=0,&C=0 \ end(cases)))
- y (t) = c 1 cos 6 t + c 2 sin 6 t + 2 15 e 3 t + 1 19 cos 5 t (\displaystyle y(t)=c_(1)\cos (\sqrt (6 ))t+c_(2)\sin (\sqrt (6))t+(\frac (2)(15))e^(3t)+(\frac (1)(19))\cos 5t)
Lagrange-Methode. Die Lagrange-Methode oder Methode zur Variation beliebiger Konstanten ist eine allgemeinere Methode zur Lösung inhomogener Differentialgleichungen, insbesondere in Fällen, in denen der Achsenabschnittsterm keine endliche Anzahl linear unabhängiger Ableitungen enthält. Zum Beispiel mit kostenlosen Konditionen tan x (\displaystyle \tan x) oder x − n (\displaystyle x^(-n)) Um eine bestimmte Lösung zu finden, muss die Lagrange-Methode verwendet werden. Mit der Lagrange-Methode können sogar Differentialgleichungen mit variablen Koeffizienten gelöst werden, allerdings wird sie in diesem Fall mit Ausnahme der Cauchy-Euler-Gleichung seltener verwendet, da die zusätzliche Lösung in der Regel nicht durch Elementarfunktionen ausgedrückt wird.
- Nehmen wir an, dass die Lösung die folgende Form hat. Seine Ableitung ist in der zweiten Zeile angegeben.
- y (x) = v 1 (x) y 1 (x) + v 2 (x) y 2 (x) (\displaystyle y(x)=v_(1)(x)y_(1)(x)+v_ (2)(x)y_(2)(x))
- y ′ = v 1 ′ y 1 + v 1 y 1 ′ + v 2 ′ y 2 + v 2 y 2 ′ (\displaystyle y"=v_(1)"y_(1)+v_(1)y_(1) „+v_(2)“y_(2)+v_(2)y_(2)“)
- Da die vorgeschlagene Lösung enthält zwei Unbekannte Größen müssen auferlegt werden zusätzlich Zustand. Wählen wir diese Zusatzbedingung in folgender Form:
- v 1 ′ y 1 + v 2 ′ y 2 = 0 (\displaystyle v_(1)"y_(1)+v_(2)"y_(2)=0)
- y ′ = v 1 y 1 ′ + v 2 y 2 ′ (\displaystyle y"=v_(1)y_(1)"+v_(2)y_(2)")
- y ″ = v 1 ′ y 1 ′ + v 1 y 1 ″ + v 2 ′ y 2 ′ + v 2 y 2 ″ (\displaystyle y""=v_(1)"y_(1)"+v_(1) y_(1)""+v_(2)"y_(2)"+v_(2)y_(2)"")
- Jetzt können wir die zweite Gleichung erhalten. Nach der Ersetzung und Umverteilung von Mitgliedern können Sie Mitglieder mit gruppieren v 1 (\displaystyle v_(1)) und Mitglieder mit v 2 (\displaystyle v_(2)). Diese Begriffe werden reduziert, weil y 1 (\displaystyle y_(1)) Und y 2 (\displaystyle y_(2)) sind Lösungen der entsprechenden homogenen Gleichung. Als Ergebnis erhalten wir das folgende Gleichungssystem
- v 1 ′ y 1 + v 2 ′ y 2 = 0 v 1 ′ y 1 ′ + v 2 ′ y 2 ′ = f (x) (\displaystyle (\begin(aligned)v_(1)"y_(1)+ v_(2)"y_(2)&=0\\v_(1)"y_(1)"+v_(2)"y_(2)"&=f(x)\\\end(aligned)))
- Dieses System kann in eine Matrixgleichung der Form transformiert werden A x = b , (\displaystyle A(\mathbf (x) )=(\mathbf (b) ),) dessen Lösung ist x = A − 1 b . (\displaystyle (\mathbf (x) )=A^(-1)(\mathbf (b) ).) Für Matrix 2 × 2 (\displaystyle 2\times 2) inverse Matrix wird ermittelt, indem man durch die Determinante dividiert, die diagonalen Elemente neu anordnet und das Vorzeichen der nichtdiagonalen Elemente ändert. Tatsächlich ist die Determinante dieser Matrix ein Wronski-Operator.
- (v 1 ′ v 2 ′) = 1 W (y 2 ′ − y 2 − y 1 ′ y 1) (0 f (x)) (\displaystyle (\begin(pmatrix)v_(1)"\\v_( 2)"\end(pmatrix))=(\frac (1)(W))(\begin(pmatrix)y_(2)"&-y_(2)\\-y_(1)"&y_(1)\ end(pmatrix))(\begin(pmatrix)0\\f(x)\end(pmatrix)))
- Ausdrücke für v 1 (\displaystyle v_(1)) Und v 2 (\displaystyle v_(2)) sind unten angegeben. Wie bei der Ordnungsreduktionsmethode erscheint in diesem Fall bei der Integration eine beliebige Konstante, die eine zusätzliche Lösung in die allgemeine Lösung der Differentialgleichung einbezieht.
- v 1 (x) = − ∫ 1 W f (x) y 2 (x) d x (\displaystyle v_(1)(x)=-\int (\frac (1)(W))f(x)y_( 2)(x)(\mathrm (d) )x)
- v 2 (x) = ∫ 1 W f (x) y 1 (x) d x (\displaystyle v_(2)(x)=\int (\frac (1)(W))f(x)y_(1) (x)(\mathrm (d) )x)
Vortrag der National Open University Intuit mit dem Titel „Lineare Differentialgleichungen n-ter Ordnung mit konstanten Koeffizienten“. - Vergleichen wir die Begriffe in f (x) (\displaystyle f(x)) mit Begriffen in, ohne auf konstante Faktoren zu achten. Es gibt drei mögliche Fälle.
Praktischer Nutzen
Differentialgleichungen stellen eine Beziehung zwischen einer Funktion und einer oder mehreren ihrer Ableitungen her. Da solche Zusammenhänge äußerst häufig vorkommen, haben Differentialgleichungen in den meisten Fällen breite Anwendung gefunden verschiedene Bereiche, und da wir in vier Dimensionen leben, sind diese Gleichungen oft Differentialgleichungen Privat Derivate. In diesem Abschnitt werden einige der wichtigsten Gleichungen dieser Art behandelt.
- Exponentielles Wachstum und Verfall. Radioaktiver Zerfall. Zinseszins. Geschwindigkeit chemische Reaktionen. Konzentration von Medikamenten im Blut. Unbegrenztes Bevölkerungswachstum. Newton-Richmann-Gesetz. In der realen Welt gibt es viele Systeme, in denen die Wachstums- oder Verfallsrate zu einem bestimmten Zeitpunkt proportional zur Menge ist dieser Moment Zeit oder kann durch das Modell gut angenähert werden. Dies liegt daran, dass die Lösung einer gegebenen Differentialgleichung, die Exponentialfunktion, eine der wichtigsten Funktionen in der Mathematik und anderen Wissenschaften ist. Allgemeiner gesagt kann das System bei kontrolliertem Bevölkerungswachstum zusätzliche Bedingungen enthalten, die das Wachstum begrenzen. In der folgenden Gleichung ist die Konstante k (\displaystyle k) kann entweder größer oder kleiner als Null sein.
- d y d x = k x (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=kx)
- Harmonische Schwingungen. Sowohl in der klassischen als auch in der Quantenmechanik ist der harmonische Oszillator einer der wichtigsten physikalische Systeme aufgrund seiner Einfachheit und breiten Anwendung zur Approximation komplexerer Systeme wie eines einfachen Pendels. In der klassischen Mechanik werden harmonische Schwingungen durch eine Gleichung beschrieben, die die Position eines materiellen Punktes mit seiner Beschleunigung durch das Hookesche Gesetz in Beziehung setzt. Dabei können auch Dämpfungs- und Antriebskräfte berücksichtigt werden. Im folgenden Ausdruck x ˙ (\displaystyle (\dot (x)))- Zeitableitung von x , (\displaystyle x,) β (\displaystyle \beta)- Parameter, der die Dämpfungskraft beschreibt, ω 0 (\displaystyle \omega _(0))- Kreisfrequenz des Systems, F (t) (\displaystyle F(t))- zeitabhängig treibende Kraft. Der harmonische Oszillator kommt auch in elektromagnetischen Schwingkreisen vor und lässt sich dort mit größerer Genauigkeit umsetzen als in mechanischen Systemen.
- x ¨ + 2 β x ˙ + ω 0 2 x = F (t) (\displaystyle (\ddot (x))+2\beta (\dot (x))+\omega _(0)^(2)x =F(t))
- Bessels Gleichung. Die Bessel-Differentialgleichung wird in vielen Bereichen der Physik verwendet, einschließlich der Lösung der Wellengleichung, der Laplace-Gleichung und der Schrödinger-Gleichung, insbesondere bei Vorliegen einer Zylinder- oder Kugelsymmetrie. Diese Differentialgleichung zweiter Ordnung mit variablen Koeffizienten ist keine Cauchy-Euler-Gleichung, daher können ihre Lösungen nicht als Elementarfunktionen geschrieben werden. Die Lösungen der Bessel-Gleichung sind die Bessel-Funktionen, die aufgrund ihrer Anwendung in vielen Bereichen gut untersucht sind. Im folgenden Ausdruck α (\displaystyle \alpha )- eine Konstante, die entspricht in Ordnung Bessel-Funktionen.
- x 2 d 2 y d x 2 + x d y d x + (x 2 − α 2) y = 0 (\displaystyle x^(2)(\frac ((\mathrm (d) )^(2)y)((\mathrm (d ) )x^(2)))+x(\frac ((\mathrm (d) )y)((\mathrm (d) )x))+(x^(2)-\alpha ^(2)) y=0)
- Maxwells Gleichungen. Zusammen mit der Lorentzkraft bilden die Maxwellschen Gleichungen die Grundlage der klassischen Elektrodynamik. Dies sind die vier partiellen Differentialgleichungen für die Elektrik E (r , t) (\displaystyle (\mathbf (E) )((\mathbf (r) ),t)) und magnetisch B (r , t) (\displaystyle (\mathbf (B) )((\mathbf (r) ),t)) Felder. In den folgenden Ausdrücken ρ = ρ (r , t) (\displaystyle \rho =\rho ((\mathbf (r) ),t))- Ladungsdichte, J = J (r , t) (\displaystyle (\mathbf (J) )=(\mathbf (J) )((\mathbf (r) ),t))- Stromdichte und ϵ 0 (\displaystyle \epsilon _(0)) Und μ 0 (\displaystyle \mu _(0))- elektrische bzw. magnetische Konstanten.
- ∇ ⋅ E = ρ ϵ 0 ∇ ⋅ B = 0 ∇ × E = − ∂ B ∂ t ∇ × B = μ 0 J + μ 0 ϵ 0 ∂ E ∂ t (\displaystyle (\begin(aligned)\nabla \cdot (\mathbf (E) )&=(\frac (\rho )(\epsilon _(0)))\\\nabla \cdot (\mathbf (B) )&=0\\\nabla \times (\mathbf (E) )&=-(\frac (\partial (\mathbf (B) ))(\partial t))\\\nabla \times (\mathbf (B) )&=\mu _(0)(\ mathbf (J) )+\mu _(0)\epsilon _(0)(\frac (\partial (\mathbf (E) ))(\partial t))\end(aligned)))
- Schrödinger-Gleichung. In der Quantenmechanik ist die Schrödinger-Gleichung die grundlegende Bewegungsgleichung, die die Bewegung von Teilchen entsprechend einer Änderung der Wellenfunktion beschreibt Ψ = Ψ (r , t) (\displaystyle \Psi =\Psi ((\mathbf (r) ),t)) mit der Zeit. Die Bewegungsgleichung wird durch das Verhalten beschrieben Hamiltonianer H^(\displaystyle (\hat (H))) - Operator, die die Energie des Systems beschreibt. Eines der bekanntesten Beispiele der Schrödinger-Gleichung in der Physik ist die Gleichung für ein einzelnes nichtrelativistisches Teilchen, das dem Potential unterliegt V (r , t) (\displaystyle V((\mathbf (r) ),t)). Viele Systeme werden durch die zeitabhängige Schrödinger-Gleichung beschrieben, und auf der linken Seite der Gleichung steht sie E Ψ , (\displaystyle E\Psi ,) Wo E (\displaystyle E)- Teilchenenergie. In den folgenden Ausdrücken ℏ (\displaystyle \hbar )- reduzierte Planck-Konstante.
- i ℏ ∂ Ψ ∂ t = H ^ Ψ (\displaystyle i\hbar (\frac (\partial \Psi )(\partial t))=(\hat (H))\Psi )
- i ℏ ∂ Ψ ∂ t = (− ℏ 2 2 m ∇ 2 + V (r , t)) Ψ (\displaystyle i\hbar (\frac (\partial \Psi )(\partial t))=\left(- (\frac (\hbar ^(2))(2m))\nabla ^(2)+V((\mathbf (r) ),t)\right)\Psi )
- Wellengleichung. Wellen sind aus Physik und Technik nicht mehr wegzudenken, sie sind in allen Arten von Systemen vorhanden. Im Allgemeinen werden Wellen durch die folgende Gleichung beschrieben: u = u (r , t) (\displaystyle u=u((\mathbf (r) ),t)) ist die gewünschte Funktion und c (\displaystyle c)- experimentell ermittelte Konstante. d'Alembert entdeckte als erster, dass die Lösung der Wellengleichung für den eindimensionalen Fall lautet beliebig Funktion mit Argument x − c t (\displaystyle x-ct), die eine Welle beliebiger Form beschreibt, die sich nach rechts ausbreitet. Die allgemeine Lösung für den eindimensionalen Fall ist eine Linearkombination dieser Funktion mit einer zweiten Funktion mit Argument x + c t (\displaystyle x+ct), was eine Welle beschreibt, die sich nach links ausbreitet. Diese Lösung wird in der zweiten Zeile vorgestellt.
- ∂ 2 u ∂ t 2 = c 2 ∇ 2 u (\displaystyle (\frac (\partial ^(2)u)(\partial t^(2)))=c^(2)\nabla ^(2)u )
- u (x , t) = f (x − c t) + g (x + c t) (\displaystyle u(x,t)=f(x-ct)+g(x+ct))
- Navier-Stokes-Gleichungen. Die Navier-Stokes-Gleichungen beschreiben die Bewegung von Flüssigkeiten. Da Flüssigkeiten in praktisch allen Bereichen der Wissenschaft und Technologie vorkommen, sind diese Gleichungen äußerst wichtig für die Vorhersage des Wetters, die Konstruktion von Flugzeugen, die Untersuchung von Meeresströmungen und die Lösung vieler anderer angewandter Probleme. Die Navier-Stokes-Gleichungen sind nichtlineare partielle Differentialgleichungen und in den meisten Fällen sehr schwer zu lösen, da die Nichtlinearität zu Turbulenzen führt und das Erhalten einer stabilen Lösung mit numerischen Methoden eine Aufteilung in sehr kleine Zellen erfordert, was erhebliche Rechenleistung erfordert. Für praktische Zwecke in der Hydrodynamik werden Methoden wie die zeitliche Mittelung zur Simulation turbulenter Strömungen eingesetzt. Komplexe Aufgaben Es gibt noch grundlegendere Fragen wie die Existenz und Eindeutigkeit von Lösungen für nichtlineare partielle Differentialgleichungen, und der Nachweis der Existenz und Eindeutigkeit einer Lösung für die Navier-Stokes-Gleichungen in drei Dimensionen gehört zu den mathematischen Problemen des Jahrtausends. Nachfolgend finden Sie die Gleichung für den inkompressiblen Flüssigkeitsfluss und die Kontinuitätsgleichung.
- ∂ u ∂ t + (u ⋅ ∇) u − ν ∇ 2 u = − ∇ h , ∂ ρ ∂ t + ∇ ⋅ (ρ u) = 0 (\displaystyle (\frac (\partial (\mathbf (u) ) )(\partial t))+((\mathbf (u) )\cdot \nabla)(\mathbf (u) )-\nu \nabla ^(2)(\mathbf (u) )=-\nabla h, \quad (\frac (\partial \rho )(\partial t))+\nabla \cdot (\rho (\mathbf (u) ))=0)
- Viele Differentialgleichungen können mit den oben genannten Methoden einfach nicht gelöst werden, insbesondere nicht mit den im letzten Abschnitt erwähnten. Dies gilt für Fälle, in denen die Gleichung variable Koeffizienten enthält und keine Cauchy-Euler-Gleichung ist, oder wenn die Gleichung nichtlinear ist, außer in einigen sehr seltenen Fällen. Allerdings können die oben genannten Methoden viele wichtige Differentialgleichungen lösen, die in verschiedenen Bereichen der Wissenschaft häufig vorkommen.
- Im Gegensatz zur Differentiation, mit der Sie die Ableitung jeder Funktion ermitteln können, kann das Integral vieler Ausdrücke nicht in Elementarfunktionen ausgedrückt werden. Verschwenden Sie also keine Zeit damit, ein Integral zu berechnen, obwohl dies unmöglich ist. Schauen Sie sich die Tabelle der Integrale an. Wenn die Lösung einer Differentialgleichung nicht durch Elementarfunktionen ausgedrückt werden kann, kann sie manchmal in Integralform dargestellt werden, und in diesem Fall spielt es keine Rolle, ob dieses Integral analytisch berechnet werden kann.
Warnungen
- Aussehen Differentialgleichungen können irreführend sein. Im Folgenden finden Sie beispielsweise zwei Differentialgleichungen erster Ordnung. Die erste Gleichung lässt sich mit den in diesem Artikel beschriebenen Methoden leicht lösen. Auf den ersten Blick eine kleine Änderung y (\displaystyle y) An y 2 (\displaystyle y^(2)) in der zweiten Gleichung macht sie nichtlinear und wird sehr schwer zu lösen.
- d y d x = x 2 + y (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=x^(2)+y)
- d y d x = x 2 + y 2 (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=x^(2)+y^(2))