Finden Sie das allgemeine Integral einer Differentialgleichung, Beispiele für Lösungen. Differentialgleichungen erster Ordnung
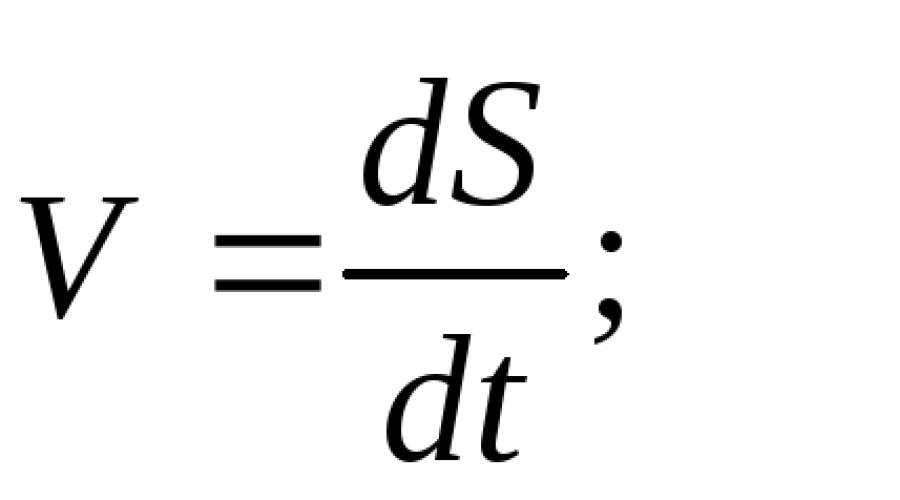
Lesen Sie auch
Die Lösung verschiedener geometrischer, physikalischer und technischer Probleme führt oft zu Gleichungen, die die unabhängigen Variablen, die ein bestimmtes Problem charakterisieren, mit einer Funktion dieser Variablen und Ableitungen dieser Funktion verschiedener Ordnung in Beziehung setzen.
Als Beispiel können wir den einfachsten Fall einer gleichmäßig beschleunigten Bewegung eines materiellen Punktes betrachten.
Es ist bekannt, dass die Verschiebung eines materiellen Punktes bei gleichmäßig beschleunigter Bewegung eine Funktion der Zeit ist und durch die Formel ausgedrückt wird:
Im Gegenzug Beschleunigung A ist zeitlich abgeleitet T von der Geschwindigkeit V, was auch eine Zeitableitung ist T vom Umzug S. Diese.

Dann erhalten wir:  - Die Gleichung verbindet die Funktion f(t) mit der unabhängigen Variablen t und der Ableitung zweiter Ordnung der Funktion f(t).
- Die Gleichung verbindet die Funktion f(t) mit der unabhängigen Variablen t und der Ableitung zweiter Ordnung der Funktion f(t).
Definition. Differentialgleichung ist eine Gleichung, die unabhängige Variablen, ihre Funktionen und Ableitungen (oder Differentiale) dieser Funktion in Beziehung setzt.
Definition. Wenn eine Differentialgleichung eine unabhängige Variable hat, heißt sie gewöhnliche Differentialgleichung , Gibt es zwei oder mehr unabhängige Variablen, so heißt eine solche Differentialgleichung partielle Differentialgleichung.
Definition. Die höchste Ordnung der in einer Gleichung vorkommenden Ableitungen wird aufgerufen Ordnung der Differentialgleichung .
Beispiel.
 - gewöhnliche Differentialgleichung 1. Ordnung. IN Gesamtansicht ist aufgenommen
- gewöhnliche Differentialgleichung 1. Ordnung. IN Gesamtansicht ist aufgenommen  .
.
 - gewöhnliche Differentialgleichung 2. Ordnung. Im Allgemeinen ist es geschrieben
- gewöhnliche Differentialgleichung 2. Ordnung. Im Allgemeinen ist es geschrieben 
 - Partielle Differentialgleichung erster Ordnung.
- Partielle Differentialgleichung erster Ordnung.
Definition. Allgemeine Lösung Die Differentialgleichung ist eine solche differenzierbare Funktion y = (x, C), die, wenn sie anstelle einer unbekannten Funktion in die ursprüngliche Gleichung eingesetzt wird, die Gleichung in die Identität umwandelt
Eigenschaften der allgemeinen Lösung.
1) Weil Ist die Konstante C ein beliebiger Wert, dann hat eine Differentialgleichung im Allgemeinen unendlich viele Lösungen.
2) Unter allen Anfangsbedingungen x = x 0, y(x 0) = y 0 gibt es einen Wert C = C 0, bei dem die Lösung der Differentialgleichung die Funktion y = (x, C 0) ist.
Definition. Man nennt eine Lösung der Form y = (x, C 0). private Lösung Differentialgleichung.
Definition. Cauchy-Problem (Augustin Louis Cauchy (1789-1857) – französischer Mathematiker) ist das Finden einer bestimmten Lösung für eine Differentialgleichung der Form y = (x, C 0), die die Anfangsbedingungen y(x 0) = y 0 erfüllt.
Satz von Cauchy. (Satz über die Existenz und Eindeutigkeit einer Lösung einer Differentialgleichung 1. Ordnung)
Wenn die FunktionF(X,
j) ist in einigen Regionen kontinuierlichDim FlugzeugXOYund hat in diesem Bereich eine stetige partielle Ableitung  , dann was auch immer der Punkt (x 0
, ja 0
) im GebietD, es gibt nur eine Lösung
, dann was auch immer der Punkt (x 0
, ja 0
) im GebietD, es gibt nur eine Lösung  Gleichungen
Gleichungen  , definiert in einem Intervall, das den Punkt x enthält 0
, wobei x = x gilt 0
Bedeutung
(X 0
) = y 0
, d.h. Es gibt eine eindeutige Lösung für die Differentialgleichung.
, definiert in einem Intervall, das den Punkt x enthält 0
, wobei x = x gilt 0
Bedeutung
(X 0
) = y 0
, d.h. Es gibt eine eindeutige Lösung für die Differentialgleichung.
Definition.
Integral
Eine Differentialgleichung ist jede Gleichung, die keine Ableitungen enthält und für die die gegebene Differentialgleichung eine Konsequenz ist. 
Beispiel. Finden gemeinsame Entscheidung Differentialgleichung  .
.
Die allgemeine Lösung der Differentialgleichung wird durch Integration der linken und rechten Seite der zuvor transformierten Gleichung gesucht auf die folgende Weise:



Jetzt integrieren wir: 




 ist die allgemeine Lösung der ursprünglichen Differentialgleichung.
ist die allgemeine Lösung der ursprünglichen Differentialgleichung.
Nehmen wir an, einige Anfangsbedingungen sind gegeben: x 0 = 1; y 0 = 2, dann gilt

Indem wir den erhaltenen Wert der Konstante in die allgemeine Lösung einsetzen, erhalten wir eine bestimmte Lösung für die gegebenen Anfangsbedingungen (Lösung des Cauchy-Problems).

Definition. Integralkurve heißt der Graph y = (x) der Lösung einer Differentialgleichung auf der XOY-Ebene.
Definition. Durch besonderen Beschluss einer Differentialgleichung ist eine solche Lösung in allen Punkten, deren Cauchy-Eindeutigkeitsbedingung genannt wird (vgl. Satz von Cauchy.) nicht erfüllt ist, d.h. In der Umgebung eines Punktes (x, y) gibt es mindestens zwei Integralkurven.
Spezielle Lösungen hängen nicht von der Konstanten C ab.
Aus der allgemeinen Lösung können für keinen Wert der Konstante C spezielle Lösungen erhalten werden. Wenn wir eine Familie von Integralkurven einer Differentialgleichung konstruieren, wird die spezielle Lösung durch eine Linie dargestellt, die an jedem Punkt mindestens eine Integralkurve berührt .
Beachten Sie, dass nicht jede Differentialgleichung spezielle Lösungen hat.
Beispiel. Finden Sie die allgemeine Lösung der Differentialgleichung:  Finden Sie eine spezielle Lösung, falls vorhanden.
Finden Sie eine spezielle Lösung, falls vorhanden.






Auch diese Differentialgleichung hat eine spezielle Lösung bei= 0. Diese Lösung kann nicht aus der allgemeinen Lösung erhalten werden, aber wenn wir sie in die ursprüngliche Gleichung einsetzen, erhalten wir eine Identität. Die Meinung, dass die Lösung j = 0 kann aus der allgemeinen Lösung mit erhalten werden MIT 1 = 0 falsch, weil C 1 = e C 0.
Erinnern wir uns an die Aufgabe, vor der wir bei der Suche nach bestimmten Integralen standen:
oder dy = f(x)dx. Ihre Lösung:
![]()
und es kommt aufs Rechnen an unbestimmtes Integral. In der Praxis kommt es häufiger vor schwierige Aufgabe: Funktion finden j, wenn bekannt ist, dass es eine Relation der Form erfüllt
Diese Beziehung bezieht sich auf die unabhängige Variable X, unbekannte Funktion j und seine Ableitungen bis zur Ordnung N inklusive, heißen .
Eine Differentialgleichung enthält eine Funktion unter dem Vorzeichen von Ableitungen (oder Differentialen) der einen oder anderen Ordnung. Die höchste Ordnung heißt Ordnung (9.1) .
![]() - erste Bestellung,
- erste Bestellung,
Zweite Bestellung
![]() - fünfte Ordnung usw.
- fünfte Ordnung usw.
Die Funktion, die eine gegebene Differentialgleichung erfüllt, wird ihre Lösung genannt , oder Integral . Es zu lösen bedeutet, alle seine Lösungen zu finden. Wenn für die gewünschte Funktion j Wenn es uns gelungen ist, eine Formel zu erhalten, die alle Lösungen angibt, dann sagen wir, dass wir ihre allgemeine Lösung gefunden haben , oder allgemeines Integral .
Gemeinsame Entscheidung
enthält N beliebige Konstanten ![]() und sieht so aus
und sieht so aus
Wenn eine Beziehung erhalten wird, die sich bezieht x, y Und N beliebige Konstanten, in einer Form, die in Bezug auf nicht zulässig ist j -
dann heißt eine solche Beziehung das allgemeine Integral der Gleichung (9.1).
Cauchy-Problem
Jede spezifische Lösung, d. h. jede spezifische Funktion, die eine gegebene Differentialgleichung erfüllt und nicht von beliebigen Konstanten abhängt, wird als besondere Lösung bezeichnet , oder ein partielles Integral. Um aus allgemeinen Lösungen (Integrale) bestimmte Lösungen zu erhalten, müssen den Konstanten bestimmte Zahlenwerte zugewiesen werden.
Der Graph einer bestimmten Lösung wird als Integralkurve bezeichnet. Die allgemeine Lösung, die alle Teillösungen enthält, ist eine Familie von Integralkurven. Bei einer Gleichung erster Ordnung hängt diese Familie von einer beliebigen Konstante für die Gleichung ab N-te Bestellung - von N beliebige Konstanten.
Das Cauchy-Problem besteht darin, eine bestimmte Lösung für die Gleichung zu finden N-te Ordnung, befriedigend N Anfangsbedingungen:
durch die n Konstanten c 1, c 2,..., c n bestimmt werden.
Differentialgleichungen 1. Ordnung
Für eine Differentialgleichung 1. Ordnung, die bezüglich der Ableitung ungelöst ist, hat sie die Form
![]()
oder für relativ erlaubt
![]()
Beispiel 3.46. Finden Sie die allgemeine Lösung der Gleichung
Lösung. Integrieren, verstehen wir
wobei C eine beliebige Konstante ist. Wenn wir C bestimmte Zahlenwerte zuweisen, erhalten wir bestimmte Lösungen, zum Beispiel:

Beispiel 3.47. Betrachten Sie eine Erhöhung des bei der Bank eingezahlten Geldbetrags vorbehaltlich der Rückstellung von 100 R Zinseszins pro Jahr. Sei Yo der anfängliche Geldbetrag und Yx der Endbetrag X Jahre. Wenn die Zinsen einmal im Jahr berechnet werden, erhalten wir
![]()
wobei x = 0, 1, 2, 3,.... Wenn die Zinsen zweimal im Jahr berechnet werden, erhalten wir
![]()
wobei x = 0, 1/2, 1, 3/2,.... Bei der Zinsberechnung N einmal im Jahr und wenn x nimmt dann sequentielle Werte 0, 1/n, 2/n, 3/n,... an
![]()

Bezeichnen Sie 1/n = h, dann sieht die vorherige Gleichheit wie folgt aus:

Mit unbegrenzter Vergrößerung N(bei ![]() ) im Limes kommen wir zum Prozess der Steigerung Geldsumme mit laufender Zinsabgrenzung:
) im Limes kommen wir zum Prozess der Steigerung Geldsumme mit laufender Zinsabgrenzung:
Somit ist klar, dass es sich um einen kontinuierlichen Wandel handelt X Das Gesetz der Geldmengenänderung wird durch eine Differentialgleichung 1. Ordnung ausgedrückt. Wobei Y x eine unbekannte Funktion ist, X- unabhängige Variable, R- konstant. Lass uns entscheiden gegebene Gleichung, dazu schreiben wir es wie folgt um:
Wo ![]() , oder
, oder ![]() , wobei P e C bezeichnet.
, wobei P e C bezeichnet.
Aus den Anfangsbedingungen Y(0) = Yo ergibt sich P: Yo = Pe o, woraus Yo = P. Daher hat die Lösung die Form:
Betrachten wir das zweite wirtschaftliche Problem. Makroökonomische Modelle werden auch durch lineare Differentialgleichungen 1. Ordnung beschrieben, die Veränderungen des Einkommens oder Outputs Y als Funktionen der Zeit beschreiben.
Beispiel 3.48. Das Volkseinkommen Y soll proportional zu seinem Wert wachsen:
und das Defizit der Staatsausgaben sei mit dem Proportionalitätskoeffizienten direkt proportional zum Einkommen Y Q. Ein Ausgabendefizit führt zu einem Anstieg der Staatsverschuldung D:
Anfangsbedingungen Y = Yo und D = Do bei t = 0. Aus der ersten Gleichung Y= Yoe kt. Wenn wir Y ersetzen, erhalten wir dD/dt = qYoe kt . Die allgemeine Lösung hat die Form
D = (q/ k) Yoe kt +С, wobei С = const, die aus den Anfangsbedingungen bestimmt wird. Wenn wir die Anfangsbedingungen ersetzen, erhalten wir Do = (q/ k)Yo + C. Also schließlich:
D = Do +(q/ k)Yo (e kt -1),
Dies zeigt, dass die Staatsverschuldung mit der gleichen relativen Rate steigt k, das gleiche wie das Nationaleinkommen.
Betrachten wir die einfachsten Differentialgleichungen N Ordnung, das sind Gleichungen der Form
Seine allgemeine Lösung kann mit erhalten werden N mal Integrationen.
Beispiel 3.49. Betrachten Sie das Beispiel y „““ = cos x.
Lösung. Integrieren, finden wir

Die allgemeine Lösung hat die Form
Lineare Differentialgleichungen
In Wirtschaft tolle Anwendung haben, überlegen Sie, solche Gleichungen zu lösen. Wenn (9.1) die Form hat:
dann heißt es linear, wobei ðo(x), ð1(x),..., ðn(x), f(x) gegebene Funktionen sind. Wenn f(x) = 0, dann heißt (9.2) homogen, andernfalls heißt es inhomogen. Die allgemeine Lösung der Gleichung (9.2) ist gleich der Summe aller ihrer speziellen Lösungen y(x) und die allgemeine Lösung der dazugehörigen homogenen Gleichung:
Wenn die Koeffizienten ð o (x), ð 1 (x),..., ð n (x) konstant sind, dann (9.2)
(9.4) heißt eine lineare Differentialgleichung mit konstanten Ordnungskoeffizienten N .
Denn (9.4) hat die Form:
Ohne Beschränkung der Allgemeinheit können wir p o = 1 setzen und (9.5) in die Form schreiben
Wir suchen nach einer Lösung (9.6) in der Form y = e kx, wobei k eine Konstante ist. Wir haben: ; y " = ke kx , y "" = k 2 e kx , ..., y (n) = kne kx . Wenn wir die resultierenden Ausdrücke in (9.6) einsetzen, erhalten wir:
(9.7) ist eine algebraische Gleichung, ihre Unbekannte ist k, es heißt charakteristisch. Die charakteristische Gleichung hat Grad N Und N Wurzeln, unter denen es sowohl vielfältig als auch komplex sein kann. Dann seien k 1 , k 2 ,..., k n real und eindeutig ![]() - besondere Lösungen (9.7) und allgemeine
- besondere Lösungen (9.7) und allgemeine
Betrachten Sie eine lineare homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten:
Seine charakteristische Gleichung hat die Form
![]() (9.9)
(9.9)
seine Diskriminante D = p 2 - 4q, je nach Vorzeichen von D sind drei Fälle möglich.
1. Wenn D>0, dann sind die Wurzeln k 1 und k 2 (9.9) reell und unterschiedlich, und die allgemeine Lösung hat die Form:
Lösung. Charakteristische Gleichung: k 2 + 9 = 0, daher k = ± 3i, a = 0, b = 3, die allgemeine Lösung hat die Form:
y = C 1 cos 3x + C 2 sin 3x.
Lineare Differentialgleichungen 2. Ordnung werden bei der Untersuchung eines webbasierten Wirtschaftsmodells mit Warenbeständen verwendet, bei dem die Preisänderungsrate P von der Größe des Lagerbestands abhängt (siehe Abschnitt 10). Falls Angebot und Nachfrage stimmen lineare Funktionen Preise, das heißt
a ist eine Konstante, die die Reaktionsgeschwindigkeit bestimmt, dann wird der Prozess der Preisänderung durch die Differentialgleichung beschrieben:

Für eine bestimmte Lösung können wir eine Konstante annehmen
sinnvoller Gleichgewichtspreis. Abweichung ![]() erfüllt die homogene Gleichung
erfüllt die homogene Gleichung
 (9.10)
(9.10)
Die charakteristische Gleichung lautet wie folgt:
![]()
Falls der Begriff positiv ist. Bezeichnen wir ![]() . Die Wurzeln der charakteristischen Gleichung k 1,2 = ± i w, daher hat die allgemeine Lösung (9.10) die Form:
. Die Wurzeln der charakteristischen Gleichung k 1,2 = ± i w, daher hat die allgemeine Lösung (9.10) die Form:
![]()
wobei C und beliebige Konstanten sind, sie werden aus den Anfangsbedingungen bestimmt. Wir haben das Gesetz der Preisänderung im Laufe der Zeit erhalten:
![]()


Bildungseinrichtung „Belarussischer Staat“.
Agrarakademie"
Abteilung für Höhere Mathematik
DIFFERENZGLEICHUNGEN ERSTER ORDNUNG
Vorlesungsskript für Studierende der Buchhaltung
Fernunterricht (NISPO)
Gorki, 2013
Differentialgleichungen erster Ordnung
Das Konzept einer Differentialgleichung. Allgemeine und besondere Lösungen
Bei der Untersuchung verschiedener Phänomene ist es oft nicht möglich, ein Gesetz zu finden, das die unabhängige Variable und die gewünschte Funktion direkt verbindet, aber es ist möglich, einen Zusammenhang zwischen der gewünschten Funktion und ihren Ableitungen herzustellen.
Die Beziehung zwischen der unabhängigen Variablen, der gewünschten Funktion und ihren Ableitungen wird aufgerufen Differentialgleichung :
Hier X- unabhängige Variable, j– die gewünschte Funktion,  - Ableitungen der gewünschten Funktion. In diesem Fall muss die Beziehung (1) mindestens eine Ableitung haben.
- Ableitungen der gewünschten Funktion. In diesem Fall muss die Beziehung (1) mindestens eine Ableitung haben.
Die Ordnung der Differentialgleichung wird als Ordnung der höchsten in der Gleichung enthaltenen Ableitung bezeichnet.
Betrachten Sie die Differentialgleichung
 .
(2)
.
(2)
Da diese Gleichung nur eine Ableitung erster Ordnung enthält, heißt sie ist eine Differentialgleichung erster Ordnung.
Wenn Gleichung (2) nach der Ableitung aufgelöst und in die Form geschrieben werden kann
 ,
(3)
,
(3)
dann heißt eine solche Gleichung in Normalform eine Differentialgleichung erster Ordnung.
In vielen Fällen empfiehlt es sich, eine Gleichung der Form zu betrachten
Was heisst eine in Differentialform geschriebene Differentialgleichung erster Ordnung.
Als  , dann kann Gleichung (3) in der Form geschrieben werden
, dann kann Gleichung (3) in der Form geschrieben werden  oder
oder  , wo wir zählen können
, wo wir zählen können  Und
Und  . Dies bedeutet, dass Gleichung (3) in Gleichung (4) umgewandelt wird.
. Dies bedeutet, dass Gleichung (3) in Gleichung (4) umgewandelt wird.
Schreiben wir Gleichung (4) in das Formular  . Dann
. Dann  ,
, ,
, , wo wir zählen können
, wo wir zählen können  , d.h. Man erhält eine Gleichung der Form (3). Somit sind die Gleichungen (3) und (4) äquivalent.
, d.h. Man erhält eine Gleichung der Form (3). Somit sind die Gleichungen (3) und (4) äquivalent.
Lösen einer Differentialgleichung
(2) oder (3) heißt jede Funktion  , was es beim Einsetzen in Gleichung (2) oder (3) in eine Identität umwandelt:
, was es beim Einsetzen in Gleichung (2) oder (3) in eine Identität umwandelt:
 oder
oder  .
.
Der Prozess, alle Lösungen einer Differentialgleichung zu finden, wird als it bezeichnet Integration
und der Lösungsgraph  Differentialgleichung heißt Integralkurve
diese Gleichung.
Differentialgleichung heißt Integralkurve
diese Gleichung.
Wenn die Lösung der Differentialgleichung implizit erhalten wird  , dann heißt es Integral
dieser Differentialgleichung.
, dann heißt es Integral
dieser Differentialgleichung.
Allgemeine Lösung
einer Differentialgleichung erster Ordnung ist eine Familie von Funktionen der Form  , abhängig von einer beliebigen Konstante MIT, von denen jede eine Lösung einer gegebenen Differentialgleichung für jeden zulässigen Wert einer beliebigen Konstante ist MIT. Somit hat die Differentialgleichung unendlich viele Lösungen.
, abhängig von einer beliebigen Konstante MIT, von denen jede eine Lösung einer gegebenen Differentialgleichung für jeden zulässigen Wert einer beliebigen Konstante ist MIT. Somit hat die Differentialgleichung unendlich viele Lösungen.
Private Entscheidung
Eine Differentialgleichung ist eine Lösung, die aus der allgemeinen Lösungsformel für einen bestimmten Wert einer beliebigen Konstante erhalten wird MIT, einschließlich  .
.
Cauchy-Problem und seine geometrische Interpretation
Gleichung (2) hat unendlich viele Lösungen. Um eine Lösung aus dieser Menge, die als privat bezeichnet wird, auszuwählen, müssen Sie einige zusätzliche Bedingungen festlegen.
Das Problem, unter gegebenen Bedingungen eine bestimmte Lösung für Gleichung (2) zu finden, heißt Cauchy-Problem . Dieses Problem ist eines der wichtigsten in der Theorie der Differentialgleichungen.
Das Cauchy-Problem lässt sich wie folgt formulieren: Finden Sie unter allen Lösungen der Gleichung (2) eine solche Lösung
 , in der die Funktion
, in der die Funktion  nimmt den angegebenen numerischen Wert an
nimmt den angegebenen numerischen Wert an  , wenn die unabhängige Variable
X
nimmt den angegebenen numerischen Wert an
, wenn die unabhängige Variable
X
nimmt den angegebenen numerischen Wert an  , d.h.
, d.h.
 ,
,
 ,
(5)
,
(5)
Wo D– Definitionsbereich der Funktion  .
.
Bedeutung  angerufen der Anfangswert der Funktion
, A
angerufen der Anfangswert der Funktion
, A
 – Anfangswert der unabhängigen Variablen
. Bedingung (5) wird aufgerufen ausgangsbedingung
oder Cauchy-Zustand
.
– Anfangswert der unabhängigen Variablen
. Bedingung (5) wird aufgerufen ausgangsbedingung
oder Cauchy-Zustand
.
Aus geometrischer Sicht lässt sich das Cauchy-Problem für die Differentialgleichung (2) wie folgt formulieren: Wählen Sie aus der Menge der Integralkurven der Gleichung (2) diejenige aus, die durchgeht angegebenen Punkt
 .
.
Differentialgleichungen mit separierbaren Variablen
Eine der einfachsten Arten von Differentialgleichungen ist eine Differentialgleichung erster Ordnung, die nicht die gewünschte Funktion enthält:
 .
(6)
.
(6)
Bedenkt, dass  , schreiben wir die Gleichung in das Formular
, schreiben wir die Gleichung in das Formular  oder
oder  . Wenn wir beide Seiten der letzten Gleichung integrieren, erhalten wir:
. Wenn wir beide Seiten der letzten Gleichung integrieren, erhalten wir:  oder
oder
 .
(7)
.
(7)
Somit ist (7) eine allgemeine Lösung für Gleichung (6).
Beispiel 1
. Finden Sie die allgemeine Lösung der Differentialgleichung  .
.
Lösung
. Schreiben wir die Gleichung in das Formular  oder
oder  . Integrieren wir beide Seiten der resultierenden Gleichung:
. Integrieren wir beide Seiten der resultierenden Gleichung:  ,
, . Wir werden es endlich aufschreiben
. Wir werden es endlich aufschreiben  .
.
Beispiel 2
. Finden Sie die Lösung der Gleichung  angesichts dessen
angesichts dessen  .
.
Lösung
. Lassen Sie uns eine allgemeine Lösung für die Gleichung finden:  ,
, ,
, ,
, . Nach Bedingung
. Nach Bedingung  ,
, . Setzen wir in die allgemeine Lösung ein:
. Setzen wir in die allgemeine Lösung ein:  oder
oder  . Wir setzen den gefundenen Wert einer beliebigen Konstante in die Formel für die allgemeine Lösung ein:
. Wir setzen den gefundenen Wert einer beliebigen Konstante in die Formel für die allgemeine Lösung ein:  . Dies ist eine bestimmte Lösung der Differentialgleichung, die die gegebene Bedingung erfüllt.
. Dies ist eine bestimmte Lösung der Differentialgleichung, die die gegebene Bedingung erfüllt.
Die gleichung
 (8)
(8)
Angerufen eine Differentialgleichung erster Ordnung, die keine unabhängige Variable enthält
. Schreiben wir es in das Formular  oder
oder  . Integrieren wir beide Seiten der letzten Gleichung:
. Integrieren wir beide Seiten der letzten Gleichung:  oder
oder  - allgemeine Lösung von Gleichung (8).
- allgemeine Lösung von Gleichung (8).
Beispiel
. Finden Sie die allgemeine Lösung der Gleichung  .
.
Lösung
. Schreiben wir diese Gleichung in der Form:  oder
oder  . Dann
. Dann  ,
, ,
, ,
, . Auf diese Weise,
. Auf diese Weise,  ist die allgemeine Lösung dieser Gleichung.
ist die allgemeine Lösung dieser Gleichung.
Gleichung des Formulars
 (9)
(9)
Integriert unter Verwendung der Variablentrennung. Dazu schreiben wir die Gleichung in das Formular  , und dann bringen wir es mithilfe der Multiplikations- und Divisionsoperationen in eine solche Form, dass ein Teil nur die Funktion von enthält X und Differential dx, und im zweiten Teil – die Funktion von bei und Differential dy. Dazu müssen beide Seiten der Gleichung mit multipliziert werden dx und dividiere durch
, und dann bringen wir es mithilfe der Multiplikations- und Divisionsoperationen in eine solche Form, dass ein Teil nur die Funktion von enthält X und Differential dx, und im zweiten Teil – die Funktion von bei und Differential dy. Dazu müssen beide Seiten der Gleichung mit multipliziert werden dx und dividiere durch  . Als Ergebnis erhalten wir die Gleichung
. Als Ergebnis erhalten wir die Gleichung
 ,
(10)
,
(10)
in dem die Variablen X Und bei getrennt. Integrieren wir beide Seiten der Gleichung (10):  . Die resultierende Beziehung ist das allgemeine Integral von Gleichung (9).
. Die resultierende Beziehung ist das allgemeine Integral von Gleichung (9).
Beispiel 3
. Gleichung integrieren  .
.
Lösung
. Lassen Sie uns die Gleichung umwandeln und die Variablen trennen:  ,
, . Integrieren wir:
. Integrieren wir:  ,
, oder ist das allgemeine Integral dieser Gleichung.
oder ist das allgemeine Integral dieser Gleichung.  .
.
Die Gleichung sei in der Form gegeben
Diese Gleichung heißt Differentialgleichung erster Ordnung mit separierbaren Variablen in symmetrischer Form.
Um die Variablen zu trennen, müssen Sie beide Seiten der Gleichung durch dividieren  :
:
 .
(12)
.
(12)
Die resultierende Gleichung heißt getrennte Differentialgleichung . Integrieren wir Gleichung (12):
 .
. (13)
(13)
Beziehung (13) ist das allgemeine Integral der Differentialgleichung (11).
Beispiel 4 . Integrieren Sie eine Differentialgleichung.
Lösung . Schreiben wir die Gleichung in das Formular
und dividiere beide Teile durch  ,
, . Die resultierende Gleichung:
. Die resultierende Gleichung:  ist eine Gleichung mit getrennten Variablen. Integrieren wir es:
ist eine Gleichung mit getrennten Variablen. Integrieren wir es:
 ,
,
 ,
,
 ,
,
 . Die letzte Gleichung ist das allgemeine Integral dieser Differentialgleichung.
. Die letzte Gleichung ist das allgemeine Integral dieser Differentialgleichung.
Beispiel 5
. Finden Sie eine bestimmte Lösung der Differentialgleichung  , die Bedingung erfüllend
, die Bedingung erfüllend  .
.
Lösung
. Bedenkt, dass  , schreiben wir die Gleichung in das Formular
, schreiben wir die Gleichung in das Formular  oder
oder  . Trennen wir die Variablen:
. Trennen wir die Variablen:  . Integrieren wir diese Gleichung:
. Integrieren wir diese Gleichung:  ,
, ,
, . Die resultierende Beziehung ist das allgemeine Integral dieser Gleichung. Nach Bedingung
. Die resultierende Beziehung ist das allgemeine Integral dieser Gleichung. Nach Bedingung  . Setzen wir es in das allgemeine Integral ein und finden wir es MIT:
. Setzen wir es in das allgemeine Integral ein und finden wir es MIT:
 ,MIT=1. Dann der Ausdruck
,MIT=1. Dann der Ausdruck  ist eine Teillösung einer gegebenen Differentialgleichung, geschrieben als Teilintegral.
ist eine Teillösung einer gegebenen Differentialgleichung, geschrieben als Teilintegral.
Lineare Differentialgleichungen erster Ordnung
Die gleichung
 (14)
(14)
angerufen lineare Differentialgleichung erster Ordnung
. Unbekannte Funktion  und seine Ableitung gehen linear in diese Gleichung ein, und die Funktionen
und seine Ableitung gehen linear in diese Gleichung ein, und die Funktionen  Und
Und  kontinuierlich.
kontinuierlich.
Wenn  , dann die Gleichung
, dann die Gleichung
 (15)
(15)
angerufen linear homogen
. Wenn  , dann wird Gleichung (14) aufgerufen linear inhomogen
.
, dann wird Gleichung (14) aufgerufen linear inhomogen
.
Um eine Lösung für Gleichung (14) zu finden, verwendet man normalerweise Substitutionsmethode (Bernoulli) , dessen Kern wie folgt ist.
Wir suchen nach einer Lösung für Gleichung (14) in Form eines Produkts zweier Funktionen
 ,
(16)
,
(16)
Wo  Und
Und  - manche kontinuierliche Funktionen. Lasst uns ersetzen
- manche kontinuierliche Funktionen. Lasst uns ersetzen  und Ableitung
und Ableitung  in Gleichung (14):
in Gleichung (14):
Funktion v Wir werden so auswählen, dass die Bedingung erfüllt ist  . Dann
. Dann  . Um eine Lösung für Gleichung (14) zu finden, ist es daher notwendig, das System der Differentialgleichungen zu lösen
. Um eine Lösung für Gleichung (14) zu finden, ist es daher notwendig, das System der Differentialgleichungen zu lösen

Die erste Gleichung des Systems ist eine lineare homogene Gleichung und kann durch die Methode der Variablentrennung gelöst werden:  ,
, ,
, ,
, ,
, . Als eine Funktion
. Als eine Funktion  Sie können eine der Teillösungen der homogenen Gleichung nehmen, d.h. bei MIT=1:
Sie können eine der Teillösungen der homogenen Gleichung nehmen, d.h. bei MIT=1:
 . Setzen wir in die zweite Gleichung des Systems ein:
. Setzen wir in die zweite Gleichung des Systems ein:  oder
oder  .Dann
.Dann  . Somit hat die allgemeine Lösung einer linearen Differentialgleichung erster Ordnung die Form
. Somit hat die allgemeine Lösung einer linearen Differentialgleichung erster Ordnung die Form  .
.
Beispiel 6
. Löse die Gleichung  .
.
Lösung
. Wir werden nach einer Lösung für die Gleichung im Formular suchen  . Dann
. Dann  . Setzen wir in die Gleichung ein:
. Setzen wir in die Gleichung ein:
 oder
oder  . Funktion v Wählen Sie so, dass die Gleichheit gilt
. Funktion v Wählen Sie so, dass die Gleichheit gilt  . Dann
. Dann  . Lösen wir die erste dieser Gleichungen mit der Methode der Variablentrennung:
. Lösen wir die erste dieser Gleichungen mit der Methode der Variablentrennung:  ,
, ,
, ,
, ,
, . Funktion v Setzen wir in die zweite Gleichung ein:
. Funktion v Setzen wir in die zweite Gleichung ein:  ,
, ,
, ,
, . Die allgemeine Lösung dieser Gleichung lautet
. Die allgemeine Lösung dieser Gleichung lautet  .
.
Fragen zur Selbstkontrolle des Wissens
Was ist eine Differentialgleichung?
Welche Ordnung hat eine Differentialgleichung?
Welche Differentialgleichung heißt Differentialgleichung erster Ordnung?
Wie wird eine Differentialgleichung erster Ordnung in Differentialform geschrieben?
Was ist die Lösung einer Differentialgleichung?
Was ist eine Integralkurve?
Was ist die allgemeine Lösung einer Differentialgleichung erster Ordnung?
Was nennt man Teillösung einer Differentialgleichung?
Wie wird das Cauchy-Problem für eine Differentialgleichung erster Ordnung formuliert?
Was ist die geometrische Interpretation des Cauchy-Problems?
Wie schreibe ich eine Differentialgleichung mit separierbaren Variablen in symmetrischer Form?
Welche Gleichung wird als lineare Differentialgleichung erster Ordnung bezeichnet?
Mit welcher Methode kann eine lineare Differentialgleichung erster Ordnung gelöst werden und was ist das Wesentliche dieser Methode?
Aufgaben für selbständiges Arbeiten
Lösen Sie Differentialgleichungen mit trennbaren Variablen:
A)  ; B)
; B)  ;
;
V)  ; G)
; G)  .
.
2. Lösen Sie lineare Differentialgleichungen erster Ordnung:
A)  ; B)
; B)  ; V)
; V)  ;
;
G)  ; D)
; D)  .
.
I. Gewöhnliche Differentialgleichungen
1.1. Grundlegende Konzepte und Definitionen
Eine Differentialgleichung ist eine Gleichung, die eine unabhängige Variable in Beziehung setzt X, die erforderliche Funktion j und seine Ableitungen oder Differentiale.
Symbolisch wird die Differentialgleichung wie folgt geschrieben:
F(x,y,y")=0, F(x,y,y")=0, F(x,y,y",y",.., y (n))=0
Eine Differentialgleichung heißt gewöhnlich, wenn die gesuchte Funktion von einer unabhängigen Variablen abhängt.
Lösen einer Differentialgleichung heißt eine Funktion, die diese Gleichung in eine Identität umwandelt.
Die Ordnung der Differentialgleichung ist die Ordnung der höchsten in dieser Gleichung enthaltenen Ableitung
Beispiele.
1. Betrachten Sie eine Differentialgleichung erster Ordnung
Die Lösung dieser Gleichung ist die Funktion y = 5 ln x. In der Tat, ersetzen y" In die Gleichung erhalten wir die Identität.
Und das bedeutet, dass die Funktion y = 5 ln x– eine Lösung dieser Differentialgleichung ist.
2. Betrachten Sie die Differentialgleichung zweiter Ordnung y" - 5y" +6y = 0. Die Funktion ist die Lösung dieser Gleichung.
Wirklich, .
Wenn wir diese Ausdrücke in die Gleichung einsetzen, erhalten wir: , – Identität.
Und das bedeutet, dass die Funktion die Lösung dieser Differentialgleichung ist.
Integrieren von Differentialgleichungen ist der Prozess, Lösungen für Differentialgleichungen zu finden.
Allgemeine Lösung der Differentialgleichung eine Funktion der Form genannt ![]() , die so viele unabhängige beliebige Konstanten enthält, wie die Ordnung der Gleichung.
, die so viele unabhängige beliebige Konstanten enthält, wie die Ordnung der Gleichung.
Teillösung der Differentialgleichung ist eine Lösung, die aus einer allgemeinen Lösung für verschiedene numerische Werte beliebiger Konstanten erhalten wird. Die Werte beliebiger Konstanten liegen bei bestimmten Anfangswerten des Arguments und der Funktion.
Der Graph einer bestimmten Lösung einer Differentialgleichung heißt Integralkurve.
Beispiele
1. Finden Sie eine bestimmte Lösung für eine Differentialgleichung erster Ordnung
xdx + ydy = 0, Wenn j= 4 bei X = 3.
Lösung. Wenn wir beide Seiten der Gleichung integrieren, erhalten wir
Kommentar. Eine durch Integration erhaltene beliebige Konstante C kann in jeder für weitere Transformationen geeigneten Form dargestellt werden. In diesem Fall ist es unter Berücksichtigung der kanonischen Kreisgleichung zweckmäßig, eine beliebige Konstante C in der Form darzustellen.
![]() - allgemeine Lösung der Differentialgleichung.
- allgemeine Lösung der Differentialgleichung.
Bestimmte Lösung der Gleichung, die die Anfangsbedingungen erfüllt j = 4 bei X = 3 ergibt sich aus der allgemeinen Lösung durch Einsetzen der Anfangsbedingungen in die allgemeine Lösung: 3 2 + 4 2 = C 2 ; C=5.
Wenn wir C=5 in die allgemeine Lösung einsetzen, erhalten wir x 2 +y 2 = 5 2 .
Dies ist eine spezielle Lösung einer Differentialgleichung, die aus einer allgemeinen Lösung unter gegebenen Anfangsbedingungen erhalten wird.
2. Finden Sie die allgemeine Lösung der Differentialgleichung
Die Lösung dieser Gleichung ist eine beliebige Funktion der Form, wobei C eine beliebige Konstante ist. Tatsächlich erhalten wir beim Einsetzen in die Gleichungen: , .
Folglich hat diese Differentialgleichung unendlich viele Lösungen, da für unterschiedliche Werte der Konstante C die Gleichheit unterschiedliche Lösungen der Gleichung bestimmt.
Durch direkte Substitution können Sie beispielsweise überprüfen, ob die Funktionen funktionieren ![]() sind Lösungen der Gleichung.
sind Lösungen der Gleichung.
Ein Problem, bei dem Sie eine bestimmte Lösung für die Gleichung finden müssen y" = f(x,y) Erfüllung der Anfangsbedingung y(x 0) = y 0, wird Cauchy-Problem genannt.
Lösung der Gleichung y" = f(x,y), die Anfangsbedingung erfüllend, y(x 0) = y 0, wird als Lösung des Cauchy-Problems bezeichnet.
Die Lösung des Cauchy-Problems hat eine einfache geometrische Bedeutung. Tatsächlich, nach diesen Definitionen, um das Cauchy-Problem zu lösen y" = f(x,y) angesichts dessen y(x 0) = y 0 bedeutet, die Integralkurve der Gleichung zu finden y" = f(x,y) die durch einen gegebenen Punkt geht M 0 (x 0,y 0).
II. Differentialgleichungen erster Ordnung
2.1. Grundlegendes Konzept
Eine Differentialgleichung erster Ordnung ist eine Gleichung der Form F(x,y,y") = 0.
Eine Differentialgleichung erster Ordnung umfasst die erste Ableitung und keine Ableitungen höherer Ordnung.
Die gleichung y" = f(x,y) heißt eine nach der Ableitung gelöste Gleichung erster Ordnung.
Die allgemeine Lösung einer Differentialgleichung erster Ordnung ist eine Funktion der Form, die eine beliebige Konstante enthält.
Beispiel. Betrachten Sie eine Differentialgleichung erster Ordnung.
Die Lösung dieser Gleichung ist die Funktion.
Tatsächlich erhalten wir, wenn wir diese Gleichung durch ihren Wert ersetzen

![]() also 3x=3x
also 3x=3x
Daher ist die Funktion eine allgemeine Lösung der Gleichung für jede Konstante C.
Finden Sie eine bestimmte Lösung dieser Gleichung, die die Anfangsbedingung erfüllt y(1)=1 Anfangsbedingungen ersetzen x = 1, y =1 In die allgemeine Lösung der Gleichung kommen wir von wo C=0.
Somit erhalten wir eine bestimmte Lösung aus der allgemeinen Lösung, indem wir den resultierenden Wert in diese Gleichung einsetzen C=0– private Lösung.
2.2. Differentialgleichungen mit separierbaren Variablen
Eine Differentialgleichung mit separierbaren Variablen ist eine Gleichung der Form: y"=f(x)g(y) oder durch Differentiale, wo f(x) Und g(y)– spezifizierte Funktionen.
Für diejenigen j, für die die Gleichung y"=f(x)g(y) ist äquivalent zur Gleichung, ![]() in dem die Variable j ist nur auf der linken Seite vorhanden und die Variable x ist nur auf der rechten Seite vorhanden. Sie sagen: „In Gl. y"=f(x)g(y Trennen wir die Variablen.“
in dem die Variable j ist nur auf der linken Seite vorhanden und die Variable x ist nur auf der rechten Seite vorhanden. Sie sagen: „In Gl. y"=f(x)g(y Trennen wir die Variablen.“
Gleichung des Formulars ![]() wird als Gleichung mit getrennten Variablen bezeichnet.
wird als Gleichung mit getrennten Variablen bezeichnet.
Integration beider Seiten der Gleichung ![]() Von X, wir bekommen G(y) = F(x) + C ist die allgemeine Lösung der Gleichung, wobei G(y) Und F(x)– einige Stammfunktionen jeweils von Funktionen und f(x), C Willkürliche Konstante.
Von X, wir bekommen G(y) = F(x) + C ist die allgemeine Lösung der Gleichung, wobei G(y) Und F(x)– einige Stammfunktionen jeweils von Funktionen und f(x), C Willkürliche Konstante.
Algorithmus zur Lösung einer Differentialgleichung erster Ordnung mit separierbaren Variablen
Beispiel 1
Löse die Gleichung y" = xy
Lösung. Ableitung einer Funktion y" Ersetzen Sie es durch
Trennen wir die Variablen
Integrieren wir beide Seiten der Gleichheit:

Beispiel 2
2yy" = 1- 3x 2, Wenn y 0 = 3 bei x 0 = 1
Dies ist eine Gleichung mit getrennten Variablen. Stellen wir es uns in Differentialen vor. Dazu schreiben wir diese Gleichung in der Form um ![]() Von hier
Von hier ![]()
Wir finden, dass wir beide Seiten der letzten Gleichheit integrieren
Ersetzen der Anfangswerte x 0 = 1, y 0 = 3 wir werden finden MIT 9=1-1+C, d.h. C = 9.
Daher wird das erforderliche Teilintegral sein ![]() oder
oder ![]()
Beispiel 3
Schreiben Sie eine Gleichung für eine Kurve, die durch einen Punkt verläuft M(2;-3) und eine Tangente mit einem Winkelkoeffizienten haben
Lösung. Je nach Zustand
Dies ist eine Gleichung mit trennbaren Variablen. Durch Division der Variablen erhalten wir: ![]()
Wenn wir beide Seiten der Gleichung integrieren, erhalten wir: 
Unter Verwendung der Anfangsbedingungen x = 2 Und y = - 3 wir werden finden C:

Daher hat die erforderliche Gleichung die Form ![]()
2.3. Lineare Differentialgleichungen erster Ordnung
Eine lineare Differentialgleichung erster Ordnung ist eine Gleichung der Form y" = f(x)y + g(x)
Wo f(x) Und g(x)- einige spezifizierte Funktionen.
Wenn g(x)=0 dann heißt die lineare Differentialgleichung homogen und hat die Form: y" = f(x)y
Wenn dann die Gleichung y" = f(x)y + g(x) heißt heterogen.
Allgemeine Lösung einer linearen homogenen Differentialgleichung y" = f(x)y wird durch die Formel gegeben: wo MIT- Willkürliche Konstante.
Insbesondere, wenn C = 0, dann ist die Lösung y = 0 Wenn linear homogene Gleichung sieht aus wie y" = ky Wo k eine Konstante ist, dann hat ihre allgemeine Lösung die Form: .
Allgemeine Lösung einer linearen inhomogenen Differentialgleichung y" = f(x)y + g(x) ergibt sich aus der Formel ![]() ,
,
diese. ist gleich der Summe der allgemeinen Lösung der entsprechenden linearen homogenen Gleichung und der besonderen Lösung dieser Gleichung.
Für eine lineare inhomogene Gleichung der Form y" = kx + b,
Wo k Und B- Einige Zahlen und eine bestimmte Lösung sind eine konstante Funktion. Daher hat die allgemeine Lösung die Form.
Beispiel. Löse die Gleichung y" + 2y +3 = 0
Lösung. Stellen wir die Gleichung im Formular dar y" = -2y - 3 Wo k = -2, b= -3 Die allgemeine Lösung ergibt sich aus der Formel.
Daher ist C eine beliebige Konstante.
2.4. Lösung linearer Differentialgleichungen erster Ordnung nach der Bernoulli-Methode
Finden einer allgemeinen Lösung für eine lineare Differentialgleichung erster Ordnung y" = f(x)y + g(x) reduziert sich auf die Lösung zweier Differentialgleichungen mit getrennten Variablen mittels Substitution y=uv, Wo u Und v- unbekannte Funktionen von X. Diese Lösungsmethode wird Bernoulli-Methode genannt.
Algorithmus zur Lösung einer linearen Differentialgleichung erster Ordnung
y" = f(x)y + g(x)
1. Geben Sie die Vertretung ein y=uv.
2. Differenzieren Sie diese Gleichheit y" = u"v + uv"
3. Ersatz j Und y" in diese Gleichung: u"v + uv" =f(x)uv + g(x) oder u"v + uv" + f(x)uv = g(x).
4. Gruppieren Sie die Terme der Gleichung so, dass u nimm es aus der Klammer:
5. Suchen Sie aus der Klammer, indem Sie sie mit Null gleichsetzen, die Funktion
Dies ist eine trennbare Gleichung: ![]()
Teilen wir die Variablen und erhalten: ![]()
Wo ![]() .
.
.
.
6. Ersetzen Sie den resultierenden Wert v in die Gleichung ein (aus Schritt 4):
![]()
und finden Sie die Funktion Dies ist eine Gleichung mit trennbaren Variablen:
![]()
7. Schreiben Sie die allgemeine Lösung in das Formular: ![]() , d.h. .
, d.h. .
Beispiel 1
Finden Sie eine bestimmte Lösung der Gleichung y" = -2y +3 = 0 Wenn y =1 bei x = 0
Lösung. Lassen Sie es uns durch Substitution lösen y=uv,.y" = u"v + uv"
Ersetzen j Und y" in diese Gleichung erhalten wir
Indem wir den zweiten und dritten Term auf der linken Seite der Gleichung gruppieren, entfernen wir den gemeinsamen Faktor u außerhalb der Klammern
Wir setzen den Ausdruck in Klammern mit Null gleich und finden nach Lösung der resultierenden Gleichung die Funktion v = v(x)
Wir erhalten eine Gleichung mit getrennten Variablen. Integrieren wir beide Seiten dieser Gleichung: Finden Sie die Funktion v:
![]()
Ersetzen wir den resultierenden Wert v in die Gleichung erhalten wir:
Dies ist eine Gleichung mit getrennten Variablen. Integrieren wir beide Seiten der Gleichung: ![]() Finden wir die Funktion u = u(x,c)
Finden wir die Funktion u = u(x,c) ![]() Lassen Sie uns eine allgemeine Lösung finden:
Lassen Sie uns eine allgemeine Lösung finden: ![]() Finden wir eine bestimmte Lösung der Gleichung, die die Anfangsbedingungen erfüllt y = 1 bei x = 0:
Finden wir eine bestimmte Lösung der Gleichung, die die Anfangsbedingungen erfüllt y = 1 bei x = 0:

III. Differentialgleichungen höherer Ordnung
3.1. Grundlegende Konzepte und Definitionen
Eine Differentialgleichung zweiter Ordnung ist eine Gleichung, die Ableitungen nicht höherer als zweiter Ordnung enthält. Im allgemeinen Fall wird eine Differentialgleichung zweiter Ordnung wie folgt geschrieben: F(x,y,y",y") = 0
Die allgemeine Lösung einer Differentialgleichung zweiter Ordnung ist eine Funktion der Form, die zwei beliebige Konstanten enthält C 1 Und C 2.
Eine besondere Lösung einer Differentialgleichung zweiter Ordnung ist eine Lösung, die aus einer allgemeinen Lösung für bestimmte Werte beliebiger Konstanten erhalten wird C 1 Und C 2.
3.2. Lineare homogene Differentialgleichungen zweiter Ordnung mit konstante Koeffizienten.
Lineare homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten wird als Gleichung der Form bezeichnet y" + py" +qy = 0, Wo P Und Q- konstante Werte.
Algorithmus zur Lösung homogener Differentialgleichungen zweiter Ordnung mit konstanten Koeffizienten
1. Schreiben Sie die Differentialgleichung in der Form: y" + py" +qy = 0.
2. Erstellen Sie die charakteristische Gleichung und bezeichnen Sie sie y" durch r 2, y" durch R, j in 1: r 2 + pr +q = 0
Der Online-Rechner ermöglicht es Ihnen, Differentialgleichungen online zu lösen. Es reicht aus, Ihre Gleichung in das entsprechende Feld einzugeben, die Ableitung der Funktion durch ein Apostroph zu kennzeichnen und auf die Schaltfläche „Gleichung lösen“ zu klicken. Und das auf der Grundlage der beliebten WolframAlpha-Website implementierte System liefert detaillierte Informationen Lösen einer Differentialgleichung absolut frei. Sie können das Cauchy-Problem auch so definieren, dass es aus der gesamten Menge besteht mögliche Lösungen Wählen Sie den Quotienten, der den gegebenen Anfangsbedingungen entspricht. Das Cauchy-Problem wird in einem separaten Feld eingetragen.
Differentialgleichung
Standardmäßig ist die Funktion in der Gleichung j ist eine Funktion einer Variablen X. Sie können jedoch eine eigene Bezeichnung für die Variable angeben; wenn Sie beispielsweise y(t) in die Gleichung schreiben, erkennt der Rechner dies automatisch j Es gibt eine Funktion aus einer Variablen T. Mit Hilfe eines Taschenrechners können Sie Differentialgleichungen lösen beliebiger Komplexität und Art: homogen und inhomogen, linear oder nichtlinear, erster Ordnung oder zweiter und höherer Ordnung, Gleichungen mit trennbaren oder nicht trennbaren Variablen usw. Lösungsunterschied. Gleichung wird in analytischer Form gegeben, hat detaillierte Beschreibung. Differentialgleichungen sind in der Physik und Mathematik sehr verbreitet. Ohne deren Berechnung ist es unmöglich, viele Probleme (insbesondere in der mathematischen Physik) zu lösen.
Einer der Schritte zur Lösung von Differentialgleichungen ist die Integration von Funktionen. Es gibt Standardmethoden zur Lösung von Differentialgleichungen. Es ist notwendig, die Gleichungen auf eine Form mit separierbaren Variablen y und x zu reduzieren und die separierten Funktionen separat zu integrieren. Dazu muss manchmal ein bestimmter Austausch vorgenommen werden.