Exponentialgleichungen online mit detaillierten Lösungen lösen. Gleichungen online
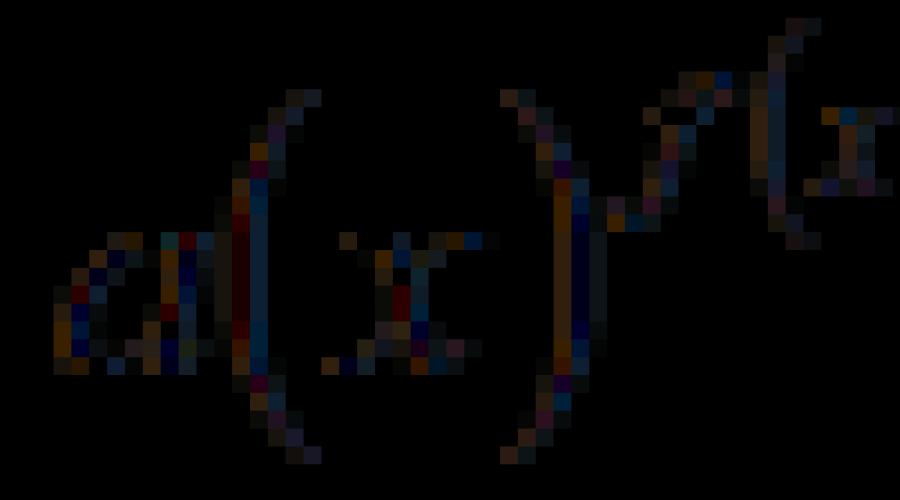
Lesen Sie auch
Dies ist die Bezeichnung für Gleichungen der Form, bei denen die Unbekannte sowohl im Exponenten als auch in der Basis der Potenz enthalten ist.
Sie können einen völlig klaren Algorithmus zum Lösen einer Gleichung der Form angeben. Dazu müssen Sie darauf achten, wann Oh) ungleich Null, Eins und minus Eins, Gradgleichheit mit den gleichen Basen (sei es positiv oder negativ) ist nur möglich, wenn die Exponenten gleich sind. Das heißt, alle Wurzeln der Gleichung sind die Wurzeln der Gleichung f(x) = g(x) Die umgekehrte Aussage ist nicht wahr, wann Oh)< 0 und Bruchwerte f(x) Und g(x) Ausdrücke Oh) f(x) Und
Oh) g(x) verlieren ihre Bedeutung. Das heißt, beim Wechsel von nach f(x) = g(x)(für und Fremdwurzeln können auftreten, die durch Vergleich mit der ursprünglichen Gleichung ausgeschlossen werden müssen. Und Fälle a = 0, a = 1, a = -1 müssen gesondert betrachtet werden.
So für komplette Lösung Gleichungen betrachten wir die Fälle:
a(x) = O f(x) Und g(x) werden positive Zahlen sein, dann ist dies die Lösung. Ansonsten nein
a(x) = 1. Die Wurzeln dieser Gleichung sind auch die Wurzeln der ursprünglichen Gleichung.
a(x) = -1. Wenn für einen Wert von x, der diese Gleichung erfüllt, f(x) Und g(x) Sind ganze Zahlen gleicher Parität (entweder beide gerade oder beide ungerade), dann ist dies die Lösung. Ansonsten nein
Wann und wir lösen die Gleichung f(x)= g(x) und indem wir die erhaltenen Ergebnisse in die ursprüngliche Gleichung einsetzen, schneiden wir die überflüssigen Wurzeln ab.
Beispiele für die Lösung von Exponentialpotenzgleichungen.
Beispiel Nr. 1.
1) x - 3 = 0, x = 3. weil 3 > 0 und 3 2 > 0, dann ist x 1 = 3 die Lösung.
2) x - 3 = 1, x 2 = 4.
3) x - 3 = -1, x = 2. Beide Indikatoren sind gerade. Diese Lösung ist x 3 = 1.
4) x - 3 ? 0 und x? ± 1. x = x 2, x = 0 oder x = 1. Für x = 0, (-3) 0 = (-3) 0 - diese Lösung ist richtig: x 4 = 0. Für x = 1, (- 2) 1 = (-2) 1 – diese Lösung ist richtig x 5 = 1.
Antwort: 0, 1, 2, 3, 4.
Beispiel Nr. 2.

Per Definition der Arithmetik Quadratwurzel: x - 1 ? 0, x ? 1.
1) x - 1 = 0 oder x = 1, = 0, 0 0 ist keine Lösung.
2) x - 1 = 1 x 1 = 2.
3) x - 1 = -1 x 2 = 0 passt nicht in ODZ.
D = (-2) - 4*1*5 = 4 - 20 = -16 - es gibt keine Wurzeln.
Exponentialgleichungen sind solche, bei denen die Unbekannte im Exponenten enthalten ist. Die einfachste Exponentialgleichung hat die Form: a x = a b, wobei a > 0, a 1, x unbekannt ist.
Die Haupteigenschaften von Potenzen, mit denen Exponentialgleichungen transformiert werden: a>0, b>0.
Bei der Entscheidung Exponentialgleichungen Verwenden Sie auch die folgenden Eigenschaften der Exponentialfunktion: y = a x, a > 0, a1:
Um eine Zahl als Potenz darzustellen, verwenden Sie die grundlegende logarithmische Identität: b = , a > 0, a1, b > 0.
Aufgaben und Tests zum Thema „Exponentialgleichungen“
- Exponentialgleichungen
Lektionen: 4 Aufgaben: 21 Tests: 1
- Exponentialgleichungen - Wichtige Themen zur Überprüfung des Einheitlichen Staatsexamens in Mathematik
Aufgaben: 14
- Systeme exponentieller und logarithmischer Gleichungen - Exponentielle und logarithmische Funktionen Klasse 11
Lektionen: 1 Aufgaben: 15 Tests: 1
- §2.1. Exponentialgleichungen lösen
Lektionen: 1 Aufgaben: 27
- §7 Exponentielle und logarithmische Gleichungen und Ungleichungen - Abschnitt 5. Exponentielle und logarithmische Funktionen, Klasse 10
Lektionen: 1 Aufgaben: 17
Um Exponentialgleichungen erfolgreich zu lösen, müssen Sie die grundlegenden Eigenschaften von Potenzen, Eigenschaften der Exponentialfunktion und die grundlegende logarithmische Identität kennen.
Beim Lösen von Exponentialgleichungen werden im Wesentlichen zwei Methoden verwendet:
- Übergang von der Gleichung a f(x) = a g(x) zur Gleichung f(x) = g(x);
- Einführung neuer Linien.
Beispiele.
1. Gleichungen auf das Einfachste reduziert. Sie werden gelöst, indem beide Seiten der Gleichung auf eine Potenz mit derselben Basis reduziert werden.
3 x = 9 x – 2.
Lösung:
3 x = (3 2) x – 2 ;
3 x = 3 2x – 4 ;
x = 2x –4;
x = 4.
Antwort: 4.
2. Gleichungen, die durch Entfernen des gemeinsamen Faktors aus Klammern gelöst werden.
Lösung:
3 x – 3 x – 2 = 24
3 x – 2 (3 2 – 1) = 24
3 x – 2 × 8 = 24
3 x – 2 = 3
x – 2 = 1
x = 3.
Antwort: 3.
3. Gleichungen, die durch eine Variablenänderung gelöst werden.
Lösung:
2 2x + 2 x – 12 = 0
Wir bezeichnen 2 x = y.
y 2 + y – 12 = 0
y 1 = - 4; y2 = 3.
a) 2 x = - 4. Die Gleichung hat keine Lösungen, weil 2 x > 0.
b) 2 x = 3; 2 x = 2 log 2 3 ; x = log 2 3.
Antwort: Protokoll 2 3.
4. Gleichungen, die Potenzen mit zwei verschiedenen (nicht aufeinander reduzierbaren) Basen enthalten.
3 × 2 x + 1 - 2 × 5 x – 2 = 5 x + 2 x – 2.
3× 2 x + 1 – 2 x – 2 = 5 x – 2 × 5 x – 2
2 x – 2 ×23 = 5 x – 2
×23
2 x – 2 = 5 x – 2
(5/2) x– 2 = 1
x – 2 = 0
x = 2.
Antwort: 2.
5. Gleichungen, die bezüglich a x und b x homogen sind.
Generelle Form: .
9 x + 4 x = 2,5 × 6 x.
Lösung:
3 2x – 2,5 × 2 x × 3 x +2 2x = 0 |: 2 2x > 0
(3/2) 2x – 2,5 × (3/2) x + 1 = 0.
Bezeichnen wir (3/2) x = y.
y 2 – 2,5y + 1 = 0,
y 1 = 2; y 2 = ½. 
Antwort: log 3/2 2; - Protokoll 3/2 2.
Besuchen Sie den YouTube-Kanal unserer Website, um über alle neuen Video-Lektionen auf dem Laufenden zu bleiben.
Erinnern wir uns zunächst an die Grundformeln der Kräfte und ihre Eigenschaften.
Produkt einer Zahl A n-mal auf sich selbst vorkommt, können wir diesen Ausdruck als a a … a=a n schreiben
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n / a m = a n - m
Potenz- oder Exponentialgleichungen– Dies sind Gleichungen, in denen die Variablen Potenzen (oder Exponenten) sind und die Basis eine Zahl ist.
Beispiele für Exponentialgleichungen:
In diesem Beispiel ist die Zahl 6 die Basis; sie steht immer unten und ist die Variable X Grad oder Indikator.
Lassen Sie uns weitere Beispiele für Exponentialgleichungen geben.
2 x *5=10
16 x - 4 x - 6=0
Schauen wir uns nun an, wie Exponentialgleichungen gelöst werden.
Nehmen wir eine einfache Gleichung:
2 x = 2 3
Dieses Beispiel kann sogar im Kopf gelöst werden. Es ist ersichtlich, dass x=3. Damit die linke und rechte Seite gleich sind, müssen Sie schließlich die Zahl 3 anstelle von x eingeben.
Sehen wir uns nun an, wie diese Entscheidung formalisiert wird:
2 x = 2 3
x = 3
Um eine solche Gleichung zu lösen, haben wir entfernt identische Gründe(also Zweier) und aufgeschrieben, was noch übrig war, das sind Grade. Wir haben die Antwort bekommen, nach der wir gesucht haben.
Fassen wir nun unsere Entscheidung zusammen.
Algorithmus zur Lösung der Exponentialgleichung:
1. Muss überprüft werden das gleiche ob die Gleichung rechts und links Basen hat. Wenn die Gründe nicht die gleichen sind, suchen wir nach Lösungen dieses Beispiel.
2. Nachdem die Basen gleich geworden sind, gleichsetzen Grad und lösen Sie die resultierende neue Gleichung.
Schauen wir uns nun ein paar Beispiele an:
Beginnen wir mit etwas Einfachem.
Die Basen auf der linken und rechten Seite entsprechen der Zahl 2, was bedeutet, dass wir die Basis wegwerfen und ihre Kräfte gleichsetzen können.
x+2=4 Man erhält die einfachste Gleichung.
x=4 – 2
x=2
Antwort: x=2
Im folgenden Beispiel können Sie sehen, dass die Basen unterschiedlich sind: 3 und 9.
3 3x - 9 x+8 = 0
Verschieben wir zunächst die Neun auf die rechte Seite, erhalten wir:
Jetzt müssen Sie die gleichen Grundlagen erstellen. Wir wissen, dass 9=3 2. Verwenden wir die Potenzformel (a n) m = a nm.
3 3x = (3 2) x+8
Wir erhalten 9 x+8 =(3 2) x+8 =3 2x+16
3 3x = 3 2x+16 Jetzt können Sie das links sehen und rechte Seite Die Basen sind gleich und gleich drei, was bedeutet, dass wir sie verwerfen und die Grade gleichsetzen können.
3x=2x+16 erhalten wir die einfachste Gleichung
3x - 2x=16
x=16
Antwort: x=16.
Schauen wir uns das folgende Beispiel an:
2 2x+4 - 10 4 x = 2 4
Zunächst schauen wir uns die Basen an, die Basen zwei und vier. Und wir brauchen, dass sie gleich sind. Wir transformieren die vier mit der Formel (a n) m = a nm.
4 x = (2 2) x = 2 2x
Und wir verwenden auch eine Formel a n a m = a n + m:
2 2x+4 = 2 2x 2 4
Zur Gleichung hinzufügen:
2 2x 2 4 - 10 2 2x = 24
Aus den gleichen Gründen haben wir ein Beispiel gegeben. Aber die anderen Zahlen 10 und 24 stören uns. Was tun mit ihnen? Wenn Sie genau hinsehen, können Sie sehen, dass wir auf der linken Seite 2 2x wiederholt haben. Hier ist die Antwort: Wir können 2 2x aus Klammern setzen:
2 2x (2 4 - 10) = 24
Berechnen wir den Ausdruck in Klammern:
2 4 — 10 = 16 — 10 = 6
Wir teilen die gesamte Gleichung durch 6:
Stellen wir uns 4=2 2 vor:
2 2x = 2 2 Basen sind gleich, wir verwerfen sie und setzen die Grade gleich.
2x = 2 ist die einfachste Gleichung. Teilen Sie es durch 2 und wir erhalten
x = 1
Antwort: x = 1.
Lösen wir die Gleichung:
9 x – 12*3 x +27= 0
Lassen Sie uns transformieren:
9 x = (3 2) x = 3 2x
Wir erhalten die Gleichung:
3 2x - 12 3 x +27 = 0
Unsere Basen sind die gleichen, gleich drei. In diesem Beispiel können Sie sehen, dass die ersten drei einen doppelten Grad haben (2x) als der zweite (nur x). In diesem Fall können Sie es lösen Ersatzmethode. Wir ersetzen die Zahl durch den kleinsten Grad:
Dann ist 3 2x = (3 x) 2 = t 2
Wir ersetzen alle x Potenzen in der Gleichung durch t:
t 2 - 12t+27 = 0
Wir bekommen quadratische Gleichung. Wenn wir die Diskriminante auflösen, erhalten wir:
D=144-108=36
t 1 = 9
t2 = 3
Zurück zur Variablen X.
Nimm t 1:
t 1 = 9 = 3 x
Das ist,
3 x = 9
3 x = 3 2
x 1 = 2
Eine Wurzel wurde gefunden. Wir suchen den zweiten von t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Antwort: x 1 = 2; x 2 = 1.
Auf der Website können Sie im Bereich HELP DECIDE Ihre Fragen stellen, wir werden Ihnen auf jeden Fall antworten.
Tritt der Gruppe bei
Staatliche Universität Belgorod
ABTEILUNG Algebra, Zahlentheorie und Geometrie
Arbeitsthema: Exponentielle Potenzgleichungen und Ungleichungen.
Diplomarbeit Student der Fakultät für Physik und Mathematik
Wissenschaftlicher Leiter:
______________________________
Rezensent: _______________________________
________________________
Belgorod. 2006
| Einführung | 3 | ||
| Thema ICH. | Analyse der Literatur zum Forschungsthema. | ||
| Thema II. | Funktionen und ihre Eigenschaften zur Lösung von Exponentialgleichungen und Ungleichungen. | ||
| I.1. | Power-Funktion und seine Eigenschaften. | ||
| I.2. | Exponentialfunktion und seine Eigenschaften. | ||
| Thema III. | Lösung exponentieller Potenzgleichungen, Algorithmus und Beispiele. | ||
| Thema IV. | Lösung exponentieller Ungleichungen, Lösungsplan und Beispiele. | ||
| Thema V. | Erfahrung in der Durchführung von Unterricht mit Schülern zum Thema: „Exponentielle Gleichungen und Ungleichungen lösen.“ | ||
| V. 1. | Unterrichtsmaterial. | ||
| V. 2. | Probleme zur unabhängigen Lösung. | ||
| Abschluss. | Schlussfolgerungen und Angebote. | ||
| Literaturverzeichnis. | |||
| Anwendungen | |||
Einführung.
„...die Freude am Sehen und Verstehen...“
A. Einstein.
In dieser Arbeit habe ich versucht, meine Erfahrungen als Mathematiklehrer zu vermitteln, zumindest teilweise meine Einstellung zum Unterrichten zu vermitteln – ein menschliches Unterfangen, in dem mathematische Wissenschaft, Pädagogik, Didaktik, Psychologie und sogar Philosophie überraschend miteinander verflochten sind.
Ich hatte die Gelegenheit, mit Kindern und Absolventen zu arbeiten, mit Kindern, die an den Stangen standen intellektuelle Entwicklung: diejenigen, die bei einem Psychiater registriert waren und sich wirklich für Mathematik interessierten
Ich hatte die Gelegenheit, viele methodische Probleme zu lösen. Ich werde versuchen, über diejenigen zu sprechen, die ich gelöst habe. Aber noch mehr sind gescheitert, und selbst bei denen, die gelöst zu sein scheinen, tauchen neue Fragen auf.
Aber noch wichtiger als das Erlebnis selbst sind die Überlegungen und Zweifel des Lehrers: Warum ist es genau so, dieses Erlebnis?
Und der Sommer ist jetzt anders und die Entwicklung der Bildung ist interessanter geworden. „Unter den Jupitern“ ist heute nicht die Suche nach einem mythischen optimalen System, um „jeden und alles“ zu unterrichten, sondern nach dem Kind selbst. Aber dann – notgedrungen – der Lehrer.
Im Schulkurs Algebra begann er mit Analysis in den Klassen 10 - 11, als er das Einheitliche Staatsexamen für den Kurs bestand weiterführende Schule und bei Aufnahmeprüfungen an Universitäten gibt es Gleichungen und Ungleichungen, die eine Unbekannte in der Basis und in Exponenten enthalten – das sind Exponentialgleichungen und Ungleichungen.
In der Schule wird ihnen wenig Beachtung geschenkt, in Lehrbüchern gibt es praktisch keine Aufgaben zu diesem Thema. Die Beherrschung der Lösungstechnik scheint mir jedoch sehr nützlich zu sein: Es steigert die geistige und geistige Leistungsfähigkeit Kreative Fähigkeiten Studenten eröffnen sich uns völlig neue Horizonte. Beim Lösen von Problemen erwerben Studierende erste Kompetenzen Forschungsarbeit, ihre mathematische Kultur wird bereichert und ihre Fähigkeiten zum logischen Denken entwickeln sich. Schulkinder entwickeln Persönlichkeitseigenschaften wie Entschlossenheit, Zielsetzung und Unabhängigkeit, die ihnen im späteren Leben von Nutzen sein werden. Und es gibt auch Wiederholung, Erweiterung und tiefe Assimilation von Lehrmaterial.
Ich begann mit der Arbeit an diesem Thema für meine Abschlussarbeit, indem ich meine Hausarbeit schrieb. Während ich die mathematische Literatur zu diesem Thema eingehend studierte und analysierte, identifizierte ich die am besten geeignete Methode zur Lösung von Exponentialgleichungen und Ungleichungen.
Es liegt darin, dass zusätzlich zum allgemein akzeptierten Ansatz bei der Lösung von Exponentialgleichungen (die Basis wird größer als 0 angenommen) und bei der Lösung der gleichen Ungleichungen (die Basis wird größer als 1 oder größer als 0, aber kleiner als 1 angenommen) Es werden auch Fälle berücksichtigt, in denen die Basen negativ sind, also gleich 0 und 1.
Eine Analyse der schriftlichen Prüfungsarbeiten der Studierenden zeigt, dass die Fragestellung mangelhaft behandelt wird negativer Wert Die Argumentation der Exponentialfunktion in Schulbüchern bereitet ihnen eine Reihe von Schwierigkeiten und führt zu Fehlern. Und sie haben auch Probleme bei der Systematisierung der erhaltenen Ergebnisse, wo durch den Übergang zu einer Gleichung – einer Konsequenz oder einer Ungleichung – einer Konsequenz Fremdwurzeln auftreten können. Um Fehler zu beseitigen, verwenden wir einen Test unter Verwendung der ursprünglichen Gleichung oder Ungleichung und eines Algorithmus zur Lösung exponentieller Gleichungen oder eines Plans zur Lösung exponentieller Ungleichungen.
Damit Studierende die Abschluss- und Aufnahmeprüfungen erfolgreich bestehen, ist es meiner Meinung nach notwendig, der Lösung von Exponentialgleichungen und Ungleichungen im Unterricht oder zusätzlich in Wahlfächern und Clubs mehr Aufmerksamkeit zu schenken.
Auf diese Weise Thema , meine These ist definiert auf die folgende Weise: „Exponentielle Potenzgleichungen und Ungleichungen.“
Ziele dieser Arbeit Sind:
1. Analysieren Sie die Literatur zu diesem Thema.
2. Geben vollständige Analyse Lösen exponentieller Potenzgleichungen und Ungleichungen.
3. Stellen Sie eine ausreichende Anzahl von Beispielen unterschiedlicher Art zu diesem Thema bereit.
4. Prüfen Sie im Klassen-, Wahlfach- und Vereinsunterricht, wie die vorgeschlagenen Methoden zur Lösung von Exponentialgleichungen und Ungleichungen wahrgenommen werden. Geben Sie entsprechende Empfehlungen zum Studium dieses Themas.
Thema Unsere Forschung besteht darin, eine Methodik zur Lösung exponentieller Gleichungen und Ungleichungen zu entwickeln.
Der Zweck und das Thema der Studie erforderten die Lösung folgender Probleme:
1. Studieren Sie die Literatur zum Thema: „Exponentielle Potenzgleichungen und Ungleichungen“.
2. Beherrschen Sie die Techniken zur Lösung von Exponentialgleichungen und Ungleichungen.
3. Wählen Sie Schulungsmaterial aus und entwickeln Sie ein Übungssystem verschiedene Level zum Thema: „Exponentielle Gleichungen und Ungleichungen lösen.“
Während der Dissertationsforschung wurden mehr als 20 Arbeiten zur Verwendung von erstellt verschiedene Methoden Lösen exponentieller Potenzgleichungen und Ungleichungen. Von hier aus bekommen wir.
Abschlussarbeitsplan:
Einführung.
Kapitel I. Analyse der Literatur zum Forschungsthema.
Kapitel II. Funktionen und ihre Eigenschaften zur Lösung von Exponentialgleichungen und Ungleichungen.
II.1. Potenzfunktion und ihre Eigenschaften.
II.2. Exponentialfunktion und ihre Eigenschaften.
Kapitel III. Lösung exponentieller Potenzgleichungen, Algorithmus und Beispiele.
Kapitel IV. Lösung exponentieller Ungleichungen, Lösungsplan und Beispiele.
Kapitel V. Erfahrungen mit der Durchführung von Unterrichtsstunden mit Schülern zu diesem Thema.
1. Schulungsmaterial.
2.Aufgaben zur eigenständigen Lösung.
Abschluss. Schlussfolgerungen und Angebote.
Liste der verwendeten Literatur.
Kapitel I analysiert die Literatur
Erste Ebene
Exponentialgleichungen. Der ultimative Leitfaden (2019)
Hallo! Heute werden wir mit Ihnen besprechen, wie Sie Gleichungen lösen können, die entweder elementar sein können (und ich hoffe, dass nach der Lektüre dieses Artikels fast alle für Sie so sein werden) und solche, die normalerweise „zum Ausfüllen“ angegeben werden. Offenbar um endlich einzuschlafen. Aber ich werde versuchen, alles Mögliche zu tun, damit Sie jetzt nicht in Schwierigkeiten geraten, wenn Sie mit solchen Gleichungen konfrontiert werden. Ich rede jetzt nicht mehr um den heißen Brei herum, verrate euch aber gleich ein kleines Geheimnis: Heute lernen wir Exponentialgleichungen.
Bevor ich mit der Analyse von Lösungsmöglichkeiten fortfahre, werde ich Ihnen gleich eine Reihe (ziemlich kleiner) Fragen skizzieren, die Sie wiederholen sollten, bevor Sie dieses Thema überstürzt angehen. Also bitte, um die besten Ergebnisse zu erzielen wiederholen:
- Eigenschaften und
- Lösung und Gleichungen
Wiederholt? Toll! Dann wird es Ihnen nicht schwer fallen zu erkennen, dass die Wurzel der Gleichung eine Zahl ist. Verstehst du genau, wie ich es gemacht habe? Ist es wahr? Dann machen wir weiter. Beantworten Sie nun meine Frage: Was ist gleich der dritten Potenz? Du hast absolut recht: . Welche Zweierpotenz ist acht? Genau – der Dritte! Weil. Versuchen wir nun, das folgende Problem zu lösen: Lassen Sie mich die Zahl einmal mit sich selbst multiplizieren und das Ergebnis erhalten. Die Frage ist, wie oft habe ich mit mir selbst multipliziert? Sie können dies natürlich direkt überprüfen:
\begin(align) & 2=2 \\ & 2\cdot 2=4 \\ & 2\cdot 2\cdot 2=8 \\ & 2\cdot 2\cdot 2\cdot 2=16 \\ \end( ausrichten)
Daraus lässt sich schließen, dass ich mal mit mir selbst multipliziert habe. Wie kann man das sonst überprüfen? So geht's: direkt per Definition des Grades: . Aber Sie müssen zugeben, wenn ich fragen würde, wie oft zwei mit sich selbst multipliziert werden müssen, um beispielsweise zu erhalten, würden Sie mir sagen: Ich mache mir nichts vor und multipliziere mit sich selbst, bis mir blau im Gesicht wird. Und er hätte völlig Recht. Denn wie kannst du Schreiben Sie alle Schritte kurz auf(und Kürze ist die Schwester des Talents)
wo - das sind die gleichen "mal", wenn man mit sich selbst multipliziert.
Ich denke, dass Sie wissen (und wenn Sie es nicht wissen, wiederholen Sie dringend, ganz dringend die Abschlüsse!), dann wird mein Problem in der Form geschrieben:
Wie können Sie vernünftigerweise zu dem Schluss kommen, dass:
Also schrieb ich unbemerkt das Einfachste auf Exponentialgleichung:
Und ich habe ihn sogar gefunden Wurzel. Finden Sie nicht, dass alles völlig trivial ist? Ich denke genau das Gleiche. Hier ist ein weiteres Beispiel für Sie:
Aber was soll man machen? Schließlich kann es nicht als Potenz einer (vernünftigen) Zahl geschrieben werden. Verzweifeln wir nicht und stellen wir fest, dass diese beiden Zahlen perfekt durch die Potenz derselben Zahl ausgedrückt werden. Welcher? Rechts: . Dann wird die ursprüngliche Gleichung in die Form umgewandelt:
Wo, wie Sie bereits verstanden haben, . Lasst uns nicht länger zögern und es aufschreiben Definition:
In unserem Fall: .
Diese Gleichungen werden gelöst, indem man sie auf die Form reduziert:
Anschließend wird die Gleichung gelöst
Tatsächlich haben wir im vorherigen Beispiel genau das getan: Wir haben Folgendes erhalten: Und wir haben die einfachste Gleichung gelöst.
Es scheint nichts Kompliziertes zu sein, oder? Lassen Sie uns zunächst an den einfachsten üben Beispiele:
Wir sehen erneut, dass die rechte und linke Seite der Gleichung als Potenzen einer Zahl dargestellt werden müssen. Auf der linken Seite ist dies zwar bereits geschehen, auf der rechten Seite steht jedoch eine Nummer. Aber es ist in Ordnung, denn meine Gleichung wird sich auf wundersame Weise in diese verwandeln:
Was musste ich hier verwenden? Welche Regel? Regel „Grad in Grad“ welches lautet:
Was ist, wenn:
Bevor wir diese Frage beantworten, füllen wir die folgende Tabelle aus:
Es fällt uns leicht zu bemerken, dass je weniger, desto weniger Wert, aber dennoch alle diese Werte Über Null. UND DAS WIRD IMMER SO SEIN!!! Die gleiche Eigenschaft gilt FÜR JEDE BASIS MIT JEDEM INDIKATOR!! (für alle und). Was können wir dann über die Gleichung schließen? Hier ist, was es ist: es hat keine Wurzeln! So wie jede Gleichung keine Wurzeln hat. Jetzt lasst uns üben und Lassen Sie uns einfache Beispiele lösen:
Lass uns das Prüfen:
1. Hier wird von Ihnen nichts verlangt außer Kenntnissen über die Eigenschaften von Graden (die ich übrigens wiederholen sollte!) In der Regel führt alles zur kleinsten Basis: , . Dann entspricht die ursprüngliche Gleichung der folgenden: Ich muss lediglich die Eigenschaften von Potenzen nutzen: Bei der Multiplikation von Zahlen mit gleicher Basis werden die Potenzen addiert, bei der Division werden sie subtrahiert. Dann bekomme ich: Nun, jetzt werde ich guten Gewissens von der Exponentialgleichung zur linearen übergehen: \begin(align)
& 2x+1+2(x+2)-3x=5 \\
& 2x+1+2x+4-3x=5 \\
&x=0. \\
\end(align)
2. Im zweiten Beispiel müssen wir vorsichtiger sein: Das Problem besteht darin, dass wir auf der linken Seite unmöglich dieselbe Zahl als Potenz darstellen können. In diesem Fall ist es manchmal nützlich stellen Zahlen als Produkt von Potenzen mit unterschiedlichen Basen, aber gleichen Exponenten dar:
Die linke Seite der Gleichung sieht so aus: Was hat uns das gebracht? Hier ist was: Zahlen mit unterschiedlichen Basen, aber gleichen Exponenten können multipliziert werden.In diesem Fall werden die Basen multipliziert, der Indikator ändert sich jedoch nicht:
In meiner Situation ergibt dies:
\begin(align)
& 4\cdot ((64)^(x))((25)^(x))=6400,\\
& 4\cdot (((64\cdot 25))^(x))=6400,\\
& ((1600)^(x))=\frac(6400)(4), \\
& ((1600)^(x))=1600, \\
&x=1. \\
\end(align)
Nicht schlecht, oder?
3. Ich mag es nicht, wenn ich unnötigerweise zwei Begriffe auf der einen Seite der Gleichung habe und keinen auf der anderen (manchmal ist das natürlich berechtigt, aber jetzt ist das nicht der Fall). Ich verschiebe den Minusterm nach rechts:
Auch jetzt schreibe ich alles in Dreierpotenzen:
Ich addiere die Grade auf der linken Seite und erhalte eine äquivalente Gleichung
Sie können die Wurzel leicht finden:
4. Wie in Beispiel drei hat der Minusterm einen Platz auf der rechten Seite!
Auf meiner linken Seite ist fast alles in Ordnung, außer was? Ja, der „falsche Grad“ der beiden stört mich. Aber ich kann das leicht beheben, indem ich schreibe: . Heureka – auf der linken Seite sind alle Basen unterschiedlich, aber alle Grade sind gleich! Lasst uns sofort vermehren!
Auch hier ist alles klar: (Wenn Sie nicht verstehen, wie ich auf magische Weise zur letzten Gleichheit gekommen bin, machen Sie eine Minute Pause, atmen Sie durch und lesen Sie die Eigenschaften des Abschlusses noch einmal ganz genau. Wer hat gesagt, dass Sie a überspringen können? Grad mit einem negativen Exponenten? Nun, hier bin ich ungefähr das Gleiche wie niemand). Jetzt bekomme ich:
\begin(align)
& ((2)^(4\left((x) -9 \right)))=((2)^(-1)) \\
& 4((x) -9)=-1 \\
& x=\frac(35)(4). \\
\end(align)
Hier sind einige Aufgaben zum Üben, auf die ich nur die Antworten gebe (allerdings in „gemischter“ Form). Lösen Sie sie, überprüfen Sie sie, und Sie und ich werden unsere Forschung fortsetzen!
Bereit? Antworten wie diese:
- irgendeine Nummer
Okay, okay, ich habe nur Witze gemacht! Hier sind einige Lösungsskizzen (einige sehr kurz!)
Glauben Sie nicht, dass es kein Zufall ist, dass ein Bruch auf der linken Seite der andere „invertiert“ ist? Es wäre eine Sünde, dies nicht auszunutzen:
Diese Regel wird sehr oft beim Lösen von Exponentialgleichungen verwendet. Denken Sie daran!
Dann sieht die ursprüngliche Gleichung so aus:
Durch Lösen dieser quadratischen Gleichung erhalten Sie die folgenden Wurzeln:
2. Eine andere Lösung: Division beider Seiten der Gleichung durch den Ausdruck links (oder rechts). Teilen Sie durch das, was rechts steht, dann erhalte ich:
Wo warum?!)
3. Ich möchte mich gar nicht wiederholen, alles wurde schon so sehr „gekaut“.
4. Äquivalent zu einer quadratischen Gleichung, Wurzeln
5. Sie müssen die in der ersten Aufgabe angegebene Formel verwenden, dann erhalten Sie Folgendes:
Aus der Gleichung ist eine triviale Identität geworden, die für jeden gilt. Dann ist die Antwort eine beliebige reelle Zahl.
Nun haben Sie das Lösen geübt einfache Exponentialgleichungen. Nun möchte ich Ihnen ein paar Lebensbeispiele geben, die Ihnen helfen zu verstehen, warum sie grundsätzlich notwendig sind. Hier werde ich zwei Beispiele nennen. Eine davon ist recht alltäglich, die andere ist jedoch eher von wissenschaftlichem als von praktischem Interesse.
Beispiel 1 (kaufmännisch) Sie haben zwar Rubel, möchten diese aber in Rubel umwandeln. Die Bank bietet Ihnen an, dieses Geld zu einem jährlichen Zinssatz mit monatlicher Kapitalisierung der Zinsen (monatliche Abgrenzung) abzunehmen. Die Frage ist: Wie viele Monate muss man ein Depot eröffnen, um den erforderlichen Endbetrag zu erreichen? Eine ziemlich banale Aufgabe, nicht wahr? Seine Lösung ist jedoch mit der Konstruktion der entsprechenden Exponentialgleichung verbunden: Sei – der Anfangsbetrag, – der Endbetrag, – der Zinssatz für die Periode, – die Anzahl der Perioden. Dann:
In unserem Fall (wenn der Zinssatz jährlich ist, wird er pro Monat berechnet). Warum wird durch geteilt? Wenn Sie die Antwort auf diese Frage nicht kennen, denken Sie an das Thema „“! Dann erhalten wir diese Gleichung:
Diese Exponentialgleichung kann nur mit einem Taschenrechner (its) gelöst werden Aussehen weist darauf hin, und dazu sind Kenntnisse in Logarithmen erforderlich, mit denen wir uns etwas später vertraut machen werden), was ich tun werde: ... Um also eine Million zu erhalten, müssen wir einen Monat lang eine Einzahlung leisten ( nicht sehr schnell, oder?).
Beispiel 2 (eher wissenschaftlich). Trotz seiner gewissen „Isolation“ empfehle ich Ihnen, auf ihn zu achten: Er „schlüpft regelmäßig in die Einheitliche Staatsprüfung!!“ (Das Problem ist der „realen“ Version entnommen) Während des Zerfalls eines radioaktiven Isotops nimmt seine Masse gemäß dem Gesetz ab, wobei (mg) die Anfangsmasse des Isotops und (min.) die seit dem Zerfall verstrichene Zeit ist Anfangsmoment (min.) ist die Halbwertszeit. Zu Beginn beträgt die Masse des Isotops mg. Seine Halbwertszeit beträgt min. Nach wie vielen Minuten beträgt die Masse des Isotops mg? Es ist in Ordnung: Wir nehmen einfach alle Daten und ersetzen sie in der uns vorgeschlagenen Formel:
Teilen wir beide Teile durch, „in der Hoffnung“, dass wir links etwas Verdauliches bekommen:
Nun, wir haben großes Glück! Es ist auf der linken Seite, dann gehen wir zur entsprechenden Gleichung über:
Wo ist min.
Wie Sie sehen, haben Exponentialgleichungen in der Praxis sehr reale Anwendungen. Jetzt möchte ich Ihnen eine andere (einfache) Möglichkeit zeigen, Exponentialgleichungen zu lösen, die darauf basiert, den gemeinsamen Faktor aus Klammern zu entfernen und die Terme dann zu gruppieren. Lassen Sie sich von meinen Worten nicht einschüchtern, Sie sind dieser Methode bereits in der 7. Klasse begegnet, als Sie Polynome studiert haben. Wenn Sie beispielsweise den Ausdruck faktorisieren müssen:
Lassen Sie uns gruppieren: den ersten und dritten Begriff sowie den zweiten und vierten. Es ist klar, dass das erste und dritte die Differenz der Quadrate sind:
und die zweite und vierte haben einen gemeinsamen Faktor von drei:
Dann entspricht der ursprüngliche Ausdruck diesem:
Woher der gemeinsame Faktor abgeleitet werden kann, ist nicht mehr schwierig:
Somit,
Das ist ungefähr das, was wir tun werden, wenn wir Exponentialgleichungen lösen: Suchen Sie nach „Gemeinsamkeiten“ zwischen den Begriffen und nehmen Sie sie aus Klammern, und dann – komme was wolle, ich glaube, dass wir Glück haben werden =)) Zum Beispiel:
Rechts ist alles andere als eine Siebenerpotenz (ich habe es überprüft!) Und links ist es etwas besser, man kann natürlich den Faktor a vom zweiten aus dem ersten Term „abhacken“ und dann austeilen mit dem, was du hast, aber lass uns vorsichtiger mit dir sein. Ich möchte mich nicht mit den Brüchen befassen, die beim „Auswählen“ zwangsläufig entstehen, also sollte ich es nicht lieber herausnehmen? Dann werde ich keine Fraktionen mehr haben: Wie man so schön sagt: Die Wölfe sind gefüttert und die Schafe sind in Sicherheit:
Berechnen Sie den Ausdruck in Klammern. Auf magische, magische Weise stellt sich das heraus (überraschenderweise, aber was sollten wir sonst noch erwarten?).
Dann reduzieren wir beide Seiten der Gleichung um diesen Faktor. Wir bekommen: , von.
Hier ist ein komplizierteres Beispiel (wirklich ziemlich viel):
Was für ein Problem! Wir haben hier keine Gemeinsamkeiten! Es ist nicht ganz klar, was jetzt zu tun ist. Tun wir, was wir können: Zuerst verschieben wir die „Vierer“ auf eine Seite und die „Fünfer“ auf die andere:
Nehmen wir nun das „Allgemeine“ links und rechts heraus:
So was jetzt? Was nützt so eine dumme Gruppe? Auf den ersten Blick ist es überhaupt nicht sichtbar, aber schauen wir genauer hin:
Nun stellen wir sicher, dass wir links nur den Ausdruck c haben und rechts alles andere. Wie machen wir das? So geht's: Teilen Sie zuerst beide Seiten der Gleichung durch (damit wir den Exponenten auf der rechten Seite loswerden) und dividieren Sie dann beide Seiten durch (damit wir den numerischen Faktor auf der linken Seite loswerden). Schließlich erhalten wir:
Unglaublich! Links haben wir einen Ausdruck und rechts einen einfachen Ausdruck. Dann kommen wir sofort zu dem Schluss
Hier ist ein weiteres Beispiel, das Sie untermauern können:
Ich bringe ihn kurze Lösung Versuchen Sie (ohne sich wirklich mit Erklärungen zu beschäftigen), alle „Feinheiten“ der Lösung selbst zu verstehen.
Nun zur endgültigen Konsolidierung des behandelten Materials. Versuchen Sie, die folgenden Probleme selbst zu lösen. Ich gebe nur kurze Empfehlungen und Tipps zur Lösung:
- Nehmen wir den gemeinsamen Faktor aus den Klammern heraus: Wobei:
- Stellen wir den ersten Ausdruck in der Form dar: , dividiere beide Seiten durch und erhalte das Ergebnis
- , dann wird die ursprüngliche Gleichung in die Form umgewandelt: Nun, jetzt ein Hinweis – schauen Sie, wo Sie und ich diese Gleichung bereits gelöst haben!
- Stellen Sie sich vor, wie, wie, ach ja, dann teilen Sie beide Seiten durch, sodass Sie die einfachste Exponentialgleichung erhalten.
- Nehmen Sie es aus den Klammern.
- Nehmen Sie es aus den Klammern.
EXPONENTÄRE GLEICHUNGEN. DURCHSCHNITTSNIVEAU
Ich gehe davon aus, dass ich den ersten Artikel gelesen habe, in dem darüber gesprochen wurde Was sind Exponentialgleichungen und wie löst man sie?, du hast es gemeistert das notwendige Minimum Kenntnisse, die zum Lösen einfacher Beispiele erforderlich sind.
Jetzt werde ich mir eine andere Methode zum Lösen von Exponentialgleichungen ansehen
„Methode zur Einführung einer neuen Variablen“ (oder Ersetzung). Er löst die meisten „schwierigen“ Probleme zum Thema Exponentialgleichungen (und nicht nur Gleichungen). Diese Methode ist eine der in der Praxis am häufigsten verwendeten. Zunächst empfehle ich Ihnen, sich mit der Thematik vertraut zu machen.
Wie Sie bereits anhand des Namens verstanden haben, besteht der Kern dieser Methode darin, eine solche Variablenänderung einzuführen, dass sich Ihre Exponentialgleichung auf wundersame Weise in eine Gleichung verwandelt, die Sie leicht lösen können. Nachdem Sie diese sehr „vereinfachte Gleichung“ gelöst haben, müssen Sie nur noch eine „umgekehrte Ersetzung“ durchführen, also vom Ersetzten zum Ersetzten zurückkehren. Lassen Sie uns das, was wir gerade gesagt haben, anhand eines sehr einfachen Beispiels veranschaulichen:
Beispiel 1:
Die Lösung dieser Gleichung erfolgt durch eine „einfache Substitution“, wie Mathematiker sie abfällig nennen. Tatsächlich ist der Ersatz hier am offensichtlichsten. Das muss man nur sehen
Dann wird die ursprüngliche Gleichung wie folgt aussehen:
Wenn wir uns zusätzlich vorstellen, wie, dann ist völlig klar, was ersetzt werden muss: natürlich . Was wird dann zur ursprünglichen Gleichung? Hier ist was:
Sie können die Wurzeln ganz einfach selbst finden: . Was sollen wir jetzt machen? Es ist Zeit, zur ursprünglichen Variablen zurückzukehren. Was habe ich vergessen zu erwähnen? Nämlich: Wenn ein bestimmter Grad durch eine neue Variable ersetzt wird (dh wenn ein Typ ersetzt wird), wird es mich interessieren nur positive Wurzeln! Warum das so ist, können Sie ganz einfach selbst beantworten. Sie und ich sind also nicht interessiert, aber die zweite Wurzel ist für uns durchaus geeignet:
Woher dann.
Antwort:
Wie Sie sehen können, hat der Ersatz im vorherigen Beispiel lediglich nach unseren Händen gefragt. Leider ist dies nicht immer der Fall. Lassen Sie uns jedoch nicht direkt zu den traurigen Dingen übergehen, sondern üben wir anhand eines weiteren Beispiels mit einem ziemlich einfachen Ersatz
Beispiel 2.
Es ist klar, dass wir höchstwahrscheinlich einen Ersatz vornehmen müssen (dies ist die kleinste der in unserer Gleichung enthaltenen Potenzen), aber bevor wir einen Ersatz einführen, muss unsere Gleichung darauf „vorbereitet“ werden, nämlich: , . Dann können Sie ersetzen, als Ergebnis erhalte ich den folgenden Ausdruck:
Oh Horror: eine kubische Gleichung mit absolut schrecklichen Formeln zu ihrer Lösung (nun ja, ehrlich gesagt). Gesamtansicht). Aber lasst uns nicht gleich verzweifeln, sondern darüber nachdenken, was wir tun sollen. Ich schlage vor, zu schummeln: Wir wissen, dass wir, um eine „schöne“ Antwort zu erhalten, diese in Form einer Dreierpotenz erhalten müssen (warum sollte das so sein?). Versuchen wir, mindestens eine Wurzel unserer Gleichung zu erraten (ich beginne mit der Vermutung mit Dreierpotenzen).
Erste Vermutung. Keine Wurzel. Ach und ah...
.
Die linke Seite ist gleich.
Rechter Teil: !
Essen! Habe die erste Wurzel erraten. Jetzt wird es einfacher!
Kennen Sie das Aufteilungsschema „Ecke“? Natürlich verwenden Sie es, wenn Sie eine Zahl durch eine andere dividieren. Aber nur wenige wissen, dass das Gleiche auch mit Polynomen möglich ist. Es gibt einen wunderbaren Satz:
Auf meine Situation übertragen bedeutet dies, dass es ohne Rest durch teilbar ist. Wie erfolgt die Teilung? So geht das:
Ich schaue mir an, mit welchem Monom ich multiplizieren sollte, um Folgendes zu erhalten:
Wenn ich den resultierenden Ausdruck subtrahiere, erhalte ich:
Womit muss ich nun multiplizieren, um zu erhalten? Es ist klar, dass ich dann Folgendes bekomme:
und subtrahiere erneut den resultierenden Ausdruck vom verbleibenden:
Nun, der letzte Schritt besteht darin, mit dem verbleibenden Ausdruck zu multiplizieren und davon zu subtrahieren:
Hurra, die Teilung ist vorbei! Was haben wir privat angesammelt? Selbstverständlich: .
Dann erhalten wir die folgende Entwicklung des ursprünglichen Polynoms:
Lösen wir die zweite Gleichung:
Es hat Wurzeln:
Dann ist die ursprüngliche Gleichung:
hat drei Wurzeln:
Die letzte Wurzel werden wir natürlich verwerfen, da sie kleiner als Null ist. Und die ersten beiden nach der umgekehrten Ersetzung ergeben uns zwei Wurzeln:
Antwort: ..
Ich wollte Sie mit diesem Beispiel keineswegs erschrecken; mein Ziel war es vielmehr zu zeigen, dass wir zwar einen recht einfachen Ersatz hatten, dieser aber dennoch zu rechtem Ergebnis führte komplexe Gleichung, dessen Lösung von uns besondere Fähigkeiten erforderte. Nun, niemand ist davor gefeit. Aber der Ersatz war in diesem Fall ziemlich offensichtlich.
Hier ist ein Beispiel mit einem etwas weniger offensichtlichen Ersatz:
Es ist überhaupt nicht klar, was wir tun sollen: Das Problem besteht darin, dass es in unserer Gleichung zwei verschiedene Basen gibt und eine Basis nicht aus der anderen gewonnen werden kann, indem man sie auf eine (natürlich vernünftige) Potenz erhöht. Doch was sehen wir? Beide Basen unterscheiden sich nur im Vorzeichen und ihr Produkt ist die Differenz der Quadrate gleich eins:
Definition:
Somit sind die Zahlen, die in unserem Beispiel die Basis bilden, konjugiert.
In diesem Fall wäre der kluge Schritt Multiplizieren Sie beide Seiten der Gleichung mit der konjugierten Zahl.
Wenn zum Beispiel ein, dann wird die linke Seite der Gleichung gleich und die rechte. Wenn wir eine Substitution vornehmen, sieht unsere ursprüngliche Gleichung wie folgt aus:
seine Wurzeln, und wenn wir uns daran erinnern, verstehen wir das.
Antwort: , .
In der Regel reicht die Ersetzungsmethode aus, um die meisten Exponentialgleichungen der „Schule“ zu lösen. Die folgenden Aufgaben sind dem Einheitlichen Staatsexamen C1 entnommen ( erhöhtes Niveau Schwierigkeiten). Sie verfügen bereits über ausreichende Kenntnisse, um diese Beispiele selbst zu lösen. Ich gebe nur den benötigten Ersatz.
- Löse die Gleichung:
- Finden Sie die Wurzeln der Gleichung:
- Löse die Gleichung: . Finden Sie alle Wurzeln dieser Gleichung, die zum Segment gehören:
Und nun noch ein paar kurze Erklärungen und Antworten:
- Hier genügt uns der Hinweis, dass... Dann ist die ursprüngliche Gleichung äquivalent zu dieser: Diese Gleichung durch Ersetzen gelöst. Führen Sie weitere Berechnungen selbst durch. Am Ende reduziert sich Ihre Aufgabe auf die Lösung einfacher trigonometrischer Probleme (abhängig von Sinus oder Cosinus). Wir werden uns in anderen Abschnitten mit Lösungen für ähnliche Beispiele befassen.
- Hier können Sie sogar auf die Substitution verzichten: Bewegen Sie einfach den Subtrahend nach rechts und stellen Sie beide Basen durch Zweierpotenzen dar: , und gehen Sie dann direkt zur quadratischen Gleichung über.
- Auch die dritte Gleichung wird ganz normal gelöst: Stellen wir uns vor, wie. Wenn wir dann ersetzen, erhalten wir eine quadratische Gleichung: dann
Du weißt doch schon, was ein Logarithmus ist, oder? Nein? Dann lesen Sie das Thema dringend!
Die erste Wurzel gehört offensichtlich nicht zum Segment, die zweite ist jedoch unklar! Aber wir werden es sehr bald erfahren! Denn (dies ist eine Eigenschaft des Logarithmus!) Vergleichen wir:
Subtrahieren Sie von beiden Seiten, dann erhalten wir:
Die linke Seite kann wie folgt dargestellt werden:
Multipliziere beide Seiten mit:
kann dann mit multipliziert werden
Dann vergleiche:
seit damals:
Dann gehört die zweite Wurzel zum erforderlichen Intervall
Antwort:
Wie du siehst, Die Auswahl der Wurzeln von Exponentialgleichungen erfordert eine ziemlich tiefe Kenntnis der Eigenschaften von Logarithmen Daher rate ich Ihnen, beim Lösen von Exponentialgleichungen so vorsichtig wie möglich zu sein. Wie Sie verstehen, ist in der Mathematik alles miteinander verbunden! Wie mein Mathematiklehrer sagte: „Mathematik kann man ebenso wie Geschichte nicht über Nacht lesen.“
In der Regel alle Die Schwierigkeit bei der Lösung der Probleme C1 liegt gerade in der Auswahl der Wurzeln der Gleichung.Üben wir mit einem weiteren Beispiel:
Es ist klar, dass die Gleichung selbst ganz einfach gelöst werden kann. Durch eine Substitution reduzieren wir unsere ursprüngliche Gleichung auf Folgendes:
Schauen wir uns zunächst die erste Wurzel an. Vergleichen wir und: seit, dann. (Eigenschaft einer logarithmischen Funktion, at). Dann ist klar, dass die erste Wurzel nicht zu unserem Intervall gehört. Nun die zweite Wurzel: . Das ist klar (da die Funktion at zunimmt). Es bleibt zu vergleichen und...
seitdem, dann zur gleichen Zeit. Auf diese Weise kann ich einen Pflock zwischen dem und „treiben“. Dieser Stift ist eine Nummer. Der erste Ausdruck ist kleiner und der zweite größer. Dann ist der zweite Ausdruck größer als der erste und die Wurzel gehört zum Intervall.
Antwort: .
Schauen wir uns abschließend ein weiteres Beispiel einer Gleichung an, bei der die Substitution völlig vom Standard abweicht:
Beginnen wir gleich damit, was getan werden kann und was im Prinzip getan werden kann, aber es ist besser, es nicht zu tun. Sie können sich alles durch die Potenzen drei, zwei und sechs vorstellen. Wohin führt es? Es wird zu nichts führen: zu einem Wirrwarr von Graden, von denen einige ziemlich schwer zu beseitigen sein werden. Was wird dann benötigt? Beachten wir, dass a Und was wird uns das bringen? Und die Tatsache, dass wir die Lösung dieses Beispiels auf die Lösung einer ziemlich einfachen Exponentialgleichung reduzieren können! Schreiben wir zunächst unsere Gleichung wie folgt um:
Teilen wir nun beide Seiten der resultierenden Gleichung durch:
Heureka! Jetzt können wir ersetzen, wir erhalten:
Nun sind Sie an der Reihe, Demonstrationsaufgaben zu lösen, und ich werde dazu nur kurze Kommentare abgeben, damit Sie nicht verwirrt werden der richtige Weg! Viel Glück!
1. Das Schwierigste! Es ist so schwer, hier einen Ersatz zu finden! Dennoch lässt sich dieses Beispiel vollständig mit lösen Hervorheben eines vollständigen Quadrats. Um es zu lösen, reicht es aus, Folgendes zu beachten:
Dann ist hier Ihr Ersatz:
(Bitte beachten Sie, dass wir hier bei unserem Ersatz die negative Wurzel nicht verwerfen können!!! Warum denken Sie?)
Um das Beispiel zu lösen, müssen Sie nun nur noch zwei Gleichungen lösen:
Beide Probleme können durch einen „Standardaustausch“ gelöst werden (aber der zweite in einem Beispiel!)
2. Merken Sie sich das und nehmen Sie einen Ersatz vor.
3. Zerlegen Sie die Zahl in Teilerzahlfaktoren und vereinfachen Sie den resultierenden Ausdruck.
4. Teilen Sie Zähler und Nenner des Bruchs durch (oder, wenn Sie möchten) und führen Sie die Ersetzung durch oder durch.
5. Beachten Sie, dass die Zahlen und konjugiert sind.
EXPONENTÄRE GLEICHUNGEN. FORTGESCHRITTENES LEVEL
Schauen wir uns außerdem einen anderen Weg an: Lösen von Exponentialgleichungen mit der Logarithmusmethode. Ich kann nicht sagen, dass das Lösen von Exponentialgleichungen mit dieser Methode sehr beliebt ist, aber in einigen Fällen kann uns nur sie dazu führen die richtige Entscheidung unsere Gleichung. Besonders häufig wird es zur Lösung des sogenannten „ gemischte Gleichungen": also solche, bei denen Funktionen unterschiedlichen Typs auftreten.
Zum Beispiel eine Gleichung der Form:
Im allgemeinen Fall kann es nur durch Logarithmen beider Seiten (z. B. zur Basis) gelöst werden, wobei die ursprüngliche Gleichung wie folgt aussieht:
Schauen wir uns das folgende Beispiel an:
Es ist klar, dass uns nur die ODZ der logarithmischen Funktion interessiert. Dies folgt jedoch nicht nur aus der ODZ des Logarithmus, sondern aus einem weiteren Grund. Ich denke, es wird Ihnen nicht schwer fallen, zu erraten, um welches es sich handelt.
Nehmen wir den Logarithmus beider Seiten unserer Gleichung zur Basis:
Wie Sie sehen, führte uns die Logarithmierung unserer ursprünglichen Gleichung schnell zur richtigen (und schönen!) Antwort. Üben wir mit einem weiteren Beispiel:
Auch hier ist nichts falsch: Nehmen wir den Logarithmus beider Seiten der Gleichung zur Basis, dann erhalten wir:
Machen wir einen Ersatz:
Allerdings haben wir etwas verpasst! Haben Sie bemerkt, wo ich einen Fehler gemacht habe? Denn dann:
was die Anforderung nicht erfüllt (überlegen Sie, woher es kommt!)
Antwort:
Versuchen Sie, die Lösung der folgenden Exponentialgleichungen aufzuschreiben:
Vergleichen Sie nun Ihre Entscheidung damit:
1. Logarithmieren wir beide Seiten zur Basis und berücksichtigen dabei Folgendes:
(die zweite Wurzel ist wegen Austausch nicht für uns geeignet)
2. Logarithmus zur Basis:
Lassen Sie uns den resultierenden Ausdruck in die folgende Form umwandeln:
EXPONENTÄRE GLEICHUNGEN. KURZE BESCHREIBUNG UND GRUNDFORMELN
Exponentialgleichung
Gleichung der Form:
angerufen die einfachste Exponentialgleichung.
Eigenschaften von Graden
Lösungsansätze
- Reduktion auf die gleiche Basis
- Reduktion auf den gleichen Exponenten
- Variablenersatz
- Vereinfachen Sie den Ausdruck und wenden Sie eines der oben genannten an.