Die größten und kleinsten Werte ohne Ableitung. Größter und kleinster Wert einer Funktion

In einer Lektion zum Thema „Verwenden der Ableitung zum Ermitteln der größten und kleinsten Werte“. kontinuierliche Funktion auf einem Intervall“ werden wir relativ einfache Probleme betrachten, den größten und kleinsten Wert einer Funktion in einem bestimmten Intervall mithilfe der Ableitung zu finden.

Thema: Derivat

Lektion: Verwenden der Ableitung, um die größten und kleinsten Werte einer stetigen Funktion über ein Intervall zu ermitteln

In dieser Lektion werden wir uns mehr ansehen einfache Aufgabe, nämlich ein Intervall wird gegeben, eine stetige Funktion auf diesem Intervall wird gegeben. Wir müssen das Beste herausfinden und kleinster Wert gegeben Funktionen auf eine gegebene zwischen.

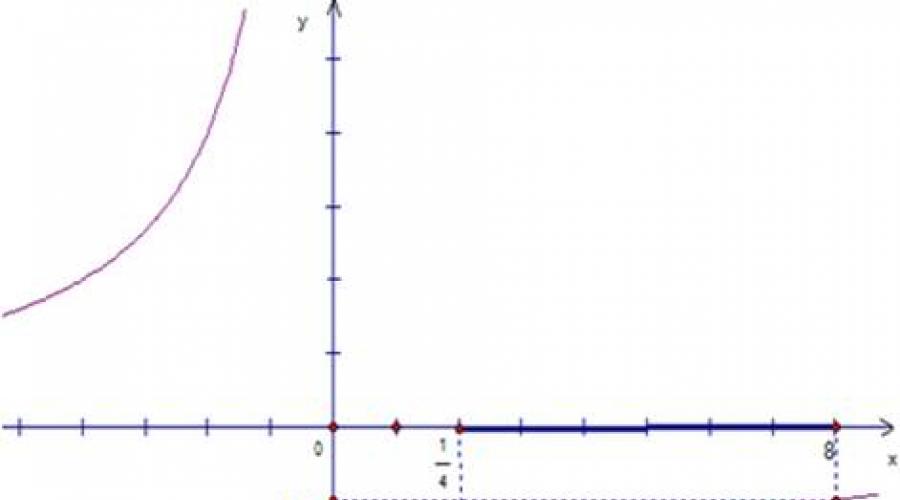
Nr. 32.1 (b). Gegeben: , . Zeichnen wir einen Graphen der Funktion (siehe Abb. 1).

Reis. 1. Graph einer Funktion.

Es ist bekannt, dass diese Funktion im Intervall zunimmt, was bedeutet, dass sie auch im Intervall zunimmt. Das heißt, wenn Sie den Wert einer Funktion an den Punkten finden und , dann sind die Änderungsgrenzen dieser Funktion, ihre größten und kleinsten Werte bekannt.

Wenn das Argument von auf 8 steigt, erhöht sich die Funktion von auf .

Antwort: ; .

Nr. 32.2 (a) Gegeben: Finden Sie den größten und kleinsten Wert der Funktion in einem gegebenen Intervall.

Lassen Sie uns diese Funktion grafisch darstellen (siehe Abb. 2).

Wenn sich das Argument über das Intervall ändert, erhöht sich die Funktion von -2 auf 2. Wenn das Argument von steigt, verringert sich die Funktion von 2 auf 0.

Reis. 2. Funktionsgraph.

Finden wir die Ableitung.

, . Wenn , dann gehört dieser Wert auch zum angegebenen Segment. Wenn, dann. Es lässt sich leicht überprüfen, ob es andere Werte annimmt und die entsprechenden stationären Punkte außerhalb des angegebenen Segments liegen. Vergleichen wir die Werte der Funktion an den Enden des Segments und an ausgewählten Punkten, an denen die Ableitung gleich Null ist. Wir werden finden

;

Antwort: ;.

Die Antwort ist also eingegangen. In diesem Fall kann die Ableitung verwendet werden oder nicht, oder Sie können die zuvor untersuchten Eigenschaften der Funktion anwenden. Dies ist nicht immer der Fall; manchmal ist die Verwendung eines Derivats die einzige Methode, mit der Sie solche Probleme lösen können.

Gegeben: , . Finden Sie den größten und kleinsten Wert der Funktion in einem bestimmten Segment.

Wenn im vorherigen Fall auf die Ableitung verzichtet werden konnte – wir wussten, wie sich die Funktion verhält, dann ist die Funktion in diesem Fall recht komplex. Daher ist die Technik, die wir in der vorherigen Aufgabe erwähnt haben, uneingeschränkt anwendbar.

1. Finden wir die Ableitung. Finden wir kritische Punkte, also kritische Punkte. Aus ihnen wählen wir diejenigen aus, die zu diesem Segment gehören: . Vergleichen wir den Wert der Funktion an den Punkten , , . Dafür werden wir finden

Lassen Sie uns das Ergebnis in der Abbildung veranschaulichen (siehe Abb. 3).

Reis. 3. Grenzen der Änderungen von Funktionswerten

Wir sehen, dass sich die Funktion im Bereich von -3 bis 4 ändert, wenn sich das Argument von 0 auf 2 ändert. Die Funktion ändert sich nicht monoton: Sie nimmt entweder zu oder ab.

Antwort: ;.

Anhand von drei Beispielen wurde die allgemeine Technik zum Ermitteln der größten und kleinsten Werte einer Funktion auf einem Intervall, in diesem Fall auf einem Segment, demonstriert.

Algorithmus zur Lösung des Problems, den größten und kleinsten Wert einer Funktion zu finden:

1. Finden Sie die Ableitung der Funktion.

2. Finden Sie die kritischen Punkte der Funktion und wählen Sie die Punkte aus, die sich auf einem bestimmten Segment befinden.

3. Finden Sie die Werte der Funktion an den Enden des Segments und an ausgewählten Punkten.

4. Vergleichen Sie diese Werte und wählen Sie den größten und den kleinsten aus.

Schauen wir uns ein anderes Beispiel an.

Finden Sie den größten und kleinsten Wert der Funktion.

Der Graph dieser Funktion wurde zuvor betrachtet (siehe Abb. 4).

Reis. 4. Funktionsgraph.

Auf dem Intervall liegt der Wertebereich dieser Funktion . Punkt - Maximalpunkt. Wenn – die Funktion zunimmt, wenn – die Funktion abnimmt. Aus der Zeichnung geht hervor, dass , - nicht existiert.

In der Lektion haben wir uns also mit dem Problem der größten und kleinsten Werte einer Funktion befasst, wenn das gegebene Intervall ein Segment ist; formulierte einen Algorithmus zur Lösung solcher Probleme.

1. Algebra und Beginn der Analysis, Klasse 10 (in zwei Teilen). Lehrbuch für allgemeinbildende Einrichtungen ( Profilebene) Hrsg. A. G. Mordkovich. -M.: Mnemosyne, 2009.

2. Algebra und Beginn der Analysis, Klasse 10 (in zwei Teilen). Problembuch für Bildungseinrichtungen (Profilebene), hrsg. A. G. Mordkovich. -M.: Mnemosyne, 2007.

3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algebra und mathematische Analyse für die 10. Klasse ( Lernprogramm für Schüler von Schulen und Klassen mit vertieftem Mathematikstudium).-M.: Prosveshchenie, 1996.

4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Eingehendes Studium der Algebra und mathematischen Analyse.-M.: Bildung, 1997.

5. Sammlung von Problemen in der Mathematik für Bewerber an Hochschulen (herausgegeben von M.I. Skanavi). - M.: Higher School, 1992.

6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebraischer Simulator.-K.: A.S.K., 1997.

7. Zvavich L.I., Shlyapochnik L.Ya., Chinkina Algebra und die Anfänge der Analysis. 8.-11. Klassen: Ein Handbuch für Schulen und Klassen mit vertieftem Mathematikstudium (didaktische Materialien). - M.: Bustard, 2002.

8. Sahakyan S.M., Goldman A.M., Denisov D.V. Probleme der Algebra und Prinzipien der Analysis (ein Handbuch für Schüler der Klassen 10-11 allgemeinbildender Einrichtungen). - M.: Prosveshchenie, 2003.

9. Karp A.P. Sammlung von Problemen zur Algebra und Prinzipien der Analyse: Lehrbuch. Zulage für die Klassen 10-11. mit Tiefgang studiert Mathematik.-M.: Bildung, 2006.

10. Glazer G.I. Geschichte der Mathematik in der Schule. Klassen 9-10 (Handbuch für Lehrer).-M.: Bildung, 1983

Zusätzliche Webressourcen

2. Portal Naturwissenschaften ().

Machen Sie es zu Hause

Nr. 46.16, 46.17 (c) (Algebra und Anfänge der Analyse, Klasse 10 (in zwei Teilen). Problembuch für allgemeinbildende Einrichtungen (Profilebene), herausgegeben von A. G. Mordkovich. - M.: Mnemozina, 2007.)

Lassen Sie die Funktion y =F(X) ist stetig im Intervall [ a, b]. Bekanntlich erreicht eine solche Funktion auf diesem Segment ihre Maximal- und Minimalwerte. Die Funktion kann diese Werte entweder am internen Punkt des Segments annehmen [ a, b] oder an der Grenze des Segments.

Um den größten und kleinsten Wert einer Funktion auf dem Segment zu finden [ a, b] notwendig:

1) Finden Sie die kritischen Punkte der Funktion im Intervall ( a, b);

2) Berechnen Sie die Werte der Funktion an den gefundenen kritischen Punkten;

3) Berechnen Sie die Werte der Funktion am Ende des Segments, also wann X=A und x = B;

4) Wählen Sie aus allen berechneten Werten der Funktion den größten und kleinsten aus.

Beispiel. Finden Sie den größten und kleinsten Wert einer Funktion

auf dem Segment.

Kritische Punkte finden:

Diese Punkte liegen innerhalb des Segments; j(1) = ‒ 3; j(2) = ‒ 4; j(0) = ‒ 8; j(3) = 1;

am Punkt X= 3 und an der Stelle X= 0.

Untersuchung einer Funktion für Konvexität und Wendepunkt.

Funktion j = F (X) angerufen konvex zwischen (A, B) , wenn sein Graph unter der an irgendeinem Punkt in diesem Intervall gezogenen Tangente liegt und aufgerufen wird konvex nach unten (konkav), wenn sein Graph über der Tangente liegt.

Der Punkt, durch den Konvexität durch Konkavität ersetzt wird oder umgekehrt, wird aufgerufen Wendepunkt.

Algorithmus zur Untersuchung von Konvexität und Wendepunkt:

1. Finden Sie kritische Punkte zweiter Art, also Punkte, an denen die zweite Ableitung gleich Null ist oder nicht existiert.

2. Zeichnen Sie kritische Punkte auf der Zahlenlinie ein und teilen Sie sie in Intervalle auf. Finden Sie das Vorzeichen der zweiten Ableitung in jedem Intervall. Wenn, dann ist die Funktion nach oben konvex, wenn, dann ist die Funktion nach unten konvex.

3. Wenn sich beim Durchlaufen eines kritischen Punktes zweiter Art das Vorzeichen ändert und an diesem Punkt die zweite Ableitung gleich Null ist, dann ist dieser Punkt die Abszisse des Wendepunktes. Finden Sie seine Ordinate.

Asymptoten des Graphen einer Funktion. Untersuchung einer Funktion für Asymptoten.

Definition. Die Asymptote des Graphen einer Funktion heißt gerade, die die Eigenschaft hat, dass der Abstand von jedem Punkt im Diagramm zu dieser Linie gegen Null tendiert, wenn sich der Punkt im Diagramm auf unbestimmte Zeit vom Ursprung entfernt.

Es gibt drei Arten von Asymptoten: vertikal, horizontal und geneigt.

Definition. Die Gerade heißt vertikale Asymptote Funktionsgrafiken y = f(x), wenn mindestens einer der einseitigen Grenzen der Funktion an diesem Punkt gleich unendlich ist, also

Wo ist der Diskontinuitätspunkt der Funktion, das heißt, sie gehört nicht zum Definitionsbereich?

Beispiel.

D ( j) = (‒ ∞; 2) (2; + ∞)

X= 2 – Bruchpunkt.

Definition. Gerade y =A angerufen horizontale Asymptote Funktionsgrafiken y = f(x) bei , wenn

Beispiel.

Definition. Gerade y =kx +B (k≠ 0) heißt schräge Asymptote Funktionsgrafiken y = f(x) bei , wo

Allgemeines Schema zum Studieren von Funktionen und zum Erstellen von Graphen.

Funktionsforschungsalgorithmusy = f(x) :

1. Finden Sie den Definitionsbereich der Funktion D (j).

2. Finden Sie (falls möglich) die Schnittpunkte des Graphen mit den Koordinatenachsen (falls möglich). X= 0 und bei j = 0).

3. Untersuchen Sie die Gleichmäßigkeit und Ungeradeheit der Funktion ( j (‒ X) = j (X) ‒ Parität; j(‒ X) = ‒ j (X) ‒ seltsam).

4. Finden Sie die Asymptoten des Funktionsgraphen.

5. Finden Sie die Intervalle der Monotonie der Funktion.

6. Finden Sie die Extrema der Funktion.

7. Finden Sie die Konvexitätsintervalle (Konkavität) und Wendepunkte des Funktionsgraphen.

8. Erstellen Sie auf der Grundlage der durchgeführten Untersuchungen einen Graphen der Funktion.

Beispiel. Erkunden Sie die Funktion und erstellen Sie ihren Graphen.

1) D (j) =

X= 4 – Bruchpunkt.

2) Wann X = 0,

(0; ‒ 5) – Schnittpunkt mit Oh.

Bei j = 0,

3) j(‒ X)= Funktion Gesamtansicht(weder gerade noch ungerade).

4) Wir untersuchen auf Asymptoten.

a) vertikal

b) horizontal

c) Finden Sie die schrägen Asymptoten wo

‒schräge Asymptotengleichung

5) B gegebene Gleichung Es besteht keine Notwendigkeit, Intervalle der Monotonie der Funktion zu finden.

6)

Diese kritischen Punkte unterteilen den gesamten Definitionsbereich der Funktion in die Intervalle (˗∞; ˗2), (˗2; 4), (4; 10) und (10; +∞). Es ist zweckmäßig, die erzielten Ergebnisse in Form der folgenden Tabelle darzustellen.

Liebe Freunde! Die Aufgabengruppe im Zusammenhang mit der Ableitung umfasst Aufgaben – die Bedingung ergibt einen Graphen einer Funktion, mehrere Punkte auf diesem Graphen und die Frage lautet:

An welchem ​​Punkt ist die Ableitung am größten (am kleinsten)?

Wiederholen wir kurz:

Die Ableitung an einem Punkt ist gleich Neigung Tangente, die durchgehtDieser Punkt in der Grafik.

Uder globale Koeffizient der Tangente wiederum gleich Tangente der Neigungswinkel dieser Tangente.

*Dies bezieht sich auf den Winkel zwischen der Tangente und der x-Achse.

1. Auf Intervallen mit zunehmender Funktion hat die Ableitung positiver Wert.

2. In Intervallen seiner Abnahme hat die Ableitung einen negativen Wert.

Betrachten Sie die folgende Skizze:

An den Punkten 1,2,4 hat die Ableitung der Funktion einen negativen Wert, da diese Punkte zu abnehmenden Intervallen gehören.

An den Punkten 3,5,6 hat die Ableitung der Funktion einen positiven Wert, da diese Punkte zu zunehmenden Intervallen gehören.

Wie Sie sehen, ist mit der Bedeutung der Ableitung alles klar, das heißt, es ist überhaupt nicht schwer zu bestimmen, welches Vorzeichen sie an einem bestimmten Punkt im Diagramm hat (positiv oder negativ).

Wenn wir außerdem gedanklich Tangenten an diesen Punkten konstruieren, werden wir sehen, dass gerade Linien, die durch die Punkte 3, 5 und 6 verlaufen, Winkel mit der oX-Achse im Bereich von 0 bis 90 ° bilden, und dass gerade Linien, die durch die Punkte 1, 2 und 4 verlaufen, Winkel bilden Mit der OX-Achse reichen die Winkel von 90° bis 180°.

*Die Beziehung ist klar: Tangenten, die durch Punkte gehen, die zu Intervallen steigender Funktionen gehören, bilden spitze Winkel mit der oX-Achse, Tangenten, die durch Punkte gehen, die zu Intervallen fallender Funktionen gehören, bilden stumpfe Winkel mit der oX-Achse.

Jetzt die wichtige Frage!

Wie verändert sich der Wert des Derivats? Immerhin ist die Tangente in verschiedene Punkte Der Graph einer stetigen Funktion bildet unterschiedliche Winkel, je nachdem, welchen Punkt im Graphen er durchläuft.

*Oder sprechend in einfacher Sprache, die Tangente liegt so, als ob sie „horizontal“ oder „vertikal“ wäre. Sehen:

Gerade Linien bilden mit der oX-Achse Winkel im Bereich von 0 bis 90 °

Gerade Linien bilden mit der oX-Achse Winkel im Bereich von 90° bis 180°

Wenn Sie also Fragen haben:

— An welchem ​​der angegebenen Punkte im Diagramm hat die Ableitung den kleinsten Wert?

- An welchem ​​der angegebenen Punkte im Diagramm hat die Ableitung den größten Wert?

Um zu antworten, muss man verstehen, wie sich der Wert des Tangens des Tangentenwinkels im Bereich von 0 bis 180 ° ändert.

*Wie bereits erwähnt, ist der Wert der Ableitung der Funktion an einem Punkt gleich dem Tangens des Neigungswinkels der Tangente an die oX-Achse.

Der Tangenswert ändert sich wie folgt:

Wenn sich der Neigungswinkel der Geraden von 0° auf 90° ändert, ändert sich der Wert der Tangente und damit der Ableitung entsprechend von 0 auf +∞;

Wenn sich der Neigungswinkel der Geraden von 90° auf 180° ändert, ändert sich der Wert der Tangente und damit die Ableitung entsprechend –∞ auf 0.

Dies ist aus dem Diagramm der Tangensfunktion deutlich zu erkennen:

In einfachen Worten:

Bei einem tangentialen Neigungswinkel von 0° bis 90°

Je näher es an 0 o liegt, desto größer ist der Wert der Ableitung nahe Null (auf der positiven Seite).

Je näher der Winkel bei 90° liegt, desto stärker steigt der Ableitungswert in Richtung +∞.

Mit einem tangentialen Neigungswinkel von 90° bis 180°

Je näher er bei 90 o liegt, desto mehr nimmt der Ableitungswert in Richtung –∞ ab.

Je näher der Winkel bei 180° liegt, desto größer ist der Wert der Ableitung nahe Null (auf der negativen Seite).

317543. Die Abbildung zeigt einen Graphen der Funktion y = F(X) und die Punkte sind markiert–2, –1, 1, 2. An welchem ​​dieser Punkte ist die Ableitung am größten? Bitte geben Sie diesen Punkt in Ihrer Antwort an.

Wir haben vier Punkte: Zwei davon gehören zu den Intervallen, in denen die Funktion abnimmt (das sind die Punkte –1 und 1) und zwei zu den Intervallen, in denen die Funktion zunimmt (das sind die Punkte –2 und 2).

Wir können sofort schließen, dass die Ableitung an den Punkten –1 und 1 einen negativen Wert hat und an den Punkten –2 und 2 einen positiven Wert. Daher ist es in diesem Fall notwendig, die Punkte –2 und 2 zu analysieren und zu bestimmen, welcher von ihnen den größten Wert hat. Konstruieren wir Tangenten, die durch die angegebenen Punkte verlaufen:

Der Wert des Tangens des Winkels zwischen der Geraden a und der Abszissenachse beträgt Größerer Wert Tangens des Winkels zwischen der Linie b und dieser Achse. Das bedeutet, dass der Wert der Ableitung am Punkt –2 am größten sein wird.

Beantworten wir die folgende Frage: An welchem ​​Punkt –2, –1, 1 oder 2 ist der Wert der Ableitung am negativsten? Bitte geben Sie diesen Punkt in Ihrer Antwort an.

Die Ableitung wird an Punkten, die zu den abnehmenden Intervallen gehören, einen negativen Wert haben. Betrachten wir also die Punkte –2 und 1. Konstruieren wir Tangenten, die durch sie verlaufen:

Wir sehen das stumpfer Winkel zwischen der Geraden b und der oX-Achse liegt „näher“ bei 180Ö , daher ist sein Tangens größer als der Tangens des Winkels, der von der Geraden a und der oX-Achse gebildet wird.

Somit ist der Wert der Ableitung am Punkt x = 1 am größten negativ.

317544. Die Abbildung zeigt den Graphen der Funktion y = F(X) und die Punkte sind markiert–2, –1, 1, 4. An welchem ​​dieser Punkte ist die Ableitung am kleinsten? Bitte geben Sie diesen Punkt in Ihrer Antwort an.

Wir haben vier Punkte: Zwei davon gehören zu den Intervallen, in denen die Funktion abnimmt (das sind die Punkte –1 und 4) und zwei zu den Intervallen, in denen die Funktion zunimmt (das sind die Punkte –2 und 1).

Wir können sofort daraus schließen, dass die Ableitung an den Punkten –1 und 4 einen negativen Wert hat und an den Punkten –2 und 1 einen positiven Wert. Daher ist es in diesem Fall notwendig, die Punkte –1 und 4 zu analysieren und zu bestimmen, welcher von ihnen den kleinsten Wert hat. Konstruieren wir Tangenten, die durch die angegebenen Punkte verlaufen:

Der Wert des Tangens des Winkels zwischen der Geraden a und der Abszissenachse wird größer sein als der Wert des Tangens des Winkels zwischen der Geraden b und dieser Achse. Das bedeutet, dass der Wert der Ableitung am Punkt x = 4 am kleinsten ist.

Antwort: 4

Ich hoffe, ich habe Sie mit der Fülle des Schreibens nicht „überfordert“. Tatsächlich ist alles sehr einfach, Sie müssen nur die Eigenschaften der Ableitung, ihre geometrische Bedeutung und wie sich der Wert des Tangens des Winkels von 0 auf 180 ° ändert, verstehen.

1. Bestimmen Sie zunächst die Vorzeichen der Ableitung an diesen Punkten (+ oder -) und wählen Sie die erforderlichen Punkte aus (abhängig von der gestellten Frage).

2. Konstruieren Sie Tangenten an diesen Punkten.

3. Markieren Sie mithilfe des Tangesoiddiagramms schematisch die Winkel und zeigen Sie sie anAlexander.

P.S.: Ich wäre Ihnen dankbar, wenn Sie mir in den sozialen Netzwerken von der Seite erzählen würden.

Manchmal gibt es in den Aufgaben B15 „schlechte“ Funktionen, für die es schwierig ist, eine Ableitung zu finden. Früher geschah dies nur bei Probeprüfungen, mittlerweile sind diese Aufgaben so alltäglich, dass sie bei der Vorbereitung auf das echte Einheitliche Staatsexamen nicht mehr außer Acht gelassen werden können.

In diesem Fall funktionieren andere Techniken, eine davon ist monoton.

Eine Funktion f (x) heißt auf der Strecke monoton wachsend, wenn für beliebige Punkte x 1 und x 2 dieser Strecke gilt:

x 1< x 2 ⇒ f (x 1) < f (x 2).

Eine Funktion f (x) heißt auf der Strecke monoton fallend, wenn für beliebige Punkte x 1 und x 2 dieser Strecke gilt:

x 1< x 2 ⇒ f (x 1) > f ( x 2).

Mit anderen Worten: Für eine zunehmende Funktion gilt: Je größer x, desto größer f(x). Für eine abnehmende Funktion gilt das Gegenteil: Je größer x, desto weniger f(x).

Beispielsweise steigt der Logarithmus monoton, wenn die Basis a > 1 ist, und nimmt monoton ab, wenn 0< a < 1. Не забывайте про область допустимых значений логарифма: x > 0.

f (x) = log a x (a > 0; a ≠ 1; x > 0)

Die arithmetische Quadratwurzel (und nicht nur die Quadratwurzel) wächst monoton über den gesamten Definitionsbereich:

Die Exponentialfunktion verhält sich ähnlich wie der Logarithmus: Sie nimmt für a > 1 zu und für 0 ab< a < 1. Но в отличие от логарифма, Exponentialfunktion definiert für alle Zahlen, nicht nur x > 0:

f (x) = a x (a > 0)

Schließlich Grad mit negativem Exponenten. Sie können sie als Bruch schreiben. Sie haben einen Bruchpunkt, an dem die Monotonie unterbrochen wird.

Alle diese Funktionen sind in nie zu finden reiner Form. Sie fügen Polynome, Brüche und anderen Unsinn hinzu, was die Berechnung der Ableitung erschwert. Schauen wir uns an, was in diesem Fall passiert.

Koordinaten des Parabelscheitelpunkts

Am häufigsten wird das Funktionsargument durch ersetzt quadratisches Trinom der Form y = ax 2 + bx + c. Sein Graph ist eine Standardparabel, an der wir interessiert sind:

1. Die Äste einer Parabel können nach oben (für a > 0) oder nach unten (a) verlaufen< 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Der Scheitelpunkt einer Parabel ist der Extrempunkt einer quadratischen Funktion, an dem diese Funktion ihr Minimum (für a > 0) oder ihr Maximum (a) annimmt< 0) значение.

Von größtem Interesse ist Scheitelpunkt einer Parabel, deren Abszisse nach der Formel berechnet wird:

Damit haben wir den Extrempunkt der quadratischen Funktion gefunden. Wenn die ursprüngliche Funktion jedoch monoton ist, ist der Punkt x 0 für sie auch ein Extrempunkt. Formulieren wir also die Schlüsselregel:

Extremumpunkte eines quadratischen Trinoms und komplexe Funktion, in dem es enthalten ist, fallen zusammen. Daher können Sie nach x 0 für ein quadratisches Trinom suchen und die Funktion vergessen.

Aus der obigen Überlegung bleibt unklar, welchen Punkt wir erhalten: Maximum oder Minimum. Allerdings sind die Aufgaben so konzipiert, dass dies keine Rolle spielt. Urteile selbst:

1. Die Problemstellung enthält kein Segment. Daher besteht keine Notwendigkeit, f(a) und f(b) zu berechnen. Es bleiben nur noch die Extrempunkte zu betrachten;
2. Aber es gibt nur einen solchen Punkt – das ist der Scheitelpunkt der Parabel x 0, deren Koordinaten buchstäblich mündlich und ohne Ableitungen berechnet werden.

Dadurch wird die Lösung des Problems erheblich vereinfacht und besteht aus nur zwei Schritten:

1. Schreiben Sie die Gleichung der Parabel y = ax 2 + bx + c auf und ermitteln Sie ihren Scheitelpunkt mit der Formel: x 0 = −b /2a ;
2. Finden Sie den Wert der ursprünglichen Funktion an dieser Stelle: f (x 0). Wenn nein zusätzliche Bedingungen Nein, das wird die Antwort sein.

Auf den ersten Blick mögen dieser Algorithmus und seine Logik kompliziert erscheinen. Ich verzichte bewusst auf ein „bloßes“ Lösungsdiagramm, da die unüberlegte Anwendung solcher Regeln mit Fehlern behaftet ist.

Schauen wir uns echte Probleme aus dem Einheitlichen Staatsexamen in Mathematik an – hier kommt diese Technik am häufigsten vor. Gleichzeitig sorgen wir dafür, dass viele B15-Probleme auf diese Weise fast oral werden.

Unter der Wurzel steht quadratische Funktion y = x 2 + 6x + 13. Der Graph dieser Funktion ist eine Parabel mit Verzweigungen nach oben, da der Koeffizient a = 1 > 0 ist.

Scheitelpunkt der Parabel:

x 0 = −b /(2a ) = −6/(2 1) = −6/2 = −3

Da die Äste der Parabel nach oben gerichtet sind, nimmt die Funktion y = x 2 + 6x + 13 im Punkt x 0 = −3 ihren Minimalwert an.

Die Wurzel wächst monoton, was bedeutet, dass x 0 der Minimalpunkt der gesamten Funktion ist. Wir haben:

Aufgabe. Finden Sie den kleinsten Wert der Funktion:

y = log 2 (x 2 + 2x + 9)

Unter dem Logarithmus gibt es wieder eine quadratische Funktion: y = x 2 + 2x + 9. Der Graph ist eine Parabel mit nach oben gerichteten Ästen, weil a = 1 > 0.

Scheitelpunkt der Parabel:

x 0 = −b /(2a ) = −2/(2 1) = −2/2 = −1

Im Punkt x 0 = −1 nimmt die quadratische Funktion also ihren Minimalwert an. Aber die Funktion y = log 2 x ist monoton, also:

y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = ... = log 2 8 = 3

Der Exponent enthält die quadratische Funktion y = 1 − 4x − x 2 . Schreiben wir es in Normalform um: y = −x 2 − 4x + 1.

Offensichtlich ist der Graph dieser Funktion eine Parabel, die nach unten verzweigt (a = −1< 0). Поэтому вершина будет точкой максимума:

x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2

Die ursprüngliche Funktion ist exponentiell, sie ist monoton, sodass der größte Wert am gefundenen Punkt x 0 = −2 liegt:

Einem aufmerksamen Leser wird wahrscheinlich auffallen, dass wir den Bereich der zulässigen Werte von Wurzel und Logarithmus nicht ausgeschrieben haben. Dies war jedoch nicht erforderlich: Im Inneren befinden sich Funktionen, deren Werte immer positiv sind.

Folgerungen aus dem Bereich einer Funktion

Manchmal reicht es nicht aus, einfach den Scheitelpunkt der Parabel zu finden, um Problem B15 zu lösen. Der Wert, den Sie suchen, kann liegen am Ende des Segments und überhaupt nicht am Extrempunkt. Wenn das Problem überhaupt kein Segment anzeigt, schauen Sie nach Bereich akzeptabler Werte ursprüngliche Funktion. Nämlich:

Bitte beachten Sie noch einmal: Null darf durchaus unter der Wurzel stehen, jedoch niemals im Logarithmus oder Nenner eines Bruchs. Sehen wir uns anhand konkreter Beispiele an, wie das funktioniert:

Aufgabe. Finden Sie den größten Wert der Funktion:

Unter der Wurzel liegt wieder eine quadratische Funktion: y = 3 − 2x − x 2 . Sein Graph ist eine Parabel, verzweigt sich aber nach unten, weil a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический Quadratwurzel einer negativen Zahl existiert nicht.

Wir schreiben den Bereich der zulässigen Werte (APV) aus:

3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]

Suchen wir nun den Scheitelpunkt der Parabel:

x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1

Der Punkt x 0 = −1 gehört zum ODZ-Segment – ​​und das ist gut so. Jetzt berechnen wir den Wert der Funktion am Punkt x 0 sowie an den Enden der ODZ:

y(−3) = y(1) = 0

Wir haben also die Zahlen 2 und 0 erhalten. Wir werden gebeten, die größte zu finden – das ist die Zahl 2.

Aufgabe. Finden Sie den kleinsten Wert der Funktion:

y = log 0,5 (6x − x 2 − 5)

Innerhalb des Logarithmus gibt es eine quadratische Funktion y = 6x − x 2 − 5. Dies ist eine Parabel mit nach unten gerichteten Zweigen, aber der Logarithmus darf keine negativen Zahlen enthalten, daher schreiben wir die ODZ aus:

6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Bitte beachten Sie: Die Ungleichung ist streng, daher gehören die Enden nicht zur ODZ. Dies unterscheidet den Logarithmus von der Wurzel, wo uns die Enden des Segments recht gut passen.

Wir suchen den Scheitelpunkt der Parabel:

x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3

Der Scheitelpunkt der Parabel passt gemäß der ODZ: x 0 = 3 ∈ (1; 5). Da uns aber die Enden des Segments nicht interessieren, berechnen wir den Wert der Funktion nur am Punkt x 0:

y min = y (3) = log 0,5 (6 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2

Die Suche nach den kleinsten und größten Werten einer Funktion auf einem Segment erinnert an einen faszinierenden Flug um ein Objekt (Funktionsgraph) mit einem Hubschrauber, bei dem man mit einer Langstreckenkanone auf bestimmte Punkte feuert und ganz besondere Punkte auswählt von diesen Punkten aus für Kontrollschüsse. Punkte werden auf eine bestimmte Art und Weise und nach bestimmten Regeln ausgewählt. Nach welchen Regeln? Wir werden weiter darüber sprechen.

Wenn die Funktion j = F(X) ist stetig im Intervall [ A, B] , dann erreicht es dieses Segment am wenigsten Und höchste Werte . Dies kann entweder in geschehen Extrempunkte oder an den Enden des Segments. Daher zu finden am wenigsten Und die größten Werte der Funktion , kontinuierlich im Intervall [ A, B] , müssen Sie seine Werte insgesamt berechnen kritische Punkte und an den Enden des Segments, und wählen Sie dann das kleinste und größte davon aus.

Angenommen, Sie möchten den größten Wert der Funktion ermitteln F(X) auf dem Segment [ A, B] . Dazu müssen Sie alle kritischen Punkte finden, die auf [ A, B] .

Kritischer Punkt nennt man den Punkt, an dem Funktion definiert, und sie Derivat entweder gleich Null oder nicht vorhanden. Dann sollten Sie die Werte der Funktion an den kritischen Punkten berechnen. Und schließlich sollte man die Werte der Funktion an kritischen Punkten und an den Enden des Segments vergleichen ( F(A) Und F(B)). Die größte dieser Zahlen wird sein der größte Wert der Funktion im Segment [A, B] .

Probleme beim Finden kleinste Funktionswerte .

Wir suchen gemeinsam nach dem kleinsten und größten Wert der Funktion

Beispiel 1. Finden Sie den kleinsten und größten Wert einer Funktion auf dem Segment [-1, 2] .

Lösung. Finden Sie die Ableitung dieser Funktion. Setzen wir die Ableitung mit Null () gleich und erhalten zwei kritische Punkte: und . Um die kleinsten und größten Werte einer Funktion auf einem bestimmten Segment zu finden, reicht es aus, ihre Werte an den Enden des Segments und am Punkt zu berechnen, da der Punkt nicht zum Segment gehört [-1, 2]. Diese Funktionswerte sind: , , . Es folgt dem kleinster Funktionswert(im Diagramm unten rot angezeigt), gleich -7, wird am rechten Ende des Segments erreicht - am Punkt , und größte(in der Grafik ebenfalls rot), beträgt am kritischen Punkt 9,-.

Wenn eine Funktion in einem bestimmten Intervall stetig ist und dieses Intervall kein Segment ist (sondern z. B. ein Intervall ist); der Unterschied zwischen einem Intervall und einem Segment: Die Randpunkte des Intervalls sind nicht im Intervall enthalten, sondern die Randpunkte des Segments sind im Segment enthalten), dann darf es unter den Werten der Funktion nicht den kleinsten und den größten geben. So ist beispielsweise die in der Abbildung unten gezeigte Funktion stetig auf ]-∞, +∞[ und hat nicht den größten Wert.

Für jedes Intervall (geschlossen, offen oder unendlich) gilt jedoch die folgende Eigenschaft stetiger Funktionen.

Beispiel 4. Finden Sie den kleinsten und größten Wert einer Funktion auf dem Segment [-1, 3] .

Lösung. Die Ableitung dieser Funktion finden wir als Ableitung des Quotienten:

.

Wir setzen die Ableitung mit Null gleich, was uns einen kritischen Punkt gibt: . Es gehört zum Segment [-1, 3] . Um die kleinsten und größten Werte einer Funktion auf einem bestimmten Segment zu finden, ermitteln wir ihre Werte an den Enden des Segments und am gefundenen kritischen Punkt:

Vergleichen wir diese Werte. Fazit: gleich -5/13, an Punkt und Höchster Wert gleich 1 am Punkt .

Wir suchen weiterhin gemeinsam nach den kleinsten und größten Werten der Funktion

Es gibt Lehrer, die den Schülern beim Thema Finden der kleinsten und größten Werte einer Funktion keine Lösungsbeispiele geben, die komplexer sind als die gerade besprochenen, also solche, bei denen die Funktion ein Polynom oder a ist Bruch, dessen Zähler und Nenner Polynome sind. Aber wir werden uns nicht auf solche Beispiele beschränken, denn unter den Lehrern gibt es solche, die die Schüler gerne zum vollständigen Denken zwingen (die Ableitungstabelle). Daher werden der Logarithmus und die trigonometrische Funktion verwendet.

Beispiel 6. Finden Sie den kleinsten und größten Wert einer Funktion auf dem Segment .

Lösung. Wir finden die Ableitung dieser Funktion als Derivat des Produkts :

Wir setzen die Ableitung mit Null gleich, was einen kritischen Punkt ergibt: . Es gehört zum Segment. Um die kleinsten und größten Werte einer Funktion auf einem bestimmten Segment zu finden, ermitteln wir ihre Werte an den Enden des Segments und am gefundenen kritischen Punkt:

Ergebnis aller Aktionen: Die Funktion erreicht ihren Minimalwert, gleich 0, am Punkt und am Punkt und Höchster Wert, gleich e², an der Stelle.

Beispiel 7. Finden Sie den kleinsten und größten Wert einer Funktion auf dem Segment .

Lösung. Finden Sie die Ableitung dieser Funktion:

Wir setzen die Ableitung mit Null gleich:

Der einzige kritische Punkt betrifft das Segment. Um die kleinsten und größten Werte einer Funktion auf einem bestimmten Segment zu finden, ermitteln wir ihre Werte an den Enden des Segments und am gefundenen kritischen Punkt:

Abschluss: Die Funktion erreicht ihren Minimalwert, gleich , am Punkt und Höchster Wert, gleich , an der Stelle .

Bei angewandten Extremalproblemen kommt es beim Finden der kleinsten (maximalen) Werte einer Funktion in der Regel darauf an, das Minimum (Maximum) zu finden. Aber nicht die Minima oder Maxima selbst sind von größerem praktischen Interesse, sondern die Werte des Arguments, bei denen sie erreicht werden. Bei der Lösung angewandter Probleme entsteht eine zusätzliche Schwierigkeit: das Zusammenstellen von Funktionen, die das betrachtete Phänomen oder den betrachteten Prozess beschreiben.

Beispiel 8. Ein Tank mit einem Fassungsvermögen von 4 Litern, der die Form eines Parallelepipeds mit quadratischer Grundfläche hat und oben offen ist, muss verzinnt sein. Welche Abmessungen sollte der Tank haben, damit er Platz findet? geringste Menge Material?

Lösung. Lassen X- Basisseite, H- Tankhöhe, S- seine unbedeckte Oberfläche, V- seine Lautstärke. Die Oberfläche des Tanks wird durch die Formel ausgedrückt, d.h. ist eine Funktion zweier Variablen. Ausdrücken S Als Funktion einer Variablen nutzen wir die Tatsache, dass , von wo . Ersetzen des gefundenen Ausdrucks H in die Formel für S:

Lassen Sie uns diese Funktion bis zum Äußersten untersuchen. Es ist überall in ]0, +∞[ , und definiert und differenzierbar

.

Wir setzen die Ableitung mit Null () gleich und finden den kritischen Punkt. Wenn die Ableitung nicht existiert, ist dieser Wert außerdem nicht im Definitionsbereich enthalten und kann daher kein Extrempunkt sein. Das ist also der einzige kritische Punkt. Überprüfen wir anhand des zweiten ausreichenden Zeichens, ob ein Extremum vorliegt. Finden wir die zweite Ableitung. Wenn die zweite Ableitung größer als Null ist (). Dies bedeutet, dass die Funktion ein Minimum erreicht . Seit dem Minimum ist das einzige Extremum dieser Funktion, es ist ihr kleinster Wert. Die Seitenlänge des Tankbodens sollte also 2 m und seine Höhe 2 m betragen.

Beispiel 9. Von Punkt A Liegt direkt an der Bahnstrecke, bis zum Punkt MIT, in einiger Entfernung davon gelegen l Es muss Fracht transportiert werden. Die Kosten für den Transport einer Gewichtseinheit pro Entfernungseinheit auf der Schiene betragen , auf der Autobahn betragen sie . Bis zu welchem ​​Punkt M Linien Eisenbahn Für den Gütertransport sollte eine Autobahn gebaut werden A V MIT war am wirtschaftlichsten (Abschnitt AB wird davon ausgegangen, dass die Eisenbahnlinie gerade ist)?