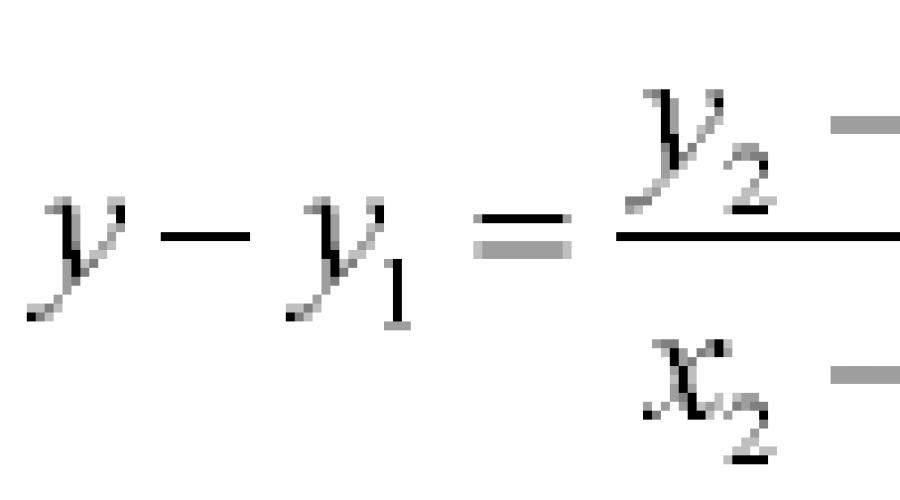
Eigenschaften einer Geraden in der euklidischen Geometrie.

Durch jeden Punkt können unendlich viele Geraden gezogen werden.

Durch zwei beliebige nicht zusammenfallende Punkte kann eine einzelne gerade Linie gezogen werden.

Zwei divergierende Linien in einer Ebene schneiden sich entweder in einem Punkt oder sind es

parallel (folgt aus dem vorherigen).

Im dreidimensionalen Raum gibt es drei Möglichkeiten für die relative Lage zweier Linien:

• Linien schneiden sich;

• Linien sind parallel;

• Geraden schneiden sich.

Gerade Linie— algebraische Kurve erster Ordnung: eine Gerade im kartesischen Koordinatensystem

ist in der Ebene durch eine Gleichung ersten Grades (lineare Gleichung) gegeben.

Allgemeine Gleichung einer Geraden.

Definition. Jede gerade Linie in der Ebene kann durch eine Gleichung erster Ordnung angegeben werden

Axt + Wu + C = 0,

und konstant A, B nicht gleichzeitig Null sind. Diese Gleichung erster Ordnung heißt allgemein

Gleichung einer Geraden. Abhängig von den Werten der Konstanten A, B Und MIT Folgende Sonderfälle sind möglich:

. C = 0, A ≠0, B ≠ 0- Eine Gerade geht durch den Ursprung

. A = 0, B ≠0, C ≠0 (By + C = 0)- Gerade parallel zur Achse Oh

. B = 0, A ≠0, C ≠ 0 (Ax + C = 0)- Gerade parallel zur Achse OU

. B = C = 0, A ≠0- Die Gerade fällt mit der Achse zusammen OU

. A = C = 0, B ≠0- Die Gerade fällt mit der Achse zusammen Oh

Die Gleichung einer Geraden lässt sich darstellen in in verschiedenen Formen je nach gegebenem

Anfangsbedingungen.

Gleichung einer Geraden aus einem Punkt und einem Normalenvektor.

Definition. In einem kartesischen rechtwinkligen Koordinatensystem ein Vektor mit den Komponenten (A, B)

senkrecht zu der durch die Gleichung gegebenen Geraden

Axt + Wu + C = 0.

Beispiel. Finden Sie die Gleichung einer Geraden, die durch einen Punkt verläuft A(1, 2) senkrecht zum Vektor (3, -1).

Lösung. Mit A = 3 und B = -1 stellen wir die Gleichung der Geraden auf: 3x - y + C = 0. Um den Koeffizienten C zu finden

Ersetzen wir die Koordinaten des gegebenen Punktes A in den resultierenden Ausdruck. Wir erhalten also: 3 - 2 + C = 0

C = -1. Gesamt: die erforderliche Gleichung: 3x - y - 1 = 0.

Gleichung einer Geraden, die durch zwei Punkte verläuft.

Gegeben seien zwei Punkte im Raum M 1 (x 1 , y 1 , z 1) Und M2 (x 2, y 2, z 2), Dann Gleichung einer Geraden,

durch diese Punkte gehen:

Wenn einer der Nenner Null ist, sollte der entsprechende Zähler gleich Null gesetzt werden. An

Ebene, die Gleichung der oben geschriebenen Geraden wird vereinfacht:

Wenn x 1 ≠ x 2 Und x = x 1, Wenn x 1 = x 2 .

Fraktion = k angerufen Neigung gerade.

Beispiel. Finden Sie die Gleichung der Geraden, die durch die Punkte A(1, 2) und B(3, 4) verläuft.

Lösung. Wenn wir die oben geschriebene Formel anwenden, erhalten wir:

Gleichung einer Geraden unter Verwendung eines Punktes und einer Steigung.

Wenn allgemeine Gleichung gerade Axt + Wu + C = 0 führen zu:

und benennen , dann heißt die resultierende Gleichung

Gleichung einer Geraden mit Steigung k.

Gleichung einer Geraden aus einem Punkt und einem Richtungsvektor.

In Analogie zum Punkt, der die Gleichung einer Geraden durch den Normalenvektor betrachtet, können Sie die Aufgabe eingeben

eine Gerade durch einen Punkt und ein Richtungsvektor einer Geraden.

Definition. Jeder Vektor ungleich Null (α 1 , α 2), deren Komponenten die Bedingung erfüllen

Aα 1 + Bα 2 = 0 angerufen Richtungsvektor einer geraden Linie.

Axt + Wu + C = 0.

Beispiel. Finden Sie die Gleichung einer Geraden mit einem Richtungsvektor (1, -1), die durch den Punkt A(1, 2) verläuft.

Lösung. Wir suchen nach der Gleichung der gewünschten Geraden in der Form: Ax + By + C = 0. Laut Definition ist

Koeffizienten müssen die folgenden Bedingungen erfüllen:

1 * A + (-1) * B = 0, d.h. A = B.

Dann hat die Geradengleichung die Form: Ax + Ay + C = 0, oder x + y + C / A = 0.

bei x = 1, y = 2 wir bekommen C/A = -3, d.h. erforderliche Gleichung:

x + y - 3 = 0

Gleichung einer Geraden in Segmenten.

Wenn in der allgemeinen Gleichung der Geraden Ах + Ву + С = 0 С≠0, dann erhalten wir durch Division durch -С:

oder wo

Die geometrische Bedeutung der Koeffizienten besteht darin, dass der Koeffizient a die Koordinate des Schnittpunkts ist

gerade mit Achse Oh, A B- Koordinate des Schnittpunkts der Linie mit der Achse OU.

Beispiel. Die allgemeine Gleichung einer Geraden ist gegeben x - y + 1 = 0. Finden Sie die Gleichung dieser Geraden in Segmenten.

C = 1, , a = -1, b = 1.

Normalgleichung einer Geraden.

Wenn beide Seiten der Gleichung Axt + Wu + C = 0 durch Zahl dividieren Was heisst

Normalisierungsfaktor, dann bekommen wir

xcosφ + ysinφ - p = 0 -Normalgleichung einer Geraden.

Das Vorzeichen ± des Normierungsfaktors muss so gewählt werden μ*C< 0.

R- die Länge der Senkrechten, die vom Ursprung zur Geraden fällt,

A φ - der Winkel, den diese Senkrechte mit der positiven Richtung der Achse bildet Oh.

Beispiel. Die allgemeine Gleichung der Geraden ist gegeben 12x - 5y - 65 = 0. Zum Schreiben erforderlich Verschiedene Arten Gleichungen

diese gerade Linie.

Die Gleichung dieser Geraden in Segmenten:

Die Gleichung dieser Geraden mit der Steigung: (durch 5 dividieren)

Gleichung einer Geraden:

cos φ = 12/13; Sünde φ= -5/13; p = 5.

Es ist zu beachten, dass nicht jede Gerade durch eine Gleichung in Segmenten dargestellt werden kann, zum Beispiel Geraden,

parallel zu den Achsen oder durch den Ursprung verlaufend.

Der Winkel zwischen geraden Linien in einer Ebene.

Definition. Wenn zwei Zeilen angegeben sind y = k 1 x + b 1 , y = k 2 x + b 2, dann der spitze Winkel zwischen diesen Linien

wird definiert als

Zwei Geraden sind parallel, wenn k 1 = k 2. Zwei Linien stehen senkrecht zueinander

Wenn k 1 = -1/ k 2 .

Satz.

Direkte Axt + Wu + C = 0 Und A 1 x + B 1 y + C 1 = 0 parallel, wenn die Koeffizienten proportional sind

A 1 = λA, B 1 = λB. Wenn auch С 1 = λС, dann fallen die Linien zusammen. Koordinaten des Schnittpunkts zweier Geraden

werden als Lösung des Gleichungssystems dieser Geraden gefunden.

Die Gleichung einer Geraden, die senkrecht zu einer gegebenen Geraden durch einen gegebenen Punkt verläuft.

Definition. Linie, die durch einen Punkt geht M 1 (x 1, y 1) und senkrecht zur Linie y = kx + b

dargestellt durch die Gleichung:

Abstand von einem Punkt zu einer Linie.

Satz. Wenn ein Punkt gegeben wird M(x 0, y 0), dann der Abstand zur Geraden Axt + Wu + C = 0 definiert als:

Nachweisen. Lassen Sie den Punkt M 1 (x 1, y 1)- die Basis einer Senkrechten, die von einem Punkt aus fällt M für ein gegebenes

Direkte. Dann der Abstand zwischen Punkten M Und M 1:

(1)

Koordinaten x 1 Und um 1 kann als Lösung des Gleichungssystems gefunden werden:

Die zweite Gleichung des Systems ist die Gleichung der durchlaufenden Geraden angegebenen Punkt M 0 senkrecht

gegebene gerade Linie. Wenn wir die erste Gleichung des Systems in die Form umwandeln:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

dann erhalten wir beim Lösen:

Wenn wir diese Ausdrücke in Gleichung (1) einsetzen, finden wir:

Der Satz ist bewiesen.

Gleichung einer geraden Linie, die durch t.u. verläuft A(ha; wa) und haben Neigung k, im Formular geschrieben

y – ua=k (x – xa).(5)

Gleichung einer Geraden, die durch zwei Punkte verläuft T. A (x 1; y 1) usw. B (x 2; y 2), hat die Form

Wenn Punkte A Und IN Definieren Sie eine gerade Linie parallel zur Ox-Achse (y 1 = y 2) oder Oy-Achse (x 1 = x 2), dann schreibt sich die Gleichung einer solchen Geraden entsprechend in die Form:

y = y 1 oder x = x 1(7)

Normalgleichung einer Geraden

Gegeben sei eine Gerade C, die durch einen gegebenen Punkt Mo(Ho;Vo) verläuft und senkrecht zum Vektor (A;B) steht. Jeder Vektor senkrecht zu einer bestimmten Linie wird als ihr bezeichnet Normalenvektor. Wählen wir einen beliebigen Punkt auf der Geraden. M (x;y). Dann, was bedeutet, dass sie Skalarprodukt. Diese Gleichheit kann in Koordinaten geschrieben werden

A(x-x o)+B(y-y o)=0 (8)

Gleichung (8) wird aufgerufen Normalgleichung einer Geraden .

Parametrische und kanonische Gleichungen der Geraden

Lass es gerade sein l durch den Ausgangspunkt gegeben M 0 (x 0; y 0) und Richtungsvektor ( a 1;a 2),. Lass t. M(x;y)– jeder Punkt, der auf einer geraden Linie liegt l. Dann ist der Vektor kollinear zum Vektor. Daher = . Wenn wir diese Gleichung in Koordinaten schreiben, erhalten wir die parametrische Gleichung der Geraden

Lassen Sie uns den Parameter t aus Gleichung (9) ausschließen. Dies ist möglich, da der Vektor ist und daher mindestens eine seiner Koordinaten von Null verschieden ist.

Sei und , dann , und deshalb,

Gleichung (10) wird aufgerufen kanonische Geradengleichung mit Führungsvektor

=(a 1; a 2). Wenn und 1 =0 und , dann nehmen die Gleichungen (9) die Form an

Diese Gleichungen geben eine gerade Linie parallel zur Achse an, OU und durch den Punkt gehen

M 0 (x 0; y 0).

x=x 0(11)

Wenn , , dann nehmen die Gleichungen (9) die Form an

Diese Gleichungen geben eine gerade Linie parallel zur O-Achse an X und durch den Punkt gehen

M 0 (x 0; y 0). Die kanonische Gleichung einer solchen Linie hat die Form

y=y 0(12)

Winkel zwischen Geraden. Die Bedingung der Parallelität und Rechtwinkligkeit zweier

Direkte

Gegeben seien zwei Geraden, definiert durch allgemeine Gleichungen:

Und

Dann der Winkel φ zwischen ihnen wird durch die Formel bestimmt:

(13)

Paralleler Zustand 2 direkt: (14)

Rechtwinkligkeitsbedingung 2 direkt: (15)

Paralleler Zustand hat in diesem Fall die Form: (17)

Rechtwinkligkeitsbedingung gerade: (18)

Wenn zwei Geraden durch kanonische Gleichungen gegeben sind:

Und

dann wird der Winkel φ zwischen diesen Linien durch die Formel bestimmt:

(19)

Paralleler Zustand gerade: (20)

Rechtwinkligkeitsbedingung Direkte: (21)

Abstand vom Punkt zur Linie

Distanz D vom Punkt M(x 1; y 1) zu einer geraden Linie Ax+By+C=0 nach der Formel berechnet

(22)

Implementierungsbeispiel praktische Arbeit

Beispiel 1. Baue Linie 3 X- 2bei+6=0.

Lösung: Um eine Gerade zu konstruieren, genügt es, zwei beliebige Punkte zu kennen, beispielsweise die Schnittpunkte mit den Koordinatenachsen. Punkt A des Schnittpunkts der Geraden mit der Ox-Achse erhält man, wenn man in die Gleichung der Geraden y = 0 einnimmt. Dann haben wir 3 X+6=0, d.h. X=-2. Auf diese Weise, A(–2;0).

Dann IN Schnittpunkt einer Geraden mit einer Achse OU hat eine Abszisse X=0; daher die Ordinate des Punktes IN ermittelt aus Gleichung –2 y+ 6=0, d.h. y=3. Auf diese Weise, IN(0;3).

Beispiel 2. Schreiben Sie eine Gleichung für eine gerade Linie, die sich auf der negativen Halbebene schneidet OU ein Segment gleich 2 Einheiten und bildet mit der Achse Oh Winkel φ =30˚.

Lösung: Die Gerade schneidet die Achse OU am Punkt IN(0;–2) und hat eine Steigung k=tg φ= = . Angenommen in Gleichung (2) k= und B= –2 erhalten wir die erforderliche Gleichung

Oder .

Beispiel 3. A(–1; 2) und

IN(0;–3). (j Zeugnis: Die Steigung der Geraden ergibt sich aus Formel (3))

Lösung: .Von hier aus haben wir . Einsetzen der Koordinaten in diese Gleichung Fernseher, wir bekommen: , d.h. Anfangskoordinate B= –3. Dann erhalten wir die Gleichung.

Beispiel 4. Allgemeine Gleichung der Zeile 2 X – 3bei– 6 = 0 führen zu einer Gleichung in Segmenten.

Lösung: Schreiben Sie es auf gegebene Gleichung als 2 X– 3bei=6 und dividiere beide Seiten durch den freien Term: . Dies ist die Gleichung dieser Geraden in Segmenten.

Beispiel 5. Durch den Punkt A(1;2) Zeichnen Sie eine gerade Linie, die gleiche Segmente auf den positiven Halbachsen der Koordinaten abschneidet.

Lösung: Die Gleichung der gewünschten Geraden habe die Form Nach Bedingung A=B. Daher nimmt die Gleichung die Form an X+ bei= A. Da Punkt A (1; 2) zu dieser Geraden gehört, erfüllen seine Koordinaten die Gleichung X + bei= A; diese. 1 + 2 = A, Wo A= 3. Damit ist die erforderliche Gleichung geschrieben auf die folgende Weise: x + y = 3, oder x + y – 3 = 0.

Beispiel 6. Für gerade Schreiben Sie die Gleichung in Segmenten. Berechnen Sie die Fläche des Dreiecks, das durch diese Linie und die Koordinatenachsen gebildet wird.

Lösung: Lassen Sie uns diese Gleichung wie folgt umwandeln: , oder .

Als Ergebnis erhalten wir die Gleichung , Das ist die Gleichung dieser Geraden in Segmenten. Das durch die gegebene Linie und die Koordinatenachsen gebildete Dreieck ist ein rechtwinkliges Dreieck mit den Schenkeln 4 und 3, daher beträgt seine Fläche S= (Quadrateinheiten)

Beispiel 7. Schreiben Sie eine Gleichung für eine Gerade, die durch den Punkt (–2; 5) verläuft, und eine Erzeugende mit der Achse Oh Winkel 45º.

Lösung: Winkelkoeffizient der gewünschten Geraden k= tan 45º = 1. Daher erhalten wir unter Verwendung von Gleichung (5). j – 5 = X– (–2), oder x – y + 7 = 0.

Beispiel 8. Schreiben Sie eine Gleichung für eine Gerade, die durch die Punkte verläuft A(–3; 5)und IN( 7; –2).

Lösung: Verwenden wir Gleichung (6):

, oder , von wo 7 X + 10bei – 29 = 0.

Beispiel 9.Überprüfen Sie, ob die Punkte liegen A(5; 2), IN(3; 1) und MIT(–1; –1) auf einer Geraden.

Lösung: Erstellen wir eine Gleichung einer geraden Linie, die durch die Punkte verläuft A Und MIT:

, oder

Ersetzen Sie die Koordinaten des Punktes in dieser Gleichung IN (xB= 3 und y B = 1) erhalten wir (3–5) / (–6) = = (1–2) / (–3), d.h. wir erhalten die richtige Gleichheit. Somit die Koordinaten des Punktes IN Erfüllen Sie die Gleichung der Geraden ( Wechselstrom), d.h. .

Beispiel 10: Schreiben Sie eine Gleichung für die Gerade, die durch den Punkt A(2;-3) verläuft.

Senkrecht =(-1;5)

Lösung: Mit Formel (8) finden wir die Gleichung dieser Geraden -1(x-2)+5(y+3)=0,

oder endlich, x – 5 y – 17=0.

Beispiel 11: Punkte werden vergeben M 1(2;-1) und M 2(4; 5). Schreiben Sie die Gleichung einer Geraden, die durch einen Punkt verläuft M 1 senkrecht zum Vektor Lösung: Der Normalenvektor der gewünschten Geraden hat die Koordinaten (2;6), daher erhalten wir mit Formel (8) die Gleichung 2(x-2)+6(y+1)=0 oder x+3y +1=0.

Beispiel 12: Und .

Lösung: ; .

Beispiel 13:

Lösung: a) ;

Beispiel 14: Berechnen Sie den Winkel zwischen Linien

Lösung:

Beispiel 15: Herausfinden gegenseitige Übereinkunft Direkte:

Lösung:

Beispiel 16: Finden Sie den Winkel zwischen den Linien und.

Lösung: .

Beispiel 17: Finden Sie die relative Position der Linien heraus:

Lösung:a ) - Geraden sind parallel;

b) – das bedeutet, dass die Linien senkrecht stehen.

Beispiel 18: Berechnen Sie den Abstand vom Punkt M(6; 8) zur Geraden

Lösung: Mit Formel (22) erhalten wir: .

Aufgaben für praktische Lektion:

Variante 1

1. Reduzieren Sie die allgemeine Gleichung der Geraden 2x+3y-6=0 auf eine Gleichung in Segmenten und berechnen Sie die Fläche des von dieser Geraden abgeschnittenen Dreiecks aus dem entsprechenden Koordinatenwinkel;

2. In ∆ABC haben die Eckpunkte die Koordinaten von Punkt A (-3;4), Punkt B (-4;-3), Punkt C (8;1). Erstellen Sie Gleichungen für Seite (AB), Höhe (VK) und Median (CM);

3. Berechnen Sie die Steigung der Geraden, die durch den Punkt M 0 (-2;4) und parallel zum Vektor (6;-1) verläuft;

4. Berechnen Sie den Winkel zwischen Linien

4. Berechnen Sie den Winkel zwischen den Linien:

a) 2x - 3y + 7 = 0 und 3x - y + 5 = 0; b) und y = 2x – 4;

5. Bestimmen Sie die relative Position von 2 Geraden und ;

, wenn die Koordinaten der Enden des Segments t.A(18;8) und t.B(-2;-6) bekannt sind.

Option 3

1. Reduzieren Sie die allgemeine Gleichung der Linie 4x-5y+20=0 auf eine Gleichung in Segmenten und berechnen Sie die Fläche des von dieser Linie abgeschnittenen Dreiecks aus dem entsprechenden Koordinatenwinkel.

2. In ∆ABC haben die Eckpunkte die Koordinaten von Punkt A (3;-2), Punkt B (7;3), Punkt

C (0;8). Erstellen Sie Gleichungen für Seite (AB), Höhe (VK) und Median (CM);

3. Berechnen Sie die Steigung der Geraden, die durch den Punkt M 0 (-1;-2) verläuft und

parallel zum Vektor (3;-5);

4. Berechnen Sie den Winkel zwischen Linien

a) 3x + y - 7 = 0 und x - y + 4 = 0; b) und ;

5. Bestimmen Sie die relative Position von 2 Geraden und y = 5x + 3;

6. Berechnen Sie den Abstand von der Mitte des Segments AB zur Geraden , wenn die Koordinaten der Enden des Segments t.A(4;-3) und t.B(-6;5) bekannt sind.

Option 4

1. Reduzieren Sie die allgemeine Gleichung der Linie 12x-5y+60=0 auf eine Gleichung in Segmenten und berechnen Sie die Länge des Segments, das von dieser Linie durch den entsprechenden Koordinatenwinkel abgeschnitten wird;

2. In ∆ABC haben die Eckpunkte die Koordinaten von Punkt A (0;-2), Punkt B (3;6), Punkt C (1;-4). Erstellen Sie Gleichungen für Seite (AB), Höhe (VK) und Median (CM);

3. Berechnen Sie die Steigung der Linie, die durch den Punkt M 0 (4;4) und parallel zum Vektor (-2;7) verläuft;

4. Berechnen Sie den Winkel zwischen Linien

a) x +4 y + 8 = 0 und 7x - 3y + 5 = 0; b) und ;

5. Bestimmen Sie die relative Position von 2 Geraden und ;

6. Berechnen Sie den Abstand von der Mitte des Segments AB zur Geraden , wenn die Koordinaten der Enden des Segments t.A(-4; 8) und t.B(0; 4) bekannt sind.

Kontrollfragen

1. Benennen Sie die Gleichungen einer Geraden in einer Ebene, wenn der Punkt, durch den sie verläuft, und ihr Richtungsvektor bekannt sind;

2. Welche Form hat die normale, allgemeine Gleichung einer Geraden auf einer Ebene?

3. Nennen Sie die Gleichung einer Geraden, die durch zwei Punkte verläuft, die Gleichung einer Geraden in Segmenten, die Gleichung einer Geraden mit einem Winkelkoeffizienten;

4. Listen Sie die Formeln zur Berechnung des Winkels zwischen Geraden auf, die durch Gleichungen mit einem Winkelkoeffizienten gegeben sind. Formulieren Sie die Bedingungen für Parallelität und Rechtwinkligkeit zweier Geraden.

5. Wie finde ich den Abstand von einem Punkt zu einer Linie?

In diesem Artikel lernen wir, wie man Gleichungen für eine Linie aufstellt, die durch einen bestimmten Punkt auf einer Ebene senkrecht zu einer bestimmten Linie verläuft. Lassen Sie uns die theoretischen Informationen studieren und präsentieren anschauliche Beispiele, wo es notwendig ist, eine solche Gleichung zu schreiben.

Yandex.RTB R-A-339285-1

Bevor Sie die Gleichung einer Geraden finden, die durch einen gegebenen Punkt senkrecht zu einer gegebenen Geraden verläuft. Der Satz wird in diskutiert weiterführende Schule. Durch einen gegebenen Punkt, der auf einer Ebene liegt, kann man eine einzelne Gerade senkrecht zu diesem Punkt ziehen. Wenn es einen dreidimensionalen Raum gibt, dann wird die Anzahl solcher Linien bis ins Unendliche ansteigen.

Definition 1

Wenn die Ebene α durch einen gegebenen Punkt M 1 senkrecht zu einer gegebenen Geraden b verläuft, dann stehen die in dieser Ebene liegenden Geraden, einschließlich der durch M 1 verlaufenden, senkrecht zu der gegebenen Geraden b.

Daraus können wir schließen, dass das Aufstellen einer Gleichung für eine Gerade, die durch einen gegebenen Punkt senkrecht zu einer gegebenen Geraden verläuft, nur für den Fall auf einer Ebene anwendbar ist.

Bei Problemen mit dem dreidimensionalen Raum muss nach der Gleichung einer Ebene gesucht werden, die durch einen bestimmten Punkt senkrecht zu einer bestimmten Linie verläuft.

Wenn wir auf einer Ebene mit einem Koordinatensystem O x y z eine Gerade b haben, dann entspricht sie der Gleichung der Geraden auf der Ebene, ein Punkt mit den Koordinaten M 1 (x 1, y 1) wird angegeben, und das ist er auch notwendig, um eine Gleichung der Geraden a zu erstellen, die durch den Punkt M 1 verläuft und senkrecht zur Geraden b steht.

Durch Bedingung haben wir die Koordinaten von Punkt M 1. Um die Gleichung einer geraden Linie zu schreiben, müssen Sie die Koordinaten des Richtungsvektors der geraden Linie a oder die Koordinaten des Normalenvektors der geraden Linie a oder den Winkelkoeffizienten der geraden Linie a haben.

Daten müssen abgerufen werden gegebene Gleichung gerade b . Gemäß der Bedingung stehen die Linien a und b senkrecht zueinander, was bedeutet, dass der Richtungsvektor der Linie b als Normalenvektor der Linie a betrachtet wird. Daraus ergibt sich, dass die Winkelkoeffizienten mit k b und k a bezeichnet werden. Sie hängen über die Beziehung k b · k a = - 1 zusammen.

Wir haben festgestellt, dass der Richtungsvektor der Geraden b die Form b → = (b x, b y) hat, daher ist der Normalenvektor n a → = (A 2, B 2), wobei die Werte A 2 = b x, B sind 2 = von y. Dann schreiben wir die allgemeine Gleichung der Linie, die durch den Punkt mit den Koordinaten M 1 (x 1 , y 1) verläuft, mit einem Normalenvektor n a → = (A 2 , B 2), mit der Form A 2 (x - x 1 ) + B 2 (y - y 1) = 0 .

Der Normalenvektor der Geraden b ist definiert und hat die Form n b → = (A 1, B 1), dann ist der Richtungsvektor der Geraden a der Vektor a → = (a x, a y), wobei die Werte a x = sind A 1, a y = B 1. Dies bedeutet, dass noch eine kanonische oder parametrische Gleichung einer Geraden a aufzustellen ist, die durch einen Punkt mit den Koordinaten M 1 (x 1, y 1) mit einem Richtungsvektor a → = (a x, a y) mit der Form x verläuft - x 1 a x = y - y 1 a y bzw. x = x 1 + a x · λ y = y 1 + a y · λ.

Nachdem Sie die Steigung k b der Geraden b ermittelt haben, können Sie die Steigung der Geraden a berechnen. Es wird gleich sein - 1 k b . Daraus folgt, dass wir die Gleichung einer geraden Linie a, die durch M 1 (x 1 , y 1) verläuft, mit einem Winkelkoeffizienten von - 1 k b in der Form y - y 1 = - 1 k b · (x - x 1) schreiben können. .

Die resultierende Gleichung einer Geraden, die durch einen gegebenen Punkt der Ebene senkrecht zu diesem verläuft. Wenn die Umstände es erfordern, können Sie zu einer anderen Form dieser Gleichung übergehen.

Beispiele lösen

Betrachten wir die Gleichung einer Geraden, die durch einen gegebenen Punkt der Ebene verläuft und senkrecht zu einer gegebenen Geraden steht.

Beispiel 1

Schreiben Sie die Gleichung der Geraden a auf, die durch den Punkt mit den Koordinaten M 1 (7, - 9) verläuft und senkrecht zur Geraden b steht, die durch die kanonische Geradengleichung x - 2 3 = y + 4 gegeben ist 1.

Lösung

Aus der Bedingung folgt, dass b → = (3, 1) der Richtungsvektor der Geraden x - 2 3 = y + 4 1 ist. Die Koordinaten des Vektors b → = 3, 1 sind die Koordinaten des Normalenvektors der Geraden a, da die Geraden a und b senkrecht zueinander stehen. Das bedeutet, dass wir n a → = (3, 1) erhalten. Nun ist es notwendig, die Gleichung einer Geraden aufzuschreiben, die durch den Punkt M 1 (7, - 9) verläuft und einen Normalenvektor mit den Koordinaten n a → = (3, 1) hat.

Wir erhalten eine Gleichung der Form: 3 · (x - 7) + 1 · (y - (- 9)) = 0 ⇔ 3 x + y - 12 = 0

Die resultierende Gleichung ist die gewünschte.

Antwort: 3 x + y - 12 = 0.

Beispiel 2

Schreiben Sie eine Gleichung für eine gerade Linie, die durch den Ursprung des Koordinatensystems O x y z senkrecht zur Geraden 2 x - y + 1 = 0 verläuft.

Lösung

Wir haben, dass n b → = (2, - 1) der Normalenvektor der gegebenen Geraden ist. Daher sind a → = (2, - 1) die Koordinaten des gewünschten Richtungsvektors der Geraden.

Stellen wir die Gleichung der durch den Ursprung verlaufenden Geraden mit dem Richtungsvektor a → = (2, - 1) fest. Wir erhalten, dass x - 0 2 = y + 0 - 1 ⇔ x 2 = y - 1 . Der resultierende Ausdruck ist die Gleichung einer Linie, die durch den Koordinatenursprung senkrecht zur Linie 2 x - y + 1 = 0 verläuft.

Antwort: x 2 = y - 1.

Beispiel 3

Schreiben Sie die Gleichung einer Geraden auf, die durch einen Punkt mit den Koordinaten M 1 (5, - 3) senkrecht zur Geraden y = - 5 2 x + 6 verläuft.

Lösung

Aus der Gleichung y = - 5 2 x + 6 hat die Steigung einen Wert von - 5 2 . Der Winkelkoeffizient einer dazu senkrechten Geraden hat den Wert - 1 - 5 · 2 = 2 · 5. Daraus schließen wir, dass die Linie, die durch den Punkt mit den Koordinaten M 1 (5, - 3) senkrecht zur Linie y = - 5 2 x + 6 verläuft, gleich y - (- 3) = 2 5 x - 5 ⇔ y ist = 2 5 x - 5 .

Antwort: y = 2 5 x - 5 .

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Eingabetaste

Gleichung einer Geraden, die durch zwei Punkte verläuft. Im Artikel" " Ich habe Ihnen versprochen, den zweiten Weg zur Lösung der vorgestellten Probleme der Ermittlung der Ableitung zu betrachten, wenn ein Graph einer Funktion und eine Tangente an diesen Graphen gegeben sind. Wir werden diese Methode in besprechen , nicht verpassen! Warum im nächsten?

Tatsache ist, dass dort die Formel für die Gleichung einer Geraden verwendet wird. Natürlich könnten wir diese Formel einfach zeigen und Ihnen raten, sie zu lernen. Aber es ist besser zu erklären, woher es kommt (wie es abgeleitet wird). Das ist notwendig! Wenn Sie es vergessen, können Sie es schnell wiederherstellenwird nicht schwierig sein. Im Folgenden wird alles im Detail beschrieben. Wir haben also zwei Punkte A auf der Koordinatenebene(x 1;y 1) und B(x 2;y 2) wird eine Gerade durch die angegebenen Punkte gezogen:

Hier ist die direkte Formel selbst:

*Das heißt, wenn wir bestimmte Koordinaten von Punkten ersetzen, erhalten wir eine Gleichung der Form y=kx+b.

**Wenn Sie sich diese Formel einfach „auswendig lernen“, besteht eine hohe Wahrscheinlichkeit, dass Sie mit den Indizes verwechselt werden X. Darüber hinaus können Indizes auf unterschiedliche Weise bezeichnet werden, zum Beispiel:

Deshalb ist es wichtig, die Bedeutung zu verstehen.

Nun die Herleitung dieser Formel. Alles ist sehr einfach!

Die Dreiecke ABE und ACF sind ähnlich scharfe Ecke(das erste Zeichen der Ähnlichkeit rechtwinklige Dreiecke). Daraus folgt, dass die Verhältnisse der entsprechenden Elemente gleich sind, das heißt:

Jetzt drücken wir diese Segmente einfach durch die Differenz der Koordinaten der Punkte aus:

Natürlich entsteht kein Fehler, wenn Sie die Beziehungen der Elemente in einer anderen Reihenfolge schreiben (Hauptsache, die Konsistenz bleibt erhalten):

Das Ergebnis wird die gleiche Geradengleichung sein. Das ist alles!

Das heißt, egal wie die Punkte selbst (und ihre Koordinaten) bezeichnet werden, wenn Sie diese Formel verstehen, werden Sie immer die Gleichung einer geraden Linie finden.

Die Formel kann mithilfe der Eigenschaften von Vektoren abgeleitet werden, das Ableitungsprinzip bleibt jedoch dasselbe, da es sich um die Proportionalität ihrer Koordinaten handelt. In diesem Fall funktioniert die gleiche Ähnlichkeit rechtwinkliger Dreiecke. Meiner Meinung nach ist die oben beschriebene Schlussfolgerung klarer)).

Ausgabe über Vektorkoordinaten anzeigen >>>

Auf der Koordinatenebene soll eine Gerade konstruiert werden, die durch zwei gegebene Punkte A(x 1;y 1) und B(x 2;y 2) verläuft. Markieren wir einen beliebigen Punkt C auf der Geraden mit Koordinaten ( X; j). Wir bezeichnen auch zwei Vektoren:

Es ist bekannt, dass für Vektoren, die auf parallelen Linien (oder auf derselben Linie) liegen, ihre entsprechenden Koordinaten proportional sind, das heißt:

— Wir schreiben die Gleichheit der Verhältnisse der entsprechenden Koordinaten auf:

Schauen wir uns ein Beispiel an:

Finden Sie die Gleichung einer Geraden, die durch zwei Punkte mit den Koordinaten (2;5) und (7:3) verläuft.

Sie müssen nicht einmal die gerade Linie selbst erstellen. Wir wenden die Formel an:

Es ist wichtig, dass Sie bei der Erstellung des Verhältnisses die Zusammenhänge verstehen. Sie können nichts falsch machen, wenn Sie schreiben:

Antwort: y=-2/5x+29/5 go y=-0,4x+5,8

Um sicherzustellen, dass die resultierende Gleichung korrekt gefunden wird, überprüfen Sie unbedingt die Koordinaten der Daten in der Bedingung der darin enthaltenen Punkte. Die Gleichungen sollten korrekt sein.

Das ist alles. Ich hoffe, das Material war für Sie nützlich.

Mit freundlichen Grüßen, Alexander.

P.S.: Ich wäre Ihnen dankbar, wenn Sie mir in den sozialen Netzwerken von der Seite erzählen würden.

Gleichung einer Geraden, die durch einen gegebenen Punkt verläuft in diese Richtung. Gleichung einer Geraden, die durch zwei gegebene Punkte verläuft. Der Winkel zwischen zwei Geraden. Der Zustand der Parallelität und Rechtwinkligkeit zweier Geraden. Bestimmen des Schnittpunkts zweier Geraden

1. Gleichung einer Geraden, die durch einen gegebenen Punkt verläuft A(X 1 , j 1) in einer bestimmten Richtung, bestimmt durch die Neigung k,

j - j 1 = k(X - X 1). (1)

Diese Gleichung definiert ein Bündel von Linien, die durch einen Punkt verlaufen A(X 1 , j 1), das Strahlzentrum genannt wird.

2. Gleichung einer Geraden, die durch zwei Punkte geht: A(X 1 , j 1) und B(X 2 , j 2), so geschrieben:

Der Winkelkoeffizient einer Geraden, die durch zwei gegebene Punkte verläuft, wird durch die Formel bestimmt

3. Winkel zwischen Geraden A Und B ist der Winkel, um den die erste Gerade gedreht werden muss A um den Schnittpunkt dieser Linien gegen den Uhrzeigersinn herum, bis er mit der zweiten Linie zusammenfällt B. Wenn zwei Geraden durch Gleichungen mit Steigung gegeben sind

j = k 1 X + B 1 ,