Finden Sie den Winkel zwischen drei Geraden. Die einfachsten Probleme mit einer geraden Linie in einer Ebene

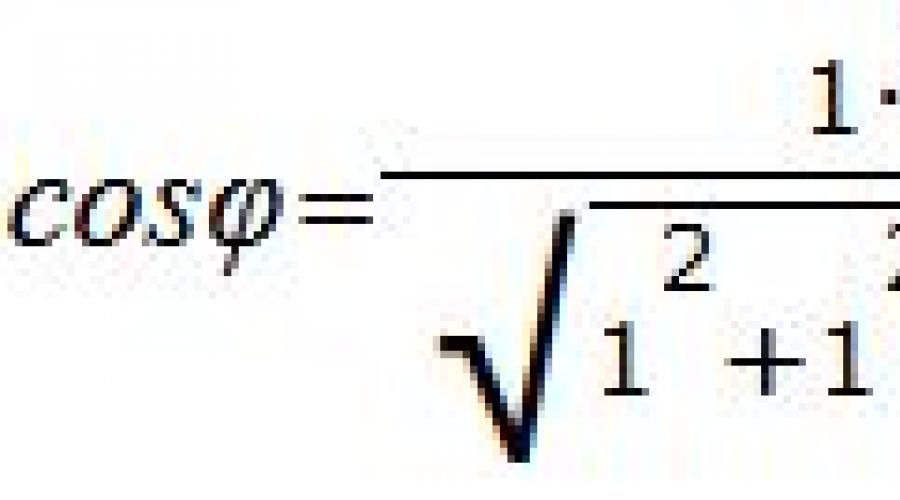
Mit dieser Hilfe Online-Rechner Sie können den Winkel zwischen geraden Linien ermitteln. Gegeben detaillierte Lösung mit Erläuterungen. Um den Winkel zwischen geraden Linien zu berechnen, stellen Sie die Abmessung ein (2, wenn eine gerade Linie auf einer Ebene betrachtet wird, 3, wenn eine gerade Linie im Raum betrachtet wird), geben Sie die Elemente der Gleichung in die Zellen ein und klicken Sie auf „Lösen“. Taste. Siehe den theoretischen Teil unten.

×

Warnung

Alle Zellen löschen?

Schließen Löschen

Anweisungen zur Dateneingabe. Zahlen werden als ganze Zahlen (Beispiele: 487, 5, -7623 usw.), Dezimalzahlen (z. B. 67, 102,54 usw.) oder Brüche eingegeben. Der Bruch muss in der Form a/b eingegeben werden, wobei a und b (b>0) Ganzzahlen oder Dezimalzahlen sind. Beispiele 45/5, 6,6/76,4, -7/6,7 usw.

1. Winkel zwischen Geraden in einer Ebene

Linien werden durch kanonische Gleichungen definiert

1.1. Bestimmen des Winkels zwischen Geraden

Lassen Sie die Linien im zweidimensionalen Raum L 1 und L

Somit können wir aus Formel (1.4) den Winkel zwischen den Geraden ermitteln L 1 und L 2. Wie aus Abb. 1 ersichtlich ist, bilden sich schneidende Linien benachbarte Winkel φ Und φ 1 . Wenn der gefundene Winkel größer als 90° ist, können Sie den minimalen Winkel zwischen Geraden ermitteln L 1 und L 2: φ 1 =180-φ .

Aus Formel (1.4) können wir die Bedingungen für Parallelität und Rechtwinkligkeit zweier Geraden ableiten.

Beispiel 1. Bestimmen Sie den Winkel zwischen Linien

Vereinfachen und lösen wir:

1.2. Bedingung für parallele Linien

Lassen φ =0. Dann cosφ=1. In diesem Fall nimmt der Ausdruck (1.4) die folgende Form an:

Beispiel 2: Bestimmen Sie, ob die Linien parallel sind

Gleichheit (1.9) ist erfüllt, daher sind die Geraden (1.10) und (1.11) parallel.

Antwort. Die Linien (1.10) und (1.11) sind parallel.

1.3. Bedingung für die Rechtwinkligkeit von Linien

Lassen φ =90°. Dann cosφ=0. In diesem Fall nimmt der Ausdruck (1.4) die folgende Form an:

Beispiel 3. Bestimmen Sie, ob die Linien senkrecht sind

Bedingung (1.13) ist erfüllt, daher stehen die Geraden (1.14) und (1.15) senkrecht zueinander.

Antwort. Die Linien (1.14) und (1.15) stehen senkrecht zueinander.

Linien werden durch allgemeine Gleichungen definiert

1.4. Bestimmen des Winkels zwischen Geraden

Lassen Sie zwei gerade Linien L 1 und L 2 werden durch allgemeine Gleichungen gegeben

Aus der Definition des Skalarprodukts zweier Vektoren ergibt sich:

Beispiel 4. Finden Sie den Winkel zwischen Linien

Werte ersetzen A 1 , B 1 , A 2 , B 2 in (1.23) erhalten wir:

Dieser Winkel ist größer als 90°. Lassen Sie uns den minimalen Winkel zwischen geraden Linien ermitteln. Subtrahieren Sie dazu diesen Winkel von 180:

Andererseits die Bedingung paralleler Linien L 1 und L 2 entspricht der Bedingung der Kollinearität von Vektoren N 1 und N 2 und kann wie folgt dargestellt werden:

Gleichheit (1.24) ist erfüllt, daher sind die Geraden (1.26) und (1.27) parallel.

Antwort. Die Linien (1.26) und (1.27) sind parallel.

1.6. Bedingung für die Rechtwinkligkeit von Linien

Bedingung für die Rechtwinkligkeit von Linien L 1 und L 2 kann durch Einsetzen aus Formel (1.20) extrahiert werden cos(φ )=0. Dann Skalarprodukt (N 1 ,N 2)=0. Wo

Gleichheit (1.28) ist erfüllt, daher stehen die Geraden (1.29) und (1.30) senkrecht zueinander.

Antwort. Die Geraden (1.29) und (1.30) stehen senkrecht aufeinander.

2. Winkel zwischen Geraden im Raum

2.1. Bestimmen des Winkels zwischen Geraden

Es sollen gerade Linien im Raum sein L 1 und L 2 sind durch kanonische Gleichungen gegeben

wo | Q 1 | und | Q 2 | Richtungsvektormodule Q 1 und Q 2 bzw. φ -Winkel zwischen Vektoren Q 1 und Q 2 .

Aus Ausdruck (2.3) erhalten wir:

.

Vereinfachen und lösen wir:

.

Finden wir den Winkel φ

WINKEL ZWISCHEN EBENEN

Betrachten Sie zwei Ebenen α 1 und α 2, die jeweils durch die Gleichungen definiert sind:

Unter Winkel zwischen zwei Ebenen werden wir eine davon verstehen Diederwinkel von diesen Ebenen gebildet. Es ist offensichtlich, dass der Winkel zwischen den Normalenvektoren und den Ebenen α 1 und α 2 gleich einem der angegebenen benachbarten Diederwinkel oder ist . Deshalb . Weil Und , Das

.

Beispiel. Bestimmen Sie den Winkel zwischen Ebenen X+2j-3z+4=0 und 2 X+3j+z+8=0.

Bedingung für die Parallelität zweier Ebenen.

Zwei Ebenen α 1 und α 2 sind genau dann parallel, wenn ihre Normalenvektoren parallel sind, und daher .

Zwei Ebenen sind also genau dann parallel zueinander, wenn die Koeffizienten der entsprechenden Koordinaten proportional sind:

oder

Bedingung der Rechtwinkligkeit von Ebenen.

Es ist klar, dass zwei Ebenen genau dann senkrecht stehen, wenn ihre Normalenvektoren senkrecht stehen, und daher oder .

Auf diese Weise, .

Beispiele.

GERADE IM RAUM.

VEKTORGLEICHUNG FÜR EINE LINIE.

PARAMETRISCHE DIREKTE GLEICHUNGEN

Die Position einer Linie im Raum wird vollständig durch die Angabe eines ihrer Fixpunkte bestimmt M 1 und ein Vektor parallel zu dieser Linie.

Ein Vektor parallel zu einer Geraden heißt Führer Vektor dieser Linie.

Also lass die gerade Linie l geht durch einen Punkt M 1 (X 1 , j 1 , z 1), liegt auf einer Linie parallel zum Vektor.

Betrachten Sie einen beliebigen Punkt M(x,y,z) auf einer geraden Linie. Aus der Abbildung geht das deutlich hervor .

Vektoren und sind kollinear, daher gibt es eine solche Zahl T, was , wo ist der Multiplikator T kann abhängig von der Position des Punktes einen beliebigen numerischen Wert annehmen M auf einer geraden Linie. Faktor T wird als Parameter bezeichnet. Nachdem wir die Radiusvektoren der Punkte bestimmt haben M 1 und M bzw. durch und erhalten wir . Diese Gleichung heißt Vektor Gleichung einer Geraden. Es zeigt dies für jeden Parameterwert T entspricht dem Radiusvektor eines Punktes M, auf einer geraden Linie liegend.

Schreiben wir diese Gleichung in Koordinatenform. Beachte das , und von hier

Die resultierenden Gleichungen werden aufgerufen parametrisch Gleichungen einer Geraden.

Beim Ändern eines Parameters T Koordinaten ändern sich X, j Und z und Punkt M bewegt sich in einer geraden Linie.

Kanonische Gleichungen des Direkten

Lassen M 1 (X 1 , j 1 , z 1) – ein Punkt, der auf einer geraden Linie liegt l, Und ist sein Richtungsvektor. Nehmen wir wieder einen beliebigen Punkt auf der Geraden M(x,y,z) und betrachte den Vektor.

Es ist klar, dass die Vektoren auch kollinear sind, daher müssen ihre entsprechenden Koordinaten proportional sein, daher

– kanonisch Gleichungen einer Geraden.

Anmerkung 1. Beachten Sie, dass die kanonischen Gleichungen der Geraden aus den parametrischen Gleichungen durch Eliminierung des Parameters erhalten werden könnten T. Tatsächlich erhalten wir aus den parametrischen Gleichungen oder .

Beispiel. Schreiben Sie die Geradengleichung auf in parametrischer Form.

Bezeichnen wir , von hier X = 2 + 3T, j = –1 + 2T, z = 1 –T.

Anmerkung 2. Die Gerade sei senkrecht zu einer der Koordinatenachsen, zum Beispiel der Achse Ochse. Dann ist der Richtungsvektor der Geraden senkrecht Ochse, somit, M=0. Folglich nehmen die parametrischen Gleichungen der Linie die Form an

Ausschließen des Parameters aus den Gleichungen T erhalten wir die Gleichungen der Geraden in der Form

Allerdings stimmen wir auch in diesem Fall zu, die kanonischen Gleichungen der Geraden formal in die Form zu schreiben . Wenn also der Nenner eines der Brüche Null ist, bedeutet dies, dass die Gerade senkrecht zur entsprechenden Koordinatenachse steht.

Ähnlich den kanonischen Gleichungen entspricht einer Geraden senkrecht zu den Achsen Ochse Und Oy oder parallel zur Achse Oz.

Beispiele.

ALLGEMEINE GLEICHUNGEN EINER GERADE ALS SCHNITTLINIEN ZWEIER EBENEN

Auf jeder geraden Linie im Weltraum gibt es unzählige Flugzeuge. Zwei beliebige davon, die sich schneiden, definieren es im Raum. Folglich stellen die Gleichungen zweier beliebiger solcher Ebenen zusammen betrachtet die Gleichungen dieser Linie dar.

Im Allgemeinen sind zwei beliebige nichtparallele Ebenen durch die allgemeinen Gleichungen gegeben

Bestimmen Sie die Gerade ihres Schnittpunkts. Diese Gleichungen heißen allgemeine Gleichungen gerade.

Beispiele.

Konstruieren Sie eine durch die Gleichungen gegebene Gerade

Um eine Gerade zu konstruieren, reicht es aus, zwei beliebige Punkte zu finden. Am einfachsten ist es, die Schnittpunkte einer Geraden mit Koordinatenebenen auszuwählen. Zum Beispiel der Schnittpunkt mit der Ebene xOy wir erhalten aus den Gleichungen der Geraden, vorausgesetzt z= 0:

Nachdem wir dieses System gelöst haben, finden wir den Punkt M 1 (1;2;0).

Ebenso vorausgesetzt j= 0, wir erhalten den Schnittpunkt der Geraden mit der Ebene xOz:

Von den allgemeinen Gleichungen einer Geraden kann man zu ihren kanonischen oder parametrischen Gleichungen übergehen. Dazu müssen Sie einen Punkt finden M 1 auf einer Geraden und dem Richtungsvektor einer Geraden.

Punktkoordinaten M 1 erhalten wir aus diesem Gleichungssystem, indem wir einer der Koordinaten einen beliebigen Wert geben. Um den Richtungsvektor zu finden, beachten Sie, dass dieser Vektor senkrecht zu beiden Normalenvektoren stehen muss Und . Daher jenseits des Richtungsvektors der Geraden l Sie können das Vektorprodukt von Normalenvektoren bilden:

.

Beispiel. Führen allgemeine Gleichungen gerade zur kanonischen Form.

Suchen wir einen Punkt, der auf einer Linie liegt. Dazu wählen wir willkürlich eine der Koordinaten aus, zum Beispiel j= 0 und löse das Gleichungssystem:

Die Normalenvektoren der die Linie definierenden Ebenen haben Koordinaten Daher ist der Richtungsvektor gerade

. Somit, l: .

WINKEL ZWISCHEN GERADE

Winkel zwischen geraden Linien im Raum nennen wir jeden der benachbarten Winkel, die durch zwei gerade Linien gebildet werden, die durch einen beliebigen Punkt parallel zu den Daten gezogen werden.

Gegeben seien zwei Geraden im Raum:

Offensichtlich kann der Winkel φ zwischen Geraden als Winkel zwischen ihren Richtungsvektoren und angenommen werden. Da wir dann die Formel für den Kosinus des Winkels zwischen Vektoren verwenden, erhalten wir

Für jeden Studenten, der sich auf das Einheitliche Staatsexamen in Mathematik vorbereitet, wird es nützlich sein, das Thema „Winkel zwischen Geraden finden“ zu wiederholen. Wie Statistiken zeigen, bereiten Aufgaben in diesem Abschnitt der Stereometrie beim Bestehen der Zertifizierungsprüfung Schwierigkeiten große Menge Studenten. Gleichzeitig finden sich Aufgaben, bei denen es darum geht, den Winkel zwischen Geraden zu ermitteln, sowohl im Grund- als auch im Einheitlichen Staatsexamen Profilebene. Das bedeutet, dass jeder sie lösen kann.

Grundlegende Momente

Es gibt 4 Arten relativer Positionen von Linien im Raum. Sie können zusammenfallen, sich schneiden, parallel sein oder sich schneiden. Der Winkel zwischen ihnen kann spitz oder gerade sein.

Um den Winkel zwischen Linien im Einheitlichen Staatsexamen oder beispielsweise beim Lösen zu ermitteln, können Schulkinder in Moskau und anderen Städten auf verschiedene Arten Probleme in diesem Abschnitt der Stereometrie lösen. Sie können die Aufgabe mit klassischen Konstruktionen lösen. Dazu lohnt es sich, die grundlegenden Axiome und Theoreme der Stereometrie zu erlernen. Der Schüler muss in der Lage sein, logisch zu denken und Zeichnungen zu erstellen, um die Aufgabe auf ein planimetrisches Problem zu übertragen.

Sie können die Koordinatenvektormethode auch mit einfachen Formeln, Regeln und Algorithmen verwenden. In diesem Fall kommt es vor allem darauf an, alle Berechnungen korrekt durchzuführen. Das Shkolkovo-Bildungsprojekt wird Ihnen helfen, Ihre Fähigkeiten zur Problemlösung in Stereometrie und anderen Abschnitten des Schulkurses zu verbessern.

Dieses Material ist einem Konzept wie dem Winkel zwischen zwei sich schneidenden Linien gewidmet. Im ersten Absatz erklären wir, was es ist und zeigen es in Abbildungen. Dann schauen wir uns die Möglichkeiten an, wie Sie den Sinus, den Cosinus dieses Winkels und den Winkel selbst ermitteln können (wir werden Fälle mit einem ebenen und dreidimensionalen Raum getrennt betrachten), geben die notwendigen Formeln an und zeigen dies anhand von Beispielen genau wie sie in der Praxis eingesetzt werden.

Yandex.RTB R-A-339285-1

Um zu verstehen, wie groß der Winkel ist, der entsteht, wenn sich zwei Linien schneiden, müssen wir uns an die Definition von Winkel, Rechtwinkligkeit und Schnittpunkt erinnern.

Definition 1

Wir nennen zwei Geraden einen Schnittpunkt, wenn sie einen gemeinsamen Punkt haben. Dieser Punkt wird als Schnittpunkt zweier Geraden bezeichnet.

Jede Gerade wird durch einen Schnittpunkt in Strahlen unterteilt. Beide Geraden bilden 4 Winkel, von denen zwei vertikal sind und zwei benachbart sind. Wenn wir das Maß eines davon kennen, können wir die übrigen bestimmen.

Nehmen wir an, wir wissen, dass einer der Winkel gleich α ist. In diesem Fall ist der dazu senkrechte Winkel ebenfalls gleich α. Um die verbleibenden Winkel zu ermitteln, müssen wir die Differenz 180° – α berechnen. Wenn α gleich 90 Grad ist, sind alle Winkel rechte Winkel. Linien, die sich im rechten Winkel schneiden, werden als Senkrechten bezeichnet (dem Begriff der Rechtwinkligkeit ist ein eigener Artikel gewidmet).

Schauen Sie sich das Bild an:

Kommen wir zur Formulierung der Hauptdefinition.

Definition 2

Der Winkel, den zwei sich schneidende Linien bilden, ist das Maß des kleineren der vier Winkel, die diese beiden Linien bilden.

Aus der Definition muss eine wichtige Schlussfolgerung gezogen werden: Die Größe des Winkels wird in diesem Fall durch eine beliebige reelle Zahl im Intervall (0, 90) ausgedrückt. Wenn die Linien senkrecht sind, ist der Winkel zwischen ihnen auf jeden Fall so gleich 90 Grad.

Die Fähigkeit, das Maß für den Winkel zwischen zwei sich schneidenden Linien zu ermitteln, ist für die Lösung vieler praktischer Probleme hilfreich. Die Lösungsmethode kann aus mehreren Optionen gewählt werden.

Zunächst können wir geometrische Methoden anwenden. Wenn wir etwas über Komplementärwinkel wissen, können wir sie anhand der Eigenschaften gleicher oder ähnlicher Figuren auf den benötigten Winkel beziehen. Wenn wir beispielsweise die Seiten eines Dreiecks kennen und den Winkel zwischen den Geraden berechnen müssen, auf denen diese Seiten liegen, dann ist der Kosinussatz für unsere Lösung geeignet. Wenn wir die Bedingung haben rechtwinkliges Dreieck, dann benötigen wir für Berechnungen auch Kenntnisse über Sinus, Cosinus und Tangens eines Winkels.

Die Koordinatenmethode eignet sich auch sehr gut zur Lösung solcher Probleme. Lassen Sie uns erklären, wie Sie es richtig verwenden.

Wir haben ein rechteckiges (kartesisches) Koordinatensystem O x y, in dem zwei Geraden gegeben sind. Bezeichnen wir sie mit den Buchstaben a und b. Die Geraden können mit einigen Gleichungen beschrieben werden. Die ursprünglichen Linien haben einen Schnittpunkt M. Wie bestimmt man den erforderlichen Winkel (nennen wir ihn α) zwischen diesen Geraden?

Beginnen wir mit der Formulierung des Grundprinzips der Winkelfindung unter gegebenen Bedingungen.

Wir wissen, dass das Konzept einer geraden Linie eng mit Konzepten wie einem Richtungsvektor und einem Normalenvektor zusammenhängt. Wenn wir eine Gleichung einer bestimmten Geraden haben, können wir daraus die Koordinaten dieser Vektoren entnehmen. Wir können dies für zwei sich schneidende Linien gleichzeitig tun.

Der Winkel zwischen zwei sich schneidenden Linien kann ermittelt werden mit:

• Winkel zwischen Richtungsvektoren;
• Winkel zwischen Normalenvektoren;
• der Winkel zwischen dem Normalenvektor einer Linie und dem Richtungsvektor der anderen.

Schauen wir uns nun jede Methode einzeln an.

1. Nehmen wir an, dass wir eine Gerade a mit einem Richtungsvektor a → = (a x, a y) und eine Gerade b mit einem Richtungsvektor b → (b x, b y) haben. Zeichnen wir nun zwei Vektoren a → und b → vom Schnittpunkt aus. Danach werden wir sehen, dass sie jeweils auf einer eigenen geraden Linie liegen. Dann haben wir vier Möglichkeiten für ihre relative Anordnung. Siehe Abbildung:

Wenn der Winkel zwischen zwei Vektoren nicht stumpf ist, dann ist es der Winkel, den wir zwischen den Schnittlinien a und b benötigen. Wenn er stumpf ist, ist der gewünschte Winkel gleich dem Winkel neben dem Winkel a →, b → ^. Somit ist α = a → , b → ^ wenn a → , b → ^ ≤ 90 ° , und α = 180 ° - a → , b → ^ wenn a → , b → ^ > 90 ° .

Basierend auf der Tatsache, dass die Kosinuswerte gleiche Winkel gleich sind, können wir die resultierenden Gleichungen wie folgt umschreiben: cos α = cos a → , b → ^ , wenn a → , b → ^ ≤ 90 ° ; cos α = cos 180° - a →, b → ^ = - cos a →, b → ^, wenn a →, b → ^ > 90°.

Im zweiten Fall wurden Reduktionsformeln verwendet. Auf diese Weise,

cos α cos a → , b → ^ , cos a → , b → ^ ≥ 0 - cos a → , b → ^ , cos a → , b → ^< 0 ⇔ cos α = cos a → , b → ^

Schreiben wir die letzte Formel in Worten:

Definition 3

Der Kosinus des Winkels, der durch zwei sich schneidende Geraden gebildet wird, ist gleich dem Modul des Kosinus des Winkels zwischen seinen Richtungsvektoren.

Die allgemeine Form der Formel für den Kosinus des Winkels zwischen zwei Vektoren a → = (a x , a y) und b → = (b x , b y) sieht folgendermaßen aus:

cos a → , b → ^ = a → , b → ^ a → b → = a x b x + a y + b y a x 2 + a y 2 b x 2 + by y 2

Daraus können wir die Formel für den Kosinus des Winkels zwischen zwei gegebenen Geraden ableiten:

cos α = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2 = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2

Dann kann der Winkel selbst mit der folgenden Formel ermittelt werden:

α = a r c cos a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2

Dabei sind a → = (a x , a y) und b → = (b x , b y) die Richtungsvektoren der gegebenen Geraden.

Lassen Sie uns ein Beispiel für die Lösung des Problems geben.

Beispiel 1

In einem rechtwinkligen Koordinatensystem auf einer Ebene sind zwei Schnittlinien a und b gegeben. Sie können durch die parametrischen Gleichungen x = 1 + 4 · λ y = 2 + λ λ ∈ R und x 5 = y - 6 - 3 beschrieben werden. Berechnen Sie den Winkel zwischen diesen Linien.

Lösung

Wir haben in unserer Bedingung eine parametrische Gleichung, was bedeutet, dass wir für diese Linie sofort die Koordinaten ihres Richtungsvektors angeben können. Dazu müssen wir die Werte der Koeffizienten für den Parameter nehmen, d.h. die Gerade x = 1 + 4 · λ y = 2 + λ λ ∈ R wird einen Richtungsvektor a → = (4, 1) haben.

Die zweite Zeile wird mit der kanonischen Gleichung x 5 = y - 6 - 3 beschrieben. Hier können wir die Koordinaten aus den Nennern entnehmen. Somit hat diese Linie einen Richtungsvektor b → = (5 , - 3) .

Als nächstes gehen wir direkt zur Bestimmung des Winkels über. Setzen Sie dazu einfach die vorhandenen Koordinaten der beiden Vektoren in die obige Formel ein: α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2 . Wir erhalten Folgendes:

α = a r c cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = a r c cos 17 17 34 = a r c cos 1 2 = 45 °

Antwort: Diese Geraden bilden einen Winkel von 45 Grad.

Wir können ein ähnliches Problem lösen, indem wir den Winkel zwischen Normalenvektoren ermitteln. Wenn wir eine Gerade a mit einem Normalenvektor n a → = (n a x , n a y) und eine Gerade b mit einem Normalenvektor n b → = (n b x , n b y) haben, dann ist der Winkel zwischen ihnen gleich dem Winkel zwischen n a → und n b → oder der Winkel, der an n a →, n b → ^ angrenzt. Diese Methode ist im Bild dargestellt:

Formeln zur Berechnung des Kosinus des Winkels zwischen sich schneidenden Linien und dieses Winkels selbst unter Verwendung der Koordinaten von Normalenvektoren sehen wie folgt aus:

cos α = cos n a →, n b → ^ = n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2 α = a r c cos n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2

Hier bezeichnen n a → und n b → die Normalenvektoren zweier gegebener Geraden.

Beispiel 2

In einem rechtwinkligen Koordinatensystem werden zwei Geraden durch die Gleichungen 3 x + 5 y – 30 = 0 und x + 4 y – 17 = 0 angegeben. Ermitteln Sie den Sinus und Cosinus des Winkels zwischen ihnen und die Größe dieses Winkels selbst.

Lösung

Die ursprünglichen Linien werden mithilfe von Normalliniengleichungen der Form A x + B y + C = 0 angegeben. Wir bezeichnen den Normalenvektor als n → = (A, B). Suchen wir die Koordinaten des ersten Normalenvektors für eine Linie und schreiben sie: n a → = (3, 5) . Für die zweite Linie x + 4 y - 17 = 0 hat der Normalenvektor die Koordinaten n b → = (1, 4). Nun addieren wir die erhaltenen Werte zur Formel und berechnen die Summe:

cos α = cos n a → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34

Wenn wir den Kosinus eines Winkels kennen, können wir seinen Sinus mithilfe der grundlegenden trigonometrischen Identität berechnen. Da der durch Geraden gebildete Winkel α nicht stumpf ist, gilt sin α = 1 - cos 2 α = 1 - 23 2 34 2 = 7 2 34.

In diesem Fall ist α = a r c cos 23 2 34 = a r c sin 7 2 34.

Antwort: cos α = 23 2 34, sin α = 7 2 34, α = a r c cos 23 2 34 = a r c sin 7 2 34

Analysieren wir den letzten Fall – das Ermitteln des Winkels zwischen Geraden, wenn wir die Koordinaten des Richtungsvektors einer Geraden und des Normalenvektors der anderen kennen.

Nehmen wir an, dass die Gerade a einen Richtungsvektor a → = (a x , a y) und die Gerade b einen Normalenvektor n b → = (n b x , n b y) hat. Wir müssen diese Vektoren vom Schnittpunkt entfernen und alle Optionen für ihre relativen Positionen berücksichtigen. Siehe im Bild:

Wenn der Winkel zwischen gegebene Vektoren nicht mehr als 90 Grad beträgt, stellt sich heraus, dass dadurch der Winkel zwischen a und b zu einem rechten Winkel ergänzt wird.

a → , n b → ^ = 90 ° - α wenn a → , n b → ^ ≤ 90 ° .

Wenn es weniger als 90 Grad beträgt, erhalten wir Folgendes:

a → , n b → ^ > 90 ° , dann a → , n b → ^ = 90 ° + α

Unter Verwendung der Regel der Kosinusgleichheit gleicher Winkel schreiben wir:

cos a → , n b → ^ = cos (90 ° - α) = sin α für a → , n b → ^ ≤ 90 ° .

cos a →, n b → ^ = cos 90 ° + α = - sin α für a →, n b → ^ > 90 °.

Auf diese Weise,

sin α = cos a → , n b → ^ , a → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , a → , n b → ^ > 90 ° ⇔ sin α = cos a → , n b → ^ , a → , n b → ^ > 0 - cos a → , n b → ^ , a → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^

Lassen Sie uns eine Schlussfolgerung formulieren.

Definition 4

Um den Sinus des Winkels zwischen zwei sich in einer Ebene schneidenden Linien zu ermitteln, müssen Sie den Modul des Kosinus des Winkels zwischen dem Richtungsvektor der ersten Linie und dem Normalenvektor der zweiten berechnen.

Schreiben wir die notwendigen Formeln auf. Den Sinus eines Winkels ermitteln:

sin α = cos a → , n b → ^ = a x n b x + a y n by a x 2 + a y 2 n b x 2 + n by 2

Den Winkel selbst finden:

α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n by 2

Hier ist a → der Richtungsvektor der ersten Linie und n b → der Normalenvektor der zweiten.

Beispiel 3

Zwei sich schneidende Geraden ergeben sich aus den Gleichungen x - 5 = y - 6 3 und x + 4 y - 17 = 0. Finden Sie den Schnittwinkel.

Lösung

Die Koordinaten des Leit- und Normalenvektors entnehmen wir den gegebenen Gleichungen. Es stellt sich heraus, dass a → = (- 5, 3) und n → b = (1, 4). Wir nehmen die Formel α = a r c sin = a x n b x + a y n by y a x 2 + a y 2 n b x 2 + n by 2 und berechnen:

α = a r c sin = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = a r c sin 7 2 34

Bitte beachten Sie, dass wir die Gleichungen aus der vorherigen Aufgabe übernommen und genau das gleiche Ergebnis erhalten haben, jedoch auf andere Weise.

Antwort:α = a r c sin 7 2 34

Lassen Sie uns eine andere Möglichkeit vorstellen, den gewünschten Winkel mithilfe der Winkelkoeffizienten gegebener Geraden zu ermitteln.

Wir haben eine Linie a, die in einem rechtwinkligen Koordinatensystem durch die Gleichung y = k 1 x + b 1 definiert ist, und eine Linie b, definiert als y = k 2 x + b 2. Dies sind Gleichungen von Geraden mit Steigungen. Um den Schnittwinkel zu ermitteln, verwenden wir die Formel:

α = a r c cos k 1 · k 2 + 1 k 1 2 + 1 · k 2 2 + 1, wobei k 1 und k 2 sind Winkelkoeffizienten gegebene Geraden. Um diesen Datensatz zu erhalten, wurden Formeln zur Bestimmung des Winkels durch die Koordinaten von Normalenvektoren verwendet.

Beispiel 4

Es gibt zwei Geraden, die sich in einer Ebene schneiden, durch Gleichungen gegeben y = - 3 5 x + 6 und y = - 1 4 x + 17 4 . Berechnen Sie den Wert des Schnittwinkels.

Lösung

Die Winkelkoeffizienten unserer Linien sind gleich k 1 = - 3 5 und k 2 = - 1 4. Fügen wir sie zur Formel α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 hinzu und berechnen wir:

α = a r c cos - 3 5 · - 1 4 + 1 - 3 5 2 + 1 · - 1 4 2 + 1 = a r c cos 23 20 34 24 · 17 16 = ar c cos 23 2 34

Antwort:α = a r c cos 23 2 34

Im Fazit dieses Absatzes ist zu beachten, dass die hier angegebenen Formeln zur Bestimmung des Winkels nicht auswendig gelernt werden müssen. Dazu reicht es aus, die Koordinaten der Hilfslinien und/oder Normalenvektoren gegebener Linien zu kennen und diese daraus bestimmen zu können verschiedene Typen Gleichungen. Aber es ist besser, sich die Formeln zur Berechnung des Kosinus eines Winkels zu merken oder aufzuschreiben.

So berechnen Sie den Winkel zwischen sich schneidenden Linien im Raum

Die Berechnung eines solchen Winkels kann auf die Berechnung der Koordinaten der Richtungsvektoren und die Bestimmung der Größe des von diesen Vektoren gebildeten Winkels reduziert werden. Für solche Beispiele wird die gleiche Argumentation wie zuvor verwendet.

Nehmen wir an, wir haben ein rechteckiges Koordinatensystem im dreidimensionalen Raum. Es enthält zwei Geraden a und b mit einem Schnittpunkt M. Um die Koordinaten der Richtungsvektoren zu berechnen, müssen wir die Gleichungen dieser Linien kennen. Bezeichnen wir die Richtungsvektoren a → = (a x , a y , a z) und b → = (b x , b y , b z) . Um den Kosinus des Winkels zwischen ihnen zu berechnen, verwenden wir die Formel:

cos α = cos a → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2

Um den Winkel selbst zu ermitteln, benötigen wir diese Formel:

α = a r c cos a x b x + a y by + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2

Beispiel 5

Wir haben eine im dreidimensionalen Raum definierte Linie mit der Gleichung x 1 = y - 3 = z + 3 - 2. Es ist bekannt, dass es die O z-Achse schneidet. Berechnen Sie den Schnittwinkel und den Kosinus dieses Winkels.

Lösung

Bezeichnen wir den Winkel, der berechnet werden muss, mit dem Buchstaben α. Schreiben wir die Koordinaten des Richtungsvektors für die erste Gerade auf – a → = (1, - 3, - 2) . Für die Anwendungsachse können wir uns am Koordinatenvektor k → = (0, 0, 1) orientieren. Wir haben die notwendigen Daten erhalten und können diese zur gewünschten Formel hinzufügen:

cos α = cos a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2

Als Ergebnis haben wir herausgefunden, dass der von uns benötigte Winkel gleich a r c cos 1 2 = 45 ° ist.

Antwort: cos α = 1 2 , α = 45 ° .

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Eingabetaste