Was ist der einbeschriebene Winkel auf dem Bogen. Eingeschriebene Winkeleigenschaften

Winkel ABC ist ein einbeschriebener Winkel. Es ruht auf dem Bogen AC, eingeschlossen zwischen seinen Seiten (Abb. 330).

Satz. Ein einbeschriebener Winkel wird durch die Hälfte des Bogens gemessen, den er schneidet.

Dies ist wie folgt zu verstehen: Ein einbeschriebener Winkel enthält so viele Winkelgrade, Minuten und Sekunden, wie Bogengrade, Minuten und Sekunden in der Hälfte des Bogens enthalten sind, auf dem er ruht.

Beim Beweis dieses Satzes müssen wir drei Fälle betrachten.

Erster Fall. Der Kreismittelpunkt liegt auf der Seite des einbeschriebenen Winkels (Abb. 331).

Sei ∠ABC ein einbeschriebener Winkel und der Mittelpunkt des Kreises O liegt auf der Seite BC. Es muss nachgewiesen werden, dass es mit dem halben Lichtbogen AC gemessen wird.

Verbinde Punkt A mit dem Mittelpunkt des Kreises. Wir erhalten die gleichschenkligen \(\Delta\)AOB, in denen AO = OB, als Radien desselben Kreises. Daher ist ∠A = ∠B.

∠AOC ist außerhalb des Dreiecks AOB, also ∠AOC = ∠A + ∠B, und da die Winkel A und B gleich sind, ist ∠B 1/2 ∠AOC.

Aber ∠AOC wird durch Lichtbogen AC gemessen, daher wird ∠B durch die Hälfte von Lichtbogen AC gemessen.

Wenn beispielsweise \(\breve(AC)\) 60°18' enthält, dann enthält ∠B 30°9'.

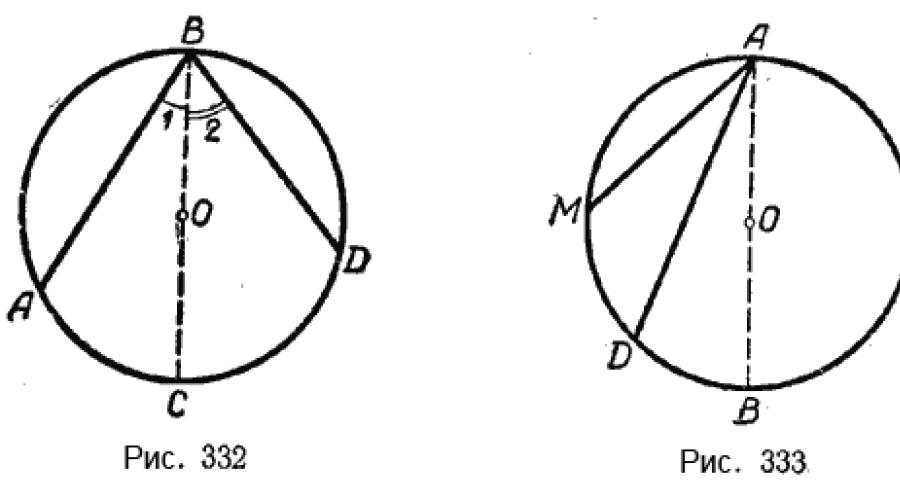
Zweiter Fall. Der Mittelpunkt des Kreises liegt zwischen den Seiten des einbeschriebenen Winkels (Abb. 332).

Sei ∠ABD ein einbeschriebener Winkel. Der Mittelpunkt des Kreises O liegt zwischen seinen Seiten. Es muss nachgewiesen werden, dass ∠ABD durch die Hälfte des Bogens AD gemessen wird.

Um dies zu beweisen, zeichnen wir den Durchmesser BC. Winkel ABD in zwei Winkel aufgeteilt: ∠1 und ∠2.

∠1 wird durch die Hälfte des Bogens AC gemessen, und ∠2 wird durch die Hälfte des Bogens CD gemessen, daher wird das gesamte ∠ABD durch 1/2 \(\breve(AC)\) + 1/2 \( \breve(CD)\), also die Hälfte des Bogens AD.

Wenn beispielsweise \(\breve(AD)\) 124° enthält, dann enthält ∠B 62°.

Dritter Fall. Der Kreismittelpunkt liegt außerhalb des einbeschriebenen Winkels (Abb. 333).

Sei ∠MAD ein einbeschriebener Winkel. Der Mittelpunkt des Kreises O liegt außerhalb der Ecke. Es muss nachgewiesen werden, dass ∠MAD durch die Hälfte des Bogens MD gemessen wird.

Zeichnen wir zum Beweis den Durchmesser AB. ∠MAD = ∠MAB - ∠DAB. Aber ∠MAB misst 1/2 \(\breve(MB)\) und ∠DAB misst 1/2 \(\breve(DB)\).

Daher misst ∠MAD 1 / 2 (\(\breve(MB) - \breve(DB))\), also 1 / 2 \(\breve(MD)\).

Wenn beispielsweise \(\breve(MD)\) 48° 38" enthält, dann enthält ∠MAD 24° 19' 8".

Konsequenzen
1. Alle einbeschriebenen Winkel, die auf demselben Bogen basieren, sind einander gleich, da sie von der Hälfte desselben Bogens gemessen werden (Abb. 334, a).

2. Ein auf einen Durchmesser bezogener einbeschriebener Winkel ist ein rechter Winkel, da er auf einem Halbkreis basiert. Die Hälfte des Kreises enthält 180 Bogengrade, was bedeutet, dass der Winkel bezogen auf den Durchmesser 90 Winkelgrade enthält (Abb. 334, b).

Meistens beginnt die Vorbereitung auf die Prüfung in Mathematik mit einer Wiederholung der grundlegenden Definitionen, Formeln und Theoreme, einschließlich des Themas "Zentral und in einem Kreiswinkel eingeschrieben". In der Regel wird dieser Abschnitt der Planimetrie studiert weiterführende Schule. Es ist nicht verwunderlich, dass viele Schüler mit der Notwendigkeit konfrontiert sind, die grundlegenden Konzepte und Theoreme zum Thema "Mittelwinkel eines Kreises" zu wiederholen. Nachdem die Schüler den Algorithmus zur Lösung solcher Probleme herausgefunden haben, können sie auf der Grundlage der Ergebnisse des einheitlichen Staatsexamens mit Wettbewerbspunkten rechnen.

Wie bereitet man sich einfach und effektiv auf die Zertifizierungsprüfung vor?

Im Studium vor dem einheitlichen Staatsexamen stehen viele Abiturienten vor dem Problem, die notwendigen Informationen zum Thema „Mittel- und Innenwinkel im Kreis“ zu finden. Nicht immer ist ein Schulbuch zur Hand. Und die Suche nach Formeln im Internet nimmt manchmal viel Zeit in Anspruch.

Fähigkeiten zu "pumpen" und Kenntnisse in einem so schwierigen Bereich der Geometrie wie der Planimetrie zu verbessern, Bildungsportal. Shkolkovo lädt Gymnasiasten und ihre Lehrer ein, den Prozess der Vorbereitung auf das einheitliche Staatsexamen neu zu gestalten. Alle Grundmaterialien werden von unseren Spezialisten in der zugänglichsten Form präsentiert. Nach Durchsicht der Informationen im Abschnitt „Theoretische Referenz“ lernen die Schüler, welche Eigenschaften der Mittelpunktswinkel eines Kreises hat, wie man seinen Wert findet usw.

Um das erworbene Wissen zu festigen und Fähigkeiten auszubauen, empfehlen wir Ihnen, die entsprechenden Übungen durchzuführen. Große Auswahl Aufgaben zum Ermitteln des Werts des in einen Kreis eingeschriebenen Winkels und anderer Parameter werden im Abschnitt "Katalog" vorgestellt. Zu jeder Übung haben unsere Experten einen detaillierten Lösungsverlauf aufgeschrieben und die richtige Antwort angegeben. Die Aufgabenliste auf der Seite wird ständig ergänzt und aktualisiert.

Gymnasiasten können sich auf die Prüfung vorbereiten, indem sie Übungen machen, z. B. den Wert des Mittelpunktswinkels und die Länge eines Kreisbogens online ermitteln, wenn sie sich in einer beliebigen russischen Region befinden.

Die erledigte Aufgabe kann bei Bedarf im Bereich „Favoriten“ gespeichert werden, um später darauf zurückzukommen und ihre Lösung noch einmal prinzipiell zu analysieren.

Eingeschriebener Winkel, Problemtheorie. Freunde! In diesem Artikel werden wir über Aufgaben sprechen, für deren Lösung es notwendig ist, die Eigenschaften eines eingeschriebenen Winkels zu kennen. Dies ist eine ganze Gruppe von Aufgaben, die in der Prüfung enthalten sind. Die meisten von ihnen werden sehr einfach in einem Schritt gelöst.

Es gibt schwierigere Aufgaben, die Ihnen jedoch keine großen Schwierigkeiten bereiten. Sie müssen die Eigenschaften des eingeschriebenen Winkels kennen. Nach und nach werden wir alle Prototypen von Aufgaben analysieren, ich lade Sie zum Blog ein!

Nun die notwendige Theorie. Erinnern Sie sich, was für ein zentraler und eingeschriebener Winkel, Sehne, Bogen, auf dem diese Winkel beruhen:

Der Mittelpunktswinkel in einem Kreis wird als flacher Winkel mit bezeichnetSpitze in seiner Mitte.

Der Teil eines Kreises, der sich innerhalb einer flachen Ecke befindetKreisbogen genannt.

Das Gradmaß eines Kreisbogens ist das Gradmaßentsprechenden Mittelwinkel.

Ein Winkel heißt in einen Kreis einbeschrieben, wenn der Scheitelpunkt des Winkels liegtauf einem Kreis, und die Seiten des Winkels schneiden diesen Kreis.

Eine Strecke, die zwei Punkte auf einem Kreis verbindet, wird aufgerufenAkkord. Die längste Sehne geht durch die Mitte des Kreises und wird aufgerufenDurchmesser.

Um Aufgaben für in einen Kreis einbeschriebene Winkel zu lösen,Sie müssen die folgenden Eigenschaften kennen:

1. Der einbeschriebene Winkel ist gleich dem halben Zentriwinkel, bezogen auf denselben Bogen.

2. Alle einbeschriebenen Winkel, die auf demselben Bogen basieren, sind gleich.

3. Alle einbeschriebenen Winkel, die derselben Sehne zugrunde liegen und deren Scheitelpunkte auf derselben Seite dieser Sehne liegen, sind gleich.

4. Jedes Winkelpaar, das auf derselben Sehne basiert und dessen Scheitelpunkte auf gegenüberliegenden Seiten der Sehne liegen, ergibt zusammen 180°.

Folgerung: Gegenüberliegende Winkel eines einem Kreis einbeschriebenen Vierecks ergeben zusammen 180 Grad.

5. Alle einbeschriebenen Winkel, bezogen auf den Durchmesser, sind gerade.

Im Allgemeinen ist diese Eigenschaft eine Folge von Eigenschaft (1), dies ist ihr besonderer Fall. Schauen Sie - der Mittelpunktswinkel ist gleich 180 Grad (und dieser entwickelte Winkel ist nichts anderes als ein Durchmesser), was bedeutet, dass der einbeschriebene Winkel C gemäß der ersten Eigenschaft gleich seiner Hälfte ist, dh 90 Grad.

Die Kenntnis dieser Eigenschaft hilft bei der Lösung vieler Probleme und ermöglicht es Ihnen oft, unnötige Berechnungen zu vermeiden. Wenn Sie es gut beherrschen, werden Sie mehr als die Hälfte dieser Art von Problemen mündlich lösen können. Zwei Konsequenzen, die gemacht werden können:

Korollar 1: Wenn einem Kreis ein Dreieck einbeschrieben ist und eine seiner Seiten mit dem Durchmesser dieses Kreises zusammenfällt, dann ist das Dreieck rechtwinklig (Spitze rechter Winkel liegt auf dem Kreis).

Korollar 2: das Zentrum der beschriebenen ungefähr rechtwinkliges Dreieck Kreis fällt mit dem Mittelpunkt seiner Hypotenuse zusammen.

Viele Prototypen stereometrischer Probleme werden ebenfalls unter Verwendung dieser Eigenschaft und dieser Folgerungen gelöst. Denken Sie an die Tatsache selbst: Wenn der Durchmesser eines Kreises eine Seite eines einbeschriebenen Dreiecks ist, dann ist dieses Dreieck rechtwinklig (der Winkel gegenüber dem Durchmesser beträgt 90 Grad). Alle anderen Schlussfolgerungen und Konsequenzen können Sie selbst ziehen, Sie müssen sie nicht lehren.

In der Regel wird die Hälfte der Aufgaben für einen einbeschriebenen Winkel mit einer Skizze, aber ohne Notation angegeben. Um den Denkprozess beim Lösen von Problemen (unten im Artikel) zu verstehen, werden die Bezeichnungen von Scheitelpunkten (Ecken) eingeführt. Auf der Prüfung können Sie dies nicht tun.Betrachten Sie die Aufgaben:

Was ist ein spitzer einbeschriebener Winkel, der eine Sehne schneidet, die gleich dem Radius des Kreises ist? Geben Sie Ihre Antwort in Grad an.

Lassen Sie uns einen zentralen Winkel für einen gegebenen einbeschriebenen Winkel bauen und die Eckpunkte bezeichnen:

Nach der Eigenschaft eines in einen Kreis eingeschriebenen Winkels:

Der Winkel AOB ist gleich 60 0 , da das Dreieck AOB gleichseitig ist und in einem gleichseitigen Dreieck alle Winkel gleich 60 0 sind. Die Seiten des Dreiecks sind gleich, da die Bedingung besagt, dass die Sehne gleich dem Radius ist.

Somit beträgt der einbeschriebene Winkel DIA 30 0 .

Antwort: 30

Finden Sie die Sehne, auf der der Winkel 30 0 ruht, eingeschrieben in einen Kreis mit Radius 3.

Dies ist im Wesentlichen das umgekehrte Problem (des vorherigen). Lassen Sie uns eine zentrale Ecke bauen.

Er ist doppelt so groß wie der eingeschriebene, dh der Winkel AOB beträgt 60 0 . Daraus können wir schließen, dass das Dreieck AOB gleichseitig ist. Somit ist die Sehne gleich dem Radius, also drei.

Antwort: 3

Der Radius des Kreises ist 1. Finden Sie den Wert eines stumpfen einbeschriebenen Winkels basierend auf einer Sehne gleich der Wurzel von zwei. Geben Sie Ihre Antwort in Grad an.

Bauen wir den Mittelwinkel:

Wenn wir den Radius und die Sehne kennen, können wir den Mittelpunktswinkel DIA finden. Dies kann mit dem Kosinussatz erfolgen. Wenn wir den Mittelpunktswinkel kennen, können wir leicht den einbeschriebenen Winkel ACB finden.

Kosinussatz: Das Quadrat jeder Seite eines Dreiecks ist gleich der Summe der Quadrate der beiden anderen Seiten, ohne das Produkt dieser Seiten mal den Kosinus des Winkels zwischen ihnen zu verdoppeln.

Daher beträgt der zweite Mittelpunktswinkel 360 0 – 90 0 = 270 0 .

Gemäß der Eigenschaft eines eingeschriebenen Winkels ist der Winkel DIA gleich seiner Hälfte, dh 135 Grad.

Antwort: 135

Finden Sie die Sehne, auf der der Winkel von 120 Grad, die Wurzel von drei, in einem Radiuskreis eingeschrieben ist.

Verbinde die Punkte A und B mit dem Mittelpunkt des Kreises. Nennen wir es O:

Wir kennen den Radius und den einbeschriebenen Winkel DIA. Wir können den Mittelpunktswinkel AOB (größer als 180 Grad) finden und dann den Winkel AOB im Dreieck AOB finden. Berechnen Sie dann mit dem Kosinussatz AB.

Aufgrund der Eigenschaft eines einbeschriebenen Winkels ist der zentrale Winkel AOB (der größer als 180 Grad ist) gleich dem zweifachen einbeschriebenen Winkel, dh 240 Grad. Das bedeutet, dass der Winkel AOB im Dreieck AOB 360 0 - 240 0 = 120 0 beträgt.

Nach dem Kosinussatz gilt:

Antwort:3

Finden Sie den einbeschriebenen Winkel basierend auf dem Bogen, der 20 % des Kreises ausmacht. Geben Sie Ihre Antwort in Grad an.

Aufgrund der Eigenschaft eines einbeschriebenen Winkels ist er halb so groß wie der Mittelpunktswinkel, der auf demselben Bogen basiert, in diesem Fall sprechen wir vom Bogen AB.

Man sagt, dass der Bogen AB 20 Prozent des Umfangs ausmacht. Das bedeutet, dass der Zentriwinkel AOB ebenfalls 20 Prozent von 360 0 beträgt.* Ein Kreis ist ein Winkel von 360 Grad. Meint,

Somit beträgt der einbeschriebene Winkel ACB 36 Grad.

Antwort: 36

Bogen eines Kreises AC, enthält keine Punkte B, beträgt 200 Grad. Und der Bogen des Kreises BC, der keine Punkte enthält EIN, beträgt 80 Grad. Finden Sie den eingeschriebenen Winkel ACB. Geben Sie Ihre Antwort in Grad an.

Lassen Sie uns der Klarheit halber die Bögen bezeichnen, deren Winkelmaße angegeben sind. Bogen entsprechend 200 Grad - blaue Farbe, der Bogen, der 80 Grad entspricht, ist rot, der Rest des Kreises ist es gelb.

Somit ist das Gradmaß des Bogens AB (gelb) und damit der Mittelpunktswinkel AOB: 360 0 – 200 0 – 80 0 = 80 0 .

Der einbeschriebene Winkel DAB ist der halbe Zentriwinkel AOB, also gleich 40 Grad.

Antwort: 40

Wie groß ist der einbeschriebene Winkel bezogen auf den Durchmesser des Kreises? Geben Sie Ihre Antwort in Grad an.

Sie müssen die Eigenschaft des einbeschriebenen Winkels kennen; verstehen, wann und wie man den Kosinussatz anwendet, mehr dazu.

Das ist alles! Ich wünsche Ihnen Erfolg!

Mit freundlichen Grüßen Alexander Krutitskikh

Mathelehrer der dritten Klasse
- Kinder, sag mir, wie viel wird 6 * 6 sein?
Die Kinder antworten im Chor:
- Sechsundsiebzig!
- Nun, wovon redest du, Kinder! Sechs mal sechs ist sechsunddreißig … naja, vielleicht 37, 38, 39 … naja, maximal 40 … aber nicht sechsundsiebzig!

P.S: Ich wäre Ihnen dankbar, wenn Sie in sozialen Netzwerken über die Website berichten.

In diesem Artikel werde ich Ihnen sagen, wie Sie Probleme lösen können, die .

Zuerst erinnern wir uns wie üblich an die Definitionen und Theoreme, die Sie kennen müssen, um Probleme auf erfolgreich zu lösen.

1.Eingeschriebener Winkel ist ein Winkel, dessen Scheitelpunkt auf dem Kreis liegt und dessen Seiten den Kreis schneiden:

2.Zentrale Ecke ist der Winkel, dessen Scheitelpunkt mit dem Mittelpunkt des Kreises zusammenfällt:

Gradgröße des Kreisbogens gemessen durch den Wert des Zentriwinkels, auf dem es ruht.

In diesem Fall ist der Gradwert des AC-Bogens gleich dem Wert des Winkels AOC.

3. Wenn der einbeschriebene und der zentrale Winkel auf demselben Bogen basieren, dann der einbeschriebene Winkel ist das Doppelte des Zentriwinkels:

4. Alle eingeschriebenen Winkel, die sich auf einen Bogen stützen, sind einander gleich:

5. Der einbeschriebene Winkel bezogen auf den Durchmesser beträgt 90°:

Wir werden mehrere Probleme lösen.

eines . Aufgabe B7 (#27887)

Lassen Sie uns den Wert des Mittelpunktswinkels finden, der auf demselben Bogen beruht:

Offensichtlich beträgt der Wert des Winkels AOC 90°, daher beträgt der Winkel ABC 45°

Antwort: 45°

2. Aufgabe B7 (Nr. 27888)

Finden Sie den Winkel ABC. Geben Sie Ihre Antwort in Grad an.

Offensichtlich beträgt der Winkel AOC 270°, dann beträgt der Winkel ABC 135°.

Antwort: 135°

3 . Aufgabe B7 (#27890)

Finden Sie den Gradwert des Bogens AC des Kreises, auf dem der Winkel ABC ruht. Geben Sie Ihre Antwort in Grad an.

Lassen Sie uns den Wert des Mittelpunktswinkels finden, der auf dem Bogen AC beruht:

Der Wert des Winkels AOC beträgt 45°, daher beträgt das Gradmaß des Bogens AC 45°.

Antwort: 45°.

vier . Aufgabe B7 (#27885)

Finden Sie den Winkel ACB, wenn die einbeschriebenen Winkel ADB und DAE auf Kreisbögen basieren, deren Gradwerte jeweils und sind. Geben Sie Ihre Antwort in Grad an.

Der Winkel ADB liegt auf dem Kreisbogen AB, daher beträgt der Wert des Zentriwinkels AOB 118°, der Winkel BDA also 59° und der angrenzende Winkel ADC 180°-59° = 121°

Ebenso beträgt der Winkel DOE 38° und der entsprechende einbeschriebene Winkel DAE 19°.

Betrachten Sie das Dreieck ADC:

Die Winkelsumme eines Dreiecks beträgt 180°.

Der Wert des Winkels ASV ist 180°- (121°+19°)=40°

Antwort: 40°

5 . Aufgabe B7 (#27872)

Die Seiten des Vierecks ABCD AB, BC, CD und AD grenzen an die Bögen des umschriebenen Kreises an, deren Gradwerte jeweils , , und sind. Finden Sie den Winkel B dieses Vierecks. Geben Sie Ihre Antwort in Grad an.

Der Winkel B liegt auf dem Bogen ADC, dessen Wert gleich der Summe der Werte der Bögen AD und CD ist, also 71°+145°=216°

Der einbeschriebene Winkel B ist gleich dem halben Wert des Bogens ADC, also 108°

Antwort: 108°

6. Aufgabe B7 (#27873)

Die Punkte A, B, C, D, die sich auf einem Kreis befinden, teilen diesen Kreis in vier Bögen AB, BC, CD und AD, deren Gradwerte jeweils als 4:2:3:6 zusammenhängen. Finden Sie den Winkel A des Vierecks ABCD. Geben Sie Ihre Antwort in Grad an.

(siehe Zeichnung der vorherigen Aufgabe)

Da wir das Verhältnis der Beträge der Bögen angegeben haben, führen wir das Einheitselement x ein. Dann wird die Größe jedes Bogens wie folgt ausgedrückt:

AB=4x, BC=2x, CD=3x, AD=6x. Alle Bögen bilden einen Kreis, dh ihre Summe beträgt 360 °.

4x+2x+3x+6x=360°, also x=24°.

Der Winkel A liegt auf den Bögen BC und CD, die zusammen einen Wert von 5x=120° haben.

Daher beträgt der Winkel A 60°

Antwort: 60°

7. Aufgabe B7 (#27874)

Viereck A B C D in einen Kreis eingeschrieben. Ecke ABC gleich , Winkel CAD

Anweisung

Wenn der Radius (R) des Kreises und die Länge des Bogens (L) entsprechend dem gewünschten Zentriwinkel (θ) bekannt sind, kann er sowohl in Grad als auch in Bogenmaß berechnet werden. Die Summe ergibt sich aus der Formel 2 * π * R und entspricht einem Mittelpunktswinkel von 360° oder zwei Pi-Zahlen, wenn anstelle von Grad das Bogenmaß verwendet wird. Gehen Sie daher von der Proportion 2*π*R/L = 360°/θ = 2*π/θ aus. Drücke daraus den Zentriwinkel im Bogenmaß θ = 2*π/(2*π*R/L) = L/R oder Grad θ = 360°/(2*π*R/L) = 180*L/(π * R) und berechnen Sie nach der resultierenden Formel.

Entsprechend der Länge der Sehne (m), die die Punkte verbindet, die den Mittelpunktswinkel (θ) definieren, kann sein Wert auch berechnet werden, wenn der Radius (R) des Kreises bekannt ist. Betrachten Sie dazu ein Dreieck, das aus zwei Radien und besteht. Das gleichschenkligen Dreiecks, alle sind bekannt, aber Sie müssen den Winkel finden, der der Basis gegenüberliegt. Der Sinus seiner Hälfte ist gleich dem Verhältnis der Länge der Basis - der Sehne - zur doppelten Länge der Seite - dem Radius. Verwenden Sie daher für Berechnungen die inverse Sinusfunktion - den Arcussinus: θ \u003d 2 * arcsin (½ * m / R).

Der Zentriwinkel kann auch in Bruchteilen einer Drehung oder aus einem vollen Winkel angegeben werden. Wenn Sie beispielsweise den Mittelpunktswinkel ermitteln möchten, der einer Vierteldrehung entspricht, teilen Sie 360° durch vier: θ = 360°/4 = 90°. Derselbe Wert im Bogenmaß sollte 2*π/4 ≈ 3,14/2 ≈ 1,57 sein. Der entwickelte Winkel entspricht einer halben vollen Umdrehung, sodass beispielsweise der Mittelwinkel, der einem Viertel davon entspricht, die Hälfte der oben berechneten Werte sowohl in Grad als auch in Bogenmaß beträgt.

Die trigonometrische Funktion des inversen Sinus wird aufgerufen Arkussinus. Es kann Werte annehmen, die innerhalb der Hälfte der Pi-Zahl liegen, sowohl positiv als auch negativ. negative Seite wenn in Radiant gemessen. In Grad gemessen liegen diese Werte jeweils im Bereich von -90° bis +90°.

Anweisung

Einige „runde“ Werte müssen nicht berechnet werden, sie sind leichter zu merken. Zum Beispiel: - wenn das Funktionsargument Null ist, dann ist der Wert des Arkussinus davon auch Null; - von 1/2 ist 30 ° oder 1/6 Pi, falls gemessen; - der Arkussinus von -1/2 ist gleich bis -30° oder -1/6 von pi in ;- Bogensinus von 1 ist 90° oder 1/2 von pi im Bogenmaß;- Bogensinus von -1 ist -90° oder -1/2 von pi im Bogenmaß;

Um die Werte dieser Funktion aus anderen Argumenten zu messen, ist es am einfachsten, den Standard-Windows-Rechner zu verwenden, falls vorhanden. Um zu beginnen, öffnen Sie das Hauptmenü über die Schaltfläche "Start" (oder durch Drücken der WIN-Taste), gehen Sie zum Abschnitt "Alle Programme" und dann zum Unterabschnitt "Zubehör" und klicken Sie auf den Punkt "Rechner".

Schalten Sie die Rechneroberfläche in den Betriebsmodus, in dem Sie rechnen können trigonometrische Funktionen. Öffnen Sie dazu in dessen Menü den Bereich „Ansicht“ und wählen Sie den Punkt „Engineering“ oder „Scientific“ (je nach verwendetem Betriebssystem).

Geben Sie den Wert des Arguments ein, aus dem der Arkustangens berechnet werden soll. Klicken Sie dazu mit der Maus auf die Schnittstellenschaltflächen des Taschenrechners, oder drücken Sie die Tasten auf , oder kopieren Sie den Wert (STRG + C) und fügen Sie ihn dann (STRG + V) in das Eingabefeld des Taschenrechners ein.

Wählen Sie die Einheiten aus, in denen Sie das Ergebnis der Funktionsberechnung erhalten möchten. Unter dem Eingabefeld befinden sich drei Optionen, aus denen Sie (durch Anklicken mit der Maus) eine auswählen müssen - , Bogenmaß oder Rad.

Aktivieren Sie das Kontrollkästchen, das die auf den Schnittstellentasten des Taschenrechners angezeigten Funktionen umkehrt. Daneben steht eine kurze Inschrift Inv.

Klicken Sie auf die Sündenschaltfläche. Der Taschenrechner invertiert die ihm zugeordnete Funktion, führt die Berechnung durch und präsentiert Ihnen das Ergebnis in den angegebenen Einheiten.

Ähnliche Videos

Eines der häufigsten geometrischen Probleme ist die Berechnung der Fläche eines Kreissegments - eines Teils eines Kreises, der von einer Sehne und einem Kreisbogen begrenzt wird, der der Sehne entspricht.

Die Fläche eines Kreissegments ist gleich der Differenz zwischen der Fläche des entsprechenden Kreissektors und der Fläche des Dreiecks, das durch die Radien des Sektors gebildet wird, der dem Segment entspricht, und der Sehne, die das Segment begrenzt.

Beispiel 1

Die Länge der Sehne, die den Kreis unterspannt, ist gleich a. Das Gradmaß des der Sehne entsprechenden Bogens beträgt 60°. Finden Sie die Fläche des Kreissegments.

Lösung

Ein aus zwei Radien und einer Sehne gebildetes Dreieck ist gleichschenklig, daher ist die Höhe, die vom Scheitelpunkt des Mittelwinkels zur Seite des durch die Sehne gebildeten Dreiecks gezogen wird, auch die Winkelhalbierende des Mittelwinkels, die ihn in zwei Hälften und den Median teilt , teilt den Akkord in zwei Hälften. Da wir wissen, dass der Sinus des Winkels β gleich dem Verhältnis des gegenüberliegenden Beins zur Hypotenuse ist, können wir den Radiuswert berechnen:

Sin 30°= a/2:R = 1/2;

Sc = πR²/360°*60° = πa²/6

Die dem Sektor entsprechende Fläche des Dreiecks wird wie folgt berechnet:

S▲=1/2*ah, wobei h die Höhe ist, die von der Spitze des Mittelwinkels bis zur Sehne gezogen wird. Nach dem Satz des Pythagoras ist h=√(R²-a²/4)= √3*a/2.

Dementsprechend ist S▲=√3/4*a².

Die Fläche des Segments, berechnet als Sceg = Sc - S▲, ist gleich:

Sseg \u003d πa² / 6 - √3 / 4 * a²

Indem Sie den Wert a durch einen Zahlenwert ersetzen, können Sie den Zahlenwert der Segmentfläche leicht berechnen.

Beispiel 2

Kreisradius ist gleich a. Das Gradmaß des dem Segment entsprechenden Bogens beträgt 60°. Finden Sie die Fläche des Kreissegments.

Lösung:

Der Bereich des Sektors entspricht angegebenen Winkel kann mit folgender Formel berechnet werden: