Was ist ein gleichschenkliger Winkel? Gleichschenkligen Dreiecks
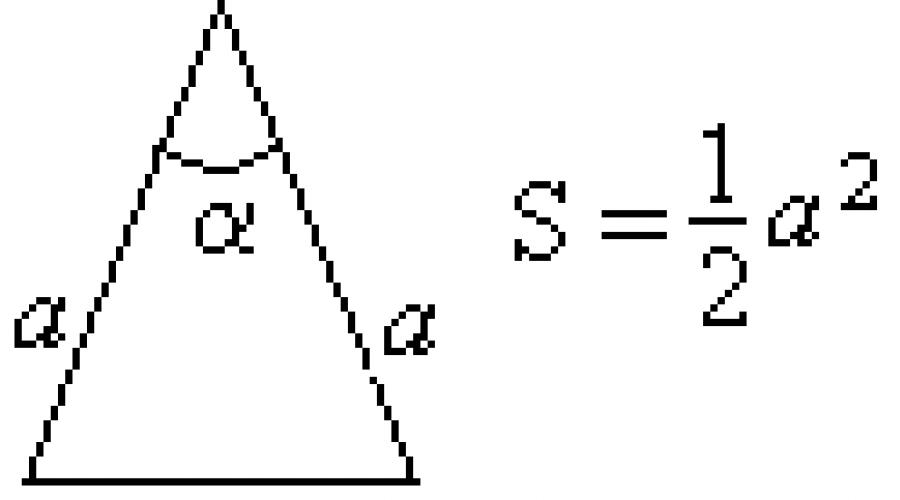
Zwei gleiche Seiten nennt man lateral, die dritte heißt Basis.
Definition 8. Wenn alle drei Seiten eines Dreiecks gleich sind, heißt das Dreieck gleichseitig.
Er ist eine private Spezies gleichschenkligen Dreiecks.
Satz 18. Die Höhe eines gleichschenkligen Dreiecks, abgesenkt zur Basis, ist gleichzeitig die Winkelhalbierende zwischen gleichen Seiten, der Median und die Symmetrieachse der Basis.
Nachweisen. Senken wir die Höhe auf die Basis des gleichschenkligen Dreiecks. Es wird es in zwei gleiche (entlang des Beins und der Hypotenuse) rechtwinklige Dreiecke teilen. Die Winkel A und C sind gleich, und die Höhe teilt auch die Basis in zwei Hälften und ist die Symmetrieachse der gesamten betrachteten Figur.
Dieser Satz lässt sich auch wie folgt formulieren:
Satz 18.1. Der Mittelwert eines gleichschenkligen Dreiecks, abgesenkt zur Basis, ist auch die Winkelhalbierende zwischen gleichen Seiten, die Höhe und die Symmetrieachse der Basis.
Satz 18.2. Die Winkelhalbierende eines gleichschenkligen Dreiecks, abgesenkt zur Basis, ist gleichzeitig Höhe, Mittelwert und Symmetrieachse der Basis.
Satz 18.3. Die Symmetrieachse eines gleichschenkligen Dreiecks ist gleichzeitig die Winkelhalbierende des Winkels zwischen gleichen Seiten, dem Median und der Höhe.
Der Beweis dieser Konsequenzen ergibt sich auch aus der Gleichheit der Dreiecke, in die ein gleichschenkliges Dreieck unterteilt ist.
Satz 19.
Die Winkel an der Basis eines gleichschenkligen Dreiecks sind gleich.
Nachweisen. Senken wir die Höhe auf die Basis des gleichschenkligen Dreiecks. Es wird in zwei gleiche rechtwinklige Dreiecke (entlang des Schenkels und der Hypotenuse) geteilt, was bedeutet, dass die entsprechenden Winkel gleich sind, d. h. ∠ A=∠ C
Die Kriterien für ein gleichschenkliges Dreieck stammen aus Satz 1 und seinen Folgerungen sowie Satz 2.
Satz 20.
Wenn zwei der angegebenen vier Linien (Höhe, Median, Winkelhalbierende, Symmetrieachse) zusammenfallen, ist das Dreieck gleichschenklig (was bedeutet, dass alle vier Linien zusammenfallen).
Satz 21.
Wenn zwei beliebige Winkel eines Dreiecks gleich sind, dann ist es gleichschenklig.
Nachweisen:Ähnlich dem Beweis des direkten Satzes, jedoch unter Verwendung des zweiten Kriteriums für die Gleichheit von Dreiecken. Der Schwerpunkt, die Mittelpunkte von Umkreis und Inkreis sowie der Schnittpunkt der Höhen eines gleichschenkligen Dreiecks liegen alle auf dessen Symmetrieachse, d. h. in der Höhe.
Ein gleichseitiges Dreieck ist für jedes seiner Seitenpaare gleichschenklig. Aufgrund der Gleichheit aller seiner Seiten sind alle drei Winkel eines solchen Dreiecks gleich. Wenn man bedenkt, dass die Summe der Winkel eines beliebigen Dreiecks gleich zwei rechten Winkeln ist, sehen wir, dass jeder Winkel eines gleichseitigen Dreiecks gleich 60° ist. Um umgekehrt sicherzustellen, dass alle Seiten eines Dreiecks gleich sind, genügt es zu überprüfen, ob zwei seiner drei Winkel gleich 60° sind.
Satz 22
. In einem gleichseitigen Dreieck fallen alle bemerkenswerten Punkte zusammen: der Schwerpunkt, die Mittelpunkte der eingeschriebenen und umschriebenen Kreise, der Schnittpunkt der Höhen (genannt Orthozentrum des Dreiecks).
Satz 23
. Wenn zwei der angegebenen vier Punkte zusammenfallen, ist das Dreieck gleichseitig und alle vier genannten Punkte fallen folglich zusammen.
Tatsächlich wird sich ein solches Dreieck gemäß dem vorherigen als gleichschenklig in Bezug auf jedes Seitenpaar herausstellen, d.h. gleichseitig. Ein gleichseitiges Dreieck wird auch regelmäßiges Dreieck genannt. Die Fläche eines gleichschenkligen Dreiecks ist gleich der Hälfte des Produkts aus dem Quadrat der Seitenseite und dem Sinus des Winkels zwischen den Seiten  Betrachten Sie diese Formel für ein gleichseitiges Dreieck, dann beträgt der Alpha-Winkel 60 Grad. Dann ändert sich die Formel wie folgt:
Betrachten Sie diese Formel für ein gleichseitiges Dreieck, dann beträgt der Alpha-Winkel 60 Grad. Dann ändert sich die Formel wie folgt:
Satz d1
. In einem gleichschenkligen Dreieck sind die zu den Seiten gezogenen Mediane gleich.
Nachweisen: Sei ABC ein gleichschenkliges Dreieck (AC = BC), AK und BL dessen Mediane. Dann sind die Dreiecke AKB und ALB gemäß dem zweiten Kriterium für die Gleichheit von Dreiecken gleich. Sie haben die gemeinsame Seite AB, die Seiten AL und BK sind gleich den Hälften der Seiten eines gleichschenkligen Dreiecks und die Winkel LAB und KBA sind gleich den Basiswinkeln eines gleichschenkligen Dreiecks. Da die Dreiecke kongruent sind, sind ihre Seiten AK und LB gleich. Aber AK und LB sind die Mediane eines gleichschenkligen Dreiecks, das an seinen Seiten gezogen wird.
Satz d2
. In einem gleichschenkligen Dreieck sind die zu den Seiten gezogenen Winkelhalbierenden gleich.
Nachweisen: Sei ABC ein gleichschenkliges Dreieck (AC = BC), AK und BL seine Winkelhalbierenden. Die Dreiecke AKB und ALB sind gemäß dem zweiten Kriterium für die Gleichheit von Dreiecken gleich. Sie haben eine gemeinsame Seite AB, die Winkel LAB und KBA sind gleich den Grundwinkeln eines gleichschenkligen Dreiecks und die Winkel LBA und KAB sind gleich den halben Grundwinkeln eines gleichschenkligen Dreiecks. Da die Dreiecke kongruent sind, sind ihre Seiten AK und LB – die Winkelhalbierenden des Dreiecks ABC – kongruent. Der Satz ist bewiesen.
Satz d3
. In einem gleichschenkligen Dreieck sind die seitlich abgesenkten Höhen gleich.
Nachweisen: Sei ABC ein gleichschenkliges Dreieck (AC = BC), AK und BL seine Höhen. Dann sind die Winkel ABL und KAB gleich, da die Winkel ALB und AKB rechte Winkel sind und die Winkel LAB und ABK gleich den Basiswinkeln eines gleichschenkligen Dreiecks sind. Folglich sind die Dreiecke ALB und AKB nach dem zweiten Kriterium für die Gleichheit von Dreiecken gleich: Sie haben eine gemeinsame Seite AB, die Winkel KAB und LBA sind entsprechend dem oben Gesagten gleich und die Winkel LAB und KBA sind gleich wie die Basiswinkel von an gleichschenkligen Dreiecks. Wenn die Dreiecke kongruent sind, sind auch ihre Seiten AK und BL kongruent. Q.E.D.
Unterrichtsthema
Gleichschenkligen Dreiecks
Der Zweck der Lektion
Machen Sie den Schülern ein gleichschenkliges Dreieck bekannt.
Entwickeln Sie weiterhin Ihre Fähigkeiten zum Konstruieren rechtwinkliger Dreiecke.
Erweitern Sie das Wissen der Schüler über die Eigenschaften gleichschenkliger Dreiecke;
Festigen Sie das theoretische Wissen bei der Lösung von Problemen.
Lernziele
In der Lage sein, den Satz über die Eigenschaften eines gleichschenkligen Dreiecks bei der Lösung von Problemen zu formulieren, zu beweisen und anzuwenden;
Setzen Sie die Entwicklung der bewussten Wahrnehmung von Lehrmaterial, des logischen Denkens, der Fähigkeiten zur Selbstkontrolle und zum Selbstwertgefühl fort;
Kognitives Interesse am Mathematikunterricht wecken;
Fördern Sie Aktivität, Neugier und Organisation.
Unterrichtsplan
1. Allgemeine Konzepte und Definitionen eines gleichschenkligen Dreiecks.
2. Eigenschaften eines gleichschenkligen Dreiecks.
3. Zeichen eines gleichschenkligen Dreiecks.
4. Fragen und Aufgaben.
Gleichschenkligen Dreiecks
Ein gleichschenkliges Dreieck ist ein Dreieck, das zwei gleiche Seiten hat, die Seiten eines gleichschenkligen Dreiecks genannt werden, und dessen dritte Seite Basis genannt wird.
Die Oberseite einer bestimmten Figur ist diejenige, die ihrer Basis gegenüberliegt.
Der Winkel, der der Basis gegenüberliegt, wird als Scheitelwinkel dieses Dreiecks bezeichnet, und die anderen beiden Winkel werden als Basiswinkel eines gleichschenkligen Dreiecks bezeichnet.
Arten von gleichschenkligen Dreiecken
Ein gleichschenkliges Dreieck kann, wie andere Figuren auch, haben verschiedene Typen. Unter den gleichschenkligen Dreiecken gibt es spitze, rechtwinklige, stumpfe und gleichseitige Dreiecke.
Ein spitzes Dreieck hat alle spitzen Winkel.
Ein rechtwinkliges Dreieck hat an seiner Spitze einen geraden Winkel und an seiner Basis spitze Winkel.
Obtuse hat stumpfer Winkel An der Spitze und an der Basis sind die Winkel scharf.
Bei einem gleichseitigen Objekt sind alle Winkel und Seiten gleich.
Eigenschaften eines gleichschenkligen Dreiecks
Entgegengesetzte Winkel in Bezug auf gleiche Seiten eines gleichschenkligen Dreiecks sind einander gleich;
Winkelhalbierende, Mittelwerte und Höhen, die aus Winkeln gegenüber gleichen Seiten eines Dreiecks gezogen werden, sind einander gleich.
Die Winkelhalbierende, der Mittelwert und die Höhe, die auf die Basis des Dreiecks gerichtet und gezeichnet sind, fallen miteinander zusammen.
Die Mittelpunkte der eingeschriebenen und umschriebenen Kreise liegen auf der zur Basis gezogenen Höhe, Winkelhalbierende und Mittellinie (sie fallen zusammen).
Winkel gegenüber gleichen Seiten eines gleichschenkligen Dreiecks sind immer spitz.
Diese Eigenschaften eines gleichschenkligen Dreiecks werden zur Lösung von Problemen genutzt.
Hausaufgaben
1. Definieren Sie ein gleichschenkliges Dreieck.
2. Was ist das Besondere an diesem Dreieck?
3. Wie unterscheidet sich ein gleichschenkliges Dreieck von einem rechtwinkligen Dreieck?
4. Nennen Sie die Eigenschaften eines gleichschenkligen Dreiecks, die Sie kennen.
5. Glauben Sie, dass es in der Praxis möglich ist, die Winkelgleichheit an der Basis zu überprüfen, und wie geht das?
Übung
Lassen Sie uns nun eine kurze Umfrage durchführen und herausfinden, wie Sie das neue Material gelernt haben.
Hören Sie sich die Fragen aufmerksam an und beantworten Sie, ob die folgende Aussage wahr ist:
1. Kann ein Dreieck als gleichschenklig betrachtet werden, wenn seine beiden Seiten gleich sind?
2. Eine Winkelhalbierende ist ein Segment, das den Scheitelpunkt eines Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet?
3. Eine Winkelhalbierende ist ein Segment, das einen Winkel halbiert, der einen Scheitelpunkt mit einem Punkt auf der gegenüberliegenden Seite verbindet?
Tipps zum Lösen von Problemen mit gleichschenkligen Dreiecken:
1. Um den Umfang eines gleichschenkligen Dreiecks zu bestimmen, reicht es aus, die Länge der Seite mit 2 zu multiplizieren und dieses Produkt mit der Länge der Basis des Dreiecks zu addieren.
2. Wenn der Umfang und die Länge der Basis eines gleichschenkligen Dreiecks in der Aufgabe bekannt sind, reicht es zum Ermitteln der Seitenlänge aus, die Länge der Basis vom Umfang abzuziehen und die gefundene Differenz durch 2 zu dividieren.
3. Und um die Länge der Basis eines gleichschenkligen Dreiecks zu ermitteln, indem Sie sowohl den Umfang als auch die Seitenlänge kennen, müssen Sie nur die Seite mit zwei multiplizieren und dieses Produkt vom Umfang unseres Dreiecks subtrahieren.
Aufgaben:
1. Identifizieren Sie unter den Dreiecken in der Abbildung ein weiteres und begründen Sie Ihre Wahl:

2. Bestimmen Sie, welche der in der Abbildung gezeigten Dreiecke gleichschenklig sind, benennen Sie ihre Basen und Seiten und berechnen Sie auch ihren Umfang.

3. Der Umfang eines gleichschenkligen Dreiecks beträgt 21 cm. Finden Sie die Seiten dieses Dreiecks, wenn eine davon 3 cm größer ist. Wie viele Lösungen kann dieses Problem haben?
4. Es ist bekannt, dass diese Dreiecke gleich sind, wenn die Seitenseite und der Winkel gegenüber der Basis eines gleichschenkligen Dreiecks gleich der Seitenseite und dem Winkel eines anderen sind. Beweisen Sie diese Aussage.
5. Überlegen Sie, ob ein gleichschenkliges Dreieck gleichseitig ist? Und wird jedes gleichseitige Dreieck gleichschenklig sein?
6. Wenn die Seiten eines gleichschenkligen Dreiecks 4 m und 5 m betragen, welchen Umfang hat es dann? Wie viele Lösungen kann dieses Problem haben?
7. Wenn einer der Winkel eines gleichschenkligen Dreiecks 91 Grad beträgt, wie groß sind dann die anderen Winkel?
8. Überlegen Sie und antworten Sie: Welche Winkel sollte ein Dreieck haben, damit es sowohl rechteckig als auch gleichschenklig ist?
Wie viele von euch wissen, was das Pascalsche Dreieck ist? Das Problem der Konstruktion des Pascalschen Dreiecks wird oft gestellt, um grundlegende Programmierkenntnisse zu testen. Im Allgemeinen bezieht sich das Pascalsche Dreieck auf die Kombinatorik und die Wahrscheinlichkeitstheorie. Was ist das denn für ein Dreieck?
Das Pascalsche Dreieck ist ein unendliches arithmetisches Dreieck oder eine dreiecksförmige Tabelle, die unter Verwendung von Binomialkoeffizienten gebildet wird. In einfachen Worten, der Scheitelpunkt und die Seiten dieses Dreiecks sind Einheiten und es selbst ist mit den Summen der beiden darüber stehenden Zahlen gefüllt. Ein solches Dreieck kann bis ins Unendliche gefaltet werden, aber wenn wir es skizzieren, erhalten wir ein gleichschenkliges Dreieck mit symmetrischen Linien relativ zu seiner vertikalen Achse.

Überlegen Sie, wo drin Alltagsleben Sind Ihnen schon einmal gleichschenklige Dreiecke begegnet? Stimmt es nicht, die Dächer von Häusern sind uralt? architektonische Strukturen Sehen sie ihnen sehr ähnlich? Erinnern Sie sich an die Grundlage der ägyptischen Pyramiden? Wo sonst sind Ihnen gleichschenklige Dreiecke begegnet?
Seit der Antike halfen gleichschenklige Dreiecke den Griechen und Ägyptern bei der Bestimmung von Entfernungen und Höhen. Die alten Griechen nutzten es beispielsweise, um aus der Ferne die Entfernung zu einem Schiff auf See zu bestimmen. Und die alten Ägypter bestimmten die Höhe ihrer Pyramiden anhand der Länge des Schlagschattens, denn... es war ein gleichschenkliges Dreieck.
Schon seit der Antike wussten die Menschen die Schönheit und Zweckmäßigkeit dieser Figur zu schätzen, da uns überall die Formen von Dreiecken umgeben. Wenn wir durch verschiedene Dörfer wandern, sehen wir die Dächer von Häusern und anderen Gebäuden, die an ein gleichschenkliges Dreieck erinnern; wenn wir in ein Geschäft gehen, sehen wir Pakete mit Lebensmitteln und Säften dreieckige Form und sogar einige menschliche Gesichter haben die Form eines Dreiecks. Diese Figur ist so beliebt, dass man sie auf Schritt und Tritt sehen kann.
Fächer > Mathematik > Mathematik 7. KlasseGleichschenkligen Dreiecks ist ein Dreieck, bei dem zwei Seiten gleich lang sind. Gleiche Seiten werden als lateral bezeichnet und die letzte wird als Basis bezeichnet. Per Definition ist ein regelmäßiges Dreieck auch gleichschenklig, aber das Gegenteil ist nicht der Fall.
Eigenschaften
- Winkel gegenüber gleichen Seiten eines gleichschenkligen Dreiecks sind einander gleich. Die aus diesen Winkeln gezogenen Winkelhalbierenden, Mittelwerte und Höhen sind ebenfalls gleich.
- Die Winkelhalbierende, der Median, die Höhe und die zur Basis gezogene Mittelsenkrechte fallen zusammen. Auf dieser Linie liegen die Mittelpunkte der ein- und umschriebenen Kreise.
- Winkel gegenüber gleichen Seiten sind immer spitz (folgt aus ihrer Gleichheit).
Lassen A- die Länge zweier gleicher Seiten eines gleichschenkligen Dreiecks, B- Länge der dritten Seite, α Und β - entsprechende Winkel, R- Radius des umschriebenen Kreises, R- Radius der Beschriftung.
Die Seiten sind wie folgt zu finden:
Winkel können auf folgende Weise ausgedrückt werden:
Der Umfang eines gleichschenkligen Dreiecks kann auf eine der folgenden Arten berechnet werden:
Die Fläche eines Dreiecks kann auf eine der folgenden Arten berechnet werden:
(Herons Formel).Zeichen
- Zwei Winkel eines Dreiecks sind gleich.
- Die Höhe stimmt mit dem Median überein.
- Die Höhe stimmt mit der Winkelhalbierenden überein.
- Die Winkelhalbierende fällt mit dem Median zusammen.
- Die beiden Höhen sind gleich.
- Die beiden Mediane sind gleich.
- Zwei Winkelhalbierende sind gleich (Satz von Steiner-Lemus).
siehe auch
Wikimedia-Stiftung. 2010.
Sehen Sie in anderen Wörterbüchern, was ein „gleichschenkliges Dreieck“ ist:
Gleichschenkliges Dreieck, ein Dreieck mit zwei Seiten gleicher Länge; Auch die Winkel an diesen Seiten sind gleich... Wissenschaftliches und technisches Enzyklopädisches Wörterbuch
Und (einfaches) Trigon, Dreieck, Mann. 1. Eine geometrische Figur, die durch drei sich gegenseitig schneidende Linien begrenzt wird, die drei Innenwinkel bilden (mat.). Stumpfes Dreieck. Spitzwinkliges Dreieck. Rechtwinkliges Dreieck.… … Wörterbuch Uschakowa
ISOSceles, aya, oe: ein gleichschenkliges Dreieck mit zwei gleichen Seiten. | Substantiv gleichschenklig und weiblich Ozhegovs erklärendes Wörterbuch. S.I. Ozhegov, N. Yu. Shvedova. 1949 1992 … Ozhegovs erklärendes Wörterbuch
Dreieck- ▲ ein Polygon mit drei Winkeln, ein Dreieck, das einfachste Polygon; wird durch 3 Punkte definiert, die nicht auf derselben Linie liegen. dreieckig. spitzer Winkel. spitzwinklig. rechtwinkliges Dreieck: Bein. Hypotenuse. gleichschenkligen Dreiecks. ▼… … Ideographisches Wörterbuch der russischen Sprache
Dreieck- TRIANGLE1, a, m von was oder mit def. Ein Objekt in Form einer geometrischen Figur, die durch drei sich schneidende Linien begrenzt wird, die drei Innenwinkel bilden. Sie sortierte die Briefe ihres Mannes, vergilbte Dreiecke von vorne. DREIECK2, a, m... ... Erklärendes Wörterbuch der russischen Substantive
Dieser Begriff hat andere Bedeutungen, siehe Dreieck (Bedeutungen). Ein Dreieck (im euklidischen Raum) ist geometrische Figur, gebildet aus drei Segmenten, die drei Punkte verbinden, die nicht auf derselben Geraden liegen. Drei Punkte,... ... Wikipedia
Dreieck (Polygon)- Dreiecke: 1 spitz, rechteckig und stumpf; 2 regelmäßig (gleichseitig) und gleichschenklig; 3 Winkelhalbierende; 4 Mediane und Schwerpunkt; 5 Höhen; 6 Orthozentrum; 7 Mittellinie. DREIECK, ein Polygon mit drei Seiten. Manchmal unter... ... Illustriertes enzyklopädisches Wörterbuch
Enzyklopädisches Wörterbuch
Dreieck- A; m. 1) a) Eine geometrische Figur, die durch drei sich schneidende Linien begrenzt wird, die drei Innenwinkel bilden. Rechteckiges, gleichschenkliges Dreieck. Berechnen Sie die Fläche des Dreiecks. b) ott. was oder mit def. Eine Figur oder ein Gegenstand dieser Form... ... Wörterbuch vieler Ausdrücke
A; m. 1. Eine geometrische Figur, die durch drei sich schneidende Linien begrenzt wird, die drei Innenwinkel bilden. Rechteckig, gleichschenklig t. Berechnen Sie die Fläche des Dreiecks. // was oder mit def. Eine Figur oder ein Objekt dieser Form. T. Dächer. T.… … Enzyklopädisches Wörterbuch
Die ersten Historiker unserer Zivilisation – die alten Griechen – erwähnen Ägypten als Geburtsort der Geometrie. Es ist schwierig, ihnen zu widersprechen, wenn man weiß, mit welch erstaunlicher Präzision die riesigen Gräber der Pharaonen errichtet wurden. Gegenseitige Übereinkunft Ebenen der Pyramiden, ihre Proportionen, Ausrichtung auf die Himmelsrichtungen – eine solche Perfektion zu erreichen wäre ohne Kenntnis der Grundlagen der Geometrie undenkbar.
Das Wort „Geometrie“ selbst kann mit „Maß der Erde“ übersetzt werden. Darüber hinaus erscheint das Wort „Erde“ nicht als Planetenteil Sonnensystem, aber als Flugzeug. Markierung von Wartungsbereichen Landwirtschaft, ist höchstwahrscheinlich die sehr ursprüngliche Grundlage der Wissenschaft der geometrischen Figuren, ihrer Typen und Eigenschaften.
Ein Dreieck ist die einfachste räumliche Figur der Planimetrie und enthält nur drei Punkte – Eckpunkte (es gibt nicht weniger). Die Grundlage der Fundamente, vielleicht ist das der Grund, warum etwas Geheimnisvolles und Altes in ihm zu sein scheint. Das allsehende Auge in einem Dreieck ist eines der frühesten bekannten okkulten Zeichen, und die Geographie seiner Verbreitung und sein Zeitrahmen sind einfach erstaunlich. Von alten ägyptischen, sumerischen, aztekischen und anderen Zivilisationen bis hin zu moderneren Gemeinschaften okkulter Liebhaber, die über den ganzen Globus verstreut sind.
Was sind Dreiecke?
Ein gewöhnliches ungleichseitiges Dreieck ist eine geschlossene geometrische Figur, die aus drei Segmenten unterschiedlicher Länge und drei Winkeln besteht, von denen keiner richtig ist. Darüber hinaus gibt es mehrere Sondertypen.
Bei einem spitzen Dreieck betragen alle Winkel weniger als 90 Grad. Mit anderen Worten: Alle Winkel eines solchen Dreiecks sind spitz.
Ein rechtwinkliges Dreieck, über das Schulkinder wegen der Fülle an Theoremen immer geweint haben, hat einen Winkel von 90 Grad oder, wie es auch genannt wird, eine Gerade.
Ein stumpfes Dreieck zeichnet sich dadurch aus, dass einer seiner Winkel stumpf ist, also mehr als 90 Grad beträgt.
Ein gleichseitiges Dreieck hat drei Seiten gleicher Länge. In einer solchen Figur sind auch alle Winkel gleich.
Und schließlich für ein gleichschenkliges Dreieck aus drei Seiten zwei sind einander gleich.
Unterscheidungsmerkmale
Die Eigenschaften eines gleichschenkligen Dreiecks bestimmen auch seinen Hauptunterschied – die Gleichheit seiner beiden Seiten. Diese gleichen Seiten werden üblicherweise als Hüften (oder häufiger als Seiten) bezeichnet, und die dritte Seite wird als „Basis“ bezeichnet.
In der betrachteten Abbildung ist a = b.
Das zweite Kriterium für ein gleichschenkliges Dreieck ergibt sich aus dem Sinussatz. Da die Seiten a und b gleich sind, sind die Sinuswerte ihrer entgegengesetzten Winkel gleich:
a/sin γ = b/sin α, woraus folgt: sin γ = sin α.
Aus der Sinusgleichheit folgt die Winkelgleichheit: γ = α.
Das zweite Vorzeichen eines gleichschenkligen Dreiecks ist also die Gleichheit zweier an der Basis angrenzender Winkel.
Drittes Zeichen. In einem Dreieck gibt es Elemente wie Höhe, Winkelhalbierende und Mittelwert.

Wenn sich bei der Lösung des Problems herausstellt, dass in dem betreffenden Dreieck zwei dieser Elemente übereinstimmen: die Höhe mit der Winkelhalbierenden; Winkelhalbierende mit Median; Median mit der Höhe – wir können definitiv schlussfolgern, dass das Dreieck gleichschenklig ist.
Geometrische Eigenschaften einer Figur
1. Eigenschaften eines gleichschenkligen Dreiecks. Eine der charakteristischen Eigenschaften der Figur ist die Gleichheit der an die Basis angrenzenden Winkel:
<ВАС = <ВСА.
2. Eine weitere Eigenschaft wurde oben besprochen: Der Median, die Winkelhalbierende und die Höhe in einem gleichschenkligen Dreieck fallen zusammen, wenn sie vom Scheitel bis zur Basis aufgebaut sind.
3. Gleichheit der Winkelhalbierenden, die von den Eckpunkten an der Basis gezogen werden:

Wenn AE die Winkelhalbierende des Winkels BAC und CD die Winkelhalbierende des Winkels BCA ist, dann gilt: AE = DC.
4. Die Eigenschaften eines gleichschenkligen Dreiecks sorgen auch für die Gleichheit der Höhen, die von den Eckpunkten an der Basis ausgehen.

Wenn wir die Höhen des Dreiecks ABC (wobei AB = BC) aus den Eckpunkten A und C konstruieren, sind die resultierenden Segmente CD und AE gleich.
5. Die von den Ecken an der Basis gezogenen Mittelwerte sind ebenfalls gleich.

Wenn also AE und DC Mediane sind, also AD = DB und BE = EC, dann ist AE = DC.
Höhe eines gleichschenkligen Dreiecks
Die Gleichheit der Seiten und Winkel mit ihnen führt einige Besonderheiten in die Berechnung der Längen der Elemente der betrachteten Figur ein.

Die Höhe in einem gleichschenkligen Dreieck teilt die Figur in zwei symmetrische rechtwinklige Dreiecke, deren Hypotenusen an den Seiten liegen. Die Höhe wird in diesem Fall nach dem Satz des Pythagoras als Bein bestimmt.
Ein Dreieck kann alle drei Seiten gleich haben, dann wird es gleichseitig genannt. Die Höhe in einem gleichseitigen Dreieck wird auf ähnliche Weise bestimmt, nur für Berechnungen reicht es aus, nur einen Wert zu kennen – die Länge der Seite dieses Dreiecks.

Sie können die Höhe auch auf andere Weise bestimmen, indem Sie beispielsweise die Basis und den angrenzenden Winkel kennen.

Median eines gleichschenkligen Dreiecks
Der betrachtete Dreieckstyp kann aufgrund seiner geometrischen Merkmale ganz einfach mit einem minimalen Satz an Ausgangsdaten gelöst werden. Da der Median in einem gleichschenkligen Dreieck sowohl seiner Höhe als auch seiner Winkelhalbierenden entspricht, unterscheidet sich der Algorithmus zu seiner Bestimmung nicht von der Vorgehensweise zur Berechnung dieser Elemente.

Beispielsweise können Sie die Länge des Medians anhand der bekannten lateralen Seite und der Größe des Scheitelwinkels bestimmen.
So bestimmen Sie den Umfang
Da die beiden Seiten der betrachteten Grundrissfigur immer gleich sind, reicht es zur Bestimmung des Umfangs aus, die Länge der Basis und die Länge einer der Seiten zu kennen.

Betrachten wir ein Beispiel, bei dem Sie den Umfang eines Dreiecks anhand einer bekannten Basis und Höhe bestimmen müssen.
Der Umfang ist gleich der Summe aus der Grundfläche und der doppelten Seitenlänge. Die laterale Seite wiederum wird mit dem Satz des Pythagoras als Hypotenuse eines rechtwinkligen Dreiecks definiert. Seine Länge ist gleich der Quadratwurzel der Summe des Quadrats der Höhe und des Quadrats der halben Grundfläche.
Fläche eines gleichschenkligen Dreiecks
Die Berechnung der Fläche eines gleichschenkligen Dreiecks bereitet in der Regel keine Schwierigkeiten. In unserem Fall gilt natürlich die universelle Regel, die Fläche eines Dreiecks als halbes Produkt aus Grundfläche und Höhe zu bestimmen. Allerdings erleichtern die Eigenschaften eines gleichschenkligen Dreiecks die Aufgabe erneut.

Nehmen wir an, dass die Höhe und der Winkel neben der Basis bekannt sind. Es ist notwendig, die Fläche der Figur zu bestimmen. Dies kann auf diese Weise erfolgen.
Da die Winkelsumme jedes Dreiecks 180° beträgt, ist es nicht schwierig, die Größe des Winkels zu bestimmen. Anschließend wird anhand des nach dem Sinussatz ermittelten Verhältnisses die Länge der Grundfläche des Dreiecks bestimmt. Alles, Grundfläche und Höhe – ausreichende Daten zur Flächenbestimmung – sind vorhanden.
Weitere Eigenschaften eines gleichschenkligen Dreiecks
Die Lage des Mittelpunkts eines um ein gleichschenkliges Dreieck umschriebenen Kreises hängt von der Größe des Scheitelwinkels ab. Wenn also ein gleichschenkliges Dreieck spitz ist, liegt der Mittelpunkt des Kreises innerhalb der Figur.
Der Mittelpunkt eines Kreises, der ein stumpfes gleichschenkliges Dreieck umschreibt, liegt außerhalb davon. Und schließlich, wenn der Winkel am Scheitelpunkt 90° beträgt, liegt der Mittelpunkt genau in der Mitte der Grundfläche und der Durchmesser des Kreises geht durch die Grundfläche selbst.
Um den Radius eines um ein gleichschenkliges Dreieck umschriebenen Kreises zu bestimmen, genügt es, die Seitenlänge durch den doppelten Kosinus des halben Scheitelwinkels zu dividieren.
In dieser Lektion wird das Thema „Gleichschenkliges Dreieck und seine Eigenschaften“ behandelt. Sie erfahren, wie gleichschenklige und gleichseitige Dreiecke aussehen und wie sie charakterisiert werden. Beweisen Sie den Satz über die Winkelgleichheit an der Basis eines gleichschenkligen Dreiecks. Betrachten Sie auch den Satz über die Winkelhalbierende (Mittelwert und Höhe), die zur Basis eines gleichschenkligen Dreiecks gezogen wird. Am Ende der Lektion lösen Sie zwei Probleme anhand der Definition und Eigenschaften eines gleichschenkligen Dreiecks.
Definition:Gleichschenklige heißt ein Dreieck, dessen beide Seiten gleich sind.
Reis. 1. Gleichschenkliges Dreieck
AB = AC – Seiten. BC - Gründung.
Die Fläche eines gleichschenkligen Dreiecks ist gleich der Hälfte des Produkts aus seiner Grundfläche und seiner Höhe.
Definition:Gleichseitig nennt man ein Dreieck, bei dem alle drei Seiten gleich sind.

Reis. 2. Gleichseitiges Dreieck
AB = BC = SA.
Satz 1: In einem gleichschenkligen Dreieck sind die Grundwinkel gleich.
Gegeben: AB = AC.
Beweisen:∠B =∠C.

Reis. 3. Zeichnen für den Satz
Nachweisen: Dreieck ABC = Dreieck ACB entsprechend dem ersten Vorzeichen (zwei gleiche Seiten und der Winkel zwischen ihnen). Aus der Gleichheit der Dreiecke folgt, dass alle entsprechenden Elemente gleich sind. Das bedeutet ∠B = ∠C, was bewiesen werden musste.
Satz 2: In einem gleichschenkligen Dreieck Halbierende zur Basis gezogen ist Median Und Höhe.
Gegeben: AB = AC, ∠1 = ∠2.
Beweisen:ÂD = DC, AD senkrecht zu BC.

Reis. 4. Zeichnung für Satz 2
Nachweisen: Dreieck ADB = Dreieck ADC gemäß dem ersten Vorzeichen (AD - allgemein, AB = AC nach Bedingung, ∠BAD = ∠DAC). Aus der Gleichheit der Dreiecke folgt, dass alle entsprechenden Elemente gleich sind. BD = DC, da ihnen gleiche Winkel gegenüberstehen. AD ist also der Median. Auch ∠3 = ∠4, da sie gegenüberliegenden gleichen Seiten liegen. Aber außerdem sind sie insgesamt gleich. Daher ist ∠3 = ∠4 = . Das bedeutet, dass AD die Höhe des Dreiecks ist, was wir beweisen mussten.
Im einzigen Fall a = b = . In diesem Fall heißen die Linien AC und BD senkrecht.
Da Winkelhalbierende, Höhe und Median das gleiche Segment sind, gelten auch folgende Aussagen:
Die Höhe eines zur Basis gezogenen gleichschenkligen Dreiecks ist der Mittelwert und die Winkelhalbierende.
Der Median eines gleichschenkligen Dreiecks, das zur Basis gezogen wird, ist die Höhe und die Winkelhalbierende.
Beispiel 1: Bei einem gleichschenkligen Dreieck ist die Basis halb so groß wie die Seite und der Umfang beträgt 50 cm. Finden Sie die Seiten des Dreiecks.
Gegeben: AB = AC, BC = AC. P = 50 cm.
Finden: BC, AC, AB.
Lösung:

Reis. 5. Zeichnen zum Beispiel 1
Bezeichnen wir die Basis BC als a, dann ist AB = AC = 2a.
2a + 2a + a = 50.
5a = 50, a = 10.
Antwort: BC = 10 cm, AC = AB = 20 cm.
Beispiel 2: Beweisen Sie, dass in einem gleichseitigen Dreieck alle Winkel gleich sind.
Gegeben: AB = BC = SA.
Beweisen:∠A = ∠B = ∠C.
Nachweisen:

Reis. 6. Zeichnen zum Beispiel
∠B = ∠C, da AB = AC, und ∠A = ∠B, da AC = BC.
Daher ist ∠A = ∠B = ∠C, was bewiesen werden musste.
Antwort: Bewährt.
In der heutigen Lektion haben wir uns ein gleichschenkliges Dreieck angesehen und seine grundlegenden Eigenschaften untersucht. In der nächsten Lektion lösen wir Aufgaben zum Thema gleichschenklige Dreiecke, zur Berechnung der Fläche eines gleichschenkligen und gleichseitigen Dreiecks.
- Alexandrov A.D., Werner A.L., Ryzhik V.I. und andere. Geometrie 7. - M.: Bildung.
- Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. und andere. Geometrie 7. 5. Aufl. - M.: Aufklärung.
- Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometrie 7 / V.F. Butuzov, S.B. Kadomtsev, V.V. Prasolova, Hrsg. Sadovnichego V.A. - M.: Bildung, 2010.
- Wörterbücher und Enzyklopädien zum Thema Akademiker ().
- Festival pädagogischer Ideen „Offene Lektion“ ().
- Kaknauchit.ru ().
1. Nr. 29. Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometrie 7 / V.F. Butuzov, S.B. Kadomtsev, V.V. Prasolova, Hrsg. Sadovnichego V.A. - M.: Bildung, 2010.
2. Der Umfang eines gleichschenkligen Dreiecks beträgt 35 cm und die Basis ist dreimal kleiner als die Seite. Finden Sie die Seiten des Dreiecks.
3. Gegeben: AB = BC. Beweisen Sie, dass ∠1 = ∠2.

4. Der Umfang eines gleichschenkligen Dreiecks beträgt 20 cm, eine seiner Seiten ist doppelt so groß wie die andere. Finden Sie die Seiten des Dreiecks. Wie viele Lösungen hat das Problem?