Was sind die Flächen eines Diederwinkels? Diederwinkel

Der Zweck der Lektion: Einführung des Konzepts des Diederwinkels und seines linearen Winkels.

Aufgaben:

Lehrreich: Betrachten Sie Aufgaben zur Anwendung dieser Konzepte und entwickeln Sie die konstruktive Fähigkeit, den Winkel zwischen Ebenen zu finden.

Entwicklung: Entwicklung kreatives Denken Studierende, persönliche Selbstentwicklung der Studierenden, Sprachentwicklung der Studierenden;

Lehrreich: Förderung einer Kultur der geistigen Arbeit, der Kommunikationskultur und der Reflexionskultur.

Unterrichtsart: Lektion im Erlernen neuen Wissens

Lehrmethoden: erklärend und anschaulich

Ausrüstung: Computer, interaktives Whiteboard.

Literatur:

Geometrie. Klassen 10-11: Lehrbuch. für 10-11 Klassen. Allgemeinbildung Institutionen: Basis und Profil. Ebenen / [L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev usw.] – 18. Auflage. – M.: Bildung, 2009. – 255 S.

Unterrichtsplan:

Zeit organisieren(2 Minuten)

Wissen aktualisieren (5 Min.)

Neues Material lernen (12 Min.)

Vertiefung des Gelernten (21 Min.)

Hausaufgaben(2 Minuten)

Zusammenfassung (3 Min.)

Während des Unterrichts:

1. Organisatorischer Moment.

Beinhaltet die Begrüßung der Klasse durch den Lehrer, die Vorbereitung des Raums für den Unterricht und die Überprüfung der Abwesenheiten.

2. Aktualisierung des Grundwissens.

Lehrer: In der letzten Lektion hast du geschrieben unabhängige Arbeit. Im Großen und Ganzen war die Arbeit gut geschrieben. Jetzt wiederholen wir es ein wenig. Wie nennt man einen Winkel in einer Ebene?

Student: Ein Winkel auf einer Ebene ist eine Figur, die aus zwei Strahlen besteht, die von einem Punkt ausgehen.

Lehrer: Wie nennt man den Winkel zwischen Linien im Raum?

Student: Der Winkel zwischen zwei sich schneidenden Linien im Raum ist der kleinste der Winkel, die die Strahlen dieser Linien mit dem Scheitelpunkt im Schnittpunkt bilden.

Student: Der Winkel zwischen sich schneidenden Linien ist der Winkel zwischen sich schneidenden Linien, jeweils parallel zu den Daten.

Lehrer: Wie heißt der Winkel zwischen einer Geraden und einer Ebene?

Student: Der Winkel zwischen einer Geraden und einer EbeneJeder Winkel zwischen einer Geraden und ihrer Projektion auf diese Ebene heißt.

3. Neues Material studieren.

Lehrer: In der Stereometrie wird neben solchen Winkeln auch eine andere Art von Winkel betrachtet – Diederwinkel. Sie haben wahrscheinlich bereits erraten, was das Thema der heutigen Lektion ist. Öffnen Sie also Ihre Notizbücher und notieren Sie das heutige Datum und das Thema der Lektion.

Schreiben Sie an die Tafel und in Notizbücher:

10.12.14.

Diederwinkel.

Lehrer : Um das Konzept eines Diederwinkels einzuführen, sollte man sich daran erinnern, dass jede gerade Linie, die in einer bestimmten Ebene gezeichnet wird, diese Ebene in zwei Halbebenen teilt(Abb. 1, a)

Lehrer : Stellen wir uns vor, wir hätten die Ebene entlang einer Geraden gebogen, so dass zwei Halbebenen mit Rand nicht mehr in derselben Ebene liegen (Abb. 1, b). Die resultierende Zahl ist der Diederwinkel. Ein Diederwinkel ist eine Figur, die aus einer Geraden und zwei Halbebenen mit einer gemeinsamen Grenze besteht, die nicht zur selben Ebene gehören. Die einen Diederwinkel bildenden Halbebenen werden als Flächen bezeichnet. Ein Diederwinkel hat zwei Seiten, daher der Name Diederwinkel. Die Gerade – die gemeinsame Grenze der Halbebenen – wird Kante des Diederwinkels genannt. Schreiben Sie die Definition in Ihr Notizbuch.

Ein Diederwinkel ist eine Figur, die aus einer Geraden und zwei Halbebenen mit einer gemeinsamen Grenze besteht, die nicht zur selben Ebene gehören.

Lehrer : Im Alltag begegnen uns oft Gegenstände, die die Form eines Diederwinkels haben. Nenne Beispiele.

Student : Halb geöffneter Ordner.

Student : Die Wand des Raumes ist mit dem Boden verbunden.

Student : Satteldächer von Gebäuden.

Lehrer : Rechts. Und solche Beispiele gibt es in Hülle und Fülle.

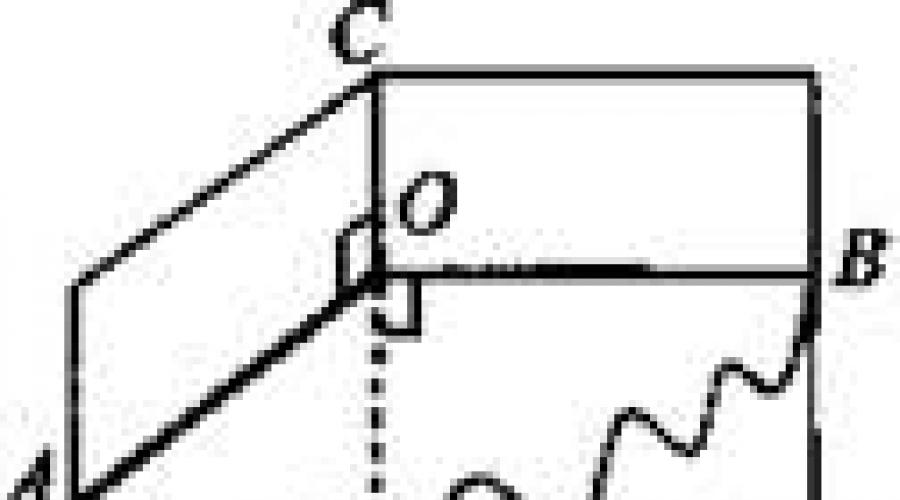
Lehrer : Wie Sie wissen, werden Winkel in einer Ebene in Grad gemessen. Sie haben wahrscheinlich eine Frage: Wie werden Diederwinkel gemessen? Es ist fertig auf die folgende Weise. Markieren wir einen Punkt am Rand des Diederwinkels und zeichnen wir von diesem Punkt aus auf jeder Fläche einen Strahl senkrecht zum Rand. Der von diesen Strahlen gebildete Winkel wird linearer Winkel des Diederwinkels genannt. Machen Sie eine Zeichnung in Ihren Notizbüchern.

Schreiben Sie an die Tafel und in Notizbücher.

UM ∈ a, JSC ⊥ a, VO ⊥ A, SABD– Diederwinkel,∠ AOB– linearer Winkel des Diederwinkels.

Lehrer : Alle linearen Winkel eines Diederwinkels sind gleich. Machen Sie sich eine weitere Zeichnung wie diese.

Lehrer : Lass es uns beweisen. Betrachten Sie zwei lineare Winkel AOB undPQR. Strahlen OA undQPliegen auf derselben Seite und sind senkrechtOQ, was bedeutet, dass sie gemeinsam Regie führen. Ebenso sind die Strahlen OB undQRCo-Regie. Bedeutet,∠ AOB= ∠ PQR(wie Winkel mit ausgerichteten Seiten).

Lehrer : Nun, die Antwort auf unsere Frage ist, wie der Diederwinkel gemessen wird.Das Gradmaß eines Diederwinkels ist das Gradmaß seines linearen Winkels. Zeichnen Sie die Bilder eines spitzen, rechten und stumpfen Diederwinkels aus dem Lehrbuch auf Seite 48 neu.

4. Konsolidierung des untersuchten Materials.

Lehrer : Zeichnungen für die Aufgaben anfertigen.

№ 1 . Gegeben: ΔABC, AC = BC, AB liegt in der Ebeneα, CD ⊥ α, C∉ α. Konstruieren Sie den linearen Winkel des DiederwinkelsCABD.

Student : Lösung:CM. ⊥ AB, Gleichstrom ⊥ AB.∠ CMD - Gesucht.

№ 2. Gegeben: ΔABC, ∠ C= 90°, BC liegt auf der Ebeneα, JSC⊥ α, A∈ α.

Konstruieren Sie den linearen Winkel des DiederwinkelsABCO.

Student : Lösung:AB ⊥ B.C., JSC⊥ BC bedeutet OS⊥ Sonne.∠ ACO - Gesucht.

№ 3 . Gegeben: ΔABC, ∠ C = 90°, AB liegt in der Ebeneα, CD⊥ α, C∉ α. Bauenlinearer DiederwinkelDABC.

Student : Lösung: CK ⊥ AB, Gleichstrom ⊥ AB,DK ⊥ AB bedeutet∠ DKC - Gesucht.

№ 4 . Gegeben:DABC- Tetraeder,TUN⊥ ABC.Konstruieren Sie den linearen Winkel des DiederwinkelsA B C D.

Student : Lösung:DM ⊥ Sonne,TUN ⊥ VS bedeutet OM⊥ Sonne;∠ OMD - Gesucht.

5. Zusammenfassung.

Lehrer: Was hast du heute im Unterricht Neues gelernt?

Studenten : Was heißt Diederwinkel, linearer Winkel, wie wird der Diederwinkel gemessen?

Lehrer : Was haben sie wiederholt?

Studenten : Was man einen Winkel in einer Ebene nennt; Winkel zwischen Geraden.

6. Hausaufgaben.

Schreiben Sie an die Tafel und in Ihr Tagebuch: Absatz 22, Nr. 167, Nr. 170.

Um Präsentationsvorschauen zu nutzen, erstellen Sie ein Google-Konto und melden Sie sich an: https://accounts.google.com

Folienunterschriften:

DIHEDRALWINKEL Mathematiklehrer GOU Sekundarschule Nr. 10 Eremenko M.A.

Hauptziele der Lektion: Einführung in das Konzept eines Diederwinkels und seines linearen Winkels. Überlegen Sie sich Aufgaben zur Anwendung dieser Konzepte.

Definition: Ein Diederwinkel ist eine Figur, die von zwei Halbebenen mit einer gemeinsamen Grenzgeraden gebildet wird.

Die Größe eines Diederwinkels ist die Größe seines linearen Winkels. AF ⊥ CD BF ⊥ CD AFB - linearer Diederwinkel ACD B

Beweisen wir, dass alle linearen Winkel eines Diederwinkels einander gleich sind. Betrachten wir zwei lineare Winkel AOB und A 1 OB 1. Die Strahlen OA und OA 1 liegen auf derselben Seite und stehen senkrecht zu OO 1, sind also gleichgerichtet. Die Strahlen OB und OB 1 sind ebenfalls gleichgerichtet. Daher ist ∠ AOB = ∠ A 1 OB 1 (wie Winkel mit gleichgerichteten Seiten).

Beispiele für Diederwinkel:

Definition: Der Winkel zwischen zwei sich schneidenden Ebenen ist der kleinste der von diesen Ebenen gebildeten Diederwinkel.

Aufgabe 1: Ermitteln Sie im Würfel A ... D 1 den Winkel zwischen den Ebenen ABC und CDD 1. Antwort: 90 o.

Aufgabe 2: Finden Sie im Würfel A ... D 1 den Winkel zwischen den Ebenen ABC und CDA 1. Antwort: 45 o.

Aufgabe 3: Finden Sie im Würfel A ... D 1 den Winkel zwischen den Ebenen ABC und BDD 1. Antwort: 90 o.

Aufgabe 4: Finden Sie im Würfel A ... D 1 den Winkel zwischen den Ebenen ACC 1 und BDD 1. Antwort: 90 o.

Aufgabe 5: Finden Sie im Würfel A ... D 1 den Winkel zwischen den Ebenen BC 1 D und BA 1 D. Lösung: Sei O der Mittelpunkt von B D. A 1 OC 1 – der lineare Winkel des Diederwinkels A 1 B D C 1.

Aufgabe 6: Im Tetraeder DABC sind alle Kanten gleich, Punkt M ist die Mitte der Kante AC. Beweisen Sie, dass ∠ DMB der lineare Winkel des Diederwinkels BACD ist.

Lösung: Die Dreiecke ABC und ADC sind regelmäßig, daher ist BM ⊥ AC und DM ⊥ AC und daher ist ∠ DMB der lineare Winkel des Diederwinkels DACB.

Aufgabe 7: Vom Scheitelpunkt B des Dreiecks ABC, dessen Seite AC in der Ebene α liegt, wird eine Senkrechte BB 1 zu dieser Ebene gezogen. Finden Sie den Abstand von Punkt B zur Geraden AC und zur Ebene α, wenn AB=2, ∠ВАС=150 0 und der Diederwinkel ВАСВ 1 gleich 45 0 ist.

Lösung: ABC ist ein stumpfes Dreieck mit dem stumpfen Winkel A, daher liegt die Basis der Höhe BC auf der Verlängerung der Seite AC. VC – Abstand von Punkt B zu AC. BB 1 – Abstand vom Punkt B zur Ebene α

2) Da AC ⊥BK, dann AC⊥KB 1 (nach Satz, Umkehrung des Satzes etwa drei Senkrechte). Daher ist ∠VKV 1 der lineare Winkel des Diederwinkels BASV 1 und ∠VKV 1 =45 0 . 3) ∆VAK: ∠A=30 0, VK=VA·sin 30 0, VK =1. ∆ВКВ 1: ВВ 1 =ВК· sin 45 0 , ВВ 1 =

TEXTTRANSKRIPT DER LEKTION:

In der Planimetrie sind die Hauptobjekte Linien, Strecken, Strahlen und Punkte. Strahlen, die von einem Punkt ausgehen, bilden eine ihrer geometrischen Formen – einen Winkel.

Wir wissen, dass der lineare Winkel in Grad und Bogenmaß gemessen wird.

Bei der Stereometrie wird den Objekten eine Ebene hinzugefügt. Eine Figur, die aus einer Geraden a und zwei Halbebenen mit einer gemeinsamen Grenze a besteht, die in der Geometrie nicht zur gleichen Ebene gehören, wird als Diederwinkel bezeichnet. Halbebenen sind die Flächen eines Diederwinkels. Die Gerade a ist eine Kante eines Diederwinkels.

Ein Diederwinkel kann wie ein linearer Winkel benannt, gemessen und konstruiert werden. Das müssen wir in dieser Lektion herausfinden.

Lassen Sie uns den Diederwinkel im ABCD-Tetraedermodell ermitteln.

Ein Diederwinkel mit der Kante AB heißt CABD, wobei die Punkte C und D zu verschiedenen Flächen des Winkels gehören und die Kante AB in der Mitte heißt

Um uns herum gibt es viele Objekte mit Elementen in Form eines Diederwinkels.

In vielen Städten sind in Parks spezielle Bänke zur Versöhnung aufgestellt. Die Bank besteht aus zwei schiefen Ebenen, die zur Mitte hin zusammenlaufen.

Beim Hausbau werden die sogenannten Satteldach. Bei diesem Haus ist das Dach in Form eines Diederwinkels von 90 Grad ausgeführt.

Der Diederwinkel wird auch in Grad oder Bogenmaß gemessen, aber wie man ihn misst.

Interessant ist, dass die Dächer der Häuser auf den Dachsparren ruhen. Und die Sparrenummantelung bildet zwei Dachschrägen in einem bestimmten Winkel.

Übertragen wir das Bild auf die Zeichnung. Um in der Zeichnung einen Diederwinkel zu finden, markiert man auf seiner Kante Punkt B. Von diesem Punkt aus werden zwei Strahlen BA und BC senkrecht zur Kante des Winkels gezeichnet. Der von diesen Strahlen gebildete Winkel ABC wird linearer Diederwinkel genannt.

Das Gradmaß eines Diederwinkels ist gleich dem Gradmaß seines linearen Winkels.

Lassen Sie uns den Winkel AOB messen.

Das Gradmaß eines gegebenen Diederwinkels beträgt sechzig Grad.

Für einen Diederwinkel können unendlich viele lineare Winkel gezeichnet werden; es ist wichtig zu wissen, dass sie alle gleich sind.

Betrachten wir zwei lineare Winkel AOB und A1O1B1. Die Strahlen OA und O1A1 liegen auf derselben Fläche und stehen senkrecht zur Geraden OO1, sind also gleichgerichtet. Die Strahlen OB und O1B1 sind ebenfalls gemeinsam gerichtet. Daher Winkel AOB gleich Winkel A1O1B1 als Winkel mit gleichgerichteten Seiten.

Ein Diederwinkel ist also durch einen linearen Winkel gekennzeichnet, und lineare Winkel sind spitz, stumpf und rechtwinklig. Betrachten wir Modelle von Diederwinkeln.

Ein stumpfer Winkel liegt vor, wenn sein linearer Winkel zwischen 90 und 180 Grad beträgt.

Ein rechter Winkel, wenn sein linearer Winkel 90 Grad beträgt.

Ein spitzer Winkel, wenn sein linearer Winkel 0 bis 90 Grad beträgt.

Lassen Sie uns eine der wichtigen Eigenschaften eines linearen Winkels beweisen.

Die Ebene des linearen Winkels steht senkrecht zur Kante des Diederwinkels.

Der Winkel AOB sei der lineare Winkel eines gegebenen Diederwinkels. Konstruktionsbedingt stehen die Strahlen AO und OB senkrecht zur Geraden a.

Die Ebene AOB verläuft durch zwei Schnittlinien AO und OB gemäß dem Satz: Eine Ebene geht durch zwei Schnittlinien, und zwar nur durch eine.

Die Linie a steht senkrecht auf zwei Schnittlinien, die in dieser Ebene liegen, was bedeutet, dass die Gerade a, basierend auf der Rechtwinkligkeit der Linie und der Ebene, senkrecht auf der Ebene AOB steht.

Um Probleme zu lösen, ist es wichtig, einen linearen Winkel eines gegebenen Diederwinkels konstruieren zu können. Konstruieren Sie einen linearen Winkel eines Diederwinkels mit der Kante AB für das Tetraeder ABCD.

Es handelt sich um einen Diederwinkel, der zum einen durch die Kante AB, eine Fläche ABD und die zweite Fläche ABC gebildet wird.

Hier ist eine Möglichkeit, es zu bauen.

Zeichnen wir eine Senkrechte vom Punkt D zur Ebene ABC. Markieren Sie Punkt M als Basis der Senkrechten. Denken Sie daran, dass bei einem Tetraeder die Basis der Senkrechten mit dem Mittelpunkt des eingeschriebenen Kreises an der Basis des Tetraeders zusammenfällt.

Zeichnen wir eine geneigte Linie vom Punkt D senkrecht zur Kante AB und markieren Sie Punkt N als Basis der geneigten Linie.

Im Dreieck DMN ist die Strecke NM die Projektion der geneigten DN auf die Ebene ABC. Nach dem Satz der drei Senkrechten steht die Kante AB senkrecht zur Projektion NM.

Das bedeutet, dass die Seiten des Winkels DNM senkrecht zur Kante AB stehen, was bedeutet, dass der konstruierte Winkel DNM der gewünschte lineare Winkel ist.

Betrachten wir ein Beispiel für die Lösung eines Problems zur Berechnung eines Diederwinkels.

Das gleichschenklige Dreieck ABC und das regelmäßige Dreieck ADB liegen nicht in derselben Ebene. Das Segment CD steht senkrecht zur Ebene ADB. Finden Sie den Diederwinkel DABC, wenn AC=CB=2 cm, AB= 4 cm.

Der Diederwinkel von DABC ist gleich seinem linearen Winkel. Lassen Sie uns diesen Winkel aufbauen.

Zeichnen wir das geneigte CM senkrecht zur Kante AB, da das Dreieck ACB gleichschenklig ist, dann fällt Punkt M mit der Mitte der Kante AB zusammen.

Die Gerade CD steht senkrecht auf der Ebene ADB, also senkrecht auf der in dieser Ebene liegenden Geraden DM. Und das Segment MD ist eine Projektion des geneigten CM auf die Ebene ADV.

Die Gerade AB steht konstruktionsbedingt senkrecht zum geneigten CM, das heißt nach dem Satz der drei Senkrechten steht sie senkrecht zur Projektion MD.

Es ergeben sich also zwei Senkrechte CM und DM zur Kante AB. Dies bedeutet, dass sie einen linearen Winkel CMD des Diederwinkels DABC bilden. Und alles was wir tun müssen, ist es aus dem CDM des rechtwinkligen Dreiecks zu finden.

Das Segment CM ist also der Median und die Höhe gleichschenkligen Dreiecks DIA, dann ist das Bein SM nach dem Satz des Pythagoras gleich 4 cm.

Aus dem rechtwinkligen Dreieck DMB ist nach dem Satz des Pythagoras das Bein DM gleich zwei Wurzeln aus drei.

Der Kosinus eines Winkels eines rechtwinkligen Dreiecks ist gleich dem Verhältnis des angrenzenden Schenkels MD zur Hypotenuse CM und entspricht drei Wurzeln aus drei mal zwei. Das bedeutet, dass der Winkel CMD 30 Grad beträgt.

In der Geometrie werden zwei zum Studium von Figuren verwendet. wichtige Eigenschaften: Längen der Seiten und Winkel zwischen ihnen. Bei räumlichen Figuren kommen zu diesen Merkmalen Diederwinkel hinzu. Schauen wir uns an, was es ist, und beschreiben wir auch die Methode zur Bestimmung dieser Winkel am Beispiel einer Pyramide.

Das Konzept des Diederwinkels

Jeder weiß, dass zwei sich schneidende Linien mit dem Scheitelpunkt an ihrem Schnittpunkt einen bestimmten Winkel bilden. Dieser Winkel kann mit einem Winkelmesser oder gemessen werden trigonometrische Funktionen um es zu berechnen. Ein Winkel, der durch zwei rechte Winkel gebildet wird, heißt linear.

Stellen Sie sich nun vor, dass es im dreidimensionalen Raum zwei Ebenen gibt, die sich in einer geraden Linie schneiden. Sie sind im Bild dargestellt.

Ein Diederwinkel ist der Winkel zwischen zwei sich schneidenden Ebenen. Genau wie linear wird es in Grad oder Bogenmaß gemessen. Wenn wir zu irgendeinem Punkt auf der Linie, entlang der sich die Ebenen schneiden, zwei in diesen Ebenen liegende Senkrechte wiederherstellen, dann ist der Winkel zwischen ihnen der gewünschte Dieder. Der einfachste Weg, diesen Winkel zu bestimmen, ist die Verwendung der Ebenengleichungen in Gesamtansicht.

Gleichung der Ebenen und Formel für den Winkel zwischen ihnen

Die Gleichung einer beliebigen Ebene im Raum wird im Allgemeinen wie folgt geschrieben:

A × x + B × y + C × z + D = 0.

Dabei sind x, y, z die Koordinaten der zur Ebene gehörenden Punkte, die Koeffizienten A, B, C, D sind einige bekannte Zahlen. Der Vorteil dieser Gleichung zur Berechnung von Diederwinkeln besteht darin, dass sie explizit die Koordinaten des Richtungsvektors der Ebene enthält. Wir werden es mit n¯ bezeichnen. Dann:

Der Vektor n¯ steht senkrecht zur Ebene. Der Winkel zwischen zwei Ebenen ist gleich dem Winkel zwischen ihren n 1 ¯ und n 2 ¯. Aus der Mathematik ist bekannt, dass der Winkel, den zwei Vektoren bilden, eindeutig aus deren Winkel bestimmt wird Skalarprodukt. Dies ermöglicht es uns, eine Formel zur Berechnung des Diederwinkels zwischen zwei Ebenen zu schreiben:

φ = arccos (|(n 1 ¯ × n 2 ¯)| / (|n 1 ¯| × |n 2 ¯|)).

Wenn wir die Koordinaten der Vektoren ersetzen, wird die Formel explizit geschrieben:

φ = arccos (|A 1 × A 2 + B 1 × B 2 + C 1 × C 2 | / (√(A 1 2 + B 1 2 + C 1 2) × √(A 2 2 + B 2 2 + C 2 2))).

Das Vorzeichen des Moduls im Zähler dient lediglich der Bestimmung scharfe Ecke, da der Diederwinkel immer kleiner oder gleich 90 ° ist.

Pyramide und ihre Ecken

Eine Pyramide ist eine Figur, die aus einem n-Eck und n Dreiecken besteht. Hier ist n eine ganze Zahl, die der Anzahl der Seiten des Polygons entspricht, das die Basis der Pyramide bildet. Diese räumliche Figur ist ein Polyeder oder Polyeder, da sie aus flachen Flächen (Seiten) besteht.

Es gibt zwei Arten von Pyramidenpolyedern:

• zwischen der Basis und der Seite (Dreieck);
• zwischen den beiden Seiten.

Wenn wir eine regelmäßige Pyramide betrachten, sind die genannten Winkel dafür nicht schwer zu bestimmen. Dazu sollten Sie anhand der Koordinaten von drei bekannten Punkten eine Ebenengleichung erstellen und dann die im obigen Absatz angegebene Formel für den Winkel φ verwenden.

Nachfolgend geben wir ein Beispiel, in dem wir zeigen, wie man Diederwinkel an der Basis einer regelmäßigen viereckigen Pyramide ermittelt.

Viereckig und der Winkel an seiner Basis

Nehmen wir an, wir hätten eine regelmäßige Pyramide mit quadratischer Grundfläche. Die Seitenlänge des Quadrats beträgt a, die Höhe der Figur beträgt h. Lassen Sie uns den Winkel zwischen der Basis der Pyramide und ihrer Seite ermitteln.

Platzieren wir den Ursprung des Koordinatensystems in der Mitte des Quadrats. Dann sind die Koordinaten der in der Abbildung gezeigten Punkte A, B, C, D gleich:

A = (a/2; -a/2; 0);

B = (a/2; a/2; 0);

C = (-a/2; a/2; 0);

Betrachten wir die Flugzeuge ACB und ADB. Offensichtlich ist der Richtungsvektor n 1 ¯ für die Ebene ACB gleich:

Um den Richtungsvektor n 2 ¯ der ADB-Ebene zu bestimmen, gehen wir wie folgt vor: Wir finden zwei beliebige Vektoren, die dazu gehören, zum Beispiel AD¯ und AB¯, und berechnen dann deren Vektorprodukt. Das Ergebnis ergibt die Koordinaten n 2 ¯. Wir haben:

AD¯ = D - A = (0; 0; h) - (a/2; -a/2; 0) = (-a/2; a/2; h);

AB¯ = B - A = (a/2; a/2; 0) - (a/2; -a/2; 0) = (0; a; 0);

n 2 ¯ = = [(-a/2; a/2; h) × (0; a; 0)] = (-a × h; 0; -a 2 /2).

Da die Multiplikation und Division eines Vektors durch eine Zahl seine Richtung nicht ändert, transformieren wir das resultierende n 2 ¯, indem wir seine Koordinaten durch -a dividieren, und erhalten:

Wir haben die Richtungsvektoren n 1 ¯ und n 2 ¯ für die Basisebenen ACB und Seitenebene ADB definiert. Es bleibt die Formel für den Winkel φ zu verwenden:

φ = arccos (|(n 1 ¯ × n 2 ¯)| / (|n 1 ¯| × |n 2 ¯|)) = arccos (a / (2 × √h 2 + a 2 /4)).

Lassen Sie uns den resultierenden Ausdruck transformieren und wie folgt umschreiben:

φ = arccos (a / √(a 2 + 4 × h 2)).

Wir haben die Formel für den Diederwinkel an der Basis für den richtigen erhalten viereckige Pyramide. Wenn Sie die Höhe der Figur und die Länge ihrer Seite kennen, können Sie den Winkel φ berechnen. Für die Cheops-Pyramide beispielsweise, deren Basisseite 230,4 Meter beträgt und deren Anfangshöhe 146,5 Meter betrug, beträgt der Winkel φ 51,8 °.

Bestimmen Sie den Diederwinkel für ein Viereck regelmäßige Pyramide Es ist auch mit der geometrischen Methode möglich. Dazu genügt eine Überlegung rechtwinkliges Dreieck, gebildet aus der Höhe h, der halben Grundlänge a/2 und dem Apothem eines gleichschenkligen Dreiecks.

Diese Lektion richtet sich an Selbststudium Thema „Diederwinkel“. In dieser Lektion lernen die Schüler eine der wichtigsten geometrischen Formen kennen, den Diederwinkel. Außerdem lernen wir in der Lektion, wie man den linearen Winkel des betrachteten Objekts bestimmt geometrische Figur und wie groß ist der Diederwinkel an der Basis der Figur?

Lassen Sie uns wiederholen, was ein Winkel in einer Ebene ist und wie er gemessen wird.

Reis. 1. Flugzeug

Betrachten wir die Ebene α (Abb. 1). Von diesem Punkt UM zwei Strahlen gehen aus - OB Und OA.

Definition. Eine Figur, die aus zwei von einem Punkt ausgehenden Strahlen besteht, wird Winkel genannt.

Der Winkel wird in Grad und Bogenmaß gemessen.

Erinnern wir uns daran, was ein Bogenmaß ist.

Reis. 2. Bogenmaß

Wenn wir einen Mittelpunktswinkel haben, dessen Bogenlänge gleich dem Radius ist, dann wird ein solcher Mittelpunktswinkel als Winkel von 1 Bogenmaß bezeichnet. ,∠ AOB= 1 rad (Abb. 2).

Beziehung zwischen Bogenmaß und Grad.

froh.

Wir haben es verstanden, ich bin froh. (). Dann,

Definition. Diederwinkel eine durch eine gerade Linie gebildete Figur heißt A und zwei Halbebenen mit einer gemeinsamen Grenze A, nicht zur selben Ebene gehörend.

Reis. 3. Halbebenen

Betrachten wir zwei Halbebenen α und β (Abb. 3). Ihre gemeinsame Grenze ist A. Diese Zahl wird als Diederwinkel bezeichnet.

Terminologie

Die Halbebenen α und β sind die Flächen eines Diederwinkels.

Gerade A ist eine Kante eines Diederwinkels.

Auf einer gemeinsamen Kante A Diederwinkel, wählen Sie einen beliebigen Punkt UM(Abb. 4). In der Halbebene α vom Punkt UM die Senkrechte wiederherstellen OA zu einer geraden Linie A. Vom selben Punkt aus UM in der zweiten Halbebene β konstruieren wir eine Senkrechte OB bis zum Rand A. Habe einen Winkel AOB, der als linearer Winkel des Diederwinkels bezeichnet wird.

Reis. 4. Diederwinkelmessung

Beweisen wir die Gleichheit aller linearen Winkel für einen gegebenen Diederwinkel.

Nehmen wir einen Diederwinkel an (Abb. 5). Wählen wir einen Punkt UM und Punkt O 1 auf einer geraden Linie A. Konstruieren wir einen linearen Winkel, der dem Punkt entspricht UM, d.h. wir zeichnen zwei Senkrechte OA Und OB in den Ebenen α bzw. β zur Kante A. Wir verstehen den Winkel AOB- linearer Winkel des Diederwinkels.

Reis. 5. Veranschaulichung des Beweises

Von diesem Punkt O 1 Zeichnen wir zwei Senkrechte OA 1 Und OB 1 bis zum Rand A in den Ebenen α bzw. β und wir erhalten den zweiten linearen Winkel A 1 O 1 B 1.

Strahlen O 1 A 1 Und OA gleichgerichtet, da sie in derselben Halbebene liegen und parallel zueinander sind wie zwei Senkrechte auf derselben Linie A.

Ebenso Strahlen Ungefähr 1 in 1 Und OB sind co-regie, das heißt ∠ AOB =∠ A 1 O 1 B 1 als Winkel mit gleichgerichteten Seiten, was bewiesen werden musste.

Die Ebene des linearen Winkels steht senkrecht zur Kante des Diederwinkels.

Beweisen: A ⊥ AOB.

Reis. 6. Beweisdarstellung

Nachweisen:

OA ⊥ A Durch den Bau, OB ⊥ A konstruktionsbedingt (Abb. 6).

Wir finden, dass die Linie A senkrecht zu zwei Schnittlinien OA Und OB aus der Ebene AOB, was bedeutet, dass es gerade ist A senkrecht zur Ebene OAV, was bewiesen werden musste.

Ein Diederwinkel wird durch seinen linearen Winkel gemessen. Das bedeutet, dass ein linearer Winkel genauso viele Grad Bogenmaß enthält wie sein Diederwinkel ebenso viele Grad Bogenmaß enthält. Dementsprechend werden folgende Arten von Diederwinkeln unterschieden.

Akut (Abb. 6)

Ein Diederwinkel ist spitz, wenn sein linearer Winkel spitz ist, d. h. .

Gerade (Abb. 7)

Ein Diederwinkel ist rechts, wenn sein linearer Winkel 90° beträgt – stumpf (Abb. 8)

Ein Diederwinkel ist stumpf, wenn sein linearer Winkel stumpf ist, d. h. .

Reis. 7. Rechter Winkel

Reis. 8. Stumpfer Winkel

Beispiele für die Konstruktion linearer Winkel in realen Figuren

ABCD- Tetraeder.

1. Konstruieren Sie einen linearen Winkel eines Diederwinkels mit einer Kante AB.

Reis. 9. Illustration des Problems

Konstruktion:

Wir sprechen von einem Diederwinkel, der durch eine Kante gebildet wird AB und Kanten ABD Und ABC(Abb. 9).

Machen wir eine direkte DN senkrecht zur Ebene ABC, N- die Basis der Senkrechten. Lassen Sie uns eine Schräge zeichnen DM senkrecht zu einer Geraden AB,M- geneigter Sockel. Aus dem Satz der drei Senkrechten schließen wir, dass die Projektion eine Schräge ist NM auch senkrecht zur Linie AB.

Das heißt, vom Punkt her M zwei Senkrechte zur Kante werden wiederhergestellt AB auf zwei seiten ABD Und ABC. Wir haben den linearen Winkel erhalten DMN.

beachte das AB, eine Kante eines Diederwinkels, senkrecht zur Ebene des linearen Winkels, d. h. der Ebene DMN. Das Problem ist behoben.

Kommentar. Der Diederwinkel kann wie folgt bezeichnet werden: DABC, Wo

AB- Kante und Punkte D Und MIT ausschlafen verschiedene Gesichter Ecke.

2. Konstruieren Sie einen linearen Winkel eines Diederwinkels mit einer Kante Wechselstrom.

Zeichnen wir eine Senkrechte DN zum Flugzeug ABC und geneigt DN senkrecht zu einer Geraden Wechselstrom. Mit dem Drei-Senkrechten-Theorem finden wir das heraus НN- Schrägprojektion DN zum Flugzeug ABC, auch senkrecht zur Linie Wechselstrom.DNH- linearer Winkel eines Diederwinkels mit einer Kante Wechselstrom.

In einem Tetraeder DABC alle Kanten sind gleich. Punkt M- Mitte der Rippe Wechselstrom. Beweisen Sie, dass der Winkel DMV- linearer Diederwinkel DUD, also ein Diederwinkel mit einer Kante Wechselstrom. Eines seiner Gesichter ist WechselstromD, zweite - DIA(Abb. 10).

Reis. 10. Illustration des Problems

Lösung:

Dreieck ADC- gleichseitig, DM- Median und damit Höhe. Bedeutet, DM ⊥ Wechselstrom. Ebenso Dreieck AINC- gleichseitig, INM- Median und damit Höhe. Bedeutet, VM ⊥ Wechselstrom.

Also vom Punkt her M Rippen Wechselstrom Der Diederwinkel stellte zwei Senkrechte wieder her DM Und VM zu dieser Kante in den Flächen des Diederwinkels.

Also, ∠ DMIN ist der lineare Winkel des Diederwinkels, der bewiesen werden musste.

Wir haben also den Diederwinkel definiert, den linearen Winkel des Diederwinkels.

In der nächsten Lektion werden wir uns mit der Rechtwinkligkeit von Linien und Ebenen befassen und dann lernen, was ein Diederwinkel an der Basis von Figuren ist.

Literaturverzeichnis zum Thema „Diederwinkel“, „Diederwinkel an der Basis geometrischer Figuren“

1. Geometrie. Klassen 10-11: Lehrbuch für allgemeinbildende Einrichtungen / Sharygin I. F. - M.: Bustard, 1999. - 208 S.: Abb.
2. Geometrie. 10. Klasse: Lehrbuch für allgemeinbildende Einrichtungen mit vertieftem und spezialisiertem Studium der Mathematik /E. V. Potoskuev, L. I. Zvalich. - 6. Auflage, Stereotyp. - M.: Bustard, 2008. - 233 S.: Abb.

1. Yaklass.ru ().
2. E-science.ru ().
3. Webmath.exponenta.ru ().
4. Tutoronline.ru ().

Hausaufgabe zum Thema „Diederwinkel“, Bestimmung des Diederwinkels an der Basis von Figuren

Geometrie. Klassen 10-11: Lehrbuch für Studierende allgemeinbildender Einrichtungen (Grund- und Profilebenen) / I. M. Smirnova, V. A. Smirnov. – 5. Auflage, korrigiert und erweitert – M.: Mnemosyne, 2008. – 288 Seiten: Abb.

Aufgaben 2, 3 S. 67.

Was ist der lineare Diederwinkel? Wie baue ich es?

ABCD- Tetraeder. Konstruieren Sie einen linearen Winkel eines Diederwinkels mit einer Kante:

A) IND B) DMIT.

ABCD.A. 1 B 1 C 1 D 1 - Würfel Konstruieren Sie den linearen Winkel des Diederwinkels Ein 1 ABC mit Rippe AB. Bestimmen Sie das Gradmaß.