Zusammenfassung andere Präsentationen

„Bestimmen Sie, ob eine Funktion gerade oder ungerade ist“ – Die Funktion ist ungerade. Ist nicht seltsam. Ist nicht einmal. Graph einer geraden Funktion. Graph einer ungeraden Funktion. Funktion. Symmetrie um die Achse. Sogar Funktionen. Ist die Funktion seltsam? Spalte. Sogar und seltsame Funktionen. Beispiel. Ist die Funktion gerade? Seltsame Funktionen.

„„Exponentialfunktion“ 11. Klasse“ – Lösen Sie die Gleichung. Definition. Überprüfe dich selbst. Exponentielle Ungleichheiten. Wenn x=0 ist, ist der Wert der Funktion 1. Testen. Exponentialgleichungen. Ableitung und Stammfunktion. Funktionaler Weg. Grundlegende Referenzsignale. Die Funktion nimmt über den gesamten Definitionsbereich zu. Exponentialfunktion. Wertebereich. Eigenschaften eines Grades mit rationalem Exponenten. Methoden zum Lösen von Gleichungen. Eigenschaften der Exponentialfunktion.

„Beispiele für logarithmische Ungleichungen“ – Finden die richtige Entscheidung. Welche Funktionen nehmen zu und welche abnehmen? Viel Glück beim Einheitlichen Staatsexamen! Graphen logarithmischer Funktionen. Zusammenfassung der Lektion. Während der Lektion zu füllender Cluster: Zunehmend. Aufgabe: lösen logarithmische Ungleichungen, vorgeschlagen in den Aufgaben des Einheitlichen Staatsexamens 2010. Setzen Sie zwischen den Zahlen m und n ein Zeichen > oder<.(m, n >0). Abnehmend. Bereiten Sie sich auf das Einheitliche Staatsexamen vor! Unterrichtsziele: Algebra 11. Klasse. Finden Sie den Definitionsbereich der Funktion.

„Eine Funktion mit einem Modul grafisch darstellen“ – Graph einer Funktion. Verstärktes Wissen über bereits erlernte Funktionen. Frage an die Klasse. Gelerntes Wissen. Y = x2 – 2x – 3. Grafische Funktionen. Verallgemeinerung. Lineare Funktion. Projektaktivitäten. Y = f(x). Lektion der Verallgemeinerung und Systematisierung von Wissen. Aktualisierung des Wissens über Funktionsgraphen. Y = lnx. Versuchen Sie, selbst Diagramme zu erstellen. Y = x – 2. Y = sinx.

„Potenzfunktionen 11. Klasse“ – Funktion y=x0. Kubische Funktion. Hyperbel. Y = x. Funktion y=x-3. Der Graph ist eine Parabel. Potenzfunktionen mit natürlicher Indikator. Funktion y = x2n-1. Funktion y = x2n. Power-Funktion. Funktion y=x-2. Funktion y=x4.

„Die geometrische Bedeutung der Ableitung einer Funktion“ – es ist mir gelungen. Berechnungsergebnisse. Grenzposition der Sekante. Finden Sie die Steigung. Sekante. Geometrische Bedeutung der Ableitung. Algorithmus zum Erstellen der Tangentengleichung. Definition. Der Wert der Ableitung der Funktion. Richtige mathematische Idee. Gleichung einer Tangente an den Graphen einer Funktion. Bilden Sie ein Paar. Gleichung einer Geraden mit Neigung. Schreiben Sie eine Gleichung für die Tangente an den Funktionsgraphen.

Das Modulzeichen ist vielleicht eines der meisten interessante Phänomene in Mathematik. In diesem Zusammenhang haben viele Schüler die Frage, wie man Funktionsgraphen erstellt, die ein Modul enthalten. Schauen wir uns dieses Problem im Detail an.

1. Diagramme von Funktionen zeichnen, die ein Modul enthalten

Beispiel 1.

Stellen Sie die Funktion y = x 2 – 8|x| grafisch dar + 12.

Lösung.

Bestimmen wir die Parität der Funktion. Der Wert für y(-x) ist derselbe wie der Wert für y(x), daher ist diese Funktion gerade. Dann ist sein Graph symmetrisch zur Oy-Achse. Wir zeichnen die Funktion y = x 2 – 8x + 12 für x ≥ 0 auf und stellen den Graphen symmetrisch bezüglich Oy für negatives x dar (Abb. 1).

Beispiel 2.

Die folgende Grafik sieht aus wie y = |x 2 – 8x + 12|.

– Wie groß ist der Wertebereich der vorgeschlagenen Funktion? (y ≥ 0).

– Wie befindet sich der Zeitplan? (Über oder berührend der x-Achse).

Dies bedeutet, dass der Graph der Funktion erhalten wird auf die folgende Weise: Erstellen Sie einen Graphen der Funktion y = x 2 – 8x + 12, lassen Sie den Teil des Graphen, der über der Ox-Achse liegt, unverändert und der Teil des Graphen, der unter der Abszissenachse liegt, wird relativ zur Ox-Achse symmetrisch angezeigt (Abb. 2).

Beispiel 3.

Um die Funktion y = |x 2 – 8|x| darzustellen + 12| Führen Sie eine Kombination von Transformationen durch:

y = x 2 – 8x + 12 → y = x 2 – 8|x| + 12 → y = |x 2 – 8|x| + 12|.

Antwort: Abbildung 3.

Die betrachteten Transformationen gelten für alle Arten von Funktionen. Machen wir eine Tabelle:

2. Zeichnen von Diagrammen von Funktionen, die „verschachtelte Module“ in der Formel enthalten

Wir haben bereits Beispiele gesehen quadratische Funktion, das das Modul enthält, sowie mit Allgemeine Regeln Erstellen von Graphen von Funktionen der Form y = f(|x|), y = |f(x)| und y = |f(|x|)|. Diese Transformationen werden uns bei der Betrachtung des folgenden Beispiels helfen.

Beispiel 4.

Betrachten Sie eine Funktion der Form y = |2 – |1 – |x|||. Der Funktionsausdruck enthält „verschachtelte Module“.

Lösung.

Lassen Sie uns die Methode der geometrischen Transformationen verwenden.

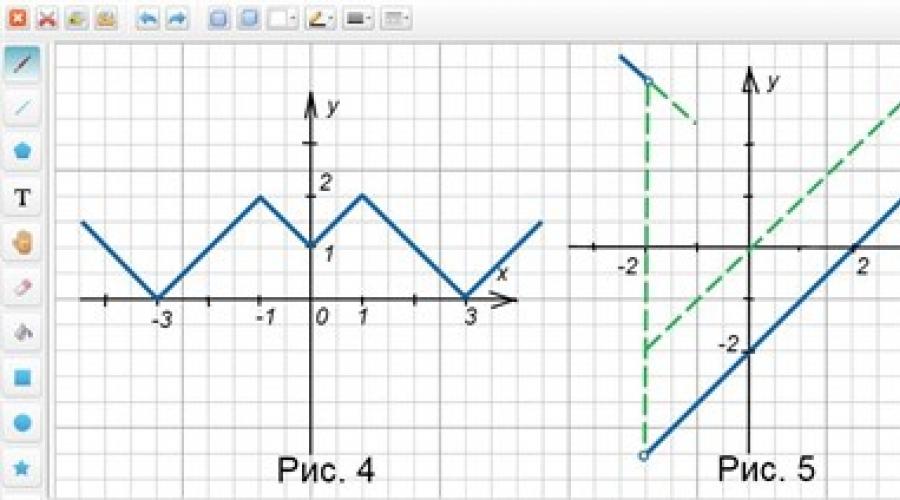
Schreiben wir eine Kette aufeinanderfolgender Transformationen auf und erstellen eine entsprechende Zeichnung (Abb. 4):

y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.

Betrachten wir Fälle, in denen Symmetrie und parallele Übersetzungstransformationen nicht die Haupttechnik beim Erstellen von Diagrammen sind.

Beispiel 5.

Konstruieren Sie einen Graphen einer Funktion der Form y = (x 2 – 4)/√(x + 2) 2.

Lösung.

Bevor wir einen Graphen erstellen, transformieren wir die Formel, die die Funktion definiert, und erhalten eine weitere analytische Zuordnung der Funktion (Abb. 5).

y = (x 2 – 4)/√(x + 2) 2 = (x– 2)(x + 2)/|x + 2|.

Erweitern wir das Modul im Nenner:

Für x > -2, y = x – 2 und für x< -2, y = -(x – 2).

Domäne D(y) = (-∞; -2)ᴗ(-2; +∞).

Wertebereich E(y) = (-4; +∞).

Die Punkte, an denen der Graph die Koordinatenachse schneidet: (0; -2) und (2; 0).

Die Funktion nimmt für alle x ab dem Intervall (-∞; -2) ab, steigt für x von -2 bis +∞.

Hier mussten wir das Vorzeichen des Moduls offenlegen und die Funktion für jeden Fall grafisch darstellen.

Beispiel 6.

Betrachten Sie die Funktion y = |x + 1| – |x – 2|.

Lösung.

Bei der Erweiterung des Vorzeichens eines Moduls ist es notwendig, jede mögliche Kombination von Vorzeichen submodularer Ausdrücke zu berücksichtigen.

Es gibt vier mögliche Fälle:

(x + 1 – x + 2 = 3, für x ≥ -1 und x ≥ 2;

(-x – 1 + x – 2 = -3, bei x< -1 и x < 2;

(x + 1 + x – 2 = 2x - 1, für x ≥ -1 und x< 2;

(-x – 1 – x + 2 = -2x + 1, bei x< -1 и x ≥ 2 – пустое множество.

Dann sieht die ursprüngliche Funktion so aus:

(3, für x ≥ 2;

y = (-3, bei x< -1;

(2x – 1, mit -1 ≤ x< 2.

Wir haben eine stückweise gegebene Funktion erhalten, deren Diagramm in Abbildung 6 dargestellt ist.

3. Algorithmus zum Erstellen von Funktionsgraphen der Form

y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + Axt + b.

Im vorherigen Beispiel war es recht einfach, die Vorzeichen des Moduls zu erkennen. Wenn es mehr Modulsummen gibt, ist es problematisch, alle möglichen Vorzeichenkombinationen submodularer Ausdrücke zu berücksichtigen. Wie konstruiert man in diesem Fall einen Graphen der Funktion?

Beachten Sie, dass der Graph eine gestrichelte Linie ist, mit Scheitelpunkten an Punkten mit den Abszissen -1 und 2. Bei x = -1 und x = 2 sind die submodularen Ausdrücke gleich Null. In der Praxis sind wir der Regel zur Erstellung solcher Diagramme näher gekommen:

Ein Graph einer Funktion der Form y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b ist eine gestrichelte Linie mit unendlichen Extremverbindungen. Um eine solche gestrichelte Linie zu konstruieren, reicht es aus, alle ihre Eckpunkte (die Abszissen der Eckpunkte sind die Nullstellen der submodularen Ausdrücke) und einen Kontrollpunkt auf den linken und rechten unendlichen Verbindungen zu kennen.

Aufgabe.

Stellen Sie die Funktion y = |x| grafisch dar + |x – 1| + |x + 1| und finden Sie seinen kleinsten Wert.

Lösung:

Nullstellen submodularer Ausdrücke: 0; -1; 1. Eckpunkte der gestrichelten Linie (0; 2); (-13); (13). Kontrollpunkt rechts (2; 6), links (-2; 6). Wir erstellen ein Diagramm (Abb. 7). min f(x) = 2.

Sie haben noch Fragen? Sie wissen nicht, wie man eine Funktion mit einem Modul grafisch darstellt?
Um Hilfe von einem Tutor zu erhalten, registrieren Sie sich.

Wenn Sie Material ganz oder teilweise kopieren, ist ein Link zur Quelle erforderlich.

Lektion 5. Konvertieren von Diagrammen mit Modulen (optionale Lektion)

09.07.2015 8999 0

Ziel: Beherrschen Sie die grundlegenden Fähigkeiten zum Konvertieren von Diagrammen mit Modulen.

I. Vermittlung des Themas und Zwecks der Lektion

II . Wiederholung und Vertiefung des behandelten Stoffes

1. Antworten auf Fragen zu Hausaufgaben(Analyse ungelöster Probleme).

2. Überwachung der Aufnahme des Stoffes (schriftliche Befragung).

Variante 1

F (x), zeichnen Sie die Funktion y = f(-x) + 2?

2. Stellen Sie die Funktion grafisch dar:

Option 2

1. Wie, wenn man den Graphen der Funktion y = kennt F (x), zeichnen Sie die Funktion y = - f(x) - 1?

2. Stellen Sie die Funktion grafisch dar:

III. Neues Material lernen

Aus dem Material der vorherigen Lektion geht hervor, dass Methoden zur Transformation von Diagrammen bei der Erstellung dieser Diagramme äußerst nützlich sind. Daher betrachten wir auch die wichtigsten Methoden zum Konvertieren von Diagrammen, die Module enthalten. Diese Methoden sind universell und für jede Funktion geeignet. Zur Vereinfachung der Konstruktion betrachten wir die stückweise lineare Funktion F (x) mit Domäne D(f ), dessen Diagramm in der Abbildung dargestellt ist. Betrachten wir drei Standardtransformationen von Graphen mit Modulen.

1) Zeichnen eines Diagramms der Funktion y = | f(x)|

f /(x), wenn Dx)>0,

Per Definition eines Moduls erhalten wir:Das bedeutet, dass man die Funktion y = | grafisch darstellen muss f(x )| Wir müssen einen Teil des Diagramms der Funktion y = speichern f(x ), für die y ≥ 0. Der Teil des Graphen der Funktion y = F (x), für das y< 0, надо симметрично отразить вверх относительно оси абсцисс.

2) Zeichnen eines Diagramms der Funktion y = f(|x|)

G/O), wenn Dx)>0,

Erweitern wir das Modul und erhalten:Daher ist es notwendig, einen Graphen der Funktion y = zu zeichnen f(|x |) müssen wir einen Teil des Graphen der Funktion y = speichern F (x), für die x ≥ 0 ist. Außerdem muss dieser Teil symmetrisch nach links relativ zur Ordinate gespiegelt sein.

3) Zeichnen Sie den Graphen der Gleichung |y| = f(x)

Per Definition des Moduls haben wir das wann F (x) ≥ 0 ist es notwendig, Graphen zweier Funktionen zu erstellen: y = f (x) und y = - f (X). Dies bedeutet, dass die Gleichung |y| grafisch dargestellt werden soll = F (x) Es ist notwendig, einen Teil des Graphen der Funktion y = zu speichern F (x), für die y ≥ 0. Außerdem muss dieser Teil relativ zur x-Achse symmetrisch nach unten gespiegelt sein.

Beachten Sie, dass die Abhängigkeit |y| = F (x) definiert keine Funktion, also bei x∈ (-2,6; 1,4) Jeder x-Wert entspricht zwei y-Werten. Daher zeigt die Abbildung genau den Graphen der Gleichung |y| = f(x).

Wir verwenden die betrachteten Methoden zur Konvertierung von Graphen mit Modulen, um Graphen komplexerer Funktionen und Gleichungen zu erstellen.

Beispiel 1

Lassen Sie uns die Funktion grafisch darstellen

Lassen Sie uns den gesamten Teil dieser Funktion hervorhebenEinen solchen Graphen erhält man durch Verschieben des Graphen der Funktion y = -1/ X 2 Einheiten nach rechts und 1 Einheit nach unten. Der Graph dieser Funktion ist eine Hyperbel.

Beispiel 2

Lassen Sie uns die Funktion grafisch darstellen

Gemäß Methode 1 speichern wir den Teil des Graphen aus Beispiel 1, für den y ≥ 0 ist. Der Teil des Graphen, für den y< 0, симметрично отразим вверх относительно оси абсцисс.

Beispiel 3

Lassen Sie uns die Funktion grafisch darstellen

Mit Methode 2 speichern wir den Teil des Diagramms aus Beispiel 1, für den x ≥ 0. Außerdem spiegeln wir diesen gespeicherten Teil relativ zur y-Achse nach links. Wir erhalten einen Graphen der Funktion, der symmetrisch zur Ordinatenachse ist.

Beispiel 4

Lassen Sie uns die Gleichung zeichnen

Gemäß Methode 3 speichern wir den Teil des Diagramms aus Beispiel 1, für den y ≥ 0 ist. Außerdem spiegeln wir diesen gespeicherten Teil relativ zur x-Achse symmetrisch nach unten. Wir erhalten ein Diagramm dieser Gleichung.

Natürlich können die betrachteten Methoden zur Konvertierung von Graphen auch zusammen verwendet werden.

Beispiel 5

Lassen Sie uns die Funktion grafisch darstellen

Wir verwenden den Graphen der Funktionkonstruiert in Beispiel 3. Um diesen Graphen zu konstruieren, speichern wir die Teile des Graphen 3, für die y ≥ 0 ist. Die Teile des Graphen 3, für die y< 0, симметрично отразим вверх относительно оси абсцисс.

In Fällen, in denen Module auf andere Weise abhängig sind (als in den Methoden 1-3), ist eine Erweiterung dieser Module erforderlich.

Beispiel 6

Lassen Sie uns die Funktion grafisch darstellen

Ausdrücke x - 1 und x + 2, die unter den Moduli-Vorzeichen enthalten sind, ändern ihr Vorzeichen an den Punkten x = 1 und X = -2 bzw. Markieren wir diese Punkte auf der Koordinatenlinie. Sie unterteilen es in drei Intervalle. Mithilfe der Moduldefinitionen erweitern wir die Module in jedem Intervall.

Wir bekommen:

1. Wann

2. Wann

3. Wann

Lassen Sie uns Diagramme dieser Funktionen erstellen und dabei die Intervalle für die Variable x berücksichtigen, in denen die Vorzeichen des Moduls offenbart wurden. Wir erhalten eine unterbrochene gerade Linie.

Sehr oft wird bei der Erstellung von Graphen von Gleichungen mit Modulen eine Koordinatenebene verwendet, um diese darzustellen. Lassen Sie uns dies anhand des folgenden Beispiels erklären.

Beispiel 7

Lassen Sie uns die Gleichung zeichnen

Der Ausdruck y - x ändert sein Vorzeichen auf der Geraden y = x. Konstruieren wir diese Gerade – die Winkelhalbierende des ersten und dritten Koordinatenwinkels. Diese Gerade teilt die Punkte der Ebene in zwei Bereiche: 1 - Punkte oberhalb der Geraden y – x; 2 - Punkte unter dieser Linie. Lassen Sie uns das Modul in solchen Bereichen erweitern. Nehmen Sie im Bereich 1 beispielsweise den Kontrollpunkt (0; 5). Wir sehen, dass für diesen Punkt der Ausdruck y - x > 0 gilt. Wenn wir das Modul erweitern, erhalten wir: y - x + y + x = 4 oder j = 2. Wir konstruieren eine solche Gerade innerhalb des ersten Bereichs. Offensichtlich gilt in Region 2 der Ausdruck y - x< 0. Раскрывая модуль, имеем: -(у - х) + у + х = 4 или х = 2. Строим эту прямую в пределах области 2. Получаем график данного уравнения.

3. Zeichnen Sie die lineare Bruchfunktion und die Gleichung grafisch auf:

4. Zeichnen Sie einen Graphen einer Funktion, Gleichung oder Ungleichung:

VIII. Zusammenfassung der Lektion

Thema: „Exponentialfunktion. Funktionalgrafische Methoden zur Lösung von Gleichungen, Ungleichungen, Systemen“

Ziel : Betrachten Sie die Aufgaben von ZNO anhand von Funktionen grafische Methoden am Beispiel einer Exponentialfunktion y = a x, a>0, a1

Lernziele:

wiederholen Sie die Eigenschaft der Monotonie und Begrenztheit der Exponentialfunktion;

Wiederholen Sie den Algorithmus zum Erstellen von Funktionsgraphen mithilfe von Transformationen.

Finden Sie mehrere Werte und mehrere Definitionen einer Funktion nach Art der Formel und Verwenden eines Diagramms;

entscheiden Exponentialgleichungen, Ungleichungen und Systeme, die Graphen und Eigenschaften von Funktionen verwenden.

Arbeiten mit Funktionsgraphen, die ein Modul enthalten;

Schauen Sie sich die Grafiken an komplexe Funktion und ihr Wertebereich;

Während des Unterrichts:

1. Einführungsrede des Lehrers. Motivation für das Studium dieses Themas

Folie 1 Exponentialfunktion. „Funktional-grafische Methoden zur Lösung von Gleichungen und Ungleichungen“

Die funktionalgrafische Methode basiert auf der Verwendung grafischer Darstellungen, der Anwendung der Eigenschaften einer Funktion und ermöglicht die Lösung vieler mathematischer Probleme.

Schieben Sie 2-3 Ziele und Lernziele.

Heute schauen wir uns die Aufgaben von ZNO an verschiedene Level Schwierigkeiten beim Einsatz funktionalgrafischer Methoden am Beispiel der Exponentialfunktion y = a x, a>o, a1. Mithilfe eines Grafikprogramms erstellen wir Illustrationen zu den Problemen.

Folie 4 Warum ist es so wichtig, die Eigenschaften der Exponentialfunktion zu kennen?

Nach dem Gesetz der Exponentialfunktion würden sich alle Lebewesen auf der Erde vermehren, wenn hierfür günstige Bedingungen gegeben wären, d. h. Es gab keine natürlichen Feinde und es gab reichlich Nahrung. Ein Beweis dafür ist die Verbreitung von Kaninchen in Australien, die es vorher nicht gab. Es reichte aus, ein paar Individuen freizulassen, und nach einiger Zeit wurde ihr Nachwuchs zu einer nationalen Katastrophe.

In Natur, Technik und Wirtschaft gibt es zahlreiche Prozesse, bei denen sich der Wert einer Größe gleich oft ändert, d. h. nach dem Gesetz der Exponentialfunktion. Diese Prozesse werden Prozesse genannt organisches Wachstum oder organische Dämpfung.

Zum Beispiel, bakterielles Wachstum V ideale Bedingungen entspricht dem Prozess des organischen Wachstums; radioaktiver Zerfall von Stoffen– der Prozess der organischen Schwächung.

Unterliegt den Gesetzen des organischen Wachstums Wachstum der Einlage bei der Sparkasse, Wiederherstellung des Hämoglobins im Blut eines Spenders oder einer verwundeten Person, die viel Blut verloren hat.

Nennen Sie Beispiele

Bewerbung im wahres Leben(Medikamentendosis).

Nachricht zur Medikamentendosierung:

Jeder weiß, dass die vom Arzt zur Behandlung empfohlenen Pillen mehrmals täglich eingenommen werden müssen, sonst sind sie wirkungslos. Die Notwendigkeit, das Arzneimittel erneut zu verabreichen, um eine konstante Konzentration im Blut aufrechtzuerhalten, wird durch die Zerstörung des Arzneimittels im Körper verursacht. Die Abbildung zeigt, wie sich die Konzentration in den meisten Fällen ändert Medikamente im Blut einer Person oder eines Tieres nach einmaliger Verabreichung. Folie 5.

Die Abnahme der Arzneimittelkonzentration kann durch eine Exponentialfunktion angenähert werden, deren Exponent die Zeit enthält. Offensichtlich muss die Zerstörungsrate des Arzneimittels im Körper proportional zur Intensität der Stoffwechselprozesse sein.

Es ist ein tragischer Fall bekannt, der sich aufgrund der Unkenntnis dieser Sucht ereignete. MIT wissenschaftlicher Punkt Sehr interessant für Psychiater und Neurophysiologen ist das Medikament LSD, das verursacht normale Leute seltsame Halluzinationen. Einige Forscher beschlossen, die Reaktion des Elefanten auf dieses Medikament zu untersuchen. Dazu nahmen sie die Menge an LSD, die Katzen wütend macht, und multiplizierten sie mit der Häufigkeit, mit der die Masse eines Elefanten größer ist als die Masse einer Katze. Dabei gingen sie davon aus, dass die Dosis des verabreichten Arzneimittels direkt proportional zur Masse sein sollte des Tieres. Die Verabreichung einer solchen Dosis LSD an einen Elefanten führte innerhalb von 5 Minuten zu dessen Tod, woraus die Autoren schlossen, dass Elefanten eine erhöhte Empfindlichkeit gegenüber dieser Droge haben. Eine Rezension dieser Arbeit, die später in der Presse erschien, nannte es einen „elefantenartigen Fehler“ der Autoren des Experiments.

2. Aktualisierung des Wissens der Studierenden.

Was bedeutet es, eine Funktion zu studieren? (eine Definition formulieren, Eigenschaften beschreiben, ein Diagramm zeichnen)

Welche Funktion heißt Exponentialfunktion? Gib ein Beispiel.

Welche grundlegenden Eigenschaften der Exponentialfunktion kennen Sie?

Bedeutungsumfang (Eingrenzung)

Domain

Monotonie (Zustand des Zunehmens und Abnehmens)

Folie 6 . Geben Sie verschiedene Funktionswerte an (gemäß der fertigen Zeichnung).

Folie 7. Benennen Sie die Bedingung für die zunehmende und abnehmende Funktion und korrelieren Sie die Formel der Funktion mit ihrem Graphen

Folie 8. Beschreiben Sie anhand der fertigen Zeichnung den Algorithmus zum Erstellen von Funktionsgraphen

Folie a) y=3 x + 2

b) y=3 x-2 – 2

3.Diagnostisches selbstständiges Arbeiten (am PC).

Die Klasse ist in zwei Gruppen aufgeteilt. Der Hauptteil der Klasse führt Testaufgaben durch. Starke Schüler lösen komplexere Aufgaben.

Selbstständige Arbeit in einem ProgrammLeistung Punkt(für den Hauptteil

Selbstständiges Arbeiten (für den starken Teil der Klasse)

Folie9. Schreiben Sie den Algorithmus zum Erstellen eines Funktionsgraphen auf, benennen Sie den Definitionsbereich, den Wertebereich und die Anstiegs- und Abfallintervalle.

Folie 10. Ordnen Sie die Funktionsformel ihrem Diagramm zu

Die Schüler überprüfen ihre Antworten, ohne Fehler zu korrigieren, die selbstständige Arbeit wird dem Lehrer übergeben

Folien 11-21. Überprüfung des Tests für den Hauptteil

4. Studieren neues Thema. Anwendung der funktionalgrafischen Methode zur Lösung von Gleichungen, Ungleichungen, Systemen, Bestimmung des Wertebereichs einer komplexen Funktion

Folien 22-23. Funktionalgrafische Methode zur Lösung von Gleichungen

Um eine Gleichung der Form f(x)=g(x) mit der funktionalgrafischen Methode zu lösen, benötigen Sie:

Konstruieren Sie Graphen der Funktionen y=f(x) und y=g(x) im selben Koordinatensystem.

Bestimmen Sie die Koordinaten des Schnittpunkts der Graphen dieser Funktionen.

Schreiben Sie die Antwort auf.

GLEICHUNGEN LÖSEN

Folie 24-25.

Hat die Gleichung eine Wurzel und wenn ja, ist sie positiv oder negativ?

FOLIE 26

5. Praktische Arbeit leisten.

GLEICHUNGEN LÖSEN. FOLIE 27-30

Diese Gleichung kann grafisch gelöst werden. Die Schüler werden gebeten, die Aufgabe zu lösen und dann die Frage zu beantworten: „Ist es notwendig, Funktionsgraphen zu erstellen, um diese Gleichung zu lösen?“ Antwort: „Die Funktion nimmt über den gesamten Definitionsbereich zu und die Funktion ab.“ Folglich haben die Graphen solcher Funktionen höchstens einen Schnittpunkt, was bedeutet, dass die Gleichung höchstens eine Wurzel hat. Durch Auswahl finden wir das „.

Lösen Sie Gleichung 3 x = (x-1) 2 + 3

Lösung: Wir verwenden die funktionale Methode zur Lösung von Gleichungen:

Weil dieses System Es hat einzige Entscheidung, dann finden wir mit der Auswahlmethode x=1

Ungleichheiten lösen. Folien 31-33

G Grafische Methoden ermöglichen die Lösung von Ungleichungen, die unterschiedliche Funktionen enthalten. Dazu muss nach der Erstellung von Diagrammen der Funktionen auf der linken und rechten Seite der Ungleichung und der Bestimmung der Abszisse des Schnittpunkts der Diagramme das Intervall bestimmt werden, in dem alle Punkte eines der Diagramme liegen oben (unten) 0 Punkte der Sekunde.

Ungleichung lösen:

a) cos x 1 + 3 x

Lösung:

Antwort: ( ; )

Lösen Sie die Ungleichung grafisch.

(Der Graph der Exponentialfunktion liegt über der Funktion auf der rechten Seite der Gleichung.)

Antwort: x>2. UM

.
Antwort: x>0.

Die Exponentialfunktion enthält das Modulzeichen im Exponenten. Folie 34-35

Wiederholen wir die Moduldefinition.

(schreibe an die Tafel)

Machen Sie sich Notizen in Ihrem Notizbuch:

1).

2).

Auf der Folie wird eine grafische Darstellung dargestellt. Erklären Sie, wie die Diagramme aufgebaut sind.

E(y)=(0;1]

Um diese Gleichung zu lösen, müssen Sie sich die Beschränktheitseigenschaft der Exponentialfunktion merken. Die Funktion nimmt Werte an > 1, a – 1 < > 1, daher ist Gleichheit nur möglich, wenn beide Seiten der Gleichung gleichzeitig gleich 1 sind. Das bedeutet, dass wir beim Lösen dieses Systems Folgendes finden X = 0.

.Ermitteln des Wertebereichs einer komplexen Funktion. Folien 36-37.

Bestimmen Sie mithilfe der Fähigkeit, einen Graphen einer quadratischen Funktion zu erstellen, nacheinander die Koordinaten des Scheitelpunkts der Parabel und ermitteln Sie den Wertebereich.

, ist der Scheitelpunkt der Parabel.

Frage: Bestimmen Sie die Art der Monotonie der Funktion.

Die Exponentialfunktion y = 16 t steigt, da 16>1.

Bei niedrigster Wert Funktionsanzeige

.

Die Grafik veranschaulicht unsere Schlussfolgerung.

Fenster. google_render_ad(); Ziel: Betrachten Sie ZNO-Probleme mit funktional-grafischen Methoden am Beispiel der Exponentialfunktion y = ax, a>0, a1

Lernziele:

l wiederhole die Eigenschaft der Monotonie und Beschränktheit der Exponentialfunktion;

l Wiederholen Sie den Algorithmus zum Erstellen von Funktionsgraphen mithilfe von Transformationen.

l Finden Sie eine Reihe von Werten und eine Reihe von Definitionen einer Funktion anhand des Formeltyps und mithilfe eines Diagramms.

l Exponentialgleichungen, Ungleichungen und Systeme mithilfe von Graphen und Eigenschaften von Funktionen lösen.

l Arbeiten mit Funktionsgraphen, die ein Modul enthalten;

l Betrachten Sie die Graphen einer komplexen Funktion und ihren Wertebereich.

Während des Unterrichts:

1. Einführungsrede des Lehrers. Motivation für das Studium dieses Themas

Folie 1 Exponentialfunktion. „Funktional-grafische Methoden zur Lösung von Gleichungen und Ungleichungen“

Die funktionalgrafische Methode basiert auf der Verwendung grafischer Darstellungen, der Anwendung der Eigenschaften einer Funktion und ermöglicht die Lösung vieler mathematischer Probleme.

Folie 2 Ziele für den Unterricht

Heute werden wir ZNO-Probleme unterschiedlicher Komplexität mit funktionalgrafischen Methoden am Beispiel der Exponentialfunktion y = ax, a>o, a1 betrachten. Mithilfe eines Grafikprogramms erstellen wir Illustrationen zu den Problemen.

Folie 3 Warum ist es so wichtig, die Eigenschaften der Exponentialfunktion zu kennen?

Nach dem Gesetz der Exponentialfunktion würden sich alle Lebewesen auf der Erde vermehren, wenn dafür günstige Bedingungen gegeben wären, das heißt, es gäbe keine natürlichen Feinde und es gäbe reichlich Nahrung. Ein Beweis dafür ist die Verbreitung von Kaninchen in Australien, die es vorher nicht gab. Es reichte aus, ein paar Individuen freizulassen, und nach einiger Zeit wurde ihr Nachwuchs zu einer nationalen Katastrophe. In Natur, Technik und Wirtschaft gibt es zahlreiche Prozesse, bei denen sich der Wert einer Größe gleich oft, also nach dem Gesetz der Exponentialfunktion, ändert. Diese Prozesse werden Prozesse genannt organisches Wachstum oder organische Dämpfung. Zum Beispiel, bakterielles Wachstum entspricht unter idealen Bedingungen dem Prozess des organischen Wachstums; radioaktiver Zerfall von Stoffen– der Prozess der organischen Schwächung. Unterliegt den Gesetzen des organischen Wachstums Wachstum der Einlage bei der Sparkasse, Wiederherstellung des Hämoglobins im Blut eines Spenders oder einer verwundeten Person, die viel Blut verloren hat. Nennen Sie Anwendungsbeispiele aus der Praxis (Medikamentendosis).

Nachricht zur Medikamentendosierung:

Jeder weiß, dass die vom Arzt zur Behandlung empfohlenen Pillen mehrmals täglich eingenommen werden müssen, sonst sind sie wirkungslos. Die Notwendigkeit, das Arzneimittel erneut zu verabreichen, um eine konstante Konzentration im Blut aufrechtzuerhalten, wird durch die Zerstörung des Arzneimittels im Körper verursacht. Die Abbildung zeigt, wie sich in den meisten Fällen die Konzentration von Medikamenten im Blut eines Menschen oder Tieres nach einer einmaligen Verabreichung verändert. Folie4.

Die Abnahme der Arzneimittelkonzentration kann durch eine Exponentialfunktion angenähert werden, deren Exponent die Zeit enthält. Offensichtlich muss die Zerstörungsrate des Arzneimittels im Körper proportional zur Intensität der Stoffwechselprozesse sein.

Es gibt einen tragischen Fall, der sich aufgrund der Unkenntnis dieser Sucht ereignete. Aus wissenschaftlicher Sicht ist die Droge LSD, die bei normalen Menschen eigenartige Halluzinationen hervorruft, für Psychiater und Neurophysiologen sehr interessant. Einige Forscher beschlossen, die Reaktion des Elefanten auf dieses Medikament zu untersuchen. Dazu nahmen sie die Menge an LSD, die Katzen wütend macht, und multiplizierten sie mit der Häufigkeit, mit der die Masse eines Elefanten größer ist als die Masse einer Katze. Dabei gingen sie davon aus, dass die Dosis des verabreichten Medikaments direkt proportional zur Masse sein sollte des Tieres. Die Verabreichung einer solchen Dosis LSD an einen Elefanten führte innerhalb von 5 Minuten zu dessen Tod, woraus die Autoren schlossen, dass Elefanten eine erhöhte Empfindlichkeit gegenüber dieser Droge haben. Eine Rezension dieser Arbeit, die später in der Presse erschien, nannte es einen „elefantenartigen Fehler“ der Autoren des Experiments.

2. Aktualisierung des Wissens der Studierenden.

· Was bedeutet es, eine Funktion zu studieren? (eine Definition formulieren, Eigenschaften beschreiben, ein Diagramm zeichnen)

· Welche Funktion heißt Exponentialfunktion? Gib ein Beispiel.

· Welche grundlegenden Eigenschaften der Exponentialfunktion kennen Sie?

Bedeutungsbereich (Begrenztheit)

· Domäne

· Monotonie (Zustand des Zunehmens und Abnehmens)

· Folie 5 . Geben Sie verschiedene Funktionswerte an (gemäß der fertigen Zeichnung).

https://pandia.ru/text/80/043/images/image004_92.jpg" width="400" height="400 src=">

https://pandia.ru/text/80/043/images/image006_59.jpg" width="400" height="400 src=">

· Folie 7. Beschreiben Sie anhand der fertigen Zeichnung den Algorithmus zum Erstellen von Funktionsgraphen

Folie a) y=3x + 2

https://pandia.ru/text/80/043/images/image009_46.jpg" width="353" height="407 src=">

3.Diagnostisches selbstständiges Arbeiten (am PC).

Die Klasse ist in zwei Gruppen aufgeteilt. Der Hauptteil der Klasse führt Testaufgaben durch. Starke Schüler lösen komplexere Aufgaben.

· Selbstständige Arbeit im ProgrammLeistungPunkt(für den Hauptteil der Lehrveranstaltung je nach Art der Prüfungsaufgaben vom ZNO mit geschlossene Form Antwort)

1. Welche Exponentialfunktion steigt?

2. Finden Sie den Definitionsbereich der Funktion.

3. Finden Sie den Wertebereich der Funktion.

4. Der Graph der Funktion wird aus dem Graphen der Exponentialfunktion durch parallele Verschiebung entlang der Achse ... um ... Einheiten ... erhalten.

5. Bestimmen Sie anhand der fertigen Zeichnung den Definitionsbereich und den Wertebereich der Funktion

6. Bestimmen Sie, bei welchem ​​Wert a die Exponentialfunktion durch den Punkt verläuft.

7. Welche Abbildung zeigt den Graphen einer Exponentialfunktion mit einer Basis größer als eins?

8. Ordnen Sie den Graphen der Funktion der Formel zu.

9. Die grafische Lösung der Ungleichung ist in der Abbildung dargestellt.

10. Lösen Sie die Ungleichung grafisch (anhand der fertigen Zeichnung)

· Selbstständiges Arbeiten (für den starken Teil der Klasse)

· Folie 8. Schreiben Sie den Algorithmus zum Erstellen eines Funktionsgraphen auf, benennen Sie den Definitionsbereich, den Wertebereich und die Anstiegs- und Abfallintervalle.

· Folie 9. Ordnen Sie die Funktionsformel ihrem Diagramm zu

7) https://pandia.ru/text/80/043/images/image018_24.jpg" width="500" height="524 src=">

https://pandia.ru/text/80/043/images/image020_21.gif" width="16 height=13" height="13">)

· Folie 11 (Überprüfungsaufgabe 8)

Die Abbildung zeigt Diagramme von Exponentialfunktionen. Ordnen Sie den Graphen der Funktion der Formel zu.

https://pandia.ru/text/80/043/images/image022_20.gif" width="78" height="27 src=">

https://pandia.ru/text/80/043/images/image024_19.gif" width="104" height="33 src=">

https://pandia.ru/text/80/043/images/image026_16.gif" width="80" height="28 src=">

https://pandia.ru/text/80/043/images/image028_11.gif" width="66" height="27 src=">

4. Ein neues Thema studieren. Anwendung der funktionalgrafischen Methode zur Lösung von Gleichungen, Ungleichungen, Systemen, Bestimmung des Wertebereichs einer komplexen Funktion

Folie 12. Funktional-grafische Methode zum Lösen von Gleichungen

Um eine Gleichung der Form f(x)=g(x) mit der funktionalgrafischen Methode zu lösen, benötigen Sie:

Konstruieren Sie Graphen der Funktionen y=f(x) und y=g(x) im selben Koordinatensystem.

Bestimmen Sie die Koordinaten des Schnittpunkts der Graphen dieser Funktionen.

Schreiben Sie die Antwort auf.

AUFGABE Nr. 1: GLEICHUNGEN LÖSEN

Folie 13.

Hat die Gleichung eine Wurzel und wenn ja, ist sie positiv oder negativ?

(4/3)x= 4

FOLIE 14

https://pandia.ru/text/80/043/images/image044_10.jpg" width="94" height="21">

https://pandia.ru/text/80/043/images/image046_3.gif" width="67" height="21">

Folie 15.

Diese Gleichung kann grafisch gelöst werden. Die Schüler werden gebeten, die Aufgabe zu lösen und dann die Frage zu beantworten: „Ist es notwendig, Funktionsgraphen zu erstellen, um diese Gleichung zu lösen?“ Antwort: „Die Funktion nimmt über den gesamten Definitionsbereich zu und die Funktion ab.“ Folglich haben die Graphen solcher Funktionen höchstens einen Schnittpunkt, was bedeutet, dass die Gleichung höchstens eine Wurzel hat. Durch Auswahl finden wir das „.

· Löse die Gleichung:

3x = (x-1) 2 + 3

Folie 16. .Lösung: Wir verwenden die funktionale Methode zum Lösen von Gleichungen:

https://pandia.ru/text/80/043/images/image051_3.gif" width="109" height="53">

Da dieses System eine eindeutige Lösung hat, finden wir x=1 mithilfe der Auswahlmethode

AUFGABE Nr. 2 Ungleichheiten lösen

Grafische Methoden ermöglichen die Lösung von Ungleichungen, die unterschiedliche Funktionen enthalten. Dazu muss nach der Erstellung von Diagrammen der Funktionen auf der linken und rechten Seite der Ungleichung und der Bestimmung der Abszisse des Schnittpunkts der Diagramme das Intervall bestimmt werden, in dem alle Punkte eines der Diagramme liegen oben (unten) 0 Punkte der Sekunde.

· Ungleichung lösen:

Folie 17.

a) cos x 1 + 3x

Folie 18. Lösung:

https://pandia.ru/text/80/043/images/image054_4.gif" width="300" height="50">

Antwort: ( ; )

Lösen Sie die Ungleichung grafisch.

Folie 19.

· Was können Sie über Funktionsgraphen sagen? https://pandia.ru/text/80/043/images/image058_2.gif" width="18" height="21 src=">>12 - 1,5x

https://pandia.ru/text/80/043/images/image060_2.gif" width="59" height="22 src=">

https://pandia.ru/text/80/043/images/image062_2.gif" width="144" height="53">(an die Tafel schreiben)

Folie 20.

Machen Sie sich Notizen in Ihrem Notizbuch:

1).

2).

Auf der Folie wird eine grafische Darstellung dargestellt. Erklären Sie, wie Graphen aufgebaut sind.

https://pandia.ru/text/80/043/images/image066_1.gif" width="12" height="23 src=">

https://pandia.ru/text/80/043/images/image068_2.gif" width="21" height="21">

https://pandia.ru/text/80/043/images/image070_3.jpg" width="400" height="400 src=">

E(y)=(0;1]

Folie 21.

Um diese Gleichung zu lösen, müssen Sie sich die Beschränktheitseigenschaft der Exponentialfunktion merken..gif" width="36" height="14"> > 1, daher ist Gleichheit nur möglich, wenn beide Seiten der Gleichung gleichzeitig gleich 1 sind. Das bedeutet, dass wir beim Lösen dieses Systems Folgendes finden X = 0.

AUFGABE 4. Ermitteln des Wertebereichs einer komplexen Funktion.

Folie 22.

Bestimmen Sie mithilfe der Fähigkeit, einen Graphen einer quadratischen Funktion zu erstellen, nacheinander die Koordinaten des Scheitelpunkts der Parabel und ermitteln Sie den Wertebereich.

Folie 23.

, ist der Scheitelpunkt der Parabel.

https://pandia.ru/text/80/043/images/image080_4.jpg" width="103" height="44">

Frage: Bestimmen Sie die Art der Monotonie der Funktion.