Rezolvarea ecuațiilor exponențiale online cu o soluție detaliată. ecuații exponențiale
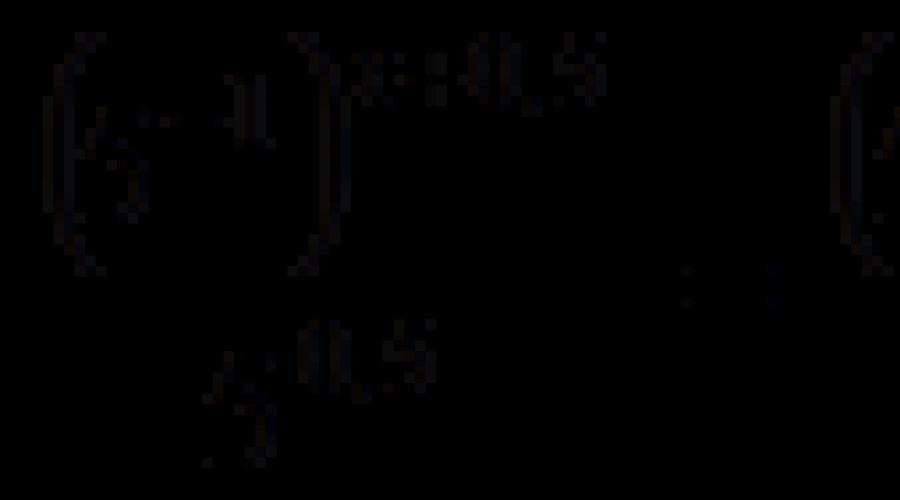
Citeste si
Prelegere: „Metode de rezolvare ecuații exponențiale».
1 . ecuații exponențiale.
Ecuațiile care conțin necunoscute în exponent se numesc ecuații exponențiale. Cea mai simplă dintre acestea este ecuația ax = b, unde a > 0 și a ≠ 1.
1) Pentru b< 0 и b = 0 это уравнение, согласно свойству 1 показательной функции, не имеет решения.
2) Pentru b > 0, folosind monotonitatea funcției și teorema rădăcinii, ecuația are o singură rădăcină. Pentru a-l găsi, b trebuie reprezentat ca b = aс, ax = bс ó x = c sau x = logab.
Ecuațiile exponențiale, prin transformări algebrice, conduc la ecuații standard, care se rezolvă prin următoarele metode:
1) metoda de reducere la o bază;
2) metoda de evaluare;
3) metoda grafica;
4) metoda introducerii de noi variabile;
5) metoda factorizării;
6) indicativ - ecuații de putere;
7) exponențial cu un parametru.
2 . Metoda de reducere la o singură bază.
Metoda se bazează pe următoarea proprietate a gradelor: dacă două grade sunt egale și bazele lor sunt egale, atunci exponenții lor sunt egali, adică, ecuația ar trebui încercată să fie redusă la forma
Exemple. Rezolvați ecuația:
1 . 3x=81;
Să reprezentăm partea dreaptă a ecuației sub forma 81 = 34 și să scriem ecuația echivalentă cu originalul 3 x = 34; x = 4. Răspuns: 4.
2. https://pandia.ru/text/80/142/images/image004_8.png" width="52" height="49"> și mergeți la ecuația pentru exponenți 3x+1 = 3 – 5x; 8x = 4; x = 0,5 Răspuns: 0,5
3. https://pandia.ru/text/80/142/images/image006_8.png" width="105" height="47">
Rețineți că numerele 0,2, 0,04, √5 și 25 sunt puteri ale lui 5. Să profităm de acest lucru și să transformăm ecuația inițială după cum urmează:
![]() ,
de unde 5-x-1 = 5-2x-2 ó - x - 1 = - 2x - 2, din care găsim soluția x = -1. Raspunsul 1.
,
de unde 5-x-1 = 5-2x-2 ó - x - 1 = - 2x - 2, din care găsim soluția x = -1. Raspunsul 1.
5. 3x = 5. Prin definiția logaritmului, x = log35. Răspuns: log35.
6. 62x+4 = 33x. 2x+8.
Să rescriem ecuația ca 32x+4.22x+4 = 32x.2x+8, adică..png" width="181" height="49 src="> Prin urmare, x - 4 =0, x = 4. Răspuns: 4.
7 . 2∙3x+1 - 6∙3x-2 - 3x = 9. Folosind proprietățile puterilor, scriem ecuația sub forma e. x+1 = 2, x =1. Raspunsul 1.


Banca de sarcini nr. 1.
Rezolvați ecuația:
Testul numărul 1.
1) 0 2) 4 3) -2 4) -4 |
|
A2 32x-8 = √3. | 1)17/4 2) 17 3) 13/2 4) -17/4 |
A3 | 1) 3;1 2) -3;-1 3) 0;2 4) fără rădăcini |
1) 7;1 2) fără rădăcini 3) -7;1 4) -1;-7 |
|
A5 | 1) 0;2; 2) 0;2;3 3) 0 4) -2;-3;0 |
A6 | 1) -1 2) 0 3) 2 4) 1 |
Testul #2
A1 | 1) 3 2) -1;3 3) -1;-3 4) 3;-1 |
A2 | 1) 14/3 2) -14/3 3) -17 4) 11 |
A3 | 1) 2;-1 2) fără rădăcini 3) 0 4) -2;1 |
A4 | 1) -4 2) 2 3) -2 4) -4;2 |
A5 | 1) 3 2) -3;1 3) -1 4) -1;3 |
3 Metoda de evaluare.
Teorema rădăcinii: dacă funcția f (x) crește (descrește) pe intervalul I, numărul a este orice valoare luată de f pe acest interval, atunci ecuația f (x) = a are o singură rădăcină pe intervalul I.
La rezolvarea ecuațiilor prin metoda estimării se utilizează această teoremă și proprietățile de monotonitate ale funcției.
Exemple. Rezolvarea ecuațiilor: 1. 4x = 5 - x.
Soluţie. Să rescriem ecuația ca 4x + x = 5.
1. dacă x \u003d 1, atunci 41 + 1 \u003d 5, 5 \u003d 5 este adevărat, atunci 1 este rădăcina ecuației.
Funcția f(x) = 4x crește pe R și g(x) = x crește pe R => h(x)= f(x)+g(x) crește pe R ca suma funcțiilor crescătoare, deci x = 1 este singura rădăcină a ecuației 4x = 5 – x. Raspunsul 1.
2.

Soluţie. Rescriem ecuația sub forma  .
.
1. dacă x = -1, atunci ![]() , 3 = 3-adevărat, deci x = -1 este rădăcina ecuației.
, 3 = 3-adevărat, deci x = -1 este rădăcina ecuației.
2. dovedesc că este unic.
3. Funcția f(x) = - scade pe R, iar g(x) = - x - scade pe R => h(x) = f(x) + g(x) - scade pe R, pe măsură ce suma a funcţiilor descrescătoare . Deci, după teorema rădăcinii, x = -1 este singura rădăcină a ecuației. Raspunsul 1.
Banca de sarcini nr 2. rezolva ecuatia

a) 4x + 1 = 6 - x;
b) 
c) 2x – 2 =1 – x;
4. Metoda de introducere a noilor variabile.
Metoda este descrisă în secțiunea 2.1. Introducerea unei noi variabile (substituție) se realizează de obicei după transformări (simplificare) termenilor ecuației. Luați în considerare exemple.
Exemple.
R Ecuația de mâncare: 1.
![]() .
.
Să rescriem altfel ecuația: https://pandia.ru/text/80/142/images/image030_0.png" width="128" height="48 src="> i.e..png" width="210" height = „45”>
Soluţie. Să rescriem altfel ecuația: 
Indicați https://pandia.ru/text/80/142/images/image035_0.png" width="245" height="57"> - nu este potrivit.
t = 4 => https://pandia.ru/text/80/142/images/image037_0.png" width="268" height="51"> - ecuație irațională. Am notat asta 
Soluția ecuației este x = 2,5 ≤ 4, deci 2,5 este rădăcina ecuației. Răspuns: 2.5.
Soluţie. Să rescriem ecuația sub forma și să împărțim ambele părți la 56x+6 ≠ 0. Obținem ecuația

2x2-6x-7 = 2x2-6x-8 +1 = 2(x2-3x-4)+1, deci..png" width="118" height="56">
Rădăcinile ecuației pătratice - t1 = 1 și t2<0, т. е..png" width="200" height="24">.
Soluţie . Rescriem ecuația sub forma
și rețineți că este o ecuație omogenă de gradul doi.
Împărțiți ecuația la 42x, obținem 
Înlocuiți https://pandia.ru/text/80/142/images/image049_0.png" width="16" height="41 src="> .

Răspuns: 0; 0,5.
Task Bank #3. rezolva ecuatia
b) ![]()
G) ![]()
Testul #3 cu o alegere de răspunsuri. Nivel minim.
A1 | 1) -0,2;2 2) log52 3) –log52 4) 2 |
А2 0,52x – 3 0,5x +2 = 0. | 1) 2;1 2) -1;0 3) fără rădăcini 4) 0 |
1) 0 2) 1; -1/3 3) 1 4) 5 |
|
A4 52x-5x - 600 = 0. | 1) -24;25 2) -24,5; 25,5 3) 25 4) 2 |
1) fără rădăcini 2) 2;4 3) 3 4) -1;2 |
Testul #4 cu o alegere de răspunsuri. Nivel general.
A1 | 1) 2;1 2) ½;0 3)2;0 4) 0 |
А2 2x – (0,5)2x – (0,5)x + 1 = 0 | 1) -1;1 2) 0 3) -1;0;1 4) 1 |
1) 64 2) -14 3) 3 4) 8 |
|
1)-1 2) 1 3) -1;1 4) 0 |
|
A5 | 1) 0 2) 1 3) 0;1 4) fără rădăcini |
5. Metoda de factorizare.
1. Rezolvați ecuația: 5x+1 - 5x-1 = 24.
Soluție..png" width="169" height="69"> , de unde
2. 6x + 6x+1 = 2x + 2x+1 + 2x+2.
Soluţie. Să scoatem 6x din partea stângă a ecuației și 2x din partea dreaptă. Obținem ecuația 6x(1+6) = 2x(1+2+4) ó 6x = 2x.
Deoarece 2x >0 pentru tot x, putem împărți ambele părți ale acestei ecuații la 2x fără teama de a pierde soluții. Obținem 3x = 1ó x = 0.
3. ![]()
Soluţie. Rezolvăm ecuația prin factorizare.
Selectăm pătratul binomului 
4. https://pandia.ru/text/80/142/images/image067_0.png" width="500" height="181">
x = -2 este rădăcina ecuației.
Ecuația x + 1 = 0 " style="border-collapse:collapse;border:none">
A1 5x-1 +5x -5x+1 = -19.
1) 1 2) 95/4 3) 0 4) -1
A2 3x+1 +3x-1 =270.
1) 2 2) -4 3) 0 4) 4
A3 32x + 32x+1 -108 = 0. x=1,5
1) 0,2 2) 1,5 3) -1,5 4) 3
1) 1 2) -3 3) -1 4) 0
A5 2x -2x-4 = 15.x=4
1) -4 2) 4 3) -4;4 4) 2
Testul #6 Nivel general.
A1 (22x-1)(24x+22x+1)=7. | 1) ½ 2) 2 3) -1;3 4) 0,2 |
A2 | 1) 2,5 2) 3;4 3) log43/2 4) 0 |
A3 2x-1-3x=3x-1-2x+2. | 1) 2 2) -1 3) 3 4) -3 |
A4 | 1) 1,5 2) 3 3) 1 4) -4 |
A5 | 1) 2 2) -2 3) 5 4) 0 |
6. Exponenţial - ecuaţii de putere.
Ecuațiile exponențiale sunt alăturate de așa-numitele ecuații de putere exponențială, adică ecuații de forma (f(x))g(x) = (f(x))h(x).
Dacă se știe că f(x)>0 și f(x) ≠ 1, atunci ecuația, ca și cea exponențială, se rezolvă prin echivalarea exponenților g(x) = f(x).
Dacă condiția nu exclude posibilitatea f(x)=0 și f(x)=1, atunci trebuie să luăm în considerare aceste cazuri atunci când rezolvăm ecuația puterii exponențiale.
1..png" width="182" height="116 src=">
2. ![]()
Soluţie. x2 +2x-8 - are sens pentru orice x, deoarece un polinom, deci ecuația este echivalentă cu mulțimea
 https://pandia.ru/text/80/142/images/image078_0.png" width="137" height="35">
https://pandia.ru/text/80/142/images/image078_0.png" width="137" height="35">
b) ![]()
7. Ecuații exponențiale cu parametri.
1. Pentru ce valori ale parametrului p are ecuația 4 (5 – 3) 2 +4p2–3p = 0 (1) singura decizie?
Soluţie. Să introducem modificarea 2x = t, t > 0, atunci ecuația (1) va lua forma t2 – (5p – 3)t + 4p2 – 3p = 0. (2)
Discriminantul ecuației (2) este D = (5p – 3)2 – 4(4p2 – 3p) = 9(p – 1)2.
Ecuația (1) are o soluție unică dacă ecuația (2) are o rădăcină pozitivă. Acest lucru este posibil în următoarele cazuri.
1. Dacă D = 0, adică p = 1, atunci ecuația (2) va lua forma t2 – 2t + 1 = 0, deci t = 1, prin urmare, ecuația (1) are o soluție unică x = 0.
2. Dacă p1, atunci 9(p – 1)2 > 0, atunci ecuația (2) are două rădăcini diferite t1 = p, t2 = 4p – 3. Mulțimea sistemelor satisface condiția problemei

Înlocuind t1 și t2 în sisteme, avem


https://pandia.ru/text/80/142/images/image084_0.png" alt="no35_11" width="375" height="54"> в зависимости от параметра a?!}
Soluţie. Lăsa  atunci ecuația (3) va lua forma t2 – 6t – a = 0. (4)
atunci ecuația (3) va lua forma t2 – 6t – a = 0. (4)
Să găsim valorile parametrului a pentru care cel puțin o rădăcină a ecuației (4) satisface condiția t > 0.
Să introducem funcția f(t) = t2 – 6t – a. Următoarele cazuri sunt posibile.
https://pandia.ru/text/80/142/images/image087.png" alt="http://1september.ru/ru/mat/2002/35/no35_14.gif" align="left" width="215" height="73 src=">где t0 - абсцисса вершины параболы и D - дискриминант квадратного трехчлена f(t);!}
https://pandia.ru/text/80/142/images/image089.png" alt="http://1september.ru/ru/mat/2002/35/no35_16.gif" align="left" width="60" height="51 src=">!}
Cazul 2. Ecuația (4) are o soluție pozitivă unică dacă
D = 0, dacă a = – 9, atunci ecuația (4) va lua forma (t – 3)2 = 0, t = 3, x = – 1.
Cazul 3. Ecuația (4) are două rădăcini, dar una dintre ele nu satisface inegalitatea t > 0. Acest lucru este posibil dacă
 https://pandia.ru/text/80/142/images/image092.png" alt="no35_17" width="267" height="63">!}
https://pandia.ru/text/80/142/images/image092.png" alt="no35_17" width="267" height="63">!}
Astfel, la a 0 ecuația (4) are o singură rădăcină pozitivă ![]() . Atunci ecuația (3) are o soluție unică
. Atunci ecuația (3) are o soluție unică 
Pentru o< – 9 уравнение (3) корней не имеет.
 în cazul în care o< – 9, то корней нет; если – 9 < a < 0, то
în cazul în care o< – 9, то корней нет; если – 9 < a < 0, то
dacă a = – 9, atunci x = – 1;
dacă a 0, atunci

Să comparăm metodele de rezolvare a ecuațiilor (1) și (3). Rețineți că atunci când rezolvarea ecuației (1) a fost redusă la o ecuație pătratică, al cărei discriminant este un pătrat complet; astfel, rădăcinile ecuației (2) au fost imediat calculate prin formula rădăcinilor ecuației pătratice, iar apoi s-au tras concluzii cu privire la aceste rădăcini. Ecuația (3) a fost redusă la o ecuație pătratică (4), al cărei discriminant nu este un pătrat perfect, prin urmare, la rezolvarea ecuației (3), este recomandabil să folosiți teoreme privind locația rădăcinilor unui trinom pătrat și un model grafic. Rețineți că ecuația (4) poate fi rezolvată folosind teorema Vieta.
Să rezolvăm ecuații mai complexe.
Sarcina 3. Rezolvați ecuația ![]()
Soluţie. ODZ: x1, x2.
Să introducem un înlocuitor. Fie 2x = t, t > 0, apoi, ca urmare a transformărilor, ecuația va lua forma t2 + 2t – 13 – a = 0. (*) Să găsim valorile lui a pentru care cel puțin o rădăcină a lui ecuația (*) îndeplinește condiția t > 0.
https://pandia.ru/text/80/142/images/image098.png" alt="http://1september.ru/ru/mat/2002/35/no35_23.gif" align="left" width="71" height="68 src=">где t0 - абсцисса вершины f(t) = t2 + 2t – 13 – a, D - дискриминант квадратного трехчлена f(t).!}
https://pandia.ru/text/80/142/images/image100.png" alt="http://1september.ru/ru/mat/2002/35/no35_25.gif" align="left" width="360" height="32 src=">!}
https://pandia.ru/text/80/142/images/image102.png" alt="http://1september.ru/ru/mat/2002/35/no35_27.gif" align="left" width="218" height="42 src=">!}
Răspuns: dacă a > - 13, a 11, a 5, atunci dacă a - 13,
a = 11, a = 5, atunci nu există rădăcini.
Bibliografie.
1. Fundamentele Guzeev ale tehnologiei educaționale.
2. Tehnologia Guzeev: de la recepție la filozofie.
M. „Director” nr. 4, 1996
3. Guzeev și forme organizaționale de educație.
4. Guzeev și practica tehnologiei educaționale integrale.
M. „Educația oamenilor”, 2001
5. Guzeev din formele lecției - seminar.
Matematica la scoala nr 2, 1987, p. 9 - 11.
6. Tehnologii educaționale Selevko.
M. „Educația poporului”, 1998
7. Scolarii Episheva invata matematica.
M. „Iluminismul”, 1990
8. Ivanov să pregătească lecții - ateliere.
Matematica la Scoala Nr.6, 1990, p. 37-40.
9. Modelul Smirnov de predare a matematicii.
Matematica la Scoala Nr.1, 1997, p. 32-36.
10. Tarasenko moduri de organizare a lucrărilor practice.
Matematica la Scoala Nr.1, 1993, p. 27 - 28.
11. Despre unul dintre tipurile de muncă individuală.
Matematica la Scoala Nr.2, 1994, p. 63 - 64.
12. Khazankin Abilități creativeşcolari.
Matematica la Scoala Nr.2, 1989, p. 10.
13. Scanavi. Editura, 1997
14. et al. Algebra şi începuturile analizei. Materiale didactice pt
15. Sarcini Krivonogov în matematică.
M. „Primul septembrie”, 2002
16. Cerkasov. Manual pentru elevii de liceu și
intrarea la universitati. „A S T – școala de presă”, 2002
17. Zhevnyak pentru solicitanții la universități.
Minsk și RF „Review”, 1996
18. Scris D. Pregătirea pentru examenul la matematică. M. Rolf, 1999
19. şi altele.Învăţarea rezolvării ecuaţiilor şi inegalităţilor.
M. „Intelectul – Centru”, 2003
20. şi altele.Materiale educaţionale şi de instruire pentru pregătirea pentru E G E.
M. „Intelect – Centru”, 2003 și 2004
21 și altele.Variante ale CMM. Centrul de testare al Ministerului Apărării al Federației Ruse, 2002, 2003
22. Ecuații Goldberg. „Quantum” nr. 3, 1971
23. Volovich M. Cum se preda cu succes matematica.
Matematică, 1997 Nr. 3.
24 Okunev pentru lecție, copii! M. Iluminismul, 1988
25. Yakimanskaya - educație orientată la școală.
26. Liimets lucreaza la lectie. M. Cunoașterea, 1975
Pe canalul de youtube al site-ului nostru pentru a fi la curent cu toate noile lecții video.
Mai întâi, să ne amintim formulele de bază ale gradelor și proprietățile lor.
Produsul unui număr A se întâmplă de n ori, putem scrie această expresie ca a a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n / a m \u003d a n - m
Putere sau ecuații exponențiale- acestea sunt ecuații în care variabilele sunt în puteri (sau exponenți), iar baza este un număr.
Exemple de ecuații exponențiale:
În acest exemplu, numărul 6 este baza, este întotdeauna în partea de jos și variabila X grad sau măsură.
Să dăm mai multe exemple de ecuații exponențiale.
2 x *5=10
16x-4x-6=0
Acum să vedem cum se rezolvă ecuațiile exponențiale?
Să luăm o ecuație simplă:
2 x = 2 3
Un astfel de exemplu poate fi rezolvat chiar și în minte. Se poate observa că x=3. La urma urmei, pentru ca părțile din stânga și din dreapta să fie egale, trebuie să puneți numărul 3 în loc de x.
Acum să vedem cum ar trebui luată această decizie:
2 x = 2 3
x = 3
Pentru a rezolva această ecuație, am eliminat aceleași temeiuri(adică doi) și a notat ce a mai rămas, acestea sunt grade. Am primit răspunsul pe care îl căutam.
Acum să rezumam soluția noastră.
Algoritm pentru rezolvarea ecuației exponențiale:
1. Trebuie verificat aceeași fie că bazele ecuației din dreapta și din stânga. Dacă temeiurile nu sunt aceleași, căutăm variante de rezolvare acest exemplu.
2. După ce bazele sunt aceleași, echivala grad și rezolvați noua ecuație rezultată.
Acum să rezolvăm câteva exemple:
Să începem simplu.
Bazele din stânga și din dreapta sunt egale cu numărul 2, ceea ce înseamnă că putem arunca baza și echivalăm gradele lor.
x+2=4 Cea mai simplă ecuație a rezultat.
x=4 - 2
x=2
Răspuns: x=2
În exemplul următor, puteți vedea că bazele sunt diferite, acestea sunt 3 și 9.
3 3x - 9 x + 8 = 0
Pentru început, le transferăm pe cele nouă în partea dreaptă, obținem:
Acum trebuie să faci aceleași baze. Știm că 9=3 2 . Să folosim formula puterii (a n) m = a nm .
3 3x \u003d (3 2) x + 8
Obținem 9 x + 8 \u003d (3 2) x + 8 \u003d 3 2 x + 16
3 3x \u003d 3 2x + 16 acum puteți vedea că în stânga și partea dreapta bazele sunt aceleași și egale cu trei, ceea ce înseamnă că le putem elimina și echivala gradele.
3x=2x+16 are cea mai simplă ecuație
3x-2x=16
x=16
Răspuns: x=16.
Să ne uităm la următorul exemplu:
2 2x + 4 - 10 4 x \u003d 2 4
În primul rând, ne uităm la baze, bazele sunt diferite două și patru. Și trebuie să fim la fel. Transformăm cvadruplul după formula (a n) m = a nm .
4 x = (2 2) x = 2 2x
Și folosim, de asemenea, o formulă a n a m = a n + m:
2 2x+4 = 2 2x 2 4
Adăugați la ecuație:
2 2x 2 4 - 10 2 2x = 24
Am dat un exemplu din aceleași motive. Dar alte numere 10 și 24 interferează cu noi. Ce să facem cu ele? Dacă te uiți cu atenție, poți vedea că în partea stângă repetăm 2 2x, iată răspunsul - putem pune 2 2x din paranteze:
2 2x (2 4 - 10) = 24
Să calculăm expresia dintre paranteze:
2 4 — 10 = 16 — 10 = 6
Împărțim întreaga ecuație la 6:
Imaginează-ți 4=2 2:
2 2x \u003d 2 2 baze sunt aceleași, aruncați-le și egalați gradele.
2x \u003d 2 s-a dovedit a fi cea mai simplă ecuație. Împărțim la 2, obținem
x = 1
Răspuns: x = 1.
Să rezolvăm ecuația:
9 x - 12*3 x +27= 0
Să transformăm:
9 x = (3 2) x = 3 2x
Obtinem ecuatia:
3 2x - 12 3 x +27 = 0
Bazele noastre sunt aceleași, egale cu trei. În acest exemplu, este clar că prima triplă are un grad de două ori (2x) decât a doua (doar x). În acest caz, puteți decide metoda de substitutie. Numărul cu gradul cel mai mic se înlocuiește cu:
Atunci 3 2x \u003d (3 x) 2 \u003d t 2
Inlocuim toate gradele cu x din ecuatie cu t:
t 2 - 12t + 27 \u003d 0
Primim ecuație pătratică. Rezolvăm prin discriminant, obținem:
D=144-108=36
t1 = 9
t2 = 3
Înapoi la Variabilă X.
Luăm t 1:
t 1 \u003d 9 \u003d 3 x
Acesta este,
3 x = 9
3 x = 3 2
x 1 = 2
S-a găsit o rădăcină. Îl căutăm pe al doilea, din t 2:
t 2 \u003d 3 \u003d 3 x
3 x = 3 1
x 2 = 1
Răspuns: x 1 \u003d 2; x 2 = 1.
Pe site puteti in sectiunea AJUTA LA DECIDE sa puneti intrebari de interes, cu siguranta iti vom raspunde.
Alăturați-vă unui grup
În această lecție, vom lua în considerare soluția unor ecuații exponențiale mai complexe, amintim principalele prevederi teoretice referitoare la funcția exponențială.
1. Definiția și proprietățile unei funcții exponențiale, o tehnică de rezolvare a celor mai simple ecuații exponențiale
Amintiți-vă definiția și principalele proprietăți ale unei funcții exponențiale. Soluția tuturor ecuațiilor și inegalităților exponențiale se bazează pe proprietăți.
Functie exponentiala este o funcție de forma , unde baza este gradul și Aici x este o variabilă independentă, un argument; y - variabilă dependentă, funcție.

Orez. 1. Graficul funcției exponențiale
Graficul prezintă un exponent crescător și descrescător, ilustrând funcția exponențială la o bază mai mare de unu și mai mică de unu, dar mai mare de zero, respectiv.
Ambele curbe trec prin punctul (0;1)
Proprietățile funcției exponențiale:
Domeniu: ;
Interval de valori: ;
Funcția este monotonă, crește cu , scade cu .
O funcție monotonă ia fiecare dintre valorile sale cu o singură valoare a argumentului.
Când argumentul crește de la minus la plus infinit, funcția crește de la zero, inclusiv, la plus infinit. Dimpotrivă, când argumentul crește de la minus la plus infinit, funcția scade de la infinit la zero, inclusiv.
2. Rezolvarea ecuațiilor exponențiale tipice
Amintiți-vă cum să rezolvați cele mai simple ecuații exponențiale. Soluția lor se bazează pe monotonitatea funcției exponențiale. Aproape toate ecuațiile exponențiale complexe sunt reduse la astfel de ecuații.
Egalitatea exponenților cu baze egale se datorează proprietății funcției exponențiale și anume monotonității acesteia.
Metoda de rezolvare:
Echivalează bazele gradelor;
Echivalează exponenții.
Să trecem la ecuații exponențiale mai complexe, scopul nostru este să reducem fiecare dintre ele la cele mai simple.
Să scăpăm de rădăcina din partea stângă și să reducem gradele la aceeași bază:
![]()
Pentru a reduce o ecuație exponențială complexă la una simplă, este adesea folosită o schimbare de variabile.
![]()
Să folosim proprietatea gradului:
Introducem un înlocuitor. Să , atunci . Cu o astfel de înlocuire, este evident că y ia strict valori pozitive. Primim:
Înmulțim ecuația rezultată cu doi și transferăm toți termenii în partea stângă:
![]()
![]()
Prima rădăcină nu satisface intervalul de valori y, o aruncăm. Primim:
![]()
Să aducem gradele la același indicator:
![]()
![]()
Introducem un înlocuitor:
Lasă atunci ![]() . Cu această înlocuire, este evident că y ia valori strict pozitive. Primim:
. Cu această înlocuire, este evident că y ia valori strict pozitive. Primim:
![]()
Știm cum să rezolvăm ecuații pătratice similare, scriem răspunsul:
Pentru a vă asigura că rădăcinile sunt găsite corect, puteți verifica conform teoremei Vieta, adică găsiți suma rădăcinilor și produsul lor și verificați cu coeficienții corespunzători ai ecuației.
Primim:
3. Tehnica de rezolvare a ecuaţiilor exponenţiale omogene de gradul II
Să studiem următoarele tip important ecuații exponențiale:
Ecuațiile de acest tip se numesc omogene de gradul doi în raport cu funcțiile f și g. Pe partea stângă există un trinom pătrat în raport cu f cu parametrul g sau un trinom pătrat în raport cu g cu parametrul f.
Metoda de rezolvare:
Această ecuație poate fi rezolvat ca un pătrat, dar este mai ușor să o faci în alt mod. Trebuie luate în considerare două cazuri:
În primul caz, obținem
În al doilea caz, avem dreptul de a împărți cu cel mai înalt grad și obținem:

Ar trebui să introduceți o schimbare de variabile, obținem o ecuație pătratică pentru y:
![]()
Rețineți că funcțiile f și g pot fi arbitrare, dar ne interesează cazul în care acestea sunt funcții exponențiale.
4. Exemple de rezolvare a ecuațiilor omogene
![]()
Să mutăm toți termenii în partea stângă a ecuației:
Deoarece funcțiile exponențiale capătă valori strict pozitive, avem dreptul de a împărți imediat ecuația la , fără a lua în considerare cazul când:
![]()
Primim:
![]()
Introducem un înlocuitor: ![]() (conform proprietăților funcției exponențiale)
(conform proprietăților funcției exponențiale)
Avem o ecuație pătratică:
![]()
Determinăm rădăcinile conform teoremei Vieta:
![]()
Prima rădăcină nu satisface intervalul de valori y, o aruncăm, obținem:
![]()
Să folosim proprietățile gradului și să reducem toate gradele la baze simple:
Este ușor de observat funcțiile f și g:
Deoarece funcțiile exponențiale capătă valori strict pozitive, avem dreptul de a împărți imediat ecuația la , fără a lua în considerare cazul când .
Ce este o ecuație exponențială? Exemple.
Deci, o ecuație exponențială... O nouă expoziție unică la expoziția noastră generală cu o mare varietate de ecuații!) Așa cum este aproape întotdeauna cazul, cuvântul cheie al oricărui termen matematic nou este adjectivul corespunzător care îl caracterizează. Deci și aici. Cuvântul cheie în termenul „ecuație exponențială” este cuvântul "demonstrativ". Ce înseamnă? Acest cuvânt înseamnă că necunoscutul (x) este în ceea ce priveşte orice grad.Și numai acolo! Acest lucru este extrem de important.
De exemplu, aceste ecuații simple:
3 x +1 = 81
5x + 5x +2 = 130
4 2 2 x -17 2 x +4 = 0
Sau chiar acești monștri:
2 sin x = 0,5
Vă rog să acordați imediat atenție unui lucru important: în temeiuri grade (de jos) - doar numere. Dar în indicatori grade (sus) - o mare varietate de expresii cu x. Absolut orice.) Totul depinde de ecuația specifică. Dacă, brusc, x iese în ecuație în altă parte, în plus față de indicator (să zicem, 3 x \u003d 18 + x 2), atunci o astfel de ecuație va fi deja o ecuație tip mixt. Astfel de ecuații nu au reguli clare de rezolvare. Prin urmare, în această lecție nu le vom lua în considerare. Spre bucuria elevilor.) Aici vom lua în considerare doar ecuaţiile exponenţiale în formă „pură”.
În general, chiar și ecuațiile exponențiale pure nu sunt rezolvate clar în toate cazurile și nu întotdeauna. Dar, printre varietatea bogată de ecuații exponențiale, există anumite tipuri care pot și ar trebui rezolvate. Aceste tipuri de ecuații sunt pe care le vom lua în considerare împreună cu dvs. Și cu siguranță vom rezolva exemplele.) Așa că ne instalăm confortabil și - la drum! Ca și în „împușcături” pe computer, călătoria noastră va trece prin niveluri.) De la elementar la simplu, de la simplu la mediu și de la mediu la complex. Pe parcurs, veți aștepta și un nivel secret - trucuri și metode pentru rezolvarea exemplelor non-standard. Cele despre care nu veți citi în majoritatea manualelor școlare... Ei bine, la final, desigur, șeful final vă așteaptă sub formă de teme.)
Nivelul 0. Care este cea mai simplă ecuație exponențială? Rezolvarea celor mai simple ecuații exponențiale.
Pentru început, să ne uităm la unele elementare sincere. Trebuie să începi de undeva, nu? De exemplu, această ecuație:
2 x = 2 2
Chiar și fără teorii, prin logică simplă și bun simț este clar că x = 2. Nu există altă cale, nu? Nicio altă valoare a lui x nu este bună... Acum să ne îndreptăm atenția asupra intrarea deciziei această ecuație exponențială grozavă:
2 x = 2 2
X = 2
Ce s-a întâmplat cu noi? Și s-au întâmplat următoarele. Noi, de fapt, am luat și... doar am aruncat aceleași baze (doi)! Complet aruncat afară. Și, ce dorește, lovește-te în ochi!
Da, într-adevăr, dacă în ecuația exponențială din stânga și dreapta sunt aceeași numere în orice grad, atunci aceste numere pot fi aruncate și pur și simplu echivalează exponenții. Matematica permite.) Și apoi puteți lucra separat cu indicatori și puteți rezolva o ecuație mult mai simplă. E grozav, nu?
Iată ideea cheie de a rezolva orice ecuație exponențială (da, exact oricare!): prin utilizarea transformări identice este necesar să se asigure că stânga și dreapta din ecuație sunt aceeași numere de bază în diferite puteri. Și apoi puteți elimina în siguranță aceleași baze și echivalați exponenții. Și lucrați cu o ecuație mai simplă.
Și acum ne amintim de regula de fier: este posibil să se elimine aceleași baze dacă și numai dacă în ecuația din stânga și din dreapta numerele de bază sunt în singurătate mândră.
Ce înseamnă, într-o izolare splendidă? Aceasta înseamnă fără vecini și coeficienți. Explic.
De exemplu, în ecuație
3 3 x-5 = 3 2 x +1
Nu poți elimina tripleții! De ce? Pentru că în stânga nu avem doar un singur trei în grad, dar muncă 3 3 x-5 . Un triplu în plus iese în cale: un coeficient, înțelegi.)
Același lucru se poate spune despre ecuație
5 3 x = 5 2 x +5 x
Și aici, toate bazele sunt aceleași - cinci. Dar în dreapta nu avem un singur grad de cinci: există suma gradelor!
Pe scurt, avem dreptul de a elimina aceleași baze numai atunci când ecuația noastră exponențială arată așa și numai așa:
Af (X) = a g (X)
Acest tip de ecuație exponențială se numește cel mai simplu. Sau stiintific, canonic . Și indiferent care ar fi ecuația răsucită din fața noastră, într-un fel sau altul, o vom reduce la o formă atât de simplă (canonică). Sau, în unele cazuri, să agregate ecuații de acest fel. Atunci cea mai simplă ecuație a noastră poate fi în vedere generala rescrie asa:
F(x) = g(x)
Si asta e. Aceasta va fi transformarea echivalentă. În același timp, absolut orice expresie cu x poate fi folosită ca f(x) și g(x). Tot ceea ce.
Poate că un student deosebit de curios se va întreba: de ce naiba aruncăm atât de ușor și pur și simplu aceleași baze din stânga și din dreapta și echivalăm exponenții? Intuiția este intuiție, dar dintr-o dată, într-o ecuație și dintr-un motiv oarecare, această abordare se va dovedi a fi greșită? Este întotdeauna legal să arunci aceleași baze? Din păcate, pentru un răspuns matematic riguros la aceasta interes Întreabă trebuie să mergi suficient de adânc și serios în teorie generală comportamentul dispozitivului și al funcției. Și puțin mai specific - în fenomen monotonitate strictă.În special, monotonitatea strictă functie exponentialay= un x. Pentru ca functie exponentialași proprietățile sale stau la baza soluției ecuațiilor exponențiale, da.) Un răspuns detaliat la această întrebare va fi dat într-o lecție specială separată dedicată rezolvării ecuațiilor complexe nestandard, folosind monotonitatea diferitelor funcții.)
A explica acest punct în detaliu acum înseamnă doar să scoți creierul unui școlar obișnuit și să-l sperii din timp cu o teorie seacă și grea. nu voi face asta.) Pentru principalul nostru acest moment sarcina - invata sa rezolvi ecuatii exponentiale! Cel mai simplu! Prin urmare, până transpiram și aruncăm cu îndrăzneală aceleași motive. Acest Poate sa, credeți-mă pe cuvânt!) Și apoi rezolvăm deja ecuația echivalentă f (x) = g (x). De regulă, este mai simplu decât exponențialul original.
Se presupune, desigur, că oamenii știu deja să rezolve cel puțin , iar ecuațiile, deja fără x în indicatori.) Cine încă nu știe cum, nu ezitați să închideți această pagină, să parcurgeți linkurile corespunzătoare și să completați vechile goluri. Altfel, îți va fi greu, da...
Tac în privința ecuațiilor iraționale, trigonometrice și a altor ecuații brutale care pot apărea și în procesul de eliminare a bazelor. Dar nu vă alarmați, deocamdată nu vom lua în considerare staniul sincer din punct de vedere al grade: este prea devreme. Ne vom antrena doar pe cele mai simple ecuații.)
Acum luați în considerare ecuațiile care necesită un efort suplimentar pentru a le reduce la cele mai simple. Pentru a le distinge, să le numim ecuații exponențiale simple. Deci, să trecem la următorul nivel!
Nivelul 1. Ecuații exponențiale simple. Recunoaște grade! indicatori naturali.
Regulile cheie în rezolvarea oricăror ecuații exponențiale sunt reguli de abordare a diplomelor. Fără aceste cunoștințe și abilități, nimic nu va funcționa. Vai. Deci, dacă sunt probleme cu diplomele, atunci pentru început ești binevenit. În plus, avem nevoie și de . Aceste transformări (până la două!) stau la baza rezolvării tuturor ecuațiilor matematicii în general. Și nu doar vitrine. Așa că, cine a uitat, faceți o plimbare și pe link: le-am pus cu un motiv.
Dar numai acțiunile cu puteri și transformări identice nu sunt suficiente. De asemenea, necesită observație personală și ingeniozitate. Avem nevoie de aceleași temeiuri, nu-i așa? Așa că examinăm exemplul și le căutăm într-o formă explicită sau deghizată!
De exemplu, această ecuație:
3 2x – 27x +2 = 0
Prima privire la temeiuri. Sunt diferite! Trei și douăzeci și șapte. Dar este prea devreme pentru a intra în panică și a cădea în disperare. Este timpul să ne amintim asta
27 = 3 3
Numerele 3 și 27 sunt rude în grad! Mai mult, rude.) Prin urmare, avem tot dreptul să scriem:
27 x +2 = (3 3) x+2
Și acum ne conectăm cunoștințele despre actiuni cu puteri(si te-am avertizat!). Există o formulă atât de utilă:
(am) n = a mn
Acum, dacă îl rulați în curs, în general se dovedește bine:
27 x +2 = (3 3) x+2 = 3 3(x +2)
Exemplul original arată acum astfel:
3 2 x – 3 3(x +2) = 0
Grozav, bazele gradelor s-au aliniat. Pentru ce ne străduiam. Jumătate din treabă este făcută.) Și acum lansăm transformarea de bază a identității - transferăm 3 3 (x +2) la dreapta. Nimeni nu a anulat acțiunile elementare ale matematicii, da.) Obținem:
3 2 x = 3 3(x +2)
Ce ne oferă acest tip de ecuație? Și faptul că acum ecuația noastră este redusă la forma canonică: stând în stânga și în dreapta aceleasi numere(triple) în puteri. Și ambii tripleți - într-o izolare splendidă. Îndepărtăm cu îndrăzneală tripleții și obținem:
2x = 3(x+2)
Rezolvăm asta și obținem:
X=-6
Cam despre asta e. Acesta este răspunsul corect.)
Și acum înțelegem cursul deciziei. Ce ne-a salvat în acest exemplu? Am fost salvați de cunoașterea gradelor tripluului. Cum anume? Noi identificat numărul 27 criptat trei! Acest truc (codificarea aceleiași baze sub numere diferite) este unul dintre cele mai populare în ecuațiile exponențiale! Doar dacă nu este cel mai popular. Da, și de asemenea, apropo. De aceea, observația și capacitatea de a recunoaște puterile altor numere în numere sunt atât de importante în ecuațiile exponențiale!
Sfaturi practice:
Trebuie să cunoașteți puterile numerelor populare. În față!
Desigur, oricine poate ridica doi la puterea a șaptea sau trei la a cincea. Nu în mintea mea, deci cel puțin pe un draft. Dar în ecuațiile exponențiale, este mult mai des necesar să nu se ridice la o putere, ci, dimpotrivă, să se afle ce număr și în ce măsură se ascunde în spatele numărului, să zicem, 128 sau 243. Și asta este deja mai mult complicat decât simpla exponențiere, vezi. Simțiți diferența, așa cum se spune!
Deoarece capacitatea de a recunoaște grade pe față este utilă nu numai la acest nivel, ci și la următoarele, iată o mică sarcină pentru tine:
Stabiliți ce puteri și ce numere sunt numere:
4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.
Răspunsuri (împrăștiate, desigur):
27 2 ; 2 10 ; 3 6 ; 7 2 ; 2 6 ; 9 2 ; 3 4 ; 4 3 ; 10 2 ; 2 5 ; 3 5 ; 7 3 ; 16 2 ; 2 7 ; 5 3 ; 2 8 ; 6 2 ; 3 3 ; 2 9 ; 2 4 ; 2 2 ; 4 5 ; 25 2 ; 4 4 ; 6 3 ; 8 2 ; 9 3 .
Da Da! Nu fi surprins că există mai multe răspunsuri decât sarcini. De exemplu, 2 8 , 4 4 și 16 2 sunt toate 256.
Nivelul 2. Ecuații exponențiale simple. Recunoaște grade! Exponenți negativi și fracționari.
La acest nivel, folosim deja cunoștințele noastre despre grade la maximum. Și anume, implicăm indicatori negativi și fracționali în acest proces fascinant! Da Da! Trebuie să creștem puterea, nu?
De exemplu, această ecuație teribilă:
![]()
Din nou, uitați-vă mai întâi la fundații. Bazele sunt diferite! Și de data aceasta nu se aseamănă nici pe departe unul cu celălalt! 5 și 0,04... Și pentru a elimina bazele, sunt necesare aceleași... Ce să faci?
E bine! De fapt, totul este la fel, doar conexiunea dintre cele cinci și 0,04 este puțin vizibilă vizual. Cum ieșim? Și să trecem la fracția obișnuită din numărul 0,04! Și acolo, vedeți, totul este format.)
0,04 = 4/100 = 1/25
Wow! Se pare că 0,04 este 1/25! Ei bine, cine ar fi crezut!)
Ei bine, cum? Acum legătura dintre numerele 5 și 1/25 este mai ușor de văzut? Asta e...
Și acum, conform regulilor de operațiuni cu puteri cu indicator negativ Poate sa cu o mână fermă scrie:
![]()
Asta e grozav. Așa că am ajuns la aceeași bază - cinci. Înlocuim acum numărul inconfortabil 0,04 din ecuație cu 5 -2 și obținem:
![]()
Din nou, conform regulilor de operare cu puteri, acum putem scrie:
(5 -2) x -1 = 5 -2(x -1)
Pentru orice eventualitate, vă reamintesc (deodată, cine nu știe) că regulile de bază pentru acțiunile cu grade sunt valabile pentru orice indicatori! Inclusiv pentru cele negative.) Așa că nu ezitați să luați și să înmulțiți indicatorii (-2) și (x-1) conform regulii corespunzătoare. Ecuația noastră devine din ce în ce mai bună:
![]()
Toate! Pe lângă cei cinci singuratici din grade din stânga și dreapta, nu există nimic altceva. Ecuația este redusă la formă canonică. Și apoi - de-a lungul pistei moletate. Îndepărtăm cele cinci și echivalăm indicatorii:
X 2 –6 X+5=-2(X-1)
Exemplul este aproape gata. Matematica elementară a claselor de mijloc rămâne - deschidem (corect!) Parantezele și colectăm totul din stânga:
X 2 –6 X+5 = -2 X+2
X 2 –4 X+3 = 0
Rezolvăm asta și obținem două rădăcini:
X 1 = 1; X 2 = 3
Asta e tot.)
Acum să ne gândim din nou. În acest exemplu, a trebuit din nou să recunoaștem același număr în grade diferite! Și anume, pentru a vedea cinci criptați în numărul 0,04. Și de data aceasta, în grad negativ! Cum am făcut-o? În mișcare - în niciun caz. Dar după trecerea de la fracție zecimală 0,04 la fracția ordinară 1/25 totul a fost evidențiat! Și apoi întreaga decizie a mers ca un ceas.)
Prin urmare, un alt sfat practic verde.
Dacă există fracții zecimale în ecuația exponențială, atunci trecem de la fracții zecimale la cele obișnuite. ÎN fracții comune este mult mai ușor să recunoști puterile multor numere populare! După recunoaștere, trecem de la fracții la puteri cu exponenți negativi.
Rețineți că o astfel de simulare în ecuațiile exponențiale apare foarte, foarte des! Și persoana nu este în subiect. Se uită, de exemplu, la numerele 32 și 0,125 și se supără. Nu-i știe că acesta este același deuce, doar în grade diferite… Dar ești deja în subiect!)
Rezolvați ecuația:
/image007.png)
În! Pare o groază liniștită... Cu toate acestea, aparențele sunt înșelătoare. Aceasta este cea mai simplă ecuație exponențială, în ciuda faptului că este terifiantă aspect. Și acum ți-o arăt.)
În primul rând, ne ocupăm de toate numerele care se află în baze și în coeficienți. Evident că sunt diferiți, da. Dar totuși ne asumăm riscul și încercăm să le facem aceeași! Să încercăm să ajungem la același număr în grade diferite. Și, de preferință, numărul cât mai mic posibil. Deci, să începem descifrarea!
Ei bine, totul este clar cu cele patru deodată - este 2 2 . Deci, deja ceva.)
Cu o fracțiune de 0,25 - nu este încă clar. Trebuie verificat. Folosim sfaturi practice - treceți de la zecimal la obișnuit:
0,25 = 25/100 = 1/4
Deja mult mai bine. Deocamdată este deja clar că 1/4 este 2 -2. Grozav, iar numărul 0,25 este, de asemenea, asemănător cu un doi.)
Până acum, bine. Dar cel mai rău număr dintre toate rămâne - rădăcina pătrată a doi! Ce să faci cu acest ardei? Poate fi reprezentată și ca o putere a doi? Si cine stie...
Ei bine, din nou urcăm în tezaurul nostru de cunoștințe despre diplome! De data aceasta, ne conectăm în plus cunoștințele despre rădăcini. De la cursul clasei a IX-a, tu și cu mine a trebuit să înduram că orice rădăcină, dacă se dorește, poate fi întotdeauna transformată într-un grad cu o fracție.
Ca aceasta:
În cazul nostru:
![]()
Cum! Se pare că rădăcina pătrată a lui doi este 2 1/2. Asta este!
Asta e bine! Toate numerele noastre incomode s-au dovedit de fapt a fi un doi criptat.) Nu mă cert, undeva criptat foarte sofisticat. Dar ne sporim și profesionalismul în rezolvarea unor astfel de cifruri! Și atunci totul este deja evident. Înlocuim numerele 4, 0,25 și rădăcina lui doi din ecuația noastră cu o putere a lui doi:
/image010.png)
Toate! Bazele tuturor gradelor din exemplu au devenit aceleași - două. Și acum sunt folosite acțiunile standard cu grade:
a mun n = a m + n
a m:a n = a m-n
(am) n = a mn
Pentru partea stângă obțineți:
2 -2 (2 2) 5 x -16 = 2 -2+2(5 x -16)
Pentru partea dreaptă va fi:
/image011.png)
Și acum ecuația noastră rea a început să arate așa:
![]()
Pentru cei care nu și-au dat seama cum exact a rezultat această ecuație, atunci întrebarea nu este despre ecuațiile exponențiale. Întrebarea este despre acțiuni cu puteri. Am rugat urgent sa repet celor care au probleme!
Iată linia de sosire! Se obține forma canonică a ecuației exponențiale! Ei bine, cum? Te-am convins că nu este atât de înfricoșător? ;) Îndepărtăm doi și echivalăm indicatorii:
![]()
Mai rămâne doar să rezolvi ecuație liniară. Cum? Cu ajutorul unor transformări identice, bineînțeles.) Rezolvă ceea ce este deja acolo! Înmulțiți ambele părți cu două (pentru a elimina fracția 3/2), mutați termenii cu X-uri la stânga, fără X-uri la dreapta, aduceți asemenea, numărați - și veți fi fericit!
Totul ar trebui să iasă frumos:
X=4
Acum să ne regândim decizia. În acest exemplu, am fost salvați de tranziția de la rădăcină pătrată La grad cu exponent 1/2. Mai mult, doar o astfel de transformare vicleană ne-a ajutat pretutindeni să ajungem la aceeași bază (deuce), care a salvat situația! Și, dacă nu ar fi, atunci am avea toate șansele să înghețăm pentru totdeauna și să nu facem niciodată față acestui exemplu, da ...
Prin urmare, nu neglijăm următorul sfat practic:
Dacă există rădăcini în ecuația exponențială, atunci trecem de la rădăcini la puteri cu exponenți fracționari. De foarte multe ori, doar o astfel de transformare clarifică situația ulterioară.
Desigur, puterile negative și fracționale sunt deja mult mai dificile. grade naturale. Cel puțin în ceea ce privește percepția vizuală și, mai ales, recunoașterea de la dreapta la stânga!
Este clar că ridicarea directă, de exemplu, a unui doi la puterea lui -3 sau a unui patru la puterea lui -3/2 nu este o problemă atât de mare. Pentru cei care știu.)
Dar du-te, de exemplu, realizezi imediat asta
0,125 = 2 -3
Sau
Aici doar regula practica si experienta bogata, da. Și, desigur, o vedere clară, Ce este un exponent negativ și un exponent fracționar.Și - sfaturi practice! Da, da, acelea verde.) Sper că, totuși, vă vor ajuta să navigați mai bine în toată varietatea pestriță de grade și să vă creșteți semnificativ șansele de succes! Deci să nu le neglijăm. nu sunt degeaba în verde scriu uneori.)
Pe de altă parte, dacă devii „tu” chiar și cu puteri exotice precum negative și fracționale, atunci posibilitățile tale de rezolvare a ecuațiilor exponențiale se vor extinde enorm și vei fi deja capabil să gestionezi aproape orice tip de ecuații exponențiale. Ei bine, dacă nu oricare, atunci 80 la sută din toate ecuațiile exponențiale - cu siguranță! Da, da, nu glumesc!
Așadar, prima noastră parte de cunoaștere a ecuațiilor exponențiale a ajuns la concluzia sa logică. Și, ca antrenament intermediar, sugerez în mod tradițional să rezolvi puțin pe cont propriu.)
Exercitiul 1.
Pentru ca cuvintele mele despre descifrarea gradelor negative și fracționale să nu fie în zadar, îmi propun să joc un mic joc!
Exprimă numărul ca putere a doi:
Răspunsuri (în dezordine):
S-a întâmplat? Grozav! Apoi facem o misiune de luptă - rezolvăm cele mai simple și simple ecuații exponențiale!
Sarcina 2.
Rezolvați ecuații (toate răspunsurile sunt o mizerie!):
5 2x-8 = 25
2 5x-4 – 16x+3 = 0
Raspunsuri:
x=16
X 1 = -1; X 2 = 2
X = 5
S-a întâmplat? Într-adevăr, mult mai ușor!
Apoi rezolvăm următorul joc:
![]()
(2 x +4) x -3 = 0,5 x 4 x -4
35 1-x = 0,2 - x 7 x
Raspunsuri:
X 1 = -2; X 2 = 2
X = 0,5
X 1 = 3; X 2 = 5
Și aceste exemple de unul au rămas? Grozav! Crești! Apoi, iată câteva exemple pe care să le gustați:
/image019.png)
Raspunsuri:
X = 6
X = 13/31
X = -0,75
X 1 = 1; X 2 = 8/3
Și s-a hotărât? Ei bine, respect! îmi scot pălăria.) Deci, lecția nu a fost în zadar și Primul nivel rezolvarea ecuațiilor exponențiale poate fi considerată stăpânită cu succes. Înainte - următoarele niveluri și ecuații mai complexe! Și noi tehnici și abordări. Și exemple non-standard. Și noi surprize.) Toate acestea - în lecția următoare!
Ceva nu a mers? Deci, cel mai probabil, problemele sunt în . Sau în . Sau ambele in acelasi timp. Aici sunt neputincios. Pot să ofer încă o dată un singur lucru - nu fi leneș și fă o plimbare prin linkuri.)
Va urma.)
Primul nivel
ecuații exponențiale. Ghid cuprinzător (2019)
Buna ziua! Astăzi vom discuta cu tine cum să rezolvi ecuații care pot fi atât elementare (și sper că, după ce am citit acest articol, aproape toate vor fi așa pentru tine), cât și cele cărora li se acordă de obicei „rămbleu”. Aparent, să adorm complet. Dar voi încerca să fac tot posibilul ca acum să nu ai probleme când te confrunți cu acest tip de ecuație. Nu voi mai bate în jurul tufișului, dar voi dezvălui imediat un mic secret: astăzi vom studia ecuații exponențiale.
Înainte de a trece la o analiză a modalităților de rezolvare a acestora, vă voi schița imediat un cerc de întrebări (destul de mic) pe care ar trebui să le repetați înainte de a vă grăbi să asaltați acest subiect. Deci, pentru cele mai bune rezultate, vă rog repeta:
- proprietăţi şi
- Soluție și ecuații
Repetat? Uimitor! Atunci nu vă va fi greu să observați că rădăcina ecuației este un număr. Ești sigur că înțelegi cum am făcut-o? Este adevarat? Apoi continuăm. Acum răspunde-mi la întrebarea, ce este egal cu a treia putere? Ai dreptate: . Opt este ce putere a doi? Așa este - al treilea! Deoarece. Ei bine, acum să încercăm să rezolvăm următoarea problemă: Lasă-mă să înmulțesc numărul cu el însuși o dată și să obțin rezultatul. Întrebarea este de câte ori m-am înmulțit singur? Desigur, puteți verifica acest lucru direct:
\begin(align) & 2=2 \\ & 2\cdot 2=4 \\ & 2\cdot 2\cdot 2=8 \\ & 2\cdot 2\cdot 2\cdot 2=16 \\ \end( alinia)
Atunci poți trage concluzia că am înmulțit ori singur. Cum altfel poate fi verificat acest lucru? Și iată cum: direct după definiția gradului: . Dar, trebuie să recunoașteți, dacă aș întreba de câte ori doi trebuie înmulțiți singuri pentru a obține, să zicem, mi-ați spune: nu mă voi păcăli și mă voi înmulți singur până nu voi fi albastru la față. Și ar avea perfectă dreptate. Pentru că cum poți notează pe scurt toate acțiunile(iar concizia este sora talentului)
unde - acesta este chiar "ori" când te înmulți singuri.
Cred că știți (și dacă nu știți, urgent, foarte urgent repetați diplomele!) că atunci problema mea va fi scrisă sub forma:
Cum puteți concluziona în mod rezonabil că:
Așa că, în liniște, am notat cel mai simplu ecuație exponențială:
Și chiar l-a găsit rădăcină. Nu crezi că totul este destul de banal? Exact asta cred si eu. Iată un alt exemplu pentru tine:
Dar ce să faci? La urma urmei, nu poate fi scris ca un grad al unui număr (rezonabil). Să nu disperăm și să observăm că ambele numere sunt perfect exprimate în termeni de putere a aceluiași număr. Ce? Dreapta: . Apoi ecuația inițială este transformată în forma:
De unde, după cum ați înțeles deja, . Să nu mai tragem și să scriem definiție:
În cazul nostru cu dumneavoastră: .
Aceste ecuații se rezolvă prin reducerea lor la forma:
cu rezolvarea ulterioară a ecuației
Noi, de fapt, am făcut asta în exemplul anterior: am primit asta. Și am rezolvat cea mai simplă ecuație cu tine.
Pare să nu fie nimic complicat, nu? Să exersăm mai întâi pe cel mai simplu. exemple:
Vedem din nou că părțile dreaptă și stângă ale ecuației trebuie reprezentate ca o putere a unui număr. Adevărat, acest lucru s-a făcut deja în stânga, dar în dreapta există un număr. Dar, la urma urmei, este în regulă, iar ecuația mea se transformă în mod miraculos în asta:
Ce a trebuit să fac aici? Ce regulă? Regulă putere la putere care scrie:
Și dacă:
Înainte de a răspunde la această întrebare, să completăm următorul tabel cu tine:
Nu ne este greu să observăm că cu cât mai puțin, cu atât valoare mai mică, dar cu toate acestea, toate aceste valori Peste zero. SI VA FI Intotdeauna ASA!!! Aceeași proprietate este valabilă PENTRU ORICE BAZĂ CU ORICE INDEX!! (pentru orice și). Atunci ce putem concluziona despre ecuație? Și iată unul: acesta nu are rădăcini! La fel ca orice ecuație nu are rădăcini. Acum să exersăm și Să rezolvăm câteva exemple simple:
Sa verificam:
1. Aici nu ți se cere nimic, decât să cunoști proprietățile puterilor (pe care, de altfel, ți-am cerut să le repeți!) De regulă, totul duce la cea mai mică bază: , . Atunci ecuația inițială va fi echivalentă cu următoarea: Tot ce am nevoie este să folosesc proprietățile puterilor: la înmulțirea numerelor cu aceeași bază, se adună exponenții, iar la împărțire se scad. Apoi voi obține: Ei bine, acum cu conștiința curată voi trece de la ecuația exponențială la cea liniară: \begin(align)
& 2x+1+2(x+2)-3x=5 \\
& 2x+1+2x+4-3x=5 \\
&x=0. \\
\end(align)
2. În al doilea exemplu, trebuie să fii mai atent: problema este că în partea stângă nu vom putea reprezenta același număr ca o putere. În acest caz, uneori este util reprezintă numere ca produs de puteri cu baze diferite, dar aceiași exponenți:
Partea stângă a ecuației va lua forma: Ce ne-a dat asta? Și iată ce: Se pot înmulți numere cu baze diferite, dar cu același exponent.În acest caz, bazele sunt înmulțite, dar exponentul nu se schimbă:
Aplicat situației mele, aceasta va da:
\begin(align)
& 4\cdot ((64)^(x))((25)^(x))=6400, \\
& 4\cdot (((64\cdot 25))^(x))=6400, \\
& ((1600)^(x))=\frac(6400)(4), \\
& ((1600)^(x))=1600, \\
&x=1. \\
\end(align)
Nu-i rău, nu?
3. Nu-mi place când am doi termeni pe o parte a ecuației și niciunul pe cealaltă (uneori, desigur, acest lucru este justificat, dar nu este cazul acum). Mutați termenul minus la dreapta:
Acum, ca și înainte, voi scrie totul prin puterile triplei:
Adun puterile din stânga și obțin o ecuație echivalentă
Îi puteți găsi cu ușurință rădăcina:
4. Ca și în exemplul trei, termenul cu minus - un loc în partea dreaptă!
În stânga, aproape totul este în regulă cu mine, cu excepția ce? Da, „gradul greșit” al zeului mă deranjează. Dar pot rezolva cu ușurință acest lucru scriind: . Eureka - în stânga, toate bazele sunt diferite, dar toate gradele sunt la fel! Ne inmultim repede!
Din nou, totul este clar: (dacă nu ați înțeles cât de magic am obținut ultima egalitate, luați o pauză de un minut, luați o pauză și citiți din nou cu mare atenție proprietățile gradului. Cine a spus că puteți sări peste grad cu exponent negativ? Ei bine, aici sunt cam la fel ca nimeni). Acum voi primi:
\begin(align)
& ((2)^(4\left((x) -9 \right)))=((2)^(-1)) \\
&4((x) -9)=-1 \\
&x=\frac(35)(4). \\
\end(align)
Iată sarcinile pe care să le exersați, la care voi da doar răspunsurile (dar într-o formă „mixtă”). Rezolvă-le, verifică și ne vom continua cercetările!
Gata? Răspunsuri ca acestea:
- orice număr
Bine, bine, glumeam! Iată schița soluțiilor (unele sunt destul de scurte!)
Nu crezi că nu este o coincidență că o fracție din stânga este o alta „inversată”? Ar fi un păcat să nu folosești asta:
Această regulă este foarte des folosită la rezolvarea ecuațiilor exponențiale, rețineți-o bine!
Atunci ecuația inițială devine:
Rezolvând această ecuație pătratică, veți obține următoarele rădăcini:
2. O altă soluție: împărțirea ambelor părți ale ecuației la expresia din stânga (sau dreapta). Voi împărți la ceea ce este în dreapta, apoi voi obține:
Unde (de ce?!)
3. Nici nu vreau să mă repet, totul a fost deja „mestecat” atât de mult.
4. echivalent cu o ecuație pătratică, rădăcinile
5. Trebuie să utilizați formula dată în prima sarcină, apoi veți obține:
Ecuația s-a transformat într-o identitate banală, ceea ce este adevărat pentru orice. Atunci răspunsul este orice număr real.
Ei bine, aici sunteți și exersați să decideți cele mai simple ecuații exponențiale. Acum vreau să vă dau câteva exemple de viață care vă vor ajuta să înțelegeți de ce sunt necesare în principiu. Aici voi da două exemple. Unul dintre ele este destul de cotidian, dar celălalt are un interes mai mult științific decât practic.
Exemplul 1 (comercial) Lasă-ți ruble, dar vrei să le transformi în ruble. Banca vă oferă să luați acești bani de la dvs. la o dobândă anuală cu o capitalizare lunară a dobânzii (cumulare lunară). Întrebarea este, pentru câte luni trebuie să deschideți un depozit pentru a încasa suma finală dorită? O sarcină destul de banală, nu-i așa? Cu toate acestea, soluția sa este legată de construcția ecuației exponențiale corespunzătoare: Fie - suma inițială, - suma finală, - rata dobânzii pentru perioada, - numărul de perioade. Apoi:
În cazul nostru (dacă rata este pe an, atunci se calculează pe lună). De ce este împărțit în? Dacă nu știți răspunsul la această întrebare, amintiți-vă de subiectul „”! Apoi obținem următoarea ecuație:
Această ecuație exponențială poate fi deja rezolvată doar cu un calculator (apariția ei sugerează acest lucru, iar acest lucru necesită cunoașterea logaritmilor, cu care ne vom familiariza puțin mai târziu), ceea ce voi face: ... Astfel, pentru a primim un milion, trebuie să facem o contribuție pentru o lună (nu foarte repede, nu?).
Exemplul 2 (mai degrabă științific).În ciuda lui, oarecare „izolare”, vă recomand să-i acordați atenție: în mod regulat „se strecoară la examen!! (sarcina este preluată din versiunea „reală”) În timpul dezintegrarii unui izotop radioactiv, masa acestuia scade conform legii, unde (mg) este masa inițială a izotopului, (min.) este timpul scurs de la momentul inițial, (min.) este timpul de înjumătățire. În momentul inițial de timp, masa izotopului este mg. Timpul său de înjumătățire este de min. În câte minute va fi masa izotopului egală cu mg? E în regulă: luăm și înlocuim toate datele din formula propusă:
Să împărțim ambele părți la, „în speranța” că în stânga obținem ceva digerabil:
Ei bine, suntem foarte norocoși! Se află în stânga, apoi să trecem la ecuația echivalentă:
Unde min.
După cum puteți vedea, ecuațiile exponențiale au o aplicație foarte reală în practică. Acum vreau să discut cu tine un alt mod (simplu) de a rezolva ecuațiile exponențiale, care se bazează pe scoaterea factorului comun din paranteze și apoi gruparea termenilor. Nu vă fie teamă de cuvintele mele, această metodă ați întâlnit deja în clasa a VII-a când ați studiat polinoamele. De exemplu, dacă trebuie să factorizați expresia:
Să grupăm: primul și al treilea termen, precum și al doilea și al patrulea. Este clar că primul și al treilea sunt diferența dintre pătrate:
iar al doilea și al patrulea au un factor comun de trei:
Atunci expresia originală este echivalentă cu aceasta:
Unde să eliminați factorul comun nu mai este dificil:
Prin urmare,
Cam așa vom acționa atunci când rezolvăm ecuații exponențiale: căutați „comunalitate” între termeni și scoateți-o din paranteze, apoi - orice ar fi, cred că vom avea noroc =)) De exemplu:
În dreapta este departe de puterea lui șapte (am verificat!) Și în stânga - puțin mai bine, puteți, desigur, să „tai” factorul a din primul termen și din al doilea, apoi să te ocupi de ce ai primit, dar să facem cu tine mai prudent. Nu vreau să mă ocup de fracțiile care sunt produse inevitabil de „selecție”, așa că nu ar trebui să suport mai bine? Atunci nu voi avea fracții: după cum se spune, lupii sunt plini și oile sunt în siguranță:
Numărați expresia dintre paranteze. Magic, magic, se dovedește că (în mod surprinzător, deși la ce să ne mai așteptăm?).
Apoi reducem ambele părți ale ecuației cu acest factor. Obținem: unde.
Iată un exemplu mai complicat (destul de puțin, într-adevăr):
Iată necazul! Nu avem un punct comun aici! Nu este complet clar ce să faci acum. Și să facem ce putem: în primul rând, vom muta „patru” într-o direcție, iar „cinci” în cealaltă:
Acum să scoatem „comunul” din stânga și din dreapta:
Deci ce acum? Care este beneficiul unei astfel de grupări stupide? La prima vedere, nu este deloc vizibil, dar haideți să privim mai profund:
Ei bine, acum să facem astfel încât în stânga să avem doar expresia c, iar în dreapta - orice altceva. Cum putem face acest lucru? Și iată cum: Împărțim mai întâi ambele părți ale ecuației cu (deci scăpăm de exponentul din dreapta), apoi împărțim ambele părți cu (deci scăpăm de factorul numeric din stânga). În sfârșit obținem:
Incredibil! În stânga avem o expresie, iar în dreapta - doar. Atunci tragem imediat concluzia că
Iată un alt exemplu de consolidat:
Îl voi aduce soluție scurtă(nu vă deranjez cu adevărat să explic), încercați să vă dați seama singur toate „subtilitățile” soluției.
Acum consolidarea finală a materialului acoperit. Încercați să rezolvați singur următoarele probleme. Voi oferi doar scurte recomandări și sfaturi pentru a le rezolva:
- Să scoatem factorul comun din paranteze:
- Reprezentăm prima expresie sub forma: , împărțim ambele părți la și obținem asta
- , apoi ecuația originală este convertită în forma: Ei bine, acum un indiciu - căutați unde am rezolvat deja această ecuație!
- Imaginați-vă cum, cum, ah, bine, apoi împărțiți ambele părți la, astfel încât să obțineți cea mai simplă ecuație exponențială.
- Scoate-l din paranteze.
- Scoate-l din paranteze.
ECUATII EXPOZIONALE. NIVEL MEDIU
Presupun că după ce am citit primul articol, care spunea ce sunt ecuațiile exponențiale și cum să le rezolvi ai stăpânit minim necesar cunoștințe necesare pentru a rezolva exemple simple.
Acum voi analiza o altă metodă de rezolvare a ecuațiilor exponențiale, aceasta este
„metoda de introducere a unei noi variabile” (sau substituție). Rezolvă majoritatea problemelor „dificile”, pe tema ecuațiilor exponențiale (și nu numai a ecuațiilor). Această metodă este una dintre cele mai frecvent utilizate în practică. În primul rând, vă recomand să vă familiarizați cu subiectul.
După cum ați înțeles deja din nume, esența acestei metode este să introduceți o astfel de schimbare a variabilei, încât ecuația dvs. exponențială să se transforme în mod miraculos într-una pe care o puteți rezolva deja cu ușurință. Tot ce vă rămâne după rezolvarea acestei „ecuații simplificate” este să faceți o „înlocuire inversă”: adică să reveniți de la înlocuit la înlocuit. Să ilustrăm ceea ce tocmai am spus cu un exemplu foarte simplu:
Exemplul 1:
Această ecuație este rezolvată printr-o „înlocuire simplă”, așa cum o numesc în mod disprețuitor matematicienii. Într-adevăr, înlocuirea de aici este cea mai evidentă. Trebuie doar văzut că
Atunci ecuația inițială devine:
Dacă ne imaginăm în plus cum, atunci este destul de clar ce trebuie înlocuit: desigur, . Ce devine atunci ecuația originală? Și iată ce:
Îi poți găsi cu ușurință rădăcinile pe cont propriu:. Ce ar trebui să facem acum? Este timpul să revenim la variabila inițială. Ce am uitat să includ? Și anume: la înlocuirea unui anumit grad cu o variabilă nouă (adică la înlocuirea unui tip), voi fi interesat de doar rădăcini pozitive! Puteți răspunde cu ușurință de ce. Astfel, nu suntem interesați de tine, dar a doua rădăcină este destul de potrivită pentru noi:
Atunci unde.
Răspuns:
După cum puteți vedea, în exemplul anterior, înlocuitorul a cerut doar mâinile noastre. Din păcate, acest lucru nu este întotdeauna cazul. Cu toate acestea, să nu trecem direct la trist, ci să exersăm pe încă un exemplu cu o înlocuire destul de simplă
Exemplul 2
Este clar că cel mai probabil va fi necesară înlocuirea (aceasta este cea mai mică dintre puterile incluse în ecuația noastră), cu toate acestea, înainte de a introduce o înlocuire, ecuația noastră trebuie să fie „pregătită” pentru aceasta, și anume: , . Apoi puteți înlocui, ca urmare voi obține următoarea expresie:
Oh groază: o ecuație cubică cu formule absolut groaznice pentru rezolvarea ei (ei bine, vorbind în termeni generali). Dar să nu disperăm imediat, ci să ne gândim la ce ar trebui să facem. Îți voi sugera să înșeli: știm că pentru a obține un răspuns „frumos”, trebuie să obținem o putere de trei (de ce ar fi asta, nu?). Și să încercăm să ghicim cel puțin o rădăcină a ecuației noastre (voi începe să ghicesc din puterile lui trei).
Prima presupunere. Nu este o rădăcină. vai și ah...
.
Partea stângă este egală.
Partea dreapta:!
Mânca! Am ghicit prima rădăcină. Acum lucrurile vor deveni mai ușoare!
Știți despre schema de împărțire „colț”? Bineînțeles că știi, îl folosești când împărți un număr la altul. Dar puțini oameni știu că același lucru se poate face cu polinoamele. Există o teoremă minunată:
Aplicabil situației mele, îmi spune ce este divizibil fără rest prin. Cum se realizează împărțirea? Așa:
Mă uit la ce monom ar trebui să înmulțesc pentru a obține Clear, apoi:
Scăd expresia rezultată din, obțin:
Acum, ce trebuie să înmulțesc pentru a obține? Este clar că pe, atunci voi obține:
și din nou scădeți expresia rezultată din cea rămasă:
Ei bine, ultimul pas, înmulțesc cu și scad din expresia rămasă:
Ura, diviziunea s-a terminat! Ce am acumulat în privat? De la sine: .
Apoi am obținut următoarea extindere a polinomului original:
Să rezolvăm a doua ecuație:
Are rădăcini:
Apoi ecuația inițială:
are trei rădăcini:
Desigur, aruncăm ultima rădăcină, deoarece este mai mică decât zero. Și primele două după înlocuirea inversă ne vor da două rădăcini:
Răspuns: ..
Prin acest exemplu, nu am vrut deloc să te sperii, ci mi-am propus să arăt că, deși am avut o înlocuire destul de simplă, totuși, a dus la un ecuație complexă, a cărui soluție a necesitat niște aptitudini speciale de la noi. Ei bine, nimeni nu este imun la asta. Dar schimbarea în acest caz a fost destul de evidentă.
Iată un exemplu cu o înlocuire puțin mai puțin evidentă:
Nu este deloc clar ce ar trebui să facem: problema este că în ecuația noastră există două baze diferite și o bază nu poate fi obținută din cealaltă ridicând-o la orice grad (rezonabil, firesc). Totuși, ce vedem? Ambele baze diferă doar prin semn, iar produsul lor este diferența de pătrate egală cu unu:
Definiție:
Astfel, numerele care sunt baze în exemplul nostru sunt conjugate.
În acest caz, mișcarea inteligentă ar fi înmulțiți ambele părți ale ecuației cu numărul conjugat.
De exemplu, pe, atunci partea stângă a ecuației va deveni egală, iar partea dreaptă. Dacă facem o înlocuire, atunci ecuația noastră originală cu tine va deveni astfel:
rădăcinile sale, atunci, dar amintindu-ne asta, obținem asta.
Răspuns: , .
De regulă, metoda înlocuirii este suficientă pentru a rezolva majoritatea ecuațiilor exponențiale „școlare”. Următoarele sarcini sunt preluate din USE C1 ( nivel ridicat dificultăți). Sunteți deja suficient de alfabetizat pentru a rezolva singur aceste exemple. Voi oferi doar înlocuirea necesară.
- Rezolvați ecuația:
- Găsiți rădăcinile ecuației:
- Rezolvați ecuația: . Găsiți toate rădăcinile acestei ecuații care aparțin segmentului:
Acum pentru câteva explicații și răspunsuri rapide:
- Aici este suficient să observăm că și. Atunci ecuația inițială va fi echivalentă cu aceasta: Această ecuație se rezolvă prin înlocuirea Efectuați singuri următoarele calcule. În final, sarcina ta se va reduce la rezolvarea celei mai simple trigonometrice (în funcție de sinus sau cosinus). Vom discuta soluția unor astfel de exemple în alte secțiuni.
- Aici puteți face chiar și fără o înlocuire: mutați pur și simplu subtrahendul la dreapta și reprezentați ambele baze prin puteri de doi: apoi treceți imediat la ecuația pătratică.
- A treia ecuație este de asemenea rezolvată într-un mod destul de standard: imaginați-vă cum. Apoi, înlocuind obținem o ecuație pătratică: atunci,
Știți deja ce este un logaritm? Nu? Atunci citeste urgent subiectul!
Prima rădăcină, evident, nu aparține segmentului, iar a doua este de neînțeles! Dar vom afla foarte curând! Din moment ce, atunci (aceasta este o proprietate a logaritmului!) Să comparăm:
Scădem din ambele părți, atunci obținem:
Partea stângă poate fi reprezentată ca:
înmulțiți ambele părți cu:
poate fi înmulțit cu, atunci
Atunci să comparăm:
de atunci:
Apoi a doua rădăcină aparține intervalului dorit
Răspuns:
Cum vedeți, selectarea rădăcinilor ecuațiilor exponențiale necesită o cunoaștere destul de profundă a proprietăților logaritmilor, așa că vă sfătuiesc să fiți cât mai atenți când rezolvați ecuații exponențiale. După cum știți, în matematică totul este interconectat! După cum obișnuia să spună profesorul meu de matematică: „Nu poți citi matematică ca istoria peste noapte”.
De regulă, toate dificultatea de a rezolva problemele C1 este tocmai alegerea rădăcinilor ecuației. Să exersăm cu un alt exemplu:
Este clar că ecuația în sine este rezolvată destul de simplu. După ce am făcut înlocuirea, reducem ecuația noastră inițială la următoarea:
Să ne uităm mai întâi la prima rădăcină. Compara si: de atunci. (proprietatea funcției logaritmice, la). Atunci este clar că nici prima rădăcină nu aparține intervalului nostru. Acum a doua rădăcină: . Este clar că (din moment ce funcția este în creștere). Rămâne de comparat și
de atunci, în acelaşi timp. Astfel, pot „conduce un cuier” între și. Acest cui este un număr. Prima expresie este mai mică decât și a doua este mai mare decât. Atunci a doua expresie este mai mare decât prima și rădăcina aparține intervalului.
Răspuns: .
În concluzie, să ne uităm la un alt exemplu de ecuație în care înlocuirea este mai degrabă nestandard:
Să începem imediat cu ce poți face și ce - în principiu, poți, dar e mai bine să nu faci asta. Este posibil - să reprezinte totul prin puterile lui trei, doi și șase. Unde duce? Da, și nu va duce la nimic: un amestec de grade, dintre care unele vor fi destul de greu de scăpat. Atunci de ce este nevoie? Să observăm că a Și ce ne va oferi? Și faptul că putem reduce soluția acestui exemplu la soluția unei ecuații exponențiale destul de simple! Mai întâi, să ne rescriem ecuația ca:
Acum împărțim ambele părți ale ecuației rezultate în:
Eureka! Acum putem înlocui, obținem:
Ei bine, acum este rândul tău să rezolvi problemele pentru demonstrație și le voi face doar comentarii scurte, ca să nu te rătăciți calea cea buna! Noroc!
1. Cel mai dificil! Să vezi un înlocuitor aici este oh, ce urât! Cu toate acestea, acest exemplu poate fi rezolvat complet folosind selectarea unui pătrat complet. Pentru a o rezolva, este suficient să rețineți că:
Deci, iată înlocuitorul tău:
(Rețineți că aici, cu înlocuirea noastră, nu putem elimina rădăcina negativă!!! Și de ce, ce credeți?)
Acum, pentru a rezolva exemplul, trebuie să rezolvați două ecuații:
Ambele sunt rezolvate prin „înlocuirea standard” (dar al doilea într-un exemplu!)
2. Observați asta și faceți o înlocuire.
3. Extindeți numărul în factori coprimi și simplificați expresia rezultată.
4. Împărțiți numărătorul și numitorul fracției la (sau dacă preferați) și faceți înlocuirea sau.
5. Rețineți că numerele și sunt conjugate.
ECUATII EXPOZIONALE. NIVEL AVANSAT
În plus, să ne uităm la un alt mod - rezolvarea ecuațiilor exponențiale prin metoda logaritmului. Nu pot spune că soluția ecuațiilor exponențiale prin această metodă este foarte populară, dar în unele cazuri doar aceasta ne poate conduce la decizia corectă ecuația noastră. Mai ales adesea este folosit pentru a rezolva așa-numitul " ecuații mixte': adică cele unde există funcții de diferite tipuri.
De exemplu, o ecuație ca:
în cazul general, poate fi rezolvată doar luând logaritmul ambelor părți (de exemplu, după bază), în care ecuația inițială se transformă în următoarea:
Să luăm în considerare următorul exemplu:
Este clar că ne interesează doar ODZ-ul funcției logaritmice. Cu toate acestea, acest lucru rezultă nu numai din ODZ al logaritmului, ci și din alt motiv. Cred că nu vă va fi greu să ghiciți care dintre ele.
Să luăm logaritmul ambelor părți ale ecuației noastre la bază:
După cum puteți vedea, luarea logaritmului ecuației noastre originale ne-a condus rapid la răspunsul corect (și frumos!). Să exersăm cu un alt exemplu:
Nici aici nu trebuie să vă faceți griji: luăm logaritmul ambelor părți ale ecuației în termeni de bază, apoi obținem:
Să facem un înlocuitor:
Totuși, am omis ceva! Ai observat unde am greșit? La urma urmei, atunci:
care nu satisface cerința (gândiți-vă de unde a venit!)
Răspuns:
Încercați să scrieți soluția ecuațiilor exponențiale de mai jos:
Acum verificați soluția cu aceasta:
1. Logaritmăm ambele părți la bază, având în vedere că:
(a doua rădăcină nu ne convine din cauza înlocuirii)
2. Logaritmul la bază:
Să transformăm expresia rezultată în următoarea formă:
ECUATII EXPOZIONALE. SCURTĂ DESCRIERE ȘI FORMULĂ DE BAZĂ
ecuație exponențială
Tip ecuație:
numit cea mai simplă ecuație exponențială.
Proprietăți de grad
Abordări ale soluției
- Reducere la aceeași bază
- Reducere la același exponent
- Substituție variabilă
- Simplificați expresia și aplicați una dintre cele de mai sus.







