Unghiul dintre două linii. Unghiul dintre liniile din spațiu
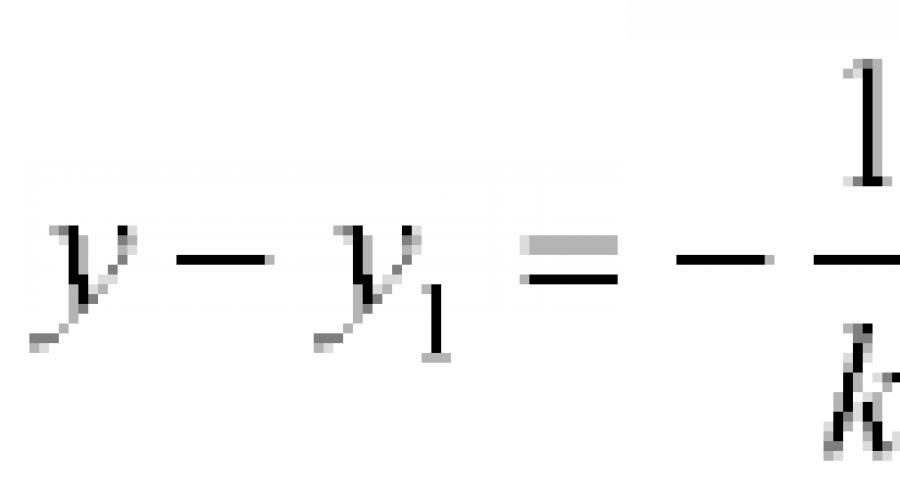
Citeste si
Va fi util pentru fiecare elev care se pregătește pentru examenul de matematică să repete subiectul „Găsirea unghiului dintre linii”. După cum arată statisticile, la trecerea unui test de certificare, sarcinile din această secțiune de stereometrie provoacă dificultăți pentru un numar mare elevi. În același timp, sarcinile care necesită găsirea unghiului dintre liniile drepte se regăsesc în USE atât de bază, cât și nivel de profil. Aceasta înseamnă că toată lumea ar trebui să le poată rezolva.
Momente de bază
Există 4 tipuri de aranjare reciprocă a liniilor în spațiu. Ele pot coincide, se intersectează, pot fi paralele sau se intersectează. Unghiul dintre ele poate fi acut sau drept.
Pentru a găsi unghiul dintre linii în examenul de stat unificat sau, de exemplu, în soluție, școlarii din Moscova și alte orașe pot folosi mai multe metode pentru rezolvarea problemelor din această secțiune a stereometriei. Puteți finaliza sarcina prin construcții clasice. Pentru a face acest lucru, merită să învățați axiomele și teoremele de bază ale stereometriei. Elevul trebuie să fie capabil să construiască logic raționament și să creeze desene pentru a aduce sarcina la o problemă planimetrică.
De asemenea, puteți utiliza metoda vector-coordonate, folosind formule, reguli și algoritmi simpli. Principalul lucru în acest caz este să efectuați corect toate calculele. Proiectul educațional Shkolkovo vă va ajuta să vă îmbunătățiți abilitățile în rezolvarea problemelor din stereometrie și alte secțiuni ale cursului școlar.
Definiție. Dacă sunt date două drepte y = k 1 x + b 1 , y = k 2 x + b 2 , atunci colt ascutitîntre aceste linii va fi definită ca
Două drepte sunt paralele dacă k 1 = k 2 . Două drepte sunt perpendiculare dacă k 1 = -1/ k 2 .
Teorema. Liniile drepte Ax + Vy + C \u003d 0 și A 1 x + B 1 y + C 1 \u003d 0 sunt paralele atunci când coeficienții A 1 \u003d λA, B 1 \u003d λB sunt proporționali. Dacă și С 1 = λС, atunci liniile coincid. Coordonatele punctului de intersecție a două drepte se găsesc ca soluție a sistemului de ecuații ale acestor drepte.
Ecuația unei drepte care trece prin punct dat
Perpendicular pe această linie
Definiție. Linia care trece prin punctul M 1 (x 1, y 1) și perpendiculară pe dreapta y \u003d kx + b este reprezentată de ecuația:

Distanța de la punct la linie
Teorema. Dacă este dat un punct M(x 0, y 0), atunci distanța până la linia Ax + Vy + C \u003d 0 este definită ca
 .
.
Dovada. Fie punctul M 1 (x 1, y 1) să fie baza perpendicularei căzute de la punctul M la dreapta dată. Atunci distanța dintre punctele M și M 1:
![]() (1)
(1)
Coordonatele x 1 și y 1 pot fi găsite ca soluție a sistemului de ecuații:

A doua ecuație a sistemului este ecuația unei linii drepte care trece prin punct dat M 0 este perpendiculară pe o dreaptă dată. Dacă transformăm prima ecuație a sistemului în forma:
A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,
apoi, rezolvand, obtinem:

Înlocuind aceste expresii în ecuația (1), găsim:

Teorema a fost demonstrată.
Exemplu. Să se determine unghiul dintre drepte: y = -3 x + 7; y = 2 x + 1.
k 1 \u003d -3; k2 = 2; tgφ =  ; φ= p /4.
; φ= p /4.
Exemplu. Arătați că dreptele 3x - 5y + 7 = 0 și 10x + 6y - 3 = 0 sunt perpendiculare.
Soluţie. Găsim: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 * k 2 \u003d -1, prin urmare, liniile sunt perpendiculare.
Exemplu. Sunt date vârfurile triunghiului A(0; 1), B (6; 5), C (12; -1). Găsiți ecuația pentru înălțimea desenată din vârful C.
Soluţie. Găsim ecuația laturii AB:  ; 4 x = 6 y - 6;
; 4 x = 6 y - 6;
2x – 3y + 3 = 0;
Ecuația de înălțime dorită este: Ax + By + C = 0 sau y = kx + b. k = . Atunci y = . pentru că înălțimea trece prin punctul C, apoi coordonatele sale satisfac această ecuație:  de unde b = 17. Total: .
de unde b = 17. Total: . 
Răspuns: 3x + 2y - 34 = 0.
Ecuația unei drepte care trece printr-un punct dat într-o direcție dată. Ecuația unei drepte care trece prin două puncte date. Unghiul dintre două linii. Condiția de paralelism și perpendicularitate a două drepte. Determinarea punctului de intersecție a două drepte
1. Ecuația unei drepte care trece printr-un punct dat A(X 1 , y 1) într-o direcție dată, determinată de pantă k,
y - y 1 = k(X - X 1). (1)
Această ecuație definește un creion de linii care trec printr-un punct A(X 1 , y 1), care se numește centrul fasciculului.
2. Ecuația unei drepte care trece prin două puncte: A(X 1 , y 1) și B(X 2 , y 2) se scrie astfel:
Panta unei drepte care trece prin două puncte date este determinată de formula
3. Unghiul dintre liniile drepte Ași B este unghiul cu care trebuie rotită prima linie dreaptă Aîn jurul punctului de intersecție al acestor linii în sens invers acelor de ceasornic până când acesta coincide cu a doua linie B. Dacă două drepte sunt date prin ecuații de pante
y = k 1 X + B 1 ,
y = k 2 X + B 2 , (4)
atunci unghiul dintre ele este determinat de formula
Trebuie remarcat faptul că la numărătorul fracției, panta primei drepte este scăzută din panta celei de-a doua drepte.
Dacă ecuațiile unei linii drepte sunt date în vedere generala
A 1 X + B 1 y + C 1 = 0,
A 2 X + B 2 y + C 2 = 0, (6)
unghiul dintre ele este determinat de formula
4. Condiții pentru paralelismul a două linii:
a) Dacă dreptele sunt date de ecuațiile (4) cu o pantă, atunci condiția necesară și suficientă pentru paralelismul lor este egalitatea pantelor lor:
k 1 = k 2 . (8)
b) Pentru cazul în care dreptele sunt date prin ecuații în forma generală (6), condiția necesară și suficientă pentru paralelismul lor este ca coeficienții la coordonatele curente corespunzătoare din ecuațiile lor să fie proporționali, i.e.
5. Condiții pentru perpendicularitatea a două drepte:
a) În cazul în care dreptele sunt date de ecuațiile (4) cu o pantă, condiția necesară și suficientă pentru perpendicularitatea lor este ca acestea factori de panta sunt reciproce ca mărime și opuse ca semn, adică
Această condiție poate fi scrisă și în formular
k 1 k 2 = -1. (11)
b) Dacă ecuațiile dreptelor sunt date în forma generală (6), atunci condiția pentru perpendicularitatea lor (necesară și suficientă) este îndeplinirea egalității
A 1 A 2 + B 1 B 2 = 0. (12)
6. Coordonatele punctului de intersecție a două drepte se găsesc prin rezolvarea sistemului de ecuații (6). Liniile (6) se intersectează dacă și numai dacă
1. Scrieți ecuațiile dreptelor care trec prin punctul M, dintre care una este paralelă, iar cealaltă perpendiculară pe dreapta dată l.
Oh-oh-oh-oh-oh ... ei bine, e minuscul, de parcă ți-ai citi propoziția pentru tine =) Cu toate acestea, atunci relaxarea va ajuta, mai ales că mi-am cumpărat azi accesorii potrivite. Prin urmare, să trecem la prima secțiune, sper că până la sfârșitul articolului voi păstra o dispoziție veselă.
Dispunerea reciprocă a două linii drepte
Cazul când sala cântă în cor. Două linii pot:
1) potrivire;
2) fi paralel: ;
3) sau se intersectează într-un singur punct: .
Ajutor pentru manechini : te rog tine minte semn matematic intersecție, va apărea foarte des. Intrarea înseamnă că linia se intersectează cu linia în punct.
Cum se determină poziția relativă a două linii?
Să începem cu primul caz:
Două drepte coincid dacă și numai dacă coeficienții lor respectivi sunt proporționali, adică există un astfel de număr „lambda” încât egalitățile
Să considerăm drepte și să compunem trei ecuații din coeficienții corespunzători: . Din fiecare ecuație rezultă că, prin urmare, aceste drepte coincid.
Într-adevăr, dacă toți coeficienții ecuației ![]() înmulțiți cu -1 (schimbați semnele) și reduceți toți coeficienții ecuației cu 2, obțineți aceeași ecuație: .
înmulțiți cu -1 (schimbați semnele) și reduceți toți coeficienții ecuației cu 2, obțineți aceeași ecuație: .
Al doilea caz când liniile sunt paralele:
Două drepte sunt paralele dacă și numai dacă coeficienții lor la variabile sunt proporționali: ![]() , dar.
, dar.
Ca exemplu, luați în considerare două linii drepte. Verificăm proporționalitatea coeficienților corespunzători pentru variabilele: ![]()
Cu toate acestea, este clar că.
Și al treilea caz, când liniile se intersectează:
Două drepte se intersectează dacă și numai dacă coeficienții lor ai variabilelor NU sunt proporționali, adică NU există o asemenea valoare a „lambda” încât egalitățile să fie îndeplinite ![]()
Deci, pentru linii drepte vom compune un sistem: ![]()
Din prima ecuație rezultă că , iar din a doua ecuație: , prin urmare, sistemul este inconsecvent(fara solutii). Astfel, coeficienții la variabile nu sunt proporționali.
Concluzie: liniile se intersectează
În problemele practice, se poate folosi schema de soluție tocmai considerată. Apropo, este foarte asemănător cu algoritmul de verificare a coliniarității vectorilor, pe care l-am luat în considerare în lecție. Conceptul de (non)dependență liniară a vectorilor. Baza vectorială. Dar există un pachet mai civilizat:
Exemplul 1
A descoperi aranjament reciproc direct: 
Soluţie pe baza studiului vectorilor de direcție ai liniilor drepte:
a) Din ecuații găsim vectorii de direcție ai dreptelor: ![]() .
.
, deci vectorii nu sunt coliniari și liniile se intersectează.
Pentru orice eventualitate, voi pune o piatră cu indicatori la răscruce:
Restul sar peste piatra si merg mai departe, direct catre Kashchei cel fara de moarte =)
b) Aflați vectorii de direcție ai dreptelor: ![]()
Liniile au același vector de direcție, ceea ce înseamnă că sunt fie paralele, fie aceleași. Aici determinantul nu este necesar.
Evident, coeficienții necunoscutelor sunt proporționale, în timp ce .
Să aflăm dacă egalitatea este adevărată: ![]()
În acest fel,
c) Aflați vectorii de direcție ai dreptelor: ![]()
Să calculăm determinantul, compus din coordonatele acestor vectori: ![]() , prin urmare, vectorii de direcție sunt coliniari. Liniile sunt fie paralele, fie coincid.
, prin urmare, vectorii de direcție sunt coliniari. Liniile sunt fie paralele, fie coincid.
Factorul de proporționalitate „lambda” este ușor de văzut direct din raportul vectorilor de direcție coliniară. Cu toate acestea, poate fi găsit și prin coeficienții ecuațiilor înșiși: ![]() .
.
Acum să aflăm dacă egalitatea este adevărată. Ambii termeni liberi sunt zero, deci:
Valoarea rezultată satisface această ecuație (orice număr o satisface în general).
Astfel, liniile coincid.
Răspuns:
Foarte curând vei învăța (sau chiar ai învățat deja) să rezolvi problema luată în considerare verbal, literal, în câteva secunde. În acest sens, nu văd niciun motiv pentru care să ofer ceva decizie independentă, este mai bine să puneți o altă cărămidă importantă în fundația geometrică:
Cum se desenează o linie paralelă cu una dată?
Pentru ignorarea acestui lucru cea mai simplă sarcină pedepsește aspru pe privighetoarea tâlharul.
Exemplul 2
Linia dreaptă este dată de ecuația . Scrieți o ecuație pentru o dreaptă paralelă care trece prin punct.
Soluţie: Notează linia necunoscută cu litera . Ce spune condiția despre ea? Linia trece prin punct. Și dacă liniile sunt paralele, atunci este evident că vectorul de direcție al dreptei „ce” este potrivit și pentru construirea dreptei „de”.
Scoatem vectorul direcție din ecuație:
Răspuns:
Geometria exemplului pare simplă: 
Verificarea analitică constă în următorii pași:
1) Verificăm ca liniile să aibă același vector de direcție (dacă ecuația dreptei nu este simplificată corespunzător, atunci vectorii vor fi coliniari).
2) Verificați dacă punctul satisface ecuația rezultată.
Verificarea analitică în cele mai multe cazuri este ușor de efectuat oral. Priviți cele două ecuații și mulți dintre voi vă vor da seama rapid cum liniile sunt paralele fără nici un desen.
Exemplele de auto-rezolvare astăzi vor fi creative. Pentru că mai trebuie să concurezi cu Baba Yaga, iar ea, știi, este o iubitoare de tot felul de ghicitori.
Exemplul 3
Scrieți o ecuație pentru o dreaptă care trece printr-un punct paralel cu dreapta dacă
Există o modalitate rațională și nu foarte rațională de a rezolva. Cel mai scurtătură- la sfarsitul lectiei.
Am lucrat puțin cu linii paralele și vom reveni la ele mai târziu. Cazul liniilor coincidente este de puțin interes, așa că să luăm în considerare o problemă care vă este bine cunoscută din programa școlară:
Cum se află punctul de intersecție a două drepte?
Dacă drept ![]() se intersectează în punctul , atunci coordonatele sale sunt soluția sisteme de ecuații liniare
se intersectează în punctul , atunci coordonatele sale sunt soluția sisteme de ecuații liniare ![]()
Cum să găsiți punctul de intersecție al liniilor? Rezolvați sistemul.
În sănătatea ta semnificația geometrică a sistemului celor doi ecuatii lineare cu două necunoscute sunt două drepte care se intersectează (cel mai adesea) pe un plan.
Exemplul 4
Aflați punctul de intersecție al dreptelor
Soluţie: Există două moduri de rezolvare - grafic și analitic.
Calea grafică este să trageți pur și simplu liniile date și să aflați punctul de intersecție direct din desen: 
Iată punctul nostru de vedere: . Pentru a verifica, ar trebui să înlocuiți coordonatele sale în fiecare ecuație a unei linii drepte, acestea ar trebui să se potrivească atât acolo, cât și acolo. Cu alte cuvinte, coordonatele unui punct sunt soluția sistemului. De fapt, am considerat o modalitate grafică de a rezolva sisteme de ecuații liniare cu două ecuații, două necunoscute.
Metoda grafică, desigur, nu este rea, dar există dezavantaje vizibile. Nu, ideea nu este că elevii de clasa a VII-a decid astfel, ideea este că va dura timp să faci un desen corect și EXACT. În plus, unele linii nu sunt atât de ușor de construit, iar punctul de intersecție în sine poate fi undeva în al treizecilea regat în afara foii de caiet.
Prin urmare, este mai oportun să căutați punctul de intersecție prin metoda analitică. Să rezolvăm sistemul: 
Pentru rezolvarea sistemului s-a folosit metoda adunării în termeni a ecuațiilor. Pentru a dezvolta abilitățile relevante, vizitați lecția Cum se rezolvă un sistem de ecuații?
Răspuns:
Verificarea este banala - coordonatele punctului de intersectie trebuie sa satisfaca fiecare ecuatie a sistemului.
Exemplul 5
Aflați punctul de intersecție al dreptelor dacă acestea se intersectează.
Acesta este un exemplu de do-it-yourself. Este convenabil să împărțiți problema în mai multe etape. Analiza stării sugerează că este necesar:
1) Scrieți ecuația unei drepte.
2) Scrieți ecuația unei drepte.
3) Aflați poziția relativă a liniilor.
4) Dacă liniile se intersectează, atunci găsiți punctul de intersecție.
Dezvoltarea unui algoritm de acțiune este tipică pentru multe probleme geometrice și mă voi concentra în mod repetat asupra acestui lucru.
Soluție completăși răspunsul la sfârșitul lecției:
O pereche de pantofi nu a fost încă uzată, deoarece am ajuns la a doua secțiune a lecției:
Linii perpendiculare. Distanța de la un punct la o linie.
Unghiul dintre linii
Să începem cu un tipic și foarte sarcină importantă. În prima parte, am învățat cum să construim o linie dreaptă paralelă cu cea dată, iar acum coliba pe pulpele de pui se va întoarce la 90 de grade:
Cum se desenează o linie perpendiculară pe una dată?
Exemplul 6
Linia dreaptă este dată de ecuația . Scrieți o ecuație pentru o dreaptă perpendiculară care trece printr-un punct.
Soluţie: Se ştie prin presupunere că . Ar fi bine să găsim vectorul direcție al dreptei. Deoarece liniile sunt perpendiculare, trucul este simplu:
Din ecuație „eliminăm” vectorul normal: , care va fi vectorul de direcție al dreptei.
Compunem ecuația unei drepte printr-un punct și un vector de direcție:
Răspuns: ![]()
Să desfășurăm schița geometrică:

Hmmm... Cer portocaliu, mare portocaliu, cămilă portocalie.
Verificarea analitică a soluției:
1) Extrageți vectorii de direcție din ecuații ![]() si cu ajutorul produs scalar al vectorilor concluzionăm că dreptele sunt într-adevăr perpendiculare: .
si cu ajutorul produs scalar al vectorilor concluzionăm că dreptele sunt într-adevăr perpendiculare: .
Apropo, puteți folosi vectori normali, este și mai ușor.
2) Verificați dacă punctul satisface ecuația rezultată ![]() .
.
Verificarea, din nou, este ușor de efectuat verbal.
Exemplul 7
Aflați punctul de intersecție al dreptelor perpendiculare, dacă ecuația este cunoscută ![]() și punct.
și punct.
Acesta este un exemplu de do-it-yourself. Există mai multe acțiuni în sarcină, deci este convenabil să aranjați soluția punct cu punct.
Călătoria noastră interesantă continuă:
Distanța de la punct la linie
În fața noastră este o fâșie dreaptă a râului și sarcina noastră este să ajungem la el în cel mai scurt drum. Nu există obstacole, iar traseul cel mai optim va fi deplasarea de-a lungul perpendicularei. Adică, distanța de la un punct la o dreaptă este lungimea segmentului perpendicular.
Distanța în geometrie se notează în mod tradițional cu litera greacă „ro”, de exemplu: - distanța de la punctul „em” la linia dreaptă „de”.
Distanța de la punct la linie ![]() este exprimat prin formula
este exprimat prin formula![]()
Exemplul 8
Aflați distanța de la un punct la o linie ![]()
Soluţie: tot ce aveți nevoie este să înlocuiți cu atenție numerele în formulă și să faceți calculele:
Răspuns: ![]()
Să executăm desenul: 
Distanța găsită de la punct la linie este exact lungimea segmentului roșu. Dacă faci un desen pe hârtie în carouri la scară de 1 unitate. \u003d 1 cm (2 celule), apoi distanța poate fi măsurată cu o riglă obișnuită.
Luați în considerare o altă sarcină conform aceluiași desen:
Sarcina este de a găsi coordonatele punctului , care este simetric față de punctul în raport cu dreapta ![]() . Vă propun să efectuați acțiunile pe cont propriu, totuși, voi schița algoritmul de soluție cu rezultate intermediare:
. Vă propun să efectuați acțiunile pe cont propriu, totuși, voi schița algoritmul de soluție cu rezultate intermediare:
1) Găsiți o dreaptă care este perpendiculară pe o dreaptă.
2) Aflați punctul de intersecție al dreptelor: ![]() .
.
Ambele acțiuni sunt discutate în detaliu în această lecție.
3) Punctul este punctul de mijloc al segmentului. Cunoaștem coordonatele mijlocului și unuia dintre capete. De formule pentru coordonatele mijlocului segmentului găsi .
Nu va fi de prisos să verificați dacă distanța este și ea egală cu 2,2 unități.
Aici pot apărea dificultăți în calcule, dar în turn un microcalculator ajută foarte mult, permițându-vă să numărați fracții comune. Am sfătuit de multe ori și o să recomand din nou.
Cum se află distanța dintre două linii paralele?
Exemplul 9
Aflați distanța dintre două drepte paralele
Acesta este un alt exemplu pentru o soluție independentă. Un mic indiciu: există nenumărate moduri de a rezolva. Debriefing la sfârșitul lecției, dar mai bine încercați să ghiciți singuri, cred că ați reușit să vă împrăștiați bine ingeniozitatea.
Unghiul dintre două linii
Oricare ar fi colțul, apoi cantul: 
În geometrie, unghiul dintre două drepte este luat ca unghi MAI MIC, din care rezultă automat că nu poate fi obtuz. În figură, unghiul indicat de arcul roșu nu este considerat a fi unghiul dintre liniile care se intersectează. Și vecinul său „verde” sau orientat opus colțul purpuriu.
Dacă liniile sunt perpendiculare, atunci oricare dintre cele 4 unghiuri poate fi luat ca unghi între ele.
Cum diferă unghiurile? Orientare. În primul rând, direcția de „defilare” colțului este esențial importantă. În al doilea rând, un unghi orientat negativ este scris cu semnul minus, de exemplu, dacă .
De ce am spus asta? Se pare că te poți descurca cu conceptul obișnuit de unghi. Cert este că în formulele prin care vom găsi unghiurile se poate obține cu ușurință un rezultat negativ, iar acest lucru nu ar trebui să vă ia prin surprindere. Un unghi cu semnul minus nu este mai rău și are o semnificație geometrică foarte specifică. În desenul pentru un unghi negativ, este imperativ să indicați orientarea acestuia (în sensul acelor de ceasornic) cu o săgeată.
Cum să găsiți unghiul dintre două linii? Există două formule de lucru:
Exemplul 10
Găsiți unghiul dintre linii
Soluţieși Metoda unu
Luați în considerare două rânduri dat de ecuaţiiîn general: ![]()
Dacă drept nu perpendicular, apoi orientat unghiul dintre ele poate fi calculat folosind formula: 
Să acordăm o atenție deosebită numitorului - exact asta produs scalar vectori de direcție ai liniilor drepte:
Dacă , atunci numitorul formulei dispare, iar vectorii vor fi ortogonali, iar liniile vor fi perpendiculare. De aceea s-a făcut o rezervă cu privire la neperpendicularitatea liniilor în formulare.
Pe baza celor de mai sus, soluția este formalizată convenabil în doi pași:
1) Calculați produs scalar vectori de direcție ai liniilor drepte:
deci liniile nu sunt perpendiculare.
2) Găsim unghiul dintre drepte prin formula:

Prin utilizarea funcție inversă ușor de găsit colțul în sine. În acest caz, folosim ciudata tangentei arcului (vezi Fig. Grafice și proprietăți ale funcțiilor elementare):![]()
Răspuns: ![]()
În răspuns, indicați valoare exacta, precum și o valoare aproximativă (de preferință atât în grade, cât și în radiani) calculată cu ajutorul unui calculator.
Ei bine, minus, deci minus, e în regulă. Iată o ilustrație geometrică: 
Nu este surprinzător că unghiul s-a dovedit a fi de orientare negativă, deoarece, în starea problemei, primul număr este o linie dreaptă și „răsucirea” unghiului a început tocmai de la aceasta.
Dacă doriți cu adevărat să obțineți un unghi pozitiv, trebuie să schimbați liniile drepte, adică să luați coeficienții din a doua ecuație ![]() , și luați coeficienții din prima ecuație . Pe scurt, trebuie să începeți cu un direct
, și luați coeficienții din prima ecuație . Pe scurt, trebuie să începeți cu un direct ![]() .
.
voi fi scurt. Unghiul dintre două linii egal cu unghiulîntre vectorii lor de direcție. Astfel, dacă reușiți să găsiți coordonatele vectorilor de direcție a \u003d (x 1; y 1; z 1) și b \u003d (x 2; y 2; z 2), puteți găsi unghiul. Mai precis, cosinusul unghiului conform formulei:
Să vedem cum funcționează această formulă pe exemple specifice:
O sarcină. Punctele E și F sunt marcate în cubul ABCDA 1 B 1 C 1 D 1 - punctele mijlocii ale muchiilor A 1 B 1 și respectiv B 1 C 1. Aflați unghiul dintre liniile AE și BF.
Deoarece muchia cubului nu este specificată, setăm AB = 1. Introducem un sistem de coordonate standard: originea este în punctul A, iar axele x, y, z sunt direcționate de-a lungul AB, AD și, respectiv, AA 1 . Segmentul unitar este egal cu AB = 1. Acum să găsim coordonatele vectorilor de direcție pentru liniile noastre.
Aflați coordonatele vectorului AE. Pentru a face acest lucru, avem nevoie de punctele A = (0; 0; 0) și E = (0,5; 0; 1). Deoarece punctul E este mijlocul segmentului A 1 B 1 , coordonatele acestuia sunt egale cu media aritmetică a coordonatelor capetelor. Rețineți că originea vectorului AE coincide cu originea, deci AE = (0,5; 0; 1).
Acum să ne ocupăm de vectorul BF. În mod similar, analizăm punctele B = (1; 0; 0) și F = (1; 0,5; 1), deoarece F - mijlocul segmentului B 1 C 1 . Avem:
BF = (1 - 1; 0,5 - 0; 1 - 0) = (0; 0,5; 1).
Deci, vectorii de direcție sunt gata. Cosinusul unghiului dintre drepte este cosinusul unghiului dintre vectorii de direcție, deci avem:
O sarcină. Într-o prismă triedră regulată ABCA 1 B 1 C 1 , ale cărei toate muchiile sunt egale cu 1, punctele D și E sunt marcate - punctele mijlocii ale muchiilor A 1 B 1 și, respectiv, B 1 C 1. Aflați unghiul dintre dreptele AD și BE.
Introducem un sistem de coordonate standard: originea este în punctul A, axa x este îndreptată de-a lungul AB, z - de-a lungul AA 1 . Îndreptăm axa y astfel încât planul OXY să coincidă cu planul ABC. Segmentul unitar este egal cu AB = 1. Aflați coordonatele vectorilor de direcție pentru liniile dorite.
Mai întâi, să găsim coordonatele vectorului AD. Luați în considerare punctele: A = (0; 0; 0) și D = (0,5; 0; 1), deoarece D - mijlocul segmentului A 1 B 1 . Deoarece începutul vectorului AD coincide cu originea, obținem AD = (0,5; 0; 1).
Acum să găsim coordonatele vectorului BE. Punctul B = (1; 0; 0) este ușor de calculat. Cu punctul E - mijlocul segmentului C 1 B 1 - puțin mai complicat. Avem:
Rămâne de găsit cosinusul unghiului:

O sarcină. Într-o prismă hexagonală regulată ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , ale cărei toate muchiile sunt egale cu 1, punctele K și L sunt marcate - punctele mijlocii ale muchiilor A 1 B 1 și B 1 C 1, respectiv. Aflați unghiul dintre liniile AK și BL.
Introducem un sistem de coordonate standard pentru o prismă: plasăm originea coordonatelor în centrul bazei inferioare, direcționăm axa x de-a lungul FC, axa y prin punctele medii ale segmentelor AB și DE și axa z. vertical în sus. Segmentul unitar este din nou egal cu AB = 1. Să scriem coordonatele punctelor de interes pentru noi:

Punctele K și L sunt punctele mijlocii ale segmentelor A 1 B 1 și respectiv B 1 C 1, deci coordonatele lor se găsesc prin media aritmetică. Cunoscând punctele, găsim coordonatele vectorilor de direcție AK și BL:
Acum să găsim cosinusul unghiului:

O sarcină. In dreapta piramida patruunghiulara SABCD, ale căror margini sunt egale cu 1, punctele E și F sunt marcate - punctele de mijloc ale laturilor SB și, respectiv, SC. Aflați unghiul dintre liniile AE și BF.
Introducem un sistem de coordonate standard: originea este în punctul A, axele x și y sunt direcționate de-a lungul AB și, respectiv, AD, iar axa z este îndreptată vertical în sus. Segmentul unitar este egal cu AB = 1.
Punctele E și F sunt punctele mijlocii ale segmentelor SB și SC, deci coordonatele lor se găsesc ca medie aritmetică a capetelor. Notăm coordonatele punctelor de interes pentru noi:
A = (0; 0; 0); B = (1; 0; 0)
Cunoscând punctele, găsim coordonatele vectorilor de direcție AE și BF:
Coordonatele vectorului AE coincid cu coordonatele punctului E, deoarece punctul A este originea. Rămâne de găsit cosinusul unghiului:




