Găsirea unei anumite soluții la ecuații diferențiale liniare. Ecuații diferențiale de ordinul întâi
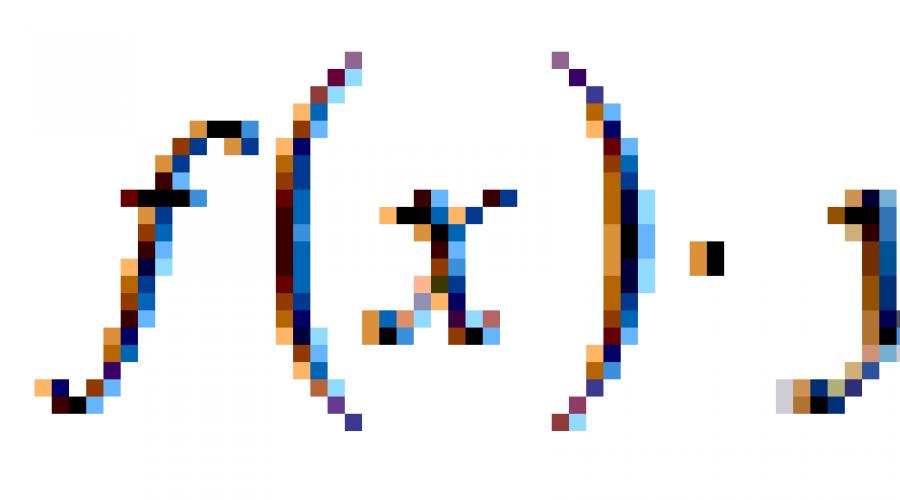
Citeste si
O ecuație diferențială este o ecuație care include o funcție și una sau mai multe dintre derivatele acesteia. În majoritatea problemelor practice, funcțiile sunt mărimi fizice, derivatele corespund ratelor de modificare a acestor mărimi, iar ecuația determină relația dintre ele.
Acest articol discută metode de rezolvare a unor tipuri de ecuații diferențiale obișnuite, ale căror soluții pot fi scrise sub forma functii elementare , adică funcții polinomiale, exponențiale, logaritmice și trigonometrice, precum și funcțiile lor inverse. Multe dintre aceste ecuații apar în viața reală, deși majoritatea celorlalte ecuații diferențiale nu pot fi rezolvate prin aceste metode, iar pentru ele răspunsul este scris ca funcții speciale sau serii de puteri, sau găsit prin metode numerice.
Pentru a înțelege acest articol, trebuie să cunoașteți calculul diferențial și integral, precum și să aveți o anumită înțelegere a derivatelor parțiale. De asemenea, se recomandă cunoașterea elementelor de bază ale algebrei liniare aplicate ecuațiilor diferențiale, în special ecuațiilor diferențiale de ordinul doi, deși cunoașterea calculului diferențial și integral este suficientă pentru a le rezolva.
Informații preliminare
- Ecuatii diferentiale au o clasificare extinsă. Acest articol vorbește despre ecuații diferențiale obișnuite, adică despre ecuații care includ o funcție a unei variabile și derivatele acesteia. Ecuațiile diferențiale obișnuite sunt mult mai ușor de înțeles și de rezolvat decât ecuații cu diferențe parțiale, care includ funcții ale mai multor variabile. Acest articol nu ia în considerare ecuațiile diferențiale parțiale, deoarece metodele de rezolvare a acestor ecuații sunt de obicei determinate de forma lor specifică.
- Mai jos sunt câteva exemple de ecuații diferențiale obișnuite.
- d y d x = k y (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=ky)
- d 2 x d t 2 + k x = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)x)((\mathrm (d) )t^(2)))+kx=0)
- Mai jos sunt câteva exemple de ecuații cu diferențe parțiale.
- ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 = 0 (\displaystyle (\frac (\partial ^(2)f)(\partial x^(2)))+(\frac (\partial ^(2) )f)(\partial y^(2)))=0)
- ∂ u ∂ t − α ∂ 2 u ∂ x 2 = 0 (\displaystyle (\frac (\partial u)(\partial t))-\alpha (\frac (\partial ^(2)u)(\partial x ^(2)))=0)
- Mai jos sunt câteva exemple de ecuații diferențiale obișnuite.
- Ordin ecuația diferențială este determinată de ordinea celei mai mari derivate incluse în această ecuație. Prima dintre ecuațiile diferențiale obișnuite de mai sus este de ordinul întâi, în timp ce a doua este de ordinul al doilea. grad se numește ecuație diferențială cel mai înalt grad, la care se ridică unul dintre termenii acestei ecuații.
- De exemplu, ecuația de mai jos este de ordinul trei și puterea a doua.
- (d 3 y d x 3) 2 + d y d x = 0 (\displaystyle \left((\frac ((\mathrm (d)) )^(3)y)((\mathrm (d) )x^(3)))\ dreapta)^(2)+(\frac ((\mathrm (d) )y)((\mathrm (d) )x))=0)
- De exemplu, ecuația de mai jos este de ordinul trei și puterea a doua.
- Ecuația diferențială este ecuație diferențială liniară dacă funcția și toate derivatele ei sunt în prima putere. În caz contrar, ecuația este ecuație diferențială neliniară. Ecuațiile diferențiale liniare sunt remarcabile prin faptul că se pot face combinații liniare din soluțiile lor, care vor fi, de asemenea, soluții ale acestei ecuații.
- Mai jos sunt câteva exemple de ecuații diferențiale liniare.
- Mai jos sunt câteva exemple de ecuații diferențiale neliniare. Prima ecuație este neliniară datorită termenului sinus.
- d 2 θ d t 2 + g l sin θ = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)\theta )((\mathrm (d) )t^(2)))+( \frac (g)(l))\sin \theta =0)
- d 2 x d t 2 + (d x d t) 2 + t x 2 = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)x)((\mathrm (d) )t^(2)))+ \left((\frac ((\mathrm (d) )x)((\mathrm (d) )t))\right)^(2)+tx^(2)=0)
- Decizie comună ecuația diferențială obișnuită nu este unică, ea include constante arbitrare de integrare. În cele mai multe cazuri, numărul de constante arbitrare este egal cu ordinea ecuației. În practică, valorile acestor constante sunt determinate de date condiții inițiale, adică prin valorile funcției și derivatelor sale la x = 0. (\displaystyle x=0.) Numărul de condiții inițiale care sunt necesare pentru a găsi decizie privată ecuație diferențială, în cele mai multe cazuri este, de asemenea, egală cu ordinea acestei ecuații.
- De exemplu, acest articol va analiza rezolvarea ecuației de mai jos. Aceasta este o ecuație diferențială liniară de ordinul doi. Soluția sa generală conține două constante arbitrare. Pentru a găsi aceste constante, este necesar să se cunoască condițiile inițiale la x (0) (\displaystyle x(0))și x′ (0) . (\displaystyle x"(0).) De obicei, condițiile inițiale sunt date la punct x = 0 , (\displaystyle x=0,), deși acest lucru nu este necesar. Acest articol va analiza, de asemenea, cum să găsiți soluții speciale pentru condiții inițiale date.
- d 2 x d t 2 + k 2 x = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)x)((\mathrm (d) )t^(2)))+k^(2 )x=0)
- x (t) = c 1 cos k x + c 2 sin k x (\displaystyle x(t)=c_(1)\cos kx+c_(2)\sin kx)
- De exemplu, acest articol va analiza rezolvarea ecuației de mai jos. Aceasta este o ecuație diferențială liniară de ordinul doi. Soluția sa generală conține două constante arbitrare. Pentru a găsi aceste constante, este necesar să se cunoască condițiile inițiale la x (0) (\displaystyle x(0))și x′ (0) . (\displaystyle x"(0).) De obicei, condițiile inițiale sunt date la punct x = 0 , (\displaystyle x=0,), deși acest lucru nu este necesar. Acest articol va analiza, de asemenea, cum să găsiți soluții speciale pentru condiții inițiale date.
Pași
Partea 1
Ecuații de ordinul întâiCând utilizați acest serviciu, unele informații pot fi transferate pe YouTube.
-
Ecuații liniare de ordinul întâi. Această secțiune discută metode de rezolvare a ecuațiilor diferențiale liniare de ordinul întâi în cazuri generale și speciale, când unii termeni sunt egali cu zero. Să ne prefacem că y = y (x) , (\displaystyle y=y(x),) p (x) (\displaystyle p(x))și q (x) (\displaystyle q(x)) sunt functii X . (\displaystyle x.)
D y d x + p (x) y = q (x) (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))+p(x)y=q(x ))
P (x) = 0. (\displaystyle p(x)=0.) Conform uneia dintre principalele teoreme analiză matematică, integrala derivatei unei funcții este și ea o funcție. Astfel, este suficient să integrezi ecuația pentru a-i găsi soluția. Trebuie remarcat însă că la calcul integrală nedefinită apare o constantă arbitrară.
- y (x) = ∫ q (x) d x (\displaystyle y(x)=\int q(x)(\mathrm (d) )x)
Q (x) = 0. (\displaystyle q(x)=0.) Folosim metoda separarea variabilelor. În acest caz, diferite variabile sunt transferate în diferite părți ale ecuației. De exemplu, puteți transfera toți membrii de la y (\displaystyle y)într-unul, și toți membrii cu x (\displaystyle x) de cealaltă parte a ecuației. De asemenea, membrii pot fi mutați d x (\displaystyle (\mathrm (d) )x)și d y (\displaystyle (\mathrm (d) )y), care sunt incluse în expresiile derivatelor, cu toate acestea, trebuie amintit că aceasta este doar o convenție, care este convenabilă atunci când se diferențiază functie complexa. O discuție despre acești termeni, care se numesc diferențiale, este în afara domeniului de aplicare al acestui articol.
- Mai întâi, trebuie să mutați variabilele pe părțile opuse ale semnului egal.
- 1 y d y = − p (x) d x (\displaystyle (\frac (1)(y))(\mathrm (d) )y=-p(x)(\mathrm (d) )x)
- Integram ambele părți ale ecuației. După integrare, pe ambele părți apar constante arbitrare, care pot fi transferate în partea dreaptă a ecuației.
- ln y = ∫ − p (x) d x (\displaystyle \ln y=\int -p(x)(\mathrm (d) )x)
- y (x) = e - ∫ p (x) d x (\displaystyle y(x)=e^(-\int p(x)(\mathrm (d) )x))
- Exemplul 1.1.În ultimul pas, am folosit regula e a + b = e a e b (\displaystyle e^(a+b)=e^(a)e^(b)) si inlocuit e C (\displaystyle e^(C)) pe C (\displaystyle C), deoarece este și o constantă arbitrară a integrării.
- d y d x - 2 y sin x = 0 (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))-2y\sin x=0)
- 1 2 y d y = sin x d x 1 2 ln y = - cos x + C ln y = - 2 cos x + C y (x) = C e )(\frac (1)(2y))(\ mathrm (d) )y&=\sin x(\mathrm (d) )x\\(\frac (1)(2))\ln y&=-\cos x+C\\\ln y&=-2\cos x+C\\y(x)&=Ce^(-2\cos x)\end(aliniat)))
P (x) ≠ 0 , q (x) ≠ 0. (\displaystyle p(x)\neq 0,\q(x)\neq 0.) Pentru a găsi soluția generală, am introdus factor integrator ca o funcție a x (\displaystyle x) pentru a reduce partea stângă la o derivată comună și a rezolva astfel ecuația.
- Înmulțiți ambele părți cu μ (x) (\displaystyle \mu (x))
- μ d y d x + μ p y = μ q (\displaystyle \mu (\frac ((\mathrm (d) )y)((\mathrm (d) )x))+\mu py=\mu q)
- Pentru a reduce partea stângă la o derivată comună, trebuie făcute următoarele transformări:
- d d x (μ y) = d μ d x y + μ d y d x = μ d y d x + μ p y (\displaystyle (\frac (\mathrm (d) )((\mathrm (d) )x))(\mu y)=(\ frac ((\mathrm (d) )\mu )((\mathrm (d) )x))y+\mu (\frac ((\mathrm (d) )y)((\mathrm (d) )x)) =\mu (\frac ((\mathrm (d) )y)((\mathrm (d) )x))+\mu py)
- Ultima egalitate înseamnă că d μ d x = μ p (\displaystyle (\frac ((\mathrm (d) )\mu )((\mathrm (d) )x))=\mu p). Acesta este un factor de integrare care este suficient pentru a rezolva orice ecuație liniară de ordinul întâi. Acum putem deriva o formulă pentru rezolvarea acestei ecuații în raport cu µ , (\displaystyle \mu ,) deși pentru antrenament este util să se facă toate calculele intermediare.
- μ (x) = e ∫ p (x) d x (\displaystyle \mu (x)=e^(\int p(x)(\mathrm (d) )x))
- Exemplul 1.2. LA acest exemplu se ia în considerare modul de găsire a unei anumite soluții a unei ecuații diferențiale cu condiții inițiale date.
- t d y d t + 2 y = t 2 , y (2) = 3 (\displaystyle t(\frac ((\mathrm (d) )y)((\mathrm (d) )t))+2y=t^(2) ,\quad y(2)=3)
- d y d t + 2 t y = t (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )t))+(\frac (2)(t))y=t)
- μ (x) = e ∫ p (t) d t = e 2 ln t = t 2 (\displaystyle \mu (x)=e^(\int p(t)(\mathrm (d) )t)=e ^(2\ln t)=t^(2))
- d d t (t 2 y) = t 3 t 2 y = 1 4 t 4 + C y (t) = 1 4 t 2 + C t 2 (\displaystyle (\begin(aligned)(\frac (\mathrm (d))) )((\mathrm (d) )t))(t^(2)y)&=t^(3)\\t^(2)y&=(\frac (1)(4))t^(4 )+C\\y(t)&=(\frac (1)(4))t^(2)+(\frac (C)(t^(2)))\end(aliniat)))
- 3 = y (2) = 1 + C 4 , C = 8 (\displaystyle 3=y(2)=1+(\frac (C)(4)),\quad C=8)
- y (t) = 1 4 t 2 + 8 t 2 (\displaystyle y(t)=(\frac (1)(4))t^(2)+(\frac (8)(t^(2)) ))
Rezolvarea ecuațiilor liniare de ordinul întâi (înregistrate de Intuit - National Open University). -
Ecuații neliniare de ordinul întâi. În această secțiune sunt luate în considerare metode de rezolvare a unor ecuații diferențiale neliniare de ordinul întâi. Deși nu există o metodă generală de rezolvare a unor astfel de ecuații, unele dintre ele pot fi rezolvate folosind metodele de mai jos.
D y d x = f (x , y) (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=f(x,y))
d y d x = h (x) g (y) . (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=h(x)g(y).) Dacă funcţia f (x , y) = h (x) g (y) (\displaystyle f(x,y)=h(x)g(y)) poate fi împărțit în funcții ale unei variabile, se numește o astfel de ecuație ecuație diferențială separabilă. În acest caz, puteți utiliza metoda de mai sus:- ∫ d y h (y) = ∫ g (x) d x (\displaystyle \int (\frac ((\mathrm (d) )y)(h(y)))=\int g(x)(\mathrm (d) )X)
- Exemplul 1.3.
- d y d x = x 3 y (1 + x 4) (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac (x^(3))( y(1+x^(4)))))
- ∫ y d y = ∫ x 3 1 + x 4 d x 1 2 y 2 = 1 4 ln (1 + x 4) + C y (x) = 1 2 ln (1 + x 4) + C (\displaystyle (\ începe(aliniat)\int y(\mathrm (d) )y&=\int (\frac (x^(3))(1+x^(4)))(\mathrm (d) )x\\(\ frac (1)(2))y^(2)&=(\frac (1)(4))\ln(1+x^(4))+C\\y(x)&=(\frac ( 1)(2))\ln(1+x^(4))+C\end(aliniat)))
D y d x = g (x , y) h (x , y) . (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac (g(x,y))(h(x,y))).) Să ne prefacem că g (x , y) (\displaystyle g(x, y))și h (x , y) (\displaystyle h(x, y)) sunt functii x (\displaystyle x)și y . (\displaystyle y.) Atunci ecuație diferențială omogenă este o ecuaţie în care g (\displaystyle g)și h (\displaystyle h) sunt funcții omogene acelasi grad. Adică, funcțiile trebuie să îndeplinească condiția g (α x , α y) = α k g (x , y) , (\displaystyle g(\alpha x,\alpha y)=\alpha ^(k)g(x,y),) Unde k (\displaystyle k) se numeste grad de omogenitate. Orice ecuație diferențială omogenă poate fi dată de un adecvat modificarea variabilelor (v = y / x (\displaystyle v=y/x) sau v = x / y (\displaystyle v=x/y)) pentru a converti într-o ecuație cu variabile separabile.
- Exemplul 1.4. Descrierea de mai sus a omogenității poate părea obscură. Să ne uităm la acest concept cu un exemplu.
- d y d x = y 3 - x 3 y 2 x (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac (y^(3)-x^ (3))(y^(2)x)))
- Pentru început, trebuie remarcat faptul că această ecuație este neliniară în raport cu y . (\displaystyle y.) De asemenea, vedem că în acest caz este imposibilă separarea variabilelor. Cu toate acestea, această ecuație diferențială este omogenă, deoarece atât numărătorul, cât și numitorul sunt omogene cu o putere de 3. Prin urmare, putem face o schimbare de variabile v=y/x. (\displaystyle v=y/x.)
- d y d x = y x - x 2 y 2 = v - 1 v 2 (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac (y)(x ))-(\frac (x^(2))(y^(2)))=v-(\frac (1)(v^(2))))
- y = v x , d y d x = d v d x x + v (\displaystyle y=vx,\quad (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=(\frac ((\mathrm) (d) )v)((\mathrm (d) )x))x+v)
- d v d x x = − 1 v 2 . (\displaystyle (\frac ((\mathrm (d) )v)((\mathrm (d) )x))x=-(\frac (1)(v^(2))).) Ca rezultat, avem o ecuație pentru v (\displaystyle v) cu variabile partajate.
- v (x) = − 3 log x + C 3 (\displaystyle v(x)=(\sqrt[(3)](-3\ln x+C)))
- y (x) = x − 3 ln x + C 3 (\displaystyle y(x)=x(\sqrt[(3)](-3\ln x+C)))
D y d x = p (x) y + q (x) y n . (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=p(x)y+q(x)y^(n).) Acest Ecuația diferențială Bernoulli- un tip special de ecuație neliniară de gradul I, a cărei soluție poate fi scrisă folosind funcții elementare.
- Înmulțiți ambele părți ale ecuației cu (1 - n) y - n (\displaystyle (1-n)y^(-n)):
- (1 - n) y - n d y d x = p (x) (1 - n) y 1 - n + (1 - n) q (x) (\displaystyle (1-n)y^(-n)(\frac ( (\mathrm (d) )y)((\mathrm (d) )x))=p(x)(1-n)y^(1-n)+(1-n)q(x))
- Folosim regula de diferențiere a unei funcții complexe din partea stângă și transformăm ecuația în ecuație liniară relativ y 1 - n , (\displaystyle y^(1-n),) care poate fi rezolvată prin metodele de mai sus.
- d y 1 - n d x = p (x) (1 - n) y 1 - n + (1 - n) q (x) (\displaystyle (\frac ((\mathrm (d) )y^(1-n)) ((\mathrm (d) )x))=p(x)(1-n)y^(1-n)+(1-n)q(x))
M (x, y) + N (x, y) d y d x = 0. (\displaystyle M(x,y)+N(x,y)(\frac ((\mathrm (d) )y)((\mathrm) (d) )x))=0.) Acest ecuația diferențială totală. Este necesar să găsiți așa-numitul funcție potențială φ (x , y) , (\displaystyle \varphi (x,y),), care îndeplinește condiția d φ d x = 0. (\displaystyle (\frac ((\mathrm (d) )\varphi )((\mathrm (d) )x))=0.)
- Pentru a îndeplini această condiție, este necesar să aveți derivat total. Derivata totală ia în considerare dependența de alte variabile. Pentru a calcula derivata totală φ (\displaystyle \varphi ) pe x , (\displaystyle x,) presupunem că y (\displaystyle y) poate depinde și de X . (\displaystyle x.)
- d φ d x = ∂ φ ∂ x + ∂ φ ∂ y d y d x (\displaystyle (\frac ((\mathrm (d))\varphi )((\mathrm (d) )x))=(\frac (\partial \varphi) )(\partial x))+(\frac (\partial \varphi )(\partial y))(\frac ((\mathrm (d) )y)((\mathrm (d) )x)))
- Compararea termenilor ne oferă M (x , y) = ∂ φ ∂ x (\displaystyle M(x,y)=(\frac (\partial \varphi)(\partial x)))și N (x, y) = ∂ φ ∂ y . (\displaystyle N(x,y)=(\frac (\partial \varphi)(\partial y)).) Acesta este un rezultat tipic pentru ecuațiile cu mai multe variabile, unde derivatele mixte ale funcțiilor netede sunt egale între ele. Uneori se numește acest caz teorema lui Clairaut. În acest caz, ecuația diferențială este o ecuație în diferențiale totale dacă este îndeplinită următoarea condiție:
- ∂ M ∂ y = ∂ N ∂ x (\displaystyle (\frac (\partial M)(\partial y))=(\frac (\partial N)(\partial x)))
- Metoda de rezolvare a ecuațiilor în diferențiale totale este similară cu găsirea de funcții potențiale în prezența mai multor derivate, pe care le vom discuta pe scurt. Mai întâi ne integrăm M (\displaystyle M) pe X . (\displaystyle x.) Pentru că M (\displaystyle M) este o funcţie şi x (\displaystyle x), și y , (\displaystyle y,) la integrare, obținem o funcție incompletă φ , (\displaystyle \varphi ,) etichetat ca φ ~ (\displaystyle (\tilde (\varphi ))). Rezultatul include și dependența de y (\displaystyle y) constanta de integrare.
- φ (x, y) = ∫ M (x, y) d x = φ ~ (x, y) + c (y) (\displaystyle \varphi (x,y)=\int M(x,y)(\mathrm (d) )x=(\tilde (\varphi ))(x,y)+c(y))
- După aceea, pentru a obține c (y) (\displaystyle c(y)) puteți lua derivata parțială a funcției rezultate în raport cu y , (\displaystyle y,) egalează rezultatul N (x, y) (\displaystyle N(x, y))și să integreze. De asemenea, se poate integra primul N (\displaystyle N), și apoi luați derivata parțială în raport cu x (\displaystyle x), ceea ce ne va permite să găsim o funcție arbitrară d(x). (\displaystyle d(x).) Ambele metode sunt potrivite și, de obicei, funcția mai simplă este aleasă pentru integrare.
- N (x , y) = ∂ φ ∂ y = ∂ φ ~ ∂ y + d c d y (\displaystyle N(x,y)=(\frac (\partial \varphi)(\partial y))=(\frac (\ parțial (\tilde (\varphi )))(\partial y))+(\frac ((\mathrm (d) )c)((\mathrm (d) )y)))
- Exemplul 1.5. Puteți lua derivate parțiale și puteți verifica dacă ecuația de mai jos este o ecuație diferențială totală.
- 3 x 2 + y 2 + 2 x y d y d x = 0 (\displaystyle 3x^(2)+y^(2)+2xy(\frac ((\mathrm (d) )y)((\mathrm (d) )x) )=0)
- φ = ∫ (3 x 2 + y 2) d x = x 3 + x y 2 + c (y) ∂ φ ∂ y = N (x , y) = 2 x y + d c d y (\displaystyle (\begin(aligned)\varphi) &=\int (3x^(2)+y^(2))(\mathrm (d) )x=x^(3)+xy^(2)+c(y)\\(\frac (\partial) \varphi )(\partial y))&=N(x,y)=2xy+(\frac ((\mathrm (d) )c)((\mathrm (d) )y))\end(aligned)))
- d c d y = 0 , c (y) = C (\displaystyle (\frac ((\mathrm (d) )c)((\mathrm (d) )y))=0,\quad c(y)=C)
- x 3 + x y 2 = C (\displaystyle x^(3)+xy^(2)=C)
- Dacă ecuația diferențială nu este o ecuație diferențială totală, în unele cazuri puteți găsi un factor de integrare care vă va permite să o convertiți într-o ecuație diferențială totală. Cu toate acestea, astfel de ecuații sunt rareori utilizate în practică, și deși factorul de integrare exista, află că se întâmplă nu asa de usor, deci aceste ecuații nu sunt luate în considerare în acest articol.
Partea 2
Ecuații de ordinul doi-
Ecuații diferențiale liniare omogene cu coeficienți constanți. Aceste ecuații sunt utilizate pe scară largă în practică, astfel încât soluția lor este de o importanță capitală. În acest caz, nu vorbim despre funcții omogene, ci despre faptul că în partea dreaptă a ecuației există 0. În secțiunea următoare, vom arăta cum corespunzătoare eterogen ecuatii diferentiale. De mai jos a (\displaystyle a)și b (\displaystyle b) sunt constante.
D 2 y d x 2 + a d y d x + b y = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )x^(2)))+a(\frac ((\mathrm (d) )y)((\mathrm (d) )x))+by=0)
Ecuație caracteristică. Această ecuație diferențială este remarcabilă prin faptul că poate fi rezolvată foarte ușor dacă acordați atenție proprietăților soluțiilor sale. Din ecuație se poate observa că y (\displaystyle y) iar derivatele sale sunt proporționale între ele. Din exemplele anterioare, care au fost luate în considerare în secțiunea privind ecuațiile de ordinul întâi, știm că numai funcția exponențială are această proprietate. Prin urmare, este posibil să se prezinte ansatz(o presupunere educată) despre care va fi soluția ecuației date.
- Soluția va lua forma unei funcții exponențiale e r x , (\displaystyle e^(rx),) Unde r (\displaystyle r) este o constantă a cărei valoare trebuie găsită. Înlocuiți această funcție în ecuație și obțineți următoarea expresie
- e r x (r 2 + a r + b) = 0 (\displaystyle e^(rx)(r^(2)+ar+b)=0)
- Această ecuație indică faptul că produsul dintre o funcție exponențială și un polinom trebuie să fie zero. Se știe că exponentul nu poate fi egal cu zero pentru nicio valoare a gradului. Prin urmare, concluzionăm că polinomul este egal cu zero. Astfel, am redus problema rezolvării unei ecuații diferențiale la o problemă mult mai simplă de rezolvare a unei ecuații algebrice, care se numește ecuație caracteristică pentru o ecuație diferențială dată.
- r 2 + a r + b = 0 (\displaystyle r^(2)+ar+b=0)
- r ± = − a ± a 2 − 4 b 2 (\displaystyle r_(\pm )=(\frac (-a\pm (\sqrt (a^(2)-4b)))(2)))
- Avem două rădăcini. Deoarece această ecuație diferențială este liniară, soluția ei generală este o combinație liniară de soluții parțiale. Deoarece aceasta este o ecuație de ordinul doi, știm că aceasta este într-adevăr soluție generală și nu există altele. O justificare mai riguroasă pentru aceasta constă în teoremele privind existența și unicitatea soluției, care pot fi găsite în manuale.
- O modalitate utilă de a verifica dacă două soluții sunt liniar independente este de a calcula Wronskian. Wronskian W (\displaystyle W)- acesta este determinantul matricei, în coloanele căreia se află funcții și derivatele lor succesive. Teorema algebrei liniare afirmă că funcțiile din Wronskian sunt liniar dependente dacă Wronskianul este egal cu zero. În această secțiune, putem testa dacă două soluții sunt liniar independente, asigurându-ne că Wronskianul este diferit de zero. Wronskianul este important în rezolvarea ecuațiilor diferențiale neomogene cu coeficienți constanți prin metoda variației parametrilor.
- w = | y 1 y 2 y 1 ′ y 2 ′ | (\displaystyle W=(\begin(vmatrix)y_(1)&y_(2)\\y_(1)"&y_(2)"\end(vmatrix)))
- În ceea ce privește algebra liniară, mulțimea tuturor soluțiilor unei ecuații diferențiale date formează un spațiu vectorial a cărui dimensiune este egală cu ordinea ecuației diferențiale. În acest spațiu, se poate alege o bază din liniar independent decizii unul de la celălalt. Acest lucru este posibil datorită faptului că funcția y (x) (\displaystyle y(x)) valabil operator liniar. Derivat este o operator liniar, deoarece transformă spațiul funcțiilor diferențiabile în spațiul tuturor funcțiilor. Ecuațiile sunt numite omogene în cazurile în care pentru un operator liniar L (\displaystyle L) este necesar să se găsească o soluție la ecuație L [ y ] = 0. (\displaystyle L[y]=0.)
Să ne întoarcem acum la câteva exemple concrete. Cazul rădăcinilor multiple ale ecuației caracteristice va fi luat în considerare puțin mai târziu, în secțiunea privind reducerea ordinii.
Dacă rădăcinile r ± (\displaystyle r_(\pm )) sunt numere reale diferite, ecuația diferențială are următoarea soluție
- y (x) = c 1 e r + x + c 2 e r − x (\displaystyle y(x)=c_(1)e^(r_(+)x)+c_(2)e^(r_(-)x ))
Două rădăcini complexe. Din teorema fundamentală a algebrei rezultă că soluțiile ecuațiilor polinomiale cu coeficienți reali au rădăcini care sunt reale sau formează perechi conjugate. Prin urmare, dacă numărul complex r = α + i β (\displaystyle r=\alpha +i\beta) este rădăcina ecuației caracteristice, atunci r ∗ = α − i β (\displaystyle r^(*)=\alpha -i\beta) este și rădăcina acestei ecuații. Astfel, soluția poate fi scrisă sub formă c 1 e (α + i β) x + c 2 e (α - i β) x , (\displaystyle c_(1)e^((\alpha +i\beta)x)+c_(2)e^( (\alpha -i\beta)x),) cu toate acestea, acesta este un număr complex și este nedorit în rezolvarea problemelor practice.
- În schimb, puteți folosi Formula lui Euler e i x = cos x + i sin x (\displaystyle e^(ix)=\cos x+i\sin x), care ne permite să scriem soluția în formular funcții trigonometrice:
- e α x (c 1 cos β x + i c 1 sin β x + c 2 cos β x − i c 2 sin β x) (\displaystyle e^(\alpha x)(c_(1)\cos \ beta x+ic_(1)\sin \beta x+c_(2)\cos \beta x-ic_(2)\sin \beta x))
- Acum poți în loc să fii constant c 1 + c 2 (\displaystyle c_(1)+c_(2)) scrie c 1 (\displaystyle c_(1)), și expresia i (c 1 - c 2) (\displaystyle i(c_(1)-c_(2))) inlocuit de c 2 . (\displaystyle c_(2).) După aceea, obținem următoarea soluție:
- y (x) = e α x (c 1 cos β x + c 2 sin β x) (\displaystyle y(x)=e^(\alpha x)(c_(1)\cos \beta x+c_ (2)\sin \beta x))
- Există o altă modalitate de a scrie soluția în termeni de amplitudine și fază, care este mai potrivită pentru problemele fizice.
- Exemplul 2.1. Să găsim soluția ecuației diferențiale prezentate mai jos cu condiții inițiale date. Pentru aceasta, este necesar să luați soluția obținută, precum și derivatul său, și înlocuiți-le în condițiile inițiale, ceea ce ne va permite să determinăm constante arbitrare.
- d 2 x d t 2 + 3 d x d t + 10 x = 0 , x (0) = 1 , x ′ (0) = − 1 (\displaystyle (\frac ((\mathrm (d)) )^(2)x)(( \mathrm (d) )t^(2)))+3(\frac ((\mathrm (d) )x)((\mathrm (d) )t))+10x=0,\quad x(0) =1,\ x"(0)=-1)
- r 2 + 3 r + 10 = 0 , r ± = − 3 ± 9 − 40 2 = − 3 2 ± 31 2 i (\displaystyle r^(2)+3r+10=0,\quad r_(\pm ) =(\frac (-3\pm (\sqrt (9-40)))(2))=-(\frac (3)(2))\pm (\frac (\sqrt (31))(2) )i)
- x (t) = e − 3 t / 2 (c 1 cos 31 2 t + c 2 sin 31 2 t) (\displaystyle x(t)=e^(-3t/2)\left(c_(1) )\cos (\frac (\sqrt (31))(2))t+c_(2)\sin (\frac (\sqrt (31))(2))t\right))
- x (0) = 1 = c 1 (\displaystyle x(0)=1=c_(1))
- x ′ (t) = − 3 2 e − 3 t / 2 (c 1 cos 31 2 t + c 2 sin 31 2 t) + e − 3 t / 2 (− 31 2 c 1 sin 31 2 t + 31 2 c 2 cos 31 2 t) (\displaystyle (\begin(aligned)x"(t)&=-(\frac (3)(2))e^(-3t/2)\left(c_ (1)\cos (\frac (\sqrt (31))(2))t+c_(2)\sin (\frac (\sqrt (31))(2))t\right)\\&+e ^(-3t/2)\left(-(\frac (\sqrt (31))(2))c_(1)\sin (\frac (\sqrt (31))(2))t+(\frac ( \sqrt (31))(2))c_(2)\cos (\frac (\sqrt (31))(2))t\right)\end(aligned)))
- x ′ (0) = − 1 = − 3 2 c 1 + 31 2 c 2 , c 2 = 1 31 (\displaystyle x"(0)=-1=-(\frac (3)(2))c_( 1)+(\frac (\sqrt (31))(2))c_(2),\quad c_(2)=(\frac (1)(\sqrt (31))))
- x (t) = e − 3 t / 2 (cos 31 2 t + 1 31 sin 31 2 t) (\displaystyle x(t)=e^(-3t/2)\left(\cos (\frac (\sqrt (31))(2))t+(\frac (1)(\sqrt (31)))\sin (\frac (\sqrt (31))(2))t\dreapta))
Rezolvarea ecuațiilor diferențiale de ordinul al n-lea cu coeficienți constanți (înregistrate de Intuit - National Open University). - Soluția va lua forma unei funcții exponențiale e r x , (\displaystyle e^(rx),) Unde r (\displaystyle r) este o constantă a cărei valoare trebuie găsită. Înlocuiți această funcție în ecuație și obțineți următoarea expresie
-
Comanda de retrogradare. Reducerea ordinului este o metodă de rezolvare a ecuațiilor diferențiale atunci când se cunoaște o soluție liniar independentă. Această metodă constă în scăderea ordinii ecuației cu una, ceea ce permite rezolvarea ecuației folosind metodele descrise în secțiunea anterioară. Să fie cunoscută soluția. Ideea principală de scădere a comenzii este să găsiți o soluție în formularul de mai jos, unde este necesar să definiți funcția v (x) (\displaystyle v(x)), substituindu-l în ecuația diferențială și găsirea v(x). (\displaystyle v(x).) Să luăm în considerare modul în care reducerea ordinii poate fi utilizată pentru a rezolva o ecuație diferențială cu coeficienți constanți și rădăcini multiple.
Rădăcini multiple ecuație diferențială omogenă cu coeficienți constanți. Reamintim că o ecuație de ordinul doi trebuie să aibă două soluții liniar independente. Dacă ecuația caracteristică are mai multe rădăcini, mulțimea soluțiilor nu formează un spațiu deoarece aceste soluții sunt dependente liniar. În acest caz, reducerea ordinului trebuie utilizată pentru a găsi o a doua soluție liniar independentă.
- Fie ca ecuația caracteristică să aibă mai multe rădăcini r (\displaystyle r). Presupunem că a doua soluție poate fi scrisă ca y (x) = e r x v (x) (\displaystyle y(x)=e^(rx)v(x)), și înlocuiți-l în ecuația diferențială. În acest caz, majoritatea termenilor, cu excepția termenului cu derivata a doua a funcției v , (\displaystyle v,) vor fi reduse.
- v ″ (x) e r x = 0 (\displaystyle v""(x)e^(rx)=0)
- Exemplul 2.2. Având în vedere următoarea ecuație, care are mai multe rădăcini r = − 4. (\displaystyle r=-4.) La înlocuire, majoritatea termenilor sunt anulați.
- d 2 y d x 2 + 8 d y d x + 16 y = 0 (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )x^(2)))+8( \frac ((\mathrm (d) )y)((\mathrm (d) )x))+16y=0)
- y = v (x) e − 4 x y ′ = v ′ (x) e − 4 x − 4 v (x) e − 4 x y ″ = v ″ (x) e − 4 x − 8 v ′ (x) e − 4 x + 16 v (x) e − 4 x (\displaystyle (\begin(aligned)y&=v(x)e^(-4x)\\y"&=v"(x)e^(-4x) )-4v(x)e^(-4x)\\y""&=v""(x)e^(-4x)-8v"(x)e^(-4x)+16v(x)e^ (-4x)\end(aliniat)))
- v ″ e − 4 x − 8 v ′ e − 4 x + 16 v e − 4 x + 8 v ′ e − 4 x − 32 v e − 4 x + 16 v e − 4 x = 0 (\displaystyle (\begin(aligned) )v""e^(-4x)&-(\cancel (8v"e^(-4x)))+(\cancel (16ve^(-4x)))\\&+(\cancel (8v"e ^(-4x)))-(\cancel (32ve^(-4x)))+(\cancel (16ve^(-4x)))=0\end(aligned)))
- Ca și ansatz-ul nostru pentru o ecuație diferențială cu coeficienți constanți, în acest caz numai derivata a doua poate fi egală cu zero. Integram de doua ori si obtinem expresia dorita pt v (\displaystyle v):
- v (x) = c 1 + c 2 x (\displaystyle v(x)=c_(1)+c_(2)x)
- Atunci soluția generală a unei ecuații diferențiale cu coeficienți constanți, dacă ecuația caracteristică are mai multe rădăcini, se poate scrie în forma următoare. Pentru comoditate, vă puteți aminti că pentru a obține independența liniară, este suficient să înmulțiți pur și simplu al doilea termen cu x (\displaystyle x). Acest set de soluții este liniar independent și astfel am găsit toate soluțiile acestei ecuații.
- y (x) = (c 1 + c 2 x) e r x (\displaystyle y(x)=(c_(1)+c_(2)x)e^(rx))
D 2 y d x 2 + p (x) d y d x + q (x) y = 0. (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )x^( 2)))+p(x)(\frac ((\mathrm (d) )y)((\mathrm (d) )x))+q(x)y=0.) Reducerea comenzii este aplicabilă dacă soluția este cunoscută y 1 (x) (\displaystyle y_(1)(x)), care poate fi găsit sau dat în enunțul problemei.
- Cautam o solutie in formular y (x) = v (x) y 1 (x) (\displaystyle y(x)=v(x)y_(1)(x))și conectați-l în această ecuație:
- v ″ y 1 + 2 v ′ y 1 ′ + p (x) v ′ y 1 + v (y 1 ″ + p (x) y 1 ′ + q (x)) = 0 (\displaystyle v""y_( 1)+2v"y_(1)"+p(x)v"y_(1)+v(y_(1)""+p(x)y_(1)"+q(x))=0)
- Pentru că y 1 (\displaystyle y_(1)) este o soluție a ecuației diferențiale, toți termenii cu v (\displaystyle v) se micsoreaza. Drept urmare, rămâne ecuație liniară de ordinul întâi. Pentru a vedea acest lucru mai clar, haideți să schimbăm variabilele w (x) = v′ (x) (\displaystyle w(x)=v"(x)):
- y 1 w ′ + (2 y 1 ′ + p (x) y 1) w = 0 (\displaystyle y_(1)w"+(2y_(1)"+p(x)y_(1))w=0 )
- w (x) = exp (∫ (2 y 1 ′ (x) y 1 (x) + p (x)) d x) (\displaystyle w(x)=\exp \left(\int \left((\) frac (2y_(1)"(x))(y_(1)(x)))+p(x)\dreapta)(\mathrm (d) )x\dreapta))
- v (x) = ∫ w (x) d x (\displaystyle v(x)=\int w(x)(\mathrm (d) )x)
- Dacă integralele pot fi calculate, obținem soluția generală ca o combinație de funcții elementare. În caz contrar, soluția poate fi lăsată în formă integrală.
- Fie ca ecuația caracteristică să aibă mai multe rădăcini r (\displaystyle r). Presupunem că a doua soluție poate fi scrisă ca y (x) = e r x v (x) (\displaystyle y(x)=e^(rx)v(x)), și înlocuiți-l în ecuația diferențială. În acest caz, majoritatea termenilor, cu excepția termenului cu derivata a doua a funcției v , (\displaystyle v,) vor fi reduse.
-
Ecuația Cauchy-Euler. Ecuația Cauchy-Euler este un exemplu de ecuație diferențială de ordinul doi cu variabile coeficienți, care are soluții exacte. Această ecuație este folosită în practică, de exemplu, pentru a rezolva ecuația Laplace în coordonate sferice.
X 2 d 2 y d x 2 + a x d y d x + b y = 0 (\displaystyle x^(2)(\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )x^(2) ))+ax(\frac ((\mathrm (d) )y)((\mathrm (d) )x))+by=0)
Ecuație caracteristică. După cum puteți vedea, în această ecuație diferențială, fiecare termen conține un factor de putere, al cărui grad este egal cu ordinul derivatei corespunzătoare.
- Astfel, se poate încerca să caute o soluție în formă y (x) = x n , (\displaystyle y(x)=x^(n),) unde să definească n (\displaystyle n), așa cum căutam o soluție sub forma unei funcții exponențiale pentru o ecuație diferențială liniară cu coeficienți constanți. După diferențiere și înlocuire, obținem
- x n (n 2 + (a - 1) n + b) = 0 (\displaystyle x^(n)(n^(2)+(a-1)n+b)=0)
- Pentru a folosi ecuația caracteristică, trebuie să presupunem că x ≠ 0 (\displaystyle x\neq 0). Punct x = 0 (\displaystyle x=0) numit punct singular regulat ecuație diferențială. Astfel de puncte sunt importante atunci când se rezolvă ecuații diferențiale folosind serii de puteri. Această ecuație are două rădăcini, care pot fi diferite și reale, multiple sau complexe conjugate.
- n ± = 1 - a ± (a - 1) 2 - 4 b 2 (\displaystyle n_(\pm )=(\frac (1-a\pm (\sqrt ((a-1)^(2)-4b) )))(2)))
Două rădăcini reale diferite. Dacă rădăcinile n ± (\displaystyle n_(\pm )) sunt reale și diferite, atunci soluția ecuației diferențiale are următoarea formă:
- y (x) = c 1 x n + + c 2 x n − (\displaystyle y(x)=c_(1)x^(n_(+))+c_(2)x^(n_(-)))
Două rădăcini complexe. Dacă ecuaţia caracteristică are rădăcini n ± = α ± β i (\displaystyle n_(\pm )=\alpha \pm \beta i), soluția este o funcție complexă.
- Pentru a transforma soluția într-o funcție reală, facem o schimbare de variabile x = e t , (\displaystyle x=e^(t),) acesta este t = ln x , (\displaystyle t=\ln x,)și folosiți formula lui Euler. Acțiuni similare au fost efectuate mai devreme la definirea constantelor arbitrare.
- y (t) = e α t (c 1 e β i t + c 2 e - β i t) (\displaystyle y(t)=e^(\alpha t)(c_(1)e^(\beta it)+ c_(2)e^(-\beta it)))
- Atunci soluția generală poate fi scrisă ca
- y (x) = x α (c 1 cos (β ln x) + c 2 sin (β ln x)) (\displaystyle y(x)=x^(\alpha )(c_(1)\ cos(\beta \ln x)+c_(2)\sin(\beta \ln x)))
Rădăcini multiple. Pentru a obține o a doua soluție liniar independentă, este necesar să reduceți din nou ordinea.
- Este nevoie de un pic de calcul, dar principiul este același: înlocuim y = v (x) y 1 (\displaystyle y=v(x)y_(1))într-o ecuație a cărei primă soluție este y 1 (\displaystyle y_(1)). După reduceri, se obține următoarea ecuație:
- v ″ + 1 x v ′ = 0 (\displaystyle v""+(\frac (1)(x))v"=0)
- Aceasta este o ecuație liniară de ordinul întâi în raport cu v′ (x) . (\displaystyle v"(x).) Soluția lui este v (x) = c 1 + c 2 ln x . (\displaystyle v(x)=c_(1)+c_(2)\ln x.) Astfel, soluția poate fi scrisă în forma următoare. Este destul de ușor de reținut - pentru a obține a doua soluție liniar independentă, aveți nevoie doar de un termen suplimentar cu ln x (\displaystyle \ln x).
- y (x) = x n (c 1 + c 2 ln x) (\displaystyle y(x)=x^(n)(c_(1)+c_(2)\ln x))
- Astfel, se poate încerca să caute o soluție în formă y (x) = x n , (\displaystyle y(x)=x^(n),) unde să definească n (\displaystyle n), așa cum căutam o soluție sub forma unei funcții exponențiale pentru o ecuație diferențială liniară cu coeficienți constanți. După diferențiere și înlocuire, obținem
-
Ecuații diferențiale liniare neomogene cu coeficienți constanți. Ecuațiile neomogene au forma L [ y (x) ] = f (x) , (\displaystyle L=f(x),) Unde f (x) (\displaystyle f(x))- așa-zisul membru gratuit. Conform teoriei ecuațiilor diferențiale, soluția generală a acestei ecuații este o suprapunere decizie privată y p (x) (\displaystyle y_(p)(x))și solutie suplimentara y c (x) . (\displaystyle y_(c)(x).) Totuși, în acest caz, o soluție anume nu înseamnă o soluție dată de condițiile inițiale, ci mai degrabă o soluție care se datorează prezenței neomogenității (membru liber). Soluția complementară este soluția ecuației omogene corespunzătoare în care f (x) = 0. (\displaystyle f(x)=0.) Soluția generală este o suprapunere a acestor două soluții, deoarece L [ y p + y c ] = L [ y p ] + L [ y c ] = f (x) (\displaystyle L=L+L=f(x)), și de când L [ y c ] = 0 , (\displaystyle L=0,) o astfel de suprapunere este într-adevăr o soluție generală.
D 2 y d x 2 + a d y d x + b y = f (x) (\displaystyle (\frac ((\mathrm (d)) )^(2)y)((\mathrm (d) )x^(2)))+a (\frac ((\mathrm (d) )y)((\mathrm (d) )x))+by=f(x))
Metoda coeficienților nedeterminați. Metoda coeficienților nedeterminați este utilizată în cazurile în care termenul liber este o combinație de exponențial, trigonometric, hiperbolic sau funcții de putere. Doar aceste funcții sunt garantate a avea un număr finit de derivate liniar independente. În această secțiune, vom găsi o soluție particulară a ecuației.
- Comparați termenii din f (x) (\displaystyle f(x)) cu termeni în ignorarea factorilor constanţi. Sunt posibile trei cazuri.
- Nu există membri identici.În acest caz, o soluție specială y p (\displaystyle y_(p)) va fi o combinație liniară de termeni din y p (\displaystyle y_(p))
- f (x) (\displaystyle f(x)) conţine membru x n (\displaystyle x^(n)) si un membru din y c , (\displaystyle y_(c),) Unde n (\displaystyle n) este zero sau un întreg pozitiv, iar acest termen corespunde unei singure rădăcini a ecuației caracteristice.În acest caz y p (\displaystyle y_(p)) va consta dintr-o combinație a funcției x n + 1 h (x) , (\displaystyle x^(n+1)h(x),) derivatele sale liniar independente, precum și alți termeni f (x) (\displaystyle f(x))și derivatele lor liniar independente.
- f (x) (\displaystyle f(x)) conţine membru h (x) , (\displaystyle h(x),) care este o lucrare x n (\displaystyle x^(n)) si un membru din y c , (\displaystyle y_(c),) Unde n (\displaystyle n) este egal cu 0 sau un număr întreg pozitiv, iar acestui termen îi corespunde multiplu rădăcina ecuației caracteristice.În acest caz y p (\displaystyle y_(p)) este o combinație liniară a funcției x n + s h (x) (\displaystyle x^(n+s)h(x))(Unde s (\displaystyle s)- multiplicitatea rădăcinii) și derivatele sale liniar independente, precum și alți membri ai funcției f (x) (\displaystyle f(x))și derivatele sale liniar independente.
- Să scriem y p (\displaystyle y_(p)) ca o combinație liniară a termenilor de mai sus. Datorită acestor coeficienți într-o combinație liniară, această metodă se numește „metoda coeficienților nedeterminați”. La apariţia celor cuprinse în y c (\displaystyle y_(c)) membrii lor pot fi aruncați din cauza prezenței constantelor arbitrare în Y c . (\displaystyle y_(c).) După aceea înlocuim y p (\displaystyle y_(p))într-o ecuație și echivalează termeni similari.
- Determinăm coeficienții. În această etapă, se obține un sistem de ecuații algebrice, care de obicei poate fi rezolvat fără probleme speciale. Soluția acestui sistem face posibilă obținerea y p (\displaystyle y_(p))și astfel rezolvăți ecuația.
- Exemplul 2.3. Considerăm o ecuație diferențială neomogenă al cărei termen liber conține un număr finit de derivate liniar independente. O soluție particulară a unei astfel de ecuații poate fi găsită prin metoda coeficienților nedeterminați.
- d 2 y d t 2 + 6 y = 2 e 3 t − cos 5 t (\displaystyle (\frac ((\mathrm (d) )^(2)y)((\mathrm (d) )t^(2) ))+6y=2e^(3t)-\cos 5t)
- y c (t) = c 1 cos 6 t + c 2 sin 6 t (\displaystyle y_(c)(t)=c_(1)\cos (\sqrt (6))t+c_(2)\sin (\sqrt(6))t)
- y p (t) = A e 3 t + B cos 5 t + C sin 5 t (\displaystyle y_(p)(t)=Ae^(3t)+B\cos 5t+C\sin 5t)
- 9 A e 3 t − 25 B cos 5 t − 25 C sin 5 t + 6 A e 3 t + 6 B cos 5 t + 6 C sin 5 t = 2 e 3 t − cos 5 t ( \displaystyle (\begin(aligned)9Ae^(3t)-25B\cos 5t&-25C\sin 5t+6Ae^(3t)\\&+6B\cos 5t+6C\sin 5t=2e^(3t)-\ cos 5t\end(aliniat)))
- ( 9 A + 6 A = 2 , A = 2 15 − 25 B + 6 B = − 1 , B = 1 19 − 25 C + 6 C = 0 , C = 0 (\displaystyle (\begin(cases)9A+ 6A) =2,&A=(\dfrac (2)(15))\\-25B+6B=-1,&B=(\dfrac (1)(19))\\-25C+6C=0,&C=0 \ sfârșitul (cazurile)))
- y (t) = c 1 cos 6 t + c 2 sin 6 t + 2 15 e 3 t + 1 19 cos 5 t (\displaystyle y(t)=c_(1)\cos (\sqrt (6) ))t+c_(2)\sin (\sqrt (6))t+(\frac (2)(15))e^(3t)+(\frac (1)(19))\cos 5t)
Metoda Lagrange. Metoda Lagrange, sau metoda de variație a constantelor arbitrare, este o metodă mai generală de rezolvare a ecuațiilor diferențiale neomogene, mai ales în cazurile în care termenul liber nu conține un număr finit de derivate liniar independente. De exemplu, cu membri gratuiti bronz x (\displaystyle \tan x) sau x − n (\displaystyle x^(-n)) pentru a găsi o anumită soluție, este necesar să folosiți metoda Lagrange. Metoda Lagrange poate fi folosită chiar și pentru a rezolva ecuații diferențiale cu coeficienți variabili, deși în acest caz, cu excepția ecuației Cauchy-Euler, este mai rar folosită, deoarece soluția suplimentară nu este de obicei exprimată în termeni de funcții elementare.
- Să presupunem că soluția are următoarea formă. Derivata sa este dată în a doua linie.
- y (x) = v 1 (x) y 1 (x) + v 2 (x) y 2 (x) (\displaystyle y(x)=v_(1)(x)y_(1)(x)+v_ (2)(x)y_(2)(x))
- y ′ = v 1 ′ y 1 + v 1 y 1 ′ + v 2 ′ y 2 + v 2 y 2 ′ (\displaystyle y"=v_(1)"y_(1)+v_(1)y_(1) „+v_(2)”y_(2)+v_(2)y_(2)”)
- Întrucât soluția propusă conține Două cantități necunoscute, este necesar să se impună adiţional condiție. Alegem această condiție suplimentară în următoarea formă:
- v 1 ′ y 1 + v 2 ′ y 2 = 0 (\displaystyle v_(1)"y_(1)+v_(2)"y_(2)=0)
- y ′ = v 1 y 1 ′ + v 2 y 2 ′ (\displaystyle y"=v_(1)y_(1)"+v_(2)y_(2)")
- y ″ = v 1 ′ y 1 ′ + v 1 y 1 ″ + v 2 ′ y 2 ′ + v 2 y 2 ″ (\displaystyle y""=v_(1)"y_(1)"+v_(1) y_(1)""+v_(2)"y_(2)"+v_(2)y_(2)"")
- Acum putem obține a doua ecuație. După înlocuirea și redistribuirea membrilor, puteți grupa membrii cu v 1 (\displaystyle v_(1)) si membrii din v 2 (\displaystyle v_(2)). Acești termeni sunt anulați deoarece y 1 (\displaystyle y_(1))și y 2 (\displaystyle y_(2)) sunt soluții ale ecuației omogene corespunzătoare. Ca rezultat, obținem următorul sistem de ecuații
- v 1 ′ y 1 + v 2 ′ y 2 = 0 v 1 ′ y 1 ′ + v 2 ′ y 2 ′ = f (x) (\displaystyle (\begin(aligned)v_(1))"y_(1)+ v_(2)"y_(2)&=0\\v_(1)"y_(1)"+v_(2)"y_(2)"&=f(x)\\\end(aliniat)))
- Acest sistem poate fi transformat într-o ecuație matriceală de formă A x = b , (\displaystyle A(\mathbf (x) )=(\mathbf (b) ),) a cărui soluție este x = A − 1 b . (\displaystyle (\mathbf (x) )=A^(-1)(\mathbf (b) ).) Pentru matrice 2 × 2 (\displaystyle 2\times 2) matricea inversă se găsește prin împărțirea la determinant, permutarea elementelor diagonale și inversarea semnului elementelor în afara diagonalei. De fapt, determinantul acestei matrice este un Wronskian.
- (v 1 ′ v 2 ′) = 1 W (y 2 ′ − y 2 − y 1 ′ y 1) (0 f (x)) (\displaystyle (\begin(pmatrix)v_(1)"\\v_( 2)"\end(pmatrix))=(\frac (1)(W))(\begin(pmatrix)y_(2)"&-y_(2)\\-y_(1)"&y_(1)\ end(pmatrix))(\begin(pmatrix)0\\f(x)\end(pmatrix)))
- Expresii pentru v 1 (\displaystyle v_(1))și v 2 (\displaystyle v_(2)) sunt enumerate mai jos. Ca și în metoda reducerii ordinului, în acest caz apare o constantă arbitrară în timpul integrării, care include o soluție suplimentară în soluția generală a ecuației diferențiale.
- v 1 (x) = − ∫ 1 W f (x) y 2 (x) d x (\displaystyle v_(1)(x)=-\int (\frac (1)(W))f(x)y_( 2)(x)(\mathrm (d) )x)
- v 2 (x) = ∫ 1 W f (x) y 1 (x) d x (\displaystyle v_(2)(x)=\int (\frac (1)(W))f(x)y_(1) (x)(\mathrm (d) )x)
Prelegerea Universității Naționale Deschise Intuit intitulată „Ecuații diferențiale lineare de ordinul n-a cu coeficienți constanți”. - Comparați termenii din f (x) (\displaystyle f(x)) cu termeni în ignorarea factorilor constanţi. Sunt posibile trei cazuri.
Uz practic
Ecuațiile diferențiale stabilesc o relație între o funcție și una sau mai multe dintre derivatele sale. Deoarece astfel de relații sunt atât de comune, ecuațiile diferențiale au găsit o aplicație largă într-o mare varietate de domenii și, deoarece trăim în patru dimensiuni, aceste ecuații sunt adesea ecuații diferențiale în privat derivate. Această secțiune discută unele dintre cele mai importante ecuații de acest tip.
- Creștere și decădere exponențială. dezintegrare radioactivă. Interes compus. Viteza reacțiilor chimice. Concentrația de medicamente în sânge. Creștere nelimitată a populației. Legea Newton-Richmann. În lumea reală, există multe sisteme în care rata de creștere sau decădere la un moment dat este proporțională cu cantitatea de acest moment timp sau poate fi bine aproximat de model. Acest lucru se datorează faptului că soluția acestei ecuații diferențiale, funcția exponențială, este una dintre cele mai importante funcții din matematică și alte științe. Mai general, în condiții de creștere controlată a populației, sistemul poate include termeni suplimentari care limitează creșterea. În ecuația de mai jos, constanta k (\displaystyle k) poate fi mai mare sau mai mică decât zero.
- d y d x = k x (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=kx)
- Vibrații armonice. Atât în mecanica clasică, cât și în cea cuantică, oscilatorul armonic este unul dintre cele mai importante sisteme fizice datorită simplității și aplicației sale largi pentru aproximarea sistemelor mai complexe precum un pendul simplu. În mecanica clasică, oscilațiile armonice sunt descrise printr-o ecuație care leagă poziția unui punct material de accelerația sa prin legea lui Hooke. În acest caz, pot fi luate în considerare și forțele de amortizare și de antrenare. În expresia de mai jos x ˙ (\displaystyle (\punct (x)))- derivată în timp a x , (\displaystyle x,) β (\displaystyle \beta) este un parametru care descrie forța de amortizare, ω 0 (\displaystyle \omega _(0))- frecvența unghiulară a sistemului, F (t) (\displaystyle F(t)) este o forță motrice dependentă de timp. Oscilatorul armonic este prezent și în circuitele oscilatoare electromagnetice, unde poate fi implementat cu o precizie mai mare decât în sistemele mecanice.
- x ¨ + 2 β x ˙ + ω 0 2 x = F (t) (\displaystyle (\ddot (x))+2\beta (\dot (x))+\omega _(0)^(2)x =F(t))
- Ecuația Bessel. Ecuația diferențială Bessel este utilizată în multe domenii ale fizicii, inclusiv soluția ecuației de undă, ecuația Laplace și ecuația Schrödinger, în special în prezența simetriei cilindrice sau sferice. Această ecuație diferențială de ordinul doi cu coeficienți variabili nu este o ecuație Cauchy-Euler, deci soluțiile sale nu pot fi scrise ca funcții elementare. Soluțiile ecuației Bessel sunt funcțiile Bessel, care sunt bine studiate datorită faptului că sunt utilizate în multe domenii. În expresia de mai jos α (\displaystyle \alpha) este o constantă care se potrivește Ordin Funcțiile Bessel.
- x 2 d 2 y d x 2 + x d y d x + (x 2 − α 2) y = 0 (\displaystyle x^(2)(\frac ((\mathrm (d) )^(2)y)((\mathrm (d) ) )x^(2)))+x(\frac ((\mathrm (d) )y)((\mathrm (d) )x))+(x^(2)-\alpha ^(2)) y=0)
- Ecuațiile lui Maxwell. Alături de forța Lorentz, ecuațiile lui Maxwell formează baza electrodinamicii clasice. Acestea sunt patru ecuații diferențiale parțiale pentru electric E (r , t) (\displaystyle (\mathbf (E) )((\mathbf (r) ),t))și magnetice B (r , t) (\displaystyle (\mathbf (B) )((\mathbf (r) ),t)) câmpuri. În expresiile de mai jos ρ = ρ (r , t) (\displaystyle \rho =\rho ((\mathbf (r) ),t))- densitatea de încărcare, J = J (r , t) (\displaystyle (\mathbf (J) )=(\mathbf (J) )((\mathbf (r) ),t)) este densitatea de curent și ϵ 0 (\displaystyle \epsilon _(0))și μ 0 (\displaystyle \mu _(0)) sunt constantele electrice și respectiv magnetice.
- ∇ ⋅ E = ρ ϵ 0 ∇ ⋅ B = 0 ∇ × E = − ∂ B ∂ t ∇ × B = μ 0 J + μ 0 ϵ 0 ∂ E ∂ t (\displaystyle (\begin(aligned)\nabla) (\mathbf (E) )&=(\frac (\rho )(\epsilon _(0)))\\\nabla \cdot (\mathbf (B) )&=0\\\nabla \times (\mathbf (E) )&=-(\frac (\partial (\mathbf (B) ))(\partial t))\\\nabla \times (\mathbf (B) )&=\mu _(0)(\ mathbf (J) )+\mu _(0)\epsilon _(0)(\frac (\partial (\mathbf (E) ))(\partial t))\end(aligned)))
- Ecuația Schrödinger.În mecanica cuantică, ecuația Schrödinger este ecuația de bază a mișcării care descrie mișcarea particulelor în conformitate cu schimbarea funcției de undă. Ψ = Ψ (r , t) (\displaystyle \Psi =\Psi ((\mathbf (r) ),t)) cu timpul. Ecuația mișcării este descrisă de comportament Hamiltonian H ^ (\displaystyle (\pălărie(H))) - operator, care descrie energia sistemului. Unul dintre exemplele binecunoscute ale ecuației Schrödinger în fizică este ecuația pentru o particulă non-relativistă, care este supusă potențialului V (r, t) (\displaystyle V((\mathbf (r)),t)). Multe sisteme sunt descrise de ecuația Schrödinger dependentă de timp, cu ecuația în partea stângă E Ψ , (\displaystyle E\Psi ,) Unde E (\displaystyle E) este energia particulei. În expresiile de mai jos ℏ (\displaystyle \hbar ) este constanta Planck redusă.
- eu ℏ ∂ Ψ ∂ t = H ^ Ψ (\displaystyle i\hbar (\frac (\partial \Psi )(\partial t))=(\hat (H))\Psi )
- i ℏ ∂ Ψ ∂ t = (− ℏ 2 2 m ∇ 2 + V (r , t)) Ψ (\displaystyle i\hbar (\frac (\partial \Psi )(\partial t))=\left(- (\frac (\hbar ^(2))(2m))\nabla ^(2)+V((\mathbf (r) ),t)\right)\Psi )
- ecuația de undă. Este imposibil să ne imaginăm fizica și tehnologia fără valuri, ele sunt prezente în toate tipurile de sisteme. În general, undele sunt descrise de ecuația de mai jos, în care u = u (r, t) (\displaystyle u=u((\mathbf (r)),t)) este funcția dorită și c (\displaystyle c)- constantă determinată experimental. d'Alembert a fost primul care a descoperit că pentru cazul unidimensional soluția ecuației de undă este orice funcția cu argument x − c t (\displaystyle x-ct), care descrie o undă arbitrară care se propagă spre dreapta. Soluția generală pentru cazul unidimensional este o combinație liniară a acestei funcții cu o a doua funcție cu un argument x + c t (\displaystyle x+ct), care descrie o undă care se propagă spre stânga. Această soluție este prezentată în a doua linie.
- ∂ 2 u ∂ t 2 = c 2 ∇ 2 u (\displaystyle (\frac (\partial ^(2)u)(\partial t^(2)))=c^(2)\nabla ^(2)u )
- u (x , t) = f (x - c t) + g (x + c t) (\displaystyle u(x,t)=f(x-ct)+g(x+ct))
- Ecuații Navier-Stokes. Ecuațiile Navier-Stokes descriu mișcarea fluidelor. Deoarece fluidele sunt prezente practic în fiecare domeniu al științei și tehnologiei, aceste ecuații sunt extrem de importante pentru predicția vremii, proiectarea aeronavelor, curenții oceanici și multe alte aplicații. Ecuațiile Navier-Stokes sunt ecuații diferențiale parțiale neliniare, iar în majoritatea cazurilor este foarte dificil de rezolvat, deoarece neliniaritatea duce la turbulențe, iar pentru a obține o soluție stabilă prin metode numerice, împărțirea în foarte mici. celulele este necesară, ceea ce necesită o putere de calcul semnificativă. În scopuri practice în hidrodinamică, metode precum media timpului sunt folosite pentru a modela curgerile turbulente. Chiar și mai multe întrebări de bază, cum ar fi existența și unicitatea soluțiilor pentru ecuațiile diferențiale parțiale neliniare, sunt probleme complexe, iar demonstrarea existenței și unicității soluțiilor pentru ecuațiile Navier-Stokes în trei dimensiuni este printre problemele matematice ale mileniului. . Mai jos sunt ecuația de curgere a fluidului incompresibil și ecuația de continuitate.
- ∂ u ∂ t + (u ⋅ ∇) u − ν ∇ 2 u = − ∇ h , ∂ ρ ∂ t + ∇ ⋅ (ρ u) = 0 (\displaystyle (\frac (\partial (\mathbf (u)))) )(\partial t))+((\mathbf (u) )\cdot \nabla)(\mathbf (u) )-\nu \nabla ^(2)(\mathbf (u) )=-\nabla h, \quad (\frac (\partial \rho )(\partial t))+\nabla \cdot (\rho (\mathbf (u) ))=0)
- Multe ecuații diferențiale pur și simplu nu pot fi rezolvate prin metodele de mai sus, în special cele menționate în ultima secțiune. Acest lucru se aplică atunci când ecuația conține coeficienți variabili și nu este o ecuație Cauchy-Euler sau când ecuația este neliniară, cu excepția câtorva cazuri foarte rare. Cu toate acestea, metodele de mai sus vă permit să rezolvați multe ecuații diferențiale importante care sunt adesea întâlnite în diferite domenii ale științei.
- Spre deosebire de diferențiere, care vă permite să găsiți derivata oricărei funcții, integrala multor expresii nu poate fi exprimată în funcții elementare. Prin urmare, nu pierdeți timpul încercând să calculați integrala acolo unde este imposibil. Uită-te la tabelul integralelor. Dacă soluția unei ecuații diferențiale nu poate fi exprimată în termeni de funcții elementare, uneori poate fi reprezentată în formă integrală, iar în acest caz nu contează dacă această integrală poate fi calculată analitic.
Avertizări
- Aspect ecuația diferențială poate induce în eroare. De exemplu, mai jos sunt două ecuații diferențiale de ordinul întâi. Prima ecuație este ușor de rezolvat folosind metodele descrise în acest articol. La prima vedere, o schimbare minoră y (\displaystyle y) pe y 2 (\displaystyle y^(2))în a doua ecuație o face neliniară și devine foarte greu de rezolvat.
- d y d x = x 2 + y (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=x^(2)+y)
- d y d x = x 2 + y 2 (\displaystyle (\frac ((\mathrm (d) )y)((\mathrm (d) )x))=x^(2)+y^(2))
Rezolvarea ecuațiilor diferențiale. Mulțumiri noastre serviciu online puteți rezolva ecuații diferențiale de orice fel și complexitate: neomogene, omogene, neliniare, liniare, de ordinul întâi, al doilea, cu sau fără variabile separabile etc. Obțineți soluția ecuațiilor diferențiale în formă analitică cu descriere detaliata. Mulți sunt interesați de: de ce este necesar să se rezolve ecuații diferențiale online? Acest tip de ecuații este foarte frecvent în matematică și fizică, unde va fi imposibil să rezolvi multe probleme fără a calcula ecuația diferențială. De asemenea, ecuațiile diferențiale sunt comune în economie, medicină, biologie, chimie și alte științe. Rezolvarea unei astfel de ecuații online vă facilitează foarte mult sarcinile, face posibilă înțelegerea mai bună a materialului și testarea dvs. Beneficiile rezolvării ecuațiilor diferențiale online. Site-ul modern de servicii matematice vă permite să rezolvați ecuații diferențiale online orice dificultăți. După cum știți, există un numar mare de tipuri de ecuații diferențiale și fiecare dintre ele are propriile metode de rezolvare. Pe serviciul nostru puteți găsi online soluția ecuațiilor diferențiale de orice ordine și tip. Pentru a obține o soluție, vă sugerăm să completați datele inițiale și să faceți clic pe butonul „Soluție”. Sunt excluse erorile în funcționarea serviciului, astfel încât puteți fi 100% sigur că ați primit răspunsul corect. Rezolvați ecuații diferențiale cu serviciul nostru. Rezolvați ecuații diferențiale online. În mod implicit, într-o astfel de ecuație, funcția y este o funcție a variabilei x. Dar vă puteți seta, de asemenea, propria desemnare a variabilei. De exemplu, dacă specificați y(t) într-o ecuație diferențială, atunci serviciul nostru va determina automat că y este o funcție a variabilei t. Ordinea întregii ecuații diferențiale va depinde de ordinea maximă a derivatei funcției prezente în ecuație. A rezolva o astfel de ecuație înseamnă a găsi funcția dorită. Serviciul nostru vă va ajuta să rezolvați ecuații diferențiale online. Nu este nevoie de mult efort din partea ta pentru a rezolva ecuația. Trebuie doar să introduceți părțile din stânga și din dreapta ale ecuației în câmpurile necesare și să faceți clic pe butonul „Soluție”. Când introduceți derivata unei funcții, este necesar să o notați cu un apostrof. În câteva secunde vei avea solutie detaliata ecuație diferențială. Serviciul nostru este absolut gratuit. Ecuații diferențiale cu variabile separabile. Dacă într-o ecuație diferențială din stânga există o expresie care depinde de y, iar pe partea dreaptă există o expresie care depinde de x, atunci o astfel de ecuație diferențială se numește cu variabile separabile. Pe partea stângă poate exista o derivată a lui y, soluția ecuațiilor diferențiale de acest fel va fi sub forma unei funcții a lui y, exprimată prin integrala părții drepte a ecuației. Dacă există o diferență a unei funcții a lui y în partea stângă, atunci ambele părți ale ecuației sunt integrate. Când variabilele dintr-o ecuație diferențială nu sunt separate, ele vor trebui împărțite pentru a obține o ecuație diferențială separată. Ecuație diferențială liniară. O ecuație diferențială se numește liniară dacă funcția și toate derivatele ei sunt de gradul întâi. Forma generală a ecuației: y'+a1(x)y=f(x). f(x) și a1(x) sunt funcții continue ale lui x. Soluția ecuațiilor diferențiale de acest tip se reduce la integrarea a două ecuații diferențiale cu variabile separate. Ordinea ecuației diferențiale. Ecuația diferențială poate fi de ordinul întâi, al doilea, al n-a. Ordinea unei ecuații diferențiale determină ordinea celei mai mari derivate conținute în ea. În serviciul nostru puteți rezolva ecuații diferențiale mai întâi online, al doilea, al treilea etc. Ordin. Soluția ecuației va fi orice funcție y=f(x), înlocuind-o în ecuație, veți obține o identitate. Procesul de găsire a unei soluții la o ecuație diferențială se numește integrare. Problema Cauchy. Dacă, pe lângă ecuația diferențială în sine, este specificată condiția inițială y(x0)=y0, atunci aceasta se numește problema Cauchy. Indicatorii y0 și x0 se adaugă la soluția ecuației și se determină valoarea unei constante arbitrare C și apoi o soluție particulară a ecuației pentru această valoare a lui C. Aceasta este soluția problemei Cauchy. Problema Cauchy se mai numește și o problemă cu condiții la limită, care este foarte comună în fizică și mecanică. Aveți și posibilitatea de a stabili problema Cauchy, adică din toate soluțiile posibile ale ecuației, alegeți una anume care îndeplinește condițiile inițiale date.
Fie deja rezolvate în raport cu derivata, fie pot fi rezolvate în raport cu derivata ![]() .
.
Rezolvarea generală a ecuațiilor diferențiale de tip pe interval X, care este dat, poate fi găsit luând integrala ambelor părți ale acestei egalități.
obține ![]() .
.
Dacă ne uităm la proprietățile integralei nedefinite, găsim soluția generală dorită:
y = F(x) + C,
Unde F(x)- unul dintre antiderivatele funcţiei f(x) intre X, A Cu este o constantă arbitrară.
Vă rugăm să rețineți că în majoritatea sarcinilor intervalul X nu indica. Aceasta înseamnă că trebuie găsită o soluție pentru toată lumea. X, pentru care și funcția dorită y, iar ecuația originală are sens.
Dacă trebuie să calculați o anumită soluție a unei ecuații diferențiale care satisface condiția inițială y(x0) = y0, apoi după calcularea integralei generale y = F(x) + C, este încă necesar să se determine valoarea constantei C=C0 folosind condiția inițială. Adică o constantă C=C0 determinată din ecuație F(x 0) + C = y 0, iar soluția particulară dorită a ecuației diferențiale va lua forma:
y = F(x) + C0.
Luați în considerare un exemplu:
Aflați soluția generală a ecuației diferențiale, verificați corectitudinea rezultatului. Să găsim o soluție particulară a acestei ecuații care să satisfacă condiția inițială .
Decizie:
După ce am integrat ecuația diferențială dată, obținem:
![]() .
.
Luăm această integrală prin metoda integrării pe părți:

Acea.,  este o soluție generală a ecuației diferențiale.
este o soluție generală a ecuației diferențiale.
Să verificăm pentru a ne asigura că rezultatul este corect. Pentru a face acest lucru, înlocuim soluția pe care am găsit-o în ecuația dată:
 .
.
Adică la  ecuația inițială se transformă într-o identitate:
ecuația inițială se transformă într-o identitate:
prin urmare, soluția generală a ecuației diferențiale a fost determinată corect.
Soluția pe care am găsit-o este soluția generală a ecuației diferențiale pentru fiecare valoare reală a argumentului X.
Rămâne de calculat o anumită soluție a EDO care ar satisface condiția inițială. Cu alte cuvinte, este necesar să se calculeze valoarea constantei Cu, la care egalitatea va fi adevărată:
 .
.
 .
.
Apoi, înlocuind C = 2în soluția generală a EDO, obținem o soluție particulară a ecuației diferențiale care satisface condiția inițială:
 .
.
Ecuație diferențială obișnuită ![]() se poate rezolva în raport cu derivata împărțind cele 2 părți ale ecuației la f(x). Această transformare va fi echivalentă dacă f(x) nu merge la zero pentru niciunul X din intervalul de integrare a ecuaţiei diferenţiale X.
se poate rezolva în raport cu derivata împărțind cele 2 părți ale ecuației la f(x). Această transformare va fi echivalentă dacă f(x) nu merge la zero pentru niciunul X din intervalul de integrare a ecuaţiei diferenţiale X.
Sunt probabile situații când, pentru unele valori ale argumentului X ∈ X funcții f(x)și g(x) se întoarce la zero în același timp. Pentru valori similare X soluția generală a ecuației diferențiale este orice funcție y, care este definit în ele, deoarece .
Dacă pentru unele valori ale argumentului X ∈ X condiția este îndeplinită, ceea ce înseamnă că în acest caz ODE nu are soluții.
Pentru toate celelalte X din interval X soluția generală a ecuației diferențiale se determină din ecuația transformată.
Să ne uităm la exemple:
Exemplul 1
Să găsim soluția generală a EDO: ![]() .
.
Decizie.
Din proprietățile funcțiilor elementare de bază, este clar că funcția de logaritm natural este definită pentru valorile nenegative ale argumentului, prin urmare, domeniul expresiei log(x+3) exista un interval X > -3 . Prin urmare, ecuația diferențială dată are sens pentru X > -3 . Cu aceste valori ale argumentului, expresiei x + 3 nu dispare, astfel încât se poate rezolva EDO în raport cu derivata împărțind cele 2 părți la x + 3.
Primim  .
.
În continuare, integrăm ecuația diferențială rezultată, rezolvată în raport cu derivata:  . Pentru a lua această integrală, folosim metoda subsumării sub semnul diferenţialului.
. Pentru a lua această integrală, folosim metoda subsumării sub semnul diferenţialului.
Ecuații diferențiale de ordinul întâi. Exemple de soluții.
Ecuații diferențiale cu variabile separabile
Ecuații diferențiale (DE). Aceste două cuvinte îl îngrozesc de obicei pe laicul obișnuit. Ecuațiile diferențiale par a fi ceva scandalos și greu de stăpânit pentru mulți studenți. Uuuuuu... ecuații diferențiale, cum aș supraviețui la toate astea?!
O astfel de opinie și o astfel de atitudine este fundamental greșită, pentru că de fapt ECUATIILE DIFERENTIALE SUNT SIMPLE SI CHIAR DISTRACTIVE. Ce trebuie să știți și să puteți învăța să rezolvați ecuații diferențiale? Pentru a studia cu succes diferențele, trebuie să fii bun la integrare și diferențiere. Cu cât subiectele sunt mai bine studiate Derivată a unei funcții a unei variabileși Integrală nedefinită, cu atât va fi mai ușor de înțeles ecuațiile diferențiale. Voi spune mai multe, dacă ai abilități de integrare mai mult sau mai puțin decente, atunci subiectul este practic stăpânit! Cu cât mai multe integrale tipuri variateștii să te decizi – cu atât mai bine. De ce? Trebuie să te integrezi mult. Și diferențiați. La fel recomand cu caldura invata sa gasesti.
În 95% din cazuri în munca de control Există 3 tipuri de ecuații diferențiale de ordinul întâi: ecuații separabile, pe care o vom trata în această lecție; ecuații omogeneși ecuații liniare neomogene. Pentru începătorii să studieze difuzoarele, vă sfătuiesc să citiți lecțiile din această secvență, iar după ce ați studiat primele două articole, nu va strica să vă consolidați abilitățile într-un atelier suplimentar - ecuaţii care se reduc la omogene.
Există și mai rare tipuri de ecuații diferențiale: ecuații în diferențiale totale, ecuații lui Bernoulli și altele. Dintre ultimele două tipuri, cele mai importante sunt ecuațiile în diferențiale totale, deoarece pe lângă acest DE, iau în considerare un material nou - integrare parțială.
Dacă mai ai doar o zi sau două, atunci pentru preparare ultra-rapidă mânca curs blitzîn format pdf.
Deci, reperele sunt setate - să mergem:
Să ne amintim mai întâi ecuațiile algebrice obișnuite. Acestea conțin variabile și numere. Cel mai simplu exemplu: . Ce înseamnă să rezolvi o ecuație obișnuită? Aceasta înseamnă să găsești set de numere care satisfac această ecuație. Este ușor de observat că ecuația copiilor are o singură rădăcină: . Pentru distracție, să facem o verificare, să înlocuim rădăcina găsită în ecuația noastră:
- se obtine egalitatea corecta, ceea ce inseamna ca solutia este gasita corect.
Difuzele sunt aranjate aproape în același mod!
Ecuație diferențială prima comandaîn general conţine:
1) variabilă independentă;
2) variabilă dependentă (funcție);
3) derivata întâi a funcției: .
În unele ecuații de ordinul 1, este posibil să nu existe „x” sau (și) „y”, dar acest lucru nu este esențial - important astfel încât în DU a fost prima derivată și nu a avut derivate de ordin superior - , etc.
Ce înseamnă ? A rezolva o ecuație diferențială înseamnă a găsi set de toate funcțiile care satisfac această ecuație. Un astfel de set de funcții are adesea forma ( este o constantă arbitrară), care este numită soluție generală a ecuației diferențiale.
Exemplul 1
Rezolvați ecuația diferențială
Muniție completă. Unde sa încep decizie?
În primul rând, trebuie să rescrieți derivatul într-o formă ușor diferită. Reamintim notația greoaie, pe care mulți dintre voi probabil l-au considerat ridicolă și inutilă. Acesta este cel care domnește în difuzoare!
În al doilea pas, să vedem dacă se poate divizarea variabilelor? Ce înseamnă separarea variabilelor? Aproximativ vorbind, pe partea stângă a trebuie să plecăm doar "jocuri", A pe drumul cel bun organiza doar x-uri. Separarea variabilelor se realizează cu ajutorul manipulărilor „școlare”: paranteze, transfer de termeni dintr-o parte în parte cu o schimbare de semn, transfer de factori de la o parte la alta conform regulii proporției etc.
Diferențiale și sunt multiplicatori completi și participanți activi la ostilități. În acest exemplu, variabilele sunt ușor separate prin factori de inversare conform regulii proporției:
Variabilele sunt separate. În partea stângă - doar "Joc", în partea dreaptă - doar "X".
Etapa următoare – integrarea ecuațiilor diferențiale. Este simplu, agățăm integrale pe ambele părți:
Desigur, trebuie luate integrale. În acest caz, acestea sunt tabelare:
După cum ne amintim, o constantă este atribuită oricărei antiderivate. Există două integrale aici, dar este suficient să scrieți constanta o dată (deoarece o constantă + o constantă este încă egală cu o altă constantă). În cele mai multe cazuri, este plasat pe partea dreaptă.
Strict vorbind, după ce integralele sunt luate, ecuația diferențială este considerată rezolvată. Singurul lucru este că „y”-ul nostru nu este exprimat prin „x”, adică soluția este prezentată în implicit formă. Soluția implicită a unei ecuații diferențiale se numește integrala generala a ecuatiei diferentiale. Adică este integrală generală.
Un răspuns în această formă este destul de acceptabil, dar există o opțiune mai bună? Să încercăm să obținem decizie comună.
Vă rog, amintiți-vă prima tehnică, este foarte comun și adesea folosit în sarcini practice: dacă un logaritm apare în partea dreaptă după integrare, atunci în multe cazuri (dar în niciun caz întotdeauna!) este de asemenea recomandabil să scrieți constanta sub logaritm.
Acesta este, ÎN LOC DEînregistrările sunt de obicei scrise ![]() .
.
De ce este nevoie de asta? Și pentru a facilita exprimarea „y”. Folosim proprietatea logaritmilor ![]() . În acest caz:
. În acest caz:
Acum logaritmii și modulele pot fi eliminate:
Funcția este prezentată explicit. Aceasta este soluția generală.
Răspuns: decizie comună: ![]() .
.
Răspunsurile la multe ecuații diferențiale sunt destul de ușor de verificat. În cazul nostru, acest lucru se face destul de simplu, luăm soluția găsită și o diferențiem:
Apoi înlocuim derivata în ecuația originală:
- se obține egalitatea corectă, ceea ce înseamnă că soluția generală satisface ecuația , care trebuia verificată.
Dând o constantă diverse sensuri, puteți obține infinit de multe decizii private ecuație diferențială. Este clar că oricare dintre funcțiile , etc. satisface ecuatia diferentiala .
Uneori se numește soluția generală familie de funcții. În acest exemplu, soluția generală ![]() - aceasta este o familie funcții liniare, sau mai bine zis, o familie de proporționalități directe.
- aceasta este o familie funcții liniare, sau mai bine zis, o familie de proporționalități directe.
După o discuție detaliată a primului exemplu, este potrivit să răspundem la câteva întrebări naive despre ecuațiile diferențiale:
1)În acest exemplu, am reușit să separăm variabilele. Este întotdeauna posibil să faci asta? Nu, nu întotdeauna. Și chiar mai des variabilele nu pot fi separate. De exemplu, în ecuații omogene de ordinul întâi trebuie înlocuit mai întâi. În alte tipuri de ecuații, de exemplu, într-o ecuație liniară neomogenă de ordinul întâi, trebuie să utilizați diverse trucuri și metode pentru a găsi o soluție generală. Ecuațiile variabile separabile pe care le considerăm în prima lecție sunt cel mai simplu tip de ecuații diferențiale.
2) Este întotdeauna posibil să se integreze o ecuație diferențială? Nu, nu întotdeauna. Este foarte ușor să vii cu o ecuație „fantezică” care nu poate fi integrată, în plus, există integrale care nu pot fi luate. Dar astfel de DE pot fi rezolvate aproximativ folosind metode speciale. D'Alembert și Cauchy garantează... ... ugh, lurkmore. Tocmai am citit multe, aproape că am adăugat "din cealaltă lume".
3) În acest exemplu, am obținut o soluție sub forma unei integrale generale ![]() . Este întotdeauna posibil să găsim o soluție generală din integrala generală, adică să exprimăm „y” într-o formă explicită? Nu, nu întotdeauna. De exemplu: . Ei bine, cum pot exprima „y” aici?! În astfel de cazuri, răspunsul trebuie scris ca o integrală generală. În plus, uneori se poate găsi o soluție generală, dar este scrisă atât de greoaie și stângace încât este mai bine să lăsați răspunsul sub forma unei integrale generale
. Este întotdeauna posibil să găsim o soluție generală din integrala generală, adică să exprimăm „y” într-o formă explicită? Nu, nu întotdeauna. De exemplu: . Ei bine, cum pot exprima „y” aici?! În astfel de cazuri, răspunsul trebuie scris ca o integrală generală. În plus, uneori se poate găsi o soluție generală, dar este scrisă atât de greoaie și stângace încât este mai bine să lăsați răspunsul sub forma unei integrale generale
4) ...poate suficient pentru moment. În primul exemplu, ne-am întâlnit încă una punct important , dar pentru a nu acoperi „manențele” cu o avalanșă de informații noi, o voi lăsa până la următoarea lecție.
Să nu ne grăbim. O altă telecomandă simplă și o altă soluție tipică:
Exemplul 2
Găsiți o anumită soluție a ecuației diferențiale care satisface condiția inițială
Decizie: după condiţia pe care se cere să se găsească soluție privată DE care satisface o condiție inițială dată. Acest tip de interogare se mai numește Problema Cauchy.
În primul rând, găsim o soluție generală. Nu există o variabilă „x” în ecuație, dar acest lucru nu ar trebui să fie jenant, principalul lucru este că are prima derivată.
Rescriem derivata în forma necesară:
Evident, variabilele pot fi împărțite, băieții la stânga, fetele la dreapta:
Integram ecuatia: ![]()
Se obține integrala generală. Aici am desenat o constantă cu o stea de accent, fapt este că foarte curând se va transforma într-o altă constantă.
Acum încercăm să convertim integrala generală într-o soluție generală (exprimați „y” în mod explicit). Ne amintim de școala veche, bună: ![]() . În acest caz:
. În acest caz:
Constanta din indicator pare cumva nu cușer, deci este de obicei coborâtă din cer pe pământ. În detaliu, se întâmplă așa. Folosind proprietatea gradelor, rescriem funcția în felul următor:
Dacă este o constantă, atunci este și o constantă, redesemnați-o cu litera:
Amintiți-vă că „demolarea” unei constante este a doua tehnică, care este adesea folosit în cursul rezolvării ecuațiilor diferențiale.
Deci solutia generala este: O familie atât de frumoasă de funcții exponențiale.
În etapa finală, trebuie să găsiți o anumită soluție care să satisfacă condiția inițială dată. Este si simplu.
Care este sarcina? Trebuie să ridic astfel de valoarea constantei pentru a satisface condiţia .
Îl poți aranja în moduri diferite, dar cel mai de înțeles, poate, va fi așa. În soluția generală, în loc de „x”, înlocuim zero, iar în loc de „y”, doi:
Acesta este,
versiune standard proiecta:
Acum înlocuim valoarea găsită a constantei în soluția generală:
– aceasta este soluția specială de care avem nevoie.
Răspuns: solutie privata:
Hai să facem o verificare. Verificarea unei anumite soluții include două etape:
În primul rând, este necesar să se verifice dacă soluția particulară găsită într-adevăr satisface condiția inițială? În loc de „x” înlocuim zero și vedem ce se întâmplă:
- da, într-adevăr, s-a obținut un deuce, ceea ce înseamnă că condiția inițială este îndeplinită.
A doua etapă este deja familiară. Luăm soluția particulară rezultată și găsim derivata:
Înlocuiți în ecuația inițială:
![]()
![]() - se obţine egalitatea corectă.
- se obţine egalitatea corectă.
Concluzie: soluția particulară este găsită corect.
Să trecem la exemple mai semnificative.
Exemplul 3
Rezolvați ecuația diferențială
Decizie: Rescriem derivata sub forma de care avem nevoie: ![]()
Evaluarea dacă variabilele pot fi separate? Poate sa. Transferăm al doilea termen în partea dreaptă cu o schimbare de semn: ![]()
Și inversăm factorii conform regulii proporției: ![]()
Variabilele sunt separate, să integrăm ambele părți: ![]()
Trebuie să te avertizez că vine ziua judecății. Daca nu ai invatat bine integrale nedefinite, a rezolvat câteva exemple, apoi nu este încotro - trebuie să le stăpânești acum.
Integrala laturii stângi este ușor de găsit, cu integrala cotangentei ne ocupăm de tehnica standard pe care am considerat-o în lecție Integrarea funcţiilor trigonometriceÎn ultimul an: ![]()
![]()
![]()
În partea dreaptă, avem un logaritm și, conform primei mele recomandări tehnice, constanta ar trebui scrisă și sub logaritm.
Acum încercăm să simplificăm integrala generală. Deoarece avem doar logaritmi, este foarte posibil (și necesar) să scăpăm de ei. Prin intermediul proprietăți cunoscute„împachetează” maxim logaritmii. Voi scrie cu mare detaliu: ![]()

Ambalajul este complet pentru a fi zdrențuit barbar: ![]()
Este posibil să exprimați „y”? Poate sa. Ambele părți trebuie să fie pătrate.
Dar nu trebuie.
Al treilea sfat tehnic: dacă pentru a obține o soluție generală trebuie să ridici la o putere sau să prinzi rădăcini, atunci În cele mai multe cazuri ar trebui să vă abțineți de la aceste acțiuni și să lăsați răspunsul sub forma unei integrale generale. Faptul este că soluția generală va arăta îngrozitor - cu rădăcini mari, semne și alte gunoi.
Prin urmare, scriem răspunsul ca o integrală generală. Este considerată o formă bună să o prezinți sub formă, adică pe partea dreaptă, dacă este posibil, lăsați doar o constantă. Nu este necesar să faceți acest lucru, dar este întotdeauna benefic să-i faceți pe plac profesorului ;-)
Răspuns: integrala generala:
! Notă: integrala generală a oricărei ecuații poate fi scrisă în mai multe moduri. Astfel, dacă rezultatul tău nu a coincis cu un răspuns cunoscut anterior, atunci asta nu înseamnă că ai rezolvat incorect ecuația.
Integrala generală este de asemenea verificată destul de ușor, principalul lucru este să poți găsi derivata unei functii definita implicit. Să diferențiem răspunsul: 
Înmulțim ambii termeni cu: 
Și împărțim la: 
Ecuația diferențială inițială a fost obținută exact, ceea ce înseamnă că integrala generală a fost găsită corect.
Exemplul 4
Găsiți o anumită soluție a ecuației diferențiale care satisface condiția inițială. Efectuați o verificare.
Acesta este un exemplu pentru decizie independentă.
Vă reamintesc că algoritmul constă din două etape:
1) găsirea unei soluții generale;
2) găsirea soluției particulare necesare.
Verificarea se efectuează și în doi pași (vezi eșantionul din Exemplul nr. 2), aveți nevoie de:
1) asigurați-vă că soluția particulară găsită satisface condiția inițială;
2) verificați dacă o anumită soluție satisface în general ecuația diferențială.
Soluție completăși răspunsul la sfârșitul lecției.
Exemplul 5
Găsiți o anumită soluție a unei ecuații diferențiale ![]() , satisfacand conditia initiala . Efectuați o verificare.
, satisfacand conditia initiala . Efectuați o verificare.
Decizie: Mai întâi, să găsim o soluție generală.Această ecuație conține deja diferențiale gata făcute și , ceea ce înseamnă că soluția este simplificată. Separarea variabilelor: 
Integram ecuatia: ![]()
Integrala din stânga este tabelară, integrala din dreapta este luată metoda de însumare a funcţiei sub semnul diferenţialului:![]()
Integrala generală a fost obținută, este posibilă exprimarea cu succes a soluției generale? Poate sa. Atârnăm logaritmi pe ambele părți. Deoarece sunt pozitive, semnele modulo sunt redundante: 
(Sper că toată lumea înțelege transformarea, astfel de lucruri ar trebui deja cunoscute)
Deci solutia generala este:
Să găsim o anumită soluție corespunzătoare condiției inițiale date.
În soluția generală, în loc de „x”, înlocuim zero și în loc de „y”, logaritmul a doi: ![]()
Design mai familiar:
Inlocuim valoarea gasita a constantei in solutia generala.
Răspuns: solutie privata:
Verificați: În primul rând, verificați dacă condiția inițială este îndeplinită:
- totul este bine.
Acum să verificăm dacă soluția particulară găsită satisface ecuația diferențială. Găsim derivata:
Să ne uităm la ecuația inițială: ![]() – se prezintă în diferențiale. Există două moduri de a verifica. Este posibil să exprimăm diferența față de derivata găsită:
– se prezintă în diferențiale. Există două moduri de a verifica. Este posibil să exprimăm diferența față de derivata găsită:
Înlocuim soluția particulară găsită și diferența rezultată în ecuația originală ![]() :
: 
Folosim identitatea logaritmică de bază: 
Se obține egalitatea corectă, ceea ce înseamnă că soluția particulară este găsită corect.
A doua modalitate de verificare este oglindită și mai familiară: din ecuație ![]() exprimă derivata, pentru aceasta împărțim toate piesele la:
exprimă derivata, pentru aceasta împărțim toate piesele la: 
Și în DE transformat înlocuim soluția particulară obținută și derivata găsită. Ca urmare a simplificărilor, ar trebui să se obțină și egalitatea corectă.
Exemplul 6
Rezolvați ecuația diferențială. Exprimați răspunsul ca o integrală generală.
Acesta este un exemplu de auto-rezolvare, soluție completă și răspuns la sfârșitul lecției.
Ce dificultăți așteaptă în rezolvarea ecuațiilor diferențiale cu variabile separabile?
1) Nu este întotdeauna evident (în special pentru un ceainic) că variabilele pot fi separate. Luați în considerare un exemplu condiționat: . Aici trebuie să scoateți factorii din paranteze: și să separați rădăcinile:. Cum să procedați în continuare este clar.
2) Dificultăți în integrarea în sine. Integrale apar adesea nu sunt cele mai simple și dacă există defecte în abilitățile de a găsi integrală nedefinită, atunci va fi dificil cu multe difuzoare. În plus, compilatorii de colecții și manuale sunt populari cu logica „deoarece ecuația diferențială este simplă, atunci cel puțin integralele vor fi mai complicate”.
3) Transformări cu o constantă. După cum toată lumea a observat, o constantă în ecuațiile diferențiale poate fi gestionată destul de liber, iar unele transformări nu sunt întotdeauna clare pentru un începător. Să ne uităm la un alt exemplu ipotetic: ![]() . În ea, este recomandabil să înmulțiți toți termenii cu 2:
. În ea, este recomandabil să înmulțiți toți termenii cu 2: ![]() . Constanta rezultată este, de asemenea, un fel de constantă, care poate fi notată prin:
. Constanta rezultată este, de asemenea, un fel de constantă, care poate fi notată prin: ![]() . Da, și deoarece există un logaritm în partea dreaptă, este recomandabil să rescrieți constanta ca o altă constantă:
. Da, și deoarece există un logaritm în partea dreaptă, este recomandabil să rescrieți constanta ca o altă constantă: ![]() .
.
Problema este că adesea nu se deranjează cu indici și folosesc aceeași literă. Ca urmare, procesul-verbal de decizie ia următoarea formă: 
Ce erezie? Iată erorile! Strict vorbind, da. Totuși, din punct de vedere de fond, nu există erori, deoarece în urma transformării unei constante variabile se obține în continuare o constantă variabilă.
Sau alt exemplu, să presupunem că în cursul rezolvării ecuației se obține o integrală generală. Acest răspuns arată urât, așa că este recomandabil să schimbați semnul fiecărui termen: ![]() . Formal, există din nou o eroare - în dreapta, ar trebui să fie scrisă . Dar este subînțeles informal că „minus ce” este încă o constantă ( care la fel de bine capătă orice valoare!), deci punerea unui „minus” nu are sens și poți folosi aceeași literă.
. Formal, există din nou o eroare - în dreapta, ar trebui să fie scrisă . Dar este subînțeles informal că „minus ce” este încă o constantă ( care la fel de bine capătă orice valoare!), deci punerea unui „minus” nu are sens și poți folosi aceeași literă.
Voi încerca să evit o abordare neglijentă și, totuși, voi pune diferiți indici pentru constante atunci când le convertesc.
Exemplul 7
Rezolvați ecuația diferențială. Efectuați o verificare.
Decizie: Această ecuație admite separarea variabilelor. Separarea variabilelor: 
Integram: 
Constanta de aici nu trebuie definită sub logaritm, deoarece nu va ieși nimic bun din ea.
Răspuns: integrala generala:
Verificați: diferențiați răspunsul (funcție implicită): 
Scăpăm de fracții, pentru aceasta înmulțim ambii termeni cu: 
S-a obținut ecuația diferențială inițială, ceea ce înseamnă că integrala generală a fost găsită corect.
Exemplul 8
Găsiți o anumită soluție pentru DE.
,
Acesta este un exemplu de do-it-yourself. Singurul indiciu este că aici obțineți o integrală generală și, mai corect, trebuie să încercați să găsiți nu o soluție anume, ci integrală privată. Soluție completă și răspuns la sfârșitul lecției.