The material metodic are scop de referință și acoperă o gamă largă de subiecte. Articolul oferă o prezentare generală a graficelor principalelor funcții elementare și ia în considerare cea mai importantă problemă - cum să construiți corect și RAPID un grafic. În cursul studierii matematicii superioare fără cunoașterea graficelor funcțiilor elementare de bază, va fi dificil, de aceea este foarte important să ne amintim cum arată graficele unei parabole, hiperbole, sinus, cosinus etc., pentru a ne aminti câteva a valorilor funcțiilor. De asemenea vom vorbi asupra unor proprietăţi ale funcţiilor de bază.

Nu pretind completitudinea și temeinicia științifică a materialelor, accentul va fi pus, în primul rând, pe practică - acele lucruri cu care trebuie să te confrunți literalmente la fiecare pas, în orice subiect de matematică superioară. Grafice pentru manechine? Se poate spune si asa.

La cererea populară din partea cititorilor cuprins pe care se poate face clic:

În plus, există un rezumat ultra-scurt pe această temă
– stăpânește 16 tipuri de diagrame studiind șase pagini!

Serios, șase, chiar și eu am fost surprins. Acest rezumat conține grafică îmbunătățită și este disponibil pentru o taxă nominală, o versiune demo poate fi vizualizată. Este convenabil să imprimați fișierul, astfel încât graficele să fie întotdeauna la îndemână. Vă mulțumim pentru susținerea proiectului!

Și începem imediat:

Cum să construiți corect axele de coordonate?

În practică, testele sunt aproape întotdeauna întocmite de către elevi în caiete separate, aliniate într-o cușcă. De ce ai nevoie de marcaje în carouri? La urma urmei, munca, în principiu, se poate face pe coli A4. Și cușca este necesară doar pentru designul de înaltă calitate și precis al desenelor.

Orice desen al unui grafic de funcții începe cu axe de coordonate.

Desenele sunt bidimensionale și tridimensionale.

Să luăm mai întâi în considerare cazul bidimensional Sistemul de coordonate carteziene:

1) Desenăm axe de coordonate. Axa se numește axa x , și axa axa y . Întotdeauna încercăm să le desenăm îngrijită și nu strâmbă. De asemenea, săgețile nu ar trebui să semene cu barba lui Papa Carlo.

2) Semnăm axele cu majuscule „x” și „y”. Nu uitați să semnați topoarele.

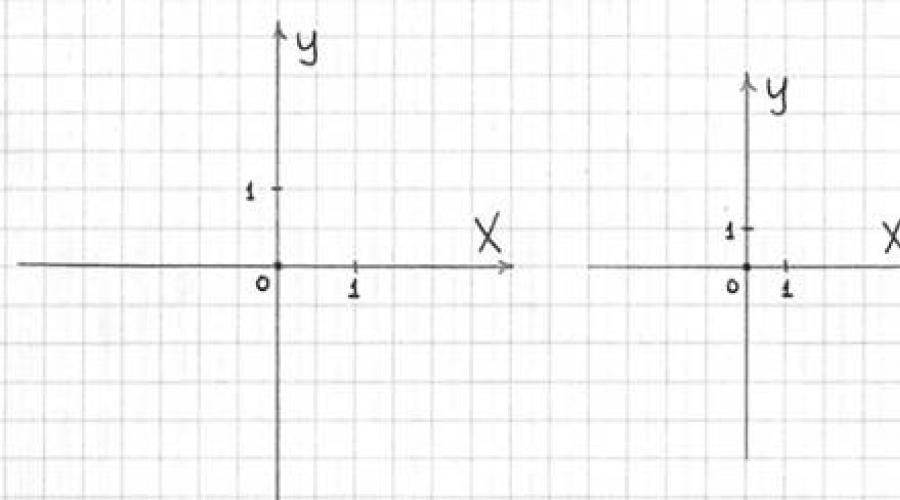
3) Setați scara de-a lungul axelor: trage zero și doi unu. Când faceți un desen, scara cea mai convenabilă și obișnuită este: 1 unitate = 2 celule (desenul din stânga) - rămâneți de ea dacă este posibil. Totuși, din când în când se întâmplă ca desenul să nu încapă pe o foaie de caiet - atunci reducem scara: 1 unitate = 1 celulă (desen din dreapta). Rareori, dar se întâmplă ca scara desenului să fie redusă (sau mărită) și mai mult

NU mâzgăliți dintr-o mitralieră... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... Căci planul de coordonate nu este un monument al lui Descartes, iar elevul nu este un porumbel. Am pus zeroși două unități de-a lungul axelor. Uneori în loc de unități, este convenabil să „detecți” alte valori, de exemplu, „două” pe axa absciselor și „trei” pe axa ordonatelor - și acest sistem (0, 2 și 3) va seta, de asemenea, grila de coordonate în mod unic.

Este mai bine să estimați dimensiunile estimate ale desenului ÎNAINTE de a fi desenat desenul.. Deci, de exemplu, dacă sarcina necesită desenarea unui triunghi cu vârfuri , , , atunci este destul de clar că scara populară 1 unitate = 2 celule nu va funcționa. De ce? Să ne uităm la subiect - aici trebuie să măsori cincisprezece centimetri în jos și, evident, desenul nu se va potrivi (sau abia se va potrivi) pe o foaie de caiet. Prin urmare, selectăm imediat o scară mai mică 1 unitate = 1 celulă.

Apropo, despre centimetri și celule de notebook. Este adevărat că sunt 15 centimetri în 30 de celule de notebook? Măsurați într-un caiet pentru dobândă 15 centimetri cu o riglă. În URSS, poate că acest lucru a fost adevărat ... Este interesant de remarcat că, dacă măsurați acești centimetri pe orizontală și pe verticală, atunci rezultatele (în celule) vor fi diferite! Strict vorbind, caietele moderne nu sunt în carouri, ci dreptunghiulare. Poate părea o prostie, dar desenarea, de exemplu, a unui cerc cu o busolă în astfel de situații este foarte incomod. Sincer să fiu, în astfel de momente începi să te gândești la corectitudinea tovarășului Stalin, care a fost trimis în lagăre pentru muncă de hack în producție, ca să nu mai vorbim de industria auto autohtonă, căderea avioanelor sau exploziile centralelor electrice.

Apropo de calitate, sau o scurtă recomandare despre papetărie. Până în prezent, majoritatea notebook-urilor sunt la vânzare, cuvinte rele ca să nu mai zic, rahat complet. Din motivul că se udă, și nu numai de la pixurile cu gel, ci și de la pixurile cu bilă! Economisiți pe hârtie. Pentru degajare lucrări de control Recomand să folosiți caietele fabricii de celuloză și hârtie din Arkhangelsk (18 coli, cușcă) sau Pyaterochka, deși este mai scump. Este indicat să alegeți un pix cu gel, chiar și cea mai ieftină reumplere chinezească cu gel este mult mai bună decât un pix, care fie untează, fie rupe hârtia. Singurul pix „competitiv” din memoria mea este Erich Krause. Ea scrie clar, frumos și stabil - fie cu tulpina plină, fie cu una aproape goală.

În plus: viziunea unui sistem de coordonate dreptunghiular prin ochii geometriei analitice este acoperită în articol Dependența liniară (non) a vectorilor. Baza vectorială, informații detaliate despre sferturile de coordonate pot fi găsite în al doilea paragraf al lecției Inegalități liniare.

carcasă 3D

Aici este aproape la fel.

1) Desenăm axe de coordonate. Standard: aplica axa – îndreptat în sus, ax – îndreptat spre dreapta, ax – în jos spre stânga strict la un unghi de 45 de grade.

2) Semnăm axele.

3) Setați scara de-a lungul axelor. Scala de-a lungul axei - de două ori mai mică decât scara de-a lungul celorlalte axe. De asemenea, rețineți că, în desenul din dreapta, am folosit un "serif" non-standard de-a lungul axei (această posibilitate a fost deja menționată mai sus). Din punctul meu de vedere, este mai precis, mai rapid și mai plăcut din punct de vedere estetic - nu trebuie să căutați mijlocul celulei la microscop și să „sculptați” unitatea până la origine.

Când faceți din nou un desen 3D - acordați prioritate scalei
1 unitate = 2 celule (desen din stânga).

Pentru ce sunt toate aceste reguli? Regulile sunt acolo pentru a fi încălcate. Ce am de gând să fac acum. Cert este că desenele ulterioare ale articolului vor fi făcute de mine în Excel, iar axele de coordonate vor arăta incorect din punct de vedere design corect. Aș putea desena toate graficele cu mâna, dar este foarte înfricoșător să le desenezi, deoarece Excel este reticent să le deseneze mult mai precis.

Grafice și proprietăți de bază ale funcțiilor elementare

Funcția liniară este dată de ecuația . Graficul funcției liniare este direct. Pentru a construi o linie dreaptă este suficient să cunoaștem două puncte.

Exemplul 1

Trasează funcția. Să găsim două puncte. Este avantajos să alegeți zero ca unul dintre puncte.

Daca atunci

Luăm un alt punct, de exemplu, 1.

Daca atunci

La pregătirea sarcinilor, coordonatele punctelor sunt de obicei rezumate într-un tabel:

Și valorile însele sunt calculate oral sau pe o schiță, calculator.

S-au găsit două puncte, să desenăm:

Când întocmim un desen, semnăm întotdeauna grafica.

Nu va fi de prisos să amintim cazuri speciale ale unei funcții liniare:

Observați cum am plasat legendele, semnăturile nu trebuie să fie ambigue atunci când studiați desenul. În acest caz, a fost foarte nedorit să se pună o semnătură lângă punctul de intersecție al liniilor sau în dreapta jos între grafice.

1) O funcție liniară de forma () se numește proporționalitate directă. De exemplu, . Graficul de proporționalitate directă trece întotdeauna prin origine. Astfel, construcția unei linii drepte este simplificată - este suficient să găsiți un singur punct.

2) O ecuație de formă definește o linie dreaptă paralelă cu axa, în special, axa însăși este dată de ecuație. Graficul funcției este construit imediat, fără a găsi niciun punct. Adică, intrarea trebuie înțeleasă după cum urmează: „y este întotdeauna egal cu -4, pentru orice valoare a lui x”.

3) O ecuație de formă definește o linie dreaptă paralelă cu axa, în special, axa însăși este dată de ecuație. Graficul funcției este de asemenea construit imediat. Intrarea ar trebui să fie înțeleasă după cum urmează: „x este întotdeauna, pentru orice valoare a lui y, egal cu 1”.

Unii se vor întreba, ei bine, de ce să-ți amintești de clasa a VI-a?! Așa este, poate așa, doar în anii de practică am întâlnit o duzină bună de studenți care au fost derutați de sarcina de a construi un grafic ca sau .

Desenarea unei linii drepte este cea mai comună acțiune atunci când faceți desene.

Linia dreaptă este discutată în detaliu în cursul geometriei analitice, iar cei care doresc pot consulta articolul Ecuația unei drepte pe un plan.

Graficul funcției patratice, graficul funcției cubice, graficul polinomial

Parabolă. Programa funcţie pătratică () este o parabolă. Luați în considerare celebrul caz:

Să ne amintim câteva proprietăți ale funcției.

Deci, soluția ecuației noastre: - în acest punct se află vârful parabolei. De ce este așa poate fi învățat din articolul teoretic despre derivată și din lecția despre extremele funcției. Între timp, calculăm valoarea corespunzătoare a lui „y”:

Deci vârful este în punct

Acum găsim alte puncte, în timp ce folosim cu nerăbdare simetria parabolei. Trebuie remarcat faptul că funcția – nu este chiar, dar, cu toate acestea, nimeni nu a anulat simetria parabolei.

În ce ordine să găsim punctele rămase, cred că va fi clar din masa finală:

Acest algoritm de construcție poate fi numit în mod figurat „navetă” sau principiul „înainte și înapoi” cu Anfisa Cehova.

Hai sa facem un desen:

Din graficele luate în considerare, îmi vine în minte o altă caracteristică utilă:

Pentru o funcție pătratică () următoarele este adevărată:

Dacă , atunci ramurile parabolei sunt îndreptate în sus.

Dacă , atunci ramurile parabolei sunt îndreptate în jos.

Cunoașterea aprofundată a curbei poate fi obținută la lecția Hiperbola și parabolă.

Parabola cubică este dată de funcția . Iată un desen cunoscut de la școală:

Enumerăm principalele proprietăți ale funcției

Graficul funcției

Reprezintă una dintre ramurile parabolei. Hai sa facem un desen:

Principalele proprietăți ale funcției:

În acest caz, axa este asimptotă verticală pentru graficul hiperbolei la .

Va fi o MARE greșeală dacă, la întocmirea unui desen, din neglijență, vei permite graficului să se intersecteze cu asimptota.

De asemenea, limite unilaterale, spune-ne că o hiperbolă nelimitat de susși nelimitat de jos.

Să explorăm funcția la infinit: , adică dacă începem să ne mișcăm de-a lungul axei la stânga (sau la dreapta) la infinit, atunci „jocurile” vor fi un pas subțire infinit de aproape se apropie de zero și, în consecință, de ramurile hiperbolei infinit de aproape se apropie de ax.

Deci axa este asimptotă orizontală pentru graficul funcției, dacă „x” tinde spre plus sau minus infinit.

Funcția este ciudat, ceea ce înseamnă că hiperbola este simetrică față de origine. Acest fapt este evident din desen, în plus, poate fi ușor verificat analitic: .

Graficul unei funcții de forma () reprezintă două ramuri ale unei hiperbole.

Dacă , atunci hiperbola este situată în primul și al treilea cadran de coordonate(vezi poza de mai sus).

Dacă , atunci hiperbola este situată în al doilea și al patrulea cadran de coordonate.

Nu este dificil de analizat regularitatea specificată a locului de reședință al hiperbolei din punctul de vedere al transformărilor geometrice ale graficelor.

Exemplul 3

Construiți ramura dreaptă a hiperbolei

Folosim metoda de construcție punctual, în timp ce este avantajos să selectăm valorile astfel încât să se împartă complet:

Hai sa facem un desen:

Nu va fi dificil să construiți ramura stângă a hiperbolei, aici ciudatenia funcției va ajuta doar. Aproximativ, în tabelul de construcție punctual, adăugați mental un minus fiecărui număr, puneți punctele corespunzătoare și desenați a doua ramură.

Informații geometrice detaliate despre linia considerată pot fi găsite în articolul Hiperbolă și parabolă.

Graficul unei funcții exponențiale

În acest paragraf, voi lua în considerare imediat funcția exponențială, deoarece în problemele de matematică superioară în 95% din cazuri este exponentul care apare.

Vă reamintesc că - acesta este un număr irațional: , acesta va fi necesar la construirea unui grafic, pe care, de fapt, îl voi construi fără ceremonie. Trei puncte probabil suficient:

Să lăsăm graficul funcției deocamdată, despre asta mai târziu.

Principalele proprietăți ale funcției:

În principiu, graficele funcțiilor arată la fel etc.

Trebuie să spun că al doilea caz este mai puțin frecvent în practică, dar apare, așa că am simțit că este necesar să îl includ în acest articol.

Graficul unei funcții logaritmice

Se consideră o funcție cu logaritm natural.
Să facem un desen în linie:

Dacă ați uitat ce este un logaritm, vă rugăm să consultați manualele școlare.

Principalele proprietăți ale funcției:

Domeniu:

Interval de valori: .

Funcția nu este limitată de mai sus: , deși încet, dar ramura logaritmului urcă până la infinit.
Să examinăm comportamentul funcției aproape de zero din dreapta: . Deci axa este asimptotă verticală pentru graficul funcției cu „x” tinde spre zero în dreapta.

Asigurați-vă că cunoașteți și rețineți valoarea tipică a logaritmului: .

În principiu, graficul logaritmului de la bază arată la fel: , , ( logaritm zecimalîn baza 10), etc. În același timp, cu cât baza este mai mare, cu atât graficul va fi mai plat.

Nu vom lua în considerare cazul, nu-mi amintesc când ultima data a construit un grafic pe o astfel de bază. Da, iar logaritmul pare a fi un invitat foarte rar în problemele de matematică superioară.

În încheierea paragrafului, voi mai spune un fapt: Funcția exponențială și funcția logaritmicăsunt două funcții reciproc inverse. Dacă te uiți îndeaproape la graficul logaritmului, poți vedea că acesta este același exponent, doar că este situat puțin diferit.

Grafice ale funcțiilor trigonometrice

Cum începe chinul trigonometric la școală? Corect. Din sinus

Să diagramăm funcția

Această linie se numește sinusoid.

Vă reamintesc că „pi” este un număr irațional:, iar în trigonometrie orbiește în ochi.

Principalele proprietăți ale funcției:

Această funcție este periodic cu punct. Ce înseamnă? Să ne uităm la tăietură. În stânga și în dreapta acestuia, exact aceeași bucată a graficului se repetă la nesfârșit.

Domeniu: , adică pentru orice valoare a lui „x” există o valoare sinus.

Interval de valori: . Funcția este limitat: , adică toate „jocurile” stau strict în segmentul .
Acest lucru nu se întâmplă: sau, mai exact, se întâmplă, dar aceste ecuații nu au o soluție.

Limite și continuitate

Seturi

Sub mulți este înțeles ca un ansamblu de obiecte omogene. Obiectele care formează o mulțime sunt numite elemente sau puncte acest set. Seturile denotă litere mari, iar elementele lor sunt inline. În cazul în care un A este un element al ansamblului A, apoi notația AÎ A. În cazul în care un b nu este un element al setului A, atunci se scrie asa: b Ï A. O mulţime care nu conţine un singur element se numeşte mulţime goală şi se notează astfel: Ø.

Dacă setul B este format dintr-o parte din elementele multimii A sau coincide cu ea, apoi setul B numit subset mulţimi şi denotă BÌ A.

Cele două seturi sunt numite egal dacă sunt formate din aceleaşi elemente.

Asociere doua seturi Ași B se numeste multime C, constând din toate elementele aparținând cel puțin unuia dintre mulțimile: C=AÈ B.

trecere doua seturi Ași B se numeste multime C, constând din toate elementele aparținând fiecăruia dintre mulțimile date: C=AÇ B.

diferență seturi Ași B se numeste multime E A, care nu aparțin setului B: .

Supliment seturi AÌ B se numeste multime C, format din toate elementele setului B, neaparținând A.

Se numesc multimi ale caror elemente sunt numere reale numeric:

în care NÌ ZÌ QÌ R, euÌ Rși R=euÈ Q.

Multe X, ale cărui elemente satisfac inegalitatea se numește segment(segment) și notat cu [ A; b]; inegalitate A<X<b – intervalși se notează cu () ; inegalități și - semiintervaleși sunt notate cu și, respectiv. De asemenea, de multe ori trebuie să vă ocupați de intervale infinite și semiintervale: , , , și . Este convenabil să le sunați pe toate la intervale .

Interval, adică setul de puncte care satisfac inegalitatea (unde), se numeste -vecinatatea punctului A.

Conceptul de funcție. Principalele proprietăți ale funcției

Dacă fiecare element X seturi X un singur element este potrivit y seturi Y, apoi spunem asta pe platou X dat funcţie y=f(X). în care X numit variabila independenta sau argument, A y – variabilă dependentă sau funcţie, A f reprezintă legea corespondenței. Multe X numit domeniul definirii funcții, ci setul Y – gamă funcții.

Există mai multe moduri de a defini funcțiile.

1) Metoda analitica - functia este data printr-o formula a formei y=f(X).

2) Metoda tabulară - funcția este definită de un tabel care conține valorile argumentului și valorile funcției corespunzătoare y=f(X).

3) Metoda grafica - imaginea graficului functiei, i.e. set de puncte ( X; y) din planul de coordonate, ale cărui abscise reprezintă valorile argumentului, iar ordonatele sunt valorile corespunzătoare ale funcției y=f(X).

4) Metoda verbală - funcția este descrisă de regula compilării ei. De exemplu, funcția Dirichlet ia valoarea 1 dacă X este un număr rațional și 0 dacă X este un număr irațional.

Se disting următoarele proprietăți principale ale funcțiilor.

1 Par și impar Funcţie y=f(X) se numește chiar, dacă pentru orice valoare X din domeniul definirii sale, f(–X)=f(X), și ciudat, dacă f(–X)=–f(X). Dacă niciuna dintre ecuațiile de mai sus nu este valabilă, atunci y=f(X) se numește functia generala. Graficul unei funcții pare este simetric față de axă Oi, iar graficul unei funcții impare este simetric față de origine.

2 Monotonie Funcţie y=f(X) se numește crescând (în scădere) pe interval X, dacă valoare mai mare unui argument din acest interval îi corespunde o valoare mai mare (mai mică) a funcției. Lăsa X 1 ,X 2 О X, X 2 >X unu . Apoi funcția crește pe interval X, dacă f(X 2)>f(X 1) și scade dacă f(X 2)<f(X 1).

Alături de funcțiile crescătoare și descrescătoare, sunt luate în considerare funcțiile nedescrescătoare și necrescătoare. Funcția este numită nedescrescătoare (necrescătoare), dacă X 1 ,X 2 О X, X 2 >X 1 inegalitatea f(X 2)≥f(X 1) (f(X 2)≤f(X 1)).

Funcțiile crescătoare și descrescătoare, precum și funcțiile necrescătoare și nedescrescătoare, se numesc monotone.

3 Limitat Funcţie y=f(X) se numește mărginit pe interval X dacă există un număr atât de pozitiv M>0, ce | f(X)|≤M pentru oricine XÎ X. În caz contrar, funcția se numește nelimitată pe X.

4 Periodicitatea Funcţie y=f(X) se numește periodic cu punct T≠0 dacă pentru oricare Xîn afara domeniului de aplicare f(X+T)=f(X). În cele ce urmează, o perioadă va fi înțeleasă ca fiind cea mai mică perioadă pozitivă a unei funcții.

Funcția este numită explicit, dacă este dat de o formulă de formă y=f(X). Dacă funcția este dată de ecuație F(X, y)=0 nu este permis în raport cu variabila dependentă y, atunci se numește implicit.

Lăsa y=f(X) este o funcție a variabilei independente definite pe mulțime X cu raza de actiune Y. Să potrivim fiecare yÎ Y sens unic XÎ X, la care f(X)=y.Apoi functia rezultata X=φ (y) definite pe platou Y cu raza de actiune X, se numește versoși notat y=f –1 (X). Grafice reciproc funcții inverse sunt simetrice față de bisectoarea primului și al treilea sferturi de coordonate.

Lasă funcția y=f(u) este o funcție a variabilei u definite pe platou U cu raza de actiune Y, și variabila u la rândul său este o funcție u=φ (X) definite pe platou X cu raza de actiune U. Apoi dat pe platou X funcţie y=f(φ (X)) se numește functie complexa (compunerea funcțiilor, suprapunerea funcțiilor, funcția unei funcții).

Funcții elementare

Principalele funcții elementare includ:

• functie de putere y=x n; y=x-nși y=X 1/ n;
• functie exponentiala y=un x;
• funcţie logaritmică y=log un x;
• funcții trigonometrice y=păcat X, y= cos X, y=tg Xși y=ctg X;
• funcții trigonometrice inverse y= arcsin X, y= arccos X, y=arctg Xși y=arctg X.

Din funcțiile elementare de bază se pot obține funcții noi folosind operații algebrice și suprapunerea funcțiilor.

Funcțiile construite din funcții elementare de bază folosind un număr finit de operații algebrice și un număr finit de operații de suprapunere se numesc elementar.

Algebric este o funcție în care se efectuează un număr finit de operații algebrice asupra argumentului. Funcțiile algebrice includ:

întreaga funcție rațională (polinom sau polinom)

funcție rațională fracțională (raportul a două polinoame)

funcție irațională (dacă operațiunile pe argument includ extragerea rădăcinilor).

Se numește orice funcție non-algebrică transcendent. Funcțiile transcendentale includ funcții exponențiale, logaritmice, trigonometrice, trigonometrice inverse.

Pentru a înțelege acest subiect, luați în considerare funcția afișată pe grafic // Să arătăm cum graficul funcției vă permite să determinați proprietățile sale.

Analizăm proprietățile unei funcții folosind un exemplu

Domeniul de aplicare al funcției este yavl. interval [ 3,5; 5.5].

Domeniul funcției yavl. interval [ 1; 3].

1. La x = -3, x = - 1, x = 1,5, x = 4,5, valoarea funcției este zero.

Valoarea argumentului, la care valoarea funcției este zero, se numește zero al funcției.

//acestea. pentru aceasta functie numerele -3;-1;1,5; 4,5 sunt zerouri.

2. Pe intervalele [ 4,5; 3) și (1; 1.5) și (4.5; 5.5] graficul funcției f este situat deasupra axei absciselor, iar la intervale (-3; -1) și (1.5; 4.5) sub axa absciselor, aceasta este explicat după cum urmează - la intervale[4,5; 3) și (1; 1.5) și (4.5; 5.5] funcția ia valori pozitive, iar pe intervalele (-3; -1) și (1,5; 4,5) sunt negative.

Fiecare dintre intervalele indicate (unde funcția ia valori de același semn) se numește interval de semn constant al funcției f.//i.e. de exemplu, dacă luăm intervalul (0; 3), atunci nu este un interval cu semn constant al funcției date.

În matematică, când se caută intervale cu semn constant al unei funcții, se obișnuiește să se indice intervale de lungime maximă. //Acestea. intervalul (2; 3) este interval de constanță funcția f, dar răspunsul trebuie să includă intervalul [ 4,5; 3) conţinând intervalul (2; 3).

3. Dacă vă deplasați de-a lungul axei x de la 4,5 la 2, veți observa că graficul funcției scade, adică valorile funcției scad. //La matematică, se obișnuiește să se spună că pe intervalul [ 4,5; 2] funcția este în scădere.

Pe măsură ce x crește de la 2 la 0, graficul funcției crește, adică. valorile funcției cresc. //La matematică, se obișnuiește să se spună că pe intervalul [ 2; 0] funcția este în creștere.

Funcția f este numită dacă pentru oricare două valori ale argumentului x1 și x2 din acest interval astfel încât x2 > x1, inegalitatea f (x2) > f (x1) este satisfăcută. // sau Funcția este apelată crescând într-un anumit interval, dacă pentru orice valoare a argumentului din acest interval, valoarea mai mare a argumentului corespunde valorii mai mari a funcției.//i.e. cu cât mai mult x, cu atât mai mult y.

Se apelează funcția f scăzând într-un anumit interval, dacă pentru oricare două valori ale argumentului x1 și x2 din acest interval astfel încât x2 > x1, inegalitatea f(x2) descrescătoare pe un anumit interval este satisfăcută, dacă pentru orice valoare a argumentului din acest interval este satisfăcută o mai mare valoarea argumentului corespunde unei valori mai mici a funcției. //acestea. cu cât mai mult x, cu atât mai puțin y.

Dacă o funcție crește pe întregul domeniu de definiție, atunci este numită crescând.

Dacă o funcție este în scădere pe întregul domeniu de definiție, atunci este numită în scădere.

Exemplul 1 grafic al funcțiilor crescătoare și, respectiv, descrescătoare.

Exemplul 2

Definiți yavl. dacă funcție liniară f(x) = 3x + 5 crescător sau descrescător?

Dovada. Să folosim definițiile. Fie x1 și x2 valori arbitrare ale argumentului și x1< x2., например х1=1, х2=7

Definiție: O funcție numerică este o corespondență care se mapează la fiecare număr x dintr-o mulțime dată singular y.

Desemnare:

unde x este o variabilă independentă (argument), y este o variabilă dependentă (funcție). Setul de valori x se numește domeniul funcției (notat D(f)). Setul de valori y se numește intervalul funcției (notat cu E(f)). Graficul unei funcții este mulțimea de puncte din planul cu coordonatele (x, f(x))

Modalități de a seta o funcție.

1. metoda analitica (folosind o formula matematica);
2. metoda tabelară (folosind un tabel);
3. metoda descriptivă (folosind o descriere verbală);
4. metoda grafică (folosind un grafic).

Proprietățile de bază ale funcției.

1. Par și impar

O funcție este numită chiar dacă
– domeniul de definire al funcției este simetric față de zero
f(-x) = f(x)

Graficul unei funcții pare este simetric față de axă 0y

O funcție se numește impar dacă
– domeniul de definire al funcției este simetric față de zero
– pentru orice x din domeniul definiției f(-x) = -f(x)

Graficul unei funcții impare este simetric față de origine.

2. Periodicitatea

Funcția f(x) se numește periodică cu o perioadă dacă pentru orice x din domeniul definiției f(x) = f(x+T) = f(x-T) .

Graficul unei funcții periodice constă în fragmente identice care se repetă la infinit.

3. Monotonie (creștere, scădere)

Funcția f(x) crește pe mulțimea P dacă pentru orice x 1 și x 2 din această mulțime, astfel încât x 1

Funcția f(x) este descrescătoare pe mulțimea P dacă pentru orice x 1 și x 2 din această mulțime, astfel încât x 1 f(x 2) .

4. Extreme

Punctul X max se numește punctul maxim al funcției f (x) dacă pentru toți x din vreo vecinătate X max , inegalitatea f (x) f (X max) este satisfăcută.

Valoarea Y max =f(X max) se numește maximul acestei funcții.

X max - punct maxim
Max are un maxim

Punctul X min se numește punctul minim al funcției f (x) dacă pentru tot x din vreo vecinătate X min, inegalitatea f (x) f (X min) este satisfăcută.

Valoarea lui Y min =f(X min) se numește minimul acestei funcții.

X min - punct minim
Y min - minim

X min , X max - puncte extreme
Y min , Y max - extrema.

5. Zerourile funcției

Zeroul funcției y = f(x) este valoarea argumentului x la care funcția dispare: f(x) = 0.

X 1, X 2, X 3 sunt zerouri ale funcției y = f(x).

Sarcini și teste pe tema „Proprietățile de bază ale unei funcții”

• Proprietățile funcției - Funcții numerice Clasa a 9-a

  Lecții: 2 Teme: 11 Teste: 1

• Proprietățile logaritmilor - Funcții exponențiale și logaritmice Gradul 11

  Lecții: 2 Teme: 14 Teste: 1

• Funcția rădăcină pătrată, proprietățile și graficul acesteia - Funcție rădăcină pătrată. Proprietățile rădăcinii pătrate gradul 8

  Lecții: 1 Teme: 9 Teste: 1

• Funcții de putere, proprietățile și graficele lor - Grade și rădăcini. Funcții de putere Clasa a 11a

  Lecții: 4 Teme: 14 Teste: 1

• Funcții - Subiecte importante pentru repetarea examenului la matematică

  Sarcini: 24

După ce ați studiat acest subiect, ar trebui să puteți găsi domeniul de definire a diferitelor funcții, să determinați intervalele de monotonitate ale unei funcții folosind grafice și să examinați funcțiile par și impar. Luați în considerare soluția unor astfel de probleme în următoarele exemple.

Exemple.

1. Găsiți domeniul funcției.

Soluţie: domeniul de aplicare al funcției se găsește din condiție