Logaritm zecimal 0 1. Logaritm
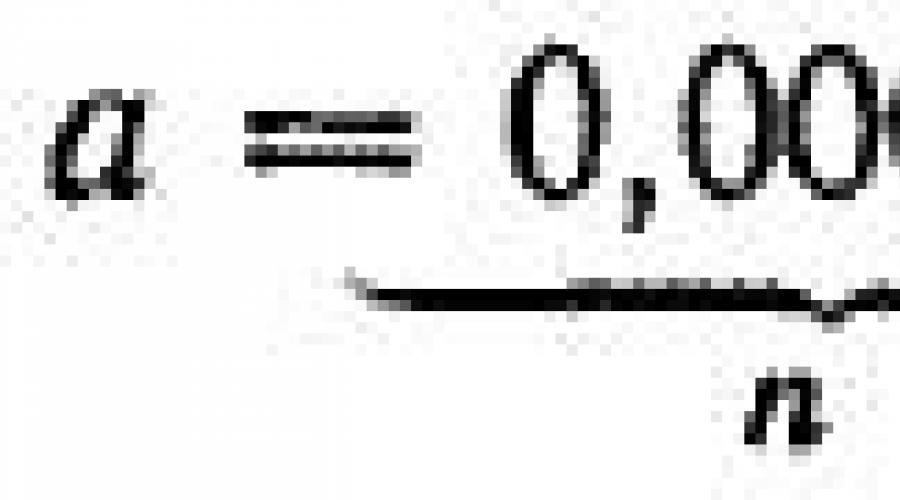
Citeste si
Adesea ia numărul zece. Se numesc logaritmi de numere la baza zece zecimal. Când se efectuează calcule cu logaritmul zecimal, este obișnuit să se opereze cu semnul lg, dar nu Buturuga; în timp ce numărul zece, care determină baza, nu este indicat. Da, înlocuim log 10 105 la simplificat lg105; A log102 pe lg2.
Pentru logaritmi zecimali sunt tipice aceleași caracteristici pe care le au logaritmii cu o bază mai mare decât unu. Și anume, logaritmii zecimali sunt caracterizați exclusiv pentru numere pozitive. Logaritmurile zecimale ale numerelor mai mari decât unu sunt pozitive, iar numerele mai mici decât unu sunt negative; dintre două numere nenegative, cel mai mare este echivalent cu logaritmul zecimal mai mare și așa mai departe. În plus, logaritmii zecimali au trăsături distinctiveși semne deosebite, care explică de ce este confortabil să preferați numărul zece ca bază a logaritmilor.
Înainte de a analiza aceste proprietăți, să aruncăm o privire la următoarele formulări.
Parte întreagă a logaritmului zecimal al unui număr A numit caracteristică, și fracționalul mantisa acest logaritm.
Caracteristica logaritmului zecimal al unui număr A indicată ca , iar mantisa ca (lg A}.
Să luăm, de exemplu, lg 2 ≈ 0,3010. În consecință, = 0, (log 2) ≈ 0,3010.
Același lucru este valabil și pentru lg 543,1 ≈2,7349. În consecință, = 2, (lg 543,1)≈ 0,7349.
Calculul logaritmilor zecimali ai numerelor pozitive din tabele este folosit pe scară largă.
Semne caracteristice ale logaritmilor zecimali.
Primul semn al logaritmului zecimal. un număr întreg nenegativ reprezentat de 1 urmat de zerouri este un număr întreg pozitiv egal cu numărul de zerouri din numărul ales .
Să luăm lg 100 = 2, lg 1 00000 = 5.
În general vorbind, dacă
Acea A= 10n , din care obținem
lg a = lg 10 n = n lg 10 =P.
Al doilea semn. Logaritm zecimal zecimală pozitivă, afișată cu unu cu zerouri înainte, este - P, Unde P- numărul de zerouri în reprezentarea acestui număr, ținând cont de zeroul numerelor întregi.
Considera , lg 0,001 = -3, lg 0,000001 = -6.
În general vorbind, dacă
,
Acea A= 10-n si se dovedeste
lga = lg 10n =-n lg 10 =-n
Al treilea semn. Caracteristica logaritmului zecimal al unui număr nenegativ mai mare decât unu este egală cu numărul de cifre din partea întreagă a acestui număr, excluzând unul.
Să analizăm această caracteristică 1) Caracteristica logaritmului lg 75.631 este echivalată cu 1.
Într-adevăr, 10< 75,631 < 100. Из этого можно сделать вывод
lg 10< lg 75,631 < lg 100,
1 < lg 75,631 < 2.
Asta implică,
lg 75,631 = 1 + b,
Deplasarea unei virgule într-o fracție zecimală la dreapta sau la stânga este echivalentă cu operația de înmulțire a acestei fracții cu o putere de zece cu un exponent întreg P(pozitiv sau negativ). Și, prin urmare, atunci când punctul zecimal dintr-o fracție zecimală pozitivă este deplasat la stânga sau la dreapta, mantisa logaritmului zecimal al acestei fracții nu se schimbă.
Deci, (log 0,0053) = (log 0,53) = (log 0,0000053).
În cele ce urmează, logaritmul zecimal este denumit pur și simplu logaritm.
Logaritmul lui unu este zero.
Logaritmi de numere 10 , 100 , 1000 etc. egal 1 ,2 ,3 etc., adică au atâtea pozitive câte zerouri sunt după unu.
Logaritmi de numere 0,1 ; 0,01 ; 0,001 etc. egal -1 , -2 , -3 etc., adică au atâtea negative câte zerouri sunt înaintea unuia (numărând și numere întregi zero).
Logaritmii numerelor rămase au o parte fracțională, numită mantisa. Partea întreagă a logaritmului este numită caracteristică.
Numerele mai mari decât unu au logaritmi pozitivi. Numerele pozitive mai mici de 1 au logaritmi negativi.
De exemplu 2, lg0,5=-0,30103, lg0,005=-2,30103.
Logaritmii negativi pentru o mai mare comoditate în găsirea logaritmului după număr și număr după logaritm nu sunt prezentați în cele de mai sus " natural forma » și în « artificial". Logaritmul negativ în formă artificială are mantisă pozitivăȘi caracteristică negativă.
De exemplu, log0,005=3,69897. Această intrare înseamnă că lg0,005=-3+0,69897=-2,30103.
Pentru a converti un logaritm negativ din natural în artificial, aveți nevoie de:
1
. creste cu unu valoare absolută caracteristicile sale;
2
. Numărul rezultat este prevăzut cu un semn minus de sus;
3
. Toate cifrele mantisei, cu excepția ultimei cifre diferite de zero, se scad din nouă; Scădeți ultima cifră diferită de zero din zece. Diferențele rezultate sunt scrise în aceleași locuri ale mantisei unde se aflau cifrele scăzute. Zerourile de la sfârșit sunt lăsate neatinse.
Exemplul 1
. lg0,05=-1,30103 duce la forma artificială:
1
. Valoarea absolută a caracteristicii 1
crestere cu 1
; primim 2
;
2
. Scriem caracteristicile formei artificiale în formă 2
și separă-l cu o virgulă;
3
. Scădeți prima cifră a mantisei 3
din 9
; primim 6
; scrie 6
pe primul loc după virgulă zecimală. În același mod, numerele apar în următoarele locuri 9(=9-0)
, 8(=9-1)
, 9(=9-0)
Și 7(=10-3)
.
Ca rezultat, obținem:
-1,30103=2,69897 .
Exemplul 2
. -0,18350
prezent sub formă artificială:
1
. Creștem 0
pe 1
, primim 1
;
2
. Avem 1
;
3
. Scădeți numerele 1
,8
,3
din 9
; figura 5
din 10
; zero de la sfârșit este lăsat neatins.
Ca rezultat, obținem:
-0,18350=1,81650 .
Pentru a converti un logaritm negativ dintr-o formă artificială într-una naturală, aveți nevoie de:
1
. Reduceți valoarea absolută a caracteristicii sale cu unul;
2
. Numărul rezultat este prevăzut cu un semn minus în stânga;
3
. Cu numerele mantisei, procedați ca și în cazul trecerii de la o formă naturală la una artificială.
Exemplul 3
. 4,689 00
prezent sub formă naturală:
1
. 4-1=3
;
2
. Avem -3
;
3
. Scăderea numerelor din mantise 6
,8
Și 9
; figura 9
din 10
; două zerouri sunt lăsate neatinse.
Ca rezultat, obținem:
4,689 00=-3,311 00 .
1 Numerele negative nu au deloc logaritmi reali..
2 Toate egalitățile ulterioare sunt aproximative până la jumătate din unitatea ultimului semn scris.
SECȚIUNEA XIII.
LOGARITMII ȘI APLICAȚIILE LOR.
§ 2. Logaritmi zecimali.
Al zecelea logaritm al numărului 1 este 0. Logaritmuri zecimale ale puterilor pozitive de 10, adică de ex. numerele 10, 100, 1000,.... sunt numere pozitive 1, 2, 3,...., deci, în general, logaritmul numărului notat cu unu cu zerouri, este egal cu numărul zerouri. Logaritmuri zecimale ale puterilor negative de 10, i.e. fracțiile 0,1, 0,01, 0,001, .... sunt numere negative -1, -2, -3 ....., astfel încât în general logaritmul unei fracții zecimale cu numărător unu este egal cu numărul negativ de zerouri a numitorului.
Logaritmii tuturor celorlalte numere comensurabile sunt incomensurabile. Astfel de logaritmi sunt calculati aproximativ, de obicei cu o precizie de o sută a miimii și, prin urmare, sunt exprimați în cinci cifre. zecimale; de exemplu, lg 3 = 0,47712.
Când se prezintă teoria logaritmilor zecimali, se presupune că toate numerele sunt compilate în funcție de sistemul zecimal al unităților și fracțiilor lor, iar toți logaritmii sunt exprimați printr-o fracție zecimală care conține 0 numere întregi, cu o creștere sau descreștere a numărului întreg. Partea fracționară a logaritmului se numește mantisă, iar întreaga creștere sau descreștere este ea caracteristică. Logaritmii numerelor mai mari decât unu sunt întotdeauna pozitivi și, prin urmare, au o caracteristică pozitivă; logaritmii numerelor mai mici decât unu sunt întotdeauna negativi, dar sunt reprezentați în așa fel încât mantisa lor să se dovedească a fi pozitivă, iar o caracteristică este negativă: de exemplu, lg 500 \u003d 0,69897 + 2 sau mai scurtă decât 2,69897 și lg 0,05 \u003d 0, 69897-2, care pentru concizie este notat ca 2,69897, punând caracteristica în locul numerelor întregi, dar cu un semn - deasupra acesteia. Astfel, logaritmul unui număr mai mare decât unu reprezintă suma aritmetică a unui număr întreg pozitiv și a unei fracții pozitive, iar logaritmul unui număr mai mic decât unu reprezintă suma algebrică a unui număr întreg negativ cu o fracție pozitivă.
Orice logaritm negativ poate fi redus la forma artificială indicată. De exemplu, avem lg 3 / 5 \u003d lg 3 - lg 5 \u003d 0,47712-0,69897 \u003d -0,22185. Pentru a converti acest logaritm adevărat într-o formă artificială, îi adăugăm 1 și după adunarea algebrică indicăm scăderea unuia pentru corecție.
Obținem lg 3 / 5 \u003d lg 0,6 \u003d (1-0,22185) -1 \u003d 0,77815-1. În acest caz, reiese că mantisa 0,77815 este cea care corespunde numărătorului 6 al acestui număr, reprezentat în sistemul zecimal sub forma unei fracții 0,6.
În reprezentarea indicată a logaritmilor zecimali, mantisele și caracteristicile lor au proprietăți importante în legătură cu desemnarea zecimală a numerelor care le corespund. Pentru a clarifica aceste proprietăți, notăm următoarele. Să luăm ca formă principală a unui număr un număr arbitrar cuprins între 1 și 10 și, exprimându-l în sistem zecimal, îl vom reprezenta sub forma a, b, c, d, e, f ...., Unde A există unul dintre cifre semnificative 1, 2, 3, 4, 5, 6, 7, 8, 9 și zecimale, b, c, d, e, f ....... esența oricăror numere, între care pot exista zerouri. Datorită faptului că numărul luat este cuprins între 1 n 10, logaritmul său este cuprins între 0 și 1 și de aceea acest logaritm constă dintr-o mantisă fără caracteristică sau cu caracteristica 0. Notăm acest logaritm sub forma 0 ,α β γ δ ε ...., Unde α, β ,γ ,δ, ε esenţa unor figuri. Acum înmulțim acest număr pe de o parte cu numerele 10, 100, 1000, .... și pe de altă parte cu numerele 0,1, 0,01, 0,001, ... și aplicăm teoremele asupra logaritmilor produsului și coeficientul. Apoi obținem o serie de numere mai mari decât unu și o serie de numere mai mici decât unu cu logaritmii lor:
lg A ,bcde f ....= 0 ,α β γ δ ε ....
lg ab,cde f ....= 1 ,α β γ δ ε ... lg 0,abcde f ....= 1 ,α β γ δ ε ....
lg abc, de f ....= 2 ,α β γ δ ε ... lg 0,0abcde f ....= 2 ,α β γ δ ε ....
lg abcd,e f ....= 3 ,α β γ δ ε ... lg 0,00abcde f ....= 3 ,α β γ δ ε ....
Când luăm în considerare aceste egalități, sunt relevate următoarele proprietăți și caracteristici mantise:
Proprietatea Mantisei. Mantisa depinde de locația și tipul cifrelor deschise ale numărului, dar nu depinde deloc de locul virgulei în desemnarea acestui număr. Mantisele logaritmilor de numere având un raport zecimal, adică cei al căror raport multiplu este egal cu orice putere pozitivă sau negativă de zece sunt la fel.
Proprietate caracteristică. Caracteristica depinde de categoria celor mai mari unități sau fracții zecimale ale unui număr, dar nu depinde deloc de tipul de cifre din desemnarea acestui număr.
Dacă sunăm la numere A ,bcde f ...., ab,cde f ...., abc, de f .... numere de cifre pozitive - primul, al doilea, al treilea etc., cifra numărului 0,abcde f .... vom lua în considerare zero și cifrele numerelor 0,0abcde f ...., 0,00abcde f ...., 0.000abcde f .... exprimă în numere negative minus unu, minus doi, minus trei etc., atunci se va putea spune în general că caracteristica logaritmului oricărui număr zecimal este cu unu mai mică decât numărul care indică cifra
101. Știind că lg 2 \u003d 0,30103, găsiți logaritmii numerelor 20,2000, 0,2 și 0,00002.
101. Știind că lg 3 \u003d 0,47712, găsiți logaritmii numerelor 300, 3000, 0,03 și 0,0003.
102. Știind că lg 5 \u003d 0,69897, găsiți logaritmii numerelor 2,5, 500, 0,25 și 0,005.
102. Știind că lg 7 \u003d 0,84510, găsiți logaritmii numerelor 0,7, 4,9, 0,049 și 0,0007.
103. Știind lg 3=0,47712 și lg 7=0,84510, găsiți logaritmii numerelor 210, 0,021, 3/7, 7/9 și 3/49.
103. Cunoscând lg 2=0,30103 și lg 7=0,84510, găsiți logaritmii numerelor 140, 0,14, 2/7, 7/8 și 2/49.
104. Cunoscând lg 3 \u003d 0,47712 și lg 5 \u003d O.69897, găsiți logaritmii numerelor 1,5, 3/5, 0,12, 5/9 și 0,36.
104. Cunoscând lg 5=0,69897 și lg 7=0,84510, găsiți logaritmii numerelor 3,5, 5/7, 0,28, 5/49 și 1,96.
Logaritmurile zecimale ale numerelor exprimate cu cel mult patru cifre sunt căutate direct din tabele, iar mantisa logaritmului dorit este găsită din tabele, iar caracteristica este setată în conformitate cu cifra numărului dat.
Dacă numărul conține mai mult de patru cifre, atunci căutarea logaritmului este însoțită de un calcul suplimentar. Regula este: pentru a găsi logaritmul unui număr care conține mai mult de patru cifre, trebuie să căutați în tabele numărul indicat de primele patru cifre și să scrieți mantisa corespunzătoare acestor patru cifre; apoi înmulțiți diferența tabelară a mantiselor cu numărul format din cifrele aruncate, în produs, aruncați atâtea cifre din dreapta câte au fost aruncate în numărul dat și adăugați rezultatul la ultimele cifre ale mantisei găsite. ; caracteristica este de a pune, în conformitate cu descărcarea unui număr dat.
Când un număr este căutat de un logaritm dat și acest logaritm este conținut în tabele, atunci numerele numărului dorit sunt găsite direct din tabele, iar cifra numărului este determinată în conformitate cu caracteristica logaritmului dat .
Dacă logaritmul dat nu este conținut în tabele, atunci căutarea unui număr este însoțită de un calcul suplimentar. Regula este: pentru a găsi un număr corespunzător unui logaritm dat, a cărui mantise nu este conținută în tabele, trebuie să găsiți cea mai apropiată mantisă mai mică și să scrieți cifrele corespunzătoare ale numărului; apoi înmulțiți diferența dintre mantisa dată și cea găsită cu 10 și împărțiți produsul la diferența tabelară; să atribuie cifra primită a coeficientului în dreapta cifrelor scrise ale numărului, motiv pentru care se va obține setul de cifre dorit; descărcarea numărului trebuie determinată în conformitate cu caracteristicile logaritmului dat.
105. Aflați logaritmii numerelor 8, 141, 954, 420, 640, 1235, 3907, 3010, 18.43, 2.05, 900.1, 0.73, 0.0028, 0.10000, 5.
105. Aflați logaritmii numerelor 15.154, 837, 510, 5002.1309-, 8900, 8.315, 790.7, 0.09, 0.6745, 0.000745, 0.000745, 0.04205
106. Găsiți logaritmii numerelor 2174.6, 1445.7, 2169.5, 8437.2, 46.472, 6.2853, 0.7893B, 0.054294, 631.074, 2.795.756, 2.795.756, 80.2853, 0.7893B
106. Aflați logaritmii numerelor 2578.4, 1323.6, 8170.5, 6245.3, 437.65, 87.268, 0.059372, 0.84938, 62.5475, 1394.63, 1394.65, 1394.65
107. Găsiți numerele corespunzătoare logaritmilor lui 3,16227, 3,59207, 2,93318, 0,41078, 1,60065, 2,756,86, 3,23528, 1,79692. 4,87800 5,14613.
107. Aflați numerele corespunzătoare logaritmilor lui 3,07372, 3,69205, 1,64904, 2,16107, 0,70364, 1,31952, 4,30814, 3,00087, 2,68,799, 2,68,95
108. Aflați numărul corespunzător logaritmilor de 3,57686, 3,16340, 2,40359, 1,09817, 4,49823, 2,83882, 1,50060, 3,30056, 1,17112, 4,0.
108. Aflați numerele corespunzătoare logaritmilor lui 3,33720, 3,09875, 0,70093, 4,04640, 2,94004, 1,41509, 2,32649, 4,14631, 3,03,39.
Logaritmii pozitivi ai numerelor mai mari decât unu sunt sumele aritmetice ale caracteristicilor și mantiselor lor. Prin urmare, acțiunile cu ei sunt efectuate conform regulilor aritmetice obișnuite.
Logaritmii negativi ai numerelor mai mici de unu sunt sumele algebrice ale unei caracteristici negative și ale unei mantise pozitive. Prin urmare, operațiunile cu acestea sunt efectuate conform regulilor algebrice, care sunt completate cu instrucțiuni speciale legate de reducerea logaritmilor negativi la forma lor normală. Forma normală a logaritmului negativ este una în care caracteristica este un număr întreg negativ și mantisa este o fracție proprie pozitivă.
Pentru a converti logaritmul reflectiv adevărat în forma sa normală artificială, trebuie să creștem valoarea absolută a termenului său întreg cu una și să faceți rezultatul o caracteristică negativă; apoi adăugați toate cifrele termenului fracționar la 9, iar ultima dintre ele la 10 și faceți rezultatul o mantisă pozitivă. De exemplu, -2,57928 = 3,42072.
Pentru a converti forma artificială normală a unui logaritm în forma sa adevărată sens negativ, trebuie să reduceți caracteristica negativă cu unul și să faceți din rezultat un termen întreg al sumei negative; apoi adăugați toate cifrele mantisei la 9, iar ultima dintre ele la 10 și faceți din rezultat un termen fracționar cu aceeași sumă negativă. De exemplu: 4,57406= -3,42594.
109. Convertiți în logaritmi artificiali -2,69537, -4, 21283, -0,54225, -1,68307, -3,53820, -5,89990.
109. Convertiți în formă artificială logaritmii -3,21729, -1,73273, -5,42936, -0,51395, -2,43780, -4,22990.
110. Aflați adevăratele valori ale logaritmilor 1.33278, 3.52793, 2.95426, 4.32725, 1.39420, 5.67990.
110. Aflați valorile reale ale logaritmilor 2.45438, 1.73977, 3.91243, 5.12912, 2.83770, 4.28990.
Regulile pentru operațiile algebrice cu logaritmi negativi sunt exprimate după cum urmează:
Pentru a aplica logaritmul negativ în forma sa artificială, trebuie să aplicați mantisa și să scădeți valoarea absolută a caracteristicii. Dacă un număr întreg pozitiv iese în evidență din adăugarea mantiselor, atunci este necesar să-l atribuiți caracteristicii rezultatului, făcându-i o corecție adecvată. De exemplu,
3,89573 + 2 ,78452 = 1 1 ,68025 = 2,68025
1 ,54978 + 2 ,94963=3 1 ,49941=2 ,49941.
Pentru a scădea logaritmul negativ în forma sa artificială, trebuie să scădeți mantisa și să adăugați valoarea absolută a caracteristicii. Dacă mantisa care trebuie scăzută este mare, atunci este necesar să se facă o corecție în caracteristica celei reduse, astfel încât să se separe o unitate pozitivă de mantisa redusă. De exemplu,
2,53798-3 ,84582=1 1 ,53798-3 ,84582 = 4,69216,
2 ,22689-1 ,64853=3 1 ,22689-1 ,64853=2 ,57836.
Pentru a multiplica un logaritm negativ cu un întreg pozitiv, trebuie să-i înmulțiți separat caracteristica și mantisa. Dacă, la înmulțirea mantisei, este alocat un număr întreg pozitiv, atunci este necesar să-l atribuiți caracteristicii rezultatului, făcându-i o corecție adecvată. De exemplu,
2 ,53729 5=10 2 ,68645=8 ,68645.
Când înmulțiți un logaritm negativ cu o sumă negativă, înlocuiți multiplicatorul cu valoarea sa adevărată.
Pentru a împărți un logaritm negativ la un număr întreg pozitiv, trebuie să-i separați separat caracteristica și mantisa. Dacă caracteristica dividendului nu este divizibilă de divizor, atunci este necesar să se facă o corecție în ea, astfel încât să se atribuie mai multe unități pozitive mantisei și să facă din caracteristică un multiplu al divizorului. De exemplu,
3 ,79432: 5=5 2 ,79432: 5=1 ,55886.
Când împărțiți un logaritm negativ la un număr negativ, trebuie să înlocuiți dividendul cu valoarea sa adevărată.
Efectuați următoarele calcule folosind tabele logaritmice și verificați rezultatele în cele mai simple cazuri folosind metodele obișnuite de acțiune:
174. Determinați volumul unui con, a cărui generatrie este de 0,9134 picioare, iar raza bazei este de 0,04278 picioare.
175. Calculați al 15-lea termen al unei progresii multiple al cărei prim termen este 2 3/5 și numitorul este 1,75.
175. Calculați primul termen al unei progresii multiple, al 11-lea termen al căruia este 649,5, iar numitorul este 1,58.
176. Determinați numărul de factori A , A 3 , A 5 R . Găsiți asta A , la care produsul a 10 factori este egal cu 100.
176. Determinați numărul de factori. A 2 , A 6 , A 10 ,.... astfel încât produsul lor să fie egal cu numărul dat R . Găsiți asta A , la care produsul a 5 factori este egal cu 10.
177. Numitorul progresiei multiple este 1,075, suma celor 10 membri ai săi este 2017,8. Găsiți primul termen.
177. Numitorul unei progresii multiple este 1,029, suma celor 20 de membri ai săi este 8743,7. Găsiți al douăzecilea termen.
178 . Exprimați numărul de termeni dintr-o progresie multiplă dat fiind primul termen A , ultimul și și numitorul q , iar apoi, alegerea unor valori numerice arbitrare A Și u , ridica q astfel încât P
178. Exprimați numărul de membri ai unei progresii multiple în funcție de primul membru A , ultimul Și și numitorul q Și Și q , ridica A astfel încât P a fost un număr întreg.
179. Determinați numărul de factori astfel încât produsul lor să fie egal cu R . Ce ar trebui să fie R pentru a A =0,5 și b =0,9 numărul de factori a fost 10.
179. Determinați numărul de factori ![]() astfel încât produsul lor să fie egal cu R
. Ce ar trebui să fie R
pentru a A
=0,2 și b
=2 numărul de factori a fost 10.
astfel încât produsul lor să fie egal cu R
. Ce ar trebui să fie R
pentru a A
=0,2 și b
=2 numărul de factori a fost 10.
180. Exprimați numărul de termeni dintr-o progresie multiplă dat fiind primul termen A , mai tarziu Și și produsul tuturor membrilor R , iar apoi, alegerea unor valori numerice arbitrare A Și R , ridica Și urmat de numitor q astfel încât Și a fost un număr întreg.
160. Exprimați numărul de membri ai unei progresii multiple în funcție de primul membru A , ultimul și și produsul tuturor termenilor R , iar apoi, alegerea unor valori numerice arbitrare Și Și R , ridica A urmat de numitor q astfel încât P a fost un număr întreg.
Rezolvați următoarele ecuații, acolo unde este posibil - fără ajutorul tabelelor și, unde nu, cu tabele:


