Calculul varianței unei variabile aleatoare. Rate absolute de variație
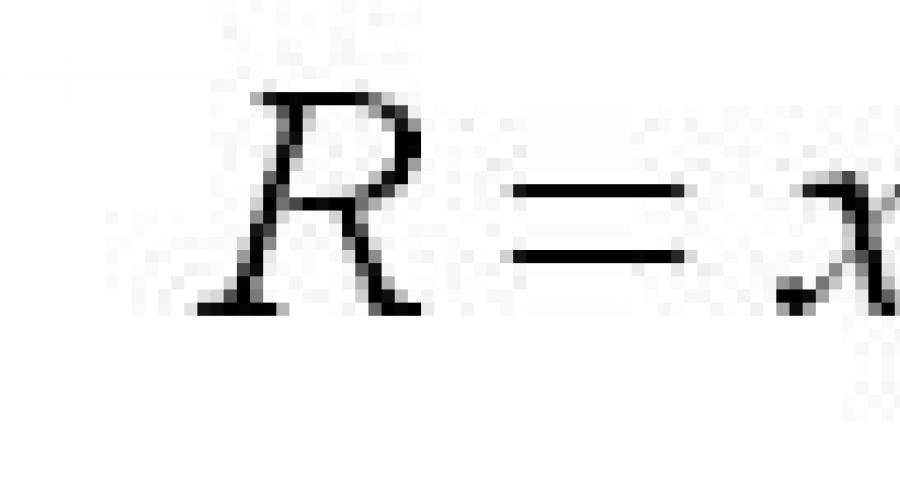
Citeste si
Pași
Calcularea variației eșantionului
-
Înregistrați valorile eșantionului.În cele mai multe cazuri, doar eșantioane din anumite populații sunt disponibile pentru statisticieni. De exemplu, de regulă, statisticienii nu analizează costul menținerii populației tuturor mașinilor din Rusia - ei analizează un eșantion aleatoriu de câteva mii de mașini. Un astfel de eșantion va ajuta la determinarea costului mediu pe mașină, dar cel mai probabil, valoarea rezultată va fi departe de cea reală.
- De exemplu, să analizăm numărul de chifle vândute într-o cafenea în 6 zile, luate în ordine aleatorie. Eșantionul are următoarea formă: 17, 15, 23, 7, 9, 13. Acesta este un eșantion, nu o populație, deoarece nu avem date despre chiflele vândute pentru fiecare zi în care cafeneaua este deschisă.
- Dacă vi se oferă o populație și nu un eșantion de valori, treceți la secțiunea următoare.
-
Notați formula pentru calcularea varianței eșantionului. Dispersia este o măsură a răspândirii valorilor unei anumite cantități. Cu cât valoarea dispersiei este mai aproape de zero, cu atât valorile sunt grupate mai aproape. Când lucrați cu un eșantion de valori, utilizați următoarea formulă pentru a calcula varianța:
- s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))-X) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2)) este dispersia. Dispersia se măsoară în unități pătrate.
- x i (\displaystyle x_(i))- fiecare valoare din eșantion.
- x i (\displaystyle x_(i)) trebuie să scădeți x̅, să-l pătrați și apoi să adăugați rezultatele.
- x̅ – medie eșantion (medie eșantion).
- n este numărul de valori din eșantion.
-
Calculați media eșantionului. Este notat cu x̅. Media eșantionului este calculată ca o medie aritmetică normală: se adună toate valorile din eșantion și apoi se împarte rezultatul la numărul de valori din eșantion.
- În exemplul nostru, adăugați valorile din eșantion: 15 + 17 + 23 + 7 + 9 + 13 = 84
Acum împărțiți rezultatul la numărul de valori din eșantion (în exemplul nostru sunt 6): 84 ÷ 6 = 14.
Media eșantionului x̅ = 14. - Media eșantionului este valoarea centrală în jurul căreia sunt distribuite valorile din eșantion. Dacă valorile din grupul de eșantion din jurul eșantionului sunt medii, atunci varianța este mică; în caz contrar, dispersia este mare.
- În exemplul nostru, adăugați valorile din eșantion: 15 + 17 + 23 + 7 + 9 + 13 = 84
-
Scădeți media eșantionului din fiecare valoare din eșantion. Acum calculează diferența x i (\displaystyle x_(i))- x̅, unde x i (\displaystyle x_(i))- fiecare valoare din eșantion. Fiecare rezultat obținut indică măsura în care o anumită valoare se abate de la media eșantionului, adică cât de departe este această valoare de media eșantionului.
- În exemplul nostru:
x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1 - Corectitudinea rezultatelor obținute este ușor de verificat, deoarece suma lor trebuie să fie egală cu zero. Aceasta este legată de definirea valorii medii, deoarece valori negative(distanțele de la valoarea medie la valori mai mici) sunt complet compensate valori pozitive(distanțele de la valori medii la mari).
- În exemplul nostru:
-
După cum sa menționat mai sus, suma diferențelor x i (\displaystyle x_(i))- x̅ trebuie să fie egal cu zero. Aceasta înseamnă că varianța medie este întotdeauna zero, ceea ce nu dă nicio idee despre răspândirea valorilor unei cantități. Pentru a rezolva această problemă, pătrați fiecare diferență x i (\displaystyle x_(i))- X. Acest lucru va duce la obținerea de numere pozitive care, atunci când sunt adunate, nu vor aduna niciodată până la 0.
- În exemplul nostru:
(x 1 (\displaystyle x_(1))-X) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
(x 2 (\displaystyle (x_(2)))-X) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - Ați găsit pătratul diferenței - x̅) 2 (\displaystyle ^(2)) pentru fiecare valoare din eșantion.
- În exemplul nostru:
-
Calculați suma diferențelor pătrate. Adică, găsiți partea formulei care este scrisă astfel: ∑[( x i (\displaystyle x_(i))-X) 2 (\displaystyle ^(2))]. Aici semnul Σ înseamnă suma diferențelor pătrate pentru fiecare valoare x i (\displaystyle x_(i))în probă. Ați găsit deja diferențele la pătrat (x i (\displaystyle (x_(i)))-X) 2 (\displaystyle ^(2)) pentru fiecare valoare x i (\displaystyle x_(i))în probă; acum doar adăugați aceste pătrate.
- În exemplul nostru: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
Împărțiți rezultatul la n - 1, unde n este numărul de valori din eșantion. Cu ceva timp în urmă, pentru a calcula varianța eșantionului, statisticienii au împărțit pur și simplu rezultatul la n; în acest caz, veți obține media varianței pătrate, care este ideală pentru a descrie varianța unui eșantion dat. Dar amintiți-vă că orice eșantion este doar o mică parte din populația generală de valori. Dacă luați un eșantion diferit și faceți aceleași calcule, veți obține un rezultat diferit. După cum se dovedește, împărțirea la n - 1 (mai degrabă decât doar n) oferă o estimare mai bună a varianței populației, care este ceea ce căutați. Împărțirea la n - 1 a devenit obișnuită, deci este inclusă în formula de calcul a varianței eșantionului.
- În exemplul nostru, eșantionul include 6 valori, adică n = 6.
Varianta eșantionului = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
- În exemplul nostru, eșantionul include 6 valori, adică n = 6.
-
Diferența dintre varianță și abaterea standard. Rețineți că formula conține un exponent, deci varianța este măsurată în unități pătrate ale valorii analizate. Uneori, o astfel de valoare este destul de dificil de utilizat; în astfel de cazuri, se utilizează abaterea standard, care este egală cu rădăcina pătrată a varianței. De aceea, varianța eșantionului se notează ca s 2 (\displaystyle s^(2)), iar abaterea standard a eșantionului ca s (\displaystyle s).
- În exemplul nostru, abaterea standard a eșantionului este: s = √33,2 = 5,76.
Calculul variației populației
-
Analizați un set de valori. Setul include toate valorile cantității luate în considerare. De exemplu, dacă studiezi vârsta locuitorilor Regiunea Leningrad, atunci populația include vârsta tuturor locuitorilor acestei zone. În cazul lucrului cu un agregat, se recomandă să creați un tabel și să introduceți valorile agregatului în acesta. Luați în considerare următorul exemplu:
- Există 6 acvarii într-o anumită cameră. Fiecare acvariu conține următorul număr de pești:
x 1 = 5 (\displaystyle x_(1)=5)
x 2 = 5 (\displaystyle x_(2)=5)
x 3 = 8 (\displaystyle x_(3)=8)
x 4 = 12 (\displaystyle x_(4)=12)
x 5 = 15 (\displaystyle x_(5)=15)
x 6 = 18 (\displaystyle x_(6)=18)
- Există 6 acvarii într-o anumită cameră. Fiecare acvariu conține următorul număr de pești:
-
Notați formula de calcul a varianței populației. Deoarece setul include toate valorile unei anumite cantități, formula de mai jos vă permite să obțineți valoare exacta varianţa populaţiei. Pentru a distinge varianța populației de varianța eșantionului (care este doar o estimare), statisticienii folosesc diverse variabile:
- σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n
- σ 2 (\displaystyle ^(2))- varianța populației (a se citi „sigma pătrat”). Dispersia se măsoară în unități pătrate.
- x i (\displaystyle x_(i))- fiecare valoare în agregat.
- Σ este semnul sumei. Adică pentru fiecare valoare x i (\displaystyle x_(i)) scădeți μ, pătrați și apoi adăugați rezultatele.
- μ este media populației.
- n este numărul de valori din populația generală.
-
Calculați media populației. Când se lucrează cu populația generală, valoarea medie a acesteia este notată ca μ (mu). Media populației este calculată ca medie aritmetică obișnuită: se adună toate valorile din populație și apoi se împarte rezultatul la numărul de valori din populație.
- Rețineți că mediile nu sunt întotdeauna calculate ca medie aritmetică.
- În exemplul nostru, media populației: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
-
Scădeți media populației din fiecare valoare din populație. Cu cât diferența este mai aproape de zero, cu atât mai aproape sens specific la media populaţiei. Găsiți diferența dintre fiecare valoare din populație și media acesteia și veți avea o primă privire asupra distribuției valorilor.
- În exemplul nostru:
x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5
- În exemplul nostru:
-
Pătrați fiecare rezultat pe care îl obțineți. Valorile diferențelor vor fi atât pozitive, cât și negative; dacă puneți aceste valori pe o linie numerică, atunci ele se vor afla la dreapta și la stânga mediei populației. Acest lucru nu este bun pentru calcularea varianței, deoarece numerele pozitive și negative se anulează reciproc. Prin urmare, pătrați fiecare diferență pentru a obține numere exclusiv pozitive.
- În exemplul nostru:
(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) pentru fiecare valoare a populației (de la i = 1 la i = 6):
(-5,5)2 (\displaystyle ^(2)) = 30,25
(-5,5)2 (\displaystyle ^(2)), Unde x n (\displaystyle x_(n)) este ultima valoare din populație. - Pentru a calcula valoarea medie a rezultatelor obținute, trebuie să găsiți suma lor și să o împărțiți la n: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2))) / n
- Acum să scriem explicația de mai sus folosind variabile: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n și obțineți o formulă pentru calcularea varianței populației.
- În exemplul nostru:
Această pagină descrie exemplu standard pentru a găsi varianța, puteți, de asemenea, să vă uitați la alte sarcini pentru a o găsi
Exemplul 1. Determinarea grupului, media grupului, între grup și variația totală
Exemplul 2. Găsirea varianței și coeficientului de variație într-un tabel de grupare
Exemplul 3. Aflarea varianței într-o serie discretă
Exemplul 4. Avem următoarele date pentru un grup de 20 de studenți prin corespondență. Este necesar să se construiască o serie de intervale a distribuției caracteristicilor, să se calculeze valoarea medie a caracteristicii și să se studieze varianța acesteia
Să construim o grupare de intervale. Să determinăm intervalul intervalului cu formula:
![]()
unde X max este valoarea maximă a caracteristicii de grupare;
X min este valoarea minimă a caracteristicii de grupare;
n este numărul de intervale:
Acceptăm n=5. Pasul este: h \u003d (192 - 159) / 5 \u003d 6,6
Să facem o grupare pe intervale

Pentru calcule suplimentare, vom construi un tabel auxiliar:

X "i - mijlocul intervalului. (de exemplu, mijlocul intervalului 159 - 165,6 \u003d 162,3)
Creșterea medie a studenților este determinată de formula mediei ponderate aritmetice:

Determinăm dispersia prin formula:
Formula poate fi convertită astfel:

Din această formulă rezultă că varianţa este diferența dintre media pătratelor opțiunilor și pătratul și media.
Varianta in seria de variatii cu intervale egale conform metodei momentelor se poate calcula în felul următor folosind a doua proprietate de dispersie (împărțirea tuturor opțiunilor la valoarea intervalului). Definiţia variance, calculat prin metoda momentelor, conform următoarei formule necesită mai puțin timp:

unde i este valoarea intervalului;
A - zero condiționat, care este convenabil să se folosească mijlocul intervalului cu cea mai mare frecvență;
m1 este pătratul momentului de ordinul întâi;
m2 - momentul de ordinul doi
Varianta caracteristicilor (dacă în populația statistică atributul se modifică în așa fel încât există doar două opțiuni care se exclud reciproc, atunci o astfel de variabilitate se numește alternativă) poate fi calculată prin formula:

Înlocuind în această formulă de dispersie q = 1- p, obținem:

Tipuri de dispersie
Varianta totala măsoară variaţia unei trăsături asupra întregii populaţii în ansamblu sub influenţa tuturor factorilor care provoacă această variaţie. Este egal cu pătratul mediu al abaterilor valori individuale caracteristica x a valorii medii globale a lui x și poate fi definită ca varianță simplă sau varianță ponderată.
Varianta intragrup caracterizează variația aleatorie, adică parte a variației, care se datorează influenței factorilor necontabiliați și nu depinde de factorul-semn care stă la baza grupării. Această varianță este egală cu pătratul mediu al abaterilor valorilor individuale ale atributului din grupul X față de media aritmetică a grupului și poate fi calculată ca varianță simplă sau ca varianță ponderată.
Prin urmare, măsuri de variație în cadrul grupului variația unei trăsături în cadrul unui grup și este determinată de formula:

unde xi - media grupului;
ni este numărul de unități din grup.
De exemplu, variațiile intra-grup, care trebuie determinate în sarcina de a studia influența calificărilor lucrătorilor asupra nivelului de productivitate a muncii în atelier, arată variații ale producției în fiecare grup cauzate de toți factorii posibili ( stare tehnica echipamente, disponibilitatea sculelor și materialelor, vârsta lucrătorilor, intensitatea muncii etc.), cu excepția diferențelor în categorie de calificare(în cadrul unui grup, toți lucrătorii au aceleași calificări).
Să calculăm înDOMNIȘOARĂEXCELAvarianţa şi abaterea standard a probei. De asemenea, calculăm varianța unei variabile aleatoare dacă distribuția ei este cunoscută.
Mai întâi luați în considerare dispersie, apoi deviație standard.
Varianta eșantionului
Varianta eșantionului (varianța eșantionului,probăvarianţă) caracterizează răspândirea valorilor în matrice relativ la .
Toate cele 3 formule sunt echivalente din punct de vedere matematic.
Din prima formulă se vede că varianța eșantionului este suma abaterilor pătrate ale fiecărei valori din matrice de la medieîmpărțit la dimensiunea eșantionului minus 1.
dispersie mostre se folosește funcția DISP(), ing. numele VAR, adică VARIANCE. De la MS EXCEL 2010, se recomandă utilizarea analogului său DISP.V() , ing. numele VARS, adică Varianta eșantionului. In plus, incepand de la versiunea de MS EXCEL 2010, exista o functie DISP.G (), ing. Numele VARP, adică VARIANCE populației care calculează dispersie Pentru populatia. Întreaga diferență se reduce la numitor: în loc de n-1 ca DISP.V() , DISP.G() are doar n în numitor. Înainte de MS EXCEL 2010, funcția VARP() a fost utilizată pentru a calcula varianța populației.
Varianta eșantionului
=PĂTRAT(Eșantion)/(NUMĂR (Eșantion)-1)
=(SUMSQ(Eșantion)-COUNT(Eșantion)*MEDIE(Eșantion)^2)/ (NUMĂR (Eșantion)-1)- formula uzuală
=SUMA((Eșantion -MEDIE(Eșantion))^2)/ (NUMĂR (Eșantion)-1) –
Varianta eșantionului este egal cu 0 numai dacă toate valorile sunt egale între ele și, în consecință, sunt egale Valoarea medie. De obicei decât mai multă valoare dispersie, cu atât este mai mare răspândirea valorilor în matrice.
Varianta eșantionului este o estimare punctuala dispersie distribuția variabilei aleatoare din care probă. Despre clădire intervale de încredere la evaluare dispersie poate fi citit in articol.
Varianta unei variabile aleatoare
A calcula dispersie variabilă aleatoare, trebuie să o știți.
Pentru dispersie variabila aleatoare X folosește adesea notația Var(X). Dispersia este egal cu pătratul abaterii de la medie E(X): Var(X)=E[(X-E(X)) 2 ]
dispersie calculat prin formula:

unde x i este valoarea pe care o poate lua variabila aleatoare și μ este valoarea medie (), p(x) este probabilitatea ca variabila aleatoare să ia valoarea x.
Dacă variabila aleatoare are , atunci dispersie calculat prin formula:

Dimensiune dispersie corespunde pătratului unității de măsură a valorilor inițiale. De exemplu, dacă valorile din eșantion sunt măsurători ale greutății piesei (în kg), atunci dimensiunea varianței ar fi kg 2 . Acest lucru poate fi dificil de interpretat, prin urmare, pentru a caracteriza răspândirea valorilor, o valoare egală cu rădăcina pătrată a dispersie – deviație standard.
Unele proprietăți dispersie:
Var(X+a)=Var(X), unde X este o variabilă aleatoare și a este o constantă.
Var(aХ)=a 2 Var(X)
Var(X)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2=E(X 2)- 2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2
Această proprietate de dispersie este utilizată în articol despre regresia liniară.
Var(X+Y)=Var(X) + Var(Y) + 2*Cov(X;Y), unde X și Y sunt variabile aleatoare, Cov(X;Y) este covarianța acestor variabile aleatoare.
Dacă variabilele aleatoare sunt independente, atunci acestea covarianta este 0 și, prin urmare, Var(X+Y)=Var(X)+Var(Y). Această proprietate a varianței este utilizată în rezultat.
Să arătăm că pentru mărimi independente Var(X-Y)=Var(X+Y). Într-adevăr, Var(X-Y)= Var(X-Y)= Var(X+(-Y))= Var(X)+Var(-Y)= Var(X)+Var(-Y)= Var(X)+(- 1) 2 Var(Y)= Var(X)+Var(Y)= Var(X+Y). Această proprietate a varianței este utilizată pentru a reprezenta grafic.
Deviația standard a eșantionului
Deviația standard a eșantionului este o măsură a cât de larg sunt împrăștiate valorile din eșantion în raport cu .
A-priorie, deviație standard este egal cu rădăcina pătrată a dispersie:

Deviație standard nu ține cont de mărimea valorilor în prelevarea de probe, ci doar gradul de împrăștiere a valorilor în jurul lor mijloc. Să luăm un exemplu pentru a ilustra acest lucru.
Să calculăm abaterea standard pentru 2 eșantioane: (1; 5; 9) și (1001; 1005; 1009). În ambele cazuri, s=4. Este evident că raportul dintre abaterea standard și valorile matricei este semnificativ diferit pentru eșantioane. Pentru astfel de cazuri, utilizați Coeficientul de variație(Coeficient de variație, CV) - raport deviație standard la medie aritmetic, exprimat ca procent.
În MS EXCEL 2007 și versiuni anterioare pentru calcul Deviația standard a eșantionului se folosește funcția =STDEV(), ing. numele STDEV, adică deviație standard. Începând cu MS EXCEL 2010, se recomandă utilizarea analogului său = STDEV.B () , ing. numele STDEV.S, adică Exemplu de deviare standard.
În plus, începând de la versiunea MS EXCEL 2010, există o funcție STDEV.G () , ing. numele STDEV.P, adică Deviația standard a populației care calculează deviație standard Pentru populatia. Întreaga diferență se reduce la numitor: în loc de n-1 ca STDEV.V() , STDEV.G() are doar n în numitor.
Deviație standard poate fi calculat și direct din formulele de mai jos (vezi fișierul exemplu)
=SQRT(SQUADROTIV(Eșantion)/(COUNT(Eșantion)-1))
=SQRT((SUMSQ(Eșantion)-COUNT(Eșantion)*MEDIE(Eșantion)^2)/(NUMĂR (Eșantion)-1))
Alte măsuri de dispersie
Funcția SQUADRIVE() calculează cu umm de abateri pătrate ale valorilor de la lor mijloc. Această funcție va returna același rezultat ca și formula =VAR.G( Probă)*VERIFICA( Probă) , Unde Probă- o referință la un interval care conține o matrice de valori ale eșantionului (). Calculele în funcția QUADROTIV() se fac după formula:

Funcția SROOT() este, de asemenea, o măsură a dispersării unui set de date. Funcția AVERAGE() calculează media valori absolute abateri de la mijloc. Această funcție va returna același rezultat ca și formula =SUMPRODUS(ABS(Eșantion-MEDIE(Eșantion)))/COUNT(Eșantion), Unde Probă- o referință la un interval care conține o serie de valori ale eșantionului.
Calculele în funcția SROOTKL () se fac după formula:

Dispersia eu
Dispersie (din latină dispersio - dispersie)
V statistici matematiceși teoria probabilității, cea mai utilizată măsură a dispersiei, adică abaterile de la medie. În sens statistic, D. este media aritmetică a abaterilor pătrate ale valorilor x i din media lor aritmetică În teoria probabilității, distribuția unei variabile aleatoare X se numește așteptarea E ( X - m x) 2 abatere la pătrat X de la ea așteptări matematice m x= E ( X). D. variabilă aleatoare X notat cu D ( X) sau prin σ 2 X. Rădăcina pătrată a lui D. (adică σ, dacă D. este σ 2) se numește abatere standard (vezi Abaterea pătrată). Pentru o variabilă aleatorie X cu o distribuție continuă de probabilitate caracterizată printr-o densitate de probabilitate (vezi Densitatea probabilității) R(X), D. se calculează prin formula În teoria probabilității mare importanță are o teoremă: D. suma termenilor independenți este egală cu suma D lor. Nu mai puțin importantă este inegalitatea Cebyshev, care permite estimarea probabilității abaterilor mari ale unei variabile aleatoare X din așteptările sale matematice. Prezența undelor D. duce la o distorsiune a formei semnalelor pe măsură ce acestea se propagă în mediu. Acest lucru se datorează faptului că undele armonice de frecvențe diferite, în care semnalul poate fi descompus, se propagă la viteze diferite (pentru mai multe detalii, vezi Unde, Viteza grupului). D. lumina când se propagă într-o prismă transparentă duce la descompunere lumină albăîn spectru (vezi Dispersia luminii).![]()
![]()
Marea Enciclopedie Sovietică. - M.: Enciclopedia Sovietică. 1969-1978 .
Sinonime:Vedeți ce este „Dispersia” în alte dicționare:
dispersie- Imprăștiind ceva. În matematică, varianța măsoară abaterea valorilor de la medie. Dispersia luminii albe duce la descompunerea acesteia în componente. Dispersia sunetului este cauza răspândirii acestuia. Se împrăștie datele stocate în… … Manualul Traducătorului Tehnic
Enciclopedia modernă
- (varianță) O măsură a împrăștierii datelor. Varianța unei mulțimi de N termeni se găsește adunând pătratele abaterilor lor de la medie și împărțind la N. Prin urmare, dacă termenii sunt xi la i = 1, 2, ..., N, iar media lor este m , varianța ...... Dicționar economic
Dispersia- (din latinescul dispersio scattering) unde, dependența vitezei de propagare a undelor într-o substanță de lungimea de undă (frecvența). Se determină dispersia proprietăți fizice mediul în care se propagă undele. De exemplu, în vid ...... Ilustrat Dicţionar enciclopedic
- (din lat. dispersio scattering) în statistica matematică și teoria probabilității, o măsură a dispersiei (abaterea de la medie). În statistică, varianța este media aritmetică a abaterilor pătrate ale valorilor observate (x1, x2,...,xn) ale unui ... ... Dicţionar enciclopedic mare
În teoria probabilității, cea mai utilizată măsură a abaterii de la medie (măsura de împrăștiere). În engleză: Dispersion Sinonime: Statistical dispersion Sinonime în engleză: Statistical dispersion Vezi și: Exemplu de populații Financiar ... ... Vocabular financiar
- [lat. dispersus împrăștiat, împrăștiat] 1) împrăștiere; 2) chimic, fizic. descompunerea unei substanțe în particule foarte mici. D. descompunerea luminii a luminii albe folosind o prismă într-un spectru; 3) mat. abatere de la medie. Dicționar de cuvinte străine. Komlev N.G.,… … Dicționar de cuvinte străine ale limbii ruse
dispersie- indicator (varianță) al dispersării datelor, corespunzător pătratului mediu al abaterii acestor date de la media aritmetică. Egal cu pătratul abaterii standard. Dicţionar psiholog practic. Moscova: AST, Harvest. S. Yu. Golovin. 1998... Marea Enciclopedie Psihologică
Scattering, scattering Dicționar de sinonime rusești. substantiv dispersie, număr de sinonime: 6 nanodispersion (1) … Dicţionar de sinonime
Dispersia este caracteristica de dispersie a valorilor unei variabile aleatoare, măsurată prin pătratul abaterilor acestora de la valoarea medie (notat cu d2). D. diferă teoretic (continuu sau discret) și empiric (tot continuu și ... ... Dicţionar economic şi matematic
Dispersia- * dispersie * dispersie 1. Imprastiere; împrăștia; variaţie (vezi). 2. Un concept teoretic probabilist care caracterizează gradul de abatere al unei variabile aleatoare de la așteptarea ei matematică. În practica biometrică, varianța eșantionului s2 ... Genetica. Dicţionar enciclopedic
Cărți
- Dispersie anormală în benzi largi de absorbție, D.S. Crăciun. Reproduce în ortografia originală a autorului ediției din 1934 (editura `Proceedings of the Academy of Sciences of the URSS`). ÎN…
Interval de variație (sau interval de variație) - este diferența dintre valorile maxime și minime ale caracteristicii:
În exemplul nostru, intervalul de variație a randamentului în ture a muncitorilor este: în prima brigadă R=105-95=10 copii, în a doua brigadă R=125-75=50 copii. (de 5 ori mai mult). Acest lucru sugerează că producția primei brigăzi este mai „stabilă”, dar a doua brigadă are mai multe rezerve pentru creșterea producției, deoarece. dacă toți muncitorii ating puterea maximă pentru această brigadă, poate produce 3 * 125 = 375 de piese, iar în brigada 1 doar 105 * 3 = 315 de piese.
Dacă valorile extreme ale atributului nu sunt tipice pentru populație, atunci se folosesc intervale de cuartile sau decile. Intervalul de quartile RQ= Q3-Q1 acoperă 50% din populație, primul interval decilă RD1 = D9-D1 acoperă 80% din date, al doilea interval decilă RD2= D8-D2 acoperă 60%.
Dezavantajul indicatorului de interval de variație este că valoarea acestuia nu reflectă toate fluctuațiile trăsăturii.
Cel mai simplu indicator de generalizare care reflectă toate fluctuațiile unei trăsături este abaterea liniară medie, care este media aritmetică a abaterilor absolute ale opțiunilor individuale de la valoarea lor medie:
,
pentru date grupate ![]() ,
,
unde хi este valoarea atributului într-o serie discretă sau mijlocul intervalului în distribuția intervalului.
În formulele de mai sus, diferențele de numărător sunt luate modulo, în caz contrar, în funcție de proprietatea mediei aritmetice, numărătorul va fi întotdeauna egal cu zero. Prin urmare, abaterea liniară medie în practica statistică este rar utilizată, doar în cazurile în care însumarea indicatorilor fără a lua în considerare semnul are sens economic. Cu ajutorul acestuia, de exemplu, sunt analizate compoziția angajaților, profitabilitatea producției și cifra de afaceri din comerțul exterior.
Varianta caracteristicilor este pătratul mediu al abaterilor variantei de la valoarea lor medie:
varianță simplă ![]() ,
,
varianță ponderată  .
.
Formula de calcul a varianței poate fi simplificată:
Astfel, varianța este egală cu diferența dintre media pătratelor variantei și pătratul mediei variantei populației:  .
.
Cu toate acestea, datorită însumării abaterilor pătrate, varianța oferă o idee distorsionată a abaterilor, astfel încât media este calculată din aceasta. deviație standard, care arată cât de mult se abate în medie variantele specifice ale atributului de la valoarea lor medie. Calculat prin extragere rădăcină pătrată din dispersie:
pentru date negrupate  ,
,
pentru seria de variații 
Cum valoare mai mică dispersia și abaterea standard, cu cât populația este mai omogenă, cu atât va fi mai fiabilă (tipic). valoarea medie.
Abaterea medie liniară și pătrată medie sunt numite numere, adică sunt exprimate în unități de măsură ale caracteristicii, sunt identice ca conținut și apropiate ca valoare.
Se recomandă calcularea indicatorilor absoluti de variație folosind tabele.
Tabelul 3 - Calculul caracteristicilor de variație (pe exemplul perioadei de date privind ieșirea în schimburi a echipelor de lucru)
Numărul de muncitori |
Mijlocul intervalului |
Valori estimate |
|||||
Total: |
|||||||
Ieșirea medie pe ture a lucrătorilor: ![]()
Abaterea liniară medie: ![]()
Dispersia ieșirii: 
Abaterea standard a producției lucrătorilor individuali de la producția medie:
.
1 Calculul dispersiei prin metoda momentelor
Calculul variațiilor este asociat cu calcule greoaie (mai ales dacă media este exprimată ca număr mare cu mai multe zecimale). Calculele pot fi simplificate folosind o formulă simplificată și proprietăți de dispersie.
Dispersia are următoarele proprietăți:
- dacă toate valorile atributului sunt reduse sau crescute cu aceeași valoare A, atunci varianța nu va scădea de la aceasta:
 ,
,
 , apoi sau
, apoi sau 
Folosind proprietățile varianței și mai întâi reducând toate variantele populației cu valoarea A, apoi împărțind la valoarea intervalului h, obținem o formulă de calcul a varianței în serii variaționale cu intervale egale. modul momentelor: ,
,
unde este dispersia calculată prin metoda momentelor;
h este valoarea intervalului seriei de variații;
– noi valori ale variantei (transformate);
A- constant, care este folosit ca mijloc al intervalului cu cea mai mare frecvență; sau varianta cu cea mai mare frecvență;  este pătratul momentului de ordinul întâi;
este pătratul momentului de ordinul întâi;
este un moment de ordinul doi.
Să calculăm varianța prin metoda momentelor pe baza datelor privind rezultatul schimburilor echipei de lucru.
Tabelul 4 - Calculul dispersiei prin metoda momentelor
Grupuri de muncitori de productie, buc. |
Numărul de muncitori |
Mijlocul intervalului |
Valori estimate |
||
Procedura de calcul:


- calculați varianța:
2 Calculul varianței unei caracteristici alternative
Printre semnele studiate de statistică se numără cele care au doar două semnificații care se exclud reciproc. Acestea sunt semne alternative. Li se acordă două valori cantitative, respectiv: opțiunile 1 și 0. Frecvența opțiunilor 1, care se notează cu p, este proporția unităților care au această caracteristică. Diferența 1-p=q este frecvența opțiunilor 0. Astfel,
xi |
|
Media aritmetică a caracteristicii alternative ![]() , deoarece p+q=1.
, deoarece p+q=1.
Varianta caracteristicilor
, deoarece 1-p=q
Astfel, varianța unui atribut alternativ este egală cu produsul dintre proporția de unități care au acest atribut și proporția de unități care nu au acest atribut.
Dacă valorile 1 și 0 sunt la fel de frecvente, adică p=q, varianța își atinge maximul pq=0,25.
Variabila de variație este utilizată în sondajele prin eșantion, de exemplu, calitatea produsului.
3 Dispersia intergrupurilor. Regula de adunare a variațiilor
Dispersia, spre deosebire de alte caracteristici ale variației, este o cantitate aditivă. Adică în agregat, care este împărțit în grupuri după criteriul factorului X , varianta rezultata y poate fi descompusă în varianță în cadrul fiecărui grup (în cadrul grupului) și varianță între grupuri (între grup). Apoi, odată cu studiul variației trăsăturii în întreaga populație în ansamblu, devine posibil să se studieze variația în fiecare grup, precum și între aceste grupuri.
Varianta totala măsoară variația unei trăsături la asupra întregii populaţii sub influenţa tuturor factorilor care au determinat această variaţie (abateri). Este egal cu pătratul mediu al abaterilor valorilor individuale ale caracteristicii la a mediei generale și poate fi calculată ca varianță simplă sau ponderată.
Varianta intergrup caracterizează variaţia caracteristicii efective la, cauzată de influența factorului-semn X care stă la baza grupării. Caracterizează variația mediilor grupului și este egal cu pătratul mediu al abaterilor mediilor grupului de la media totală:  ,
,
unde este media aritmetică a grupului i;
– numărul de unități din i-a grupă (frecvența i-a grupă);
este media totală a populației.
Varianta intragrup reflectă variația aleatorie, adică acea parte a variației care este cauzată de influența unor factori necontabiliați și nu depinde de factorul-atribut care stă la baza grupării. Caracterizează variația valorilor individuale în raport cu mediile de grup, este egal cu pătratul mediu al abaterilor valorilor individuale ale trăsăturii laîn cadrul unui grup din media aritmetică a acestui grup (media grupului) și se calculează ca o varianță simplă sau ponderată pentru fiecare grup: ![]() sau
sau ![]() ,
,
unde este numărul de unități din grup.
Pe baza variațiilor intra-grup pentru fiecare grup, este posibil să se determine media generală a variațiilor în cadrul grupului:
.
Relația dintre cele trei varianțe se numește reguli de adăugare a varianței, conform căruia varianța totală este egală cu suma varianței intergrup și media variațiilor intragrup:
Exemplu. Când se studiază influența categorie tarifară(calificarea) lucrătorilor asupra nivelului de productivitate a muncii lor, s-au obţinut următoarele date.
Tabelul 5 - Distribuția lucrătorilor în funcție de producția medie orară.
№ p/n |
Muncitori din categoria a 4-a |
Muncitori din categoria a 5-a |
|||||
De lucru |
De lucru |
||||||
1 |
7 |
7-10=-3 |
9 |
1 |
14 |
14-15=-1 |
1 |
ÎN acest exemplu lucrătorii sunt împărțiți în două grupe după un criteriu factori X- calificări, care se caracterizează prin rangul lor. Trăsătura efectivă - producția - variază atât sub influența sa (variația intergrup), cât și datorită altor factori aleatori (variația intragrup). Provocarea este de a măsura aceste variații folosind trei variații: total, între grup și în interiorul grupului. Coeficientul empiric de determinare arată proporția de variație a caracteristicii rezultate la sub influența unui semn factor X. Restul variației totale la cauzate de modificări ale altor factori.
În exemplu, coeficientul empiric de determinare este: ![]() sau 66,7%,
sau 66,7%,
Aceasta înseamnă că 66,7% din variația productivității muncii a lucrătorilor se datorează diferențelor de calificare, iar 33,3% se datorează influenței altor factori.
Relația de corelație empirică arată strânsoarea relației dintre grupare și caracteristicile efective. Se calculează ca rădăcină pătrată a coeficientului empiric de determinare:
Raportul de corelație empirică, precum și , pot lua valori de la 0 la 1.
Dacă nu există nicio conexiune, atunci =0. În acest caz, =0, adică mediile grupului sunt egale între ele și nu există nicio variație intergrup. Aceasta înseamnă că semnul de grupare - factorul nu afectează formarea variației generale.
Dacă relația este funcțională, atunci =1. În acest caz, varianța mediilor grupului este egală cu varianța totală (), adică nu există o variație intragrup. Aceasta înseamnă că caracteristica de grupare determină complet variația caracteristicii rezultate care este studiată.
Cu cât valoarea relației de corelație este mai apropiată de unul, cu atât mai aproape, mai aproape de dependența funcțională, relația dintre trăsături.
Pentru o evaluare calitativă a strângerii legăturii dintre semne se folosesc relațiile Chaddock.
În exemplu ![]() , ceea ce indică legătură strânsăîntre productivitatea muncitorilor şi calificările acestora.
, ceea ce indică legătură strânsăîntre productivitatea muncitorilor şi calificările acestora.