Cele mai mari și cele mai mici valori fără derivată. Cea mai mare și cea mai mică valoare a funcției

În lecția cu tema „Folosirea unei derivate pentru a găsi cele mai mari și cele mai mici valori functie continua pe interval” vor fi considerate probleme relativ simple de a găsi cele mai mari și mai mici valori ale unei funcții pe un interval dat folosind o derivată.

Tema: Derivată

Lecție: Folosirea unei derivate pentru a găsi cele mai mari și cele mai mici valori ale unei funcții continue pe un interval

În această lecție, ne vom uita la mai multe o sarcină simplă, și anume, se va da un interval, se va da o funcție continuă pe acest interval. Trebuie să aflăm cel mai mult cea mai mică valoare dat funcții pe un dat interval.

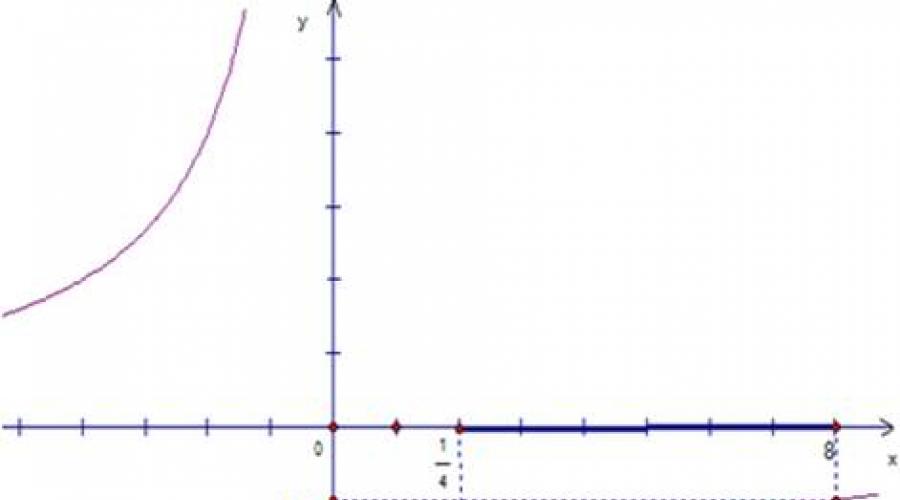
Nr. 32.1 (b). Dat: , . Să desenăm un grafic al funcției (vezi Fig. 1).

Orez. 1. Graficul unei funcții.

Se știe că această funcție crește pe interval , ceea ce înseamnă că crește și pe interval . Deci, dacă găsiți valoarea funcției în punctele și , atunci limitele de schimbare ale acestei funcții, valoarea ei cea mai mare și cea mai mică, vor fi cunoscute.

Când argumentul crește de la la 8, funcția crește de la la .

Răspuns: ; .

№ 32.2 (a) dat: Găsiți cele mai mari și cele mai mici valori ale funcției pe un interval dat.

Să construim un grafic al acestei funcții (vezi Fig. 2).

Dacă argumentul se schimbă pe intervalul , atunci funcția crește de la -2 la 2. Dacă argumentul crește de la , atunci funcția scade de la 2 la 0.

Orez. 2. Graficul unei funcții.

Să găsim derivata.

, . Dacă , atunci această valoare aparține și segmentului dat. Daca atunci . Este ușor de verificat dacă ia alte valori, punctele staționare corespunzătoare trec dincolo de segmentul dat. Să comparăm valorile funcției la capetele segmentului și în punctele selectate în care derivata este egală cu zero. Sa gasim

;

Răspuns: ;.

Deci, răspunsul este primit. Derivatul în acest caz poate fi folosit, nu îl puteți folosi, aplicați proprietățile funcției care au fost studiate mai devreme. Nu este întotdeauna cazul, uneori utilizarea unui derivat este singura metodă care vă permite să rezolvați astfel de probleme.

Dat: , . Găsiți cea mai mare și cea mai mică valoare a funcției pe segmentul dat.

Dacă în cazul precedent a fost posibil să se facă fără derivată - știam cum se comportă funcția, atunci în acest caz funcția este destul de complicată. Prin urmare, metodologia pe care am menționat-o în sarcina anterioară este pe deplin aplicabilă.

1. Găsiți derivata. Să găsim puncte critice, deci, - puncte critice. Dintre acestea, le selectăm pe cele care aparțin acestui segment: . Să comparăm valoarea funcției la punctele , , . Pentru aceasta găsim

Ilustram rezultatul in figura (vezi Fig. 3).

Orez. 3. Limitele de modificare a valorilor funcției

Vedem că dacă argumentul se schimbă de la 0 la 2, funcția se schimbă de la -3 la 4. Funcția nu se schimbă monoton: fie crește, fie scade.

Răspuns: ;.

Deci, folosind trei exemple, a fost demonstrată o tehnică generală pentru găsirea valorilor mai mari și cele mai mici ale unei funcții pe un interval, în acest caz, pe un segment.

Algoritm pentru rezolvarea problemei de a găsi cele mai mari și mai mici valori ale funcției:

1. Aflați derivata funcției.

2. Găsiți punctele critice ale funcției și selectați acele puncte care se află pe un segment dat.

3. Găsiți valorile funcției la capetele segmentului și la punctele selectate.

4. Comparați aceste valori și alegeți cea mai mare și cea mai mică.

Să luăm în considerare încă un exemplu.

Găsiți cea mai mare și cea mai mică valoare a funcției , .

Anterior, a fost luat în considerare graficul acestei funcții (vezi Fig. 4).

Orez. 4. Graficul unei funcții.

Pe interval, intervalul acestei funcții . Punctul este punctul maxim. Când - funcția crește, când - funcția scade. Din desen se poate observa că , - nu există.

Deci, în lecție am luat în considerare problema celei mai mari și mai mici valori a unei funcții, când un interval dat este un segment; a formulat un algoritm pentru rezolvarea unor astfel de probleme.

1. Algebra și începutul analizei, nota 10 (în două părți). Manual pentru instituțiile de învățământ ( nivel de profil) ed. A. G. Mordkovici. -M.: Mnemosyne, 2009.

2. Algebra și începutul analizei, nota 10 (în două părți). Caiet de sarcini pentru instituțiile de învățământ (nivel de profil), ed. A. G. Mordkovici. -M.: Mnemosyne, 2007.

3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Algebră și analiză matematică pentru nota 10 ( tutorial pentru elevii școlilor și claselor cu studiu aprofundat al matematicii).-M .: Educație, 1996.

4. Galitsky M.L., Moshkovich M.M., Shvartburd S.I. Un studiu aprofundat al algebrei și al analizei matematice.-M .: Education, 1997.

5. Culegere de probleme de matematică pentru candidații la universitățile tehnice (sub redacția M.I.Skanavi).-M.: Liceul, 1992.

6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Antrenor algebric.-K.: A.S.K., 1997.

7. Zvavich L.I., Shlyapochnik L.Ya., Chinkina Algebra și începuturile analizei. 8-11 celule: Un manual pentru școli și clase cu studiu aprofundat al matematicii (materiale didactice) - M .: Drofa, 2002.

8. Saakyan S.M., Goldman A.M., Denisov D.V. Tasks in Algebra and the Beginnings of Analysis (un manual pentru elevii din clasele 10-11 ale instituțiilor de învățământ general).-M .: Educație, 2003.

9. Karp A.P. Culegere de probleme de algebră și începuturile analizei: manual. alocație pentru 10-11 celule. cu o adâncime studiu matematică.-M.: Educaţie, 2006.

10. Glazer G.I. Istoria matematicii la scoala. Clasele 9-10 (un ghid pentru profesori).-M.: Enlightenment, 1983

Resurse web suplimentare

2. Portal Stiintele Naturii ().

face acasa

Nr. 46.16, 46.17 (c) (Algebra și începutul analizei, nota 10 (în două părți). Caiet de sarcini pentru instituțiile de învățământ general (nivel de profil) editat de A. G. Mordkovich. - M .: Mnemozina, 2007.)

Lasă funcția y=f(X) continuu pe segmentul [ a, b]. După cum se știe, o astfel de funcție își atinge valorile maxime și minime în acest interval. Funcția poate lua aceste valori fie într-un punct interior al segmentului [ a, b], sau la limita segmentului.

Pentru a găsi cele mai mari și cele mai mici valori ale unei funcții pe intervalul [ a, b] necesar:

1) găsiți punctele critice ale funcției în intervalul ( a, b);

2) calculați valorile funcției la punctele critice găsite;

3) calculați valorile funcției la capetele segmentului, adică pt X=Ași x = b;

4) dintre toate valorile calculate ale funcției, alegeți cea mai mare și cea mai mică.

Exemplu. Găsiți cele mai mari și cele mai mici valori ale unei funcții

pe segment.

Găsirea punctelor critice:

Aceste puncte se află în interiorul segmentului; y(1) = ‒ 3; y(2) = ‒ 4; y(0) = ‒ 8; y(3) = 1;

la punct X= 3 și la punct X= 0.

Investigarea unei funcții pentru convexitate și un punct de inflexiune.

Funcţie y = f (X) numit convexă intre (A, b) , dacă graficul său se află sub o tangentă desenată în orice punct al acestui interval și se numește convex în jos (concav) dacă graficul său se află deasupra tangentei.

Se numește punctul de tranziție prin care convexitatea este înlocuită cu concavitate sau invers punct de inflexiune.

Algoritm pentru studiul convexității și punctului de inflexiune:

1. Aflați punctele critice de al doilea fel, adică punctele în care derivata a doua este egală cu zero sau nu există.

2. Pune punctele critice pe dreapta numerică, împărțind-o în intervale. Aflați semnul derivatei a doua pe fiecare interval; dacă , atunci funcția este convexă în sus, dacă, atunci funcția este convexă în jos.

3. Dacă, la trecerea printr-un punct critic de al doilea fel, acesta își schimbă semnul și în acest punct derivata a doua este egală cu zero, atunci acest punct este abscisa punctului de inflexiune. Găsiți-i ordonata.

Asimptotele graficului unei funcții. Investigarea unei funcții în asimptote.

Definiție. Asimptota graficului unei funcții se numește Drept, care are proprietatea că distanța de la orice punct al graficului până la această linie tinde spre zero cu o îndepărtare nelimitată a punctului grafic de la origine.

Există trei tipuri de asimptote: vertical, orizontal și înclinat.

Definiție. Apelat direct asimptotă verticală graficul funcției y = f(x), dacă cel puțin una dintre limitele unilaterale ale funcției în acest punct este egală cu infinit, adică

unde este punctul de discontinuitate al funcției, adică nu aparține domeniului definiției.

Exemplu.

D( y) = (‒ ∞; 2) (2; + ∞)

X= 2 - punctul de rupere.

Definiție. Drept y=A numit asimptotă orizontală graficul funcției y = f(x) la , dacă

Exemplu.

Definiție. Drept y=kx +b (k≠ 0) se numește asimptotă oblică graficul funcției y = f(x) unde

Schema generală pentru studiul funcțiilor și a graficului.

Algoritm de cercetare a funcțieiy = f(x) :

1. Găsiți domeniul funcției D (y).

2. Găsiți (dacă este posibil) punctele de intersecție ale graficului cu axele de coordonate (cu X= 0 și la y = 0).

3. Investigați funcțiile pare și impare ( y (‒ X) = y (X) ‒ paritate; y(‒ X) = ‒ y (X) ‒ ciudat).

4. Găsiți asimptotele graficului funcției.

5. Găsiți intervalele de monotonitate ale funcției.

6. Aflați extremele funcției.

7. Aflați intervalele de convexitate (concavitate) și punctele de inflexiune ale graficului funcției.

8. Pe baza cercetărilor efectuate, construiți un grafic al funcției.

Exemplu. Investigați funcția și trasați graficul acesteia.

1) D (y) =

X= 4 - punctul de rupere.

2) Când X = 0,

(0; – 5) – punctul de intersecție cu oi.

La y = 0,

3) y(‒ X)= funcţie vedere generala(nici par, nici impar).

4) Investigam pentru asimptote.

a) verticală

b) orizontală

c) găsi asimptote oblice unde

‒ecuația de asimptotă oblică

5) B ecuația dată nu este necesar să se găsească intervale de monotonitate ale funcției.

6)

Aceste puncte critice împart întregul domeniu al funcției pe intervalul (˗∞; ˗2), (˗2; 4), (4; 10) și (10; +∞). Este convenabil să prezentați rezultatele obținute sub forma următorului tabel.

Dragi prieteni! Grupul de sarcini legate de derivată include sarcini - în condiție, este dat graficul funcției, mai multe puncte pe acest grafic și întrebarea este:

În ce moment este valoarea derivatei cea mai mare (mai mică)?

Să repetăm ​​pe scurt:

Derivata la un punct este coeficient unghiular tangente care trece prinacest punct din grafic.

Lacoeficientul global al tangentei la rândul său egal cu tangenta panta acestei tangente.

*Acest lucru se referă la unghiul dintre tangentă și axa x.

1. Pe intervale de funcție crescătoare, derivata are valoare pozitivă.

2. Pe intervalele scăderii sale, derivata are valoare negativă.

Luați în considerare următoarea schiță:

La punctele 1,2,4, derivata funcției are o valoare negativă, deoarece aceste puncte aparțin intervalelor descrescătoare.

La punctele 3,5,6, derivata funcției are o valoare pozitivă, deoarece aceste puncte aparțin intervalelor de creștere.

După cum puteți vedea, totul este clar cu valoarea derivatei, adică nu este dificil să determinați ce semn are (pozitiv sau negativ) la un anumit punct al graficului.

Mai mult, dacă construim mental tangente în aceste puncte, vom vedea că liniile care trec prin punctele 3, 5 și 6 formează unghiuri cu axa oX situată în intervalul de la 0 la 90 °, iar liniile care trec prin punctele 1, 2 și 4 formează cu axa oX, unghiuri cuprinse între 90 o și 180 o.

* Relația este clară: tangentele care trec prin puncte aparținând intervalelor de funcții crescătoare formează unghiuri ascuțite cu axa oX, tangentele care trec prin puncte aparținând intervalelor de funcții descrescătoare formează unghiuri obtuze cu axa oX.

Acum întrebarea importantă!

Cum se modifică valoarea instrumentului derivat? La urma urmei, tangenta puncte diferite Graficul unei funcții continue formează unghiuri diferite, în funcție de punctul prin care trece.

* Sau, vorbind limbaj simplu, tangenta este situată, parcă, „mai orizontal” sau „mai vertical”. Uite:

Liniile drepte formează unghiuri cu axa oX variind de la 0 la 90 o

Liniile drepte formează unghiuri cu axa oX variind de la 90 o până la 180 o

Deci, dacă există întrebări:

- în care dintre punctele date din grafic valoarea derivatei are cea mai mică valoare?

- în care dintre punctele date din grafic valoarea derivatei are cea mai mare valoare?

atunci pentru răspuns este necesar să înțelegem cum se modifică valoarea tangentei unghiului tangentei în intervalul de la 0 la 180 o.

* După cum sa menționat deja, valoarea derivatei funcției într-un punct este egală cu tangentei pantei tangentei la axa x.

Valoarea tangentei se modifică după cum urmează:

Când panta dreptei se modifică de la 0 o la 90 o, valoarea tangentei și, prin urmare, derivata, se modifică de la 0 la +∞, respectiv;

Când panta dreptei se schimbă de la 90 o la 180 o, valoarea tangentei și, prin urmare, derivata, se modifică în consecință –∞ la 0.

Acest lucru poate fi văzut clar din graficul funcției tangente:

In termeni simpli:

Când unghiul de înclinare al tangentei este de la 0 o până la 90 o

Cu cât este mai aproape de 0 o, cu atât valoarea derivatei va fi mai mare aproape de zero (pe partea pozitivă).

Cu cât unghiul este mai aproape de 90°, cu atât valoarea derivatei va crește spre +∞.

Când unghiul de înclinare al tangentei este de la 90 o până la 180 o

Cu cât este mai aproape de 90 o, cu atât valoarea derivatei va scădea spre –∞.

Cu cât unghiul este mai aproape de 180 o, cu atât valoarea derivatei va fi mai aproape de zero (pe partea negativă).

317543. Figura prezintă un grafic al funcției y = f(X) și puncte marcate–2, –1, 1, 2. În care dintre aceste puncte este cea mai mare valoarea derivatei? Vă rugăm să indicați acest punct în răspunsul dvs.

Avem patru puncte: două dintre ele aparțin intervalelor la care funcția scade (sunt punctele –1 și 1) și două intervalelor la care funcția crește (sunt punctele –2 și 2).

Putem concluziona imediat că la punctele -1 și 1 derivata are o valoare negativă, la punctele -2 și 2 are o valoare pozitivă. Prin urmare, în acest caz, este necesar să se analizeze punctele -2 și 2 și să se determine care dintre ele va avea cea mai mare valoare. Să construim tangente care trec prin punctele indicate:

Valoarea tangentei unghiului dintre dreapta a și axa absciselor va fi mai multă valoare tangenta unghiului dintre linia b si aceasta axa. Aceasta înseamnă că valoarea derivatei în punctul -2 va fi cea mai mare.

Să răspundem la următoarea întrebare: în care dintre punctele -2, -1, 1 sau 2 este valoarea derivatei cea mai mare negativă? Vă rugăm să indicați acest punct în răspunsul dvs.

Derivata va avea o valoare negativă în punctele aparținând intervalelor descrescătoare, deci luați în considerare punctele -2 și 1. Să construim tangentele care trec prin ele:

Noi vedem asta unghi obtuzîntre linia b și axa oX este „mai aproape” de 180 O , deci tangenta sa va fi mai mare decât tangenta unghiului format de dreapta a și axa x.

Astfel, în punctul x = 1, valoarea derivatei va fi cea mai mare negativă.

317544. Figura prezintă un grafic al funcției y = f(X) și puncte marcate–2, –1, 1, 4. În care dintre aceste puncte este valoarea derivatei cea mai mică? Vă rugăm să indicați acest punct în răspunsul dvs.

Avem patru puncte: două dintre ele aparțin intervalelor la care funcția scade (sunt punctele –1 și 4) și două intervalelor la care funcția crește (sunt punctele –2 și 1).

Putem concluziona imediat că la punctele -1 și 4 derivata are valoare negativă, la punctele -2 și 1 are valoare pozitivă. Prin urmare, în acest caz, este necesar să se analizeze punctele –1 și 4 și să se determine care dintre ele va avea cea mai mică valoare. Să construim tangente care trec prin punctele indicate:

Valoarea tangentei unghiului dintre linia a și axa absciselor va fi mai mare decât valoarea tangentei unghiului dintre dreapta b și această axă. Aceasta înseamnă că valoarea derivatei în punctul x = 4 va fi cea mai mică.

Raspuns: 4

Sper că nu te-am „supraîncărcat” cu cantitatea de scris. De fapt, totul este foarte simplu, trebuie doar să înțelegeți proprietățile derivatei, semnificația ei geometrică și modul în care valoarea tangentei unghiului se modifică de la 0 la 180 o.

1. Mai întâi, determină semnele derivatei în aceste puncte (+ sau -) și selectează punctele necesare (în funcție de întrebarea pusă).

2. Construiți tangente în aceste puncte.

3. Folosind graficul tangesoid, marcați schematic colțurile și afișațiAlexandru.

P.S: Aș fi recunoscător dacă ai spune despre site în rețelele de socializare.

Uneori, în problemele B15 există funcții „proaste” pentru care este greu de găsit derivata. Anterior, acest lucru era doar pe sonde, dar acum aceste sarcini sunt atât de comune încât nu mai pot fi ignorate atunci când se pregătesc pentru acest examen.

În acest caz, funcționează alte trucuri, dintre care unul este - monoton.

Funcția f (x) se numește monoton crescătoare pe segment dacă pentru orice puncte x 1 și x 2 ale acestui segment este adevărat:

x 1< x 2 ⇒ f (x 1) < f (x2).

Funcția f (x) se numește monoton descrescătoare pe segment dacă pentru orice puncte x 1 și x 2 ale acestui segment este adevărat:

x 1< x 2 ⇒ f (x 1) > f( x2).

Cu alte cuvinte, pentru o funcție crescătoare, cu cât x este mai mare, cu atât f(x) este mai mare. Pentru o funcție descrescătoare, opusul este adevărat: cu cât x , cu cât Mai puțin f(x).

De exemplu, logaritmul crește monoton dacă baza a > 1 și scade monoton dacă 0< a < 1. Не забывайте про область допустимых значений логарифма: x > 0.

f (x) = log a x (a > 0; a ≠ 1; x > 0)

Rădăcina pătrată aritmetică (și nu numai pătrată) crește monoton pe întregul domeniu de definiție:

Funcția exponențială se comportă similar cu logaritmul: crește pentru a > 1 și scade pentru 0< a < 1. Но в отличие от логарифма, functie exponentiala definit pentru toate numerele, nu doar x > 0:

f (x) = a x (a > 0)

În cele din urmă, grade cu exponent negativ. Le puteți scrie ca fracție. Au un punct de rupere în care monotonia este ruptă.

Toate aceste caracteristici nu se găsesc niciodată în formă pură. La acestea se adaugă polinoame, fracții și alte prostii, din cauza cărora devine dificil să se calculeze derivata. Ce se întâmplă în acest caz - acum vom analiza.

Coordonatele vârfurilor parabolei

Cel mai adesea, argumentul funcției este înlocuit cu trinom pătrat de forma y = ax 2 + bx + c . Graficul său este o parabolă standard, în care ne interesează:

1. Ramuri de parabolă - pot merge în sus (pentru a > 0) sau în jos (a< 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Vârful parabolei este punctul extremum al unei funcții pătratice, la care această funcție își ia cea mai mică (pentru a > 0) sau cea mai mare (a< 0) значение.

De cel mai mare interes este vârful unei parabole, a cărei abscisă se calculează cu formula:

Deci, am găsit punctul extremum al funcției pătratice. Dar dacă funcția originală este monotonă, pentru ea punctul x 0 va fi și un punct extremum. Astfel, formulăm regula cheie:

Punctele extreme ale trinomului pătrat și functie complexa, în care intră, sunt aceleași. Prin urmare, puteți căuta x 0 pentru un trinom pătrat și uitați de funcție.

Din raționamentul de mai sus, rămâne neclar ce fel de punct obținem: un maxim sau un minim. Cu toate acestea, sarcinile sunt concepute special, astfel încât să nu conteze. Judecă singur:

1. Nu există niciun segment în starea problemei. Prin urmare, nu este necesar să se calculeze f(a) și f(b). Rămâne să luăm în considerare doar punctele extremum;
2. Dar există un singur astfel de punct - acesta este vârful parabolei x 0, ale cărui coordonate sunt calculate literalmente oral și fără derivate.

Astfel, soluția problemei este mult simplificată și redusă la doar doi pași:

1. Scrieți ecuația parabolei y = ax 2 + bx + c și găsiți vârful acesteia folosind formula: x 0 = −b /2a;
2. Găsiți valoarea funcției inițiale în acest punct: f (x 0). Dacă niciunul conditii suplimentare nu, acesta ar fi raspunsul.

La prima vedere, acest algoritm și justificarea lui pot părea complicate. Nu postez în mod deliberat o schemă de soluții „nudă”, deoarece aplicarea necugetă a unor astfel de reguli este plină de erori.

Luați în considerare sarcinile reale de la examenul de probă la matematică - aici este cea mai comună tehnică. În același timp, ne vom asigura că în acest fel multe probleme ale B15 devin aproape verbale.

Sub rădăcină este funcţie pătratică y \u003d x 2 + 6x + 13. Graficul acestei funcții este o parabolă cu ramuri în sus, deoarece coeficientul a \u003d 1\u003e 0.

Partea de sus a parabolei:

x 0 \u003d -b / (2a) \u003d -6 / (2 1) \u003d -6 / 2 \u003d -3

Deoarece ramurile parabolei sunt îndreptate în sus, în punctul x 0 \u003d −3, funcția y \u003d x 2 + 6x + 13 ia cea mai mică valoare.

Rădăcina crește monoton, deci x 0 este punctul minim al întregii funcții. Avem:

Sarcină. Găsiți cea mai mică valoare a funcției:

y = log 2 (x 2 + 2x + 9)

Sub logaritm este din nou o funcție pătratică: y \u003d x 2 + 2x + 9. Graficul este o parabolă cu ramuri în sus, deoarece a = 1 > 0.

Partea de sus a parabolei:

x 0 \u003d -b / (2a) \u003d -2 / (2 1) \u003d -2/2 \u003d -1

Deci, în punctul x 0 = −1, funcția pătratică ia cea mai mică valoare. Dar funcția y = log 2 x este monotonă, deci:

y min = y (−1) = log 2 ((−1) 2 + 2 (−1) + 9) = ... = log 2 8 = 3

Exponentul este o funcție pătratică y = 1 − 4x − x 2 . Să o rescriem în formă normală: y = −x 2 − 4x + 1.

În mod evident, graficul acestei funcții este o parabolă, ramificate în jos (a = -1< 0). Поэтому вершина будет точкой максимума:

x 0 = −b /(2a ) = −(−4)/(2 (−1)) = 4/(−2) = −2

Funcția originală este exponențială, este monotonă, deci cea mai mare valoare va fi în punctul găsit x 0 = −2:

Un cititor atent va observa cu siguranță că nu am scris zona valorilor permise ale rădăcinii și logaritmului. Dar acest lucru nu a fost necesar: în interior există funcții ale căror valori sunt întotdeauna pozitive.

Consecințele din sfera unei funcții

Uneori, pentru a rezolva problema B15, nu este suficient să găsim vârful parabolei. Valoarea dorită poate fi la sfârșitul segmentului, dar nu la punctul extremum. Dacă sarcina nu specifică deloc un segment, priviți interval de toleranță functia originala. Și anume:

Fiți atenți din nou: zero poate fi sub rădăcină, dar niciodată în logaritmul sau numitorul unei fracții. Să vedem cum funcționează cu exemple specifice:

Sarcină. Găsiți cea mai mare valoare a funcției:

Sub rădăcină se află din nou o funcție pătratică: y \u003d 3 - 2x - x 2. Graficul său este o parabolă, dar se ramifică în jos deoarece a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический Rădăcină pătrată dintr-un număr negativ nu există.

Scriem zona valorilor permise (ODZ):

3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]

Acum găsiți vârful parabolei:

x 0 = −b /(2a ) = −(−2)/(2 (−1)) = 2/(−2) = −1

Punctul x 0 = −1 aparține segmentului ODZ - și acest lucru este bun. Acum luăm în considerare valoarea funcției în punctul x 0, precum și la sfârșitul ODZ:

y(−3) = y(1) = 0

Deci, am primit numerele 2 și 0. Ni se cere să găsim cel mai mare - acesta este numărul 2.

Sarcină. Găsiți cea mai mică valoare a funcției:

y = log 0,5 (6x - x 2 - 5)

În interiorul logaritmului există o funcție pătratică y \u003d 6x - x 2 - 5. Aceasta este o parabolă cu ramuri în jos, dar nu pot exista numere negative în logaritm, așa că scriem ODZ:

6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Vă rugăm să rețineți: inegalitatea este strictă, astfel încât capetele nu aparțin ODZ. În acest fel, logaritmul diferă de rădăcină, unde capetele segmentului ni se potrivesc destul de bine.

Căutând vârful parabolei:

x 0 = −b /(2a ) = −6/(2 (−1)) = −6/(−2) = 3

Vârful parabolei se potrivește de-a lungul ODZ: x 0 = 3 ∈ (1; 5). Dar din moment ce capetele segmentului nu ne interesează, considerăm valoarea funcției doar în punctul x 0:

y min = y (3) = log 0,5 (6 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2

Procesul de găsire a celor mai mici și mai mari valori ale unei funcții pe un segment amintește de un zbor fascinant în jurul unui obiect (un grafic al unei funcții) pe un elicopter cu tragere dintr-un tun cu rază lungă de acțiune în anumite puncte și alegând dintre aceste puncte puncte foarte speciale pentru lovituri de control. Punctele sunt selectate într-un anumit mod și în conformitate cu anumite reguli. După ce reguli? Vom vorbi mai departe despre asta.

Dacă funcţia y = f(X) continuu pe segmentul [ A, b] , apoi ajunge pe acest segment cel mai puţin Și cele mai mari valori . Acest lucru se poate întâmpla fie în puncte extremum sau la capetele segmentului. Prin urmare, pentru a găsi cel mai puţin Și cele mai mari valori ale funcției , continuu pe segmentul [ A, b] , trebuie să-i calculați valorile în totalitate puncte criticeși la capetele segmentului, apoi alegeți cel mai mic și cel mai mare dintre ele.

Să fie, de exemplu, să se determine valoarea maximă a funcției f(X) pe segmentul [ A, b] . Pentru a face acest lucru, găsiți toate punctele sale critice situate pe [ A, b] .

punct critic se numeste punctul in care functie definita, si ea derivat fie este zero, fie nu există. Apoi ar trebui să calculați valorile funcției în punctele critice. Și, în sfârșit, ar trebui să comparăm valorile funcției în punctele critice și la capetele segmentului ( f(A) Și f(b) ). Cel mai mare dintre aceste numere va fi cea mai mare valoare a funcției de pe segment [A, b] .

Problema găsirii cele mai mici valori ale funcției .

Căutăm împreună cele mai mici și cele mai mari valori ale funcției

Exemplul 1. Găsiți cele mai mici și cele mai mari valori ale unei funcții pe segment [-1, 2] .

Soluţie. Găsim derivata acestei funcții. Echivalează derivata cu zero () și obține două puncte critice: și . Pentru a găsi cele mai mici și mai mari valori ale unei funcții pe un anumit segment, este suficient să-i calculați valorile la capetele segmentului și în punctul , deoarece punctul nu aparține segmentului [-1, 2] . Aceste valori ale funcției sunt următoarele: , , . Rezultă că cea mai mică valoare a funcției(marcat cu roșu pe graficul de mai jos), egal cu -7, este atins la capătul din dreapta al segmentului - în punctul , și cel mai mare(de asemenea roșu pe grafic), este egal cu 9, - în punctul critic .

Dacă funcția este continuă într-un anumit interval și acest interval nu este un segment (dar este, de exemplu, un interval; diferența dintre un interval și un segment: punctele limită ale intervalului nu sunt incluse în interval, ci punctele de limită ale segmentului sunt incluse în segment), apoi printre valorile funcției este posibil să nu fie cel mai mic și cel mai mare. Deci, de exemplu, funcția descrisă în figura de mai jos este continuă pe ]-∞, +∞[ și nu are cea mai mare valoare.

Cu toate acestea, pentru orice interval (închis, deschis sau infinit), este valabilă următoarea proprietate a funcțiilor continue.

Exemplul 4. Găsiți cele mai mici și cele mai mari valori ale unei funcții pe segment [-1, 3] .

Soluţie. Găsim derivata acestei funcții ca derivată a coeficientului:

.

Echivalăm derivata cu zero, ceea ce ne oferă un punct critic: . Aparține intervalului [-1, 3] . Pentru a găsi cele mai mici și mai mari valori ale unei funcții pe un anumit segment, găsim valorile acesteia la capetele segmentului și în punctul critic găsit:

Să comparăm aceste valori. Concluzie: egal cu -5/13, la punctul și cea mai mare valoare egal cu 1 la punctul .

Continuăm să căutăm împreună cele mai mici și cele mai mari valori ale funcției

Sunt profesori care, pe tema găsirii celor mai mici și mai mari valori ale unei funcții, nu dau elevilor exemple mai complicate decât cele luate în considerare, adică acelea în care funcția este un polinom sau o fracție, numărătorul. iar numitorul cărora sunt polinoame. Dar nu ne vom limita la astfel de exemple, deoarece printre profesori sunt iubitori de a-i face pe elevi să gândească în întregime (tabelul derivatelor). Prin urmare, se vor folosi logaritmul și funcția trigonometrică.

Exemplul 6. Găsiți cele mai mici și cele mai mari valori ale unei funcții pe segment .

Soluţie. Găsim derivata acestei funcții ca derivat al produsului :

Echivalăm derivata cu zero, ceea ce dă un punct critic: . Aparține segmentului. Pentru a găsi cele mai mici și mai mari valori ale unei funcții pe un anumit segment, găsim valorile acesteia la capetele segmentului și în punctul critic găsit:

Rezultatul tuturor acțiunilor: funcția își atinge valoarea minimă, egal cu 0, într-un punct și într-un punct și cea mai mare valoare egal cu e² , la punctul .

Exemplul 7. Găsiți cele mai mici și cele mai mari valori ale unei funcții pe segment .

Soluţie. Găsim derivata acestei funcții:

Echivalează derivata cu zero:

Singurul punct critic aparține segmentului . Pentru a găsi cele mai mici și mai mari valori ale unei funcții pe un anumit segment, găsim valorile acesteia la capetele segmentului și în punctul critic găsit:

Concluzie: funcția își atinge valoarea minimă, egal cu , la punctul și cea mai mare valoare, egal cu , la punctul .

În problemele extreme aplicate, găsirea celor mai mici (mai mari) valori ale funcției, de regulă, se reduce la găsirea minimului (maximului). Dar nu minimele sau maximele în sine prezintă un interes practic mai mare, ci valorile argumentului la care sunt atinse. La rezolvarea problemelor aplicate, apare o dificultate suplimentară - compilarea funcțiilor care descriu fenomenul sau procesul luat în considerare.

Exemplul 8 Un rezervor cu o capacitate de 4, avand forma unui paralelipiped cu baza patrata si deschis in varf, trebuie sa fie cositorit. Care ar trebui să fie dimensiunile rezervorului, astfel încât să ia cea mai mică cantitate material?

Soluţie. Lăsa X- partea de bază h- inaltimea rezervorului, S- suprafața sa fără acoperire, V- volumul acestuia. Suprafața rezervorului este exprimată prin formula , adică este o funcție a două variabile. A exprima Sîn funcție de o variabilă, folosim faptul că , de unde . Înlocuind expresia găsită hîn formula pentru S:

Să examinăm această funcție pentru un extremum. Este definită și diferențiabilă peste tot în ]0, +∞[ , și

.

Echivalăm derivata cu zero () și găsim punctul critic. În plus, la , derivata nu există, dar această valoare nu este inclusă în domeniul definiției și, prin urmare, nu poate fi un punct extremum. Deci, - singurul punct critic. Să verificăm prezența unui extremum folosind al doilea semn suficient. Să găsim derivata a doua. Când derivata a doua este mai mare decât zero (). Aceasta înseamnă că atunci când funcția atinge un minim . Pentru că asta minim - singurul extrem al acestei funcții, este cea mai mică valoare a acesteia. Deci, partea bazei rezervorului ar trebui să fie egală cu 2 m și înălțimea acestuia.

Exemplul 9 Din paragraf A, situat pe linia de cale ferata, pana la punct CU, la distanță de el l, mărfurile trebuie transportate. Costul transportului unei unități de greutate pe unitate de distanță pe calea ferată este egal cu , iar pe autostradă este egal cu . Până în ce punct M linii calea ferata ar trebui construită o autostradă astfel încât transportul mărfurilor din A V CU a fost cel mai economic AB se presupune că calea ferată este dreaptă)?