Scrieți ecuația planului prin puncte. Distanța până la avion de la punct
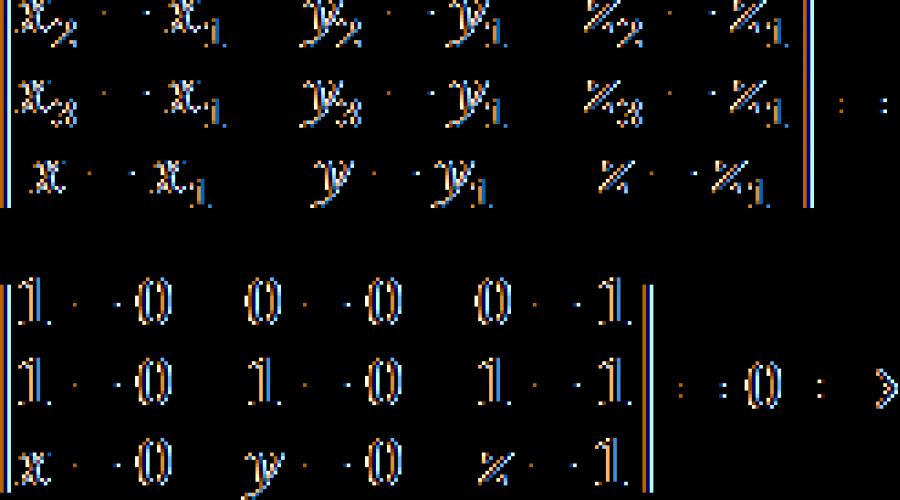
Citeste si
În această lecție, ne vom uita la cum să folosim determinantul pentru a compune ecuația plană. Dacă nu știți ce este un determinant, mergeți la prima parte a lecției - „Matrice și determinanți”. Altfel, riști să nu înțelegi nimic din materialul de astăzi.
Ecuația unui plan cu trei puncte
De ce avem nevoie de ecuația planului? Este simplu: știind asta, putem calcula cu ușurință unghiuri, distanțe și alte prostii în problema C2. În general, această ecuație este indispensabilă. Prin urmare, formulăm problema:
Sarcină. Există trei puncte în spațiu care nu se află pe aceeași linie dreaptă. Coordonatele lor:
M = (x 1 , y 1 , z 1);
N \u003d (x 2, y 2, z 2);
K \u003d (x 3, y 3, z 3);Este necesar să scrieți ecuația planului care trece prin aceste trei puncte. Și ecuația ar trebui să arate așa:
Ax + By + Cz + D = 0
unde numerele A , B , C și D sunt coeficienții pe care, de fapt, doriți să îi găsiți.
Ei bine, cum să obțineți ecuația planului, dacă sunt cunoscute doar coordonatele punctelor? Cel mai simplu mod este să înlocuiți coordonatele în ecuația Ax + By + Cz + D = 0. Obțineți un sistem de trei ecuații care este ușor de rezolvat.
Mulți studenți consideră această soluție extrem de obositoare și nesigură. Examenul de matematică de anul trecut a arătat că probabilitatea de a face o eroare de calcul este foarte mare.
Prin urmare, cei mai avansați profesori au început să caute soluții mai simple și mai elegante. Și au găsit-o! Adevărat, tehnica obținută este mai probabil să fie legată de matematica superioară. Personal, a trebuit să răsfoiesc întreaga listă federală de manuale pentru a mă asigura că avem dreptul de a folosi această tehnică fără nicio justificare și dovezi.
Ecuația planului prin determinant
Destul de dezgustări, să trecem la treabă. Pentru început, o teoremă despre modul în care determinantul matricei și ecuația planului sunt legate.
Teorema. Să fie date coordonatele a trei puncte prin care trebuie trasat planul: M = (x 1 , y 1 , z 1 ); N \u003d (x 2, y 2, z 2); K \u003d (x 3, y 3, z 3). Atunci ecuația acestui plan poate fi scrisă în termeni de determinant:
De exemplu, să încercăm să găsim o pereche de avioane care apar de fapt în problemele C2. Uită-te la cât de repede contează totul:
A 1 = (0, 0, 1);
B = (1, 0, 0);
C1 = (1, 1, 1);
Compunem determinantul și îl echivalăm cu zero:

Deschiderea determinantului:
a = 1 1 (z − 1) + 0 0 x + (−1) 1 y = z − 1 − y;
b = (−1) 1 x + 0 1 (z − 1) + 1 0 y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
După cum puteți vedea, când am calculat numărul d, am „periat” puțin ecuația, astfel încât variabilele x , y și z să intre în succesiunea corectă. Asta e tot! Ecuația avionului este gata!
Sarcină. Scrieți o ecuație pentru un plan care trece prin punctele:
A = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);
Înlocuiți imediat coordonatele punctelor din determinant:
Extinderea din nou a determinantului:
a = 1 1 z + 0 1 x + 1 0 y = z;
b = 1 1 x + 0 0 z + 1 1 y = x + y;
d \u003d a - b \u003d z - (x + y) \u003d z - x - y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;
Deci, ecuația plană se obține din nou! Din nou, la ultimul pas, a trebuit să schimb semnele din el pentru a obține o formulă mai „frumoasă”. Nu este necesar să faceți acest lucru în această soluție, dar este totuși recomandat - pentru a simplifica soluția ulterioară a problemei.
După cum puteți vedea, acum este mult mai ușor să scrieți ecuația planului. Substituim punctele în matrice, calculăm determinantul - și gata, ecuația este gata.
Acesta ar putea fi sfârșitul lecției. Cu toate acestea, mulți studenți uită constant ce este în interiorul determinantului. De exemplu, care linie conține x 2 sau x 3 și care linie doar x . Pentru a rezolva în sfârșit acest lucru, să urmărim de unde provine fiecare număr.
De unde vine formula cu determinantul?
Deci, să ne dăm seama de unde vine o ecuație atât de dură cu un determinant. Acest lucru vă va ajuta să vă amintiți și să îl aplicați cu succes.
Toate planurile care apar în problema C2 sunt definite de trei puncte. Aceste puncte sunt întotdeauna marcate pe desen sau chiar indicate direct în textul problemei. În orice caz, pentru a compila ecuația, trebuie să le scriem coordonatele:
M = (x 1 , y 1 , z 1);
N \u003d (x 2, y 2, z 2);
K \u003d (x 3, y 3, z 3).
Luați în considerare încă un punct pe planul nostru cu coordonate arbitrare:
T = (x, y, z)
Luăm orice punct din primele trei (de exemplu, punctul M ) și desenăm vectori din acesta către fiecare dintre cele trei puncte rămase. Obținem trei vectori:
MN = (x 2 - x 1, y 2 - y 1, z 2 - z 1);
MK = (x3-x1, y3-y1,z3-z1);
MT = (x - x 1 , y - y 1 , z - z 1).
Acum să facem o matrice pătrată din acești vectori și să echivalăm determinantul acesteia cu zero. Coordonatele vectorilor vor deveni rândurile matricei - și vom obține același determinant care este indicat în teoremă:
Această formulă înseamnă că volumul cutiei construite pe vectorii MN , MK și MT este egal cu zero. Prin urmare, toți cei trei vectori se află în același plan. În special, un punct arbitrar T = (x, y, z) este exact ceea ce căutam.
Înlocuirea punctelor și rândurilor determinantului
Determinanții au niște proprietăți minunate care fac și mai ușor de făcut rezolvarea problemei C2. De exemplu, nu contează pentru noi din ce punct să desenăm vectori. Prin urmare, următorii determinanți dau aceeași ecuație plană ca cea de mai sus:
De asemenea, puteți schimba liniile determinantului. Ecuația va rămâne neschimbată. De exemplu, multor oameni le place să scrie o linie cu coordonatele punctului T = (x; y; z) în partea de sus. Vă rog, dacă vă convine:
Pe unii îi încurcă faptul că una dintre linii conține variabile x , y și z , care nu dispar la înlocuirea punctelor. Dar nu ar trebui să dispară! Înlocuind numerele în determinant, ar trebui să obțineți următoarea construcție:

Apoi determinantul este extins conform schemei date la începutul lecției și se obține ecuația standard a planului:
Ax + By + Cz + D = 0
Aruncă o privire la un exemplu. El este ultimul din lecția de astăzi. Voi schimba în mod deliberat liniile pentru a mă asigura că răspunsul va fi aceeași ecuație a planului.
Sarcină. Scrieți o ecuație pentru un plan care trece prin punctele:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1).
Deci, luăm în considerare 4 puncte:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1);
T = (x, y, z).
Mai întâi, să facem un determinant standard și să-l echivalăm cu zero:
Deschiderea determinantului:
a = 0 1 (z − 1) + 1 0 (x − 1) + (−1) (−1) y = 0 + 0 + y;
b = (−1) 1 (x − 1) + 1 (−1) (z − 1) + 0 0 y = 1 − x + 1 − z = 2 − x − z;
d \u003d a - b \u003d y - (2 - x - z) \u003d y - 2 + x + z \u003d x + y + z - 2;
d = 0 ⇒ x + y + z − 2 = 0;
Asta e, avem răspunsul: x + y + z − 2 = 0 .
Acum să rearanjam câteva rânduri în determinant și să vedem ce se întâmplă. De exemplu, să scriem o linie cu variabilele x, y, z nu în partea de jos, ci în partea de sus:
Să extindem din nou determinantul rezultat:
a = (x − 1) 1 (−1) + (z − 1) (−1) 1 + y 0 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) 1 0 + y (−1) (−1) + (x − 1) 1 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;
Avem exact aceeași ecuație plană: x + y + z − 2 = 0. Deci, chiar nu depinde de ordinea rândurilor. Rămâne să scrieți răspunsul.
Deci, am văzut că ecuația planului nu depinde de succesiunea de drepte. Este posibil să se efectueze calcule similare și să se demonstreze că ecuația planului nu depinde de punctul ale cărui coordonate le scădem din celelalte puncte.
În problema considerată mai sus, am folosit punctul B 1 = (1, 0, 1), dar a fost foarte posibil să luăm C = (1, 1, 0) sau D 1 = (0, 1, 1). În general, orice punct cu coordonate cunoscute se află pe planul dorit.
Poate fi setat căi diferite(un punct și un vector, două puncte și un vector, trei puncte etc.). Cu acest lucru în minte poate avea ecuația planului tipuri diferite. De asemenea, în anumite condiții, planurile pot fi paralele, perpendiculare, intersectante etc. Vom vorbi despre asta în acest articol. Vom învăța cum să scriem ecuația generală a planului și nu numai.
Forma normală a ecuației
Să presupunem că există un spațiu R 3 care are un sistem de coordonate dreptunghiular XYZ. Setăm vectorul α, care va fi eliberat din punctul inițial O. Prin capătul vectorului α desenăm planul P, care va fi perpendicular pe acesta.
Notăm cu P un punct arbitrar Q=(x, y, z). Vom semna vectorul rază al punctului Q cu litera p. Lungimea vectorului α este p=IαI și Ʋ=(cosα,cosβ,cosγ).
Acesta este un vector unitar care arată lateral, la fel ca vectorul α. α, β și γ sunt unghiurile care se formează între vectorul Ʋ și direcțiile pozitive ale axelor spațiale x, y, z, respectiv. Proiecția unui punct QϵП pe vectorul Ʋ este valoare constantă, care este egal cu p: (p,Ʋ) = p(p≥0).
Această ecuație are sens când p=0. Singurul lucru este că planul P în acest caz va intersecta punctul O (α=0), care este originea, iar vectorul unitar Ʋ eliberat din punctul O va fi perpendicular pe P, indiferent de direcția acestuia, ceea ce înseamnă că vectorul Ʋ este determinat din semn exact. Ecuația anterioară este ecuația planului nostru P, exprimată în formă vectorială. Dar în coordonate va arăta astfel:
P aici este mai mare sau egal cu 0. Am găsit ecuația unui plan în spațiu în forma sa normală.
Ecuația generală
Dacă înmulțim ecuația în coordonate cu orice număr care nu este egal cu zero, obținem o ecuație echivalentă cu cea dată, care determină același plan. Va arata asa:

Aici A, B, C sunt numere care sunt simultan diferite de zero. Această ecuație este denumită ecuația planului general.
Ecuații plane. Cazuri speciale
Ecuația în vedere generala se poate modifica dacă este disponibil conditii suplimentare. Să luăm în considerare unele dintre ele.
Să presupunem că coeficientul A este 0. Aceasta înseamnă că planul dat este paralel cu axa dată Ox. În acest caz, forma ecuației se va schimba: Ву+Cz+D=0.
În mod similar, forma ecuației se va schimba în următoarele condiții:
- În primul rând, dacă B = 0, atunci ecuația se va schimba în Ax + Cz + D = 0, ceea ce va indica paralelismul cu axa Oy.
- În al doilea rând, dacă С=0, atunci ecuația este transformată în Ах+Ву+D=0, ceea ce va indica paralelismul cu axa dată Oz.
- În al treilea rând, dacă D=0, ecuația va arăta ca Ax+By+Cz=0, ceea ce va însemna că planul intersectează O (originea).
- În al patrulea rând, dacă A=B=0, atunci ecuația se va schimba în Cz+D=0, ceea ce se va dovedi paralel cu Oxy.
- În al cincilea rând, dacă B=C=0, atunci ecuația devine Ax+D=0, ceea ce înseamnă că planul către Oyz este paralel.
- În al șaselea rând, dacă A=C=0, atunci ecuația va lua forma Ву+D=0, adică va raporta paralelismul la Oxz.
Tip de ecuație în segmente
În cazul în care numerele A, B, C, D sunt diferite de zero, forma ecuației (0) poate fi după cum urmează:
x/a + y/b + z/c = 1,
în care a \u003d -D / A, b \u003d -D / B, c \u003d -D / C.
Obținem ca rezultat. Merită remarcat faptul că acest plan va intersecta axa Ox într-un punct cu coordonatele (a,0,0), Oy - (0,b,0) și Oz - (0,0,c) .

Ținând cont de ecuația x/a + y/b + z/c = 1, este ușor de reprezentat vizual poziția planului în raport cu un sistem de coordonate dat.
Coordonate vectoriale normale
Vectorul normal n la planul P are coordonatele care sunt coeficienții ecuație generală plan dat, adică n (A, B, C).

Pentru a determina coordonatele normalei n, este suficient să cunoaștem ecuația generală a unui plan dat.
Când se utilizează ecuația în segmente, care are forma x/a + y/b + z/c = 1, precum și când se utilizează ecuația generală, se pot scrie coordonatele oricărui vector normal al unui plan dat: (1 /a + 1/b + 1/ Cu).
Trebuie remarcat faptul că vectorul normal ajută la rezolvarea diferitelor probleme. Cele mai frecvente sunt sarcinile care constau in demonstrarea perpendicularitatii sau paralelismului planurilor, probleme in gasirea unghiurilor intre plane sau unghiurilor intre plane si drepte.
Vedere a ecuației planului în funcție de coordonatele punctului și ale vectorului normal
Un vector diferit de zero n perpendicular pe un plan dat se numește normal (normal) pentru un plan dat.
Să presupunem că în spațiul de coordonate (sistem de coordonate dreptunghiulare) Oxyz sunt date:
- punctul Mₒ cu coordonatele (xₒ,yₒ,zₒ);
- vector zero n=A*i+B*j+C*k.

Este necesar să se compună o ecuație pentru un plan care va trece prin punctul Mₒ perpendicular pe normala n.
În spațiu, alegem orice punct arbitrar și îl notăm cu M (x y, z). Fie vectorul rază al oricărui punct M (x, y, z) r=x*i+y*j+z*k, iar vectorul rază al punctului Mₒ (xₒ,yₒ,zₒ) - rₒ=xₒ* i+yₒ *j+zₒ*k. Punctul M va aparține planului dat dacă vectorul MₒM este perpendicular pe vectorul n. Scriem condiția de ortogonalitate folosind produsul scalar:
[MₒM, n] = 0.
Deoarece MₒM \u003d r-rₒ, ecuația vectorială a planului va arăta astfel:
Această ecuație poate lua o altă formă. Pentru aceasta, se folosesc proprietățile produsului scalar și partea stângă ecuații. = - . Dacă se notează c, atunci se va obține următoarea ecuație: - c \u003d 0 sau \u003d c, care exprimă constanța proiecțiilor pe vectorul normal al vectorilor de rază ai punctelor date care aparțin planului.
Acum puteți obține forma de coordonate de scriere a ecuației vectoriale a planului nostru = 0. Deoarece r-rₒ = (x-xₒ)*i + (y-yₒ)*j + (z-zₒ)*k și n = A*i+B *j+C*k, avem:
Rezultă că avem o ecuație pentru un plan care trece printr-un punct perpendicular pe normala n:
A*(x-xₒ)+B*(y-yₒ)C*(z-zₒ)=0.
Vedere a ecuației plane în funcție de coordonatele a două puncte și un vector coliniar cu planul
Definim două puncte arbitrare M′ (x′,y′,z′) și M″ (x″,y″,z″), precum și vectorul a (a′,a″,a‴).
Acum putem compune o ecuație pentru un plan dat, care va trece prin punctele disponibile M′ și M ″, precum și orice punct M cu coordonatele (x, y, z) în paralel vector dat A.
În acest caz, vectorii M′M=(x-x′;y-y′;z-z′) și M″M=(x″-x′;y″-y′;z″-z′) trebuie să fie coplanari cu vectorul a=(a′,a″,a‴), ceea ce înseamnă că (M′M, M″M, a)=0.
Deci, ecuația noastră a unui plan în spațiu va arăta astfel:

Tipul ecuației unui plan care intersectează trei puncte
Să presupunem că avem trei puncte: (x′, y′, z′), (x″,y″,z″), (x‴,y‴,z‴), care nu aparțin aceleiași drepte. Este necesar să scrieți ecuația planului care trece prin cele trei puncte date. Teoria geometriei susține că acest tip de plan există cu adevărat, doar că este singurul și inimitabil. Deoarece acest plan intersectează punctul (x′, y′, z′), forma ecuației sale va fi după cum urmează:
Aici A, B, C sunt diferite de zero în același timp. De asemenea, planul dat intersectează încă două puncte: (x″,y″,z″) și (x‴,y‴,z‴). În acest sens, trebuie îndeplinite următoarele condiții:

Acum putem compune un sistem omogen cu necunoscute u, v, w:

În a noastră cazul x,y sau z este un punct arbitrar care satisface ecuația (1). Ținând cont de ecuația (1) și de sistemul de ecuații (2) și (3), sistemul de ecuații indicat în figura de mai sus satisface vectorul N (A, B, C), care este netrivial. De aceea determinantul acestui sistem este egal cu zero.

Ecuația (1), pe care am obținut-o, este ecuația planului. Trece exact prin 3 puncte, iar acest lucru este ușor de verificat. Pentru a face acest lucru, trebuie să ne extindem determinantul asupra elementelor din primul rând. Din proprietățile existente ale determinantului rezultă că planul nostru intersectează simultan trei puncte date inițial (x′, y′, z′), (x″,y″,z″), (x‴,y‴,z‴) . Adică am rezolvat sarcina stabilită înaintea noastră.
Unghiul diedric dintre plane
Un unghi diedru este un spațial figură geometrică, format din două semiplane care emană dintr-o linie dreaptă. Cu alte cuvinte, aceasta este partea din spațiu care este limitată de aceste semiplanuri.
Să presupunem că avem două plane cu următoarele ecuații:

Știm că vectorii N=(A,B,C) și N¹=(A¹,B¹,C¹) sunt perpendiculari conform planurilor date. În acest sens, unghiul φ dintre vectorii N și N¹ este egal cu unghiul (diedrul), care se află între aceste plane. Produs scalar se pare ca:
NN¹=|N||N¹|cos φ,
tocmai pentru că
cosφ= NN¹/|N||N¹|=(AA¹+BB¹+CC¹)/((√(A²+B²+C²))*(√(A¹)²+(B¹)²+(C¹)²)).

Este suficient să luăm în considerare faptul că 0≤φ≤π.
De fapt, două plane care se intersectează formează două unghiuri (diedrice): φ 1 și φ 2 . Suma lor este egală cu π (φ 1 + φ 2 = π). În ceea ce privește cosinusurile lor, valorile lor absolute sunt egale, dar diferă în semne, adică cos φ 1 =-cos φ 2. Dacă în ecuația (0) înlocuim A, B și C cu numerele -A, -B și respectiv -C, atunci ecuația pe care o obținem va determina același plan, singurul unghi φ din ecuația cos φ= NN 1 /| N||N 1 | va fi înlocuit cu π-φ.
Ecuația planului perpendicular
Planurile se numesc perpendiculare dacă unghiul dintre ele este de 90 de grade. Folosind materialul prezentat mai sus, putem găsi ecuația unui plan perpendicular pe altul. Să presupunem că avem două plane: Ax+By+Cz+D=0 și A¹x+B¹y+C¹z+D=0. Putem afirma că vor fi perpendiculare dacă cosφ=0. Aceasta înseamnă că NN¹=AA¹+BB¹+CC¹=0.
Ecuația planului paralel
Paralele sunt două plane care nu conțin puncte comune.
Condiția (ecuațiile lor sunt aceleași ca în paragraful anterior) este ca vectorii N și N¹, care sunt perpendiculari pe ei, să fie coliniari. Aceasta înseamnă că sunt îndeplinite următoarele condiții de proporționalitate:
A/A¹=B/B1=C/C1.
Dacă condițiile de proporționalitate sunt extinse - A/A¹=B/B¹=C/C¹=DD¹,
aceasta indică faptul că aceste planuri coincid. Aceasta înseamnă că ecuațiile Ax+By+Cz+D=0 și A¹x+B¹y+C¹z+D¹=0 descriu un plan.
Distanța până la avion de la punct
Să presupunem că avem un plan P, care este dat de ecuația (0). Este necesar să găsiți distanța până la acesta de la punctul cu coordonatele (xₒ,yₒ,zₒ)=Qₒ. Pentru a face acest lucru, trebuie să aduceți ecuația planului P în formă normală:
(ρ,v)=p (p≥0).
În acest caz, ρ(x,y,z) este vectorul rază a punctului nostru Q situat pe P, p este lungimea perpendicularei pe P care a fost eliberată din punctul zero, v este vectorul unitar care este situat în direcția a.
Diferența ρ-ρº a vectorului rază a unui punct Q=(x,y,z) aparținând lui P, precum și vectorul rază a unui punct dat Q 0 =(xₒ,yₒ,zₒ) este un astfel de vector, valoare absolută a cărui proiecție pe v este egală cu distanța d, care trebuie găsită de la Q 0 \u003d (xₒ, yₒ, zₒ) la P:
D=|(ρ-ρ 0 ,v)|, dar
(ρ-ρ 0 ,v)= (ρ,v)-(ρ 0 ,v) =р-(ρ 0 ,v).
Deci se dovedește
d=|(ρ 0 ,v)-p|.
Astfel vom găsi valoare absolută expresia rezultată, adică d.
Folosind limbajul parametrilor, obținem ceea ce este evident:
d=|Axₒ+Vuₒ+Czₒ|/√(A²+B²+C²).
Dacă punctul dat Q 0 este de cealaltă parte a planului P, precum și originea, atunci între vectorul ρ-ρ 0 și v este deci:
d=-(ρ-ρ 0 ,v)=(ρ 0 ,v)-p>0.
În cazul în care punctul Q 0, împreună cu originea, este situat pe aceeași parte a lui P, atunci unghiul creat este ascuțit, adică:
d \u003d (ρ-ρ 0, v) \u003d p - (ρ 0, v)>0.
Ca urmare, rezultă că în primul caz (ρ 0 ,v)> р, în al doilea (ρ 0 ,v)<р.
Planul tangent și ecuația acestuia
Planul tangent la suprafață în punctul de contact Mº este planul care conține toate tangentele posibile la curbele trasate prin acest punct de pe suprafață.
Cu această formă a ecuației de suprafață F (x, y, z) \u003d 0, ecuația planului tangent la punctul tangent Mº (xº, yº, zº) va arăta astfel:
F x (xº, yº, zº)(x- xº)+ F x (xº, yº, zº)(y-yº)+ F x (xº, yº, zº)(z-zº)=0.
Dacă specificați suprafața în formă explicită z=f (x, y), atunci planul tangent va fi descris de ecuația:
z-zº = f(xº, yº)(x- xº)+f(xº, yº)(y-yº).
Intersecția a două planuri
În sistemul de coordonate (dreptunghiular) se află Oxyz, sunt date două plane П′ și П″, care se intersectează și nu coincid. Deoarece orice plan situat într-un sistem de coordonate dreptunghiular este determinat de ecuația generală, vom presupune că P′ și P″ sunt date de ecuațiile A′x+B′y+C′z+D′=0 și A″x +B″y+ С″z+D″=0. În acest caz, avem normala n′ (A′, B′, C′) a planului P′ și normala n″ (A″, B″, C″) a planului P″. Deoarece planurile noastre nu sunt paralele și nu coincid, acești vectori nu sunt coliniari. Folosind limbajul matematicii, putem scrie această condiție astfel: n′≠ n″ ↔ (A′, B′, C′) ≠ (λ*A″,λ*B″,λ*C″), λϵR. Fie ca linia care se află la intersecția dintre P′ și P″ se notează cu litera a, în acest caz a = P′ ∩ P″.
a este o linie dreaptă formată din mulțimea tuturor punctelor planelor (comune) П′ și П″. Aceasta înseamnă că coordonatele oricărui punct aparținând dreptei a trebuie să îndeplinească simultan ecuațiile A′x+B′y+C′z+D′=0 și A″x+B″y+C″z+D″= 0. Aceasta înseamnă că coordonatele punctului vor fi o soluție particulară a următorului sistem de ecuații:

Ca urmare, se dovedește că soluția (generală) a acestui sistem de ecuații va determina coordonatele fiecăruia dintre punctele dreptei, care va acționa ca punct de intersecție al lui П′ și П″ și va determina dreapta linia a în sistemul de coordonate Oxyz (dreptunghiular) în spațiu.
În cadrul acestui material, vom analiza cum să găsim ecuația unui plan dacă cunoaștem coordonatele celor trei puncte diferite ale sale care nu se află pe o singură dreaptă. Pentru a face acest lucru, trebuie să ne amintim ce este un sistem de coordonate dreptunghiular în spațiul tridimensional. În primul rând, introducem principiul de bază al acestei ecuații și arătăm cum să o folosim în rezolvarea unor probleme specifice.
Yandex.RTB R-A-339285-1
Pentru început, trebuie să ne amintim o axiomă, care sună astfel:
Definiția 1
Dacă trei puncte nu coincid unul cu celălalt și nu se află pe o singură linie dreaptă, atunci în spațiul tridimensional trece un singur plan prin ele.
Cu alte cuvinte, dacă avem trei puncte diferite ale căror coordonate nu coincid și care nu pot fi conectate printr-o dreaptă, atunci putem determina planul care trece prin el.
Să presupunem că avem un sistem de coordonate dreptunghiular. Să o notăm O x y z . Conține trei puncte M cu coordonatele M 1 (x 1, y 1, z 1) , M 2 (x 2 , y 2 , z 2) , M 3 (x 3 , y 3 , z 3) care nu pot fi conectate drept linia. Pe baza acestor condiții, putem scrie ecuația planului de care avem nevoie. Există două abordări pentru a rezolva această problemă.
1. Prima abordare folosește ecuația generală a planului. În formă literală, se scrie ca A (x - x 1) + B (y - y 1) + C (z - z 1) = 0. Cu acesta, puteți seta într-un sistem de coordonate dreptunghiular un anumit plan alfa, care trece prin primul punct dat M 1 (x 1 , y 1 , z 1) . Rezultă că vectorul plan normal α va avea coordonatele A , B , C .
Definiția lui N
Cunoscând coordonatele vectorului normal și coordonatele punctului prin care trece planul, putem scrie ecuația generală a acestui plan.
De aici vom merge mai departe.
Astfel, în funcție de condițiile problemei, avem coordonatele punctului dorit (chiar trei), prin care trece avionul. Pentru a găsi ecuația, trebuie să calculați coordonatele vectorului său normal. Notează-l n → .
Amintiți-vă regula: orice vector diferit de zero al unui plan dat este perpendicular pe vectorul normal al aceluiași plan. Atunci avem că n → va fi perpendicular pe vectorii alcătuiți din punctele inițiale M 1 M 2 → și M 1 M 3 → . Atunci putem nota n → ca produs vectorial de forma M 1 M 2 → · M 1 M 3 → .
Deoarece M 1 M 2 → = (x 2 - x 1, y 2 - y 1, z 2 - z 1) și M 1 M 3 → = x 3 - x 1, y 3 - y 1, z 3 - z 1 (demonstrațiile acestor egalități sunt date în articolul dedicat calculării coordonatelor unui vector din coordonatele punctelor), atunci rezultă că:
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 - x 1 y 2 - y 1 z 2 - z 1 x 3 - x 1 y 3 - y 1 z 3 - z 1
Dacă calculăm determinantul, vom obține coordonatele vectorului normal n → de care avem nevoie. Acum putem scrie ecuația de care avem nevoie pentru un plan care trece prin trei puncte date.
2. A doua abordare pentru găsirea unei ecuații care trece prin M 1 (x 1, y 1, z 1) , M 2 (x 2 , y 2 , z 2) , M 3 (x 3 , y 3 , z 3) este bazat pe un astfel de concept precum complanaritatea vectorilor.
Dacă avem o mulțime de puncte M (x, y, z), atunci într-un sistem de coordonate dreptunghiular ele definesc un plan pentru punctele date M 1 (x 1 , y 1 , z 1) , M 2 (x 2 , y) 2 , z 2 ) , M 3 (x 3 , y 3 , z 3) numai dacă vectorii M 1 M → = (x - x 1 , y - y 1 , z - z 1) , M 1 M 2 → = ( x 2 - x 1 , y 2 - y 1 , z 2 - z 1) și M 1 M 3 → = (x 3 - x 1 , y 3 - y 1 , z 3 - z 1) vor fi coplanare.
Pe diagramă va arăta astfel:
Aceasta va însemna că produsul mixt al vectorilor M 1 M → , M 1 M 2 → , M 1 M 3 → va fi egal cu zero: M 1 M → · M 1 M 2 → · M 1 M 3 → = 0 , deoarece aceasta este condiția principală pentru comparație: M 1 M → = (x - x 1 , y - y 1 , z - z 1) , M 1 M 2 → = (x 2 - x 1 , y 2 - y 1 ) , z 2 - z 1 ) și M 1 M 3 → = (x 3 - x 1 , y 3 - y 1 , z 3 - z 1) .
Scriem ecuația rezultată sub formă de coordonate:
După ce calculăm determinantul, putem obține ecuația planului de care avem nevoie pentru trei puncte care nu se află pe o singură dreaptă M 1 (x 1, y 1, z 1) , M 2 (x 2 , y 2 , z ) 2), M3 (x3, y3, z3).
Din ecuația rezultată, puteți merge la ecuația planului în segmente sau la ecuația normală a planului, dacă condițiile problemei o cer.
În paragraful următor, vom da exemple despre modul în care abordările pe care le-am indicat sunt implementate în practică.
Exemple de sarcini pentru alcătuirea unei ecuații a unui plan care trece prin 3 puncte
Anterior, am identificat două abordări care pot fi utilizate pentru a găsi ecuația dorită. Să vedem cum sunt folosite în rezolvarea problemelor și când să le alegem pe fiecare.
Exemplul 1
Există trei puncte care nu se află pe o singură dreaptă, cu coordonatele M 1 (- 3 , 2 , - 1) , M 2 (- 1 , 2 , 4) , M 3 (3 , 3 , - 1) . Scrieți o ecuație pentru un plan care trece prin ele.
Soluţie
Folosim ambele metode pe rând.
1. Aflați coordonatele celor doi vectori de care avem nevoie M 1 M 2 → , M 1 M 3 → :
M 1 M 2 → = - 1 - - 3, 2 - 2, 4 - - 1 ⇔ M 1 M 2 → = (2, 0, 5) M 1 M 3 → = 3 - - 3, 3 - 2, - 1 - - 1 ⇔ M 1 M 3 → = 6 , 1 , 0
Acum calculăm produsul lor vectorial. În acest caz, nu vom descrie calculele determinantului:
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = - 5 i → + 30 j → + 2 k →
Avem un vector normal al planului care trece prin cele trei puncte cerute: n → = (- 5 , 30 , 2) . În continuare, trebuie să luăm unul dintre puncte, de exemplu, M 1 (- 3 , 2 , - 1) și să scriem ecuația pentru planul cu vectorul n → = (- 5 , 30 , 2) . Obținem că: - 5 (x - (- 3)) + 30 (y - 2) + 2 (z - (- 1)) = 0 ⇔ - 5 x + 30 y + 2 z - 73 = 0
Aceasta este ecuația planului de care avem nevoie, care trece prin trei puncte.
2. Folosim o abordare diferită. Scriem ecuația pentru un plan cu trei puncte M 1 (x 1, y 1, z 1) , M 2 (x 2 , y 2 , z 2) , M 3 (x 3 , y 3 , z 3) în urmatoarea forma:
x - x 1 y - y 1 z - z 1 x 2 - x 1 y 2 - y 1 z 2 - z 1 x 3 - x 1 y 3 - y 1 z 3 - z 1 = 0
Aici puteți înlocui datele din starea problemei. Deoarece x 1 = - 3, y 1 = 2, z 1 = - 1, x 2 = - 1, y 2 = 2, z 2 = 4, x 3 = 3, y 3 = 3, z 3 = - 1, ca rezultat vom obține:
x - x 1 y - y 1 z - z 1 x 2 - x 1 y 2 - y 1 z 2 - z 1 x 3 - x 1 y 3 - y 1 z 3 - z 1 = x - (- 3) y - 2 z - (- 1) - 1 - (- 3) 2 - 2 4 - (- 1) 3 - (- 3) 3 - 2 - 1 - (- 1) = = x + 3 y - 2 z + 1 2 0 5 6 1 0 = - 5 x + 30 y + 2 z - 73
Avem ecuația de care avem nevoie.
Răspuns:- 5x + 30y + 2z - 73 .
Dar dacă punctele date se află încă pe aceeași linie dreaptă și trebuie să compunem o ecuație plană pentru ele? Aici trebuie spus imediat că această condiție nu va fi pe deplin corectă. Prin astfel de puncte pot trece infinit de avioane, deci este imposibil să se calculeze un singur răspuns. Să luăm în considerare o astfel de problemă pentru a demonstra incorectitudinea unei astfel de formulări a întrebării.
Exemplul 2
Avem un sistem de coordonate dreptunghiular în spațiu 3D care conține trei puncte cu coordonatele M 1 (5 , - 8 , - 2) , M 2 (1 , - 2 , 0) , M 3 (- 1 , 1 , 1) . Este necesar să scrieți o ecuație pentru un avion care trece prin ea.
Soluţie
Folosim prima metodă și începem prin a calcula coordonatele a doi vectori M 1 M 2 → și M 1 M 3 → . Să le calculăm coordonatele: M 1 M 2 → = (- 4 , 6 , 2) , M 1 M 3 → = - 6 , 9 , 3 .
Produsul vectorial va fi egal cu:
M 1 M 2 → × M 1 M 3 → = i → j → k → - 4 6 2 - 6 9 3 = 0 i ⇀ + 0 j → + 0 k → = 0 →
Deoarece M 1 M 2 → × M 1 M 3 → = 0 → , atunci vectorii noștri vor fi coliniari (recitiți articolul despre ei dacă ați uitat definiția acestui concept). Astfel, punctele inițiale M 1 (5 , - 8 , - 2) , M 2 (1 , - 2 , 0) , M 3 (- 1 , 1 , 1) sunt pe aceeași dreaptă, iar problema noastră are infinit multe opțiuni de răspuns.
Dacă folosim a doua metodă, obținem:
x - x 1 y - y 1 z - z 1 x 2 - x 1 y 2 - y 1 z 2 - z 1 x 3 - x 1 y 3 - y 1 z 3 - z 1 = 0 ⇔ x - 5 y - (- 8) z - (- 2) 1 - 5 - 2 - (- 8) 0 - (- 2) - 1 - 5 1 - (- 8) 1 - (- 2) = 0 ⇔ ⇔ x - 5 y + 8z + 2 - 4 6 2 - 6 9 3 = 0 ⇔ 0 ≡ 0
Din egalitatea rezultată mai rezultă că punctele date M 1 (5 , - 8 , - 2) , M 2 (1 , - 2 , 0) , M 3 (- 1 , 1 , 1) sunt pe aceeași linie.
Dacă doriți să găsiți cel puțin un răspuns la această problemă dintr-un număr infinit de opțiuni, atunci trebuie să urmați acești pași:
1. Scrieți ecuația dreptei M 1 M 2, M 1 M 3 sau M 2 M 3 (dacă este necesar, consultați materialul despre această acțiune).
2. Luați un punct M 4 (x 4 , y 4 , z 4) care nu se află pe dreapta M 1 M 2 .
3. Scrieți ecuația unui plan care trece prin trei puncte diferite M 1 , M 2 și M 4 care nu se află pe o singură dreaptă.
Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter
Primul nivel
Coordonate și vectori. Ghid cuprinzător (2019)
În acest articol, voi și cu mine vom începe o discuție despre o „baghetă magică” care vă va permite să reduceți multe probleme din geometrie la aritmetică simplă. Această „baghetă” îți poate face viața mult mai ușoară, mai ales atunci când te simți nesigur în construirea unor figuri spațiale, secțiuni etc. Toate acestea necesită o anumită imaginație și abilități practice. Metoda, pe care vom începe să o luăm în considerare aici, vă va permite să abstrageți aproape complet din toate tipurile de construcții și raționamente geometrice. Metoda este numită "metoda coordonate". În acest articol, vom lua în considerare următoarele întrebări:
- Planul de coordonate
- Puncte și vectori în plan
- Construirea unui vector din două puncte
- Lungimea vectorului (distanța dintre două puncte).
- Coordonatele punctului de mijloc
- Produsul punctual al vectorilor
- Unghiul dintre doi vectori
Cred că ai ghicit deja de ce metoda coordonatelor se numește așa? Este adevărat că a primit un astfel de nume, deoarece nu operează cu obiecte geometrice, ci cu caracteristicile lor numerice (coordonatele). Iar transformarea în sine, care face posibilă trecerea de la geometrie la algebră, constă în introducerea unui sistem de coordonate. Dacă figura originală era plată, atunci coordonatele sunt bidimensionale, iar dacă figura este tridimensională, atunci coordonatele sunt tridimensionale. În acest articol, vom lua în considerare doar cazul bidimensional. Și scopul principal al articolului este de a vă învăța cum să utilizați câteva tehnici de bază ale metodei coordonatelor (uneori se dovedesc a fi utile atunci când rezolvați probleme de planimetrie în partea B a examenului de stat unificat). Următoarele două secțiuni pe această temă sunt dedicate discuției despre metodele de rezolvare a problemelor C2 (problema stereometriei).
Unde ar fi logic să începem să discutăm despre metoda coordonatelor? Probabil cu conceptul de sistem de coordonate. Amintește-ți când ai cunoscut-o prima dată. Mi se pare că în clasa a VII-a, când ai aflat despre existența unei funcții liniare, de exemplu. Permiteți-mi să vă reamintesc că ați construit-o punct cu punct. Vă amintiți? Ați ales un număr arbitrar, l-ați înlocuit în formulă și ați calculat în acest fel. De exemplu, dacă, atunci, dacă, atunci etc. Ce ați obținut ca rezultat? Și ați primit puncte cu coordonate: și. Apoi, ați desenat o „cruce” (sistem de coordonate), ați ales o scară pe ea (câte celule veți avea ca un singur segment) și ați marcat punctele primite pe ea, pe care apoi le-ați conectat cu o linie dreaptă, rezultatul linia este graficul funcției.
Există câteva lucruri care trebuie explicate puțin mai detaliat:
1. Alegeți un singur segment din motive de comoditate, astfel încât totul să se potrivească frumos și compact în imagine
2. Se presupune că axa merge de la stânga la dreapta, iar axa merge de jos în sus
3. Se intersectează în unghi drept, iar punctul de intersecție a lor se numește origine. Este marcat cu o literă.
4. În înregistrarea coordonatei unui punct, de exemplu, în stânga între paranteze este coordonata punctului de-a lungul axei, iar în dreapta, de-a lungul axei. În special, înseamnă pur și simplu că punctul
5. Pentru a seta orice punct pe axa de coordonate, trebuie să specificați coordonatele acestuia (2 numere)
6. Pentru orice punct situat pe axă,
7. Pentru orice punct situat pe axă,
8. Axa se numește axa x
9. Axa se numește axa y
Acum să facem următorul pas cu tine: marchează două puncte. Conectați aceste două puncte cu o linie. Si sa punem sageata ca si cand am desenam un segment din punct in punct: adica ne vom face segmentul directionat!

Vă amintiți care este alt nume pentru un segment regizat? Așa e, se numește vector!
Astfel, dacă conectăm un punct la un punct, iar începutul va fi punctul A, iar sfârșitul va fi punctul B, atunci obținem un vector. Construcția asta ați făcut-o și în clasa a VIII-a, vă amintiți?
Se pare că vectorii, ca și punctele, pot fi notați cu două numere: aceste numere se numesc coordonatele vectorului. Întrebare: credeți că este suficient să cunoaștem coordonatele începutului și sfârșitului vectorului pentru a găsi coordonatele acestuia? Se dovedește că da! Și este foarte ușor de făcut:
Astfel, deoarece în vector punctul este începutul și sfârșitul, vectorul are următoarele coordonate:
De exemplu, dacă, atunci coordonatele vectorului
Acum să facem invers, să găsim coordonatele vectorului. Ce trebuie să schimbăm pentru asta? Da, trebuie să schimbați începutul și sfârșitul: acum începutul vectorului va fi într-un punct, iar sfârșitul într-un punct. Apoi:
Privește cu atenție, care este diferența dintre vectori și? Singura lor diferență sunt semnele din coordonate. Ele sunt opuse. Acest fapt este scris astfel:
Uneori, dacă nu este specificat în mod specific care punct este începutul vectorului și care este sfârșitul, atunci vectorii sunt notați nu cu două litere mari, ci cu o literă mică, de exemplu: etc.
Acum puțin practicăși găsiți coordonatele următorilor vectori:
Examinare:
Acum rezolvați problema puțin mai dificil:
Un tor vectorial cu resturi on-cha într-un punct are co-or-di-on-you. Find-di-te abs-cis-su puncte.
La fel este destul de prozaic: fie coordonatele punctului. Apoi
Am compilat sistemul determinând care sunt coordonatele unui vector. Atunci punctul are coordonate. Ne interesează abscisa. Apoi
Răspuns:
Ce altceva poți face cu vectorii? Da, aproape totul este la fel ca cu numerele obișnuite (cu excepția faptului că nu puteți împărți, dar puteți înmulți în două moduri, dintre care unul îl vom discuta aici puțin mai târziu)
- Vectorii pot fi stivuiți unul cu celălalt
- Vectorii pot fi scăzuți unul de la altul
- Vectorii pot fi înmulțiți (sau împărțiți) cu un număr arbitrar diferit de zero
- Vectorii pot fi înmulțiți între ei
Toate aceste operații au o reprezentare geometrică destul de vizuală. De exemplu, regula triunghiului (sau paralelogramului) pentru adunare și scădere:



Un vector se întinde sau se micșorează sau își schimbă direcția atunci când este înmulțit sau împărțit cu un număr:

Totuși, aici ne va interesa întrebarea ce se întâmplă cu coordonatele.
1. Când adunăm (scădem) doi vectori, adunăm (scădem) coordonatele acestora element cu element. Acesta este:
2. La înmulțirea (împărțirea) unui vector cu un număr, toate coordonatele acestuia sunt înmulțite (împărțite) cu acest număr:
De exemplu:
· Find-di-suma ko-or-di-nat century-to-ra.

Să găsim mai întâi coordonatele fiecărui vector. Ambele au aceeași origine - punctul de origine. Capatele lor sunt diferite. Apoi, . Acum calculăm coordonatele vectorului Apoi suma coordonatelor vectorului rezultat este egală cu.
Răspuns:
Acum rezolvați singur următoarea problemă:
· Aflați suma coordonatelor vectorului

Verificăm:
Să luăm acum în considerare următoarea problemă: avem două puncte pe planul de coordonate. Cum să găsești distanța dintre ele? Fie primul punct și al doilea. Să notăm distanța dintre ele ca . Să facem următorul desen pentru claritate:

Ce am facut? În primul rând, am conectat punctele și, de asemenea, am trasat o linie paralelă cu axa din punct și am trasat o linie paralelă cu axa din punct. S-au intersectat într-un punct, formând o figură minunată? De ce este minunată? Da, tu și cu mine știm aproape totul despre un triunghi dreptunghic. Ei bine, teorema lui Pitagora, cu siguranță. Segmentul dorit este ipotenuza acestui triunghi, iar segmentele sunt catetele. Care sunt coordonatele punctului? Da, sunt ușor de găsit din imagine: Deoarece segmentele sunt paralele cu axele și, respectiv, lungimile lor sunt ușor de găsit: dacă notăm lungimile segmentelor, respectiv prin, atunci
Acum să folosim teorema lui Pitagora. Știm lungimile catetelor, vom găsi ipotenuza:
Astfel, distanța dintre două puncte este suma rădăcină a diferențelor pătrate față de coordonate. Sau - distanța dintre două puncte este lungimea segmentului care le conectează. Este ușor de observat că distanța dintre puncte nu depinde de direcție. Apoi:
Din aceasta tragem trei concluzii:
Să exersăm puțin la calcularea distanței dintre două puncte:
De exemplu, dacă, atunci distanța dintre și este
Sau să mergem altfel: găsiți coordonatele vectorului
Și găsiți lungimea vectorului:
După cum puteți vedea, este la fel!
Acum exersează puțin pe cont propriu:
Sarcină: găsiți distanța dintre punctele date:
Verificăm:
Iată încă câteva probleme pentru aceeași formulă, deși sună puțin diferit:
1. Find-di-te pătratul lungimii pleoapei-la-ra.

2. Nai-di-te pătrat de pleoapă lungime-to-ra

Bănuiesc că le poți descurca cu ușurință? Verificăm:
1. Și asta pentru atenție) Am găsit deja coordonatele vectorilor înainte: . Atunci vectorul are coordonate. Pătratul lungimii sale va fi:
2. Aflați coordonatele vectorului
Atunci pătratul lungimii sale este
Nimic complicat, nu? Aritmetică simplă, nimic mai mult.
Următoarele puzzle-uri nu pot fi clasificate fără ambiguitate, ele sunt mai degrabă pentru erudiția generală și capacitatea de a desena imagini simple.
1. Găsiți-di-cele sinus ale unghiului pe-clo-pe-de-taie, conectați-un-n-al-lea punct, cu axa absciselor.
 Și
Și
Cum o vom face aici? Trebuie să găsiți sinusul unghiului dintre și axa. Și unde putem căuta sinusul? Așa este, într-un triunghi dreptunghic. Deci, ce trebuie să facem? Construiește acest triunghi!

Deoarece coordonatele punctului și, atunci segmentul este egal, iar segmentul. Trebuie să găsim sinusul unghiului. Permiteți-mi să vă reamintesc că sinusul este raportul dintre catetul opus și ipotenuză
Ce ne rămâne de făcut? Aflați ipotenuza. O poți face în două moduri: folosind teorema lui Pitagora (picioarele sunt cunoscute!) sau folosind formula distanței dintre două puncte (de fapt la fel ca prima metodă!). Voi merge pe a doua cale:
Răspuns:
Următoarea sarcină ți se va părea și mai ușoară. Ea - pe coordonatele punctului.
Sarcina 2. Din punct de vedere, per-pen-di-ku-lar este coborât pe axa abs-ciss. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
Hai sa facem un desen:

Baza perpendicularei este punctul în care se intersectează cu axa x (axa) pentru mine, acesta este un punct. Figura arată că are coordonatele: . Ne interesează abscisa - adică componenta „X”. Ea este egală.
Răspuns: .
Sarcina 3.În condițiile problemei anterioare, găsiți suma distanțelor de la punct la axele de coordonate.
Sarcina este în general elementară dacă știți care este distanța de la un punct la axe. Ştii? Sper, dar totuși vă reamintesc:
Deci, în desenul meu, situat puțin mai sus, am descris deja o astfel de perpendiculară? Ce axa este? la axa. Și atunci ce lungime are? Ea este egală. Acum trageți singur o perpendiculară pe axă și găsiți-i lungimea. Va fi egal, nu? Atunci suma lor este egală.
Răspuns: .
Sarcina 4.În condițiile problemei 2, găsiți ordonata punctului simetric față de punctul din jurul axei x.
Cred că înțelegi intuitiv ce este simetria? Foarte multe obiecte o au: multe clădiri, mese, avioane, multe forme geometrice: o minge, un cilindru, un pătrat, un romb etc. În linii mari, simetria poate fi înțeleasă astfel: o figură este formată din două (sau mai multe) jumătăți identice. Această simetrie se numește axială. Ce este atunci o axă? Aceasta este exact linia de-a lungul căreia figura poate fi, relativ vorbind, „tăiată” în jumătăți identice (în această imagine, axa de simetrie este dreaptă):

Acum să revenim la sarcina noastră. Știm că căutăm un punct care este simetric față de axă. Atunci această axă este axa de simetrie. Deci, trebuie să marchem un punct, astfel încât axa să taie segmentul în două părți egale. Încercați să marcați singur un astfel de punct. Acum compară cu soluția mea:

Ați făcut la fel? Amenda! La punctul găsit, ne interesează ordonata. Ea este egală
Răspuns:
Acum spuneți-mi, după ce m-am gândit o secundă, care va fi abscisa punctului simetric față de punctul A în jurul axei y? Care este răspunsul tău? Răspuns corect: .
În general, regula poate fi scrisă astfel:
Un punct simetric față de un punct în jurul axei x are coordonatele:
Un punct simetric față de un punct în jurul axei y are coordonatele:
Ei bine, acum este chiar înfricoșător. sarcină: Găsiți coordonatele unui punct care este simetric față de un punct, în raport cu originea. Mai întâi gândești singur și apoi uită-te la desenul meu!

Răspuns:
Acum problema paralelogramului:
Sarcina 5: Punctele sunt ver-shi-na-mi-pa-ral-le-lo-gram-ma. Găsește-dee-te sau-dee-on-tu puncte.

Puteți rezolva această problemă în două moduri: logic și metoda coordonatelor. Voi aplica mai întâi metoda coordonatelor, apoi vă voi spune cum puteți decide diferit.
Este destul de clar că abscisa punctului este egală. (se află pe perpendiculara trasată de la punct la axa x). Trebuie să găsim ordonata. Să profităm de faptul că figura noastră este un paralelogram, ceea ce înseamnă că. Găsiți lungimea segmentului folosind formula pentru distanța dintre două puncte:
Coborâm perpendiculara care leagă punctul cu axa. Punctul de intersecție este notat cu o literă.

Lungimea segmentului este egală. (găsiți singur problema, unde am discutat acest moment), apoi vom găsi lungimea segmentului folosind teorema lui Pitagora:
Lungimea segmentului este exact aceeași cu ordonatele sale.
Răspuns: .
O altă soluție (voi oferi doar o poză care o ilustrează)

Progresul soluției:
1. Cheltuiește
2. Găsiți coordonatele punctului și lungimea
3. Demonstrează că.
Încă unul problema lungimii tăiate:
Punctele sunt-la-yut-xia top-shi-on-mi tri-unghi-no-ka. Găsiți lungimea liniei mediane, par-ral-lel-noy.

Îți amintești ce este linia de mijloc a unui triunghi? Atunci pentru tine această sarcină este elementară. Dacă nu vă amintiți, atunci vă voi aminti: linia de mijloc a unui triunghi este o linie care leagă punctele medii ale laturilor opuse. Este paralel cu baza și egal cu jumătate din ea.
Baza este un segment. A trebuit să-i căutăm lungimea mai devreme, este egală. Atunci lungimea liniei mediane este la jumătate mai lungă și egală.
Răspuns: .
Comentariu: Această problemă poate fi rezolvată într-un alt mod, la care vom reveni puțin mai târziu.
Între timp, iată câteva sarcini pentru tine, exersează-le, sunt destul de simple, dar ajută la „umplerea mâinii” folosind metoda coordonatelor!
1. Punctele apar-la-yut-xia top-shi-on-mi tra-pe-tion. Găsiți lungimea liniei mediane.

2. Puncte și yav-la-yut-xia ver-shi-na-mi pa-ral-le-lo-gram-ma. Găsește-dee-te sau-dee-on-tu puncte.

3. Găsiți lungimea de la tăiere, conectați al doilea punct și

4. Găsiți zona pentru fi-gu-ry-roșu-shen-noy pe planul ko-or-di-nat-noy.

5. Un cerc centrat pe na-cha-le ko-or-di-nat trece printr-un punct. Find-de-te-i ra-di-mustache.

6. Nai-di-te ra-di-us circle-no-sti, describe-san-noy lângă unghiul drept-no-ka, vârfurile-shi-ny a ceva-ro-go au co-or - di-na-tu co-din-reply-dar

Solutii:
1. Se știe că linia mediană a unui trapez este egală cu jumătate din suma bazelor sale. Baza este egală, dar baza. Apoi
Răspuns:
2. Cel mai simplu mod de a rezolva această problemă este să observați că (regula paralelogramului). Calculați coordonatele vectorilor și nu este dificil: . La adăugarea vectorilor, coordonatele sunt adăugate. Apoi are coordonate. Punctul are aceleași coordonate, deoarece începutul vectorului este un punct cu coordonate. Ne intereseaza ordonata. Ea este egală.
Răspuns:
3. Acționăm imediat după formula distanței dintre două puncte:
Răspuns:
4. Privește imaginea și spune, între care două cifre este „storsă” zona umbrită? Este prins între două pătrate. Apoi, aria figurii dorite este egală cu aria pătratului mare minus aria celui mic. Latura pătratului mic este un segment care leagă punctele și lungimea acestuia este
Atunci aria pătratului mic este
Facem același lucru cu un pătrat mare: latura sa este un segment care leagă punctele și lungimea sa este egală cu
Atunci aria pătratului mare este
Aria figurii dorite este găsită prin formula:
Răspuns:
5. Dacă cercul are originea ca centru și trece printr-un punct, atunci raza lui va fi exact egală cu lungimea segmentului (fă un desen și vei înțelege de ce acest lucru este evident). Aflați lungimea acestui segment:
Răspuns:
6. Se știe că raza unui cerc circumscris unui dreptunghi este egală cu jumătate din diagonala acestuia. Să găsim lungimea oricăreia dintre cele două diagonale (la urma urmei, într-un dreptunghi sunt egale!)
Răspuns:
Ei bine, ai gestionat totul? Nu a fost atât de greu să-mi dau seama, nu-i așa? Există o singură regulă aici - să puteți face o imagine vizuală și pur și simplu să „citiți” toate datele din ea.
Mai avem foarte puțin. Mai sunt literalmente două puncte pe care aș dori să le discut.
Să încercăm să rezolvăm această problemă simplă. Lăsați două puncte și să fie date. Găsiți coordonatele mijlocului segmentului. Soluția la această problemă este următoarea: fie punctul să fie mijlocul dorit, apoi are coordonatele:
Acesta este: coordonatele mijlocului segmentului = media aritmetică a coordonatelor corespunzătoare ale capetelor segmentului.
Această regulă este foarte simplă și de obicei nu provoacă dificultăți elevilor. Să vedem în ce probleme și cum se folosește:
1. Find-di-te or-di-na-tu se-re-di-us from-cut, connect-nya-yu-th-th point and

2. Punctele sunt yav-la-yut-xia ver-shi-na-mi-che-you-reh-coal-no-ka. Find-di-te or-di-na-tu puncte de re-re-se-che-niya lui dia-go-on-lei.

3. Find-di-te abs-cis-su al centrului cercului, descrie-san-noy lângă dreptunghi-no-ka, vârfurile-shi-avem ceva-ro-go co-or-di- na-tu co-de la-vet-stvenno-dar.

Solutii:
1. Prima sarcină este doar un clasic. Acționăm imediat prin determinarea punctului de mijloc al segmentului. Are coordonate. ordonata este egală.
Răspuns:
2. Este ușor de observat că patrulaterul dat este un paralelogram (chiar și un romb!). Puteți dovedi singuri calculând lungimile laturilor și comparându-le între ele. Ce știu despre un paralelogram? Diagonalele sale sunt tăiate în două de punctul de intersecție! Aha! Deci, care este punctul de intersecție al diagonalelor? Acesta este mijlocul oricăreia dintre diagonale! Voi alege, în special, diagonala. Atunci punctul are coordonate.Ordonata punctului este egală cu.
Răspuns:
3. Care este centrul cercului circumscris dreptunghiului? El coincide cu punctul de intersecție al diagonalelor sale. Ce știi despre diagonalele unui dreptunghi? Sunt egale, iar punctul de intersecție este împărțit la jumătate. Sarcina a fost redusă la cea anterioară. Luați, de exemplu, diagonala. Atunci, dacă este centrul cercului circumscris, atunci este mijlocul. Caut coordonate: Abscisa este egală.
Răspuns:
Acum exersează puțin pe cont propriu, voi da doar răspunsurile la fiecare problemă ca să te poți verifica singur.
1. Nai-di-te ra-di-us circle-no-sti, descrie-san-noy lângă triunghi-no-ka, vârfurile cineva-ro-go au ko-or-di -no misters

2. Găsește-di-te or-di-na-tu centrul cercului, descrie san-noy lângă triunghi-no-ka, vârfurile-shi-avem coordonatele ceva-ro-go
3. Ce fel de ra-di-y-sa ar trebui să existe un cerc cu un centru într-un punct astfel încât să atingă axa abs-ciss?

4. Găsiți-di-te sau-di-pe-acel punct de re-re-se-che-ing al axei și de la tăiere, conecta-nya-yu-al-lea punct și

Raspunsuri:
A mers totul? Chiar sper! Acum - ultima împingere. Acum fii deosebit de atent. Materialul pe care îl voi explica acum nu este relevant doar pentru problemele simple ale metodei coordonatelor din partea B, ci se găsește și în problema C2.
Pe care dintre promisiunile mele nu le-am ținut încă? Îți amintești ce operații pe vectori am promis să introduc și pe care le-am introdus în cele din urmă? Sunt sigur că nu am uitat nimic? Uitat! Am uitat să explic ce înseamnă multiplicarea vectorilor.
Există două moduri de a înmulți un vector cu un vector. În funcție de metoda aleasă, vom obține obiecte de altă natură:
Produsul vectorial este destul de complicat. Cum se face și de ce este nevoie, vom discuta cu tine în următorul articol. Și în aceasta ne vom concentra pe produsul scalar.
Există deja două moduri care ne permit să-l calculăm:
După cum ați ghicit, rezultatul ar trebui să fie același! Deci, să ne uităm mai întâi la primul mod:
Punctați produsul prin coordonate
Găsiți: - notație comună pentru produsul punctual
Formula de calcul este următoarea:
Adică produsul punctual = suma produselor coordonatelor vectorilor!
Exemplu:
Find-dee-te

Soluţie:
Găsiți coordonatele fiecărui vector:
Calculăm produsul scalar cu formula:
Răspuns:
Vezi tu, absolut nimic complicat!
Ei bine, acum încearcă singur:
Find-di-te scalar-noe pro-from-ve-de-nie century-to-ditch and

Ai reușit? Poate a observat un mic truc? Sa verificam:
Coordonate vectoriale, ca în sarcina anterioară! Răspuns: .
Pe lângă coordonate, există o altă modalitate de a calcula produsul scalar, și anume, prin lungimile vectorilor și cosinusul unghiului dintre ei:
Indică unghiul dintre vectorii și.
Adică produsul scalar este egal cu produsul lungimilor vectorilor și cosinusul unghiului dintre ei.
De ce avem nevoie de această a doua formulă, dacă avem prima, care este mult mai simplă, măcar nu există cosinus în ea. Și avem nevoie de ea pentru ca din prima și a doua formulă să putem deduce cum să găsim unghiul dintre vectori!
Să ne amintim de formula pentru lungimea unui vector!
Apoi, dacă conectez aceste date în formula produsului punctual, obțin:
Dar în alt fel:
Deci ce avem? Acum avem o formulă pentru a calcula unghiul dintre doi vectori! Uneori, pentru concizie, se scrie și așa:
Adică, algoritmul pentru calcularea unghiului dintre vectori este următorul:
- Calculăm produsul scalar prin coordonate
- Aflați lungimile vectorilor și înmulțiți-le
- Împărțiți rezultatul punctului 1 la rezultatul punctului 2
Să exersăm cu exemple:
1. Găsiți unghiul dintre pleoape-la-ra-mi și. Dați răspunsul în grade.

2. În condițiile problemei anterioare, găsiți cosinusul dintre vectori
Să facem asta: te voi ajuta să rezolvi prima problemă și să încerci să o faci singur pe a doua! De acord? Atunci să începem!
1. Acești vectori sunt vechii noștri prieteni. Am luat deja în considerare produsul lor scalar și a fost egal. Coordonatele lor sunt: , . Apoi găsim lungimile lor:
Atunci căutăm cosinusul dintre vectori:
Care este cosinusul unghiului? Acesta este colțul.
Răspuns:
Ei bine, acum rezolvă singur a doua problemă și apoi compară! Voi da doar o soluție foarte scurtă:
2. are coordonate, are coordonate.
Fie unghiul dintre vectori și, apoi
Răspuns:
Trebuie menționat că sarcinile direct pe vectori și metoda coordonatelor din partea B a lucrării de examen sunt destul de rare. Cu toate acestea, marea majoritate a problemelor C2 pot fi rezolvate cu ușurință prin introducerea unui sistem de coordonate. Deci, puteți considera acest articol ca pe o fundație, pe baza căreia vom realiza construcții destul de complicate de care vom avea nevoie pentru a rezolva probleme complexe.
COORDONATE ȘI VECTORI. NIVEL INTERMEDIAR
Tu și cu mine continuăm să studiem metoda coordonatelor. În ultima parte, am derivat o serie de formule importante care permit:
- Găsiți coordonatele vectoriale
- Găsiți lungimea unui vector (alternativ: distanța dintre două puncte)
- Adăugați, scădeți vectori. Înmulțiți-le cu un număr real
- Găsiți punctul de mijloc al unui segment
- Calculați produsul scalar al vectorilor
- Găsiți unghiul dintre vectori
Desigur, întreaga metodă de coordonate nu se încadrează în aceste 6 puncte. Stă la baza unei astfel de științe precum geometria analitică, pe care o veți face cunoștință la universitate. Vreau doar să construiesc o fundație care să vă permită să rezolvați problemele într-o singură stare. examen. Ne-am dat seama de sarcinile părții B în Acum este timpul să trecem la un nivel calitativ nou! Acest articol va fi dedicat unei metode de rezolvare a acelor probleme C2 în care ar fi rezonabil să trecem la metoda coordonatelor. Acest caracter rezonabil este determinat de ceea ce trebuie găsit în problemă și de ce cifră este dată. Deci, aș folosi metoda coordonatelor dacă întrebările sunt:
- Aflați unghiul dintre două plane
- Aflați unghiul dintre o dreaptă și un plan
- Găsiți unghiul dintre două drepte
- Aflați distanța de la un punct la un plan
- Aflați distanța de la un punct la o linie
- Găsiți distanța de la o linie dreaptă la un avion
- Aflați distanța dintre două linii
Dacă cifra dată în starea problemei este un corp de revoluție (bilă, cilindru, con...)
Cifrele potrivite pentru metoda coordonatelor sunt:
- cuboid
- Piramida (triunghiulara, patrangulara, hexagonala)
De asemenea, din experiența mea este nepotrivit să se folosească metoda coordonatelor pentru:
- Găsirea zonelor de secțiuni
- Calcule ale volumelor corpurilor
Cu toate acestea, trebuie remarcat imediat că trei situații „nefavorabile” pentru metoda coordonatelor sunt destul de rare în practică. În majoritatea sarcinilor, poate deveni salvatorul tău, mai ales dacă nu ești foarte puternic în construcții tridimensionale (care sunt uneori destul de complicate).
Care sunt toate cifrele pe care le-am enumerat mai sus? Nu mai sunt plate, precum pătrat, triunghi, cerc, ci voluminoase! În consecință, trebuie să luăm în considerare nu un sistem de coordonate bidimensional, ci un sistem de coordonate tridimensional. Se construiește destul de ușor: doar pe lângă abscisă și ordonate, vom introduce o altă axă, axa aplicată. Figura arată schematic poziția lor relativă:

Toate sunt reciproc perpendiculare, se intersectează într-un punct, pe care îl vom numi origine. Se va nota axa absciselor, ca mai înainte, axa ordonatelor - , iar axa aplicată introdusă - .
Dacă mai devreme fiecare punct din plan a fost caracterizat de două numere - abscisa și ordonata, atunci fiecare punct din spațiu este deja descris de trei numere - abscisa, ordonata, aplicata. De exemplu:

În consecință, abscisa punctului este egală, ordonata este , iar aplicația este .
Uneori, abscisa unui punct este denumită și proiecția punctului pe axa absciselor, ordonata este proiecția punctului pe axa ordonatelor, iar aplicatul este proiecția punctului pe axa aplicată. În consecință, dacă este dat un punct, atunci un punct cu coordonate:
numită proiecția unui punct pe un plan
numită proiecția unui punct pe un plan
Se ridică o întrebare firească: toate formulele derivate pentru cazul bidimensional sunt valabile în spațiu? Răspunsul este da, sunt justi și au același aspect. Pentru un mic detaliu. Cred că ai ghicit deja care. În toate formulele, va trebui să adăugăm încă un termen responsabil pentru axa aplicată. Și anume.
1. Dacă sunt date două puncte: , atunci:
- Coordonatele vectoriale:
- Distanța dintre două puncte (sau lungimea vectorului)
- Mijlocul segmentului are coordonate
2. Dacă sunt dați doi vectori: și, atunci:
- Produsul lor punctual este:
- Cosinusul unghiului dintre vectori este:
Cu toate acestea, spațiul nu este atât de simplu. După cum înțelegeți, adăugarea unei alte coordonate introduce o varietate semnificativă în spectrul figurilor „care trăiesc” în acest spațiu. Și pentru o narațiune ulterioară, trebuie să introduc ceva, aproximativ vorbind, „generalizare” a liniei drepte. Această „generalizare” va fi un avion. Ce știi despre avion? Încercați să răspundeți la întrebarea, ce este un avion? Este foarte greu de spus. Cu toate acestea, toți ne imaginăm intuitiv cum arată:

În linii mari, acesta este un fel de „frunză” nesfârșită aruncată în spațiu. „Infinitul” trebuie înțeles că planul se extinde în toate direcțiile, adică aria sa este egală cu infinitul. Cu toate acestea, această explicație „pe degete” nu dă nici cea mai mică idee despre structura avionului. Și ne va interesa.
Să ne amintim una dintre axiomele de bază ale geometriei:
- O linie dreaptă trece prin două puncte diferite dintr-un plan, în plus, doar unul:

Sau analogul său în spațiu:

Desigur, vă amintiți cum să obțineți ecuația unei linii drepte din două puncte date, acest lucru nu este deloc dificil: dacă primul punct are coordonate: iar al doilea, atunci ecuația liniei drepte va fi după cum urmează:
Ai trecut prin asta în clasa a VII-a. În spațiu, ecuația unei drepte arată astfel: să avem două puncte cu coordonate: , atunci ecuația unei drepte care trece prin ele are forma:
De exemplu, o linie trece prin puncte:
Cum ar trebui să fie înțeles acest lucru? Acest lucru trebuie înțeles după cum urmează: un punct se află pe o dreaptă dacă coordonatele sale satisfac următorul sistem:
Nu ne va interesa foarte mult ecuația unei linii drepte, dar trebuie să acordăm atenție conceptului foarte important al vectorului de direcție al unei linii drepte. - orice vector diferit de zero situat pe o linie dată sau paralel cu aceasta.

De exemplu, ambii vectori sunt vectori de direcție ai unei linii drepte. Fie un punct situat pe o linie dreaptă și vectorul său de direcție. Atunci ecuația unei linii drepte poate fi scrisă sub următoarea formă:
Încă o dată, nu voi fi foarte interesat de ecuația unei linii drepte, dar chiar am nevoie să vă amintiți ce este un vector de direcție! Din nou: este ORICE vector diferit de zero situat pe o linie sau paralel cu aceasta.
Retrage ecuația în trei puncte a unui plan nu mai este atât de banal și, de obicei, nu este acoperit într-un curs de liceu. Dar în zadar! Această tehnică este vitală atunci când recurgem la metoda coordonatelor pentru a rezolva probleme complexe. Totuși, presupun că ești plin de dorință de a învăța ceva nou? Mai mult, îți vei putea impresiona profesorul de la universitate atunci când se va dovedi că știi deja să folosești tehnica care se studiază de obicei în cursul geometriei analitice. Asadar, haideti sa începem.
Ecuația unui plan nu este prea diferită de ecuația unei drepte pe un plan, și anume, are forma:
unele numere (nu toate egale cu zero), dar variabile, de exemplu: etc. După cum puteți vedea, ecuația unui plan nu este foarte diferită de ecuația unei linii drepte (funcție liniară). Totuși, îți amintești ce ne-am certat cu tine? Am spus că dacă avem trei puncte care nu se află pe o singură dreaptă, atunci ecuația planului este restabilită în mod unic din ele. Dar cum? Voi încerca să vă explic.
Deoarece ecuația plană este:
Și punctele aparțin acestui plan, atunci când înlocuim coordonatele fiecărui punct în ecuația planului, ar trebui să obținem identitatea corectă:
Astfel, este nevoie de a rezolva trei ecuații deja cu necunoscute! Dilemă! Cu toate acestea, putem întotdeauna presupune că (pentru aceasta trebuie să împărțim prin). Astfel, obținem trei ecuații cu trei necunoscute:
Cu toate acestea, nu vom rezolva un astfel de sistem, ci vom scrie expresia criptică care decurge din el:
Ecuația unui plan care trece prin trei puncte date
\[\stanga| (\begin(array)(*(20)(c))(x - (x_0))&((x_1) - (x_0))&((x_2) - (x_0))\\(y - (y_0) )&((y_1) - (y_0))&((y_2) - (y_0))\\(z - (z_0))&((z_1) - (z_0))&((z_2) - (z_0)) \end(matrice)) \right| = 0\]
Stop! Ce altceva este asta? Un modul foarte neobișnuit! Totuși, obiectul pe care îl vezi în fața ta nu are nimic de-a face cu modulul. Acest obiect se numește determinant de ordinul trei. De acum înainte, când te ocupi de metoda coordonatelor dintr-un avion, vei întâlni adesea acești determinanți. Ce este un determinant de ordinul trei? Destul de ciudat, este doar un număr. Rămâne să înțelegem ce număr specific vom compara cu determinantul.
Să scriem mai întâi determinantul de ordinul trei într-o formă mai generală:
Unde sunt niște numere. Mai mult, prin primul index înțelegem numărul rândului, iar prin index - numărul coloanei. De exemplu, înseamnă că numărul dat se află la intersecția celui de-al doilea rând și a treia coloană. Să ne punem următoarea întrebare: cum anume vom calcula un astfel de determinant? Adică, cu ce număr specific îl vom compara? Pentru determinantul exact al celui de-al treilea ordin, există o regulă triunghiulară euristică (vizuală), arată astfel:

- Produsul elementelor diagonalei principale (de la stânga sus la dreapta jos) produsul elementelor care formează primul triunghi „perpendicular” pe diagonala principală produsul elementelor care formează al doilea triunghi „perpendicular” pe principalul diagonală
- Produsul elementelor diagonalei secundare (din colțul din dreapta sus până în stânga jos) produsul elementelor care formează primul triunghi „perpendicular” al diagonalei secundare produsul elementelor care formează al doilea triunghi „perpendicular” a diagonalei secundare
- Atunci determinantul este egal cu diferența dintre valorile obținute la pas și
Dacă scriem toate acestea în numere, atunci obținem următoarea expresie:
Cu toate acestea, nu trebuie să memorați metoda de calcul în această formă, este suficient să păstrați triunghiurile în cap și însăși ideea a ceea ce se adaugă la ce și ce se scade apoi din ce).
Să ilustrăm metoda triunghiului cu un exemplu:
1. Calculați determinantul:
Să ne dăm seama ce adăugăm și ce scădem:
Termeni care vin cu un „plus”:
Aceasta este diagonala principală: produsul elementelor este
Primul triunghi, „perpendicular pe diagonala principală: produsul elementelor este
Al doilea triunghi, „perpendicular pe diagonala principală: produsul elementelor este
Adăugăm trei numere:
Termeni care vin cu un „minus”
Aceasta este o diagonală laterală: produsul elementelor este
Primul triunghi, „perpendicular pe diagonala secundară: produsul elementelor este
Al doilea triunghi, „perpendicular pe diagonala secundară: produsul elementelor este
Adăugăm trei numere:
Tot ce rămâne de făcut este să scădem din suma termenilor plus suma termenilor minus:
Prin urmare,
După cum puteți vedea, nu există nimic complicat și supranatural în calcularea determinanților de ordinul trei. Este pur și simplu important să vă amintiți despre triunghiuri și să nu faceți greșeli de aritmetică. Acum încercați să vă calculați:
Verificăm:
- Primul triunghi perpendicular pe diagonala principală:
- Al doilea triunghi perpendicular pe diagonala principală:
- Suma termenilor plus:
- Primul triunghi perpendicular pe diagonala laterală:
- Al doilea triunghi, perpendicular pe diagonala laterală:
- Suma termenilor cu minus:
- Suma termenilor plus minus suma termenilor minus:
Iată încă câțiva factori determinanți pentru tine, calculează-le singur valorile și compară cu răspunsurile:
Raspunsuri:
Ei bine, totul s-a potrivit? Grozav, atunci poți merge mai departe! Dacă există dificultăți, atunci sfatul meu este acesta: pe internet există o grămadă de programe pentru calcularea determinantului online. Tot ce aveți nevoie este să găsiți propriul determinant, să îl calculați singur și apoi să îl comparați cu ceea ce calculează programul. Și așa mai departe până când rezultatele încep să se potrivească. Sunt sigur că acest moment nu va întârzia să apară!
Acum să revenim la determinantul pe care l-am scris când am vorbit despre ecuația unui plan care trece prin trei puncte date:
Tot ce trebuie să faceți este să calculați valoarea acestuia direct (folosind metoda triunghiului) și să setați rezultatul egal cu zero. Desigur, deoarece sunt variabile, veți obține o expresie care depinde de ele. Această expresie va fi ecuația unui plan care trece prin trei puncte date care nu se află pe o singură dreaptă!
Să ilustrăm acest lucru cu un exemplu simplu:
1. Construiți ecuația planului care trece prin puncte
Compunem un determinant pentru aceste trei puncte:
Simplificare:
Acum îl calculăm direct după regula triunghiurilor:
\[(\left| (\begin(array)(*(20)(c))(x + 3)&2&6\\(y - 2)&0&1\\(z + 1)&5&0\end(array)) \ dreapta| = \left((x + 3) \right) \cdot 0 \cdot 0 + 2 \cdot 1 \cdot \left((z + 1) \right) + \left((y - 2) \right) \cdot 5 \cdot 6 - )\]
Astfel, ecuația planului care trece prin puncte este:
Acum încercați să rezolvați singur o problemă și apoi o vom discuta:
2. Aflați ecuația planului care trece prin puncte
Ei bine, hai să discutăm soluția acum:
Facem un determinant:
Și calculează-i valoarea:
Atunci ecuația planului are forma:
Sau, reducând cu, obținem:
Acum două sarcini pentru autocontrol:
- Construiți ecuația unui plan care trece prin trei puncte:
Raspunsuri:
S-a potrivit totul? Din nou, dacă există anumite dificultăți, atunci sfatul meu este următorul: ia trei puncte din capul tău (cu un grad mare de probabilitate să nu se întindă pe o singură linie dreaptă), construiește un avion pe ele. Și apoi verificați-vă online. De exemplu, pe site:
Totuși, cu ajutorul determinanților, vom construi nu numai ecuația planului. Amintiți-vă, v-am spus că pentru vectori nu este definit doar produsul punctual. Există, de asemenea, un vector, precum și un produs mixt. Și dacă produsul scalar a doi vectori va fi un număr, atunci produsul vectorial al doi vectori va fi un vector, iar acest vector va fi perpendicular pe cei dați:

Mai mult, modulul său va fi egal cu aria paralelogramului construit pe vectori și. Vom avea nevoie de acest vector pentru a calcula distanța de la un punct la o linie. Cum putem calcula produsul încrucișat al vectorilor și dacă sunt date coordonatele lor? În ajutorul nostru ne vine din nou determinantul ordinului al treilea. Cu toate acestea, înainte de a trece la algoritmul de calcul al produsului încrucișat, trebuie să fac o mică digresiune lirică.
Această digresiune se referă la vectorii de bază.
Schematic ele sunt prezentate în figură:

De ce crezi că se numesc de bază? Adevărul este că:
Sau in poza:

Valabilitatea acestei formule este evidentă, deoarece:
produs vectorial
Acum pot începe să introduc produsul încrucișat:
Produsul vectorial al doi vectori este un vector care se calculează conform următoarei reguli:
Acum să dăm câteva exemple de calcul al produsului încrucișat:
Exemplul 1: Găsiți produsul încrucișat al vectorilor:
Rezolvare: fac un determinant:
Si il calculez:
Acum, de la scrierea prin vectori de bază, voi reveni la notația vectorială obișnuită:
Prin urmare:
Acum încearcă.
Gata? Verificăm:
Și în mod tradițional două sarcini de controlat:
- Găsiți produsul încrucișat al următorilor vectori:
- Găsiți produsul încrucișat al următorilor vectori:
Raspunsuri:
Produs mixt a trei vectori
Ultima construcție de care am nevoie este produsul mixt a trei vectori. El, ca un scalar, este un număr. Există două moduri de a o calcula. - prin determinant, - prin produsul mixt.
Și anume, să presupunem că avem trei vectori:
Apoi produsul mixt a trei vectori, notat cu poate fi calculat ca:
1. - adică produsul mixt este produsul scalar al unui vector și produsul vectorial al altor doi vectori
De exemplu, produsul mixt a trei vectori este:
Încercați să îl calculați singur folosind produsul vectorial și asigurați-vă că rezultatele se potrivesc!
Și din nou - două exemple pentru o soluție independentă:
Raspunsuri:
Alegerea sistemului de coordonate
Ei bine, acum avem toate bazele necesare de cunoștințe pentru a rezolva probleme stereometrice complexe în geometrie. Cu toate acestea, înainte de a trece direct la exemplele și algoritmii pentru rezolvarea acestora, cred că va fi util să ne oprim asupra următoarei întrebări: cum exact alegeți un sistem de coordonate pentru o anumită figură. La urma urmei, alegerea poziției relative a sistemului de coordonate și a figurii în spațiu este cea care va determina în cele din urmă cât de greoaie vor fi calculele.
Vă reamintesc că în această secțiune avem în vedere următoarele cifre:
- cuboid
- Prismă dreaptă (triunghiulară, hexagonală...)
- Piramida (triunghiulara, patruunghiulara)
- Tetraedrul (la fel ca piramida triunghiulara)
Pentru un cuboid sau cub, recomand următoarea construcție:

Adică voi plasa figura „în colț”. Cubul și cutia sunt figuri foarte bune. Pentru ei, puteți găsi întotdeauna cu ușurință coordonatele vârfurilor sale. De exemplu, dacă (așa cum se arată în imagine)

atunci coordonatele vârfurilor sunt:
Desigur, nu trebuie să vă amintiți acest lucru, dar este de dorit să vă amintiți cum să poziționați cel mai bine un cub sau o cutie dreptunghiulară.
prismă dreaptă
Prisma este o figură mai dăunătoare. Îl puteți aranja în spațiu în diferite moduri. Cu toate acestea, cred că următoarea este cea mai bună opțiune:
Prisma triunghiulara:

Adică punem una dintre laturile triunghiului în întregime pe axă, iar unul dintre vârfuri coincide cu originea.
Prisma hexagonala:

Adică, unul dintre vârfuri coincide cu originea, iar una dintre laturi se află pe axă.
Piramida patruunghiulara si hexagonala:

O situație asemănătoare cu un cub: combinăm două laturi ale bazei cu axele de coordonate, combinăm unul dintre vârfuri cu originea. Singura dificultate mică va fi să calculați coordonatele punctului.
Pentru o piramidă hexagonală - la fel ca și pentru o prismă hexagonală. Sarcina principală va fi din nou găsirea coordonatelor vârfului.

Tetraedrul (piramida triunghiulara)

Situația este foarte asemănătoare cu cea pe care am dat-o pentru prisma triunghiulară: un vârf coincide cu originea, o latură se află pe axa de coordonate.
Ei bine, acum tu și cu mine suntem în sfârșit aproape de a începe să rezolvăm problemele. Din ceea ce am spus chiar la începutul articolului, ați putea trage următoarea concluzie: majoritatea problemelor C2 se încadrează în 2 categorii: probleme pentru unghi și probleme pentru distanță. În primul rând, vom lua în considerare problemele pentru găsirea unui unghi. Ei, la rândul lor, sunt împărțiți în următoarele categorii (pe măsură ce complexitatea crește):
Probleme pentru găsirea colțurilor
- Găsirea unghiului dintre două drepte
- Aflarea unghiului dintre două plane
Să luăm în considerare aceste probleme secvențial: să începem prin a găsi unghiul dintre două drepte. Haide, ține minte, tu și cu mine am rezolvat exemple similare înainte? Vă amintiți, pentru că aveam deja ceva asemănător... Căutăm un unghi între doi vectori. Vă reamintesc, dacă sunt dați doi vectori: și, atunci unghiul dintre ei se găsește din relația:
Acum avem un obiectiv - găsirea unghiului dintre două linii drepte. Să trecem la „imaginea plată”:

Câte unghiuri obținem când două drepte se intersectează? Deja lucruri. Adevărat, doar două dintre ele nu sunt egale, în timp ce altele sunt verticale față de ei (și, prin urmare, coincid cu ei). Deci, ce unghi ar trebui să luăm în considerare unghiul dintre două drepte: sau? Aici regula este: unghiul dintre două linii drepte nu este întotdeauna mai mare de grade. Adică din două unghiuri, vom alege întotdeauna unghiul cu cea mai mică măsură a gradului. Adică, în această imagine, unghiul dintre cele două linii este egal. Pentru a nu te deranja să găsești de fiecare dată cel mai mic dintre cele două unghiuri, matematicienii vicleni au sugerat să folosești modulul. Astfel, unghiul dintre două linii drepte este determinat de formula:
Tu, ca cititor atent, ar fi trebuit să ai o întrebare: de unde, de fapt, obținem exact aceste numere de care avem nevoie pentru a calcula cosinusul unui unghi? Răspuns: le vom lua din vectorii de direcție ai liniilor! Astfel, algoritmul pentru găsirea unghiului dintre două linii este următorul:
- Aplicam formula 1.
Sau mai detaliat:
- Căutăm coordonatele vectorului de direcție al primei drepte
- Căutăm coordonatele vectorului de direcție al celei de-a doua linii
- Calculați modulul produsului lor scalar
- Căutăm lungimea primului vector
- Căutăm lungimea celui de-al doilea vector
- Înmulțiți rezultatele de la punctul 4 cu rezultatele de la punctul 5
- Împărțim rezultatul punctului 3 la rezultatul punctului 6. Obținem cosinusul unghiului dintre drepte
- Dacă acest rezultat ne permite să calculăm exact unghiul, îl căutăm
- În caz contrar, scriem prin arccosinus
Ei bine, acum este momentul să trecem la sarcini: voi demonstra soluția primelor două în detaliu, voi prezenta soluția alteia pe scurt și voi da doar răspunsuri la ultimele două sarcini, trebuie să vă faceți singuri toate calculele pentru ei.
Sarcini:
1. În tet-ra-ed-re dreapta, găsește-di-te unghiul dintre tu-so-that tet-ra-ed-ra și partea me-di-a-noy bo-ko-how.
2. În șase-coal-pi-ra-mi-de-dreapta înainte, suta-ro-na-os-no-va-niya sunt cumva egale, iar nervurile laterale sunt egale, găsiți unghiul dintre dreapta linii şi.
3. Lungimile tuturor muchiilor dreptacilor four-you-rech-coal-noy pi-ra-mi-dy sunt egale între ele. Găsiți unghiul dintre liniile drepte și dacă from-re-zok - you-so-that data pi-ra-mi-dy, punctul este se-re-di-pe coasta ei bo-ko-th
4. Pe marginea cubului de la-me-che-până la un punct astfel încât Find-di-te unghiul dintre liniile drepte și
5. Punct - se-re-di-pe marginile cubului Nai-di-te unghiul dintre liniile drepte si.
Nu întâmplător am plasat sarcinile în această ordine. Deși nu ați avut încă timp să începeți să navigați prin metoda coordonatelor, eu însumi voi analiza cele mai „problematice” figuri și vă voi lăsa să vă ocupați de cel mai simplu cub! Treptat trebuie să înveți cum să lucrezi cu toate figurile, voi crește complexitatea sarcinilor de la subiect la subiect.
Să începem să rezolvăm problemele:
1. Desenați un tetraedru, plasați-l în sistemul de coordonate așa cum am sugerat mai devreme. Deoarece tetraedrul este regulat, atunci toate fețele sale (inclusiv baza) sunt triunghiuri regulate. Deoarece nu ni se dă lungimea laturii, o pot lua egală. Cred că înțelegi că unghiul nu va depinde cu adevărat de cât de mult va fi „întins” tetraedrul nostru?. De asemenea, voi desena înălțimea și mediana în tetraedru. Pe parcurs, îi voi desena baza (ne va veni și la îndemână).

Trebuie să găsesc unghiul dintre și. Ce știm? Știm doar coordonatele punctului. Deci, trebuie să găsim mai multe coordonate ale punctelor. Acum ne gândim: un punct este un punct de intersecție al înălțimilor (sau bisectoarelor sau medianelor) unui triunghi. Un punct este un punct ridicat. Punctul este punctul de mijloc al segmentului. Apoi în sfârșit trebuie să găsim: coordonatele punctelor: .
Să începem cu cel mai simplu: coordonatele punctului. Priviți figura: este clar că aplicația unui punct este egală cu zero (punctul se află pe un plan). Ordonata sa este egală (pentru că este mediana). Este mai greu să-i găsești abscisa. Cu toate acestea, acest lucru se face cu ușurință pe baza teoremei lui Pitagora: Luați în considerare un triunghi. Ipotenuza sa este egală, iar unul dintre catete este egal. Atunci:
În sfârșit avem:
Acum să găsim coordonatele punctului. Este clar că aplicația sa este din nou egală cu zero, iar ordonata sa este aceeași cu cea a unui punct, adică. Să-i găsim abscisa. Acest lucru se face destul de banal dacă cineva își amintește asta înălțimile unui triunghi echilateral se împart la punctul de intersecție în proporție numărând de sus. Deoarece:, atunci abscisa dorită a punctului, egală cu lungimea segmentului, este egală cu:. Astfel, coordonatele punctului sunt:
Să găsim coordonatele punctului. Este clar că abscisa și ordonata ei coincid cu abscisa și ordonata punctului. Și aplicația este egală cu lungimea segmentului. - acesta este unul dintre catetele triunghiului. Ipotenuza unui triunghi este un segment - un catet. Este căutat din motivele pe care le-am evidențiat cu caractere aldine:
Punctul este punctul de mijloc al segmentului. Apoi trebuie să ne amintim formula pentru coordonatele mijlocului segmentului:
Asta e, acum putem căuta coordonatele vectorilor de direcție:
Ei bine, totul este gata: înlocuim toate datele în formula:
Prin urmare,
Răspuns:
Nu ar trebui să vă fie frică de astfel de răspunsuri „îngrozitoare”: pentru problemele C2 aceasta este o practică obișnuită. Mai degrabă aș fi surprins de răspunsul „frumos” din această parte. De asemenea, după cum ați observat, practic nu am recurs la altceva decât la teorema lui Pitagora și la proprietatea înălțimilor unui triunghi echilateral. Adică, pentru a rezolva problema stereometrică, am folosit chiar minimul de stereometrie. Câștigul din aceasta este parțial „stins” prin calcule destul de greoaie. Dar sunt destul de algoritmici!
2. Desenați o piramidă hexagonală regulată împreună cu sistemul de coordonate, precum și baza acesteia:

Trebuie să găsim unghiul dintre linii și. Astfel, sarcina noastră se reduce la găsirea coordonatelor punctelor: . Vom găsi coordonatele ultimelor trei din desenul mic și vom găsi coordonatele vârfului prin coordonatele punctului. Multă muncă, dar trebuie să încep!
a) Coordonata: este clar ca aplicata si ordonata ei sunt zero. Să găsim abscisa. Pentru a face acest lucru, luați în considerare un triunghi dreptunghic. Din păcate, în ea nu cunoaștem decât ipotenuza, care este egală cu. Vom încerca să găsim piciorul (pentru că este clar că lungimea de două ori a piciorului ne va da abscisa punctului). Cum o putem căuta? Să ne amintim ce fel de figură avem la baza piramidei? Acesta este un hexagon obișnuit. Ce înseamnă? Aceasta înseamnă că toate laturile și toate unghiurile sunt egale. Trebuie să găsim un astfel de colț. Vreo idee? Există o mulțime de idei, dar există o formulă:
Suma unghiurilor unui n-gon regulat este .
Astfel, suma unghiurilor unui hexagon regulat este de grade. Atunci fiecare dintre unghiuri este egal cu:
Să ne uităm din nou la imagine. Este clar că segmentul este bisectoarea unghiului. Atunci unghiul este de grade. Apoi:
Atunci unde.
Deci are coordonate
b) Acum putem găsi cu ușurință coordonatele punctului: .
c) Aflați coordonatele punctului. Deoarece abscisa coincide cu lungimea segmentului, este egală. Găsirea ordonatei nu este, de asemenea, foarte dificilă: dacă conectăm punctele și și notăm punctul de intersecție al dreptei, să spunem pentru. (fa-te singur construcție simplă). Atunci, astfel, ordonata punctului B este egală cu suma lungimilor segmentelor. Să ne uităm din nou la triunghi. Apoi
Apoi din Atunci punctul are coordonate
d) Acum găsiți coordonatele punctului. Luați în considerare un dreptunghi și demonstrați că. Astfel, coordonatele punctului sunt:
e) Rămâne de găsit coordonatele vârfului. Este clar că abscisa și ordonata ei coincid cu abscisa și ordonata punctului. Să găsim o aplicație. De atunci. Luați în considerare un triunghi dreptunghic. După starea problemei, marginea laterală. Aceasta este ipotenuza triunghiului meu. Atunci înălțimea piramidei este piciorul.
Atunci punctul are coordonatele:
Gata, am coordonatele tuturor punctelor de interes pentru mine. Caut coordonatele vectorilor de direcție ai liniilor drepte:
Căutăm unghiul dintre acești vectori:
Răspuns:
Din nou, atunci când am rezolvat această problemă, nu am folosit niciun truc sofisticat, cu excepția formulei pentru suma unghiurilor unui n-gon regulat, precum și a definiției cosinusului și sinusului unui triunghi dreptunghic.
3. Deoarece din nou nu ni se dau lungimile marginilor din piramidă, le voi considera egale cu unu. Astfel, deoarece TOATE muchiile, și nu doar cele laterale, sunt egale între ele, atunci la baza piramidei și eu se află un pătrat, iar fețele laterale sunt triunghiuri regulate. Să descriem o astfel de piramidă, precum și baza ei pe un plan, marcând toate datele date în textul problemei:

Căutăm unghiul dintre și. Voi face calcule foarte scurte când voi căuta coordonatele punctelor. Va trebui să le „decriptați”:
b) - mijlocul segmentului. Coordonatele ei:
c) Voi găsi lungimea segmentului folosind teorema lui Pitagora într-un triunghi. Voi găsi prin teorema lui Pitagora într-un triunghi.
Coordonate:
d) - mijlocul segmentului. Coordonatele sale sunt
e) Coordonate vectoriale
f) Coordonate vectoriale
g) Căutarea unui unghi:
Cubul este cea mai simplă figură. Sunt sigur că poți să-ți dai seama singur. Răspunsurile la problemele 4 și 5 sunt următoarele:
Găsirea unghiului dintre o dreaptă și un plan
Ei bine, timpul pentru puzzle-uri simple s-a terminat! Acum exemplele vor fi și mai dificile. Pentru a găsi unghiul dintre o dreaptă și un plan, vom proceda după cum urmează:
- Folosind trei puncte, construim ecuația planului
,
folosind un determinant de ordinul trei. - Prin două puncte căutăm coordonatele vectorului de direcție al dreptei:
- Aplicam formula pentru a calcula unghiul dintre o dreapta si un plan:
După cum puteți vedea, această formulă este foarte asemănătoare cu cea pe care am folosit-o pentru a găsi unghiurile dintre două linii. Structura părții drepte este aceeași, iar în stânga căutăm acum un sinus, și nu un cosinus, ca înainte. Ei bine, a fost adăugată o acțiune urâtă - căutarea ecuației avionului.
Să nu lăsăm la raft exemple de rezolvare:
1. Os-no-va-ni-em straight-my prize-we are-la-et-xia egal-dar-poor-ren-ny triangle-nick you-with-th that prize-we are egal. Aflați unghiul dintre linie dreaptă și plan
2. Intr-un pa-ral-le-le-pi-pe-de dreptunghiular dinspre Vest Nai-di-te unghiul dintre dreapta si plan
3. În prisma cu șase cărbuni din dreapta, toate marginile sunt egale. Aflați unghiul dintre linie dreaptă și plan.
4. În pi-ra-mi-de triunghiular drept cu os-but-va-ni-em din vestul coastei unghiul Nai-di-te, planul ob-ra-zo-van -ny al osului. -no-va-niya și straight-my, trecând prin se-re-di-na coastelor și
5. Lungimile tuturor marginilor pi-ra-mi-dy dreptunghiulare cu vârf sunt egale între ele. Aflați unghiul dintre linie dreaptă și plan, dacă punctul este se-re-di-pe muchia bo-ko-in-a a pi-ra-mi-dy.
Din nou, voi rezolva primele două probleme în detaliu, pe a treia - pe scurt, iar ultimele două vă las pe voi să le rezolvați singur. În plus, ai avut deja de-a face cu piramide triunghiulare și patrulatere, dar nu încă cu prisme.
Solutii:
1. Desenați o prismă, precum și baza acesteia. Să-l combinăm cu sistemul de coordonate și să marchem toate datele care sunt date în enunțul problemei:

Îmi cer scuze pentru nerespectarea unor proporții, dar pentru rezolvarea problemei acest lucru, de fapt, nu este atât de important. Avionul este doar „peretele din spate” al prismei mele. Este suficient să ghicim că ecuația unui astfel de plan are forma:
Cu toate acestea, acest lucru poate fi afișat și direct:
Alegem trei puncte arbitrare pe acest plan: de exemplu, .
Să facem ecuația planului:
Exercițiu pentru tine: calculează singur acest determinant. ai reusit? Atunci ecuația planului are forma:
Sau pur și simplu
Prin urmare,
Pentru a rezolva exemplul, trebuie să găsesc coordonatele vectorului de direcție al dreptei. Deoarece punctul a coincis cu originea, coordonatele vectorului vor coincide pur și simplu cu coordonatele punctului.Pentru a face acest lucru, găsim mai întâi coordonatele punctului.
Pentru a face acest lucru, luați în considerare un triunghi. Să desenăm o înălțime (este și o mediană și o bisectoare) de sus. Deoarece, atunci ordonata punctului este egală. Pentru a găsi abscisa acestui punct, trebuie să calculăm lungimea segmentului. După teorema lui Pitagora avem:
Atunci punctul are coordonatele:
Un punct este un „ridicat” pe un punct:
Atunci coordonatele vectorului:
Răspuns:
După cum puteți vedea, nu este nimic fundamental dificil în rezolvarea unor astfel de probleme. De fapt, „dreapta” unei figuri, cum ar fi o prismă, simplifică puțin mai mult procesul. Acum să trecem la următorul exemplu:
2. Desenăm un paralelipiped, desenăm un plan și o linie dreaptă în el și, de asemenea, desenăm separat baza sa inferioară:

În primul rând, găsim ecuația planului: coordonatele celor trei puncte aflate în el:
(primele două coordonate sunt obținute într-un mod evident și puteți găsi cu ușurință ultima coordonată din imaginea punctului). Apoi compunem ecuația planului:
Noi calculăm:
Căutăm coordonatele vectorului de direcție: este clar că coordonatele acestuia coincid cu coordonatele punctului, nu-i așa? Cum să găsesc coordonatele? Acestea sunt coordonatele punctului, ridicate de-a lungul axei aplicate cu una! . Atunci căutăm unghiul dorit:
Răspuns:
3. Desenați o piramidă hexagonală obișnuită, apoi desenați în ea un plan și o linie dreaptă.

Aici este chiar problematic să desenezi un avion, ca să nu mai vorbim de soluția acestei probleme, dar metoda coordonatelor nu-i pasă! Principalul său avantaj constă în versatilitatea sa!
Avionul trece prin trei puncte: . Căutăm coordonatele lor:
1) . Afișați singur coordonatele ultimelor două puncte. Pentru aceasta, va trebui să rezolvați problema cu o piramidă hexagonală!
2) Construim ecuația planului:
Căutăm coordonatele vectorului: . (Vezi din nou problema piramidei triunghiulare!)
3) Căutăm un unghi:
Răspuns:
După cum puteți vedea, nu există nimic supranatural de dificil în aceste sarcini. Trebuie doar să fii foarte atent cu rădăcinile. La ultimele două probleme, voi da doar răspunsuri:
După cum puteți vedea, tehnica de rezolvare a problemelor este aceeași peste tot: sarcina principală este să găsiți coordonatele vârfurilor și să le înlocuiți în niște formule. Rămâne să luăm în considerare încă o clasă de probleme pentru calcularea unghiurilor, și anume:
Calcularea unghiurilor dintre două plane
Algoritmul de soluție va fi următorul:
- Pentru trei puncte căutăm ecuația primului plan:
- Pentru celelalte trei puncte, căutăm ecuația celui de-al doilea plan:
- Aplicam formula:
După cum puteți vedea, formula este foarte asemănătoare cu cele două anterioare, cu ajutorul cărora am căutat unghiuri între drepte și între o dreaptă și un plan. Așa că să-ți amintești de acesta nu va fi dificil pentru tine. Să trecem direct la problemă:
1. O sută de ro-pe baza prismei triunghiulare drepte este egală, iar dia-go-nalul feței laterale este egală. Găsiți unghiul dintre plan și planul bazei premiului.
2. În dreapta înainte four-you-re-coal-noy pi-ra-mi-de, toate muchiile cuiva sunt egale, găsiți sinusul unghiului dintre plan și planul Ko-Stu, trecând prin punctul de per-pen-di-ku-lyar-dar drept-meu.
3. Într-o prismă obișnuită cu patru cărbuni, laturile os-no-va-nia sunt egale, iar marginile laterale sunt egale. Pe marginea de la-me-che-până la punct astfel încât. Aflați unghiul dintre plane și
4. În prisma dreptunghiulară, laturile bazelor sunt egale, iar marginile laterale sunt egale. Pe marginea de la-me-che-la un punct astfel încât Găsiți unghiul dintre avioane și.
5. În cub, găsiți co-sinusul unghiului dintre plane și
Rezolvarea problemelor:
1. Desenez o prismă triunghiulară regulată (la bază - un triunghi echilateral) și marchez pe ea planurile care apar în starea problemei:

Trebuie să găsim ecuațiile a două plane: Ecuația de bază se obține trivial: puteți face determinantul corespunzător pentru trei puncte, dar voi face ecuația imediat:
Acum să găsim ecuația Punctul are coordonatele Punctul - Deoarece - mediana și înălțimea triunghiului, este ușor de găsit prin teorema lui Pitagora într-un triunghi. Atunci punctul are coordonate: Găsiți aplicația punctului Pentru a face acest lucru, luați în considerare un triunghi dreptunghic
Apoi obținem următoarele coordonate: Compunem ecuația planului.
Calculăm unghiul dintre plane:
Răspuns:
2. Realizarea unui desen:
Cel mai dificil este să înțelegeți ce fel de plan misterios este, care trece printr-un punct perpendicular. Ei bine, principalul lucru este ce este? Principalul lucru este atenția! Într-adevăr, linia este perpendiculară. Linia este de asemenea perpendiculară. Apoi, planul care trece prin aceste două drepte va fi perpendicular pe linie și, apropo, va trece prin punct. Acest plan trece și prin vârful piramidei. Apoi avionul dorit - Și avionul ne este deja dat. Căutăm coordonatele punctelor.
Găsim coordonatele punctului prin punct. Este ușor de dedus dintr-un mic desen că coordonatele punctului vor fi următoarele: Ce mai rămâne acum de găsit pentru a găsi coordonatele vârfului piramidei? Mai trebuie să-i calculăm înălțimea. Acest lucru se face folosind aceeași teoremă a lui Pitagora: mai întâi, demonstrați că (trivial din triunghiuri mici care formează un pătrat la bază). Deoarece prin condiție avem:
Acum totul este gata: coordonatele vârfurilor:
Compunem ecuația planului:
Ești deja un expert în calculul determinanților. Veți primi cu ușurință:
Sau altfel (dacă înmulțim ambele părți cu rădăcina a două)
Acum să găsim ecuația planului:
(Nu ați uitat cum obținem ecuația avionului, nu? Dacă nu înțelegeți de unde provine acest minus, atunci reveniți la definiția ecuației avionului! S-a dovedit întotdeauna că avionul a aparținut originii!)
Calculăm determinantul:
(Poți observa că ecuația planului a coincis cu ecuația dreptei care trece prin puncte și! Gândește-te de ce!)
Acum calculăm unghiul:
Trebuie să găsim sinusul:
Răspuns:
3. O întrebare dificilă: ce este o prismă dreptunghiulară, ce crezi? Este doar un paralelipiped binecunoscut pentru tine! Desen imediat! Nici măcar nu puteți înfățișa baza separat, nu este de folos aici:

Planul, așa cum am observat mai devreme, este scris ca o ecuație:
Acum facem un avion
Compunem imediat ecuația planului:
Caut un unghi
Acum răspunsurile la ultimele două probleme:
Ei bine, acum este momentul să luăm o pauză, pentru că tu și cu mine suntem grozavi și am făcut o treabă grozavă!
Coordonate și vectori. Nivel avansat
În acest articol, vom discuta cu tine o altă clasă de probleme care pot fi rezolvate folosind metoda coordonatelor: problemele de distanță. Și anume, vom lua în considerare următoarele cazuri:
- Calcularea distanței dintre liniile oblice.
Am ordonat sarcinile date pe măsură ce complexitatea lor crește. Cel mai ușor este de găsit distanta punct la plan iar cel mai greu este să găsești distanța dintre liniile care se intersectează. Deși, desigur, nimic nu este imposibil! Să nu amânăm și să trecem imediat la luarea în considerare a primei clase de probleme:
Calcularea distanței de la un punct la un plan
De ce avem nevoie pentru a rezolva această problemă?
1. Coordonatele punctului
Deci, de îndată ce obținem toate datele necesare, aplicăm formula:
Ar trebui să știți deja cum construim ecuația planului din problemele anterioare pe care le-am analizat în ultima parte. Să trecem imediat la treabă. Schema este următoarea: 1, 2 - te ajut să te decizi, iar în detaliu, 3, 4 - doar răspunsul, iei singur decizia și compari. A început!
Sarcini:
1. Dat un cub. Lungimea muchiei cubului este Find-di-te distanța de la se-re-di-ny de la tăiat la plat
2. Având în vedere dreapta-vil-naya patru-you-rekh-coal-naya pi-ra-mi-da Bo-ko-voe marginea sută-ro-pe os-no-va-nia este egală. Găsiți-di-acele distanțe de la un punct la un plan unde - se-re-di-pe margini.
3. În pi-ra-mi-de triunghiular drept cu os-but-va-ni-em, cealaltă margine este egală, iar o sută de ro-on os-no-vaniya este egală. Găsiți-di-acele distanțe de la vârf la avion.
4. În prisma cu șase cărbuni din dreapta, toate marginile sunt egale. Găsiți-di-acele distanțe de la un punct la un plan.
Solutii:
1. Desenați un cub cu margini simple, construiți un segment și un plan, notați mijlocul segmentului cu litera
 .
.
În primul rând, să începem cu unul ușor: găsiți coordonatele unui punct. De atunci (amintiți-vă de coordonatele mijlocului segmentului!)
Acum compunem ecuația planului pe trei puncte
\[\stanga| (\begin(array)(*(20)(c))x&0&1\\y&1&0\\z&1&1\end(array)) \right| = 0\]
Acum pot începe să găsesc distanța:
2. Reîncepem cu un desen, pe care notăm toate datele!
Pentru o piramidă, ar fi util să-i desenați baza separat.

Nici chiar faptul că desenez ca laba de pui nu ne va împiedica să rezolvăm cu ușurință această problemă!
Acum este ușor să găsiți coordonatele unui punct
Deoarece coordonatele punctului
2. Deoarece coordonatele punctului a sunt mijlocul segmentului, atunci
Putem găsi cu ușurință coordonatele a încă două puncte din plan.Compunem ecuația planului și o simplificăm:
\[\stanga| (\left| (\begin(array)(*(20)(c))x&1&(\frac(3)(2))\\y&0&(\frac(3)(2))\\z&0&(\frac( (\sqrt 3 ))(2))\end(array)) \right|) \right| = 0\]
Deoarece punctul are coordonatele: , atunci calculăm distanța:
Răspuns (foarte rar!):
Ei bine, ai inteles? Mi se pare că totul aici este la fel de tehnic ca în exemplele pe care le-am analizat împreună cu dumneavoastră în partea anterioară. Deci sunt sigur că, dacă ați stăpânit acel material, atunci nu vă va fi greu să rezolvați celelalte două probleme. Vă voi da doar răspunsurile:
Calcularea distanței de la o linie la un plan
De fapt, nu este nimic nou aici. Cum pot fi situate o linie și un plan unul față de celălalt? Au toate posibilitățile: să se intersecteze, sau o dreaptă este paralelă cu planul. Care crezi că este distanța de la linie la planul cu care se intersectează linia dată? Mi se pare că este clar că o astfel de distanță este egală cu zero. Caz neinteresant.

Al doilea caz este mai complicat: aici distanța este deja diferită de zero. Cu toate acestea, deoarece linia este paralelă cu planul, atunci fiecare punct al dreptei este echidistant de acest plan:

Prin urmare:
Și asta înseamnă că sarcina mea a fost redusă la cea anterioară: căutăm coordonatele oricărui punct de pe linie, căutăm ecuația planului, calculăm distanța de la punct la plan. De fapt, astfel de sarcini la examen sunt extrem de rare. Am reușit să găsesc o singură problemă, iar datele din ea erau de așa natură încât metoda coordonatelor nu i-a fost foarte aplicabilă!
Acum să trecem la o altă clasă de probleme, mult mai importantă:
Calcularea distanței dintre un punct și o linie
De ce vom avea nevoie?
1. Coordonatele punctului de la care căutăm distanța:
2. Coordonatele oricărui punct situat pe o linie dreaptă
3. Coordonatele vectorului de direcție ale dreptei
Ce formulă folosim?
Ce înseamnă pentru tine numitorul acestei fracții și, prin urmare, ar trebui să fie clar: aceasta este lungimea vectorului de direcție al dreptei. Iată un numărător foarte complicat! Expresia înseamnă modulul (lungimea) produsului vectorial al vectorilor și Cum se calculează produsul vectorial, am studiat în partea anterioară a lucrării. Reîmprospătează-ți cunoștințele, ne va fi foarte util acum!
Astfel, algoritmul de rezolvare a problemelor va fi următorul:
1. Căutăm coordonatele punctului de la care căutăm distanța:
2. Căutăm coordonatele oricărui punct de pe dreapta până la care căutăm distanța:
3. Construirea unui vector
4. Construim vectorul direcție al dreptei
5. Calculați produsul încrucișat
6. Căutăm lungimea vectorului rezultat:
7. Calculați distanța:
Avem mult de lucru, iar exemplele vor fi destul de complexe! Așa că acum concentrează-ți toată atenția!
1. Dana este un pi-ra-mi-da triunghiular dreptaci cu un vârf. O sută de ro-pe os-no-va-niya pi-ra-mi-dy este egal, you-so-ta este egal. Găsiți-di-acele distanțe de la se-re-di-ny a muchiei bo-ko-a-a până la linia dreaptă, unde punctele și sunt se-re-di-ny ale coastelor și co-from-vet -stven-dar.
2. Lungimile nervurilor și unghiul drept-no-para-ral-le-le-pi-pe-da sunt egale, respectiv, și Find-di-te distanța de la top-shi-ny la straight-my
3. În prisma dreaptă cu șase cărbuni, toate marginile unui roi sunt egale aflați-di-acea distanță de la un punct la o linie dreaptă
Solutii:
1. Facem un desen îngrijit, pe care notăm toate datele:

Avem mult de lucru pentru tine! Mai întâi aș dori să descriu în cuvinte ce vom căuta și în ce ordine:
1. Coordonatele punctelor și
2. Coordonatele punctului
3. Coordonatele punctelor și
4. Coordonatele vectorilor şi
5. Produsul lor încrucișat
6. Lungimea vectorului
7. Lungimea produsului vectorial
8. Distanța de la până la
Ei bine, avem mult de lucru! Să ne suflecăm mânecile!
1. Pentru a afla coordonatele înălțimii piramidei, trebuie să cunoaștem coordonatele punctului.Aplicata lui este zero, iar ordonata este egală cu abscisa lui. În cele din urmă, am obținut coordonatele:
Coordonatele punctului
2. - mijlocul segmentului
3. - mijlocul segmentului
punct de mijloc
4.Coordonate
Coordonatele vectoriale
5. Calculați produsul vectorial:

6. Lungimea vectorului: cel mai simplu mod este să înlocuiți că segmentul este linia de mijloc a triunghiului, ceea ce înseamnă că este egal cu jumătatea bazei. Asa de.
7. Considerăm lungimea produsului vectorial:
8. În cele din urmă, găsiți distanța:
Puff, asta-i tot! Sincer, vă spun: rezolvarea acestei probleme prin metode tradiționale (prin construcții) ar fi mult mai rapidă. Dar aici am redus totul la un algoritm gata făcut! Cred că algoritmul de soluție este clar pentru tine? Prin urmare, vă voi cere să rezolvați singur cele două probleme rămase. Comparați răspunsurile?
Din nou, repet: este mai ușor (mai rapid) să rezolvi aceste probleme prin construcții, decât să apelezi la metoda coordonatelor. Am demonstrat acest mod de a rezolva doar pentru a vă arăta o metodă universală care vă permite să „nu terminați nimic”.
În cele din urmă, luați în considerare ultima clasă de probleme:
Calcularea distanței dintre liniile oblice
Aici algoritmul de rezolvare a problemelor va fi similar cu cel anterior. Ce avem:
3. Orice vector care leagă punctele primei și celei de-a doua linii:
Cum găsim distanța dintre linii?
Formula este:
Numătorul este modulul produsului mixt (l-am introdus în partea anterioară), iar numitorul este același ca în formula anterioară (modulul produsului vectorial al vectorilor de direcție ai liniilor, distanța dintre care avem cauta).
Îți voi aminti că

Apoi formula distanței poate fi rescrisă ca:
Împărțiți acest determinant la determinant! Deși, sincer să fiu, nu am chef de glume aici! Această formulă, de fapt, este foarte greoaie și duce la calcule destul de complicate. Dacă aș fi în locul tău, l-aș folosi doar ca ultimă soluție!
Să încercăm să rezolvăm câteva probleme folosind metoda de mai sus:
1. În prisma triunghiulară dreaptă, toate muchiile sunt cumva egale, găsiți distanța dintre liniile drepte și.
2. Având în vedere o prismă triunghiulară în formă de dreapta înainte, toate marginile os-no-va-niya ale cuiva sunt egale cu Se-che-tion, trecând prin cealaltă nervură și nervurile se-re-di-nu sunt yav-la-et-sya square-ra-tom. Find-di-te dis-sto-I-nie între straight-we-mi și
Eu o decid pe prima, iar pe baza ei, tu decizi pe a doua!
1. Desenez o prismă și marchez liniile și

Coordonatele punctului C: atunci
Coordonatele punctului
Coordonatele vectoriale
Coordonatele punctului
Coordonatele vectoriale
Coordonatele vectoriale
\[\left((B,\overrightarrow (A(A_1)) \overrightarrow (B(C_1)) ) \right) = \left| (\begin(array)(*(20)(l))(\begin(array)(*(20)(c))0&1&0\end(array))\\(\begin(array)(*(20) (c))0&0&1\end(array))\\(\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \frac(1) (2))&1\end(matrice))\end(matrice)) \right| = \frac((\sqrt 3 ))(2)\]
Considerăm produsul încrucișat dintre vectorii și
\[\overrightarrow (A(A_1)) \cdot \overrightarrow (B(C_1)) = \left| \begin(array)(l)\begin(array)(*(20)(c))(\overrightarrow i )&(\overrightarrow j )&(\overrightarrow k )\end(array)\\\begin(array) )(*(20)(c))0&0&1\end(array)\\\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \ frac(1)(2))&1\end(matrice)\end(matrice) \right| - \frac((\sqrt 3 ))(2)\overrightarrow k + \frac(1)(2)\overrightarrow i \]
Acum luăm în considerare lungimea sa:
Răspuns:
Acum încercați să finalizați cu atenție a doua sarcină. Răspunsul la aceasta va fi:.
Coordonate și vectori. Scurtă descriere și formule de bază
Un vector este un segment direcționat. - începutul vectorului, - sfârşitul vectorului.
Vectorul este notat cu sau.
Valoare absolută vector - lungimea segmentului care reprezintă vectorul. Desemnat ca.
Coordonatele vectoriale:
,
unde sunt capetele vectorului \displaystyle a .
Suma vectorilor: .
Produsul vectorilor:
Produsul punctual al vectorilor:
Ecuația plană. Cum se scrie o ecuație pentru un avion?
Aranjamentul reciproc al avioanelor. Sarcini
Geometria spațială nu este cu mult mai complicată decât geometria „plată”, iar zborurile noastre în spațiu încep cu acest articol. Pentru a înțelege subiectul, trebuie să înțelegeți bine vectori, în plus, este de dorit să fiți familiarizați cu geometria planului - vor exista multe asemănări, multe analogii, astfel încât informațiile vor fi digerate mult mai bine. Într-o serie de lecții mele, lumea 2D se deschide cu un articol Ecuația unei drepte pe un plan. Dar acum Batman a părăsit televizorul cu ecran plat și se lansează din Cosmodromul Baikonur.
Să începem cu desene și simboluri. Schematic, planul poate fi desenat ca un paralelogram, ceea ce dă impresia de spațiu: 
Avionul este infinit, dar avem ocazia să înfățișăm doar o bucată din el. În practică, pe lângă paralelogram, se desenează și un oval sau chiar un nor. Din motive tehnice, îmi este mai convenabil să înfățișez avionul în acest fel și în această poziție. Planurile reale, pe care le vom lua în considerare în exemple practice, pot fi aranjate după bunul plac - luați mental desenul în mâini și răsuciți-l în spațiu, dând planului orice pantă, orice unghi.
Notaţie: se obișnuiește să se desemneze avioanele cu litere mici grecești, aparent pentru a nu le confunda cu direct în avion sau cu drept în spațiu. Sunt obișnuit să folosesc litera . În desen, este litera „sigma” și deloc o gaură. Deși, un avion gol, este cu siguranță foarte amuzant.
În unele cazuri, este convenabil să folosiți aceleași litere grecești cu indice pentru a desemna avioane, de exemplu, .
Este evident că planul este determinat în mod unic de trei puncte diferite care nu se află pe aceeași linie dreaptă. Prin urmare, denumirile de trei litere ale avioanelor sunt destul de populare - în funcție de punctele care le aparțin, de exemplu, etc. Adesea literele sunt cuprinse între paranteze: ![]() , pentru a nu confunda planul cu o altă figură geometrică.
, pentru a nu confunda planul cu o altă figură geometrică.
Pentru cititorii experimentați, voi oferi meniu de comenzi rapide:
- Cum se scrie o ecuație pentru un plan folosind un punct și doi vectori?
- Cum se scrie o ecuație pentru un plan folosind un punct și un vector normal?
și nu vom lâncevi în așteptări lungi:
Ecuația generală a planului
Ecuația generală a planului are forma , unde coeficienții sunt simultan nenuli.
O serie de calcule teoretice și probleme practice sunt valabile atât pentru baza ortonormală obișnuită, cât și pentru baza afină a spațiului (dacă uleiul este ulei, reveniți la lecție Dependența liniară (non) a vectorilor. Baza vectorială). Pentru simplitate, vom presupune că toate evenimentele au loc pe o bază ortonormală și un sistem de coordonate dreptunghiular cartezian.
Și acum să antrenăm puțină imaginație spațială. E în regulă dacă o ai rău, acum o vom dezvolta puțin. Chiar și jocul pe nervi necesită practică.
În cel mai general caz, când numerele nu sunt egale cu zero, planul intersectează toate cele trei axe de coordonate. De exemplu, așa:

Repet încă o dată că avionul continuă la nesfârșit în toate direcțiile și avem ocazia să ne înfățișăm doar o parte din el.
Luați în considerare cele mai simple ecuații ale planelor:
Cum să înțelegem această ecuație? Gândiți-vă la asta: „Z” ÎNTOTDEAUNA, pentru orice valoare a lui „X” și „Y” este egal cu zero. Aceasta este ecuația planului de coordonate „nativ”. Într-adevăr, formal ecuația poate fi rescrisă după cum urmează: ![]() , de unde este clar că nu ne pasă, ce valori iau „x” și „y”, este important ca „z” să fie egal cu zero.
, de unde este clar că nu ne pasă, ce valori iau „x” și „y”, este important ca „z” să fie egal cu zero.
În mod similar:
este ecuația planului de coordonate ;
este ecuația planului de coordonate.
Să complicăm puțin problema, să considerăm un plan (aici și mai departe în paragraf presupunem că coeficienții numerici nu sunt egali cu zero). Să rescriem ecuația sub forma: . Cum să-l înțelegi? „X” este ÎNTOTDEAUNA, pentru orice valoare a lui „y” și „z” este egală cu un anumit număr. Acest plan este paralel cu planul de coordonate. De exemplu, un plan este paralel cu un plan și trece printr-un punct.
În mod similar:
- ecuaţia planului, care este paralelă cu planul de coordonate;
- ecuația unui plan care este paralel cu planul de coordonate.
Adăugați membri: . Ecuația poate fi rescrisă astfel: , adică „Z” poate fi orice. Ce înseamnă? „X” și „Y” sunt conectate printr-un raport care trasează o anumită linie dreaptă în plan (veți recunoaște ecuația unei drepte într-un plan?). Deoarece Z poate fi orice, această linie este „replicată” la orice înălțime. Astfel, ecuația definește un plan paralel cu axa de coordonate
În mod similar:
- ecuația planului, care este paralelă cu axa de coordonate;
- ecuația planului, care este paralelă cu axa de coordonate.
Dacă termenii liberi sunt zero, atunci planurile vor trece direct prin axele corespunzătoare. De exemplu, clasicul „proporționalitate directă”:. Desenați o linie dreaptă în plan și înmulțiți-o mental în sus și în jos (deoarece „z” este oricare). Concluzie: planul dat de ecuație trece prin axa de coordonate.
Încheiem trecerea în revistă: ecuația planului ![]() trece prin origine. Ei bine, aici este destul de evident că punctul satisface ecuația dată.
trece prin origine. Ei bine, aici este destul de evident că punctul satisface ecuația dată.
Și, în sfârșit, cazul care este prezentat în desen: - planul este prieten cu toate axele de coordonate, în timp ce întotdeauna „taie” un triunghi care poate fi situat în oricare dintre cei opt octanți.
Inegalități liniare în spațiu
Pentru a înțelege informațiile, este necesar să studiezi bine inegalități liniare în plan pentru că multe lucruri vor fi asemănătoare. Paragraful va fi o scurtă prezentare generală cu câteva exemple, deoarece materialul este destul de rar în practică.
Dacă ecuația definește un plan, atunci inegalitățile
cere semi-spații. Dacă inegalitatea nu este strictă (ultimele două din listă), atunci soluția inegalității, în plus față de semi-spațiu, include planul însuși.
Exemplul 5
Găsiți vectorul normal unitar al planului ![]() .
.
Soluţie: Un vector unitar este un vector a cărui lungime este unu. Să notăm acest vector cu . Este destul de clar că vectorii sunt coliniari: 
În primul rând, eliminăm vectorul normal din ecuația planului: .
Cum să găsiți vectorul unitar? Pentru a găsi vectorul unitar, aveți nevoie fiecare coordonata vectorială împărțită la lungimea vectorului.
Să rescriem vectorul normal în forma și să îi găsim lungimea:
Conform celor de mai sus:
Răspuns: ![]()
Verificare: , care a fost necesar să se verifice.
Cititorii care au studiat cu atenție ultimul paragraf al lecției, probabil au observat asta coordonatele vectorului unitar sunt exact cosinusurile de direcție ale vectorului:
Să ne abatem de la problema dezasamblată: când vi se oferă un vector arbitrar diferit de zero, iar prin condiție se cere să-i găsească cosinusurile direcției (vezi ultimele sarcini ale lecției Produsul punctual al vectorilor), atunci, de fapt, găsiți și un vector unitar coliniar cu cel dat. De fapt, două sarcini într-o sticlă.
Necesitatea de a găsi un vector normal unitar apare în unele probleme de analiză matematică.
Ne-am dat seama de pescuitul vectorului normal, acum vom răspunde la întrebarea opusă:
Cum se scrie o ecuație pentru un plan folosind un punct și un vector normal?
Această construcție rigidă a unui vector normal și a unui punct este bine cunoscută de o țintă de săgeți. Vă rugăm să întindeți mâna înainte și să selectați mental un punct arbitrar din spațiu, de exemplu, o pisică mică într-un bufet. Evident, prin acest punct, poți desena un singur plan perpendicular pe mâna ta.
Ecuația unui plan care trece printr-un punct perpendicular pe vector este exprimată prin formula: