Tangenta la graficul unei functii liniare. Ecuația tangentei la graficul funcției

22.09.2019

Citeste si

Ce face Comitetul de Investigații al Federației Ruse: principalele sarcini și competențe

Ceea ce a făcut ca sistemul energetic al Uralilor să se cutremure astfel încât Belarusul a simțit-o

Candidatul republican Donald Trump a câștigat alegerile prezidențiale din SUA

Ce alarmă de pornire automată este mai bună - comparație între modele și producători

Articolul oferă o explicație detaliată a definițiilor, semnificația geometrică a derivatului cu denumiri grafice. Ecuația dreptei tangente va fi luată în considerare cu exemple, se vor găsi ecuațiile tangentei la curbe de ordinul 2.

Yandex.RTB R-A-339285-1 Definiție 1

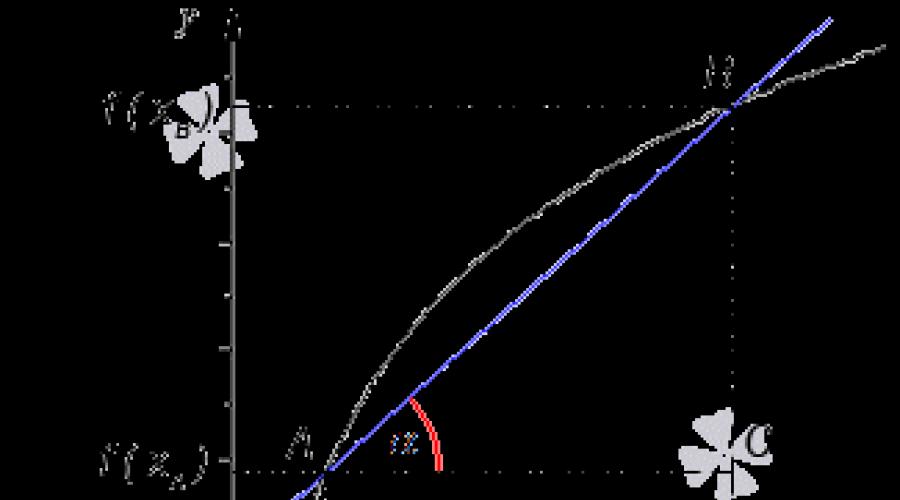
Unghiul de înclinare al dreptei y \u003d k x + b se numește unghiul α, care este măsurat de la direcția pozitivă a axei x la linia dreaptă y \u003d k x + b în direcția pozitivă.

În figură, direcția bou este indicată printr-o săgeată verde și un arc verde, iar unghiul de înclinare printr-un arc roșu. Linia albastră se referă la o linie dreaptă.

Definiția 2

Pantă dreapta y = k x + b se numeşte coeficient numeric k .

Panta este egală cu panta dreptei, cu alte cuvinte k = t g α .

Panta dreptei este 0 numai atunci când o x este paralelă și panta este egală cu zero, deoarece tangenta lui zero este 0. Deci, forma ecuației va fi y = b.
Dacă unghiul de înclinare al dreptei y = k x + b este ascuțit, atunci condițiile sunt 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 și există o creștere a graficului.
Dacă α \u003d π 2, atunci locația dreptei este perpendiculară pe x. Egalitatea este specificată de egalitatea x = c, valoarea c fiind un număr real.
Dacă unghiul de înclinare al dreptei y = k x + b este obtuz, atunci corespunde condițiilor π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает sens negativ, iar graficul este în scădere.

Definiția 3

O secantă este o dreaptă care trece prin 2 puncte ale funcției f (x). Cu alte cuvinte, o secanta este o linie dreaptă care trece prin oricare două puncte din graficul unei anumite funcții.

Figura arată că A B este o secante, iar f (x) este o curbă neagră, α este un arc roșu, indicând unghiul de înclinare al secantei.

Când panta unei drepte este egală cu tangentei unghiului de înclinare, este clar că tangenta dintr-un triunghi dreptunghic A B C poate fi găsită în raport cu catetul opus celui alăturat.

Definiția 4

Obținem formula pentru găsirea secantei formei:

k = t g α = B C A C = f (x B) - f x A x B - x A , unde abscisele punctelor A și B sunt valorile x A , x B și f (x A) , f (x B) sunt funcțiile de valori în aceste puncte.

În mod evident, panta secantei este definită folosind egalitatea k \u003d f (x B) - f (x A) x B - x A sau k \u003d f (x A) - f (x B) x A - x B, iar ecuația trebuie scrisă ca y = f (x B) - f (x A) x B - x A x - x A + f (x A) sau
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Secanta împarte vizual graficul în 3 părți: la stânga punctului A, de la A la B, la dreapta lui B. Figura de mai jos arată că există trei secante care sunt considerate a fi aceleași, adică sunt setați folosind o ecuație similară.

Prin definiție, este clar că linia și secanta ei coincid în acest caz.

O secanta poate intersecta graficul unei funcții date de mai multe ori. Dacă există o ecuație de forma y \u003d 0 pentru secante, atunci numărul de puncte de intersecție cu sinusoida este infinit.

Definiția 5

Tangenta la graficul functiei f (x) in punctul x 0 ; f (x 0) se numește dreptă care trece printr-un punct dat x 0; f (x 0) , cu prezența unui segment care are multe x valori apropiate de x 0 .

Exemplul 1

Să aruncăm o privire mai atentă la exemplul de mai jos. Atunci se poate observa că linia dată de funcția y = x + 1 este considerată a fi tangentă la y = 2 x în punctul cu coordonatele (1 ; 2) . Pentru claritate, este necesar să luați în considerare graficele cu valori apropiate de (1; 2). Funcția y = 2 x este marcată cu negru, linia albastră este tangenta, punctul roșu este punctul de intersecție.

Evident, y \u003d 2 x se îmbină cu linia y \u003d x + 1.

Pentru a determina tangentei, ar trebui să luăm în considerare comportamentul tangentei A B pe măsură ce punctul B se apropie la infinit de punctul A. Pentru claritate, prezentăm o figură.

Secanta A B, indicată de linia albastră, tinde spre poziția tangentei însăși, iar unghiul de înclinare al secantei α va începe să se apropie de unghiul de înclinare al tangentei însăși α x.

Definiția 6

Tangenta la graficul funcției y \u003d f (x) în punctul A este poziția limită a secantei A B la B care tinde spre A, adică B → A.

Acum ne întoarcem la considerarea semnificației geometrice a derivatei unei funcții într-un punct.

Să trecem la considerarea secantei A B pentru funcția f (x), unde A și B cu coordonatele x 0, f (x 0) și x 0 + ∆ x, f (x 0 + ∆ x) și ∆ x este notat ca un increment al argumentului . Acum funcția va lua forma ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Pentru claritate, să facem o poză ca exemplu.

Luați în considerare rezultatul triunghi dreptunghic A B C. Folosim definiția tangentei pentru soluție, adică obținem raportul ∆ y ∆ x = t g α . Din definiţia unei tangente rezultă că lim ∆ x → 0 ∆ y ∆ x = t g α x . Conform regulii derivatei într-un punct, avem că derivata f (x) în punctul x 0 se numește limita raportului dintre incrementul funcției și incrementul argumentului, unde ∆ x → 0, atunci notată f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Rezultă că f „(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, unde k x este notat ca panta tangentei.

Adică, obținem că f ' (x) poate exista în punctul x 0 și, precum și tangenta la graficul dat a funcției în punctul de contact egal cu x 0 , f 0 (x 0) , unde valoarea pantei tangentei în punctul este egală cu derivata în punctul x 0 . Atunci obținem că k x = f "(x 0) .

Sensul geometric al derivatei unei funcții într-un punct este că este dat conceptul existenței unei tangente la graficul în același punct.

Pentru a scrie ecuația oricărei drepte în plan, este necesar să existe o pantă cu punctul prin care trece. Desemnarea sa este luată ca x 0 la intersecție.

Ecuația tangentei la graficul funcției y \u003d f (x) în punctul x 0, f 0 (x 0) ia forma y \u003d f "(x 0) x - x 0 + f (x 0) .

Înseamnă că valoarea finală a derivatei f „(x 0) poate determina poziția tangentei, adică vertical în condiția lim x → x 0 + 0 f” (x) = ∞ și lim x → x 0 - 0 f „(x ) = ∞ sau absență deloc în condiția lim x → x 0 + 0 f „(x) ≠ lim x → x 0 - 0 f „(x) .

Locația tangentei depinde de valoarea pantei sale k x \u003d f "(x 0). Când este paralel cu axa x, obținem că k k \u003d 0, atunci când este paralel cu aproximativ y - k x \u003d ∞ și forma ecuației tangente x \u003d x 0 crește cu k x > 0, scade pe măsură ce k x< 0 .

Exemplul 2

Compilați ecuația tangentei la graficul funcției y \u003d e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 într-un punct cu coordonatele (1; 3) cu definiția unghiului de înclinare.

Soluţie

Prin presupunere, avem că funcția este definită pentru toate numerele reale. Obținem că punctul cu coordonatele specificate de condiția (1 ; 3) este punctul de contact, atunci x 0 = - 1 , f (x 0) = - 3 .

Este necesar să găsim derivata în punctul cu valoarea - 1 . Înțelegem asta

y "= e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" = = e x + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = e x + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Valoarea lui f ’ (x) în punctul de contact este panta tangentei, care este egală cu tangentei pantei.

Atunci k x = t g α x = y „(x 0) = 3 3

Rezultă că α x = a r c t g 3 3 = π 6

Răspuns: ecuația tangentei ia forma

y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3

Pentru claritate, dăm un exemplu într-o ilustrație grafică.

Culoarea neagră este utilizată pentru graficul funcției originale, Culoarea albastră- imaginea tangentei, punctul roșu - punctul de contact. Figura din dreapta arată o vedere mărită.

Exemplul 3

Aflați existența unei tangente la graficul unei funcții date
y = 3 x - 1 5 + 1 în punctul cu coordonatele (1 ; 1) . Scrieți o ecuație și determinați unghiul de înclinare.

Soluţie

Prin presupunere, avem că domeniul funcției date este mulțimea tuturor numerelor reale.

Să trecem la găsirea derivatei

y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Dacă x 0 = 1 , atunci f ' (x) nu este definit, dar limitele sunt scrise ca lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + ∞ și lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , ceea ce înseamnă existență tangentă verticală la punctul (1; 1) .

Răspuns: ecuația va lua forma x \u003d 1, unde unghiul de înclinare va fi egal cu π 2.

Să-l graficăm pentru claritate.

Exemplul 4

Aflați punctele graficului funcției y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , unde

Tangenta nu există;
Tangenta este paralelă cu x;
Tangenta este paralelă cu dreapta y = 8 5 x + 4 .

Soluţie

Este necesar să se acorde atenție domeniului definiției. Prin presupunere, avem că funcția este definită pe mulțimea tuturor numerelor reale. Extindeți modulul și rezolvați sistemul cu intervale x ∈ - ∞ ; 2 şi [-2; +∞). Înțelegem asta

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)

Funcția trebuie diferențiată. Avem asta

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)

Când x = - 2, atunci derivata nu există deoarece limitele unilaterale nu sunt egale în acel punct:

lim x → - 2 - 0 y "(x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Calculăm valoarea funcției în punctul x \u003d - 2, de unde obținem asta

y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, adică tangenta la punctul (- 2; - 2) nu va exista.
Tangenta este paralelă cu x când panta este zero. Apoi k x \u003d t g α x \u003d f "(x 0). Adică, este necesar să se găsească valorile unui astfel de x atunci când derivata funcției o transformă la zero. Adică, valorile \u200b\u200de f '(x) și vor fi puncte de atingere, unde tangenta este paralelă cu x .

Când x ∈ - ∞ ; - 2 , atunci - 1 5 (x 2 + 12 x + 35) = 0 , iar pentru x ∈ (- 2 ; + ∞) obținem 1 5 (x 2 - 4 x + 3) = 0 .

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Calculăm valorile corespunzătoare ale funcției

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Prin urmare - 5; 8 5 , - 4 ; 4 3 , 1 ; 85, 3; 4 3 sunt considerate a fi punctele dorite ale graficului funcției.

Luați în considerare o reprezentare grafică a soluției.

Linia neagră este graficul funcției, punctele roșii sunt punctele de atingere.

Când liniile sunt paralele, pantele sunt egale. Apoi este necesar să căutați punctele graficului funcției, unde panta va fi egală cu valoarea 8 5 . Pentru a face acest lucru, trebuie să rezolvați o ecuație de forma y "(x) = 8 5. Atunci, dacă x ∈ - ∞; - 2, obținem că - 1 5 (x 2 + 12 x + 35) = 8 5, iar dacă x ∈ ( - 2 ; + ∞) , atunci 1 5 (x 2 - 4 x + 3) = 8 5 .

Prima ecuație nu are rădăcini deoarece discriminantul este mai mic decât zero. Să scriem asta

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

O altă ecuație are două rădăcini reale, deci

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Să trecem la găsirea valorilor funcției. Înțelegem asta

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Puncte cu valori - 1; 4 15, 5; 8 3 sunt punctele în care tangentele sunt paralele cu dreapta y = 8 5 x + 4 .

Răspuns: linie neagră - graficul funcției, linie roșie - graficul y \u003d 8 5 x + 4, linie albastră - tangente în puncte - 1; 4 15, 5; 8 3 .

Existența unui număr infinit de tangente pentru funcții date este posibilă.

Exemplul 5

Scrieți ecuațiile tuturor tangentelor disponibile ale funcției y = 3 cos 3 2 x - π 4 - 1 3 , care sunt perpendiculare pe dreapta y = - 2 x + 1 2 .

Soluţie

Pentru a întocmi ecuația tangentei, este necesar să se găsească coeficientul și coordonatele punctului de contact, pe baza condiției de perpendicularitate a dreptelor. Definiția sună așa: produsul pantelor care sunt perpendiculare pe drepte este egal cu - 1, adică se scrie ca k x · k ⊥ = - 1. Din condiția avem că panta este perpendiculară pe dreapta și este egală cu k ⊥ = - 2, atunci k x = - 1 k ⊥ = - 1 - 2 = 1 2 .

Acum trebuie să găsim coordonatele punctelor de atingere. Trebuie să găsiți x, după care valoarea sa pentru o funcție dată. Rețineți că din sensul geometric al derivatei la punct
x 0 obținem acel k x \u003d y "(x 0) . Din această egalitate, găsim valorile x \u200b\u200bpentru punctele de atingere.

Înțelegem asta

y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 \u003d - 9 2 sin 3 2 x 0 - π 4 ⇒ k x \u003d y "(x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9

Acest ecuație trigonometrică va fi folosit pentru a calcula ordonatele punctelor de atingere.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk sau 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk sau 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk sau x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z este mulțimea numerelor întregi.

S-au găsit x puncte de contact. Acum trebuie să mergeți la căutarea valorilor y:

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 sau y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 sau y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 sau y 0 = - 4 5 + 1 3

De aici obținem că 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 sunt puncte de atingere.

Răspuns: ecuaţiile necesare se vor scrie ca

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Pentru o reprezentare vizuală, luați în considerare funcția și tangenta pe linia de coordonate.

Figura arată că locația funcției este pe intervalul [-10; 10 ] , unde linia neagră este graficul funcției, liniile albastre sunt tangente care sunt perpendiculare pe dreapta dată de forma y = - 2 x + 1 2 . Punctele roșii sunt puncte de atingere.

Ecuațiile canonice ale curbelor de ordinul 2 nu sunt funcții cu o singură valoare. Ecuațiile tangente ale acestora sunt compilate după scheme binecunoscute.

Tangenta la cerc

Pentru a stabili un cerc centrat într-un punct x c e n t e r ; y c e n t e r și raza R, se utilizează formula x - x c e n t e r 2 + y - y c e n t e r 2 = R 2.

Această egalitate poate fi scrisă ca unirea a două funcții:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

Prima funcție este în partea de sus și a doua în partea de jos, așa cum se arată în figură.

Să se întocmească o ecuaţie a unui cerc într-un punct x 0 ; y 0 , care este situat în semicercul superior sau inferior, ar trebui să găsiți ecuația graficului funcției de forma y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r sau y \u003d - R 2 - x - x c e n t e r 2 + y c e n t e r la punctul specificat.

Când în punctele x c e n t e r ; y c e n t e r + R și x ce n t e r ; y c e n t e r - R tangente pot fi date de ecuațiile y = y c e n t e r + R și y = y c e n t e r - R , iar în punctele x c e n t e r + R ; y c e n t e r şi
x c e n t e r - R ; y c e n t e r va fi paralel cu y, atunci vom obține ecuații de forma x = x c e n t e r + R și x = x c e n t e r - R .

Tangenta la elipsa

Când elipsa este centrată pe x ce n t e r ; y c e n t e r cu semiaxele a și b , atunci poate fi dat folosind ecuația x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .

O elipsă și un cerc pot fi notate prin combinarea a două funcții, și anume, semielipsa superioară și inferioară. Atunci obținem asta

y = b a a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a a 2 - (x - x c e n t e r) 2 + y c e n t e r

Dacă tangentele sunt situate la vârfurile elipsei, atunci ele sunt paralele cu x sau despre y. Pentru claritate, luați în considerare figura de mai jos.

Exemplul 6

Scrieți ecuația tangentei la elipsa x - 3 2 4 + y - 5 2 25 = 1 în punctele cu valorile x egale cu x = 2 .

Soluţie

Este necesar să găsiți puncte de atingere care să corespundă valorii x = 2. Facem o substituție în ecuația existentă a elipsei și obținem asta

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Apoi 2; 5 3 2 + 5 și 2 ; - 5 3 2 + 5 sunt punctele tangente care aparțin semielipsei superioare și inferioare.

Să trecem la găsirea și rezolvarea ecuației unei elipse în raport cu y. Înțelegem asta

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Este evident că semielipsa superioară este specificată folosind o funcție de forma y = 5 + 5 2 4 - x - 3 2 , iar cea inferioară y = 5 - 5 2 4 - x - 3 2 .

Aplicam algoritmul standard pentru a formula ecuatia tangentei la graficul unei functii intr-un punct. Scriem că ecuația pentru prima tangentă la punctul 2 ; 5 3 2 + 5 vor arăta ca

y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Obținem că ecuația celei de-a doua tangente cu valoarea din punct
2; - 5 3 2 + 5 devine

y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Grafic, tangentele sunt notate după cum urmează:

Tangenta la hiperbola

Când hiperbola are un centru în punctul x c e n t e r ; y c e n t e r şi vârfuri x c e n t e r + α ; y c e n t e r şi x c e n t e r - α ; y c e n t e r , inegalitatea x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 este dată dacă cu vârfuri x c e n t e r ; y c e n t e r + b și x c e n t e r ; y c e n t e r - b este dat atunci de inegalitatea x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

O hiperbolă poate fi reprezentată ca două funcții combinate ale formei

y = b a (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a (x - x c e n t e r) 2 - a 2 + y c e n t e r sau y = b a (x - x c e n t e r) 2 + a 2 + y c e n t e r e = - x c e n t e (x - x c e n t e r) ) 2 + a 2 + y c e n t e r

În primul caz, avem că tangentele sunt paralele cu y, iar în al doilea, sunt paralele cu x.

Rezultă că pentru a găsi ecuația unei tangente la o hiperbolă este necesar să aflăm cărei funcție îi aparține punctul tangentei. Pentru a determina acest lucru, este necesar să faceți o înlocuire în ecuații și să le verificați pentru identitate.

Exemplul 7

Scrieți ecuația tangentei la hiperbola x - 3 2 4 - y + 3 2 9 = 1 la punctul 7; - 3 3 - 3 .

Soluţie

Este necesar să se transforme înregistrarea soluției de găsire a hiperbolei folosind 2 funcții. Înțelegem asta

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 sau y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Este necesar să aflăm cărei funcție îi aparține punctul dat cu coordonatele 7; - 3 3 - 3 .

Evident, pentru a verifica prima funcție, aveți nevoie de y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 , atunci punctul nu aparține graficului, deoarece egalitatea nu este satisfăcută.

Pentru a doua funcție, avem că y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , ceea ce înseamnă că punctul aparține graficului dat. De aici ar trebui să găsiți coeficientul de pantă.

Înțelegem asta

y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Răspuns: ecuaţia tangentei poate fi reprezentată ca

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Este vizualizat astfel:

Tangenta la parabolă

Pentru a compune ecuația tangentei la parabola y \u003d a x 2 + b x + c în punctul x 0, y (x 0) , trebuie să utilizați algoritmul standard, apoi ecuația va lua forma y \u003d y " (x 0) x - x 0 + y ( x 0) O astfel de tangentă la vârf este paralelă cu x.

Parabola x = a y 2 + b y + c ar trebui definită ca unirea a două funcții. Prin urmare, trebuie să rezolvăm ecuația pentru y. Înțelegem asta

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Să o reprezentam grafic ca:

Pentru a afla dacă un punct x 0 , y (x 0) aparține unei funcții, urmați ușor algoritmul standard. O astfel de tangentă va fi paralelă cu y față de parabolă.

Exemplul 8

Scrieți ecuația tangentei la graficul x - 2 y 2 - 5 y + 3 când avem o pantă tangentei de 150 °.

Soluţie

Începem soluția reprezentând parabola ca două funcții. Înțelegem asta

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Valoarea pantei este egală cu valoarea derivatei în punctul x 0 al acestei funcții și este egală cu tangentei pantei.

Primim:

k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3

De aici determinăm valoarea lui x pentru punctele de contact.

Prima funcție va fi scrisă ca

y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Evident, nu există rădăcini reale, deoarece am primit o valoare negativă. Concluzionăm că nu există o tangentă cu un unghi de 150 ° pentru o astfel de funcție.

A doua funcție va fi scrisă ca

y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Avem că punctele de atingere - 23 4 ; - 5 + 3 4 .

Răspuns: ecuația tangentei ia forma

y = - 1 3 x - 23 4 + - 5 + 3 4

Să-l grafic astfel:

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Acest program de matematică găsește ecuația tangentei la graficul funcției $f(x) $ într-un punct specificat de utilizator $a $.

Programul nu numai că afișează ecuația tangentei, dar afișează și procesul de rezolvare a problemei.

Acest calculator online poate fi util elevilor de liceu scoli de invatamant generalîn pregătire pentru munca de controlși examene, la testarea cunoștințelor înainte de examen, părinții pentru a controla rezolvarea multor probleme de matematică și algebră. Sau poate este prea scump pentru tine să angajezi un tutor sau să cumperi noi manuale? Sau vrei doar să o faci cât mai curând posibil? teme pentru acasă matematica sau algebra? În acest caz, puteți folosi și programele noastre cu o soluție detaliată.

În acest fel, vă puteți conduce propriul antrenament și/sau vă puteți antrena frati mai mici sau surori, în timp ce nivelul de educație în domeniul sarcinilor în curs de rezolvare crește.

Dacă trebuie să găsiți derivata unei funcții, atunci pentru aceasta avem sarcina Găsiți derivată.

Dacă nu sunteți familiarizat cu regulile de introducere a funcțiilor, vă recomandăm să vă familiarizați cu acestea.

Introduceți expresia funcției $f(x)$ și numărul $a$ Găsiți ecuația tangentei

S-a constatat că unele scripturi necesare pentru a rezolva această sarcină nu au fost încărcate și este posibil ca programul să nu funcționeze.
Este posibil să aveți AdBlock activat.
În acest caz, dezactivați-l și reîmprospătați pagina.

Aveți JavaScript dezactivat în browser.
JavaScript trebuie să fie activat pentru ca soluția să apară.
Iată instrucțiuni despre cum să activați JavaScript în browserul dvs.

Deoarece Sunt o mulțime de oameni care doresc să rezolve problema, cererea ta este pusă în coadă.
După câteva secunde, soluția va apărea mai jos.
Va rugam asteptati sec...

daca tu observat o eroare în soluție, apoi puteți scrie despre asta în Formularul de feedback .
Nu uita indicați ce sarcină tu decizi ce intra in campuri.

Jocurile, puzzle-urile, emulatorii noștri:

Un pic de teorie.

Panta unei drepte

Amintiți-vă că programul funcție liniară$y=kx+b$ este o linie dreaptă. Se numește numărul $k=tg \alpha $. panta unei drepte, iar unghiul $\alpha $ este unghiul dintre această linie și axa Ox

Dacă $k>0$, atunci \(0 Dacă \(kEcuația tangentei la graficul funcției

Dacă punctul M (a; f (a)) aparține graficului funcției y \u003d f (x) și dacă în acest punct este posibil să se deseneze o tangentă la graficul funcției care nu este perpendiculară pe axa x, apoi din semnificația geometrică a derivatei rezultă că panta tangentei este egală cu f "(a). În continuare, vom dezvolta un algoritm de compilare a ecuației tangentei la graficul oricărei funcții.

Să fie date funcția y \u003d f (x) și punctul M (a; f (a)) de pe graficul acestei funcții; să se știe că f "(a) există. Să compunem ecuația tangentei la graficul unei funcții date într-un punct dat. Această ecuație, ca și ecuația oricărei drepte care nu este paralelă cu axa y , are forma y \u003d kx + b, deci problema este de a găsi valorile coeficienților k și b.

Totul este clar cu panta k: se știe că k \u003d f "(a). Pentru a calcula valoarea lui b, folosim faptul că linia dreaptă dorită trece prin punctul M (a; f (a)) Aceasta înseamnă că, dacă înlocuim coordonatele punctului M în ecuația unei linii drepte, obținem egalitatea corectă: \ (f (a) \u003d ka + b \), adică \ (b \u003d f (a) ) - ka \).

Rămâne să înlocuiți valorile găsite ale coeficienților k și b în ecuația unei linii drepte:

$$ y=kx+b $$ $$ y=kx+ f(a) - ka $$ $$ y=f(a)+ k(x-a) $$ $$ y=f(a)+ f"(a) )(x-a) $$

Am primit ecuația tangentei la graficul funcției$y = f(x) $ în punctul $x=a $.

Algoritm pentru găsirea ecuației tangentei la graficul funcției $y=f(x)$
1. Desemnați abscisa punctului de contact cu litera \ (a \)
2. Calculați $f(a)$
3. Găsiți $f"(x) $ și calculați $f"(a) $
4. Înlocuiți numerele găsite \ (a, f (a), f "(a) \) în formula \ (y \u003d f (a) + f "(a) (x-a) \)

Cărți (manuale) Rezumate ale examenului de stat unificat și teste OGE online Jocuri, puzzle-uri Reprezentarea grafică a funcțiilor Dicționarul ortografic al limbii ruse Dicționarul argoului pentru tineri Catalogul școlilor din Rusia Catalogul școlilor secundare din Rusia Catalogul universităților din Rusia Lista sarcinilor Găsirea GCD și LCM Simplificarea unui polinom (înmulțirea polinoamelor)

Ecuația tangentei la graficul funcției

P. Romanov, T. Romanova,
Magnitogorsk,
Regiunea Chelyabinsk

Ecuația tangentei la graficul funcției

Articolul a fost publicat cu sprijinul Complexului Hotelier ITAKA+. Stând în orașul constructorilor de nave Severodvinsk, nu vă veți confrunta cu problema găsirii de locuințe temporare. , Pe net complex hotelier„ITAKA +” http://itakaplus.ru, puteți închiria ușor și rapid un apartament în oraș, pentru orice perioadă, cu plata zilnică.

Pe stadiul prezent dezvoltarea educației ca una dintre sarcinile sale principale este formarea unei personalități cu gândire creativ. Capacitatea de creativitate la elevi poate fi dezvoltată doar dacă aceștia sunt implicați sistematic în elementele de bază. activitati de cercetare. Fundația pentru ca elevii să-și folosească forțele creative, abilitățile și talentele este formată de cunoștințe și abilități cu drepturi depline. În acest sens, problema formării unui sistem de cunoștințe și abilități de bază pentru fiecare subiect al cursului de matematică școlară este de o importanță nu mică. În același timp, abilitățile cu drepturi depline ar trebui să fie scopul didactic nu al sarcinilor individuale, ci al sistemului lor atent gândit. În sensul cel mai larg, un sistem este înțeles ca un set de elemente interconectate care interacționează care au integritate și o structură stabilă.

Luați în considerare o metodologie pentru a-i învăța pe elevi cum să întocmească o ecuație a unei tangente la un grafic de funcție. În esență, toate sarcinile pentru găsirea ecuației tangentei sunt reduse la necesitatea de a selecta din mulțimea (snop, familie) de linii pe acelea dintre ele care satisfac o anumită cerință - sunt tangente la graficul unei anumite funcții. În acest caz, setul de linii din care se efectuează selecția poate fi specificat în două moduri:

a) un punct situat pe planul xOy (creion central de linii);
b) coeficient unghiular (mănunchi paralel de linii).

În acest sens, la studierea temei „Tangentă la graficul unei funcții” pentru a izola elementele sistemului, am identificat două tipuri de sarcini:

1) sarcini pe o tangentă, punct prin care trece;
2) sarcini pe o tangentă dată de panta acesteia.

Învățarea rezolvării problemelor pe o tangentă s-a realizat folosind algoritmul propus de A.G. Mordkovici. Diferența sa fundamentală față de cele deja cunoscute este că abscisa punctului tangent se notează cu litera a (în loc de x0), în legătură cu care ecuația tangentei ia forma

y \u003d f (a) + f "(a) (x - a)

(comparați cu y \u003d f (x 0) + f "(x 0) (x - x 0)). Aceasta tehnica metodica, în opinia noastră, permite elevilor să realizeze rapid și ușor unde în ecuația tangentă generală sunt scrise coordonatele punctului curent și unde sunt punctele de atingere.

Algoritm pentru compilarea ecuației tangentei la graficul funcției y = f(x)

1. Desemnați cu litera a abscisa punctului de contact.
2. Găsiți f(a).
3. Găsiți f „(x) și f „(a).
4. Înlocuiți numerele găsite a, f (a), f "(a) în ecuație generală tangentă y \u003d f (a) \u003d f "(a) (x - a).

Acest algoritm poate fi compilat pe baza selecției independente a operațiilor de către elevi și a secvenței de execuție a acestora.

Practica a arătat că soluția consecventă a fiecăreia dintre sarcinile cheie folosind algoritmul vă permite să vă formați capacitatea de a scrie ecuația tangentei la graficul funcției în etape, iar pașii algoritmului servesc drept puncte forte pentru acțiuni. . Această abordare corespunde teoriei formării treptate a acțiunilor mentale dezvoltată de P.Ya. Galperin și N.F. Talizina.

În primul tip de sarcini au fost identificate două sarcini cheie:

tangenta trece printr-un punct situat pe curbă (problema 1);
tangenta trece printr-un punct care nu se află pe curbă (Problema 2).

Sarcina 1. Echivalează tangenta cu graficul funcției în punctul M(3; – 2).

Soluţie. Punctul M(3; – 2) este punctul de contact, deoarece

1. a = 3 - abscisa punctului de atingere.
2. f(3) = – 2.
3. f "(x) \u003d x 2 - 4, f "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 este ecuația tangentei.

Sarcina 2. Scrieți ecuațiile tuturor tangentelor la graficul funcției y = - x 2 - 4x + 2, trecând prin punctul M(- 3; 6).

Soluţie. Punctul M(– 3; 6) nu este un punct tangent, deoarece f(– 3) 6 (Fig. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - ecuație tangentă.

Tangenta trece prin punctul M(– 3; 6), prin urmare, coordonatele ei satisfac ecuația tangentei.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = - 4, a 2 = - 2.

Dacă a = – 4, atunci ecuația tangentei este y = 4x + 18.

Dacă a \u003d - 2, atunci ecuația tangentei are forma y \u003d 6.

În al doilea tip, sarcinile cheie vor fi următoarele:

tangenta este paralelă cu o dreaptă (problema 3);
tangenta trece la un anumit unghi la dreapta dată (Problema 4).

Sarcina 3. Scrieți ecuațiile tuturor tangentelor la graficul funcției y \u003d x 3 - 3x 2 + 3, paralele cu dreapta y \u003d 9x + 1.

Soluţie.

1. a - abscisa punctului de atingere.
2. f(a) = a 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.

Dar, pe de altă parte, f "(a) \u003d 9 (condiția de paralelism). Deci, trebuie să rezolvăm ecuația 3a 2 - 6a \u003d 9. Rădăcinile sale a \u003d - 1, a \u003d 3 (Fig. . 3).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 este ecuația tangentei;

1) a = 3;
2) f(3) = 3;
3) f „(3) = 9;
4) y = 3 + 9(x - 3);

y = 9x – 24 este ecuația tangentei.

Sarcina 4. Scrieți ecuația tangentei la graficul funcției y = 0,5x 2 - 3x + 1, trecând cu un unghi de 45 ° la dreapta y = 0 (Fig. 4).

Soluţie. Din condiția f "(a) \u003d tg 45 ° găsim a: a - 3 \u003d 1^a=4.

1. a = 4 - abscisa punctului de atingere.
2. f(4) = 8 - 12 + 1 = - 3.
3. f "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).

y \u003d x - 7 - ecuația tangentei.

Este ușor de demonstrat că rezolvarea oricărei alte probleme se reduce la rezolvarea uneia sau mai multor probleme cheie. Luați în considerare următoarele două probleme ca exemplu.

1. Scrieți ecuațiile tangentelor la parabola y = 2x 2 - 5x - 2, dacă tangentele se intersectează în unghi drept și una dintre ele atinge parabola în punctul cu abscisa 3 (Fig. 5).

Soluţie. Deoarece abscisa punctului de contact este dată, prima parte a soluției se reduce la problema cheie 1.

1. a = 3 - abscisa punctului de atingere al uneia dintre laturi unghi drept.
2. f(3) = 1.
3. f "(x) \u003d 4x - 5, f "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - ecuația primei tangente.

Lasă a este unghiul de înclinare al primei tangente. Deoarece tangentele sunt perpendiculare, atunci este unghiul de înclinare al celei de-a doua tangente. Din ecuația y = 7x – 20 a primei tangente avem tg a = 7. Găsiți

Aceasta înseamnă că panta celei de-a doua tangente este .

Soluția ulterioară se reduce la sarcina cheie 3.

Fie B(c; f(c)) punctul tangent al celei de-a doua drepte, atunci

1. - abscisa celui de-al doilea punct de contact.
2.
3.
4.
este ecuația celei de-a doua tangente.

Notă. Coeficientul unghiular al tangentei poate fi găsit mai ușor dacă elevii cunosc raportul dintre coeficienții dreptelor perpendiculare k 1 k 2 = - 1.

2. Scrieți ecuațiile tuturor tangentelor comune la graficele de funcții

Soluţie. Problema se reduce la găsirea absciselor punctelor tangente comune, adică la rezolvarea problemei cheie 1 în vedere generala, alcătuind un sistem de ecuații și soluția lui ulterioară (Fig. 6).

1. Fie a abscisa punctului de atingere situat pe graficul funcției y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f „(a) = 2a + 1.
4. y \u003d a 2 + a + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - a 2.

1. Fie c abscisa punctului tangent situat pe graficul funcției
2.
3. f „(c) = c.
4.

Din moment ce tangentele sunt comune, atunci

Deci y = x + 1 și y = - 3x - 3 sunt tangente comune.

Scopul principal al sarcinilor luate în considerare este de a pregăti elevii pentru auto-recunoașterea tipului de sarcină cheie atunci când rezolvă mai multe sarcini provocatoare care necesită anumite abilități de cercetare (capacitatea de a analiza, compara, generaliza, formula o ipoteză etc.). Astfel de sarcini includ orice sarcină în care sarcina cheie este inclusă ca componentă. Să luăm ca exemplu problema (invers cu problema 1) de a găsi o funcție din familia tangentelor sale.

3. Pentru ce b și c sunt liniile y \u003d x și y \u003d - 2x tangente la graficul funcției y \u003d x 2 + bx + c?

Soluţie.

Fie t abscisa punctului de contact al dreptei y = x cu parabola y = x 2 + bx + c; p este abscisa punctului de contact al dreptei y = - 2x cu parabola y = x 2 + bx + c. Atunci ecuația tangentei y = x va lua forma y = (2t + b)x + c - t 2 , iar ecuația tangentei y = - 2x va lua forma y = (2p + b)x + c - p 2 .

Compuneți și rezolvați un sistem de ecuații

Răspuns:

Sarcini pentru soluție independentă

1. Scrieți ecuațiile tangentelor trasate la graficul funcției y = 2x 2 - 4x + 3 în punctele de intersecție ale graficului cu dreapta y = x + 3.

Răspuns: y \u003d - 4x + 3, y \u003d 6x - 9,5.

2. Pentru ce valori ale lui a trece tangenta trasată la graficul funcției y \u003d x 2 - ax în punctul graficului cu abscisa x 0 \u003d 1 prin punctul M (2; 3) ?

Răspuns: a = 0,5.

3. Pentru ce valori ale lui p linia y = px - 5 atinge curba y = 3x 2 - 4x - 2?

Răspuns: p 1 \u003d - 10, p 2 \u003d 2.

4. Aflați toate punctele comune ale graficului funcției y = 3x - x 3 și tangenta trasată la acest grafic prin punctul P(0; 16).

Răspuns: A(2; - 2), B(- 4; 52).

5. Aflați cea mai scurtă distanță dintre parabolă y = x 2 + 6x + 10 și linie

Răspuns:

6. Pe curba y \u003d x 2 - x + 1, găsiți punctul în care tangenta la grafic este paralelă cu linia y - 3x + 1 \u003d 0.

Răspuns: M(2; 3).

7. Scrieți ecuația tangentei la graficul funcției y = x 2 + 2x - | 4x | care îl atinge în două puncte. Faceți un desen.

Răspuns: y = 2x - 4.

8. Demonstrați că dreapta y = 2x – 1 nu intersectează curba y = x 4 + 3x 2 + 2x. Găsiți distanța dintre cele mai apropiate puncte ale acestora.

Răspuns:

9. Pe parabola y \u003d x 2, sunt luate două puncte cu abscise x 1 \u003d 1, x 2 \u003d 3. Prin aceste puncte se trasează o secantă. În ce punct al parabolei tangenta la aceasta va fi paralelă cu secantei desenate? Scrieți ecuațiile secantei și tangentei.

Răspuns: y \u003d 4x - 3 - ecuație secante; y = 4x – 4 este ecuația tangentei.

10. Aflați unghiul q între tangentele la graficul funcției y \u003d x 3 - 4x 2 + 3x + 1, desenate în puncte cu abscisele 0 și 1.

Răspuns: q = 45°.

11. În ce puncte tangenta la graficul funcției formează un unghi de 135° cu axa Ox?

Răspuns: A(0; - 1), B(4; 3).

12. În punctul A(1; 8) la curbă se trasează o tangentă. Aflați lungimea segmentului tangentei cuprins între axele de coordonate.

Răspuns:

13. Scrieți ecuația tuturor tangentelor comune la graficele funcțiilor y \u003d x 2 - x + 1 și y \u003d 2x 2 - x + 0,5.

Răspuns: y = - 3x și y = x.

14. Aflați distanța dintre tangente la graficul funcției paralel cu axa x.

Răspuns:

15. Determinați la ce unghiuri intersectează parabola y \u003d x 2 + 2x - 8 axa x.

Răspuns: q 1 \u003d arctan 6, q 2 \u003d arctan (- 6).

16. Pe graficul funcţiei găsiți toate punctele, tangenta la fiecare dintre ele la acest grafic intersectează semiaxele pozitive ale coordonatelor, decupând segmente egale din ele.

Răspuns: A(-3; 11).

17. Linia y = 2x + 7 și parabola y = x 2 – 1 se intersectează în punctele M și N. Aflați punctul de intersecție K al dreptelor tangente la parabolă în punctele M și N.

Răspuns: K(1; - 9).

18. Pentru ce valori ale lui b este linia y \u003d 9x + b tangentă la graficul funcției y \u003d x 3 - 3x + 15?

Raspunsul 1; 31.

19. Pentru ce valori ale lui k linia y = kx – 10 are un singur punct comun cu graficul funcției y = 2x 2 + 3x – 2? Pentru valorile găsite ale lui k, determinați coordonatele punctului.

Răspuns: k 1 = - 5, A(- 2; 0); k2 = 11, B(2; 12).

20. Pentru ce valori ale lui b trece tangenta trasată la graficul funcției y = bx 3 – 2x 2 – 4 în punctul cu abscisa x 0 = 2 prin punctul M(1; 8)?

Răspuns: b = - 3.

21. O parabolă cu un vârf pe axa x este tangentă la o dreaptă care trece prin punctele A(1; 2) și B(2; 4) în punctul B. Aflați ecuația parabolei.

Răspuns:

22. La ce valoare a coeficientului k atinge parabola y \u003d x 2 + kx + 1 de axa Ox?

Răspuns: k = q 2.

23. Aflați unghiurile dintre dreapta y = x + 2 și curba y = 2x 2 + 4x - 3.

29. Aflați distanța dintre tangentele la graficul generatoarelor de funcții cu direcția pozitivă a axei Ox la un unghi de 45 °.

Răspuns:

30. Aflați locul vârfurilor tuturor parabolelor de forma y = x 2 + ax + b atingând dreapta y = 4x - 1.

Răspuns: linie dreaptă y = 4x + 3.

Literatură

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra și începuturile analizei: 3600 de probleme pentru școlari și solicitanții la universitate. - M., Butarda, 1999.
2. Mordkovich A. Al patrulea seminar pentru tineri profesori. Subiectul este „Aplicații derivate”. - M., „Matematică”, Nr. 21/94.
3. Formarea de cunoștințe și deprinderi pe baza teoriei asimilării treptate a acțiunilor mentale. / Ed. P.Ya. Galperin, N.F. Talizina. - M., Universitatea de Stat din Moscova, 1968.

Tutorialul video „Ecuația tangentei la graficul unei funcții” demonstrează material educațional pentru însușirea temei. În cadrul lecției video este prezentat materialul teoretic necesar formării conceptului de ecuație a tangentei la graficul unei funcții la un punct dat, algoritmul de găsire a unei astfel de tangente, exemple de rezolvare a problemelor folosind teoreticul studiat. sunt descrise materiale.

Tutorialul video folosește metode care îmbunătățesc vizibilitatea materialului. În vizualizare sunt inserate desene, diagrame, sunt date comentarii vocale importante, sunt aplicate animații, evidențierea culorilor și alte instrumente.

Lecția video începe cu prezentarea subiectului lecției și imaginea unei tangente la graficul unei funcții y=f(x) în punctul M(a;f(a)). Se știe că panta tangentei trasate la grafic într-un punct dat este egală cu derivata funcției f΄(a) într-un punct dat. Tot din cursul algebrei se cunoaste ecuatia dreptei y=kx+m. Schematic este prezentată soluția problemei găsirii ecuației tangentei într-un punct, ceea ce se reduce la găsirea coeficienților k, m. Cunoscând coordonatele punctului aparținând graficului funcției, putem găsi m înlocuind valoarea coordonatelor în ecuația tangentei f(a)=ka+m. Din el găsim m=f(a)-ka. Astfel, cunoscând valoarea derivatei într-un punct dat și coordonatele punctului, putem reprezenta ecuația tangentei în acest fel y=f(a)+f΄(a)(x-a).

Urmează un exemplu de întocmire a unei ecuații tangente, urmând schema. Dată o funcție y=x 2 , x=-2. Acceptând a=-2, găsim valoarea funcției în acest punct f(a)= f(-2)=(-2) 2 =4. Determinăm derivata funcției f΄(х)=2х. În acest moment, derivata este egală cu f΄(a)= f΄(-2)=2 (-2)=-4. Pentru a compila ecuația se găsesc toți coeficienții a=-2, f(a)=4, f΄(a)=-4, deci ecuația tangentei y=4+(-4)(x+2). Simplificand ecuația, obținem y \u003d -4-4x.

În exemplul următor, se propune formularea ecuației tangentei de la origine la graficul funcției y=tgx. În acest punct a=0, f(0)=0, f΄(х)=1/cos 2 x, f΄(0)=1. Deci ecuația tangentei arată ca y=x.

Ca o generalizare, procesul de compilare a ecuației tangentei la graficul funcției la un moment dat este formalizat ca un algoritm format din 4 pași:

Se introduce o desemnare pentru abscisa punctului de contact;
f(a) se calculează;
Se determină F΄(х) și se calculează f΄(a). Valorile găsite a, f(a), f΄(a) sunt substituite în formula ecuației tangente y=f(a)+f΄(a)(x-a).

Exemplul 1 ia în considerare compilarea ecuației tangentei la graficul funcției y \u003d 1 / x în punctul x \u003d 1. Folosim un algoritm pentru a rezolva problema. Pentru această funcție în punctul a=1, valoarea funcției f(a)=-1. Derivată a funcției f΄(х)=1/х 2 . În punctul a=1, derivata f΄(a)= f΄(1)=1. Folosind datele obținute, este compilată ecuația tangentei y \u003d -1 + (x-1) sau y \u003d x-2.

În exemplul 2, trebuie să găsiți ecuația tangentei la graficul funcției y \u003d x 3 +3x 2 -2x-2. Condiția principală este paralelismul tangentei și a dreptei y \u003d -2x + 1. În primul rând, găsim panta tangentei, egală cu panta dreptei y \u003d -2x + 1. Deoarece f΄(a)=-2 pentru această linie dreaptă, atunci k=-2 pentru tangenta dorită. Găsim derivata funcției (x 3 + 3x 2 -2x-2) ΄ \u003d 3x 2 + 6x-2. Știind că f΄(a)=-2, găsim coordonatele punctului 3а 2 +6а-2=-2. Rezolvând ecuația, obținem 1 \u003d 0 și 2 \u003d -2. Folosind coordonatele găsite, puteți găsi ecuația tangentei folosind un algoritm binecunoscut. Găsim valoarea funcției în punctele f(a 1)=-2, f(a 2)=-18. Valoarea derivatei în punctul f΄(а 1)= f΄(а 2)=-2. Înlocuind valorile găsite în ecuația tangentei, obținem pentru primul punct a 1 \u003d 0 y \u003d -2x-2, iar pentru al doilea punct a 2 \u003d -2 ecuația tangentei y \u003d -2x- 22.

Exemplul 3 descrie formularea ecuației tangentei pentru desenarea acesteia în punctul (0;3) la graficul funcției y=√x. Decizia se ia conform algoritmului cunoscut. Punctul de atingere are coordonatele x=a, unde a>0. Valoarea funcției în punctul f(a)=√x. Derivata funcției f΄(х)=1/2√х, deci, în punctul dat f΄(а)=1/2√а. Înlocuind toate valorile obținute în ecuația tangentei, obținem y \u003d √a + (x-a) / 2√a. Transformând ecuația, obținem y=x/2√a+√a/2. Știind că tangenta trece prin punctul (0; 3), găsim valoarea lui a. Găsiți a din 3=√a/2. Prin urmare √a=6, a=36. Găsim ecuația tangentei y \u003d x / 12 + 3. Figura prezintă graficul funcției luate în considerare și tangenta dorită construită.

Elevilor li se reamintesc egalitățile aproximative Δy=≈f΄(x)Δx și f(x+Δx)-f(x)≈f΄(x)Δx. Luând x=a, x+Δx=x, Δx=x-a, obținem f(x)- f(a)≈f΄(a)(x-a), deci f(x)≈f(a)+ f΄( a)(x-a).

În exemplul 4, este necesar să găsim valoarea aproximativă a expresiei 2.003 6 . Deoarece este necesar să găsim valoarea funcției f (x) \u003d x 6 în punctul x \u003d 2.003, putem folosi formula binecunoscută, luând f (x) \u003d x 6, a \u003d 2 , f (a) \u003d f (2) \u003d 64, f ΄(x)=6х 5 . Derivată în punctul f΄(2)=192. Prin urmare, 2,003 6 ≈65-192 0,003. După calcularea expresiei, obținem 2,003 6 ≈64,576.

Lecția video „Ecuația tangentei la graficul unei funcții” este recomandată pentru utilizare într-o lecție tradițională de matematică la școală. Pentru un profesor de învățământ la distanță, materialul video va ajuta la explicarea subiectului mai clar. Videoclipul poate fi recomandat pentru a fi luat în considerare de către studenți, dacă este necesar, pentru a-și aprofunda înțelegerea subiectului.

INTERPRETAREA TEXTULUI:

Știm că dacă punctul M (a; f (a)) (em cu coordonatele a și eff din a) aparține graficului funcției y \u003d f (x) și dacă în acest punct se poate desena o tangentă la graficul funcției, nu perpendicular pe abscisa axei, atunci panta tangentei este f "(a) (ef curs de la a).

Să fie date o funcție y = f(x) și un punct M (a; f(a)) și se știe de asemenea că f´(a) există. Să compunem ecuația tangentei la graficul unei funcții date într-un punct dat. Această ecuație, ca și ecuația oricărei drepte care nu este paralelă cu axa y, are forma y = kx + m (y este egal cu ka x plus em), deci sarcina este de a găsi valorile coeficienților k și m. (ka și em)

Panta k \u003d f "(a). Pentru a calcula valoarea lui m, folosim faptul că linia dreaptă dorită trece prin punctul M (a; f (a)). Aceasta înseamnă că dacă înlocuim coordonatele lui punctul M din ecuația dreptei, obținem egalitatea corectă : f(a) = ka+m, de unde constatăm că m = f(a) - ka.

Rămâne să înlocuiți valorile găsite ale coeficienților ki și m în ecuația unei linii drepte:

y = kx+(f(a)-ka);

y = f(a)+k(x-a);

y= f(A)+ f"(A) (X- A). ( Y este egal cu eff dintr-o cursă plus ef dintr-un înmulțit cu x minus a).

Am obținut ecuația tangentei la graficul funcției y = f(x) în punctul x=a.

Dacă, să spunem, y \u003d x 2 și x \u003d -2 (adică a \u003d -2), atunci f (a) \u003d f (-2) \u003d (-2) 2 \u003d 4; f´(x) \u003d 2x, deci f "(a) \u003d f´(-2) \u003d 2 (-2) \u003d -4. (atunci eff din a este egal cu patru, eff prim din x este egal cu doi x, ceea ce înseamnă cursa ef de la a este egal cu minus patru)

Înlocuind în ecuație valorile găsite a \u003d -2, f (a) \u003d 4, f "(a) \u003d -4, obținem: y \u003d 4 + (-4) (x + 2) , adică y \u003d -4x -4.

(y este egal cu minus patru x minus patru)

Compuneți ecuația tangentei la graficul funcției y \u003d tgx (y egal cu tangenta x) la origine. Avem: a = 0, f(0) = tg0=0;

f"(x)= , deci f"(0) = l. Înlocuind valorile găsite a=0, f(a)=0, f´(a) = 1 în ecuație, obținem: y=x.

Ne generalizăm pașii pentru găsirea ecuației tangentei la graficul funcției în punctul x folosind algoritmul.

ALGORITM PENTRU COMPUNEREA ECUAȚIEI FUNCȚIEI tangente la GRAFUL y \u003d f (x):

1) Desemnați abscisa punctului de contact cu litera a.

2) Calculați f(a).

3) Aflați f´(x) și calculați f´(a).

4) Înlocuiți numerele găsite a, f(a), f´(a) în formulă y= f(A)+ f"(A) (X- A).

Exemplul 1. Scrieți ecuația tangentei la graficul funcției y \u003d - în

punctul x = 1.

Soluţie. Să folosim algoritmul, ținând cont de faptul că în acest exemplu

2) f(a)=f(1)=-=-1

3) f´(x)=; f´(a)= f´(1)= =1.

4) Înlocuiți cele trei numere găsite: a \u003d 1, f (a) \u003d -1, f "(a) \u003d 1 în formulă. Obținem: y \u003d -1 + (x-1), y \u003d x-2.

Răspuns: y = x-2.

Exemplul 2. Având în vedere o funcție y = x 3 +3x 2 -2x-2. Scrieți ecuația tangentei la graficul funcției y \u003d f (x), paralelă cu dreapta y \u003d -2x +1.

Folosind algoritmul de compilare a ecuației tangente, ținem cont că în acest exemplu f(x) = x 3 +3x 2 -2x-2, dar abscisa punctului de atingere nu este specificată aici.

Să începem să vorbim așa. Tangenta dorită trebuie să fie paralelă cu linia dreaptă y \u003d -2x + 1. Și liniile paralele au pante egale. Prin urmare, panta tangentei este egală cu panta dreptei date: k cas. = -2. Hok cas. = f "(a). Astfel, putem găsi valoarea lui a din ecuația f ´ (a) \u003d -2.

Să găsim derivata funcției y=f(X):

f"(X) \u003d (x 3 + 3x 2 -2x-2)´ \u003d 3x 2 + 6x-2;f„(a) \u003d 3a 2 + 6a-2.

Din ecuația f "(a) \u003d -2, adică. 3а 2 +6а-2\u003d -2 găsim un 1 \u003d 0, un 2 \u003d -2. Aceasta înseamnă că există două tangente care îndeplinesc condițiile problemei: una într-un punct cu abscisă 0, cealaltă într-un punct cu abscisă -2.

Acum puteți acționa conform algoritmului.

1) a 1 \u003d 0 și 2 \u003d -2.

2) f(a 1) = 0 3 +3 0 2 -2∙0-2=-2; f(a2)= (-2) 3 +3 (-2) 2 -2 (-2)-2=6;

3) f „(a 1) = f” (a 2) = -2.

4) Înlocuind valorile a 1 = 0, f (a 1) = -2, f "(a 1) = -2 în formulă, obținem:

y=-2-2(x-0), y=-2x-2.

Înlocuind valorile a 2 \u003d -2, f (a 2) \u003d 6, f "(a 2) \u003d -2 în formulă, obținem:

y=6-2(x+2), y=-2x+2.

Răspuns: y=-2x-2, y=-2x+2.

Exemplul 3. Din punctul (0; 3) trageți o tangentă la graficul funcției y \u003d. Soluţie. Să folosim algoritmul de compilare a ecuației tangente, având în vedere că în acest exemplu f(x) = . Rețineți că aici, ca și în exemplul 2, abscisa punctului de atingere nu este indicată în mod explicit. Cu toate acestea, acționăm conform algoritmului.

1) Fie x = a abscisa punctului de contact; este clar că a > 0.

3) f´(x)=()´=; f´(a) =.

4) Înlocuind valorile a, f(a) = , f "(a) = în formula

y \u003d f (a) + f "(a) (x-a), primim:

Prin condiție, tangenta trece prin punctul (0; 3). Înlocuind valorile x = 0, y = 3 în ecuație, obținem: 3 = , iar apoi =6, a =36.

După cum puteți vedea, în acest exemplu, abia la pasul al patrulea al algoritmului am reușit să găsim abscisa punctului de atingere. Înlocuind valoarea a =36 în ecuație, obținem: y=+3

Pe fig. Figura 1 prezintă o ilustrare geometrică a exemplului considerat: este trasat un grafic al funcției y \u003d, este trasată o linie dreaptă y \u003d +3.

Răspuns: y = +3.

Știm că pentru funcția y = f(x), care are o derivată în punctul x, egalitatea aproximativă este valabilă: Δyf´(x)Δx

sau, mai detaliat, f(x+Δx)-f(x) f´(x) Δx (ef din x plus delta x minus ef din x este aproximativ egal cu ef prim de la x la delta x).

Pentru comoditatea unui raționament suplimentar, schimbăm notația:

în loc de x vom scrie A,

în loc de x + Δx vom scrie x

în loc de Δx vom scrie x-a.

Atunci egalitatea aproximativă scrisă mai sus va lua forma:

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (ef din x este aproximativ egal cu eff dintr-o cursă plus ef din a, înmulțit cu diferența dintre x și a).

Exemplul 4. Găsiți o valoare aproximativă expresie numerică 2,003 6 .

Soluţie. Vorbim despre găsirea valorii funcției y \u003d x 6 în punctul x \u003d 2.003. Să folosim formula f(x)f(a)+f´(a)(x-a), având în vedere că în acest exemplu f(x)=x 6 , a = 2,f(a) = f(2) = 2 6 =64; x \u003d 2,003, f "(x) \u003d 6x 5 și, prin urmare, f" (a) \u003d f "(2) \u003d 6 2 5 \u003d 192.

Ca rezultat, obținem:

2,003 6 64+192 0,003, i.e. 2,003 6 = 64,576.

Dacă folosim un calculator, obținem:

2,003 6 = 64,5781643...

După cum puteți vedea, acuratețea aproximării este destul de acceptabilă.

În stadiul actual de dezvoltare a educației, una dintre sarcinile sale principale este formarea unei personalități care gândesc creativ. Capacitatea de creativitate la studenți poate fi dezvoltată numai dacă aceștia sunt implicați sistematic în bazele activităților de cercetare. Fundația pentru ca elevii să-și folosească forțele creative, abilitățile și talentele este formată de cunoștințe și abilități cu drepturi depline. În acest sens, problema formării unui sistem de cunoștințe și abilități de bază pentru fiecare subiect al cursului de matematică școlară este de o importanță nu mică. În același timp, abilitățile cu drepturi depline ar trebui să fie scopul didactic nu al sarcinilor individuale, ci al sistemului lor atent gândit. În sensul cel mai larg, un sistem este înțeles ca un set de elemente interconectate care interacționează care au integritate și o structură stabilă.

a) un punct situat pe planul xOy (creion central de linii);
b) coeficient unghiular (mănunchi paralel de linii).

În acest sens, la studierea temei „Tangentă la graficul unei funcții” pentru a izola elementele sistemului, am identificat două tipuri de sarcini:

1) sarcini pe o tangentă dată de un punct prin care trece;
2) sarcini pe o tangentă dată de panta acesteia.

y \u003d f (a) + f "(a) (x - a)

(comparați cu y \u003d f (x 0) + f "(x 0) (x - x 0)). Această tehnică metodologică, în opinia noastră, permite elevilor să realizeze rapid și ușor unde sunt scrise coordonatele punctului curent în ecuația tangentei generale și unde sunt punctele de contact.

Algoritm pentru compilarea ecuației tangentei la graficul funcției y = f(x)

1. Desemnați cu litera a abscisa punctului de contact.
2. Găsiți f(a).
3. Găsiți f „(x) și f „(a).
4. Înlocuiți numerele găsite a, f (a), f "(a) în ecuația generală a tangentei y \u003d f (a) \u003d f "(a) (x - a).

Acest algoritm poate fi compilat pe baza selecției independente a operațiilor de către elevi și a secvenței de execuție a acestora.

În primul tip de sarcini au fost identificate două sarcini cheie:

tangenta trece printr-un punct situat pe curbă (problema 1);
tangenta trece printr-un punct care nu se află pe curbă (Problema 2).

Sarcina 1. Echivalează tangenta cu graficul funcției în punctul M(3; – 2).

Soluţie. Punctul M(3; – 2) este punctul de contact, deoarece

1. a = 3 - abscisa punctului de atingere.
2. f(3) = – 2.
3. f "(x) \u003d x 2 - 4, f "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 este ecuația tangentei.

Sarcina 2. Scrieți ecuațiile tuturor tangentelor la graficul funcției y = - x 2 - 4x + 2, trecând prin punctul M(- 3; 6).

Soluţie. Punctul M(– 3; 6) nu este un punct tangent, deoarece f(– 3) 6 (Fig. 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - ecuație tangentă.

Tangenta trece prin punctul M(– 3; 6), prin urmare, coordonatele ei satisfac ecuația tangentei.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a 1 = - 4, a 2 = - 2.

Dacă a = – 4, atunci ecuația tangentei este y = 4x + 18.

Dacă a \u003d - 2, atunci ecuația tangentei are forma y \u003d 6.

În al doilea tip, sarcinile cheie vor fi următoarele:

tangenta este paralelă cu o dreaptă (problema 3);
tangenta trece la un anumit unghi la dreapta dată (Problema 4).

Sarcina 3. Scrieți ecuațiile tuturor tangentelor la graficul funcției y \u003d x 3 - 3x 2 + 3, paralele cu dreapta y \u003d 9x + 1.

1. a - abscisa punctului de atingere.
2. f(a) = a 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.

Dar, pe de altă parte, f "(a) \u003d 9 (condiția de paralelism). Deci, trebuie să rezolvăm ecuația 3a 2 - 6a \u003d 9. Rădăcinile sale a \u003d - 1, a \u003d 3 (Fig. . 3).

4. 1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 este ecuația tangentei;

1) a = 3;
2) f(3) = 3;
3) f „(3) = 9;
4) y = 3 + 9(x - 3);

y = 9x – 24 este ecuația tangentei.

Sarcina 4. Scrieți ecuația tangentei la graficul funcției y = 0,5x 2 - 3x + 1, trecând cu un unghi de 45 ° la dreapta y = 0 (Fig. 4).

Soluţie. Din condiția f "(a) \u003d tg 45 ° găsim a: a - 3 \u003d 1 ^ a \u003d 4.

1. a = 4 - abscisa punctului de atingere.
2. f(4) = 8 - 12 + 1 = - 3.
3. f "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).

y \u003d x - 7 - ecuația tangentei.

Este ușor de demonstrat că rezolvarea oricărei alte probleme se reduce la rezolvarea uneia sau mai multor probleme cheie. Luați în considerare următoarele două probleme ca exemplu.

1. Scrieți ecuațiile tangentelor la parabola y = 2x 2 - 5x - 2, dacă tangentele se intersectează în unghi drept și una dintre ele atinge parabola în punctul cu abscisa 3 (Fig. 5).

Soluţie. Deoarece abscisa punctului de contact este dată, prima parte a soluției se reduce la problema cheie 1.

1. a \u003d 3 - abscisa punctului de contact al uneia dintre laturile unghiului drept.
2. f(3) = 1.
3. f "(x) \u003d 4x - 5, f "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - ecuația primei tangente.

Fie a panta primei tangente. Deoarece tangentele sunt perpendiculare, atunci este unghiul de înclinare al celei de-a doua tangente. Din ecuația y = 7x – 20 a primei tangente avem tg a = 7. Aflați

Aceasta înseamnă că panta celei de-a doua tangente este .

Soluția ulterioară se reduce la sarcina cheie 3.

Fie B(c; f(c)) punctul tangent al celei de-a doua drepte, atunci

1. - abscisa celui de-al doilea punct de contact.
2.
3.
4.
este ecuația celei de-a doua tangente.

Notă. Coeficientul unghiular al tangentei poate fi găsit mai ușor dacă elevii cunosc raportul dintre coeficienții dreptelor perpendiculare k 1 k 2 = - 1.

2. Scrieți ecuațiile tuturor tangentelor comune la graficele de funcții

Soluţie. Sarcina se reduce la găsirea absciselor punctelor de contact ale tangentelor comune, adică la rezolvarea problemei cheie 1 într-o formă generală, alcătuirea unui sistem de ecuații și apoi rezolvarea acestuia (Fig. 6).

1. Fie a abscisa punctului de atingere situat pe graficul funcției y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f „(a) = 2a + 1.
4. y \u003d a 2 + a + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - a 2.

1. Fie c abscisa punctului tangent situat pe graficul funcției
2.
3. f „(c) = c.
4.

Din moment ce tangentele sunt comune, atunci

Deci y = x + 1 și y = - 3x - 3 sunt tangente comune.

Scopul principal al sarcinilor luate în considerare este pregătirea elevilor pentru auto-recunoașterea tipului de sarcină cheie atunci când rezolvă sarcini mai complexe care necesită anumite abilități de cercetare (capacitatea de a analiza, compara, generaliza, prezenta o ipoteză etc.). Astfel de sarcini includ orice sarcină în care sarcina cheie este inclusă ca componentă. Să luăm ca exemplu problema (invers cu problema 1) de a găsi o funcție din familia tangentelor sale.

3. Pentru ce b și c sunt liniile y \u003d x și y \u003d - 2x tangente la graficul funcției y \u003d x 2 + bx + c?

Compuneți și rezolvați un sistem de ecuații

Răspuns:

f(x)=
a=