Găsiți online soluții parțiale ale ecuațiilor diferențiale. Rezolvarea celor mai simple ecuații diferențiale de ordinul întâi
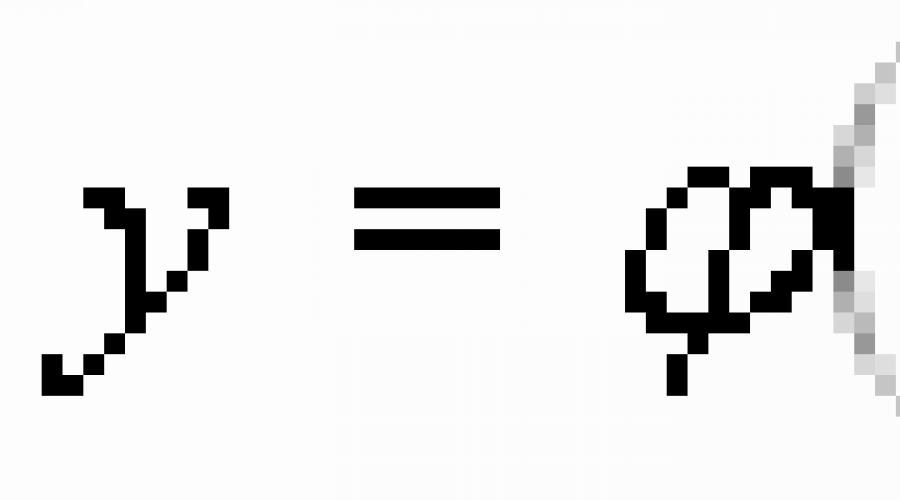
Citeste si
I. Ecuații diferențiale obișnuite
1.1. Concepte de bază și definiții
O ecuație diferențială este o ecuație care leagă o variabilă independentă X, funcția dorită yși derivatele sau diferențialele sale.
Simbolic, ecuația diferențială se scrie după cum urmează:
F(x,y,y")=0, F(x,y,y")=0, F(x,y,y",y",.., y(n))=0
O ecuație diferențială se numește obișnuită dacă funcția dorită depinde de o variabilă independentă.
Prin rezolvarea ecuației diferențiale se numește o astfel de funcție care transformă această ecuație într-o identitate.
Ordinea ecuației diferențiale este ordinul celei mai mari derivate din această ecuație
Exemple.
1. Considerăm ecuația diferențială de ordinul întâi
Soluția acestei ecuații este funcția y = 5 ln x. Într-adevăr, prin înlocuire y"în ecuație, obținem - o identitate.
Și asta înseamnă că funcția y = 5 ln x– este soluția acestei ecuații diferențiale.
2. Considerăm ecuația diferențială de ordinul doi y" - 5y" + 6y = 0. Funcția este soluția acestei ecuații.
Într-adevăr, .
Înlocuind aceste expresii în ecuație, obținem: , - identitate.
Și asta înseamnă că funcția este soluția acestei ecuații diferențiale.
Integrarea ecuațiilor diferențiale este procesul de găsire a soluțiilor ecuațiilor diferențiale.
Soluția generală a ecuației diferențiale se numește o funcție a formei ![]() , care include tot atâtea constante arbitrare independente câte ordinea ecuației.
, care include tot atâtea constante arbitrare independente câte ordinea ecuației.
Rezolvarea parțială a ecuației diferențiale se numește soluția obținută din soluția generală pentru diferite valori numerice ale constantelor arbitrare. Valorile constantelor arbitrare se găsesc la anumite valori inițiale ale argumentului și funcției.
Graficul unei anumite soluții a unei ecuații diferențiale se numește curba integrala.
Exemple
1. Găsiți o anumită soluție pentru o ecuație diferențială de ordinul întâi
xdx + ydy = 0, Dacă y= 4 at X = 3.
Soluţie. Integrând ambele părți ale ecuației, obținem
Cometariu. O constantă arbitrară C obținută ca rezultat al integrării poate fi reprezentată în orice formă convenabilă pentru transformări ulterioare. În acest caz, ținând cont de ecuația canonică a cercului, este convenabil să se reprezinte o constantă arbitrară С sub forma .
![]() - decizie comună ecuație diferențială.
- decizie comună ecuație diferențială.
O soluție particulară a unei ecuații care îndeplinește condițiile inițiale y = 4 at X = 3 se găsește din general prin substituirea condițiilor inițiale în soluția generală: 3 2 + 4 2 = C 2 ; C=5.
Înlocuind C=5 în soluția generală, obținem x2+y2 = 5 2 .
Aceasta este o soluție particulară a ecuației diferențiale obținute din soluția generală în condiții inițiale date.
2. Aflați soluția generală a ecuației diferențiale
Rezolvarea acestei ecuații este orice funcție de forma , unde C este o constantă arbitrară. Într-adevăr, substituind în ecuații, obținem: , .
Prin urmare, această ecuație diferențială are un număr infinit de soluții, deoarece pentru diferite valori ale constantei C, egalitatea determină soluții diferite ale ecuației.
De exemplu, prin substituție directă, se poate verifica dacă funcțiile ![]() sunt soluții ale ecuației .
sunt soluții ale ecuației .
O problemă în care este necesar să se găsească o anumită soluție a ecuației y" = f(x, y) satisfacerea conditiei initiale y(x0) = y0, se numește problema Cauchy.
Soluția ecuației y" = f(x, y), îndeplinind condiția inițială, y(x0) = y0, se numește o soluție la problema Cauchy.
Rezolvarea problemei Cauchy are un sens geometric simplu. Într-adevăr, conform acestor definiții, pentru a rezolva problema Cauchy y" = f(x, y) dat fiind y(x0) = y0, înseamnă a găsi curba integrală a ecuației y" = f(x, y) care trece prin punct dat M0 (x0,y 0).
II. Ecuații diferențiale de ordinul întâi
2.1. Noțiuni de bază
O ecuație diferențială de ordinul întâi este o ecuație de formă F(x,y,y") = 0.
Ecuația diferențială de ordinul întâi include derivata întâi și nu include derivate de ordin superior.
Ecuația y" = f(x, y) se numește ecuație de ordinul întâi rezolvată în raport cu derivata.
O soluție generală a unei ecuații diferențiale de ordinul întâi este o funcție de forma , care conține o constantă arbitrară.
Exemplu. Să considerăm o ecuație diferențială de ordinul întâi.
Soluția acestei ecuații este funcția .
Într-adevăr, înlocuind în această ecuație cu valoarea ei, obținem

![]() acesta este 3x=3x
acesta este 3x=3x
Prin urmare, funcția este o soluție generală a ecuației pentru orice constantă C.
Găsiți o soluție particulară a acestei ecuații care satisface condiția inițială y(1)=1Înlocuirea condițiilor inițiale x=1, y=1în soluția generală a ecuației , obținem de unde C=0.
Astfel, se obține o soluție particulară din cea generală prin substituirea în această ecuație a valorii rezultate C=0 este o decizie privată.
2.2. Ecuații diferențiale cu variabile separabile
O ecuație diferențială cu variabile separabile este o ecuație de forma: y"=f(x)g(y) sau prin diferenţiale , unde f(x)Și g(y) sunt date funcții.
Pentru cei y, pentru care , ecuația y"=f(x)g(y) este echivalentă cu ecuația ![]() în care variabila y este prezentă doar pe partea stângă, iar variabila x este prezentă doar pe partea dreaptă. Ei spun, „în ecuație y"=f(x)g(y separarea variabilelor.
în care variabila y este prezentă doar pe partea stângă, iar variabila x este prezentă doar pe partea dreaptă. Ei spun, „în ecuație y"=f(x)g(y separarea variabilelor.
Tip ecuație ![]() se numește ecuație de variabilă separată.
se numește ecuație de variabilă separată.
După integrarea ambelor părți ale ecuației ![]() De X, primim G(y) = F(x) + C este soluția generală a ecuației, unde G(y)Și F(x) sunt niste antiderivate, respectiv, ale functiilor si f(x), C constantă arbitrară.
De X, primim G(y) = F(x) + C este soluția generală a ecuației, unde G(y)Și F(x) sunt niste antiderivate, respectiv, ale functiilor si f(x), C constantă arbitrară.
Algoritm pentru rezolvarea unei ecuații diferențiale de ordinul întâi cu variabile separabile
Exemplul 1
rezolva ecuatia y" = xy
Soluţie. Derivată a unei funcții y"înlocui cu
separăm variabilele
Să integrăm ambele părți ale egalității:

Exemplul 2
2aa" = 1- 3x 2, Dacă y 0 = 3 la x0 = 1
Aceasta este o ecuație de variabilă separată. Să o reprezentăm în diferențe. Pentru a face acest lucru, rescriem această ecuație sub forma ![]() De aici
De aici ![]()
Integrând ambele părți ale ultimei egalități, găsim
Înlocuirea valorilor inițiale x 0 = 1, y 0 = 3 găsi CU 9=1-1+C, adică C = 9.
Prin urmare, integrala parțială dorită va fi ![]() sau
sau ![]()
Exemplul 3
Scrieți o ecuație pentru o curbă care trece printr-un punct M(2;-3)şi având o tangentă cu pantă
Soluţie. Conform conditiei
Aceasta este o ecuație de variabilă separabilă. Împărțind variabilele, obținem: ![]()
Integrând ambele părți ale ecuației, obținem: 
Folosind condițiile inițiale, x=2Și y=-3 găsi C:

Prin urmare, ecuația dorită are forma ![]()
2.3. Liniar ecuatii diferentiale prima comanda
O ecuație diferențială liniară de ordinul întâi este o ecuație de formă y" = f(x)y + g(x)
Unde f(x)Și g(x)- unele funcţii date.
Dacă g(x)=0 atunci ecuația diferențială liniară se numește omogenă și are forma: y" = f(x)y
Dacă atunci ecuația y" = f(x)y + g(x) numite eterogene.
Soluție generală a unei ecuații diferențiale liniare omogene y" = f(x)y dat de formula: unde CU este o constantă arbitrară.
În special, dacă C \u003d 0, atunci solutia este y=0 Dacă este liniară ecuație omogenă are forma y" = ky Unde k este o constantă, atunci soluția sa generală are forma: .
Rezolvarea generală a unei ecuații diferențiale liniare neomogene y" = f(x)y + g(x) dat de formula ![]() ,
,
acestea. este egală cu suma soluției generale a ecuației liniare omogene corespunzătoare și a soluției particulare a acestei ecuații.
Pentru o ecuație liniară neomogenă de formă y" = kx + b,
Unde kȘi b- unele numere și o anumită soluție vor fi o funcție constantă. Prin urmare, soluția generală are forma .
Exemplu. rezolva ecuatia y" + 2y +3 = 0
Soluţie. Reprezentăm ecuația sub formă y" = -2y - 3 Unde k=-2, b=-3 Soluția generală este dată de formula .
Prin urmare, unde C este o constantă arbitrară.
2.4. Rezolvarea ecuațiilor diferențiale liniare de ordinul întâi prin metoda Bernoulli
Găsirea unei soluții generale pentru o ecuație diferențială liniară de ordinul întâi y" = f(x)y + g(x) reduce la rezolvarea a două ecuații diferențiale cu variabile separate folosind substituția y=uv, Unde uȘi v- funcții necunoscute de la X. Această metodă de soluție se numește metoda Bernoulli.
Algoritm pentru rezolvarea unei ecuații diferențiale liniare de ordinul întâi
y" = f(x)y + g(x)
1. Introduceți o înlocuire y=uv.
2. Diferențiază această egalitate y"=u"v + uv"
3. Înlocuitor yȘi y" V ecuația dată: u"v + uv" =f(x)uv + g(x) sau u"v + uv" + f(x)uv = g(x).
4. Grupați termenii ecuației astfel încât u scoate-l din paranteze:
5. Din paranteză, echivalându-l cu zero, găsiți funcția
Aceasta este o ecuație separabilă: ![]()
Împărțiți variabilele și obțineți: ![]()
Unde ![]() .
.
.
.
6. Înlocuiți valoarea primită vîn ecuație (de la punctul 4):
![]()
și găsiți funcția Aceasta este o ecuație separabilă:
![]()
7. Scrieți soluția generală sub forma: ![]() , adică .
, adică .
Exemplul 1
Găsiți o anumită soluție a ecuației y" = -2y +3 = 0 Dacă y=1 la x=0
Soluţie. Să rezolvăm cu înlocuire y=uv,.y"=u"v + uv"
Înlocuind yȘi y"în această ecuație, obținem
Grupând al doilea și al treilea termen din partea stângă a ecuației, scoatem factorul comun u din paranteze
Echivalăm expresia dintre paranteze cu zero și, după ce am rezolvat ecuația rezultată, găsim funcția v = v(x)
Avem o ecuație cu variabile separate. Integram ambele părți ale acestei ecuații: Găsiți funcția v:
![]()
Înlocuiți valoarea rezultată vîn ecuație obținem:
Aceasta este o ecuație de variabilă separată. Integram ambele parti ale ecuatiei: ![]() Să găsim funcția u = u(x,c)
Să găsim funcția u = u(x,c) ![]() Să găsim o soluție generală:
Să găsim o soluție generală: ![]() Să găsim o soluție particulară a ecuației care satisface condițiile inițiale y=1 la x=0:
Să găsim o soluție particulară a ecuației care satisface condițiile inițiale y=1 la x=0:

III. Ecuații diferențiale de ordin superior
3.1. Concepte de bază și definiții
O ecuație diferențială de ordinul doi este o ecuație care conține derivate nu mai mari decât ordinul doi. În cazul general, ecuația diferențială de ordinul doi se scrie astfel: F(x,y,y",y") = 0
Soluția generală a unei ecuații diferențiale de ordinul doi este o funcție de forma , care include două constante arbitrare C1Și C2.
O soluție particulară a unei ecuații diferențiale de ordinul doi este o soluție obținută din cea generală pentru unele valori ale constantelor arbitrare C1Și C2.
3.2. Ecuații diferențiale liniare omogene de ordinul doi cu rapoarte constante.
Ecuație diferențială liniară omogenă de ordinul doi cu coeficienți constanți se numește ecuație de formă y" + py" + qy = 0, Unde pȘi q sunt valori constante.
Algoritm pentru rezolvarea ecuațiilor diferențiale omogene de ordinul doi cu coeficienți constanți
1. Scrieți ecuația diferențială sub forma: y" + py" + qy = 0.
2. Compuneți ecuația sa caracteristică, notând y" prin r2, y" prin r, yîn 1: r2 + pr +q = 0
Rezolvarea ecuațiilor diferențiale. Mulțumiri noastre serviciu online puteți rezolva ecuații diferențiale de orice fel și complexitate: neomogene, omogene, neliniare, liniare, de ordinul întâi, al doilea, cu sau fără variabile separabile etc. Obțineți soluția ecuațiilor diferențiale în formă analitică cu descriere detaliata. Mulți sunt interesați de: de ce este necesar să se rezolve ecuații diferențiale online? Acest tip de ecuații este foarte frecvent în matematică și fizică, unde va fi imposibil să rezolvi multe probleme fără a calcula ecuația diferențială. De asemenea, ecuațiile diferențiale sunt comune în economie, medicină, biologie, chimie și alte științe. Rezolvarea unei astfel de ecuații online vă facilitează foarte mult sarcinile, face posibilă înțelegerea mai bună a materialului și testarea dvs. Beneficiile rezolvării ecuațiilor diferențiale online. Site-ul modern de servicii matematice vă permite să rezolvați ecuații diferențiale online orice dificultăți. După cum știți, există un numar mare de tipuri de ecuații diferențiale și fiecare dintre ele are propriile metode de rezolvare. Pe serviciul nostru puteți găsi online soluția ecuațiilor diferențiale de orice ordine și tip. Pentru a obține o soluție, vă sugerăm să completați datele inițiale și să faceți clic pe butonul „Soluție”. Sunt excluse erorile în funcționarea serviciului, astfel încât puteți fi 100% sigur că ați primit răspunsul corect. Rezolvați ecuații diferențiale cu serviciul nostru. Rezolvați ecuații diferențiale online. În mod implicit, într-o astfel de ecuație, funcția y este o funcție a variabilei x. Dar vă puteți seta, de asemenea, propria desemnare a variabilei. De exemplu, dacă specificați y(t) într-o ecuație diferențială, atunci serviciul nostru va determina automat că y este o funcție a variabilei t. Ordinea întregii ecuații diferențiale va depinde de ordinea maximă a derivatei funcției prezente în ecuație. A rezolva o astfel de ecuație înseamnă a găsi funcția necesară. Serviciul nostru vă va ajuta să rezolvați ecuații diferențiale online. Nu este nevoie de mult efort din partea ta pentru a rezolva ecuația. Trebuie doar să introduceți părțile din stânga și din dreapta ale ecuației în câmpurile necesare și să faceți clic pe butonul „Soluție”. Când introduceți derivata unei funcții, este necesar să o notați cu un apostrof. În câteva secunde vei avea solutie detaliata ecuație diferențială. Serviciul nostru este absolut gratuit. Ecuații diferențiale cu variabile separabile. Dacă într-o ecuație diferențială din stânga există o expresie care depinde de y, iar pe partea dreaptă există o expresie care depinde de x, atunci o astfel de ecuație diferențială se numește cu variabile separabile. Pe partea stângă poate exista o derivată a lui y, soluția ecuațiilor diferențiale de acest fel va fi sub forma unei funcții a lui y, exprimată prin integrala părții drepte a ecuației. Dacă există o diferență a unei funcții a lui y în partea stângă, atunci ambele părți ale ecuației sunt integrate. Când variabilele dintr-o ecuație diferențială nu sunt separate, ele vor trebui împărțite pentru a obține o ecuație diferențială separată. Ecuație diferențială liniară. O ecuație diferențială se numește liniară dacă funcția și toate derivatele ei sunt de gradul întâi. Forma generală ecuații: y'+a1(x)y=f(x). f(x) și a1(x) sunt funcții continue din x. Soluția ecuațiilor diferențiale de acest tip se reduce la integrarea a două ecuații diferențiale cu variabile separate. Ordinea ecuației diferențiale. Ecuația diferențială poate fi de ordinul întâi, al doilea, al n-a. Ordinea unei ecuații diferențiale determină ordinea celei mai mari derivate conținute în ea. În serviciul nostru puteți rezolva ecuații diferențiale mai întâi online, al doilea, al treilea etc. Ordin. Soluția ecuației va fi orice funcție y=f(x), înlocuind-o în ecuație, veți obține o identitate. Procesul de găsire a unei soluții la o ecuație diferențială se numește integrare. Problema Cauchy. Dacă, pe lângă ecuația diferențială în sine, este specificată condiția inițială y(x0)=y0, atunci aceasta se numește problema Cauchy. Indicatorii y0 și x0 se adaugă la soluția ecuației și se determină valoarea unei constante arbitrare C și apoi o soluție particulară a ecuației pentru această valoare a lui C. Aceasta este soluția problemei Cauchy. Problema Cauchy se mai numește și o problemă cu condiții la limită, care este foarte comună în fizică și mecanică. Aveți și ocazia să setați problema Cauchy, adică din toate solutii posibile din ecuație, alegeți un coeficient care îndeplinește condițiile inițiale date.
Ecuație diferențială (DE)
este ecuația,
unde sunt variabile independente, y este o funcție și sunt derivate parțiale.
Ecuație diferențială obișnuită este o ecuație diferențială care are o singură variabilă independentă, .
Ecuație diferențială parțială este o ecuație diferențială care are două sau mai multe variabile independente.
Cuvintele „ordinare” și „derivate parțiale” pot fi omise dacă este clar ce ecuație este luată în considerare. În cele ce urmează, sunt luate în considerare ecuațiile diferențiale obișnuite.
Ordinea ecuației diferențiale este ordinul celei mai mari derivate.
Iată un exemplu de ecuație de ordinul întâi:
Iată un exemplu de ecuație de ordinul al patrulea:
Uneori, o ecuație diferențială de ordinul întâi este scrisă în termeni de diferențiale:
În acest caz, variabilele x și y sunt egale. Adică, variabila independentă poate fi fie x, fie y. În primul caz, y este o funcție a lui x. În al doilea caz, x este o funcție a lui y. Dacă este necesar, putem aduce această ecuație într-o formă în care derivata y′ intră în mod explicit.
Împărțind această ecuație la dx, obținem:
.
Din moment ce și , rezultă că
.
Rezolvarea ecuațiilor diferențiale
Derivate din functii elementare sunt exprimate în termeni de funcţii elementare. Integralele funcțiilor elementare nu sunt adesea exprimate în termeni de funcții elementare. Cu ecuațiile diferențiale, situația este și mai proastă. Ca rezultat al soluției, puteți obține:
- dependența explicită a unei funcții de o variabilă;
Rezolvarea unei ecuații diferențiale este funcția y = u (X), care este definit, este de n ori diferențiabil și .
- dependenta implicita sub forma unei ecuatii de tip Φ (x, y) = 0 sau sisteme de ecuații;
Integrală a ecuației diferențiale este o soluție a unei ecuații diferențiale care are o formă implicită.
- dependența exprimată prin funcții elementare și integrale din acestea;
Rezolvarea unei ecuații diferențiale în cuadraturi - aceasta este găsirea unei soluții sub forma unei combinații de funcții elementare și integrale ale acestora.
- soluţia poate să nu fie exprimată în termeni de funcţii elementare.
Întrucât soluția ecuațiilor diferențiale se reduce la calculul integralelor, soluția include o mulțime de constante C 1 , C 2 , C 3 , ... C n . Numărul de constante este egal cu ordinea ecuației. Integrală parțială a unei ecuații diferențiale este integrala generală pentru valorile date ale constantelor C 1 , C 2 , C 3 , ... , C n .
Referinte:
V.V. Stepanov, Curs de ecuații diferențiale, LKI, 2015.
N.M. Gunther, R.O. Kuzmin, Culegere de probleme de matematică superioară, Lan, 2003.
6.1. CONCEPTE ȘI DEFINIȚII DE BAZĂ
La hotărâre diverse sarcini matematică și fizică, biologie și medicină, destul de des nu este posibil să se stabilească imediat o dependență funcțională sub forma unei formule care leagă variabile care descriu procesul studiat. De obicei, trebuie să folosim ecuații care conțin, pe lângă variabila independentă și funcția necunoscută, și derivatele acesteia.
Definiție. Se numește o ecuație care leagă o variabilă independentă, o funcție necunoscută și derivatele acesteia de diferite ordine diferenţial.
Funcția necunoscută este de obicei indicată y(x) sau pur și simplu y, iar derivatele sale sunt y", y" etc.
Sunt posibile și alte notații, de exemplu: dacă y= x(t), atunci x"(t), x""(t) sunt derivatele sale și t este o variabilă independentă.
Definiție. Dacă funcția depinde de o variabilă, atunci ecuația diferențială se numește obișnuită. Forma generală ecuație diferențială obișnuită:
sau
Funcții FȘi f poate să nu conțină unele argumente, dar pentru ca ecuațiile să fie diferențiale, prezența unei derivate este esențială.
Definiție.Ordinea ecuației diferențiale este ordinul celei mai mari derivate incluse în ea.
De exemplu, x 2 y"- y= 0, y" + sin X= 0 sunt ecuații de ordinul întâi și y"+ 2 y"+ 5 y= X este o ecuație de ordinul doi.
La rezolvarea ecuațiilor diferențiale se folosește operația de integrare, care este asociată cu apariția unei constante arbitrare. Dacă se aplică acţiunea de integrare n ori, atunci, evident, soluția va conține n constante arbitrare.
6.2. ECUAȚII DIFERENȚIALE DE ORDIN I
Forma generală ecuație diferențială de ordinul întâi este definit de expresia
Ecuația poate să nu conțină în mod explicit XȘi y, dar conține în mod necesar y”.
Dacă ecuația poate fi scrisă ca
atunci obținem o ecuație diferențială de ordinul întâi rezolvată în raport cu derivata.
Definiție. Soluția generală a ecuației diferențiale de ordinul întâi (6.3) (sau (6.4)) este mulțimea soluțiilor  , Unde CU este o constantă arbitrară.
, Unde CU este o constantă arbitrară.
Graficul pentru rezolvarea unei ecuații diferențiale se numește curba integrala.
Oferind o constantă arbitrară CU valori diferite, este posibil să se obțină anumite soluții. La suprafață xOy soluția generală este o familie de curbe integrale corespunzătoare fiecărei soluții particulare.
Dacă ai stabilit un punct A(x0, y0), prin care trebuie să treacă curba integrală, apoi, de regulă, din mulţimea funcţiilor ![]() unul poate fi evidențiat - o soluție specială.
unul poate fi evidențiat - o soluție specială.
Definiție.Decizie privată a unei ecuații diferențiale este soluția acesteia care nu conține constante arbitrare.
Dacă ![]() este o soluție generală, apoi din condiție
este o soluție generală, apoi din condiție
 poți găsi un permanent CU. Se numește condiția condiția inițială.
poți găsi un permanent CU. Se numește condiția condiția inițială.
Problema găsirii unei anumite soluții a unei ecuații diferențiale (6.3) sau (6.4) care satisface condiția inițială  la
la ![]() numit problema Cauchy. Această problemă are întotdeauna o soluție? Răspunsul este conținut în următoarea teoremă.
numit problema Cauchy. Această problemă are întotdeauna o soluție? Răspunsul este conținut în următoarea teoremă.
teorema lui Cauchy(teorema existenței și unicității soluției). Lăsați ecuația diferențială y"= f(x, y) funcţie f(x, y) si ea
derivat parțial  definită şi continuă în unele
definită şi continuă în unele
zone D, conţinând un punct  Apoi în zonă D există
Apoi în zonă D există
singura decizie ecuație care satisface condiția inițială ![]() la
la 
Teorema lui Cauchy afirmă că în anumite condiții există o curbă integrală unică y= f(x), trecând printr-un punct  Puncte în care nu sunt îndeplinite condițiile teoremei
Puncte în care nu sunt îndeplinite condițiile teoremei
Pisicile sunt numite special. Pauze în aceste puncte f(x, y) sau.
Fie mai multe curbe integrale trec printr-un punct singular, fie niciuna.
Definiție. Dacă soluția (6.3), (6.4) se găsește sub forma f(X y, c)= 0 nu este permis în raport cu y, atunci se numește integrală comună ecuație diferențială.
Teorema lui Cauchy garantează doar că există o soluție. Deoarece nu există o metodă unică pentru găsirea unei soluții, vom lua în considerare doar câteva tipuri de ecuații diferențiale de ordinul întâi care sunt integrabile în pătrate.
Definiție. Ecuația diferențială se numește integrabil în cuadraturi, dacă căutarea soluţiei sale se reduce la integrarea funcţiilor.
6.2.1. Ecuații diferențiale de ordinul întâi cu variabile separabile
Definiție. O ecuație diferențială de ordinul întâi se numește ecuație cu variabile separabile,
Partea dreaptă a ecuației (6.5) este produsul a două funcții, fiecare dintre ele depinde de o singură variabilă.
De exemplu, ecuația  este o ecuație cu separare
este o ecuație cu separare
trecerea variabilelor  și ecuația
și ecuația 
nu poate fi reprezentat sub forma (6.5).
Dat fiind  , rescriem (6.5) ca
, rescriem (6.5) ca 
Din această ecuație obținem o ecuație diferențială cu variabile separate, în care diferențialele conțin funcții care depind doar de variabila corespunzătoare:

Integrarea termen cu termen, avem

unde C= C 2 - C 1 este o constantă arbitrară. Expresia (6.6) este integrala generală a ecuației (6.5).
Împărțind ambele părți ale ecuației (6.5) la , putem pierde acele soluții pentru care,  Într-adevăr, dacă
Într-adevăr, dacă  la
la 
Acea  este evident o soluție a ecuației (6.5).
este evident o soluție a ecuației (6.5).
Exemplul 1 Găsiți o soluție satisfăcătoare a ecuației
condiție: y= 6 at X= 2 (y(2) = 6).
Soluţie. Să înlocuim la" pentru atunci  . Înmulțiți ambele părți cu
. Înmulțiți ambele părți cu
dx,întrucât în integrarea ulterioară este imposibil să plece dx la numitor:

iar apoi împărțind ambele părți la  obținem ecuația,
obținem ecuația,
care poate fi integrat. Integram: 

Apoi  ; potențarea, obținem y = C . (x + 1) - ob-
; potențarea, obținem y = C . (x + 1) - ob-
soluţie.
Pe baza datelor inițiale, determinăm o constantă arbitrară prin substituirea lor în soluția generală
În sfârșit, obținem y= 2(x + 1) este o soluție particulară. Luați în considerare câteva exemple de rezolvare a ecuațiilor cu variabile separabile.
Exemplul 2 Găsiți o soluție pentru ecuație 
Soluţie. Dat fiind  , primim
, primim  .
.
Integrând ambele părți ale ecuației, avem

Unde 
Exemplul 3 Găsiți o soluție pentru ecuație Soluţie.Împărțim ambele părți ale ecuației la acei factori care depind de o variabilă care nu coincide cu variabila sub semnul diferențial, adică prin ![]() și să integreze. Apoi primim
și să integreze. Apoi primim

și, în sfârșit

Exemplul 4 Găsiți o soluție pentru ecuație
Soluţie.Știind ce vom obține. Secțiune-
variabile lim. Apoi 

Integrarea, obținem

Cometariu.În exemplele 1 și 2, funcția dorită y exprimată în mod explicit (soluție generală). În exemplele 3 și 4 - implicit (integrală generală). Pe viitor, forma deciziei nu va fi specificată.
Exemplul 5 Găsiți o soluție pentru ecuație Soluţie.

Exemplul 6 Găsiți o soluție pentru ecuație  satisfăcător
satisfăcător
condiție voi)= 1.
Soluţie. Scriem ecuația sub forma 
Înmulțirea ambelor părți ale ecuației cu dxși mai departe, primim

Integrând ambele părți ale ecuației (integrala din partea dreaptă este luată pe părți), obținem 
Dar după condiție y= 1 la X= e. Apoi
Înlocuiți valorile găsite CUîntr-o soluție generală:

Expresia rezultată se numește o soluție particulară a ecuației diferențiale.
6.2.2. Ecuații diferențiale omogene de ordinul întâi
Definiție. Se numește ecuația diferențială de ordinul întâi omogen dacă poate fi reprezentat ca

Prezentăm un algoritm pentru rezolvarea unei ecuații omogene.
1. În schimb y introduceți o nouă funcție Apoi ![]() și, prin urmare
și, prin urmare 

2. Din punct de vedere al funcției u ecuația (6.7) ia forma
adică, înlocuirea reduce ecuația omogenă la o ecuație cu variabile separabile.
3. Rezolvând ecuația (6.8), găsim mai întâi u, apoi y= ux.
Exemplul 1 rezolva ecuatia  Soluţie. Scriem ecuația sub forma
Soluţie. Scriem ecuația sub forma
Facem o înlocuire:  Apoi
Apoi 
Să înlocuim 
Înmulțiți cu dx:  Împarte la Xși pe
Împarte la Xși pe  Apoi
Apoi

Integrând ambele părți ale ecuației în raport cu variabilele corespunzătoare, avem

sau, revenind la vechile variabile, ajungem în sfârșit

Exemplul 2rezolva ecuatia  Soluţie.Lăsa
Soluţie.Lăsa  Apoi
Apoi

Împărțiți ambele părți ale ecuației la x2:  Să deschidem parantezele și să rearanjam termenii:
Să deschidem parantezele și să rearanjam termenii:


Trecând la vechile variabile, ajungem la rezultatul final:

Exemplul 3Găsiți o soluție pentru ecuație  dat fiind
dat fiind

Soluţie.Efectuarea unei înlocuiri standard  primim
primim

sau 

sau

Deci soluția particulară are forma  Exemplul 4 Găsiți o soluție pentru ecuație
Exemplul 4 Găsiți o soluție pentru ecuație
Soluţie.

Exemplul 5Găsiți o soluție pentru ecuație  Soluţie.
Soluţie.

Muncă independentă
Găsiți o soluție pentru ecuații diferențiale cu variabile separabile (1-9).

Găsiți o soluție pentru ecuații diferențiale omogene (9-18).

6.2.3. Câteva aplicații ale ecuațiilor diferențiale de ordinul întâi
Problema dezintegrarii radioactive
Rata de descompunere a Ra (radiului) în fiecare moment de timp este proporțională cu masa sa disponibilă. Aflați legea dezintegrarii radioactive a lui Ra dacă se știe că la momentul inițial a existat Ra și timpul de înjumătățire al lui Ra este de 1590 de ani.
Soluţie. Fie în momentul de față masa Ra X= x(t) g, și  Atunci rata de dezintegrare a lui Ra este
Atunci rata de dezintegrare a lui Ra este

Conform sarcinii 
Unde k
Separând variabilele din ultima ecuație și integrând, obținem
Unde 
Pentru determinare C folosim condiția inițială: ![]() .
.
Apoi ![]() prin urmare,
prin urmare, 
Factorul de proporționalitate k determina din condiție suplimentară:
Avem
De aici  și formula dorită
și formula dorită

Problema ratei de reproducere a bacteriilor
Rata de reproducere a bacteriilor este proporțională cu numărul lor. La momentul inițial erau 100 de bacterii. În 3 ore numărul lor s-a dublat. Găsiți dependența de timp a numărului de bacterii. De câte ori va crește numărul bacteriilor în decurs de 9 ore?
Soluţie. Lăsa X- numărul de bacterii în acest moment t. Apoi, conform condiției, 
Unde k- coeficient de proporţionalitate.
De aici  Se ştie din condiţia că
Se ştie din condiţia că  . Mijloace,
. Mijloace,
Din condiția suplimentară  . Apoi
. Apoi
Funcția necesară: 
Deci, la t= 9 X= 800, adică în 9 ore numărul bacteriilor a crescut de 8 ori.
Sarcina de a crește cantitatea de enzimă
În cultura drojdiei de bere, rata de creștere a enzimei active este proporțională cu cantitatea sa inițială. X. Cantitatea inițială de enzimă A dublat într-o oră. Găsiți dependența
x(t).
Soluţie. După condiție, ecuația diferențială a procesului are forma 
de aici

Dar  . Mijloace, C= Ași apoi
. Mijloace, C= Ași apoi ![]()
Se mai stie ca 
Prin urmare,
6.3. ECUATII DIFERENTIALE DE ORDINUL AL DOILEA
6.3.1. Noțiuni de bază
Definiție.Ecuație diferențială de ordinul doi se numește relația care leagă variabila independentă, funcția dorită și derivatele sale prima și a doua.
În cazuri speciale, x poate fi absent în ecuație, la sau y". Totuşi, ecuaţia de ordinul doi trebuie să conţină în mod necesar y". În cazul general, ecuația diferențială de ordinul doi se scrie astfel:
sau, dacă este posibil, în forma permisă pentru derivata a doua:
Ca și în cazul unei ecuații de ordinul întâi, o ecuație de ordinul doi poate avea o soluție generală și una particulară. Soluția generală arată astfel:
Găsirea unei soluții private
în condiţii iniţiale – dat
număr) este numit problema Cauchy. Din punct de vedere geometric, aceasta înseamnă că este necesară găsirea curbei integrale la= y(x), trecând printr-un punct dat  și având o tangentă în acest punct, care este de aproximativ
și având o tangentă în acest punct, care este de aproximativ
furci cu direcție pozitivă a axei Bou unghi dat. e.  (Fig. 6.1). Problema Cauchy are o soluție unică dacă partea dreaptă a ecuației (6.10),
(Fig. 6.1). Problema Cauchy are o soluție unică dacă partea dreaptă a ecuației (6.10),  nepre-
nepre-
este discontinuă și are derivate parțiale continue în raport cu tu, tu"într-o vecinătate a punctului de plecare

Pentru a găsi constantă  inclus într-o anumită soluție, este necesar să se permită sistemul
inclus într-o anumită soluție, este necesar să se permită sistemul

Orez. 6.1. curba integrala

Fie deja rezolvate în raport cu derivata, fie pot fi rezolvate în raport cu derivata ![]() .
.
Rezolvarea generală a ecuațiilor diferențiale de tip pe interval X, care este dat, poate fi găsit luând integrala ambelor părți ale acestei egalități.
obține ![]() .
.
Privind proprietățile integrală nedefinită, atunci găsim soluția generală dorită:
y = F(x) + C,
Unde F(x)- unul dintre antiderivatele funcţiei f(x) intre X, A CU este o constantă arbitrară.
Vă rugăm să rețineți că în majoritatea sarcinilor intervalul X nu indica. Aceasta înseamnă că trebuie găsită o soluție pentru toată lumea. X, pentru care și funcția dorită y, iar ecuația originală are sens.
Dacă trebuie să calculați o anumită soluție a unei ecuații diferențiale care satisface condiția inițială y(x0) = y0, apoi după calcul integrală comună y = F(x) + C, este încă necesar să se determine valoarea constantei C=C0 folosind condiția inițială. Adică o constantă C=C0 determinată din ecuație F(x 0) + C = y 0, iar soluția particulară dorită a ecuației diferențiale va lua forma:
y = F(x) + C0.
Luați în considerare un exemplu:
Aflați soluția generală a ecuației diferențiale, verificați corectitudinea rezultatului. Să găsim o soluție particulară a acestei ecuații care să satisfacă condiția inițială .
Soluţie:
După ce am integrat ecuația diferențială dată, obținem:
![]() .
.
Luăm această integrală prin metoda integrării pe părți:

Acea.,  este o soluție generală a ecuației diferențiale.
este o soluție generală a ecuației diferențiale.
Să verificăm pentru a ne asigura că rezultatul este corect. Pentru a face acest lucru, înlocuim soluția pe care am găsit-o în ecuația dată:
 .
.
Adică la  ecuația inițială se transformă într-o identitate:
ecuația inițială se transformă într-o identitate:
prin urmare, soluția generală a ecuației diferențiale a fost determinată corect.
Soluția pe care am găsit-o este soluția generală a ecuației diferențiale pentru fiecare valoare reală a argumentului X.
Rămâne de calculat o anumită soluție a EDO care ar satisface condiția inițială. Cu alte cuvinte, este necesar să se calculeze valoarea constantei CU, la care egalitatea va fi adevărată:
 .
.
 .
.
Apoi, înlocuind C = 2în soluția generală a EDO, obținem o soluție particulară a ecuației diferențiale care satisface condiția inițială:
 .
.
Ecuație diferențială obișnuită ![]() se poate rezolva în raport cu derivata împărțind cele 2 părți ale ecuației la f(x). Această transformare va fi echivalentă dacă f(x) nu merge la zero pentru niciunul X din intervalul de integrare a ecuaţiei diferenţiale X.
se poate rezolva în raport cu derivata împărțind cele 2 părți ale ecuației la f(x). Această transformare va fi echivalentă dacă f(x) nu merge la zero pentru niciunul X din intervalul de integrare a ecuaţiei diferenţiale X.
Sunt probabile situații când, pentru unele valori ale argumentului X ∈ X funcții f(x)Și g(x) se întoarce la zero în același timp. Pentru valori similare X soluția generală a ecuației diferențiale este orice funcție y, care este definit în ele, deoarece .
Dacă pentru unele valori ale argumentului X ∈ X condiția este îndeplinită, ceea ce înseamnă că în acest caz ODE nu are soluții.
Pentru toate celelalte X din interval X soluția generală a ecuației diferențiale se determină din ecuația transformată.
Să ne uităm la exemple:
Exemplul 1
Să găsim soluția generală a EDO: ![]() .
.
Soluţie.
Din proprietățile funcțiilor elementare de bază, este clar că funcția de logaritm natural este definită pentru valorile nenegative ale argumentului, prin urmare, domeniul expresiei log(x+3) exista un interval X > -3 . Prin urmare, ecuația diferențială dată are sens pentru X > -3 . Cu aceste valori ale argumentului, expresiei x + 3 nu dispare, astfel încât se poate rezolva EDO în raport cu derivata împărțind cele 2 părți la x + 3.
Primim  .
.
În continuare, integrăm ecuația diferențială rezultată, rezolvată în raport cu derivata:  . Pentru a lua această integrală, folosim metoda subsumării sub semnul diferenţialului.
. Pentru a lua această integrală, folosim metoda subsumării sub semnul diferenţialului.