Die physikalische Bedeutung einer Tangente. Physikalische Bedeutung der Ableitungsfunktion

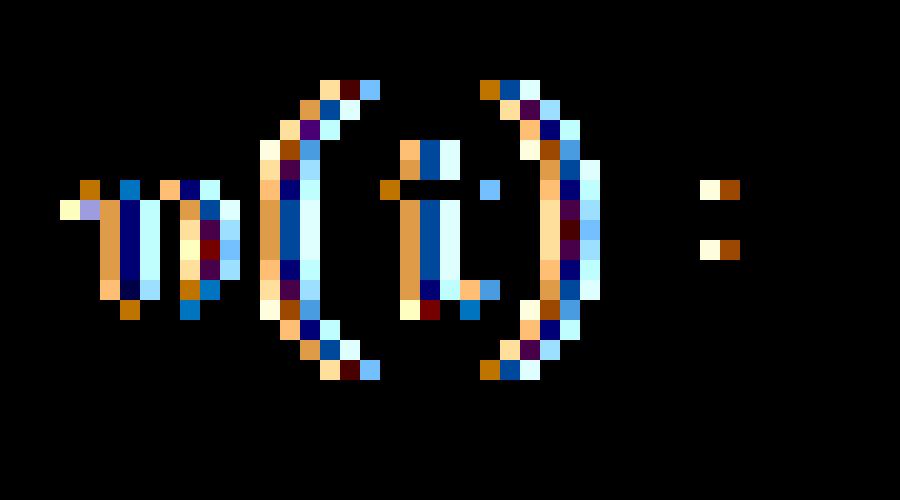
Lernziele:

Lehrreich:

• Schaffen Sie Bedingungen, damit die Schüler die physikalische Bedeutung der Ableitung sinnvoll verarbeiten können.
• Fördern Sie die Ausbildung von Fähigkeiten und Fertigkeiten praktischer Nutzen Derivat zur Lösung verschiedener physikalischer Probleme.

Lehrreich:

• Förderung der Entwicklung mathematischer Ansichten und kognitiven Interesses bei Studierenden durch Offenlegung der praktischen Notwendigkeit und theoretischen Bedeutung des Themas.
• Schaffen Sie Bedingungen für die Verbesserung der Denkfähigkeiten der Schüler: Vergleichen, Analysieren, Verallgemeinern.

Lehrreich:

• Fördern Sie das Interesse an Mathematik.

Unterrichtsart: Eine Lektion in der Beherrschung neuen Wissens.

Arbeitsformen: frontal, individuell, Gruppe.

Ausrüstung: Computer, interaktives Whiteboard, Präsentation, Lehrbuch.

Unterrichtsaufbau:

1. Zeit organisieren, ein Unterrichtsziel festlegen
2. Neues Material lernen
3. Primäre Konsolidierung von neuem Material
4. Selbstständige Arbeit
5. Zusammenfassung der Lektion. Betrachtung.

Während des Unterrichts

ICH. Organisatorischer Moment, Festlegung des Unterrichtsziels (2 Min.)

II. Neues Material lernen (10 Min.)

Lehrer: In den vorherigen Lektionen haben wir uns mit den Regeln zur Berechnung von Ableitungen vertraut gemacht und gelernt, Ableitungen von linearen Potenzen zu finden. trigonometrische Funktionen. Wir haben gelernt, was die geometrische Bedeutung einer Ableitung ist. Heute werden wir im Unterricht lernen, wo dieses Konzept in der Physik verwendet wird.

Erinnern Sie sich dazu an die Definition der Ableitung (Folie 2)

Kommen wir nun zum Physikkurs (Folie 3)

Die Schüler denken, merken sich physikalische Konzepte und Formeln.

Lassen Sie den Körper sich gemäß dem Gesetz bewegen S(t)= f(t) Betrachten Sie den Weg, den der Körper während der Zeit von t 0 bis t 0 + Δ t zurücklegt, wobei Δt das Inkrement des Arguments ist. Zum Zeitpunkt t 0 hat der Körper den Weg S(t 0) zurückgelegt, zum Zeitpunkt t 0 +Δt - den Weg S(t 0 +Δt). Daher hat der Körper während der Zeit Δt den Weg S(t 0 +Δt) – S(t 0) durchlaufen, d.h. Wir haben das Funktionsinkrement erhalten. Durchschnittsgeschwindigkeit Körperbewegungen während dieser Zeitspanne υ==

Je kürzer das Zeitintervall t, desto genauer können wir herausfinden, mit welcher Geschwindigkeit sich der Körper im Moment t bewegt. Nachdem wir t →0 gerichtet haben, erhalten wir die momentane Geschwindigkeit – den numerischen Wert der Geschwindigkeit im Moment t dieser Bewegung.

υ= , bei Δt→0 Geschwindigkeit ist die Ableitung des Weges nach der Zeit.

Folie 4

Erinnern wir uns an die Definition von Beschleunigung.

Anhand des oben präsentierten Materials können wir schließen, dass bei t a(t)= υ’(t) Beschleunigung ist eine Ableitung der Geschwindigkeit.

Als nächstes erscheinen auf der interaktiven Tafel Formeln für Stromstärke, Winkelgeschwindigkeit, EMK usw. Die Schüler addieren momentane Datenwerte physikalische Quantitäten durch das Konzept der Ableitung. (Bei Abwesenheit Interaktives Whiteboard Präsentation verwenden)

Folien 5-8

Die Studierenden formulieren das Fazit.

Abschluss:(Folie 9) Die Ableitung ist die Änderungsrate einer Funktion. (Funktionen von Weg, Koordinaten, Geschwindigkeit, magnetischem Fluss usw.)

υ (x)=f ’(x)

Lehrer: Wir sehen, dass der Zusammenhang zwischen den quantitativen Eigenschaften der unterschiedlichsten von der Physik untersuchten Prozesse, technische Wissenschaften, Chemie, ist analog zur Beziehung zwischen Weg und Geschwindigkeit. Sie können viele Probleme angeben, zu deren Lösung es auch erforderlich ist, die Änderungsrate einer bestimmten Funktion zu ermitteln, zum Beispiel: die Konzentration einer Lösung zu einem bestimmten Zeitpunkt zu ermitteln, die Strömungsgeschwindigkeit einer Flüssigkeit zu ermitteln, den Winkel Rotationsgeschwindigkeit eines Körpers, lineare Dichte an einem Punkt usw. Einige dieser Probleme werden wir nun lösen.

III. Festigen erworbener Kenntnisse (Gruppenarbeit) (15 Min.)

Anschließend Diskussion im Vorstand

Klären Sie vor der Lösung von Problemen die Maßeinheiten physikalischer Größen.

Geschwindigkeit – [m/s]
Beschleunigung – [m/s 2 ]
Stärke – [N]
Energie – [J]

Aufgabe 1 Gruppe

Der Punkt bewegt sich nach dem Gesetz s(t)=2t³-3t (s ist der Weg in Metern, t ist die Zeit in Sekunden). Berechnen Sie die Geschwindigkeit des Punktes und seine Beschleunigung zum Zeitpunkt 2s

Aufgabe 2 Gruppe

Das Schwungrad dreht sich um eine Achse nach dem Gesetz φ(t)= t 4 -5t. Finden Sie seine Winkelgeschwindigkeit ω zum Zeitpunkt 2s (φ ist der Drehwinkel im Bogenmaß, ω ist die Winkelgeschwindigkeit rad/s)

Aufgabe 3 Gruppe

Ein 2 kg schwerer Körper bewegt sich geradlinig nach dem Gesetz x(t)=2-3t+2t²

Ermitteln Sie die Geschwindigkeit des Körpers und seine kinetische Energie 3 s nach Beginn der Bewegung. Welche Kraft wirkt zu diesem Zeitpunkt auf den Körper? (t wird in Sekunden gemessen, x wird in Metern gemessen)

Aufgabe 4

Der Punkt führt oszillierende Bewegungen nach dem Gesetz x(t)=2sin3t aus. Beweisen Sie, dass die Beschleunigung proportional zur x-Koordinate ist.

IV. Unabhängige Lösung der Probleme Nr. 272, 274, 275, 277

[A. N. Kolmogorov, A. M. Abramov und andere. „Algebra und Anfänge der Analysis, Klassen 10-11“] 12 Min

Physikalische Bedeutung von Derivat. Das Einheitliche Staatsexamen in Mathematik umfasst eine Gruppe von Problemen, deren Lösung Kenntnisse und Verständnis der physikalischen Bedeutung der Ableitung erfordert. Insbesondere gibt es Probleme, bei denen das Bewegungsgesetz eines bestimmten Punktes (Objekts) durch eine Gleichung ausgedrückt wird und es erforderlich ist, seine Geschwindigkeit zu einem bestimmten Zeitpunkt der Bewegung oder zu der Zeit, nach der das Objekt bewegt wird, zu ermitteln wird eine bestimmte Geschwindigkeit erreichen.Die Aufgaben sind sehr einfach, sie können in einer Aktion gelöst werden. Also:

Gegeben sei das Bewegungsgesetz eines materiellen Punktes x (t) entlang der Koordinatenachse, wobei x die Koordinate des sich bewegenden Punktes und t die Zeit ist.

Die Geschwindigkeit zu einem bestimmten Zeitpunkt ist die Ableitung der Koordinate nach der Zeit. Dies ist die mechanische Bedeutung der Ableitung.

Ebenso ist die Beschleunigung die Ableitung der Geschwindigkeit nach der Zeit:

Die physikalische Bedeutung der Ableitung ist also Geschwindigkeit. Dies kann die Bewegungsgeschwindigkeit, die Änderungsrate eines Prozesses (z. B. das Wachstum von Bakterien), die Arbeitsgeschwindigkeit (usw.) sein, es gibt viele angewandte Probleme.

Darüber hinaus müssen Sie die Ableitungstabelle (Sie müssen sie genau wie die Multiplikationstabelle kennen) und die Differenzierungsregeln kennen. Konkret sind zur Lösung der genannten Probleme Kenntnisse der ersten sechs Ableitungen notwendig (siehe Tabelle):

Betrachten wir die Aufgaben:

x (t) = t 2 – 7t – 20

wobei x t die Zeit in Sekunden ist, gemessen vom Beginn der Bewegung an. Finden Sie seine Geschwindigkeit (in Metern pro Sekunde) zum Zeitpunkt t = 5 s.

Die physikalische Bedeutung einer Ableitung ist Geschwindigkeit (Bewegungsgeschwindigkeit, Änderungsgeschwindigkeit eines Prozesses, Arbeitsgeschwindigkeit usw.)

Finden wir das Gesetz der Geschwindigkeitsänderung: v (t) = x′(t) = 2t – 7 m/s.

Bei t = 5 haben wir:

Antwort: 3

Entscheide dich selbst:

Der materielle Punkt bewegt sich geradlinig nach dem Gesetz x (t) = 6t 2 – 48t + 17, wobei X- Entfernung vom Referenzpunkt in Metern, T- Zeit in Sekunden, gemessen ab Beginn der Bewegung. Finden Sie seine Geschwindigkeit (in Metern pro Sekunde) zum Zeitpunkt t = 9 s.

Der materielle Punkt bewegt sich geradlinig nach dem Gesetz x (t) = 0,5t 3 – 3t 2 + 2t, wo XT- Zeit in Sekunden, gemessen ab Beginn der Bewegung. Finden Sie seine Geschwindigkeit (in Metern pro Sekunde) zum Zeitpunkt t = 6 s.

Ein materieller Punkt bewegt sich gemäß dem Gesetz geradlinig

x (t) = –t 4 + 6t 3 + 5t + 23

Wo X- Entfernung vom Referenzpunkt in Metern,T- Zeit in Sekunden, gemessen ab Beginn der Bewegung. Finden Sie seine Geschwindigkeit (in Metern pro Sekunde) zum Zeitpunkt t = 3 s.

Ein materieller Punkt bewegt sich gemäß dem Gesetz geradlinig

x(t) = (1/6)t 2 + 5t + 28

Dabei ist x der Abstand vom Referenzpunkt in Metern, t die Zeit in Sekunden, gemessen vom Beginn der Bewegung an. Zu welchem ​​Zeitpunkt (in Sekunden) betrug seine Geschwindigkeit 6 m/s?

Finden wir das Gesetz der Geschwindigkeitsänderung:

Um herauszufinden, zu welchem ​​ZeitpunktTdie Geschwindigkeit 3 ​​m/s betrug, muss die Gleichung gelöst werden:

Antwort: 3

Entscheide dich selbst:

Der materielle Punkt bewegt sich geradlinig nach dem Gesetz x (t) = t 2 – 13t + 23, wobei X- Entfernung vom Referenzpunkt in Metern, T- Zeit in Sekunden, gemessen ab Beginn der Bewegung. Zu welchem ​​Zeitpunkt (in Sekunden) betrug seine Geschwindigkeit 3 ​​m/s?

Ein materieller Punkt bewegt sich gemäß dem Gesetz geradlinig

x (t) = (1/3) t 3 – 3t 2 – 5t + 3

Wo X- Entfernung vom Referenzpunkt in Metern, T- Zeit in Sekunden, gemessen ab Beginn der Bewegung. Zu welchem ​​Zeitpunkt (in Sekunden) betrug seine Geschwindigkeit 2 m/s?

Ich möchte darauf hinweisen, dass Sie sich beim Einheitlichen Staatsexamen nicht nur auf diese Art von Aufgaben konzentrieren sollten. Sie können völlig unerwartet Probleme aufwerfen, die das Gegenteil der dargestellten sind. Wenn das Gesetz der Geschwindigkeitsänderung gegeben ist und es darum geht, das Bewegungsgesetz zu finden.

Hinweis: In diesem Fall müssen Sie das Integral der Geschwindigkeitsfunktion finden (auch dies ist ein einstufiges Problem). Wenn Sie die zu einem bestimmten Zeitpunkt zurückgelegte Strecke ermitteln möchten, müssen Sie die Zeit in die resultierende Gleichung einsetzen und die Strecke berechnen. Wir werden jedoch auch solche Probleme analysieren, verpassen Sie es nicht!Ich wünsche Ihnen Erfolg!

Mit freundlichen Grüßen Alexander Krutitskikh.

P.S.: Ich wäre Ihnen dankbar, wenn Sie mir in den sozialen Netzwerken von der Seite erzählen würden.

Betrachten Sie den Graphen einer Funktion y = f(x).

Markieren wir darauf einen bestimmten Punkt A mit den Koordinaten (x, f(x)) und nicht weit davon entfernt einen Punkt B mit den Koordinaten (x+h, f(x+h). Zeichnen wir eine Gerade (AB) durch diese Punkte. Betrachten Sie den Ausdruck . Die Differenz f(x+h)-f(x) ist gleich dem Abstand BL und der Abstand AL ist gleich h. Das Verhältnis BL/AL ist der Tangens ε des Winkels – der Neigungswinkel der Geraden (AB). Stellen wir uns nun vor, dass der Wert von h sehr, sehr klein ist. Dann fällt die Gerade (AB) fast mit der Tangente am Punkt x an den Graphen der Funktion y = f(x) zusammen.

Lassen Sie uns also einige Definitionen geben.

Die Ableitung der Funktion y = f(x) am Punkt x heißt Grenzwert des Verhältnisses da h gegen Null geht. Sie schreiben:

Die geometrische Bedeutung der Ableitung ist der Tangens des Tangentenwinkels.

Die Ableitung hat auch eine physikalische Bedeutung. IN Grundschule Geschwindigkeit wurde als Distanz geteilt durch Zeit definiert. Allerdings in wahres Leben Die Geschwindigkeit beispielsweise eines Autos ist nicht während der gesamten Fahrt konstant. Der Weg sei eine Funktion der Zeit – S(t). Legen wir den Zeitpunkt t fest. In einem kurzen Zeitraum von t bis t+h wird das Auto den Weg S(t+h)-S(t) zurücklegen. Über einen kurzen Zeitraum hinweg ändert sich die Geschwindigkeit nicht wesentlich, daher können Sie die Geschwindigkeitsdefinition von verwenden Grundschule . Und da h gegen Null geht, ist dies die Ableitung.

Mathematische Probleme finden in vielen Wissenschaften Anwendung. Hierzu zählen nicht nur Physik, Chemie, Technik und Wirtschaftswissenschaften, sondern auch Medizin, Ökologie und weitere Disziplinen. Einer von wichtige Konzepte, die beherrscht werden muss, um Lösungen für wichtige Dilemmata zu finden, ist die Ableitung einer Funktion. Seine physikalische Bedeutung ist gar nicht so schwer zu erklären, wie es denjenigen erscheinen mag, die mit dem Wesen des Themas nicht vertraut sind. Sie müssen nur finden passende Beispiele dies im wirklichen Leben und in gewöhnlichen Alltagssituationen. Tatsächlich bewältigt jeder Autofahrer jeden Tag eine ähnliche Aufgabe, wenn er auf den Tacho schaut und die Geschwindigkeit seines Autos zu einem bestimmten Zeitpunkt ermittelt. Schließlich ist es genau dieser Parameter, der die Essenz der physikalischen Bedeutung der Ableitung enthält.

So finden Sie Geschwindigkeit

Jeder Fünftklässler kann die Geschwindigkeit einer Person auf der Straße leicht bestimmen, indem er die zurückgelegte Strecke und die Fahrzeit kennt. Teilen Sie dazu den ersten der angegebenen Werte durch den zweiten. Aber nicht jeder junge Mathematiker weiß das dieser Moment ermittelt das Verhältnis der Inkremente einer Funktion und ihres Arguments. Wenn Sie sich die Bewegung tatsächlich in Form eines Diagramms vorstellen, indem Sie den Weg entlang der Ordinatenachse und die Zeit entlang der Abszisse auftragen, wird es genau so sein.

Allerdings kann sich die Geschwindigkeit eines Fußgängers oder eines anderen Objekts, die wir über einen großen Abschnitt des Weges bestimmen und die Bewegung als gleichmäßig betrachten, durchaus ändern. In der Physik sind viele Bewegungsformen bekannt. Es kann nicht nur mit gemacht werden konstante Beschleunigung, sondern verlangsamen und erhöhen sich auf willkürliche Weise. Es ist zu beachten, dass in diesem Fall die die Bewegung beschreibende Linie keine Gerade mehr ist. Grafisch kann es die komplexesten Konfigurationen annehmen. Aber für jeden Punkt im Diagramm können wir immer eine Tangente zeichnen, dargestellt durch eine lineare Funktion.

Um den Parameter der Verschiebungsänderung in Abhängigkeit von der Zeit zu verdeutlichen, ist es notwendig, die gemessenen Segmente zu kürzen. Wenn sie verschwindend klein werden, ist die berechnete Geschwindigkeit augenblicklich. Diese Erfahrung hilft uns, eine Ableitung zu definieren. Aus solchen Überlegungen ergibt sich auch logisch seine physikalische Bedeutung.

Aus geometrischer Sicht

Es ist bekannt, dass je größer die Geschwindigkeit des Körpers ist, desto steiler ist der Graph der Zeitabhängigkeit der Verschiebung und damit der Neigungswinkel der Tangente an den Graphen an einem bestimmten Punkt. Ein Indikator für solche Änderungen kann der Tangens des Winkels zwischen der Abszissenachse und der Tangente sein. Genau dies bestimmt den Wert der Ableitung und errechnet sich aus dem Verhältnis der Längen der Gegenseite zur Nachbarseite in rechtwinkliges Dreieck, gebildet durch eine Senkrechte, die von einem bestimmten Punkt zur Abszissenachse fällt.

Dies ist die geometrische Bedeutung der ersten Ableitung. Der physikalische Aspekt offenbart sich darin, dass der Wert der gegenüberliegenden Seite in unserem Fall die zurückgelegte Strecke und die benachbarte Seite die Zeit darstellt. In diesem Fall ist ihr Verhältnis die Geschwindigkeit. Und wieder kommen wir zu dem Schluss, dass die Momentangeschwindigkeit, die bestimmt wird, wenn beide Intervalle zum Infinitesimalen tendieren, das Wesentliche ist und ihre physikalische Bedeutung anzeigt. Zweite Ableitung in in diesem Beispiel Es kommt zu einer Beschleunigung des Körpers, die wiederum den Grad der Geschwindigkeitsänderung anzeigt.

Beispiele für die Suche nach Ableitungen in der Physik

Die Ableitung ist ein Indikator für die Änderungsrate jeder Funktion, auch wenn es sich nicht um Bewegung im wörtlichen Sinne des Wortes handelt. Um dies deutlich zu veranschaulichen, hier einige konkrete Beispiele. Angenommen, die Stromstärke ändert sich mit der Zeit nach folgendem Gesetz: ICH= 0,4t 2 . Es ist erforderlich, den Wert der Geschwindigkeit zu ermitteln, mit der sich dieser Parameter am Ende der 8. Sekunde des Prozesses ändert. Beachten Sie, dass der gewünschte Wert selbst, wie aus der Gleichung hervorgeht, ständig zunimmt.

Zur Lösung ist es notwendig, die erste Ableitung zu finden, deren physikalische Bedeutung bereits zuvor besprochen wurde. Hier dI/ dt = 0,8 T. Als nächstes finden wir es unter T=8 , stellen wir fest, dass die Rate, mit der die Stromänderungen auftreten, gleich ist 6,4 A/ C. Hierbei wird davon ausgegangen, dass die Stromstärke in Ampere und die Zeit dementsprechend in Sekunden gemessen wird.

Alles ist veränderbar

Sichtbar die Umwelt, bestehend aus Materie, unterliegt ständigen Veränderungen und ist in der Bewegung verschiedener darin ablaufender Prozesse. Zur Beschreibung können verschiedene Parameter herangezogen werden. Wenn sie durch eine Abhängigkeit verbunden sind, werden sie mathematisch in Form einer Funktion geschrieben, die ihre Änderungen deutlich zeigt. Und wo Bewegung ist (in welcher Form sie auch immer ausgedrückt werden mag), gibt es auch eine Ableitung, über deren physikalische Bedeutung wir uns gerade Gedanken machen.

Im folgenden Beispiel geht es darum. Nehmen wir an, die Körpertemperatur ändert sich gemäß dem Gesetz T=0,2 T 2 . Sie sollten die Aufheizgeschwindigkeit am Ende der 10. Sekunde ermitteln. Die Lösung des Problems erfolgt auf ähnliche Weise wie im vorherigen Fall beschrieben. Das heißt, wir finden die Ableitung und ersetzen sie durch den Wert T= 10 , wir bekommen T= 0,4 T= 4. Dies bedeutet, dass die endgültige Antwort 4 Grad pro Sekunde beträgt, d. h. der Erwärmungsprozess und die Temperaturänderung, gemessen in Grad, erfolgen mit genau dieser Geschwindigkeit.

Praktische Probleme lösen

Natürlich kann im wirklichen Leben alles viel komplizierter sein als bei theoretischen Problemen. In der Praxis wird der Wert von Mengen meist im Rahmen eines Experiments ermittelt. In diesem Fall werden Instrumente verwendet, die bei Messungen mit einem bestimmten Fehler Messwerte liefern. Daher muss man sich bei der Berechnung mit Näherungswerten der Parameter auseinandersetzen und auf Rundungen unbequemer Zahlen sowie andere Vereinfachungen zurückgreifen. Nachdem wir dies berücksichtigt haben, gehen wir noch einmal zu Problemen über die physikalische Bedeutung der Ableitung über, wobei wir berücksichtigen, dass es sich lediglich um eine Art mathematisches Modell der komplexesten Prozesse in der Natur handelt.

Vulkanausbruch

Stellen wir uns vor, dass ein Vulkan ausbricht. Wie gefährlich kann er sein? Um dieses Problem zu klären, müssen viele Faktoren berücksichtigt werden. Wir werden versuchen, einen davon zu berücksichtigen.

Aus dem Mund des „Feuermonsters“ werden Steine ​​senkrecht nach oben geschleudert, wobei sie vom Moment ihres Herauskommens an eine Anfangsgeschwindigkeit haben. Es muss berechnet werden, welche maximale Höhe sie erreichen können.

Um den gewünschten Wert zu finden, erstellen wir eine Gleichung für die Abhängigkeit der Höhe H, gemessen in Metern, von anderen Werten. Dazu gehören Anfangsgeschwindigkeit und -zeit. Wir gehen davon aus, dass der Beschleunigungswert bekannt ist und ungefähr 10 m/s 2 beträgt.

Partielle Ableitung

Betrachten wir nun die physikalische Bedeutung der Ableitung einer Funktion aus einem etwas anderen Blickwinkel, da die Gleichung selbst möglicherweise nicht eine, sondern mehrere Variablen enthält. Beispielsweise wurde im vorherigen Problem die Abhängigkeit der Höhe des Aufstiegs von Steinen, die aus der Mündung eines Vulkans geschleudert wurden, nicht nur durch eine Änderung der Zeiteigenschaften, sondern auch durch den Wert der Anfangsgeschwindigkeit bestimmt. Letzterer galt als konstanter, fester Wert. Aber bei anderen Problemen mit ganz anderen Voraussetzungen könnte alles anders sein. Wenn die Mengen, auf die es ankommt komplexe Funktion, mehrere, Berechnungen werden gemäß den folgenden Formeln durchgeführt.

Die physikalische Bedeutung der häufigen Ableitung sollte wie im Normalfall ermittelt werden. Dies ist die Änderungsrate einer Funktion an einem bestimmten Punkt, wenn der Parameter der Variablen zunimmt. Sie wird so berechnet, dass alle anderen Komponenten als Konstanten angenommen werden, nur eine wird als Variable betrachtet. Dann läuft alles nach den üblichen Regeln ab.

Wenn man die physikalische Bedeutung der Ableitung versteht, ist es nicht schwer, Beispiele für die Lösung komplizierter und komplexer Probleme zu nennen, deren Antwort mit diesem Wissen gefunden werden kann. Wenn wir eine Funktion haben, die den Kraftstoffverbrauch in Abhängigkeit von der Geschwindigkeit des Autos beschreibt, können wir berechnen, bei welchen Parametern des letzteren der Benzinverbrauch am geringsten ist.

In der Medizin lässt sich vorhersagen, wie der menschliche Körper auf ein vom Arzt verschriebenes Medikament reagiert. Die Einnahme des Arzneimittels beeinflusst verschiedene physiologische Indikatoren. Dazu gehören Veränderungen des Blutdrucks, der Herzfrequenz, der Körpertemperatur und mehr. Sie hängen alle von der eingenommenen Dosis ab Medizin. Diese Berechnungen helfen, den Behandlungsverlauf vorherzusagen, sowohl bei günstigen Erscheinungsformen als auch bei unerwünschten Ereignissen, die sich fatal auf Veränderungen im Körper des Patienten auswirken können.

Zweifellos ist es wichtig, die physikalische Bedeutung der Ableitung in technischen Angelegenheiten zu verstehen, insbesondere in der Elektrotechnik, Elektronik, Design und Konstruktion.

Bremswege

Betrachten wir das nächste Problem. Das mit konstanter Geschwindigkeit fahrende Auto, das sich der Brücke näherte, musste 10 Sekunden vor der Einfahrt abbremsen, wie der Fahrer bemerkte Verkehrszeichen, das Fahren mit Geschwindigkeiten über 36 km/h verbietet. Hat der Fahrer gegen die Regeln verstoßen, wenn sein Bremsweg durch die Formel S = 26t - t 2 beschrieben werden kann?

Nachdem wir die erste Ableitung berechnet haben, finden wir eine Formel für die Geschwindigkeit, wir erhalten v = 28 - 2t. Als nächstes ersetzen wir den Wert t=10 in den angegebenen Ausdruck.

Da dieser Wert in Sekunden ausgedrückt wurde, ergibt sich eine Geschwindigkeit von 8 m/s, also 28,8 km/h. Daraus lässt sich erkennen, dass der Fahrer rechtzeitig mit der Bremsung begonnen hat und nicht gegen die Verkehrsregeln und damit gegen die auf dem Schild angegebene Geschwindigkeitsbegrenzung verstoßen hat.

Dies beweist die Bedeutung der physikalischen Bedeutung der Ableitung. Ein Beispiel zur Lösung dieses Problems zeigt am deutlichsten, wie vielfältig dieses Konzept ist verschiedene Bereiche Leben. Auch in alltäglichen Situationen.

Ableitung in der Wirtschaftswissenschaft

Bis zum 19. Jahrhundert arbeiteten Ökonomen hauptsächlich mit Durchschnittswerten, sei es die Arbeitsproduktivität oder der Preis hergestellter Produkte. Doch irgendwann wurden Grenzwerte notwendiger, um in diesem Bereich sinnvolle Prognosen erstellen zu können. Diese beinhalten Grenznutzen, Einnahmen oder Kosten. Diese Erkenntnis gab den Anstoß zur Schaffung eines völlig neuen Instruments der Wirtschaftsforschung, das seit mehr als hundert Jahren existiert und weiterentwickelt wird.

Um solche Berechnungen zu erstellen, bei denen Konzepte wie Minimum und Maximum dominieren, ist es lediglich notwendig, die geometrische und physikalische Bedeutung der Ableitung zu verstehen. Unter den Schöpfern theoretische Basis Zu diesen Disziplinen zählen so prominente englische und österreichische Ökonomen wie W. S. Jevons, K. Menger und andere. Natürlich ist es nicht immer praktisch, in wirtschaftlichen Berechnungen Grenzwerte zu verwenden. Und zum Beispiel passen vierteljährliche Berichte nicht unbedingt in das bestehende Schema, dennoch ist die Anwendung einer solchen Theorie in vielen Fällen sinnvoll und effektiv.

Die Ableitung der Funktion f (x) am Punkt x0 ist die Grenze (falls vorhanden) des Verhältnisses des Inkrements der Funktion am Punkt x0 zum Inkrement des Arguments Δx, wenn das Inkrement des Arguments dazu tendiert Null und wird mit f '(x0) bezeichnet. Das Finden der Ableitung einer Funktion wird Differenzierung genannt.
Die Ableitung einer Funktion hat folgende physikalische Bedeutung: die Ableitung einer Funktion in angegebenen Punkt- Änderungsrate der Funktion an einem bestimmten Punkt.

Geometrische Bedeutung der Ableitung. Die Ableitung am Punkt x0 ist gleich Neigung Tangente an den Graphen der Funktion y=f(x) an diesem Punkt.

Physikalische Bedeutung von Derivat. Wenn sich ein Punkt entlang der x-Achse bewegt und sich seine Koordinate gemäß dem Gesetz x(t) ändert, dann beträgt die Momentangeschwindigkeit des Punktes:

Das Konzept des Differentials, seine Eigenschaften. Differenzierungsregeln. Beispiele.

Definition. Das Differential einer Funktion an einem Punkt x ist der lineare Hauptteil des Inkrements der Funktion. Das Differential der Funktion y = f(x) ist gleich dem Produkt seiner Ableitung und dem Inkrement der unabhängigen Variablen x ( Streit).

Es ist so geschrieben:

oder

Oder


Differenzielle Eigenschaften
Das Differential hat ähnliche Eigenschaften wie die Ableitung:





ZU Grundregeln der Differenzierung enthalten:
1) Platzieren eines konstanten Faktors außerhalb des Vorzeichens der Ableitung
2) Ableitung einer Summe, Ableitung einer Differenz
3) Ableitung des Funktionsprodukts
4) Ableitung des Quotienten zweier Funktionen (Ableitung eines Bruchs)

Beispiele.
Beweisen wir die Formel: Per Definition der Ableitung gilt:

Über das Vorzeichen des Grenzübergangs hinaus kann daher ein beliebiger Faktor angenommen werden (dies ist aus den Eigenschaften des Grenzübergangs bekannt).

Zum Beispiel: Finden Sie die Ableitung einer Funktion
Lösung: Wenden wir die Regel an, den Multiplikator außerhalb des Vorzeichens der Ableitung zu platzieren :

Sehr oft ist es notwendig, zunächst die Form der differenzierbaren Funktion zu vereinfachen, um die Ableitungstabelle und die Regeln zum Auffinden von Ableitungen verwenden zu können. Die folgenden Beispiele bestätigen dies deutlich.

Differenzierungsformeln. Anwendung des Differentials in Näherungsberechnungen. Beispiele.

Durch die Verwendung eines Differentials in Näherungsberechnungen können Sie ein Differential verwenden, um die Werte einer Funktion anzunähern.
Beispiele.
Berechnen Sie anhand des Differentials ungefähr
Berechnen gegebener Wert Wenden wir die Formel aus der Theorie an
Lassen Sie uns eine Funktion in Betracht ziehen und den gegebenen Wert in der Form darstellen
dann lasst uns rechnen

Wenn wir alles in die Formel einsetzen, erhalten wir schließlich
Antwort:

16. L'Hopitals Regel zur Offenlegung von Unsicherheiten der Form 0/0 oder ∞/∞. Beispiele.
Grenze des Verhältnisses von zwei Infinitesimalen oder zwei Infinitesimalen große Mengen ist gleich der Grenze des Verhältnisses ihrer Ableitungen.

1)

17. Zunehmende und abnehmende Funktion. Extremum der Funktion. Algorithmus zur Untersuchung einer Funktion auf Monotonie und Extremum. Beispiele.

Funktion erhöht sich auf einem Intervall, wenn für zwei beliebige Punkte dieses Intervalls, die durch die Beziehung verbunden sind, die Ungleichung wahr ist. Also, höherer Wert Das Argument entspricht einem größeren Wert der Funktion und sein Diagramm verläuft „von unten nach oben“. Die Demonstrationsfunktion nimmt im Laufe des Intervalls zu

Ebenso die Funktion nimmt ab auf einem Intervall, wenn für zwei beliebige Punkte eines gegebenen Intervalls, so dass die Ungleichung wahr ist. Das heißt, ein größerer Wert des Arguments entspricht einem kleineren Wert der Funktion und ihr Diagramm verläuft „von oben nach unten“. Unsere nimmt in Abständen ab, nimmt in Abständen ab .

Extreme Ein Punkt wird als Maximalpunkt der Funktion y=f(x) bezeichnet, wenn die Ungleichung für alle x in seiner Umgebung gilt. Der Wert der Funktion am Maximalpunkt wird aufgerufen Maximum der Funktion und bezeichnen.
Ein Punkt heißt Minimalpunkt der Funktion y=f(x), wenn die Ungleichung für alle x in seiner Umgebung gilt. Der Wert der Funktion am Minimalpunkt wird aufgerufen minimale Funktion und bezeichnen.
Unter der Umgebung eines Punktes versteht man das Intervall , wobei eine ausreichend kleine positive Zahl ist.
Die minimalen und maximalen Punkte werden als Extrempunkte bezeichnet, und die den Extrempunkten entsprechenden Funktionswerte werden als Extrempunkte bezeichnet Extrema der Funktion.

Um die Funktion zu erkunden zur Monotonie, verwenden Sie das folgende Schema:
- Finden Sie den Definitionsbereich der Funktion;
- Finden Sie die Ableitung der Funktion und den Definitionsbereich der Ableitung;
- Finden Sie die Nullstellen der Ableitung, d.h. der Wert des Arguments, bei dem die Ableitung gleich Null ist;
- Markieren Sie die Zahlenstrahlen allgemeiner Teil der Definitionsbereich einer Funktion und der Definitionsbereich ihrer Ableitung und darauf - die Nullstellen der Ableitung;
- Bestimmen Sie die Vorzeichen der Ableitung für jedes der resultierenden Intervalle;
- Bestimmen Sie anhand der Vorzeichen der Ableitung, in welchen Intervallen die Funktion zunimmt und in welchen sie abnimmt;
- Schreiben Sie die entsprechenden Intervalle durch Semikolons getrennt.

Forschungsalgorithmus kontinuierliche Funktion y = f(x) für Monotonie und Extrema:
1) Finden Sie die Ableitung f ′(x).
2) Finden Sie stationäre (f ′(x) = 0) und kritische (f ′(x) existiert nicht) Punkte der Funktion y = f(x).
3) Markieren Sie stationäre und kritische Punkte auf der Zahlengeraden und bestimmen Sie die Vorzeichen der Ableitung auf den resultierenden Intervallen.
4) Ziehen Sie Rückschlüsse auf die Monotonie der Funktion und ihrer Extrempunkte.

18. Konvexität der Funktion. Wendepunkte. Algorithmus zum Studieren einer Funktion für Konvexität (Konkavität) Beispiele.

konvex nach unten auf dem X-Intervall, wenn sein Graph an keinem Punkt des X-Intervalls tiefer als die Tangente an ihn liegt.

Die zu differenzierende Funktion wird aufgerufen konvex nach oben auf dem X-Intervall, wenn sein Graph an keinem Punkt im X-Intervall höher liegt als die Tangente an ihn.

Die Punktformel heißt Wendepunkt des Diagramms Funktion y=f(x), wenn an einem bestimmten Punkt eine Tangente an den Graphen der Funktion vorhanden ist (sie kann parallel zur Oy-Achse sein) und es eine solche Nachbarschaft des Formelpunkts gibt, innerhalb derer nach links und rechts des Punktes M hat der Graph der Funktion unterschiedliche Konvexitätsrichtungen.

Intervalle für Konvexität finden:

Wenn die Funktion y=f(x) eine endliche zweite Ableitung im Intervall X hat und wenn die Ungleichung gilt (), dann hat der Graph der Funktion bei X eine nach unten (oben) gerichtete Konvexität.
Mit diesem Satz können Sie die Konkavitäts- und Konvexitätsintervalle einer Funktion ermitteln; Sie müssen lediglich die Ungleichungen bzw. im Definitionsbereich der ursprünglichen Funktion lösen.

Beispiel: Finden Sie die Intervalle heraus, in denen der Graph der Funktion liegt. Finden Sie die Intervalle heraus, in denen der Graph der Funktion liegt hat eine nach oben gerichtete Konvexität und eine nach unten gerichtete Konvexität. hat eine nach oben gerichtete Konvexität und eine nach unten gerichtete Konvexität.
Lösung: Der Definitionsbereich dieser Funktion ist die gesamte Menge der reellen Zahlen.
Finden wir die zweite Ableitung.

Der Definitionsbereich der zweiten Ableitung fällt mit dem Definitionsbereich der ursprünglichen Funktion zusammen. Um die Konkavitäts- und Konvexitätsintervalle herauszufinden, reicht es daher aus, und dementsprechend zu lösen. Daher ist die Funktion in der Intervallformel nach unten konvex und in der Intervallformel nach oben konvex.

19) Asymptoten der Funktion. Beispiele.

Die Gerade heißt vertikale Asymptote Graph einer Funktion, wenn mindestens einer von Grenzwerte oder gleich oder .

Kommentar. Eine Gerade kann keine vertikale Asymptote sein, wenn die Funktion im Punkt stetig ist. Daher sollten vertikale Asymptoten an den Unstetigkeitspunkten der Funktion gesucht werden.

Die Gerade heißt horizontale Asymptote Graph der Funktion, wenn mindestens einer der Grenzwerte oder gleich ist.

Kommentar. Der Graph einer Funktion kann nur eine rechte oder nur eine linke horizontale Asymptote haben.

Die Gerade heißt schräge Asymptote Funktionsgraph wenn

BEISPIEL:

Übung. Finden Sie Asymptoten des Graphen einer Funktion

Lösung. Funktionsumfang:

a) vertikale Asymptoten: Gerade - vertikale Asymptote, da

b) horizontale Asymptoten: Wir finden den Grenzwert der Funktion im Unendlichen:

das heißt, es gibt keine horizontalen Asymptoten.

c) schräge Asymptoten:

Somit ist die schräge Asymptote: .

Antwort. Die vertikale Asymptote ist gerade.

Die schräge Asymptote ist gerade.

20) Allgemeines Schema Erforschung der Funktion und Zeichnen des Diagramms. Beispiel.

A.
Finden Sie die ODZ- und Diskontinuitätspunkte der Funktion.

B. Finden Sie die Schnittpunkte des Funktionsgraphen mit den Koordinatenachsen.

2. Führen Sie eine Untersuchung der Funktion mit der ersten Ableitung durch, d. h. ermitteln Sie die Extrempunkte der Funktion und die Intervalle der Zunahme und Abnahme.

3. Untersuchen Sie die Funktion mithilfe der Ableitung zweiter Ordnung, d. h. finden Sie die Wendepunkte des Funktionsgraphen und die Intervalle seiner Konvexität und Konkavität.

4. Finden Sie die Asymptoten des Funktionsgraphen: a) vertikal, b) schräg.

5. Erstellen Sie auf der Grundlage der Recherche einen Graphen der Funktion.

Beachten Sie, dass es vor dem Zeichnen eines Diagramms nützlich ist, zu bestimmen, ob eine bestimmte Funktion ungerade oder gerade ist.

Denken Sie daran, dass eine Funktion auch dann aufgerufen wird, wenn eine Änderung des Vorzeichens des Arguments den Wert der Funktion nicht ändert: f(-x) = f(x) und eine Funktion heißt ungerade wenn f(-x) = -f(x).

In diesem Fall reicht es aus, die Funktion zu untersuchen und ihren Graphen zu zeichnen positive Werte Argumente der ODZ. Für negative Werte des Arguments wird der Graph auf der Grundlage vervollständigt, dass er für eine gerade Funktion symmetrisch zur Achse ist Oy und für ungerade relativ zum Ursprung.

Beispiele. Erkunden Sie Funktionen und erstellen Sie ihre Diagramme.

Funktionsdomäne D(y)= (–∞; +∞). Es gibt keine Bruchstellen.

Schnittpunkt mit Achse Ochse: X = 0,y= 0.

Die Funktion ist ungerade und kann daher nur auf dem Intervall untersucht werden.