Allgemeines Schema zum Studieren einer Funktion und zum Erstellen eines Diagramms online. Untersuchung einer Funktion mit Methoden der Differentialrechnung
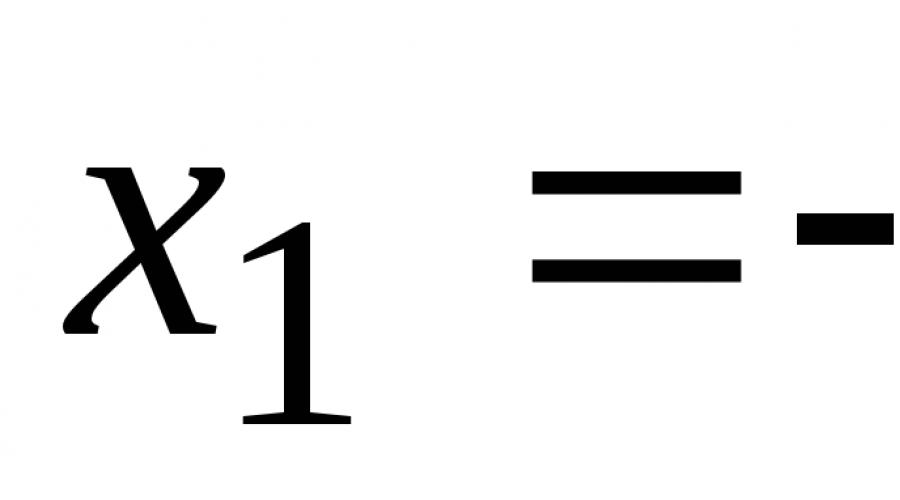
Lesen Sie auch
Das Studium einer Funktion erfolgt nach einem klaren Schema und erfordert vom Studierenden solide Kenntnisse grundlegender mathematischer Konzepte wie Definitions- und Wertebereich, Kontinuität der Funktion, Asymptote, Extrempunkte, Parität, Periodizität usw . Der Studierende muss in der Lage sein, Funktionen frei zu differenzieren und Gleichungen zu lösen, die teilweise sehr komplex sein können.
Das heißt, diese Aufgabe testet eine erhebliche Wissensschicht, wobei jede Lücke, die darin besteht, zu einem Hindernis für den Erwerb wird die richtige Entscheidung. Besonders häufig treten Schwierigkeiten bei der Erstellung von Funktionsgraphen auf. Dieser Fehler fällt dem Lehrer sofort auf und kann Ihrer Note großen Schaden zufügen, selbst wenn alles andere richtig gemacht wurde. Hier kannst du finden Probleme bei der Online-Funktionsforschung: Studienbeispiele, Download-Lösungen, Bestellaufträge.
Erkunden Sie eine Funktion und zeichnen Sie ein Diagramm: Beispiele und Lösungen online
Wir haben für Sie viele vorgefertigte Funktionsstudien vorbereitet, sowohl kostenpflichtig im Lösungsbuch als auch kostenlos im Abschnitt Beispiele für Funktionsstudien. Anhand dieser gelösten Aufgaben können Sie sich detailliert mit der Methodik zur Durchführung ähnlicher Aufgaben vertraut machen und Ihre Recherche analog durchführen.
Wir bieten vorgefertigte Beispiele vollständige Untersuchung und Darstellung von Funktionen der gängigsten Typen: Polynome, gebrochene rationale, irrationale, exponentielle, logarithmische, trigonometrische Funktionen. Jedem gelösten Problem liegt ein vorgefertigter Graph mit hervorgehobenen Schlüsselpunkten, Asymptoten, Maxima und Minima bei; die Lösung erfolgt mithilfe eines Algorithmus zur Untersuchung der Funktion.
In jedem Fall werden Ihnen die gelösten Beispiele eine große Hilfe sein, da sie die gängigsten Funktionstypen abdecken. Wir bieten Ihnen Hunderte bereits gelöster Probleme, aber wie Sie wissen, gibt es auf der Welt unendlich viele mathematische Funktionen, und Lehrer sind große Experten darin, immer schwierigere Aufgaben für arme Schüler zu erfinden. Also, liebe Studierende, qualifizierte Hilfe wird Ihnen nicht schaden.
Lösung benutzerdefinierter Funktionsforschungsprobleme
In diesem Fall bieten Ihnen unsere Partner einen weiteren Service an - Vollständige Funktionsrecherche online auf Bestellung. Die Aufgabe wird für Sie unter Einhaltung aller Anforderungen an einen Algorithmus zur Lösung solcher Probleme erledigt, was Ihrem Lehrer sehr gefallen wird.
Wir führen für Sie eine vollständige Untersuchung der Funktion durch: Wir finden den Definitionsbereich und den Wertebereich, prüfen auf Kontinuität und Diskontinuität, stellen Parität her, überprüfen Ihre Funktion auf Periodizität und finden die Schnittpunkte mit den Koordinatenachsen . Und natürlich weiter mit der Hilfe Differentialrechnung: Wir werden Asymptoten finden, Extrema und Wendepunkte berechnen und den Graphen selbst konstruieren.
Die Wahrung Ihrer Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Daten verwenden und speichern. Bitte lesen Sie unsere Datenschutzpraktiken durch und teilen Sie uns mit, wenn Sie Fragen haben.
Erhebung und Nutzung personenbezogener Daten
Unter personenbezogenen Daten versteht man Daten, die dazu genutzt werden können, eine bestimmte Person zu identifizieren oder mit ihr in Kontakt zu treten.
Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie mit uns Kontakt aufnehmen.
Nachfolgend finden Sie einige Beispiele für die Arten personenbezogener Daten, die wir möglicherweise sammeln, und wie wir diese Informationen verwenden können.
Welche personenbezogenen Daten erfassen wir:
- Wenn Sie auf der Website eine Bewerbung einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer, Ihrer E-Mail-Adresse usw.
Wie wir Ihre persönlichen Daten verwenden:
- Die von uns erfassten personenbezogenen Daten ermöglichen es uns, Sie mit einzigartigen Angeboten, Werbeaktionen und anderen Veranstaltungen sowie bevorstehenden Veranstaltungen zu kontaktieren.
- Von Zeit zu Zeit können wir Ihre persönlichen Daten verwenden, um wichtige Mitteilungen und Mitteilungen zu versenden.
- Wir können personenbezogene Daten auch für interne Zwecke verwenden, beispielsweise zur Durchführung von Audits, Datenanalysen und verschiedenen Forschungsarbeiten, um die von uns bereitgestellten Dienste zu verbessern und Ihnen Empfehlungen zu unseren Diensten zu geben.
- Wenn Sie an einer Verlosung, einem Wettbewerb oder einer ähnlichen Aktion teilnehmen, können wir die von Ihnen bereitgestellten Informationen zur Verwaltung solcher Programme verwenden.
Weitergabe von Informationen an Dritte
Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.
Ausnahmen:
- Falls erforderlich, in Übereinstimmung mit dem Gesetz, Gerichtsverfahren, in Gerichtsverfahren und/oder auf der Grundlage öffentlicher Anfragen oder Anfragen von Regierungsbehörden in der Russischen Föderation – um Ihre personenbezogenen Daten offenzulegen. Wir können auch Informationen über Sie offenlegen, wenn wir zu dem Schluss kommen, dass eine solche Offenlegung aus Sicherheits-, Strafverfolgungs- oder anderen Gründen von öffentlicher Bedeutung notwendig oder angemessen ist.
- Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den jeweiligen Nachfolger-Dritten weitergeben.
Schutz personenbezogener Daten
Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer –, um Ihre persönlichen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung zu schützen.
Respektieren Sie Ihre Privatsphäre auf Unternehmensebene
Um sicherzustellen, dass Ihre persönlichen Daten sicher sind, kommunizieren wir Datenschutz- und Sicherheitsstandards an unsere Mitarbeiter und setzen Datenschutzpraktiken strikt durch.
Um die Funktion vollständig zu studieren und ihren Graphen darzustellen, wird empfohlen, das folgende Schema zu verwenden:
1) Finden Sie den Definitionsbereich der Funktion;
2) Finden Sie die Diskontinuitätspunkte der Funktion und der vertikalen Asymptoten (falls vorhanden);
3) Untersuchen Sie das Verhalten der Funktion im Unendlichen und finden Sie horizontale und schräge Asymptoten.
4) Untersuchen Sie die Funktion auf Parität (Seltsamkeit) und Periodizität (für trigonometrische Funktionen);
5) Finden Sie Extrema und Intervalle der Monotonie der Funktion;
6) Bestimmen Sie die Konvexitätsintervalle und Wendepunkte;
7) Finden Sie die Schnittpunkte mit den Koordinatenachsen und, wenn möglich, einige zusätzliche Punkte, die den Graphen verdeutlichen.
Das Studium der Funktion erfolgt gleichzeitig mit der Konstruktion ihres Graphen.
Beispiel 9 Erkunden Sie die Funktion und erstellen Sie ein Diagramm.
1. Definitionsbereich: ;
2. Die Funktion weist an Punkten Diskontinuität auf  ,
, ;
;
Wir untersuchen die Funktion auf das Vorhandensein vertikaler Asymptoten.
 ;
; ,
,
 ─ vertikale Asymptote.
─ vertikale Asymptote.
 ;
; ,
,
 ─ vertikale Asymptote.
─ vertikale Asymptote.
3. Wir untersuchen die Funktion auf das Vorhandensein schräger und horizontaler Asymptoten.
Gerade  ─ schräge Asymptote, wenn
─ schräge Asymptote, wenn  ,
,
 .
.
 ,
, .
.
Gerade  ─ horizontale Asymptote.
─ horizontale Asymptote.
4. Die Funktion ist gerade weil  . Die Parität der Funktion gibt die Symmetrie des Diagramms relativ zur Ordinatenachse an.
. Die Parität der Funktion gibt die Symmetrie des Diagramms relativ zur Ordinatenachse an.
5. Finden Sie die Monotonieintervalle und Extrema der Funktion.
Finden wir die kritischen Punkte, d.h. Punkte, an denen die Ableitung 0 ist oder nicht existiert:  ;
; . Wir haben drei Punkte
. Wir haben drei Punkte  ;
;
 . Diese Punkte unterteilen die gesamte reale Achse in vier Intervalle. Definieren wir die Zeichen
. Diese Punkte unterteilen die gesamte reale Achse in vier Intervalle. Definieren wir die Zeichen  auf jedem von ihnen.
auf jedem von ihnen.

Auf den Intervallen (-∞; -1) und (-1; 0) nimmt die Funktion zu, auf den Intervallen (0; 1) und (1; +∞) ─ ab. Beim Passieren eines Punktes  Die Ableitung ändert das Vorzeichen von Plus nach Minus, daher weist die Funktion an diesem Punkt ein Maximum auf
Die Ableitung ändert das Vorzeichen von Plus nach Minus, daher weist die Funktion an diesem Punkt ein Maximum auf  .
.
6. Finden Sie die Intervalle der Konvexität und Wendepunkte.

Finden wir die Punkte, an denen  ist 0 oder existiert nicht.
ist 0 oder existiert nicht.
 hat keine wirklichen Wurzeln.
hat keine wirklichen Wurzeln.  ,
,
 ,
,

Punkte  Und
Und  Teilen Sie die reale Achse in drei Intervalle. Definieren wir das Zeichen
Teilen Sie die reale Achse in drei Intervalle. Definieren wir das Zeichen  in jedem Intervall.
in jedem Intervall.

Somit ist die Kurve über die Intervalle  Und
Und  konvex nach unten, im Intervall (-1;1) konvex nach oben; Es gibt keine Wendepunkte, da die Funktion an Punkten liegt
konvex nach unten, im Intervall (-1;1) konvex nach oben; Es gibt keine Wendepunkte, da die Funktion an Punkten liegt  Und
Und  unentschlossen.
unentschlossen.
7. Finden Sie die Schnittpunkte mit den Achsen.
Mit Achse  Der Graph der Funktion schneidet sich im Punkt (0; -1) und mit der Achse
Der Graph der Funktion schneidet sich im Punkt (0; -1) und mit der Achse  der Graph schneidet sich nicht, weil Der Zähler dieser Funktion hat keine echten Wurzeln.
der Graph schneidet sich nicht, weil Der Zähler dieser Funktion hat keine echten Wurzeln.
Der Graph der gegebenen Funktion ist in Abbildung 1 dargestellt.

Abbildung 1 ─ Funktionsgraph 
Anwendung des Derivatkonzepts in der Wirtschaftswissenschaft. Elastizitätsfunktion
Um wirtschaftliche Prozesse zu untersuchen und andere angewandte Probleme zu lösen, wird häufig das Konzept der Elastizität einer Funktion verwendet.
Definition. Elastizitätsfunktion  heißt Grenze des Verhältnisses des relativen Inkrements der Funktion
heißt Grenze des Verhältnisses des relativen Inkrements der Funktion  zum relativen Inkrement der Variablen
zum relativen Inkrement der Variablen  bei
bei  , . (VII)
, . (VII)
Die Elastizität einer Funktion gibt ungefähr an, um wie viel Prozent sich die Funktion ändert  wenn sich die unabhängige Variable ändert
wenn sich die unabhängige Variable ändert  um 1 %.
um 1 %.
Die Elastizitätsfunktion wird bei der Analyse von Nachfrage und Verbrauch verwendet. Wenn die Nachfrageelastizität (in absoluten Werten)  , dann gilt die Nachfrage als elastisch, wenn
, dann gilt die Nachfrage als elastisch, wenn  ─ neutral wenn
─ neutral wenn  ─ unelastisch im Verhältnis zum Preis (oder Einkommen).
─ unelastisch im Verhältnis zum Preis (oder Einkommen).
Beispiel 10 Berechnen Sie die Elastizität der Funktion  und ermitteln Sie den Wert des Elastizitätsindex für
und ermitteln Sie den Wert des Elastizitätsindex für  = 3.
= 3.
Lösung: Nach Formel (VII) beträgt die Elastizität der Funktion:
Sei also x=3  .Das heißt, wenn die unabhängige Variable um 1 % steigt, erhöht sich der Wert der abhängigen Variablen um 1,42 %.
.Das heißt, wenn die unabhängige Variable um 1 % steigt, erhöht sich der Wert der abhängigen Variablen um 1,42 %.
Beispiel 11 Lassen Sie die Nachfrage funktionieren  bezüglich des Preises
bezüglich des Preises  sieht aus wie
sieht aus wie  , Wo
, Wo  ─ konstanter Koeffizient. Finden Sie den Wert des Elastizitätsindikators der Nachfragefunktion zum Preis x = 3 Den. Einheiten
─ konstanter Koeffizient. Finden Sie den Wert des Elastizitätsindikators der Nachfragefunktion zum Preis x = 3 Den. Einheiten
Lösung: Berechnen Sie die Elastizität der Nachfragefunktion mit Formel (VII)
Glauben  Geldeinheiten erhalten wir
Geldeinheiten erhalten wir  . Das bedeutet, dass es seinen Preis hat
. Das bedeutet, dass es seinen Preis hat  Geldeinheiten Eine Preiserhöhung um 1 % führt zu einem Rückgang der Nachfrage um 6 %, d. h. Die Nachfrage ist elastisch.
Geldeinheiten Eine Preiserhöhung um 1 % führt zu einem Rückgang der Nachfrage um 6 %, d. h. Die Nachfrage ist elastisch.
Führen Sie eine vollständige Studie durch und zeichnen Sie die Funktion grafisch auf
y(x)=x2+81−x.y(x)=x2+81−x.
1) Der Umfang der Funktion. Da die Funktion ein Bruch ist, müssen wir die Nullstellen des Nenners finden.
1−x=0,⇒x=1,1−x=0,⇒x=1.
Wir schließen den einzigen Punkt x=1x=1 aus dem Definitionsbereich der Funktion aus und erhalten:
D(y)=(−∞;1)∪(1;+∞).D(y)=(−∞;1)∪(1;+∞).
2) Lassen Sie uns das Verhalten der Funktion in der Nähe des Unstetigkeitspunkts untersuchen. Finden wir einseitige Grenzen:
Da die Grenzen gleich unendlich sind, ist der Punkt x=1x=1 eine Unstetigkeit zweiter Art, die Gerade x=1x=1 eine vertikale Asymptote.
3) Bestimmen wir die Schnittpunkte des Funktionsgraphen mit den Koordinatenachsen.
Finden wir die Schnittpunkte mit der Ordinatenachse OyOy, für die wir x=0x=0 setzen:
Somit hat der Schnittpunkt mit der OyOy-Achse die Koordinaten (0;8)(0;8).
Finden wir die Schnittpunkte mit der Abszissenachse OxOx, für die wir y=0y=0 setzen:
![]()
Die Gleichung hat keine Wurzeln, daher gibt es keine Schnittpunkte mit der OxOx-Achse.
Beachten Sie, dass x2+8>0x2+8>0 für jedes xx gilt. Daher gilt für x∈(−∞;1)x∈(−∞;1) die Funktion y>0y>0( positive Werte, der Graph liegt über der x-Achse), für x∈(1;+∞)x∈(1;+∞) die Funktion y<0y<0 (принимает отрицательные значения, график находится ниже оси абсцисс).
4) Die Funktion ist weder gerade noch ungerade, weil:
5) Untersuchen wir die Funktion auf Periodizität. Die Funktion ist nicht periodisch, da es sich um eine gebrochenrationale Funktion handelt.
6) Untersuchen wir die Funktion auf Extrema und Monotonie. Dazu ermitteln wir die erste Ableitung der Funktion:
![]()
Setzen wir die erste Ableitung mit Null gleich und finden stationäre Punkte (an denen y′=0y′=0):
Wir haben drei kritische Punkte: x=−2,x=1,x=4x=−2,x=1,x=4. Teilen wir den gesamten Definitionsbereich der Funktion mit diesen Punkten in Intervalle auf und bestimmen wir die Vorzeichen der Ableitung in jedem Intervall:

Für x∈(−∞;−2),(4;+∞)x∈(−∞;−2),(4;+∞) ist die Ableitung y′<0y′<0, поэтому функция убывает на данных промежутках.
Für x∈(−2;1),(1;4)x∈(−2;1),(1;4) der Ableitung y′>0y′>0 nimmt die Funktion in diesen Intervallen zu.
In diesem Fall ist x=−2x=−2 ein lokaler Minimalpunkt (die Funktion nimmt ab und dann zu), x=4x=4 ist ein lokaler Maximalpunkt (die Funktion nimmt zu und dann ab).
Suchen wir die Werte der Funktion an diesen Punkten: ![]()
![]()
Somit ist der minimale Punkt (−2;4)(−2;4), der maximale Punkt ist (4;−8)(4;−8).
7) Lassen Sie uns die Funktion auf Knicke und Konvexität untersuchen. Finden wir die zweite Ableitung der Funktion:
Setzen wir die zweite Ableitung mit Null gleich:
![]()
Die resultierende Gleichung hat keine Wurzeln, daher gibt es keine Wendepunkte. Wenn außerdem x∈(−∞;1)x∈(−∞;1) y′′>0y″>0 erfüllt ist, d. h. die Funktion konkav ist, wenn x∈(1;+∞)x∈( 1;+ ∞) wird durch y'' erfüllt<0y″<0, то есть функция выпуклая.
8) Untersuchen wir das Verhalten der Funktion im Unendlichen, also bei .
Da die Grenzen unendlich sind, gibt es keine horizontalen Asymptoten.
Versuchen wir, schräge Asymptoten der Form y=kx+by=kx+b zu bestimmen. Wir berechnen die Werte von k,bk,b mit bekannten Formeln:
![]()
Wir haben herausgefunden, dass die Funktion eine schräge Asymptote y=−x−1y=−x−1 hat.
9) Zusätzliche Punkte. Berechnen wir den Wert der Funktion an einigen anderen Punkten, um den Graphen genauer zu erstellen.
y(−5)=5,5;y(2)=−12;y(7)=−9,5.y(−5)=5,5;y(2)=−12;y(7)=−9,5.
10) Basierend auf den erhaltenen Daten erstellen wir einen Graphen, ergänzen ihn mit den Asymptoten x=1x=1 (blau), y=−x−1y=−x−1 (grün) und markieren die charakteristischen Punkte (lila Schnittpunkt mit der Ordinate). Achse, orangefarbene Extrema, schwarze Zusatzpunkte):

Aufgabe 4: Geometrische, wirtschaftliche Probleme (ich habe keine Ahnung, was, hier ist eine ungefähre Auswahl von Problemen mit Lösungen und Formeln) 
Beispiel 3.23. A
Lösung. X Und j j
y = a - 2×a/4 =a/2. Da x = a/4 der einzige kritische Punkt ist, prüfen wir, ob sich das Vorzeichen der Ableitung beim Durchgang durch diesen Punkt ändert. Für xa/4 S " > 0 und für x >a/4 S "< 0, значит, в точке x=a/4 функция S имеет максимум. Значение функции S(a/4) = a/4(a - a/2) = a 2 /8 (кв. ед).Поскольку S непрерывна на и ее значения на концах S(0) и S(a/2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.
Beispiel 3.24.
Lösung.
R = 2, H = 16/4 = 4.
Beispiel 3.22. Finden Sie die Extrema der Funktion f(x) = 2x 3 - 15x 2 + 36x - 14.
Lösung. Da f "(x) = 6x 2 - 30x +36 = 6(x -2)(x - 3), dann sind die kritischen Punkte der Funktion x 1 = 2 und x 2 = 3. Extrema können nur bei liegen Diese Punkte. Wenn also die Ableitung beim Durchgang durch den Punkt x 1 = 2 ihr Vorzeichen von Plus nach Minus ändert, hat die Funktion an diesem Punkt ein Maximum. Beim Durchgang durch den Punkt x 2 = 3 ändert die Ableitung ihr Vorzeichen von Minus zu plus, daher hat die Funktion am Punkt x 2 = 3 ein Minimum. Nachdem wir die Funktionswerte an den Punkten berechnet haben
x 1 = 2 und x 2 = 3, wir finden die Extrema der Funktion: Maximum f(2) = 14 und Minimum f(3) = 13.
Beispiel 3.23. Es ist notwendig, in der Nähe der Steinmauer einen rechteckigen Bereich zu errichten, der an drei Seiten mit Drahtgeflecht eingezäunt ist und die vierte Seite an die Mauer angrenzt. Dafür gibt es A laufende Meter Maschenweite. Bei welchem Seitenverhältnis wird die Website die größte Fläche haben?
Lösung. Bezeichnen wir die Seiten der Plattform mit X Und j. Die Fläche des Geländes beträgt S = xy. Lassen j- Dies ist die Länge der Seite neben der Wand. Dann muss aufgrund der Bedingung die Gleichheit 2x + y = a gelten. Daher ist y = a - 2x und S = x(a - 2x), wobei
0 ≤ x ≤ a/2 (die Länge und Breite des Pads dürfen nicht negativ sein). S " = a - 4x, a - 4x = 0 bei x = a/4, daher
y = a - 2×a/4 =a/2. Da x = a/4 der einzige kritische Punkt ist, prüfen wir, ob sich das Vorzeichen der Ableitung beim Durchgang durch diesen Punkt ändert. Für xa/4 S " > 0 und für x >a/4 S "< 0, значит, в точке x=a/4 функция S имеет максимум. Значение функции S(a/4) = a/4(a - a/2) = a 2 /8 (кв. ед).Поскольку S непрерывна на и ее значения на концах S(0) и S(a/2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.
Beispiel 3.24. Es ist erforderlich, einen geschlossenen zylindrischen Tank mit einem Fassungsvermögen von V=16p ≈ 50 m 3 herzustellen. Welche Abmessungen sollte der Tank haben (Radius R und Höhe H), damit für seine Herstellung möglichst wenig Material verbraucht wird?
Lösung. Die Gesamtoberfläche des Zylinders beträgt S = 2pR(R+H). Wir kennen das Volumen des Zylinders V = pR 2 N Þ N = V/pR 2 =16p/ pR 2 = 16/ R 2 . Das bedeutet S(R) = 2p(R 2 +16/R). Wir finden die Ableitung dieser Funktion:
S " (R) = 2p(2R- 16/R 2) = 4p (R- 8/R 2). S " (R) = 0 für R 3 = 8, daher
R = 2, H = 16/4 = 4.
Verwandte Informationen.
Heute laden wir Sie ein, mit uns einen Funktionsgraphen zu erkunden und zu erstellen. Nachdem Sie diesen Artikel sorgfältig studiert haben, müssen Sie nicht lange schwitzen, um diese Art von Aufgabe zu erledigen. Es ist nicht einfach, einen Funktionsgraphen zu studieren und zu erstellen; es ist eine umfangreiche Arbeit, die maximale Aufmerksamkeit und Genauigkeit der Berechnungen erfordert. Um den Stoff verständlicher zu machen, werden wir die gleiche Funktion Schritt für Schritt studieren und alle unsere Aktionen und Berechnungen erklären. Willkommen in der erstaunlichen und faszinierenden Welt der Mathematik! Gehen!
Domain
Um eine Funktion zu untersuchen und grafisch darzustellen, müssen Sie mehrere Definitionen kennen. Funktion ist eines der wichtigsten (Grund-)Konzepte der Mathematik. Es spiegelt die Abhängigkeit zwischen mehreren Variablen (zwei, drei oder mehr) bei Änderungen wider. Die Funktion zeigt auch die Abhängigkeit von Mengen.
Stellen Sie sich vor, wir haben zwei Variablen, die einen bestimmten Änderungsbereich aufweisen. Y ist also eine Funktion von x, vorausgesetzt, dass jeder Wert der zweiten Variablen einem Wert der zweiten entspricht. In diesem Fall ist die Variable y abhängig und wird Funktion genannt. Es ist üblich zu sagen, dass die Variablen x und y in sind. Zur besseren Verdeutlichung dieser Abhängigkeit wird ein Graph der Funktion erstellt. Was ist ein Graph einer Funktion? Dies ist eine Menge von Punkten auf der Koordinatenebene, wobei jeder x-Wert einem y-Wert entspricht. Diagramme können unterschiedlich sein – Gerade, Hyperbel, Parabel, Sinuswelle usw.
Es ist unmöglich, eine Funktion ohne Recherche grafisch darzustellen. Heute lernen wir, wie man Forschung durchführt und einen Graphen einer Funktion erstellt. Es ist sehr wichtig, sich während des Studiums Notizen zu machen. Dadurch wird die Bewältigung der Aufgabe deutlich erleichtert. Der bequemste Forschungsplan:
- Domain.
- Kontinuität.
- Gerade oder ungerade.
- Periodizität.
- Asymptoten.
- Nullen.
- Zeichenkonstanz.
- Zunehmend und abnehmend.
- Extreme.
- Konvexität und Konkavität.
Beginnen wir mit dem ersten Punkt. Finden wir den Definitionsbereich, also die Intervalle, in denen unsere Funktion existiert: y=1/3(x^3-14x^2+49x-36). In unserem Fall existiert die Funktion für alle Werte von x, das heißt, der Definitionsbereich ist gleich R. Dies kann wie folgt geschrieben werden: xÎR.
Kontinuität
Jetzt untersuchen wir die Diskontinuitätsfunktion. In der Mathematik entstand der Begriff „Kontinuität“ als Ergebnis des Studiums der Bewegungsgesetze. Was ist unendlich? Raum, Zeit, einige Abhängigkeiten (ein Beispiel ist die Abhängigkeit der Variablen S und t bei Bewegungsproblemen), die Temperatur eines erhitzten Objekts (Wasser, Bratpfanne, Thermometer usw.), eine durchgehende Linie (also eine, die kann gezeichnet werden, ohne es vom Blatt abzuheben (Bleistift).

Ein Graph gilt als kontinuierlich, wenn er nicht irgendwann abbricht. Eines der offensichtlichsten Beispiele für einen solchen Graphen ist eine Sinuskurve, die Sie im Bild in diesem Abschnitt sehen können. Eine Funktion ist an einem Punkt x0 stetig, wenn eine Reihe von Bedingungen erfüllt sind:
- eine Funktion ist an einem bestimmten Punkt definiert;
- die rechten und linken Grenzen an einem Punkt sind gleich;
- der Grenzwert ist gleich dem Wert der Funktion am Punkt x0.
Wenn mindestens eine Bedingung nicht erfüllt ist, gilt die Funktion als fehlgeschlagen. Und die Punkte, an denen die Funktion unterbrochen wird, werden normalerweise als Unterbrechungspunkte bezeichnet. Ein Beispiel für eine Funktion, die bei der grafischen Darstellung „abbricht“, ist: y=(x+4)/(x-3). Darüber hinaus existiert y am Punkt x = 3 nicht (da eine Division durch Null unmöglich ist).
In der Funktion, die wir untersuchen (y=1/3(x^3-14x^2+49x-36)) erwies sich alles als einfach, da der Graph stetig sein wird.
Gerade ungerade

Untersuchen Sie nun die Funktion auf Parität. Zunächst eine kleine Theorie. Eine gerade Funktion erfüllt die Bedingung f(-x)=f(x) für jeden Wert der Variablen x (aus dem Wertebereich). Beispiele beinhalten:
- Modul x (der Graph sieht aus wie eine Daw, die Winkelhalbierende des ersten und zweiten Viertels des Graphen);
- x im Quadrat (Parabel);
- Kosinus x (Kosinus).
Beachten Sie, dass alle diese Diagramme symmetrisch sind, wenn sie in Bezug auf die y-Achse (d. h. die y-Achse) betrachtet werden.
Was nennt man dann eine ungerade Funktion? Dies sind jene Funktionen, die die Bedingung f(-x)=-f(x) für jeden Wert der Variablen x erfüllen. Beispiele:
- Hyperbel;
- kubische Parabel;
- Sinusoid;
- Tangente und so weiter.
Bitte beachten Sie, dass diese Funktionen symmetrisch zum Punkt (0:0), also zum Ursprung, sind. Basierend auf dem, was in diesem Abschnitt des Artikels gesagt wurde, müssen eine gerade und eine ungerade Funktion die Eigenschaft haben: x gehört zur Definitionsmenge und auch -x.
Lassen Sie uns die Funktion auf Parität untersuchen. Wir können sehen, dass sie auf keine der Beschreibungen passt. Daher ist unsere Funktion weder gerade noch ungerade.
Asymptoten
Beginnen wir mit einer Definition. Eine Asymptote ist eine Kurve, die möglichst nahe am Graphen liegt, d. h. der Abstand von einem bestimmten Punkt geht gegen Null. Insgesamt gibt es drei Arten von Asymptoten:
- vertikal, also parallel zur y-Achse;
- horizontal, also parallel zur x-Achse;
- geneigt.
Was den ersten Typ betrifft, sollte an einigen Stellen nach diesen Zeilen gesucht werden:
- Lücke;
- Enden des Definitionsbereichs.
In unserem Fall ist die Funktion stetig und der Definitionsbereich ist gleich R. Folglich gibt es keine vertikalen Asymptoten.
Der Graph einer Funktion hat eine horizontale Asymptote, die die folgende Anforderung erfüllt: wenn x gegen Unendlich oder minus Unendlich tendiert und der Grenzwert einer bestimmten Zahl entspricht (z. B. a). In diesem Fall ist y=a die horizontale Asymptote. In der von uns untersuchten Funktion gibt es keine horizontalen Asymptoten.
Eine schräge Asymptote existiert nur, wenn zwei Bedingungen erfüllt sind:
- lim(f(x))/x=k;
- lim f(x)-kx=b.
Dann kann es mit der Formel y=kx+b ermittelt werden. Auch in unserem Fall gibt es keine schrägen Asymptoten.
Funktionsnullstellen

Der nächste Schritt besteht darin, den Graphen der Funktion auf Nullstellen zu untersuchen. Es ist auch sehr wichtig zu beachten, dass die Aufgabe, die Nullstellen einer Funktion zu finden, nicht nur beim Studium und Aufbau eines Funktionsgraphen auftritt, sondern auch als eigenständige Aufgabe und als Möglichkeit zur Lösung von Ungleichungen. Möglicherweise müssen Sie die Nullstellen einer Funktion in einem Diagramm finden oder die mathematische Notation verwenden.
Das Ermitteln dieser Werte wird Ihnen helfen, die Funktion genauer darzustellen. Vereinfacht ausgedrückt ist der Nullpunkt einer Funktion der Wert der Variablen x, bei dem y = 0 ist. Wenn Sie in einem Diagramm nach den Nullstellen einer Funktion suchen, sollten Sie auf die Punkte achten, an denen sich das Diagramm mit der x-Achse schneidet.
Um die Nullstellen der Funktion zu finden, müssen Sie die folgende Gleichung lösen: y=1/3(x^3-14x^2+49x-36)=0. Nach Durchführung der notwendigen Berechnungen erhalten wir folgende Antwort:
Zeichenkonstanz
Die nächste Stufe der Forschung und Konstruktion einer Funktion (Graph) besteht darin, Intervalle mit konstantem Vorzeichen zu finden. Das bedeutet, dass wir bestimmen müssen, in welchen Intervallen die Funktion einen positiven Wert und in welchen Intervallen sie einen negativen Wert annimmt. Die im letzten Abschnitt gefundenen Nullfunktionen helfen uns dabei. Wir müssen also eine gerade Linie erstellen (getrennt vom Diagramm) und die Nullstellen der Funktion in der richtigen Reihenfolge vom kleinsten zum größten entlang dieser Linie verteilen. Jetzt müssen Sie bestimmen, welches der resultierenden Intervalle ein „+“-Zeichen und welches ein „-“ hat.
In unserem Fall nimmt die Funktion in Intervallen einen positiven Wert an:
- von 1 bis 4;
- von 9 bis unendlich.
Negative Bedeutung:
- von minus unendlich bis 1;
- von 4 bis 9.
Das lässt sich ganz einfach feststellen. Setzen Sie eine beliebige Zahl aus dem Intervall in die Funktion ein und sehen Sie, welches Vorzeichen die Antwort hat (Minus oder Plus).
Zunehmende und abnehmende Funktion
Um eine Funktion zu untersuchen und zu konstruieren, müssen wir wissen, wo der Graph ansteigt (entlang der Oy-Achse nach oben geht) und wo er abfällt (entlang der y-Achse nach unten kriecht).

Eine Funktion nimmt nur dann zu, wenn ein größerer Wert der Variablen x einem größeren Wert von y entspricht. Das heißt, x2 ist größer als x1 und f(x2) ist größer als f(x1). Und wir beobachten ein völlig entgegengesetztes Phänomen mit einer abnehmenden Funktion (je mehr x, desto weniger y). Um die Intervalle der Zunahme und Abnahme zu bestimmen, müssen Sie Folgendes herausfinden:
- Definitionsbereich (wir haben ihn bereits);
- Ableitung (in unserem Fall: 1/3(3x^2-28x+49);
- Lösen Sie die Gleichung 1/3(3x^2-28x+49)=0.
Nach Berechnungen erhalten wir das Ergebnis:
Wir erhalten: Die Funktion nimmt in den Intervallen von minus Unendlich bis 7/3 und von 7 bis Unendlich zu und in dem Intervall von 7/3 bis 7 ab.
Extreme

Die untersuchte Funktion y=1/3(x^3-14x^2+49x-36) ist stetig und existiert für jeden Wert der Variablen x. Der Extrempunkt zeigt das Maximum und Minimum einer bestimmten Funktion. In unserem Fall gibt es keine, was die Konstruktionsaufgabe erheblich vereinfacht. Ansonsten können sie auch mit der Ableitungsfunktion ermittelt werden. Sobald Sie sie gefunden haben, vergessen Sie nicht, sie auf der Karte zu markieren.
Konvexität und Konkavität
Wir untersuchen die Funktion y(x) weiter. Jetzt müssen wir es auf Konvexität und Konkavität prüfen. Die Definitionen dieser Konzepte sind recht schwer zu verstehen, es ist besser, alles anhand von Beispielen zu analysieren. Zum Test: Eine Funktion ist konvex, wenn sie eine nicht fallende Funktion ist. Stimmen Sie zu, das ist unverständlich!
Wir müssen die Ableitung einer Funktion zweiter Ordnung finden. Wir erhalten: y=1/3(6x-28). Setzen wir nun die rechte Seite mit Null gleich und lösen die Gleichung. Antwort: x=14/3. Wir haben den Wendepunkt gefunden, also den Ort, an dem der Graph von der Konvexität zur Konkavität wechselt oder umgekehrt. Im Intervall von minus Unendlich bis 14/3 ist die Funktion konvex, und von 14/3 bis plus Unendlich ist sie konkav. Es ist auch sehr wichtig zu beachten, dass der Wendepunkt im Diagramm glatt und weich sein sollte und keine scharfen Ecken vorhanden sein sollte.
Zusätzliche Punkte definieren
Unsere Aufgabe besteht darin, die Funktion zu untersuchen und einen Graphen zu erstellen. Wir haben die Studie abgeschlossen; die Erstellung eines Graphen der Funktion ist jetzt nicht mehr schwierig. Für eine genauere und detailliertere Wiedergabe einer Kurve oder Geraden auf der Koordinatenebene können Sie mehrere Hilfspunkte finden. Sie sind recht einfach zu berechnen. Nehmen wir zum Beispiel x=3, lösen die resultierende Gleichung und finden y=4. Oder x=5 und y=-5 und so weiter. Sie können so viele Zusatzpunkte nehmen, wie Sie für den Bau benötigen. Mindestens 3-5 davon werden gefunden.
Zeichnen eines Diagramms

Wir mussten die Funktion (x^3-14x^2+49x-36)*1/3=y untersuchen. Alle notwendigen Markierungen während der Berechnungen wurden auf der Koordinatenebene vorgenommen. Jetzt müssen Sie nur noch ein Diagramm erstellen, also alle Punkte verbinden. Das Verbinden der Punkte sollte reibungslos und genau erfolgen, das ist eine Frage der Geschicklichkeit – ein wenig Übung und Ihr Zeitplan werden perfekt sein.