Fonction inverse x. Fonctions mutuellement inverses
Lire aussi
Supposons que nous ayons une fonction y = f (x) strictement monotone (décroissante ou croissante) et continue sur le domaine x ∈ a ; b; sa plage de valeurs est y ∈ c ; d , et sur l'intervalle c ; d en même temps, nous aurons une fonction x = g (y) avec une plage de valeurs a ; b. La deuxième fonction sera également continue et strictement monotone. Par rapport à y = f (x) ce sera une fonction inverse. C'est-à-dire qu'on peut parler de fonction inverse x \u003d g (y) lorsque y \u003d f (x) sur un intervalle donné diminuera ou augmentera.
Ces deux fonctions, f et g , seront mutuellement inverses.
Yandex.RTB R-A-339285-1
Pourquoi avons-nous besoin du concept de fonctions inverses ?
Nous en avons besoin pour résoudre les équations y = f (x) , qui sont écrites uniquement en utilisant ces expressions.
Disons que nous devons trouver une solution à l'équation cos (x) = 1 3 . Ses solutions sont deux points : x = ± a r c o c s 1 3 + 2 π k , k ∈ Z
Inverses l'une par rapport à l'autre seront, par exemple, les fonctions arccosinus et cosinus.
Analysons plusieurs problèmes pour trouver des fonctions inverses de celles données.
Exemple 1
Condition: quelle est la fonction inverse pour y = 3 x + 2 ?
La solution
Le domaine des définitions et le domaine des valeurs de la fonction spécifiée dans la condition est l'ensemble de tous les nombres réels. Essayons de résoudre équation donnéeà x , c'est-à-dire en exprimant x à y .
Nous obtenons x = 1 3 y - 2 3 . C'est la fonction inverse dont nous avons besoin, mais ici y sera un argument et x sera une fonction. Réorganisons-les pour obtenir une notation plus familière :
Réponse: la fonction y = 1 3 x - 2 3 sera inverse pour y = 3 x + 2 .
Les deux fonctions mutuellement inverses peuvent être tracées de la manière suivante:
Nous voyons la symétrie des deux graphiques par rapport à y = x . Cette ligne est la bissectrice des premier et troisième quadrants. Nous avons obtenu une preuve d'une des propriétés des fonctions mutuellement inverses, dont nous parlerons plus tard.
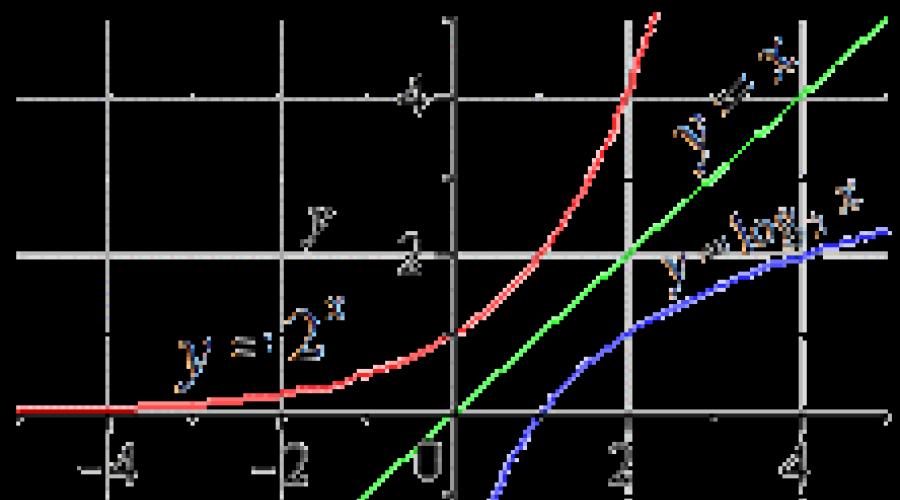
Prenons un exemple dans lequel vous devez trouver la fonction logarithmique, l'inverse d'une exponentielle donnée.
Exemple 2
Condition: déterminer quelle fonction sera inverse pour y = 2 x .
La solution
Pour une fonction donnée, le domaine de définition est tous les nombres réels. La plage de valeurs se situe dans l'intervalle 0 ; +∞ . Maintenant, nous devons exprimer x par y, c'est-à-dire résoudre l'équation indiquée par x. On obtient x = log 2 y . Réorganisez les variables et obtenez y = log 2 x .
En conséquence, nous avons obtenu des fonctions exponentielles et logarithmiques, qui seront mutuellement inverses l'une de l'autre sur tout le domaine de définition.
Réponse: y = log 2 x .
Sur le graphique, les deux fonctions ressembleront à ceci :

Propriétés de base des fonctions mutuellement inverses
Dans cette sous-section, nous énumérons les principales propriétés des fonctions y = f (x) et x = g (y) qui sont mutuellement inverses.
Définition 1
- Nous avons déjà dérivé la première propriété plus tôt : y = f (g (y)) et x = g (f (x)) .
- La deuxième propriété découle de la première : le domaine de définition y = f (x) coïncidera avec le domaine de la fonction inverse x = g (y) , et vice versa.
- Les graphiques des fonctions inverses seront symétriques par rapport à y = x .
- Si y = f (x) augmente, alors x = g (y) augmentera également, et si y = f (x) diminue, alors x = g (y) diminuera également.
Nous vous conseillons de bien considérer les notions de domaine de définition et d'étendue des fonctions et de ne jamais les confondre. Disons que nous avons deux fonctions mutuellement inverses y = f (x) = a x et x = g (y) = log a y . Selon la première propriété, y = f (g (y)) = a log a y . Cette égalité ne sera vraie que si valeurs positives y , et le logarithme n'est pas défini pour les négatifs, alors ne vous précipitez pas pour noter qu'un log a y = y . Assurez-vous de vérifier et d'ajouter que cela n'est vrai que pour y positif.
Mais l'égalité x \u003d f (g (x)) \u003d log a a x \u003d x sera vraie pour toutes les valeurs réelles de x.
N'oubliez pas ce point, surtout si vous devez travailler avec des fonctions trigonométriques et trigonométriques inverses. Donc, a r c sin sin 7 π 3 ≠ 7 π 3 parce que la plage de l'arcsinus est π 2 ; π 2 et 7 π 3 n'y sont pas inclus. La bonne entrée sera
a r c sin sin 7 π 3 \u003d a r c sin sin 2 π + π 3 \u003d \u003d \u003d sous la forme d'un s u l p r i o n i o n \u003d a r c sin sin π 3 \u003d π 3
Mais sin a r c sin 1 3 \u003d 1 3 est l'égalité correcte, c'est-à-dire sin (a r c sin X) = x pour x ∈ - 1 ; 1 et a r c sin (sin x) = x pour x ∈ - π 2 ; π 2 . Soyez toujours prudent avec la portée et la portée des fonctions inverses!
- Fonctions de base mutuellement inverses : puissance
Si nous avons une fonction puissance y = x a , alors pour x > 0 la fonction puissance x = y 1 a lui sera également inverse. Remplaçons les lettres et obtenons respectivement y = x a et x = y 1 a.
Sur le graphique, ils ressembleront à ceci (cas avec coefficient positif et négatif a):

- Fonctions de base mutuellement inverses : exponentielles et logarithmiques
Prenons a, qui sera un nombre positif, non égal à 1 .
Graphiques pour les fonctions avec a > 1 et a< 1 будут выглядеть так:

- Fonctions de base mutuellement inverses : trigonométriques et trigonométriques inverses
Si nous devons tracer la branche principale du sinus et de l'arc sinus, cela ressemblera à ceci (indiqué dans la zone claire en surbrillance).
Travaux finis
CES TRAVAUX
Beaucoup est déjà en retard et maintenant vous êtes diplômé, si, bien sûr, vous écrivez votre thèse à temps. Mais la vie est une chose telle que ce n'est que maintenant qu'il devient clair pour vous que, ayant cessé d'être étudiant, vous perdrez toutes les joies étudiantes, dont beaucoup que vous n'avez pas essayées, remettant tout à plus tard. Et maintenant, au lieu de rattraper ton retard, tu bricoles ta thèse ? Il existe une excellente solution : téléchargez la thèse dont vous avez besoin sur notre site Web - et vous aurez instantanément beaucoup de temps libre !
Les travaux de diplôme ont été défendus avec succès dans les principales universités de la République du Kazakhstan.
Coût des travaux à partir de 20 000 tenge
TRAVAUX DE COURS
Le projet de cours est le premier travail pratique sérieux. C'est avec la rédaction d'un mémoire que commence la préparation à l'élaboration des projets de fin d'études. Si un étudiant apprend à énoncer correctement le contenu du sujet dans un projet de cours et à le rédiger correctement, il n'aura plus de problèmes à l'avenir ni pour la rédaction de rapports, ni pour la rédaction de thèses, ni pour la mise en œuvre d'autres tâches pratiques. Afin d'aider les étudiants à rédiger ce type de travail d'étudiant et de clarifier les questions qui se posent au cours de sa préparation, en fait, cette section d'information a été créée.
Coût des travaux à partir de 2 500 tenge
THÈMES DE MAÎTRISE
À l'heure actuelle, dans les établissements d'enseignement supérieur du Kazakhstan et des pays de la CEI, le niveau d'enseignement supérieur est très courant. enseignement professionnel, qui suit après le baccalauréat - maîtrise. Dans la magistrature, les étudiants étudient dans le but d'obtenir un diplôme de maîtrise, qui est reconnu dans la plupart des pays du monde plus qu'un baccalauréat, et est également reconnu par les employeurs étrangers. Le résultat de la formation à la magistrature est la soutenance d'un mémoire de maîtrise.
Nous vous fournirons un matériel analytique et textuel à jour, le prix comprend 2 articles scientifiques et un résumé.
Coût des travaux à partir de 35 000 tenge
RAPPORTS DE PRATIQUE
Après avoir terminé tout type de pratique étudiante (éducative, industrielle, de premier cycle), un rapport est requis. Ce document sera la preuve Travaux pratiquesétudiant et la base pour la formation des évaluations pour la pratique. Habituellement, pour rédiger un rapport de stage, il est nécessaire de collecter et d'analyser des informations sur l'entreprise, de tenir compte de la structure et du calendrier de travail de l'organisation dans laquelle se déroule le stage, d'établir plan de calendrier et décrivez votre activités pratiques.
Nous vous aiderons à rédiger un rapport de stage en tenant compte des spécificités des activités d'une entreprise particulière.
Définition d'une fonction inverse et de ses propriétés : lemme sur la monotonie mutuelle des fonctions directes et inverses ; symétrie des graphiques de fonctions directes et inverses ; théorèmes sur l'existence et la continuité de la fonction inverse pour une fonction strictement monotone sur un segment, un intervalle et un demi-intervalle. Exemples de fonctions inverses. Un exemple de solution à un problème. Preuves de propriétés et de théorèmes.
Définition et propriétés
Définition de la fonction inverse
Soit la fonction ayant un domaine X et un ensemble de valeurs Y . Et laissez-lui la propriété:
pour tous .
Alors pour tout élément de l'ensemble Y, un seul élément de l'ensemble X peut être associé, pour lequel . Cette correspondance définit une fonction appelée fonction inverseà . La fonction inverse est notée comme suit :
.
Il découle de la définition que
;
pour tous ;
pour tous .
Propriété sur la symétrie des graphes de fonctions directes et inverses
Les graphiques des fonctions directes et inverses sont symétriques par rapport à la ligne directe.
Théorème sur l'existence et la continuité de la fonction inverse sur un segment
Soit la fonction continue et strictement croissante (décroissante) sur l'intervalle . Alors sur l'intervalle la fonction inverse est définie et continue, strictement croissante (décroissante).
Pour une fonction croissante. Pour descendre - .
Théorème sur l'existence et la continuité de la fonction inverse sur un intervalle
Soit la fonction continue et strictement croissante (décroissante) sur un intervalle ouvert fini ou infini. Alors la fonction inverse est définie et continue sur l'intervalle strictement croissant (décroissant).
Pour une fonction croissante.
Pour la descente : .
De manière similaire, on peut formuler un théorème sur l'existence et la continuité d'une fonction inverse sur un demi-intervalle.
Si la fonction est continue et strictement croissante (diminue) sur le demi-intervalle ou , alors sur le demi-intervalle ou la fonction inverse est définie, qui strictement augmente (diminue). Ici .
S'il est strictement croissant, alors les intervalles et correspondent aux intervalles et . S'ils sont strictement décroissants, alors les intervalles et correspondent aux intervalles et .
Ce théorème se démontre de la même manière que le théorème sur l'existence et la continuité de la fonction inverse sur un intervalle.
Exemples de fonctions inverses
Arcsinus

Parcelles y= péché x et fonction inverse y = arcsin x.
Considérez la fonction trigonométrique sinus: . Il est défini et continu pour toutes les valeurs de l'argument , mais n'est pas monotone. Cependant, si le domaine de définition est restreint, alors les sections monotones peuvent être distinguées. Ainsi, sur le segment , la fonction est définie, continue, strictement croissante et prenant des valeurs de -1 avant de +1 . Par conséquent, il a une fonction inverse sur lui, qui s'appelle l'arcsinus. L'arc sinus a un domaine de définition et un ensemble de valeurs.
Logarithme

Parcelles y= 2x et fonction inverse y = bûche 2 x.
La fonction exponentielle est définie, continue et strictement croissante pour toutes les valeurs de l'argument . L'ensemble de ses valeurs est un intervalle ouvert. La fonction inverse est le logarithme de base deux. Il a une portée et un ensemble de valeurs.
Racine carrée

Parcelles y=x 2 et fonction inverse.
Fonction de puissance est défini et continu pour tous . L'ensemble de ses valeurs est un demi-intervalle. Mais il n'est pas monotone pour toutes les valeurs de l'argument. Cependant, sur le demi-intervalle, il est continu et strictement croissant de manière monotone. Par conséquent, si, comme domaine, nous prenons l'ensemble , alors il existe une fonction inverse, qui s'appelle racine carrée. La fonction inverse a un domaine de définition et un ensemble de valeurs.
Exemple. Preuve de l'existence et de l'unicité d'une racine de degré n
Montrer que l'équation , où n est un nombre naturel, est un nombre réel non négatif, a seule décision sur l'ensemble des nombres réels, . Cette solution est appelée racine nième de a. Autrement dit, vous devez montrer que tout nombre non négatif a une racine unique de degré n.
Considérons une fonction de variable x :
(P1) .
Montrons qu'elle est continue.
En utilisant la définition de la continuité, nous montrons que
.
On applique la formule binomiale de Newton :
(P2)
.
Appliquons les propriétés arithmétiques des limites de la fonction . Puisque , alors seul le premier terme est non nul :
.
La continuité a été prouvée.
Montrons que la fonction (P1) est strictement croissante lorsque .
Prenons des nombres arbitraires reliés par des inégalités :
,
,
.
Nous devons montrer cela. Introduisons des variables. Alors . Puisque , il ressort de (A2) que . Ou
.
L'augmentation stricte est prouvée.
Trouvez l'ensemble des valeurs de fonction pour .
À ce point , .
Trouvons la limite.
Pour cela, appliquez l'inégalité de Bernoulli. Quand nous avons:
.
Depuis , puis et .
En appliquant la propriété des inégalités de fonctions infiniment grandes, on trouve que .
De cette façon, , .
Selon le théorème de la fonction inverse, une fonction inverse est définie et continue sur un intervalle. Autrement dit, pour tout, il existe un unique qui satisfait l'équation. Puisque nous avons , cela signifie que pour tout , l'équation a une solution unique, qui s'appelle la racine du degré n à partir du nombre x :
.
Preuves de propriétés et théorèmes
Preuve du lemme sur la monotonie mutuelle des fonctions directes et inverses
Soit la fonction ayant un domaine X et un ensemble de valeurs Y . Montrons qu'il a une fonction inverse. Sur la base de , nous devons prouver que
pour tous .
Supposons le contraire. Qu'il y ait des nombres , donc . Laissez en même temps. Sinon, nous changeons la notation pour qu'elle soit . Alors, du fait de la stricte monotonie de f , l'une des inégalités doit être vraie :
si f est strictement croissante ;
si f est strictement décroissante.
C'est-à-dire . Il y avait une contradiction. Il a donc une fonction inverse.
Soit la fonction strictement croissante. Montrons que la fonction inverse est aussi strictement croissante. Introduisons la notation :
. Autrement dit, nous devons prouver que si , alors .
Supposons le contraire. Laissez , mais .
Si donc . Cette affaire est sortie.
Laisser . Alors, du fait de la stricte augmentation de la fonction , , ou . Il y avait une contradiction. Par conséquent, seul le cas est possible.
Le lemme est démontré pour une fonction strictement croissante. Ce lemme se démontre de manière similaire pour une fonction strictement décroissante.
Preuve d'une propriété sur la symétrie des graphes de fonctions directes et inverses
Soit un point arbitraire du graphe de la fonction directe :
(2.1)
.
Montrons que le point , symétrique au point A par rapport à la droite , appartient au graphe de la fonction inverse :
.
Il résulte de la définition de la fonction inverse que
(2.2)
.
Il faut donc montrer (2.2).

Graphique de la fonction inverse y = f -1 fois) est symétrique au graphe de la fonction directe y = f (X) par rapport à la droite y = x .
A partir des points A et S, nous déposons des perpendiculaires sur les axes de coordonnées. Alors
,
.
Par le point A, nous traçons une ligne perpendiculaire à la ligne. Laissez les droites se croiser au point C. On construit un point S sur la droite tel que . Alors le point S sera symétrique au point A par rapport à la droite.
Considérons les triangles et . Ils ont deux côtés de même longueur : et, et angles égaux entre eux: . Ils sont donc congruents. Alors
.
Considérons un triangle. Depuis
.
Idem pour le triangle :
.
Alors
.
Maintenant on trouve :
;
.
Donc, équation (2.2) :
(2.2)
est satisfait car , et (2.1) est satisfait :
(2.1)
.
Puisque nous avons choisi arbitrairement le point A, cela s'applique à tous les points du graphique :
tous les points du graphe de la fonction, réfléchis symétriquement par rapport à la droite, appartiennent au graphe de la fonction inverse.
Ensuite, nous pouvons échanger nos places. En conséquence, nous obtenons
tous les points du graphe de la fonction, réfléchis symétriquement par rapport à la droite, appartiennent au graphe de la fonction.
Il s'ensuit que les graphes des fonctions et sont symétriques par rapport à la droite.
La propriété a été prouvée.
Preuve du théorème sur l'existence et la continuité de la fonction inverse sur un intervalle
Soit désigne le domaine de définition de la fonction - le segment .
1. Montrons que l'ensemble des valeurs de la fonction est l'intervalle :
,
où .
En effet, puisque la fonction est continue sur le segment , alors, d'après le théorème de Weierstrass, elle atteint son minimum et son maximum sur celui-ci. Ensuite, selon le théorème de Bolzano-Cauchy, la fonction prend toutes les valeurs du segment. Autrement dit, pour tout existe , pour lequel . Puisqu'il y a un minimum et un maximum, la fonction ne prend sur le segment que les valeurs de l'ensemble .
2. Puisque la fonction est strictement monotone, alors selon ce qui précède, il existe une fonction inverse , qui est également strictement monotone (augmente si augmente et diminue si diminue). Le domaine de la fonction inverse est l'ensemble et l'ensemble des valeurs est l'ensemble.
3. Maintenant, nous prouvons que la fonction inverse est continue.
3.1. Soit un point intérieur quelconque du segment : . Montrons que la fonction inverse est continue en ce point.
Qu'il corresponde au point . Puisque la fonction inverse est strictement monotone, c'est-à-dire le point intérieur du segment :
.
D'après la définition de la continuité, il faut prouver que pour tout il existe une fonction telle que
(3.1)
pour tous .
Notez que nous pouvons prendre arbitrairement petit. En effet, si nous avons trouvé une fonction telle que les inégalités (3.1) soient satisfaites pour des valeurs suffisamment petites de , alors elles le seront automatiquement pour toute grande valeur de , si nous posons pour .
Prenons-le si petit que les points et appartiennent au segment :
.
Introduisons et arrangeons la notation :
.
On transforme la première inégalité (3.1) :
(3.1)
pour tous .
;
;
;
(3.2)
.
Comme il est strictement monotone, il s'ensuit que
(3.3.1)
, si augmente ;
(3.3.2)
s'il diminue.
Comme la fonction inverse est aussi strictement monotone, les inégalités (3.3) impliquent les inégalités (3.2).

Pour tout ε > 0 existe δ, donc |f -1 (y) - f -1 (y 0) |< ε pour tout |y - y 0 | < δ .
Les inégalités (3.3) définissent un intervalle ouvert dont les extrémités sont séparées du point par des distances et . Soit la plus petite de ces distances :
.
En raison de la stricte monotonie de , , . C'est pourquoi . Alors l'intervalle sera compris dans l'intervalle défini par les inégalités (3.3). Et pour toutes les valeurs qui lui appartiennent, les inégalités (3.2) seront remplies.
Donc, nous avons trouvé que pour suffisamment petit , existe , de sorte que
à .
Changeons maintenant de notation.
Pour assez petit , il existe tel que
à .
Cela signifie que la fonction inverse est continue aux points intérieurs.
3.2. Considérons maintenant les extrémités du domaine de définition. Ici, tous les arguments restent les mêmes. Seuls les voisinages unilatéraux de ces points doivent être pris en compte. Au lieu d'un point, il y aura ou , et au lieu d'un point - ou .
Ainsi, pour une fonction croissante , .
à .
La fonction inverse est continue à , car pour tout suffisamment petit il y a , de sorte que
à .
Pour une fonction décroissante , .
La fonction inverse est continue à , car pour tout suffisamment petit il y a , de sorte que
à .
La fonction inverse est continue à , car pour tout suffisamment petit il y a , de sorte que
à .
Le théorème a été démontré.
Preuve du théorème sur l'existence et la continuité de la fonction inverse sur l'intervalle
Soit désigne le domaine de la fonction - un intervalle ouvert. Soit l'ensemble de ses valeurs. D'après ce qui précède, il existe une fonction inverse qui a un domaine de définition, un ensemble de valeurs et qui est strictement monotone (augmente si elle augmente et diminue si elle diminue). Il nous reste à prouver que
1) l'ensemble est un intervalle ouvert , et que
2) la fonction inverse est continue sur elle.
Ici .
1. Montrons que l'ensemble des valeurs de la fonction est un intervalle ouvert :
.
Comme tout ensemble non vide dont les éléments ont une opération de comparaison, l'ensemble des valeurs de fonction a des bornes inférieure et supérieure :
.
Ici, et peuvent être des nombres finis ou des symboles et .
1.1. Montrons que les points et n'appartiennent pas à l'ensemble des valeurs de la fonction. Autrement dit, l'ensemble de valeurs ne peut pas être un segment.
Si ou est pointe à l'infini: ou , alors un tel point n'est pas un élément de l'ensemble. Elle ne peut donc pas appartenir à un ensemble de valeurs.
Soit (ou ) un nombre fini. Supposons le contraire. Soit le point (ou ) appartenir à l'ensemble des valeurs de la fonction . C'est-à-dire qu'il existe telle pour laquelle (ou ). Prendre des points et satisfaire les inégalités :
.
Comme la fonction est strictement monotone, alors
, si f augmente ;
si f est décroissante.
Autrement dit, nous avons trouvé un point auquel la valeur de la fonction est inférieure (supérieure à
). Mais cela contredit la définition de la face inférieure (supérieure), selon laquelle
pour tous
.
Par conséquent, les points
et
ne peut pas appartenir à un ensemble de valeurs
les fonctions
.
1.2. Montrons maintenant que l'ensemble de valeurs est un intervalle , plutôt qu'une union d'intervalles et de points. c'est-à-dire pour tout point existe , Pour qui .
D'après les définitions des faces inférieure et supérieure, en tout voisinage des points
et
contient au moins un élément de l'ensemble
.
Laisser
- un nombre arbitraire appartenant à l'intervalle
:
.
Alors pour le quartier
existe
,
Pour qui
.
Pour le quartier
existe
,
Pour qui
.
Parce que le
et
,
alors
.
Alors
(4.1.1)
si
augmente;
(4.1.2)
si
diminue.
Les inégalités (4.1) sont faciles à prouver par contradiction. Mais vous pouvez utiliser , selon lequel sur le plateau
il existe une fonction inverse
,
qui est strictement croissante si
et décroît strictement si
.
On obtient alors immédiatement les inégalités (4.1).
Nous avons donc un segment
,
où
si
augmente;
si
diminue.
Aux extrémités du segment, la fonction prend les valeurs
et
.
Parce que le
,
alors par le théorème de Bolzano-Cauchy, il y a un point
,
Pour qui
.
Parce que le , nous avons ainsi montré que pour tout existe , Pour qui . Cela signifie que l'ensemble des valeurs de la fonction est un intervalle ouvert .
2. Montrons maintenant que la fonction inverse est continue en un point quelconque intervalle : . Pour ce faire, appliquez-vous au segment . Parce que le , alors la fonction inverse continue sur le segment , y compris au point .
Le théorème a été démontré.
Références:
O.I. Démons. Conférences sur l'analyse mathématique. Partie 1. Moscou, 2004.
CM. Nikolsky. Cours d'analyse mathématique. Tome 1. Moscou, 1983.
Expressions correspondantes qui se transforment l'une en l'autre. Pour comprendre ce que cela signifie, il convient de considérer exemple concret. Disons que nous avons y = cos(x). Si nous prenons le cosinus de l'argument, alors nous pouvons trouver la valeur de y. Évidemment, pour cela, vous devez avoir x. Mais que se passe-t-il si le jeu est initialement donné ? C'est là qu'on entre dans le vif du sujet. Pour résoudre le problème, l'utilisation d'une fonction inverse est nécessaire. Dans notre cas, il s'agit de l'arc cosinus.
Après toutes les transformations, on obtient : x = arccos(y).
Autrement dit, pour trouver une fonction inverse d'une fonction donnée, il suffit d'exprimer simplement un argument à partir de celle-ci. Mais cela ne fonctionne que si le résultat aura une seule valeur (plus à ce sujet plus tard).
À vue générale on peut écrire ce fait comme suit : f(x) = y, g(y) = x.
Définition
Soit f une fonction dont le domaine est l'ensemble X et dont le domaine est l'ensemble Y. Alors s'il existe g dont les domaines effectuent des tâches opposées, alors f est réversible.
De plus, dans ce cas g est unique, ce qui signifie qu'il existe exactement une fonction qui satisfait cette propriété (ni plus, ni moins). Ensuite, on l'appelle la fonction inverse et, par écrit, elle est notée comme suit: g (x) \u003d f -1 (x).
En d'autres termes, ils peuvent être considérés comme une relation binaire. La réversibilité n'a lieu que lorsqu'un élément de l'ensemble correspond à une valeur d'une autre.
Il n'y a pas toujours de fonction inverse. Pour ce faire, chaque élément y є Y doit correspondre au plus à un x є X. Alors f est appelé bijectif ou injection. Si f -1 appartient à Y, alors chaque élément de cet ensemble doit correspondre à un certain x ∈ X. Les fonctions possédant cette propriété sont appelées surjections. C'est vrai par définition si Y est une image f, mais ce n'est pas toujours le cas. Pour être inverse, une fonction doit être à la fois une injection et une surjection. De telles expressions sont appelées bijections.
Exemple : fonctions carré et racine
La fonction est définie sur R. Une partition d'un segment [, b] est un ensemble de points τ = (x, x 1,..., x n 1, x n ) [, b] tel que = x< x 1 < < x n 1
Cours Etude d'une fonction et construction de son graphe Résumé : La fonction est étudiée pour la monotonie, l'extremum, la convexité-concavité, l'existence d'asymptotes
Sujet. Fonction. Méthodes de tâche. Fonction implicite. Fonction inverse. Classification des fonctions Éléments de la théorie des ensembles. Concepts de base L'un des concepts de base des mathématiques modernes est le concept d'ensemble.
Sujet 2.1 Fonctions numériques. Fonction, ses propriétés et graphe Soit X et Y certains ensembles de nombres Si chacun selon une règle F se voit attribuer un élément unique, alors nous disons que
L'algèbre et le début de l'analyse, XI L'ALGÈBRE ET LE DÉBUT DE L'ANALYSE Fédération Russe les étudiants prennent
LA. Strauss, IV. Tâches de Barinova avec un paramètre dans les directives d'examen d'État unifié y=-x 0 -a- -a x -5 Ulyanovsk 05 Strauss L.A. Tâches avec un paramètre dans l'examen [Texte] : des lignes directrices/ LA Strauss, IV.
Chapitre 3. Recherche de fonctions à l'aide de dérivées 3.1. Extremums et monotonicité Considérons une fonction y = f () définie sur un intervalle I R. On dit qu'elle a un maximum local au point
Sujet. Équations logarithmiques, inégalités et systèmes d'équations I. Consignes générales
Ce que nous allons étudier : Leçon sur le thème : Recherche des points d'extremums de fonctions. 1. Introduction. 2) Points de minimum et maximum. 3) Extremum de la fonction. 4) Comment calculer les extremums ? 5) Exemples les gars, voyons voir
1 SA Lavrenchenko Conférence 13 Fonctions exponentielles et logarithmiques 1 Le concept d'une fonction exponentielle Définition 11 fonction exponentielle est appelée une fonction de la forme constante positive de base, où Fonction
Webinaire 5 Sujet : Révision Préparation à l'examen d'État unifié (tâche 8) Tâche 8 Trouver toutes les valeurs du paramètre a, pour chacune desquelles l'équation a a 0 a sept ou huit solutions Soit, puis t t Équation initiale
Université technique d'État de Moscou nommée d'après N.E. Faculté Bauman des sciences fondamentales Département de modélisation mathématique А.Н. Kanatnikov, A.P. Kryshenko
informations générales Tâches avec paramètres Équations avec un module de tâche de type C 5 1 Préparation à l'examen d'État unifié Dikhtyar M.B. une. Valeur absolue, ou le module du nombre x, est le nombre x lui-même, si x 0 ; nombre x,
I. V. Yakovlev Matériaux sur les mathématiques MathUs.ru Logarithme Dans cet article, nous définissons le logarithme, dérivons le principal formules logarithmiques, nous donnons des exemples de calculs avec des logarithmes, et considérons également
13. Dérivées partielles d'ordres supérieurs Soit = avoir et défini sur D O. Les fonctions et sont aussi appelées dérivées partielles du premier ordre d'une fonction ou dérivées partielles premières d'une fonction. et en général
Ministère de l'éducation et des sciences de la Fédération de Russie Établissement d'enseignement budgétaire de l'État fédéral l'enseignement supérieur"UNIVERSITÉ TECHNIQUE D'ÉTAT DE NIZHNY NOVGOROD IM RE
CONTENU DE L'ALGÈBRE ET LE DÉBUT DE L'ANALYSE DES FONCTIONS...10 Propriétés de base des fonctions...11 Pair et impair...11 Périodicité...12 Zéros de la fonction...12 Monotonie (croissance, décroissance)...13 Extrêmes (maximum
INTRODUCTION À L'ANALYSE MATHÉMATIQUE Cours magistral. La notion d'ensemble. Propriétés de base de la définition de fonction. Principal fonctions élémentaires CONTENU : Éléments de théorie des ensembles Ensemble de nombres réels Numérique
Sujet 36 "Propriétés des fonctions" Nous analyserons les propriétés d'une fonction en utilisant l'exemple du graphe d'une fonction arbitraire y = f (x) : 1. Le domaine d'une fonction est l'ensemble de toutes les valeurs de la variable x qui correspondent
Asymptotes Représentation graphique d'une fonction Système de coordonnées cartésiennes Fonction fractionnaire linéaire Trinôme carré Fonction linéaire Extremum local Ensemble de valeurs du trinôme carré Ensemble de valeurs de fonction
Université fédérale de l'Oural, Institut de mathématiques et d'informatique, Département d'algèbre et de mathématiques discrètes Remarques introductives Ce cours est consacré à l'étude du plan. Le matériel qu'il contient
ÉQUATIONS DIFFÉRENTIELLES 1. Concepts de base équation différentielleà l'égard de quelque fonction, on appelle une équation qui relie cette fonction avec ses variables indépendantes et avec ses dérivées.
MATHÉMATIQUES UTILISER les devoirs C5 7 Inégalités (méthode des aires) Indications et solutions Matériel de référence Sources Koryanov A G Bryansk Envoyez vos commentaires et suggestions à : [courriel protégé] TÂCHES AVEC PARAMÈTRES
Sujet 41 "Tâches avec un paramètre" Les principales formulations de tâches avec un paramètre : 1) Rechercher toutes les valeurs de paramètre, chacune satisfaisant à une certaine condition.) Résoudre une équation ou une inégalité avec
Sujet 39. "Dérivées de fonctions" La fonction La dérivée d'une fonction au point x 0 est appelée la limite du rapport de l'incrément de la fonction à l'incrément de la variable, c'est-à-dire = lim = lim + () Tableau des dérivés : Dérivé
Département de mathématiques et d'informatique Éléments de mathématiques supérieures Complexe pédagogique et méthodologique pour les étudiants de l'enseignement secondaire professionnel étudiant à l'aide des technologies à distance Module Théorie des limites Compilé par: Professeur associé
Dérivée d'une fonction Sa géométrie et signification physique Définitions de base de la technique de différenciation Soit f () défini sur (,) a, b un point fixe, incrément d'argument au point,
Différenciation d'une fonction implicite Considérons la fonction (,) = C (C = const) Cette équation définit une fonction implicite () Supposons que nous ayons résolu cette équation et trouvé une expression explicite = () Nous pouvons maintenant
Ministère de l'éducation et des sciences de la Fédération de Russie Yaroslavsky Université d'État nommé d'après PG Demidov Département d'analyse discrète COLLECTE DE PROBLÈMES POUR UNE SOLUTION INDÉPENDANTE SUR LE SUJET LIMITE DE FONCTION
Conférence scientifique et pratique régionale de l'éducation, de la recherche et travail de conceptionélèves de la 6e à la 11e année "Questions appliquées et fondamentales de mathématiques" Aspects méthodologiques de l'étude des mathématiques Utilisation
Limites et continuité. Limite d'une fonction Soit la fonction = f) définie dans un voisinage du point = a. En même temps, au point a même, la fonction n'est pas nécessairement définie. Définition. Le nombre b est appelé la limite
Unified State Examination in Mathematics, 7 year demo Part A Trouver la valeur de l'expression 6p p avec p = Solution Utiliser la propriété du diplôme : Substituer dans l'expression résultante Correct
0.5 Équations et inégalités logarithmiques. Livres d'occasion :. Algèbre et début d'analyse 0 - édité par A.N. Kolmogorov. Indépendant et papiers de test en algèbre 0 - édité par E.P. Ershov
Système de tâches sur le thème "Équation tangentielle" Déterminer le signe pente tangente tracée au graphe de la fonction y f (), aux points d'abscisse a, b, c a) b) Préciser les points auxquels la dérivée
Inégalités avec un paramètre dans l'examen d'État unifié VV Silvestrov
Équations algébriques où Définition. L'algébrique est une équation de la forme 0, P () 0, des nombres réels. 0 0 variable s'appelle l'inconnue, et les nombres 0, les coefficients
Équations d'une droite et d'un plan Équation d'une droite sur un plan.. Équation générale droit. Un signe de parallélisme et de perpendicularité des lignes. En coordonnées cartésiennes, chaque droite du plan Oxy est définie par
Graphique de la dérivée d'une fonction Intervalles de monotonie d'une fonction Exemple 1. La figure montre un graphique y =f (x) de la dérivée de la fonction f (x) définie sur l'intervalle (1;13). Trouver les intervalles de la fonction croissante
Exemples de problèmes et de questions de base de MA pour la limite de séquence du semestre Simple Calculer la limite de séquence l i m 2 n 6 n 2 + 9 n 6 4 n 6 n 4 6 4 n 6 2 2 Calculer la limite de séquence
Problèmes de géométrie analytique, Mech-Math, Université d'État de Moscou Problème Dan est un tétraèdre O Exprimer le vecteur EF en termes de vecteurs O O O avec le début au milieu E de l'arête O et se terminant au point F de l'intersection des médianes du triangle Solution Soit
Enoncé du problème Méthode de la bissection Méthode des cordes (méthode des parties proportionnelles 4 Méthode de Newton (méthode des tangentes) 5 Méthode des itérations (méthode des approximations successives) Enoncé du problème Soit donné
1. Expressions et transformations 1.1 Racine du degré n Notion de racine du degré n Propriétés de la racine du degré n : La racine du produit et le produit des racines : simplifier l'expression ; trouver des valeurs Racine d'un quotient
CONFÉRENCE N4. Différentiel d'une fonction du premier ordre et des ordres supérieurs. Invariance de la forme différentielle. Dérivés d'ordres supérieurs. Application du différentiel dans les calculs approximatifs. 1. Le concept de différentiel ....
MODULE 7 "Fonctions exponentielles et logarithmiques". Généralisation de la notion de diplôme. Racine du ème degré et ses propriétés. Équations irrationnelles.. Degré avec exposant rationnel.. Fonction exponentielle..
13. Exposant et logarithme Pour compléter la preuve de la proposition 12.8, il nous reste à donner une définition et à prouver une proposition. Définition 13.1. Une série a i est dite absolument convergente si
MINISTÈRE DE L'ÉDUCATION ET DES SCIENCES DE LA FÉDÉRATION DE RUSSIE UNIVERSITÉ D'ÉTAT DE NOVOSSIBIRSK CENTRE ÉDUCATIF ET SCIENTIFIQUE SPÉCIALISÉ Mathématiques 10e année RECHERCHE DE FONCTIONS Novosibirsk Pour vérification
CONFÉRENCE N. Champ scalaire. Dérivée directionnelle. Pente. Plan tangent et normale à la surface. Extrema d'une fonction de plusieurs variables. Extremum conditionnel Champ scalaire. Dérivé par rapport à
MINISTÈRE DE L'ÉDUCATION ET DES SCIENCES DE LA FÉDÉRATION DE RUSSIE UNIVERSITÉ D'ÉTAT DE NOVOSSIBIRSK CENTRE ÉDUCATIF ET SCIENTIFIQUE SPÉCIALISÉ Mathématiques Niveau 0 LIMITES DES SÉQUENCES Novosibirsk Intuitif