L'article fournit une explication détaillée des définitions, de la signification géométrique de la dérivée avec symboles graphiques. L'équation d'une droite tangente sera considérée avec des exemples, les équations d'une tangente aux courbes du 2ème ordre seront trouvées.

Yandex.RTB R-A-339285-1 Définition 1

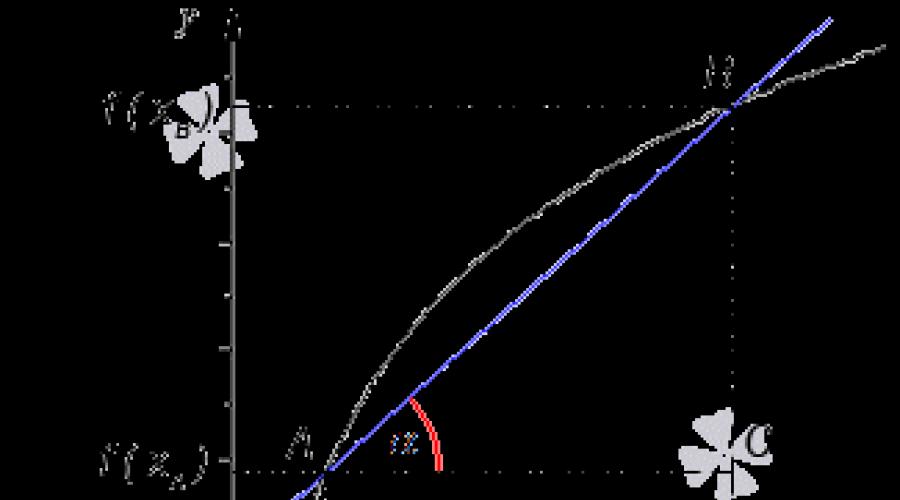
L'angle d'inclinaison de la droite y = k x + b est appelé angle α, qui est mesuré depuis la direction positive de l'axe x jusqu'à la droite y = k x + b dans la direction positive.

Sur la figure, la direction x est indiquée par une flèche verte et un arc vert, et l'angle d'inclinaison par un arc rouge. La ligne bleue fait référence à la ligne droite.

Définition 2

Facteur de pente la droite y = k x + b est appelée coefficient numérique k.

Le coefficient angulaire est égal à la tangente de la droite, autrement dit k = t g α.

• L'angle d'inclinaison d'une droite n'est égal à 0 que si elle est parallèle à x et que la pente est égale à zéro, car la tangente de zéro est égale à 0. Cela signifie que la forme de l’équation sera y = b.
• Si l'angle d'inclinaison de la droite y = k x + b est aigu, alors les conditions 0 sont remplies< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0, et il y a une augmentation dans le graphique.
• Si α = π 2, alors l'emplacement de la droite est perpendiculaire à x. L'égalité est spécifiée par x = c, la valeur c étant un nombre réel.
• Si l'angle d'inclinaison de la droite y = k x + b est obtus, alors il correspond aux conditions π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает Sens négatif, et le graphique diminue.

Définition 3

Une sécante est une droite qui passe par 2 points de la fonction f (x). En d’autres termes, une sécante est une ligne droite passant par deux points quelconques du graphique d’une fonction donnée.

La figure montre que A B est une sécante, et f (x) est une courbe noire, α est un arc rouge, indiquant l'angle d'inclinaison de la sécante.

Lorsque le coefficient angulaire d'une droite est égal à la tangente de l'angle d'inclinaison, il est clair que la tangente d'un triangle rectangle A B C peut être trouvée par le rapport du côté opposé au côté adjacent.

Définition 4

On obtient une formule pour trouver une sécante de la forme :

k = t g α = B C A C = f (x B) - f x A x B - x A, où les abscisses des points A et B sont les valeurs x A, x B, et f (x A), f (x B) sont les fonctions de valeurs en ces points.

Évidemment, le coefficient angulaire de la sécante est déterminé à l'aide de l'égalité k = f (x B) - f (x A) x B - x A ou k = f (x A) - f (x B) x A - x B , et l'équation doit être écrite sous la forme y = f (x B) - f (x A) x B - x A x - x A + f (x A) ou
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

La sécante divise visuellement le graphique en 3 parties : à gauche du point A, de A à B, à droite de B. La figure ci-dessous montre qu'il existe trois sécantes qui sont considérées comme coïncidentes, c'est-à-dire qu'elles sont définies à l'aide d'un équation similaire.

Par définition, il est clair que la droite et sa sécante coïncident dans ce cas.

Une sécante peut couper plusieurs fois le graphique d’une fonction donnée. S'il existe une équation de la forme y = 0 pour une sécante, alors le nombre de points d'intersection avec la sinusoïde est infini.

Définition 5

Tangente au graphique de la fonction f (x) au point x 0 ; f (x 0) est une droite passant par un point donné x 0 ; f (x 0), avec la présence d'un segment qui a de nombreuses valeurs x proches de x 0.

Exemple 1

Regardons de plus près l'exemple ci-dessous. Il est alors clair que la droite définie par la fonction y = x + 1 est considérée comme tangente à y = 2 x au point de coordonnées (1 ; 2). Pour plus de clarté, il est nécessaire de considérer des graphiques dont les valeurs sont proches de (1 ; 2). La fonction y = 2 x est représentée en noir, la ligne bleue est la ligne tangente et le point rouge est le point d'intersection.

Évidemment, y = 2 x fusionne avec la droite y = x + 1.

Pour déterminer la tangente, nous devons considérer le comportement de la tangente A B lorsque le point B s'approche du point A à l'infini. Pour plus de clarté, nous présentons un dessin.

La sécante A B, indiquée par la ligne bleue, tend vers la position de la tangente elle-même, et l'angle d'inclinaison de la sécante α commencera à tendre vers l'angle d'inclinaison de la tangente elle-même α x.

Définition 6

La tangente au graphique de la fonction y = f (x) au point A est considérée comme la position limite de la sécante A B lorsque B tend vers A, c'est-à-dire B → A.

Passons maintenant à la signification géométrique de la dérivée d'une fonction en un point.

Passons à considérer la sécante A B pour la fonction f (x), où A et B de coordonnées x 0, f (x 0) et x 0 + ∆ x, f (x 0 + ∆ x), et ∆ x est noté comme l'incrément de l'argument. Maintenant, la fonction prendra la forme ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Pour plus de clarté, donnons un exemple de dessin.

Considérons le résultat triangle rectangle A B C. Nous utilisons la définition de la tangente pour résoudre, c'est-à-dire que nous obtenons la relation ∆ y ∆ x = t g α . De la définition d'une tangente, il résulte que lim ∆ x → 0 ∆ y ∆ x = t g α x . D'après la règle de la dérivée en un point, on a que la dérivée f (x) au point x 0 est appelée la limite du rapport de l'incrément de la fonction à l'incrément de l'argument, où ∆ x → 0 , alors nous le notons f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Il s'ensuit que f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, où k x est noté la pente de la tangente.

Autrement dit, nous constatons que f ' (x) peut exister au point x 0, et comme la tangente à un graphique donné de la fonction au point de tangence égale à x 0, f 0 (x 0), où la valeur de la pente de la tangente au point est égale à la dérivée au point x 0 . Ensuite, nous obtenons que k x = f " (x 0) .

La signification géométrique de la dérivée d'une fonction en un point est que la notion de l'existence d'une tangente au graphique en ce même point est donnée.

Pour écrire l’équation d’une droite quelconque sur un plan, il faut disposer d’un coefficient angulaire avec le point par lequel elle passe. Sa notation est prise x 0 à l'intersection.

L'équation tangente au graphique de la fonction y = f (x) au point x 0, f 0 (x 0) prend la forme y = f "(x 0) x - x 0 + f (x 0).

Cela signifie que la valeur finale de la dérivée f "(x 0) peut déterminer la position de la tangente, c'est-à-dire verticalement, à condition que lim x → x 0 + 0 f "(x) = ∞ et lim x → x 0 - 0 f "(x ) = ∞ ou absence totale sous la condition lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .

L'emplacement de la tangente dépend de la valeur de son coefficient angulaire k x = f "(x 0). Lorsqu'elle est parallèle à l'axe o x, on obtient que k k = 0, lorsqu'elle est parallèle à o y - k x = ∞, et la forme du équation tangente x = x 0 augmente lorsque k x > 0, diminue lorsque k x< 0 .

Exemple 2

Compilez une équation pour la tangente au graphique de la fonction y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 au point de coordonnées (1 ; 3) et déterminez l'angle d'inclinaison.

Solution

Par condition, nous avons que la fonction est définie pour tous les nombres réels. Nous constatons que le point avec les coordonnées spécifiées par la condition (1 ; 3) est un point de tangence, alors x 0 = - 1, f (x 0) = - 3.

Il faut trouver la dérivée au point de valeur - 1. Nous obtenons cela

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

La valeur de f' (x) au point de tangence est la pente de la tangente, qui est égale à la tangente de la pente.

Alors k x = t g α x = y " (x 0) = 3 3

Il s'ensuit que α x = a r c t g 3 3 = π 6

Répondre: l'équation tangente prend la forme

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Pour plus de clarté, nous donnons un exemple dans une illustration graphique.

La couleur noire est utilisée pour le graphique de la fonction originale, Couleur bleue– image d'une tangente, point rouge – point de tangence. La figure de droite montre une vue agrandie.

Exemple 3

Déterminer l'existence d'une tangente au graphique d'une fonction donnée
y = 3 · x - 1 5 + 1 au point de coordonnées (1 ; 1) . Écrivez une équation et déterminez l’angle d’inclinaison.

Solution

Par condition, nous avons que le domaine de définition d'une fonction donnée est considéré comme l'ensemble de tous les nombres réels.

Passons à la recherche de la dérivée

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Si x 0 = 1, alors f' (x) n'est pas défini, mais les limites s'écrivent sous la forme lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ et lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , ce qui signifie que existence tangente verticale au point (1 ; 1).

Répondre: l'équation prendra la forme x = 1, où l'angle d'inclinaison sera égal à π 2.

Pour plus de clarté, décrivons-le graphiquement.

Exemple 4

Trouvez les points sur le graphique de la fonction y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, où

1. Il n'y a pas de tangente ;
2. La tangente est parallèle à x ;
3. La tangente est parallèle à la droite y = 8 5 x + 4.

Solution

Il faut faire attention à la portée de la définition. Par condition, on a que la fonction est définie sur l’ensemble de tous les nombres réels. Nous développons le module et résolvons le système avec des intervalles x ∈ - ∞ ; 2 et [ - 2 ; + ∞) . Nous obtenons cela

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

Il faut différencier la fonction. Nous avons ça

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

Lorsque x = − 2, alors la dérivée n'existe pas car les limites unilatérales ne sont pas égales à ce stade :

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

On calcule la valeur de la fonction au point x = - 2, où on obtient ça

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, c'est-à-dire la tangente au point ( - 2 ; - 2) n'existera pas.
2. La tangente est parallèle à x lorsque la pente est nulle. Alors k x = t g α x = f "(x 0). Autrement dit, il est nécessaire de trouver les valeurs d'un tel x lorsque la dérivée de la fonction le transforme à zéro. C'est-à-dire les valeurs de f' (x) seront les points de tangence, où la tangente est parallèle à x .

Quand x ∈ - ∞ ; - 2, alors - 1 5 (x 2 + 12 x + 35) = 0, et pour x ∈ (- 2 ; + ∞) on obtient 1 5 (x 2 - 4 x + 3) = 0.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Calculer les valeurs de fonction correspondantes

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 et 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

D'où - 5 ; 8 5, - 4 ; 4 3, 1 ; 8 5, 3; 4 3 sont considérés comme les points requis du graphe de fonction.

Regardons une représentation graphique de la solution.

La ligne noire est le graphique de la fonction, les points rouges sont les points de tangence.

1. Lorsque les droites sont parallèles, les coefficients angulaires sont égaux. Ensuite, il faut rechercher les points sur le graphique de fonction où la pente sera égale à la valeur 8 5. Pour ce faire, il faut résoudre une équation de la forme y "(x) = 8 5. Alors, si x ∈ - ∞; - 2, on obtient que - 1 5 (x 2 + 12 x + 35) = 8 5, et si x ∈ ( - 2 ; + ∞), alors 1 5 (x 2 - 4 x + 3) = 8 5.

La première équation n’a pas de racine puisque le discriminant est inférieur à zéro. Écrivons ça

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Une autre équation a deux racines réelles, alors

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Passons à la recherche des valeurs de la fonction. Nous obtenons cela

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Points avec des valeurs - 1 ; 4 15, 5; 8 3 sont les points auxquels les tangentes sont parallèles à la droite y = 8 5 x + 4.

Répondre: ligne noire – graphique de la fonction, ligne rouge – graphique de y = 8 5 x + 4, ligne bleue – tangentes aux points - 1 ; 4 15, 5; 8 3.

Il peut y avoir une infinité de tangentes pour des fonctions données.

Exemple 5

Écrivez les équations de toutes les tangentes disponibles de la fonction y = 3 cos 3 2 x - π 4 - 1 3, qui sont situées perpendiculairement à la droite y = - 2 x + 1 2.

Solution

Pour compiler l'équation tangente, il est nécessaire de trouver le coefficient et les coordonnées du point tangent, en fonction de la condition de perpendiculaire des lignes. La définition est la suivante : le produit des coefficients angulaires perpendiculaires aux droites est égal à - 1, c'est-à-dire s'écrit k x · k ⊥ = - 1. De la condition nous avons que le coefficient angulaire est situé perpendiculairement à la droite et est égal à k ⊥ = - 2, alors k x = - 1 k ⊥ = - 1 - 2 = 1 2.

Vous devez maintenant trouver les coordonnées des points de contact. Vous devez trouver x puis sa valeur pour une fonction donnée. Notez que d'après la signification géométrique de la dérivée au point
x 0 on obtient que k x = y" (x 0). De cette égalité on retrouve les valeurs de x pour les points de contact.

Nous obtenons cela

y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 péché 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 péché 3 2 x 0 - π 4 = 1 2 ⇒ péché 3 2 x 0 - π 4 = - 1 9

Ce équation trigonométrique sera utilisé pour calculer les ordonnées des points tangents.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk ou 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk ou 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk ou x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z est un ensemble d'entiers.

x points de contact ont été trouvés. Vous devez maintenant passer à la recherche des valeurs de y :

y 0 = 3 cos 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - péché 2 3 2 x 0 - π 4 - 1 3 ou y 0 = 3 - 1 - péché 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 ou y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 ou y 0 = - 4 5 + 1 3

De là, nous obtenons que 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 sont les points de tangence.

Répondre: les équations nécessaires s'écriront sous la forme

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈Z

Pour une représentation visuelle, considérons une fonction et une tangente sur une ligne de coordonnées.

La figure montre que la fonction est située sur l'intervalle [ - 10 ; 10 ], où la ligne noire est le graphique de la fonction, les lignes bleues sont des tangentes situées perpendiculairement à la ligne donnée de la forme y = - 2 x + 1 2. Les points rouges sont des points de contact.

Les équations canoniques des courbes du 2ème ordre ne sont pas des fonctions à valeur unique. Les équations tangentes pour eux sont compilées selon des schémas connus.

Tangente à un cercle

Définir un cercle de centre au point x centre ; y centre et rayon R, appliquez la formule x - x centre 2 + y - y centre 2 = R 2 .

Cette égalité peut s'écrire comme une union de deux fonctions :

y = R 2 - x - x centre 2 + y centre y = - R 2 - x - x centre 2 + y centre

La première fonction est située en haut et la seconde en bas, comme le montre la figure.

Compiler l'équation d'un cercle au point x 0 ; y 0 , qui est situé dans le demi-cercle supérieur ou inférieur, vous devriez trouver l'équation du graphique d'une fonction de la forme y = R 2 - x - x c e n t e r 2 + y c e n t e r ou y = - R 2 - x - x c e n t e r 2 + y centrez-vous au point indiqué.

Quand aux points x centre ; y centre + R et x centre ; y centre - R les tangentes peuvent être données par les équations y = y centre + R et y = y centre - R , et aux points x centre + R ; y centre et
x centre - R ; y centre sera parallèle à o y, alors on obtient des équations de la forme x = x c e n t e r + R et x = x c e n t e r - R .

Tangente à une ellipse

Lorsque l'ellipse a un centre en x centre ; y c e n t e r avec les demi-axes a et b, alors il peut être spécifié en utilisant l'équation x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.

Une ellipse et un cercle peuvent être désignés en combinant deux fonctions, à savoir la demi-ellipse supérieure et inférieure. Ensuite, nous obtenons cela

y = b a · a 2 - (x - x centre) 2 + y centre y = - b a · a 2 - (x - x centre) 2 + y centre

Si les tangentes sont situées aux sommets de l’ellipse, alors elles sont parallèles par rapport à x ou par rapport à y. Ci-dessous, pour plus de clarté, considérons la figure.

Exemple 6

Écrivez l'équation de la tangente à l'ellipse x - 3 2 4 + y - 5 2 25 = 1 aux points avec des valeurs de x égales à x = 2.

Solution

Il faut trouver les points tangents qui correspondent à la valeur x = 2. Nous substituons l'équation existante de l'ellipse et trouvons que

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Puis 2 ; 5 3 2 + 5 et 2 ; - 5 3 2 + 5 sont les points tangents qui appartiennent à la demi-ellipse supérieure et inférieure.

Passons à la recherche et à la résolution de l'équation de l'ellipse par rapport à y. Nous obtenons cela

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Évidemment, la demi-ellipse supérieure est spécifiée à l'aide d'une fonction de la forme y = 5 + 5 2 4 - x - 3 2, et la demi-ellipse inférieure y = 5 - 5 2 4 - x - 3 2.

Appliquons un algorithme standard pour créer une équation pour une tangente au graphique d'une fonction en un point. Écrivons que l'équation de la première tangente au point 2 ; 5 3 2 + 5 ressemblera à

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

On trouve que l'équation de la deuxième tangente de valeur au point
2 ; - 5 3 2 + 5 prend la forme

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Graphiquement, les tangentes sont désignées comme suit :

Tangente à l'hyperbole

Lorsqu'une hyperbole a un centre en x centre ; y centre et sommets x centre + α ; y centre et x centre - α ; y centre, l'inégalité x - x centre 2 α 2 - y - y centre 2 b 2 = 1 a lieu, si avec les sommets x centre ; y centre + b et x centre ; y c e n t e r - b , alors est spécifié en utilisant l'inégalité x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Une hyperbole peut être représentée comme deux fonctions combinées de la forme

y = b a · (x - x centre) 2 - a 2 + y centre = - b a · (x - x centre) 2 - a 2 + y centre ou y = b a · (x - x centre) 2 + a 2 + y centre = - b a · (x - x centre) 2 + a 2 + y centre

Dans le premier cas nous avons que les tangentes sont parallèles à y, et dans le second elles sont parallèles à x.

Il s'ensuit que pour trouver l'équation de la tangente à une hyperbole, il faut savoir à quelle fonction appartient le point de tangence. Pour déterminer cela, il est nécessaire de substituer les équations et de vérifier l'identité.

Exemple 7

Écrivez une équation pour la tangente à l'hyperbole x - 3 2 4 - y + 3 2 9 = 1 au point 7 ; - 3 3 - 3 .

Solution

Il est nécessaire de transformer l'enregistrement solution pour trouver une hyperbole à l'aide de 2 fonctions. Nous obtenons cela

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 et y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Il est nécessaire d'identifier à quelle fonction appartient un point donné de coordonnées 7 ; - 3 3 - 3 .

Évidemment, pour vérifier la première fonction il faut y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, alors le point n'appartient pas au graphe, puisque l'égalité ne tient pas.

Pour la deuxième fonction, nous avons que y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, ce qui signifie que le point appartient au graphique donné. De là, vous devriez trouver la pente.

Nous obtenons cela

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Répondre: l'équation tangente peut être représentée comme

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

C'est clairement représenté comme ceci :

Tangente à une parabole

Pour créer une équation pour la tangente à la parabole y = a x 2 + b x + c au point x 0, y (x 0), vous devez utiliser un algorithme standard, alors l'équation prendra la forme y = y "(x 0) x - x 0 + y ( x 0). Une telle tangente au sommet est parallèle à x.

Vous devez définir la parabole x = a y 2 + b y + c comme l'union de deux fonctions. Nous devons donc résoudre l’équation de y. Nous obtenons cela

x = une y 2 + par y + c ⇔ une y 2 + par y + c - x = 0 D = b 2 - 4 une (c - x) y = - b + b 2 - 4 une (c - x) 2 une y = - b - b 2 - 4 une (c - x) 2 une

Représentons-le graphiquement comme suit :

Pour savoir si un point x 0, y (x 0) appartient à une fonction, procédez doucement selon l'algorithme standard. Une telle tangente sera parallèle à o y par rapport à la parabole.

Exemple 8

Écrivez l'équation de la tangente au graphique x - 2 y 2 - 5 y + 3 lorsque l'on a un angle tangent de 150°.

Solution

Nous commençons la solution en représentant la parabole comme deux fonctions. Nous obtenons cela

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

La valeur de la pente est égale à la valeur de la dérivée au point x 0 de cette fonction et est égale à la tangente de l'angle d'inclinaison.

On a:

k x = y "(x 0) = t g α x = t g 150 ° = - 1 3

À partir de là, nous déterminons la valeur x pour les points de contact.

La première fonction s’écrira sous la forme

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Évidemment, il n’y a pas de véritables racines, puisque nous avons obtenu une valeur négative. Nous concluons qu’il n’existe pas de tangente d’angle de 150° pour une telle fonction.

La deuxième fonction s’écrira sous la forme

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Nous avons que les points de contact sont 23 4 ; - 5 + 3 4 .

Répondre: l'équation tangente prend la forme

y = - 1 3 x - 23 4 + - 5 + 3 4

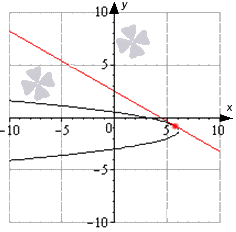
Représentons-le graphiquement de cette façon :

Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée

Ce programme mathématique trouve l'équation de la tangente au graphique de la fonction \(f(x)\) en un point spécifié par l'utilisateur \(a\).

Le programme affiche non seulement l'équation tangente, mais affiche également le processus de résolution du problème.

Ce calculateur en ligne peut être utile aux lycéens écoles secondaires en préparation pour essais et des examens, lors du test des connaissances avant l'examen d'État unifié, permettant aux parents de contrôler la solution de nombreux problèmes de mathématiques et d'algèbre. Ou peut-être que cela vous coûte trop cher d’embaucher un tuteur ou d’acheter de nouveaux manuels ? Ou souhaitez-vous simplement le faire le plus rapidement possible ? devoirs en mathématiques ou en algèbre ? Dans ce cas, vous pouvez également utiliser nos programmes avec des solutions détaillées.

De cette façon, vous pouvez organiser votre propre formation et/ou votre propre formation. frères plus jeunes ou sœurs, tandis que le niveau d'éducation dans le domaine des problèmes à résoudre augmente.

Si vous avez besoin de trouver la dérivée d'une fonction, nous avons pour cela la tâche Trouver la dérivée.

Si vous ne connaissez pas les règles de saisie des fonctions, nous vous recommandons de vous familiariser avec elles.

Entrez l'expression de fonction \(f(x)\) et le nombre \(a\)

f(x)=
une =

Trouver l'équation tangente

Il a été découvert que certains scripts nécessaires à la résolution de ce problème n'étaient pas chargés et que le programme pouvait ne pas fonctionner.
Vous avez peut-être activé AdBlock.
Dans ce cas, désactivez-le et actualisez la page.

Javascript est désactivé sur votre navigateur.
Pour que la solution apparaisse, vous devez activer JavaScript.
Voici les instructions pour activer JavaScript dans votre navigateur.

Parce que Il y a beaucoup de personnes prêtes à résoudre le problème, votre demande a été mise en file d'attente.
Dans quelques secondes, la solution apparaîtra ci-dessous.
S'il vous plaît, attendez seconde...

Si tu remarqué une erreur dans la solution, vous pourrez alors écrire à ce sujet dans le formulaire de commentaires.
N'oubliez pas indiquer quelle tâche tu décides quoi entrez dans les champs.

Nos jeux, puzzles, émulateurs :

Un peu de théorie.

Pente directe

Rappelons que le calendrier fonction linéaire\(y=kx+b\) est une ligne droite. Le nombre \(k=tg \alpha \) est appelé pente d'une droite, et l'angle \(\alpha \) est l'angle entre cette ligne et l'axe Ox

Si \(k>0\), alors \(0 Si \(kEquation de la tangente au graphe de la fonction

Si le point M(a; f(a)) appartient au graphe de la fonction y = f(x) et si à ce point une tangente peut être tracée au graphe de la fonction qui n'est pas perpendiculaire à l'axe des x, puis de la signification géométrique de la dérivée, il s'ensuit que le coefficient angulaire de la tangente est égal à f "(a). Ensuite, nous développerons un algorithme pour composer une équation pour une tangente au graphique de n'importe quelle fonction.

Soit une fonction y = f(x) et un point M(a; f(a)) sur le graphique de cette fonction ; faisons savoir que f"(a) existe. Créons une équation pour la tangente au graphique d'une fonction donnée en un point donné. Cette équation, comme l'équation de toute droite non parallèle à l'axe des ordonnées, a pour forme y = kx + b, la tâche est donc de trouver les valeurs des coefficients k et b.

Tout est clair avec le coefficient angulaire k : on sait que k = f"(a). Pour calculer la valeur de b, on utilise le fait que la droite recherchée passe par le point M(a; f(a)) . Cela signifie que si l'on substitue les coordonnées du point M dans l'équation d'une droite, on obtient l'égalité correcte : \(f(a)=ka+b\), c'est-à-dire \(b = f(a) - ka\).

Il reste à substituer les valeurs trouvées des coefficients k et b dans l'équation de la droite :

$$ y=kx+b $$ $$ y=kx+ f(a) - ka $$ $$ y=f(a)+ k(x-a) $$ $$ y=f(a)+ f"(a )(x-a) $$

Nous avons reçu équation de la tangente au graphique d'une fonction\(y = f(x) \) au point \(x=a \).

Algorithme pour trouver l'équation de la tangente au graphique de la fonction \(y=f(x)\)
1. Désignons l'abscisse du point tangent par la lettre \(a\)
2. Calculer \(f(a)\)
3. Trouvez \(f"(x)\) et calculez \(f"(a)\)
4. Remplacez les nombres trouvés \(a, f(a), f"(a) \) dans la formule \(y=f(a)+ f"(a)(x-a) \)

Livres (manuels) Résumés de l'examen d'État unifié et des tests de l'examen d'État unifié en ligne Jeux, puzzles Tracer des graphiques de fonctions Dictionnaire orthographique de la langue russe Dictionnaire de l'argot de la jeunesse Catalogue des écoles russes Catalogue des établissements d'enseignement secondaire de Russie Catalogue des universités russes Catalogue des universités russes Liste des problèmes Trouver GCD et LCM Simplifier un polynôme (multiplication de polynômes)

Équation de la tangente au graphique d'une fonction

P. Romanov, T. Romanova,
Magnitogorsk,
Région de Tcheliabinsk

Équation de la tangente au graphique d'une fonction

L'article a été publié avec le soutien du complexe hôtelier ITAKA+. En séjournant dans la ville des constructeurs navals de Severodvinsk, vous ne rencontrerez pas le problème de trouver un logement temporaire. , En ligne complexe hôtelier« ITHAKA+ » http://itakaplus.ru, vous pouvez louer facilement et rapidement un appartement en ville, pour n'importe quelle période, avec un paiement journalier.

Sur scène moderne développement de l'éducation, l'une de ses tâches principales est la formation d'une personnalité à la pensée créative. La capacité de créativité des étudiants ne peut être développée que s'ils sont systématiquement attirés par les bases activités de recherche. La base permettant aux étudiants d'utiliser leurs pouvoirs créatifs, leurs capacités et leurs talents est constituée de connaissances et de compétences à part entière. À cet égard, le problème de la formation d'un système de connaissances et de compétences de base pour chaque sujet du cours de mathématiques scolaire n'est pas négligeable. Dans le même temps, des compétences à part entière devraient être l'objectif didactique non pas de tâches individuelles, mais d'un système soigneusement pensé de celles-ci. Au sens le plus large, un système est compris comme un ensemble d’éléments en interaction interconnectés, intègres et dotés d’une structure stable.

Considérons une technique pour apprendre aux étudiants à écrire une équation pour une tangente au graphique d'une fonction. Essentiellement, tous les problèmes liés à la recherche de l'équation tangente se résument à la nécessité de sélectionner parmi un ensemble (faisceau, famille) de droites celles qui satisfont à une certaine exigence - elles sont tangentes au graphique d'une certaine fonction. Dans ce cas, l'ensemble des lignes à partir duquel la sélection est effectuée peut être précisé de deux manières :

a) un point situé sur le plan xOy (crayon central de lignes) ;
b) coefficient angulaire (faisceau parallèle de lignes droites).

A cet égard, en étudiant le thème « Tangente au graphe d'une fonction » afin d'isoler les éléments du système, nous avons identifié deux types de problèmes :

1) problèmes tangents, donné par le point, par lequel il passe ;
2) problèmes sur une tangente donnée par sa pente.

La formation à la résolution de problèmes tangents a été réalisée à l'aide de l'algorithme proposé par A.G. Mordkovitch. Sa différence fondamentale avec celles déjà connues est que l'abscisse du point tangent est désignée par la lettre a (au lieu de x0), et donc l'équation tangente prend la forme

y = f(une) + f "(une)(x – une)

(à comparer avec y = f(x 0) + f "(x 0)(x – x 0)). Ceci technique méthodique, à notre avis, permet aux étudiants de comprendre rapidement et facilement où dans l'équation tangente générale sont écrites les coordonnées du point actuel et où se trouvent les points tangents.

Algorithme de composition de l'équation tangente au graphique de la fonction y = f(x)

1. Désignons l'abscisse du point tangent par la lettre a.
2. Trouvez f(a).
3. Trouvez f "(x) et f "(a).
4. Remplacez les nombres trouvés a, f(a), f "(a) dans équation générale tangente y = f(a) = f "(a)(x – a).

Cet algorithme peut être compilé sur la base de l’identification indépendante des opérations par les étudiants et de la séquence de leur mise en œuvre.

La pratique a montré que la solution séquentielle de chacun des problèmes clés à l'aide d'un algorithme permet de développer les compétences d'écriture de l'équation d'une tangente au graphique d'une fonction par étapes, et les étapes de l'algorithme servent de points de référence pour les actions. . Cette approche correspond à la théorie de la formation progressive des actions mentales développée par P.Ya. Galperin et N.F. Talyzina.

Dans le premier type de tâches, deux tâches clés ont été identifiées :

• la tangente passe par un point situé sur la courbe (problème 1) ;
• la tangente passe par un point ne se trouvant pas sur la courbe (problème 2).

Tâche 1. Écrivez une équation pour la tangente au graphique de la fonction au point M(3; – 2).

Solution. Le point M(3; – 2) est un point tangent, puisque

1. a = 3 – abscisse du point tangent.
2.f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – équation tangente.

Problème 2. Écrivez les équations de toutes les tangentes au graphique de la fonction y = – x 2 – 4x + 2 passant par le point M(– 3 ; 6).

Solution. Le point M(– 3; 6) n'est pas un point tangent, puisque f(– 3) 6 (Fig.2).

2. f(une) = – une 2 – 4une + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – équation tangente.

La tangente passe par le point M(– 3; 6), donc ses coordonnées satisfont à l'équation de la tangente.

6 = – une 2 – 4une + 2 – 2(une + 2)(– 3 – une),
une 2 + 6une + 8 = 0^ un 1 = – 4, un 2 = – 2.

Si a = – 4, alors l’équation tangente est y = 4x + 18.

Si a = – 2, alors l’équation tangente a la forme y = 6.

Dans le deuxième type, les tâches clés seront les suivantes :

• la tangente est parallèle à une ligne (problème 3) ;
• la tangente passe sous un certain angle par rapport à la ligne donnée (problème 4).

Problème 3. Écrivez les équations de toutes les tangentes au graphique de la fonction y = x 3 – 3x 2 + 3, parallèle à la droite y = 9x + 1.

Solution.

1. a – abscisse du point tangent.
2. f(une) = une 3 – 3une 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Mais, d'un autre côté, f "(a) = 9 (condition de parallélisme). Cela signifie que nous devons résoudre l'équation 3a 2 – 6a = 9. Ses racines sont a = – 1, a = 3 (Fig. 3 ).

4. 1) une = – 1 ;
2) f(– 1) = – 1;
3) f "(– 1) = 9 ;
4) y = – 1 + 9(x + 1) ;

y = 9x + 8 – équation tangente ;

1) une = 3 ;
2) f(3) = 3;
3) f "(3) = 9 ;
4) y = 3 + 9(x – 3);

y = 9x – 24 – équation tangente.

Problème 4. Écrivez l'équation de la tangente au graphique de la fonction y = 0,5x 2 – 3x + 1, passant sous un angle de 45° par rapport à la droite y = 0 (Fig. 4).

Solution. A partir de la condition f "(a) = tan 45° on trouve a : a – 3 = 1^une = 4.

1. a = 4 – abscisse du point tangent.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – équation tangente.

Il est facile de montrer que la solution à tout autre problème revient à résoudre un ou plusieurs problèmes clés. Considérons les deux problèmes suivants à titre d'exemple.

1. Écrivez les équations des tangentes à la parabole y = 2x 2 – 5x – 2, si les tangentes se coupent à angle droit et que l'une d'elles touche la parabole au point d'abscisse 3 (Fig. 5).

Solution. L’abscisse du point tangent étant donnée, la première partie de la solution se réduit au problème clé 1.

1. a = 3 – abscisse du point de tangence d'un des côtés angle droit.
2.f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – équation de la première tangente.

Laissez un – angle d'inclinaison de la première tangente. Puisque les tangentes sont perpendiculaires, alors l’angle d’inclinaison de la deuxième tangente est égal à. De l’équation y = 7x – 20 de la première tangente nous avons tg a = 7. Trouvons

Cela signifie que la pente de la deuxième tangente est égale à .

La solution supplémentaire se résume à la tâche clé 3.

Soit B(c; f(c)) le point de tangence de la deuxième droite, alors

1. – abscisse du deuxième point de tangence.
2.
3.
4.
– équation de la deuxième tangente.

Note. Le coefficient angulaire de la tangente peut être trouvé plus facilement si les élèves connaissent le rapport des coefficients des droites perpendiculaires k 1 k 2 = – 1.

2. Écrivez les équations de toutes les tangentes communes aux graphiques de fonctions

Solution. Le problème revient à trouver l'abscisse des points de tangence des tangentes communes, c'est-à-dire à résoudre le problème clé 1 dans vue générale, élaborant un système d'équations et sa solution ultérieure (Fig. 6).

1. Soit a l'abscisse du point tangent situé sur le graphique de la fonction y = x 2 + x + 1.
2. f(une) = une 2 + une + 1.
3. f"(a) = 2a + 1.
4. y = une 2 + une + 1 + (2a + 1)(x – une) = (2a + 1)x + 1 – une 2 .

1. Soit c l'abscisse du point tangent situé sur le graphique de la fonction
2.
3. f"(c) = c.
4.

Puisque les tangentes sont générales, alors

Donc y = x + 1 et y = – 3x – 3 sont des tangentes communes.

L'objectif principal des tâches considérées est de préparer les étudiants à reconnaître de manière indépendante le type de problème clé lors de la résolution de problèmes plus approfondis. tâches complexes, nécessitant certaines compétences de recherche (capacité d'analyser, de comparer, de généraliser, d'émettre une hypothèse, etc.). Ces tâches incluent toute tâche dans laquelle la tâche clé est incluse en tant que composant. Considérons comme exemple le problème (inverse du problème 1) de trouver une fonction à partir de la famille de ses tangentes.

3. Pour quoi b et c sont les droites y = x et y = – 2x tangentes au graphique de la fonction y = x 2 + bx + c ?

Solution.

Soit t l'abscisse du point de tangence de la droite y = x avec la parabole y = x 2 + bx + c ; p est l'abscisse du point de tangence de la droite y = – 2x avec la parabole y = x 2 + bx + c. Alors l'équation tangente y = x prendra la forme y = (2t + b)x + c – t 2 , et l'équation tangente y = – 2x prendra la forme y = (2p + b)x + c – p 2 .

Composons et résolvons un système d'équations

Répondre:

Problèmes à résoudre de manière autonome

1. Écrivez les équations des tangentes tracées au graphique de la fonction y = 2x 2 – 4x + 3 aux points d'intersection du graphique avec la droite y = x + 3.

Réponse : y = – 4x + 3, y = 6x – 9,5.

2. Pour quelles valeurs de a la tangente tracée au graphe de la fonction y = x 2 – hache au point du graphe d'abscisse x 0 = 1 passe-t-elle par le point M(2 ; 3) ?

Réponse : a = 0,5.

3. Pour quelles valeurs de p la droite y = px – 5 touche-t-elle la courbe y = 3x 2 – 4x – 2 ?

Réponse : p 1 = – 10, p 2 = 2.

4. Trouver tous les points communs du graphique de la fonction y = 3x – x 3 et la tangente tracée à ce graphique passant par le point P(0; 16).

Réponse : A(2 ; – 2), B(– 4 ; 52).

5. Trouvez la distance la plus courte entre la parabole y = x 2 + 6x + 10 et la ligne droite

Répondre:

6. Sur la courbe y = x 2 – x + 1, trouvez le point où la tangente au graphique est parallèle à la droite y – 3x + 1 = 0.

Réponse : M(2 ; 3).

7. Écrivez l'équation de la tangente au graphique de la fonction y = x 2 + 2x – | 4x |, qui le touche en deux points. Faites un dessin.

Réponse : y = 2x – 4.

8. Montrer que la droite y = 2x – 1 ne coupe pas la courbe y = x 4 + 3x 2 + 2x. Trouvez la distance entre leurs points les plus proches.

Répondre:

9. Sur la parabole y = x 2, deux points sont pris en abscisses x 1 = 1, x 2 = 3. Une sécante est tracée par ces points. En quel point de la parabole la tangente à celle-ci sera-t-elle parallèle à la sécante ? Écrivez les équations sécantes et tangentes.

Réponse : y = 4x – 3 – équation sécante ; y = 4x – 4 – équation tangente.

10. Trouvez l'angle q entre les tangentes au graphique de la fonction y = x 3 – 4x 2 + 3x + 1, tracées aux points d'abscisses 0 et 1.

Réponse : q = 45°.

11. En quels points la tangente au graphique de la fonction forme-t-elle un angle de 135° avec l'axe Ox ?

Réponse : A(0 ; – 1), B(4 ; 3).

12. Au point A(1; 8) de la courbe une tangente est tracée. Trouvez la longueur du segment tangent entre les axes de coordonnées.

Répondre:

13. Écrivez l'équation de toutes les tangentes communes aux graphiques des fonctions y = x 2 – x + 1 et y = 2x 2 – x + 0,5.

Réponse : y = – 3x et y = x.

14. Trouver la distance entre les tangentes au graphique de la fonction parallèle à l’axe des x.

Répondre:

15. Déterminez sous quels angles la parabole y = x 2 + 2x – 8 coupe l'axe des x.

Réponse : q 1 = arctan 6, q 2 = arctan (– 6).

16. Graphique de fonction trouver tous les points dont la tangente à chacun desquels à ce graphique coupe les demi-axes positifs des coordonnées, en coupant des segments égaux.

Réponse : A(– 3 ; 11).

17. La droite y = 2x + 7 et la parabole y = x 2 – 1 se coupent aux points M et N. Trouvez le point K d'intersection des droites tangentes à la parabole aux points M et N.

Réponse : K(1 ; – 9).

18. Pour quelles valeurs de b la droite y = 9x + b est-elle tangente au graphique de la fonction y = x 3 – 3x + 15 ?

Réponse 1; 31.

19. Pour quelles valeurs de k la droite y = kx – 10 n'a-t-elle qu'un seul point commun avec le graphique de la fonction y = 2x 2 + 3x – 2 ? Pour les valeurs trouvées de k, déterminez les coordonnées du point.

Réponse : k 1 = – 5, A(– 2 ; 0) ; k 2 = 11, B(2; 12).

20. Pour quelles valeurs de b la tangente tracée au graphique de la fonction y = bx 3 – 2x 2 – 4 au point d'abscisse x 0 = 2 passe-t-elle par le point M(1 ; 8) ?

Réponse : b = – 3.

21. Une parabole dont le sommet est sur l'axe Ox touche la droite passant par les points A(1; 2) et B(2; 4) au point B. Trouvez l'équation de la parabole.

Répondre:

22. A quelle valeur du coefficient k la parabole y = x 2 + kx + 1 touche-t-elle l'axe Ox ?

Réponse : k = d 2.

23. Trouvez les angles entre la droite y = x + 2 et la courbe y = 2x 2 + 4x – 3.

29. Trouvez la distance entre les tangentes au graphique de la fonction et les génératrices avec la direction positive de l'axe Ox à un angle de 45°.

Répondre:

30. Trouvez le lieu des sommets de toutes les paraboles de la forme y = x 2 + ax + b tangente à la droite y = 4x – 1.

Réponse : droite y = 4x + 3.

Littérature

1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algèbre et débuts de l'analyse : 3600 problèmes pour les écoliers et ceux qui entrent à l'université. – M., Outarde, 1999.
2. Mordkovich A. Quatrième séminaire pour les jeunes enseignants. Sujet : Applications dérivées. – M., « Mathématiques », n° 21/94.
3. Formation de connaissances et de compétences basées sur la théorie de l'assimilation progressive des actions mentales. / Éd. P.Ya. Galperina, N.F. Talyzina. – M., Université d'État de Moscou, 1968.

La leçon vidéo « L'équation d'une tangente au graphique d'une fonction » présente du matériel pédagogique pour maîtriser le sujet. Au cours de la leçon vidéo, le matériel théorique nécessaire pour formuler le concept de l'équation d'une tangente au graphique d'une fonction en un point donné, un algorithme pour trouver une telle tangente et des exemples de résolution de problèmes en utilisant le matériel théorique étudié sont décrits. .

Le didacticiel vidéo utilise des méthodes qui améliorent la clarté du matériel. La présentation contient des dessins, des diagrammes, des commentaires vocaux importants, des animations, des surlignages et d'autres outils.

La leçon vidéo commence par une présentation du sujet de la leçon et une image d'une tangente au graphique d'une fonction y=f(x) au point M(a;f(a)). On sait que le coefficient angulaire de la tangente tracée au graphique en un point donné est égal à la dérivée de la fonction f΄(a) en ce point. Grâce au cours d'algèbre, nous connaissons également l'équation de la droite y=kx+m. La solution au problème de trouver l'équation tangente en un point est présentée schématiquement, ce qui se réduit à trouver les coefficients k, m. Connaissant les coordonnées d'un point appartenant au graphique de la fonction, nous pouvons trouver m en substituant la valeur des coordonnées dans l'équation tangente f(a)=ka+m. À partir de là, nous trouvons m=f(a)-ka. Ainsi, connaissant la valeur de la dérivée en un point donné et les coordonnées du point, on peut représenter l'équation tangente de cette manière y=f(a)+f΄(a)(x-a).

Ce qui suit est un exemple de composition d’une équation tangente en suivant le diagramme. Étant donné la fonction y=x 2 , x=-2. En prenant a=-2, on trouve la valeur de la fonction en un point donné f(a)= f(-2)=(-2) 2 =4. On détermine la dérivée de la fonction f΄(x)=2x. À ce stade, la dérivée est égale à f΄(a)= f΄(-2)=2·(-2)=-4. Pour composer l'équation, tous les coefficients a=-2, f(a)=4, f΄(a)=-4 ont été trouvés, donc l'équation tangente est y=4+(-4)(x+2). En simplifiant l'équation, nous obtenons y = -4-4x.

L'exemple suivant propose de construire une équation pour la tangente à l'origine du graphique de la fonction y=tgx. En un point donné a=0, f(0)=0, f΄(x)=1/cos 2 x, f΄(0)=1. L’équation tangente ressemble donc à y=x.

En généralisation, le processus de composition d'une équation tangente au graphique d'une fonction en un certain point est formalisé sous la forme d'un algorithme composé de 4 étapes :

• Entrez la désignation a pour l'abscisse du point tangent ;
• f(a) est calculé ;
• f΄(x) est déterminé et f΄(a) est calculé. Les valeurs trouvées de a, f(a), f΄(a) sont substituées dans la formule de l'équation tangente y=f(a)+f΄(a)(x-a).

L'exemple 1 considère la composition de l'équation tangente au graphique de la fonction y=1/x au point x=1. Pour résoudre le problème, nous utilisons un algorithme. Pour une fonction donnée au point a=1, la valeur de la fonction f(a)=-1. Dérivée de la fonction f΄(x)=1/x 2. Au point a=1 la dérivée f΄(a)= f΄(1)=1. A partir des données obtenues, l'équation tangente y=-1+(x-1), ou y=x-2, est établie.

Dans l'exemple 2, il faut trouver l'équation de la tangente au graphique de la fonction y=x 3 +3x 2 -2x-2. La condition principale est le parallélisme de la tangente et de la droite y=-2x+1. Tout d’abord, on trouve le coefficient angulaire de la tangente, égal au coefficient angulaire de la droite y=-2x+1. Puisque f΄(a)=-2 pour une droite donnée, alors k=-2 pour la tangente souhaitée. On trouve la dérivée de la fonction (x 3 +3x 2 -2x-2)΄=3x 2 +6x-2. Sachant que f΄(a)=-2, on trouve les coordonnées du point 3a 2 +6a-2=-2. Après avoir résolu l’équation, nous obtenons 1 =0 et 2 =-2. En utilisant les coordonnées trouvées, vous pouvez trouver l'équation tangente à l'aide d'un algorithme bien connu. On retrouve la valeur de la fonction aux points f(a 1)=-2, f(a 2)=-18. La valeur de la dérivée au point f΄(а 1)= f΄(а 2)=-2. En substituant les valeurs trouvées dans l'équation tangente, nous obtenons pour le premier point a 1 =0 y=-2x-2, et pour le deuxième point a 2 =-2 l'équation tangente y=-2x-22.

L'exemple 3 décrit la composition de l'équation tangente pour la tracer au point (0;3) au graphique de la fonction y=√x. La solution est réalisée à l'aide d'un algorithme bien connu. Le point tangent a les coordonnées x=a, où a>0. La valeur de la fonction au point f(a)=√x. La dérivée de la fonction f΄(х)=1/2√х, donc en un point donné f΄(а)=1/2√а. En substituant toutes les valeurs obtenues dans l'équation tangente, nous obtenons y = √a + (x-a)/2√a. En transformant l'équation, nous obtenons y=x/2√а+√а/2. Sachant que la tangente passe par le point (0;3), on trouve la valeur de a. On trouve a à partir de 3=√a/2. Donc √a=6, a=36. On retrouve l'équation tangente y=x/12+3. La figure montre le graphique de la fonction considérée et la tangente souhaitée construite.

Il est rappelé aux élèves les égalités approximatives Δy=≈f΄(x)Δxet f(x+Δx)-f(x)≈f΄(x)Δx. En prenant x=a, x+Δx=x, Δx=x-a, on obtient f(x)- f(a)≈f΄(a)(x-a), donc f(x)≈f(a)+ f΄( a)(x-a).

Dans l'exemple 4, il faut trouver la valeur approximative de l'expression 2,003 6. Puisqu'il faut trouver la valeur de la fonction f(x)=x 6 au point x=2,003, on peut utiliser la formule bien connue, en prenant f(x)=x 6, a=2, f(a )= f(2)=64, f ΄(x)=6x 5. Dérivée au point f΄(2)=192. Par conséquent, 2,003 6 ≈65-192·0,003. Après avoir calculé l'expression, nous obtenons 2,003 6 ≈64,576.

La leçon vidéo « L'équation d'une tangente au graphique d'une fonction » est recommandée pour une utilisation dans un cours de mathématiques traditionnel à l'école. Pour un enseignant qui enseigne à distance, le matériel vidéo aidera à expliquer le sujet plus clairement. La vidéo peut être recommandée aux étudiants pour qu'ils la revoient indépendamment si nécessaire pour approfondir leur compréhension du sujet.

DÉCODAGE DE TEXTE :

On sait que si un point M (a; f(a)) (em de coordonnées a et ef de a) appartient au graphe de la fonction y = f (x) et si à ce point il est possible de tracer une tangente au graphique de la fonction qui n'est pas perpendiculaire à l'axe des abscisses, alors le coefficient angulaire de la tangente est égal à f"(a) (eff premier de a).

Soit une fonction y = f(x) et un point M (a; f(a)), et on sait également que f´(a) existe. Créons une équation pour la tangente au graphique d'une fonction donnée en un point donné. Cette équation, comme l'équation de toute droite non parallèle à l'axe des ordonnées, a la forme y = kx+m (le y est égal à ka x plus em), la tâche est donc de trouver les valeurs de les coefficients k et m (ka et em)

Coefficient d'angle k= f"(a). Pour calculer la valeur de m, on utilise le fait que la droite souhaitée passe par le point M(a; f (a)). Cela signifie que si l'on substitue les coordonnées du point M dans l'équation de la droite, on obtient l'égalité correcte : f(a) = ka+m, d'où on trouve que m = f(a) - ka.

Il reste à substituer les valeurs trouvées des coefficients ki et m dans l'équation de la droite :

y = kx+(f(a) -ka);

y = f(a)+k(x-a);

oui= F(un)+ F"(un) (X- un). ( y est égal à ef de a plus ef prime de a, multiplié par x moins a).

Nous avons obtenu l'équation de la tangente au graphique de la fonction y = f(x) au point x=a.

Si, disons, y = x 2 et x = -2 (c'est-à-dire a = -2), alors f (a) = f (-2) = (-2) 2 = 4 ; f´(x) = 2x, ce qui signifie f"(a) = f´(-2) = 2·(-2) = -4. (alors le ef de a est égal à quatre, le ef du premier de x est égal à deux x, ce qui signifie ef premier à partir de a est égal à moins quatre)

En remplaçant les valeurs trouvées a = -2, f(a) = 4, f"(a) = -4 dans l'équation, nous obtenons : y = 4+(-4)(x+2), c'est-à-dire y = -4x -4.

(E est égal à moins quatre x moins quatre)

Créons une équation pour la tangente au graphique de la fonction y = tgx(grec égal à la tangente x) à l'origine. On a : a = 0, f(0) = tan0=0 ;

f"(x)= , ce qui signifie f"(0) = l. En remplaçant les valeurs trouvées a=0, f(a)=0, f´(a) = 1 dans l'équation, nous obtenons : y=x.

Résumons nos étapes pour trouver l'équation de la tangente au graphique d'une fonction au point x à l'aide d'un algorithme.

ALGORITHME DE DÉVELOPPEMENT D'UNE ÉQUATION POUR UNE TANGENTE AU GRAPHE DE LA FONCTION y = f(x) :

1) Désigner l'abscisse du point de tangence par la lettre a.

2) Calculez f(a).

3) Trouvez f´(x) et calculez f´(a).

4) Remplacez les nombres trouvés a, f(a), f´(a) dans la formule oui= F(un)+ F"(un) (X- un).

Exemple 1. Créer une équation pour la tangente au graphique de la fonction y = - dans

point x = 1.

Solution. Utilisons l'algorithme, en tenant compte du fait que dans dans cet exemple

2) f(a)=f(1)=- =-1

3) f´(x)=; f´(une)= f´(1)= =1.

4) Remplacez les trois nombres trouvés : a = 1, f(a) = -1, f"(a) = 1 dans la formule. Nous obtenons : y = -1+(x-1), y = x-2 .

Réponse : y = x-2.

Exemple 2. Étant donné la fonction y = x3 +3x2 -2x-2. Notez l'équation de la tangente au graphique de la fonction y = f(x), parallèle à la droite y = -2x +1.

En utilisant l'algorithme de composition de l'équation tangente, on prend en compte que dans cet exemple f(x) = x3 +3x2 -2x-2, mais l'abscisse du point tangent n'est pas indiquée ici.

Commençons par penser comme ça. La tangente souhaitée doit être parallèle à la droite y = -2x+1. Et les lignes parallèles ont des coefficients angulaires égaux. Cela signifie que le coefficient angulaire de la tangente est égal au coefficient angulaire de la droite donnée : k tangente. = -2. Hok cas. = f"(a). Ainsi, nous pouvons trouver la valeur de a à partir de l'équation f ´(a) = -2.

Trouvons la dérivée de la fonction y=F(X):

F"(X)= (x 3 +3x 2 -2x-2)´ =3x 2 +6x-2 ;F"(une)= 3a 2 +6a-2.

D'après l'équation f"(a) = -2, c'est-à-dire 3a 2 +6a-2=-2 on trouve un 1 =0, un 2 =-2. Cela signifie qu'il existe deux tangentes qui satisfont aux conditions du problème : l'une au point d'abscisse 0, l'autre au point d'abscisse -2.

Vous pouvez maintenant suivre l'algorithme.

1) un 1 =0 et 2 =-2.

2) f(une 1)= 0 3 +3·0 2 -2∙0-2=-2; f(une 2)= (-2) 3 +3·(-2) 2 -2·(-2)-2=6;

3) f"(une 1) = f"(une 2) = -2.

4) En remplaçant les valeurs a 1 = 0, f(a 1) = -2, f"(a 1) = -2 dans la formule, nous obtenons :

y=-2-2(x-0), y=-2x-2.

En remplaçant les valeurs a 2 = -2, f(a 2) =6, f"(a 2) = -2 dans la formule, nous obtenons :

y=6-2(x+2), y=-2x+2.

Réponse : y=-2x-2, y=-2x+2.

Exemple 3. A partir du point (0; 3) tracez une tangente au graphique de la fonction y = . Solution. Utilisons l'algorithme pour composer l'équation tangente, en tenant compte du fait que dans cet exemple f(x) = . A noter qu'ici, comme dans l'exemple 2, l'abscisse du point tangent n'est pas explicitement indiquée. Néanmoins, nous suivons l'algorithme.

1) Soit x = a l'abscisse du point de tangence ; il est clair que a >0.

3) f´(x)=()´=; f´(une) =.

4) Remplacer les valeurs de a, f(a) = , f"(a) = dans la formule

y=f (a) +f "(a) (x-a), on a:

Par condition, la tangente passe par le point (0 ; 3). En substituant les valeurs x = 0, y = 3 dans l'équation, nous obtenons : 3 = , puis =6, a =36.

Comme vous pouvez le voir, dans cet exemple, ce n'est qu'à la quatrième étape de l'algorithme que nous avons réussi à trouver l'abscisse du point tangent. En substituant la valeur a =36 dans l'équation, nous obtenons : y=+3

En figue. La figure 1 montre une illustration géométrique de l'exemple considéré : un graphique de la fonction y = est construit, une droite est tracée y = +3.

Réponse : y = +3.

On sait que pour une fonction y = f(x), qui a une dérivée au point x, l'égalité approximative est valable : Δyf´(x)Δx (delta y est approximativement égal à l'eff premier de x multiplié par delta x)

ou, plus en détail, f(x+Δx)-f(x) f´(x) Δx (eff de x plus delta x moins ef de x est approximativement égal à ef prime de x par delta x).

Pour faciliter la discussion ultérieure, modifions la notation :

au lieu de x nous écrirons UN,

au lieu de x+Δx on écrira x

au lieu de Δx nous écrirons x-a.

Alors l’égalité approximative écrite ci-dessus prendra la forme :

f(x)-f(a)f´(a)(x-a)

f(x)f(a)+f´(a)(x-a). (eff de x est approximativement égal à ef de a plus ef prime de a, multiplié par la différence entre x et a).

Exemple 4 : Trouver une valeur approximative expression numérique 2,003 6 .

Solution. Nous parlons de trouver la valeur de la fonction y = x 6 au point x = 2,003. Utilisons la formule f(x)f(a)+f´(a)(x-a), en tenant compte du fait que dans cet exemple f(x)=x 6, a = 2,f(a) = f(2) = 2 6 =64 ; x = 2,003, f"(x) = 6x 5 et, donc, f"(a) = f"(2) = 6 2 5 =192.

En conséquence nous obtenons :

2,003 6 64+192 · 0,003, soit 2,0036 =64,576.

Si on utilise une calculatrice, on obtient :

2,003 6 = 64,5781643...

Comme vous pouvez le constater, la précision de l’approximation est tout à fait acceptable.

Au stade actuel de développement de l'éducation, l'une de ses tâches principales est la formation d'une personnalité à la pensée créative. La capacité de créativité des étudiants ne peut être développée que s'ils sont systématiquement impliqués dans les bases des activités de recherche. La base permettant aux étudiants d'utiliser leurs pouvoirs créatifs, leurs capacités et leurs talents est constituée de connaissances et de compétences à part entière. À cet égard, le problème de la formation d'un système de connaissances et de compétences de base pour chaque sujet du cours de mathématiques scolaire n'est pas négligeable. Dans le même temps, des compétences à part entière devraient être l'objectif didactique non pas de tâches individuelles, mais d'un système soigneusement pensé de celles-ci. Au sens le plus large, un système est compris comme un ensemble d’éléments en interaction interconnectés, intègres et dotés d’une structure stable.

Considérons une technique pour apprendre aux étudiants à écrire une équation pour une tangente au graphique d'une fonction. Essentiellement, tous les problèmes liés à la recherche de l'équation tangente se résument à la nécessité de sélectionner parmi un ensemble (faisceau, famille) de droites celles qui satisfont à une certaine exigence - elles sont tangentes au graphique d'une certaine fonction. Dans ce cas, l'ensemble des lignes à partir duquel la sélection est effectuée peut être précisé de deux manières :

a) un point situé sur le plan xOy (crayon central de lignes) ;
b) coefficient angulaire (faisceau parallèle de lignes droites).

A cet égard, en étudiant le thème « Tangente au graphe d'une fonction » afin d'isoler les éléments du système, nous avons identifié deux types de problèmes :

1) problèmes sur une tangente donnés par le point par lequel elle passe ;
2) problèmes sur une tangente donnée par sa pente.

La formation à la résolution de problèmes tangents a été réalisée à l'aide de l'algorithme proposé par A.G. Mordkovitch. Sa différence fondamentale avec celles déjà connues est que l'abscisse du point tangent est désignée par la lettre a (au lieu de x0), et donc l'équation tangente prend la forme

y = f(une) + f "(une)(x – une)

(à comparer avec y = f(x 0) + f "(x 0)(x – x 0)). Cette technique méthodologique, à notre avis, permet aux étudiants de comprendre rapidement et facilement où sont écrites les coordonnées du point actuel l'équation générale de la tangente et où sont les points de contact.

Algorithme de composition de l'équation tangente au graphique de la fonction y = f(x)

1. Désignons l'abscisse du point tangent par la lettre a.
2. Trouvez f(a).
3. Trouvez f "(x) et f "(a).
4. Remplacez les nombres trouvés a, f(a), f "(a) dans l'équation tangente générale y = f(a) = f "(a)(x – a).

Cet algorithme peut être compilé sur la base de l’identification indépendante des opérations par les étudiants et de la séquence de leur mise en œuvre.

La pratique a montré que la solution séquentielle de chacun des problèmes clés à l'aide d'un algorithme permet de développer les compétences d'écriture de l'équation d'une tangente au graphique d'une fonction par étapes, et les étapes de l'algorithme servent de points de référence pour les actions. . Cette approche correspond à la théorie de la formation progressive des actions mentales développée par P.Ya. Galperin et N.F. Talyzina.

Dans le premier type de tâches, deux tâches clés ont été identifiées :

• la tangente passe par un point situé sur la courbe (problème 1) ;
• la tangente passe par un point ne se trouvant pas sur la courbe (problème 2).

Tâche 1. Écrivez une équation pour la tangente au graphique de la fonction au point M(3; – 2).

Solution. Le point M(3; – 2) est un point tangent, puisque

1. a = 3 – abscisse du point tangent.
2.f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – équation tangente.

Problème 2. Écrivez les équations de toutes les tangentes au graphique de la fonction y = – x 2 – 4x + 2 passant par le point M(– 3 ; 6).

Solution. Le point M(– 3 ; 6) n'est pas un point de tangence, puisque f(– 3) 6 (Fig. 2).

2. f(une) = – une 2 – 4une + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – équation tangente.

La tangente passe par le point M(– 3; 6), donc ses coordonnées satisfont à l'équation de la tangente.

6 = – une 2 – 4une + 2 – 2(une + 2)(– 3 – une),
un 2 + 6a + 8 = 0 ^ un 1 = – 4, un 2 = – 2.

Si a = – 4, alors l’équation tangente est y = 4x + 18.

Si a = – 2, alors l’équation tangente a la forme y = 6.

Dans le deuxième type, les tâches clés seront les suivantes :

• la tangente est parallèle à une ligne (problème 3) ;
• la tangente passe sous un certain angle par rapport à la ligne donnée (problème 4).

Problème 3. Écrivez les équations de toutes les tangentes au graphique de la fonction y = x 3 – 3x 2 + 3, parallèle à la droite y = 9x + 1.

1. a – abscisse du point tangent.
2. f(une) = une 3 – 3une 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Mais, d'un autre côté, f "(a) = 9 (condition de parallélisme). Cela signifie que nous devons résoudre l'équation 3a 2 – 6a = 9. Ses racines sont a = – 1, a = 3 (Fig. 3 ).

4. 1) une = – 1 ;
2) f(– 1) = – 1;
3) f "(– 1) = 9 ;
4) y = – 1 + 9(x + 1) ;

y = 9x + 8 – équation tangente ;

1) une = 3 ;
2) f(3) = 3;
3) f "(3) = 9 ;
4) y = 3 + 9(x – 3);

y = 9x – 24 – équation tangente.

Problème 4. Écrivez l'équation de la tangente au graphique de la fonction y = 0,5x 2 – 3x + 1, passant sous un angle de 45° par rapport à la droite y = 0 (Fig. 4).

Solution. A partir de la condition f "(a) = tan 45° on trouve a : a – 3 = 1 ^ a = 4.

1. a = 4 – abscisse du point tangent.
2. f(4) = 8 – 12 + 1 = – 3.
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – équation tangente.

Il est facile de montrer que la solution à tout autre problème revient à résoudre un ou plusieurs problèmes clés. Considérons les deux problèmes suivants à titre d'exemple.

1. Écrivez les équations des tangentes à la parabole y = 2x 2 – 5x – 2, si les tangentes se coupent à angle droit et que l'une d'elles touche la parabole au point d'abscisse 3 (Fig. 5).

Solution. L’abscisse du point tangent étant donnée, la première partie de la solution se réduit au problème clé 1.

1. a = 3 – abscisse du point de tangence d'un des côtés de l'angle droit.
2.f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – équation de la première tangente.

Soit a l'angle d'inclinaison de la première tangente. Puisque les tangentes sont perpendiculaires, alors l’angle d’inclinaison de la deuxième tangente est égal à. De l’équation y = 7x – 20 de la première tangente nous avons tg a = 7. Trouvons

Cela signifie que la pente de la deuxième tangente est égale à .

La solution supplémentaire se résume à la tâche clé 3.

Soit B(c; f(c)) le point de tangence de la deuxième droite, alors

1. – abscisse du deuxième point de tangence.
2.
3.
4.
– équation de la deuxième tangente.

Note. Le coefficient angulaire de la tangente peut être trouvé plus facilement si les élèves connaissent le rapport des coefficients des droites perpendiculaires k 1 k 2 = – 1.

2. Écrivez les équations de toutes les tangentes communes aux graphiques de fonctions

Solution. La tâche revient à trouver l'abscisse des points tangents des tangentes communes, c'est-à-dire résoudre le problème clé 1 sous forme générale, établir un système d'équations puis le résoudre (Fig. 6).

1. Soit a l'abscisse du point tangent situé sur le graphique de la fonction y = x 2 + x + 1.
2. f(une) = une 2 + une + 1.
3. f"(a) = 2a + 1.
4. y = une 2 + une + 1 + (2a + 1)(x – une) = (2a + 1)x + 1 – une 2 .

1. Soit c l'abscisse du point tangent situé sur le graphique de la fonction
2.
3. f"(c) = c.
4.

Puisque les tangentes sont générales, alors

Donc y = x + 1 et y = – 3x – 3 sont des tangentes communes.

L'objectif principal des tâches considérées est de préparer les étudiants à reconnaître de manière autonome le type de problème clé lors de la résolution de problèmes plus complexes qui nécessitent certaines compétences de recherche (capacité d'analyser, de comparer, de généraliser, d'émettre une hypothèse, etc.). Ces tâches incluent toute tâche dans laquelle la tâche clé est incluse en tant que composant. Considérons comme exemple le problème (inverse du problème 1) de trouver une fonction à partir de la famille de ses tangentes.

3. Pour quoi b et c sont les droites y = x et y = – 2x tangentes au graphique de la fonction y = x 2 + bx + c ?

Soit t l'abscisse du point de tangence de la droite y = x avec la parabole y = x 2 + bx + c ; p est l'abscisse du point de tangence de la droite y = – 2x avec la parabole y = x 2 + bx + c. Alors l'équation tangente y = x prendra la forme y = (2t + b)x + c – t 2 , et l'équation tangente y = – 2x prendra la forme y = (2p + b)x + c – p 2 .

Composons et résolvons un système d'équations

Répondre: