Calcul de la variance d'une variable aléatoire. Taux de variation absolus
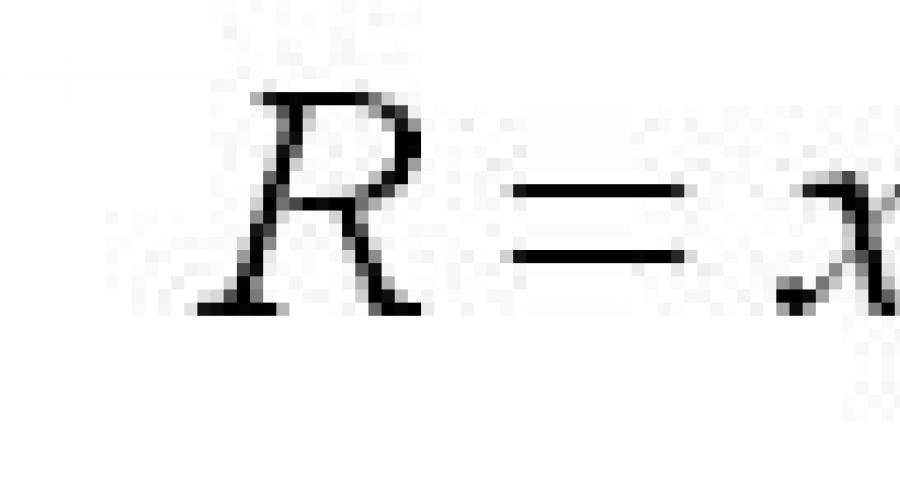
Lire aussi
Pas
Exemple de calcul de variance
-
Enregistrez les valeurs de l'échantillon. Dans la plupart des cas, seuls des échantillons de certaines populations sont à la disposition des statisticiens. Par exemple, en règle générale, les statisticiens n'analysent pas le coût du maintien de la population de toutes les voitures en Russie - ils analysent un échantillon aléatoire de plusieurs milliers de voitures. Un tel échantillon aidera à déterminer le coût moyen par voiture, mais très probablement, la valeur résultante sera loin de la valeur réelle.
- Par exemple, analysons le nombre de petits pains vendus dans un café en 6 jours, pris dans un ordre aléatoire. L'échantillon a la forme suivante : 17, 15, 23, 7, 9, 13. Il s'agit d'un échantillon, pas d'une population, car nous n'avons pas de données sur les petits pains vendus pour chaque jour d'ouverture du café.
- Si vous disposez d'une population et non d'un échantillon de valeurs, passez à la section suivante.
-
Notez la formule de calcul de la variance de l'échantillon. La dispersion est une mesure de la propagation des valeurs d'une certaine quantité. Plus la valeur de dispersion est proche de zéro, plus les valeurs sont regroupées. Lorsque vous travaillez avec un échantillon de valeurs, utilisez la formule suivante pour calculer la variance :
- s 2 (\displaystyle s^(2)) = ∑[(x je (\displaystyle x_(i))-X) 2 (\ style d'affichage ^ (2))] / (n - 1)
- s 2 (\displaystyle s^(2)) est la dispersion. La dispersion est mesurée en unités carrées.
- x je (\displaystyle x_(i))- chaque valeur de l'échantillon.
- x je (\displaystyle x_(i)) vous devez soustraire x̅, le mettre au carré, puis ajouter les résultats.
- x̅ – moyenne de l'échantillon (moyenne de l'échantillon).
- n est le nombre de valeurs dans l'échantillon.
-
Calculez la moyenne de l'échantillon. Il est noté x̅. La moyenne de l'échantillon est calculée comme une moyenne arithmétique normale : additionnez toutes les valeurs de l'échantillon, puis divisez le résultat par le nombre de valeurs de l'échantillon.
- Dans notre exemple, additionnez les valeurs de l'échantillon : 15 + 17 + 23 + 7 + 9 + 13 = 84
Divisez maintenant le résultat par le nombre de valeurs dans l'échantillon (dans notre exemple il y en a 6) : 84 ÷ 6 = 14.
Moyenne de l'échantillon x̅ = 14. - La moyenne de l'échantillon est la valeur centrale autour de laquelle les valeurs de l'échantillon sont distribuées. Si les valeurs de l'échantillon se regroupent autour de la moyenne de l'échantillon, la variance est faible ; sinon, la dispersion est grande.
- Dans notre exemple, additionnez les valeurs de l'échantillon : 15 + 17 + 23 + 7 + 9 + 13 = 84
-
Soustrayez la moyenne de l'échantillon de chaque valeur de l'échantillon. Calculez maintenant la différence x je (\displaystyle x_(i))- x̅, où x je (\displaystyle x_(i))- chaque valeur de l'échantillon. Chaque résultat obtenu indique dans quelle mesure une valeur particulière s'écarte de la moyenne de l'échantillon, c'est-à-dire à quel point cette valeur est éloignée de la moyenne de l'échantillon.
- Dans notre exemple :
x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1 - L'exactitude des résultats obtenus est facile à vérifier, puisque leur somme doit être égale à zéro. Ceci est lié à la définition de la valeur moyenne, puisque valeurs négatives(distances entre la valeur moyenne et les valeurs inférieures) sont entièrement compensées valeurs positives(distances des moyennes aux grandes valeurs).
- Dans notre exemple :
-
Comme indiqué ci-dessus, la somme des différences x je (\displaystyle x_(i))- x̅ doit être égal à zéro. Cela signifie que la variance moyenne est toujours nulle, ce qui ne donne aucune idée de la dispersion des valeurs d'une certaine quantité. Pour résoudre ce problème, mettez chaque différence au carré x je (\displaystyle x_(i))- X. Ainsi, vous n'obtiendrez que des nombres positifs qui, une fois additionnés, ne totaliseront jamais 0.
- Dans notre exemple :
(x 1 (\displaystyle x_(1))-X) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
(x 2 (\displaystyle (x_(2))-X) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
9 2 = 81
(-7) 2 = 49
(-5) 2 = 25
(-1) 2 = 1 - Vous avez trouvé le carré de la différence - x̅) 2 (\ style d'affichage ^ (2)) pour chaque valeur de l'échantillon.
- Dans notre exemple :
-
Calculer la somme des différences au carré. Autrement dit, trouvez la partie de la formule qui s'écrit comme suit : ∑[( x je (\displaystyle x_(i))-X) 2 (\ style d'affichage ^ (2))]. Ici, le signe Σ signifie la somme des différences au carré pour chaque valeur x je (\displaystyle x_(i)) dans l'échantillon. Vous avez déjà trouvé les différences au carré (x je (\displaystyle (x_(i))-X) 2 (\ style d'affichage ^ (2)) pour chaque valeur x je (\displaystyle x_(i)) dans l'échantillon ; maintenant, ajoutez simplement ces carrés.
- Dans notre exemple : 9 + 1 + 81 + 49 + 25 + 1 = 166 .
-
Divisez le résultat par n - 1, où n est le nombre de valeurs dans l'échantillon. Il y a quelque temps, pour calculer la variance de l'échantillon, les statisticiens divisaient simplement le résultat par n ; dans ce cas, vous obtiendrez la moyenne de la variance au carré, ce qui est idéal pour décrire la variance d'un échantillon donné. Mais rappelez-vous que tout échantillon ne représente qu'une petite partie de la population générale de valeurs. Si vous prenez un échantillon différent et faites les mêmes calculs, vous obtiendrez un résultat différent. Il s'avère que la division par n - 1 (plutôt que par n) donne une meilleure estimation de la variance de la population, ce que vous recherchez. La division par n - 1 est devenue courante, elle est donc incluse dans la formule de calcul de la variance de l'échantillon.
- Dans notre exemple, l'échantillon comprend 6 valeurs, c'est-à-dire n = 6.
Écart d'échantillon = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
- Dans notre exemple, l'échantillon comprend 6 valeurs, c'est-à-dire n = 6.
-
La différence entre la variance et l'écart type. Notez que la formule contient un exposant, de sorte que la variance est mesurée en unités au carré de la valeur analysée. Parfois, une telle valeur est assez difficile à exploiter; dans de tels cas, l'écart type est utilisé, qui est égal à la racine carrée de la variance. C'est pourquoi la variance de l'échantillon est notée s 2 (\displaystyle s^(2)), et l'écart-type de l'échantillon comme s (\ displaystyle s).
- Dans notre exemple, l'écart type de l'échantillon est : s = √33,2 = 5,76.
Calcul de la variance de la population
-
Analyser un ensemble de valeurs. L'ensemble comprend toutes les valeurs de la quantité considérée. Par exemple, si vous étudiez l'âge des habitants Région de Léningrad, alors la population comprend l'âge de tous les habitants de cette zone. Dans le cas où vous travaillez avec un agrégat, il est recommandé de créer un tableau et d'y saisir les valeurs de l'agrégat. Considérez l'exemple suivant :
- Il y a 6 aquariums dans une certaine pièce. Chaque aquarium contient le nombre suivant de poissons :
x 1 = 5 (\displaystyle x_(1)=5)
x 2 = 5 (\displaystyle x_(2)=5)
x 3 = 8 (\displaystyle x_(3)=8)
x 4 = 12 (\displaystyle x_(4)=12)
x 5 = 15 (\displaystyle x_(5)=15)
x 6 = 18 (\displaystyle x_(6)=18)
- Il y a 6 aquariums dans une certaine pièce. Chaque aquarium contient le nombre suivant de poissons :
-
Notez la formule de calcul de la variance de la population.Étant donné que l'ensemble comprend toutes les valeurs d'une certaine quantité, la formule ci-dessous vous permet d'obtenir valeur exacteécart démographique. Pour distinguer la variance de la population de la variance de l'échantillon (qui n'est qu'une estimation), les statisticiens utilisent diverses variables :
- σ 2 (\ style d'affichage ^ (2)) = (∑(x je (\displaystyle x_(i)) - μ) 2 (\ style d'affichage ^ (2))) / n
- σ 2 (\ style d'affichage ^ (2))- la variance de la population (lue comme "sigma au carré"). La dispersion est mesurée en unités carrées.
- x je (\displaystyle x_(i))- chaque valeur dans l'agrégat.
- Σ est le signe de la somme. C'est-à-dire que pour chaque valeur x je (\displaystyle x_(i)) soustrayez μ, mettez-le au carré, puis additionnez les résultats.
- μ est la moyenne de la population.
- n est le nombre de valeurs dans la population générale.
-
Calculez la moyenne de la population. Lorsque l'on travaille avec la population générale, sa valeur moyenne est notée μ (mu). La moyenne de la population est calculée comme la moyenne arithmétique habituelle : additionnez toutes les valeurs de la population, puis divisez le résultat par le nombre de valeurs de la population.
- Gardez à l'esprit que les moyennes ne sont pas toujours calculées comme la moyenne arithmétique.
- Dans notre exemple, la population moyenne : μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
-
Soustrayez la moyenne de la population de chaque valeur de la population. Plus la différence est proche de zéro, plus signification spécifiqueà la moyenne de la population. Trouvez la différence entre chaque valeur de la population et sa moyenne, et vous aurez un premier aperçu de la distribution des valeurs.
- Dans notre exemple :
x 1 (\displaystyle x_(1))-μ = 5 - 10,5 = -5,5
x 2 (\displaystyle x_(2))-μ = 5 - 10,5 = -5,5
x 3 (\displaystyle x_(3))-μ = 8 - 10,5 = -2,5
x 4 (\displaystyle x_(4))- µ = 12 - 10,5 = 1,5
x 5 (\displaystyle x_(5))- µ = 15 - 10,5 = 4,5
x 6 (\displaystyle x_(6))- µ = 18 - 10,5 = 7,5
- Dans notre exemple :
-
Mettez au carré chaque résultat que vous obtenez. Les valeurs de différence seront à la fois positives et négatives ; si vous placez ces valeurs sur une droite numérique, elles se situeront à droite et à gauche de la moyenne de la population. Ce n'est pas bon pour calculer la variance, car les nombres positifs et négatifs s'annulent. Par conséquent, mettez chaque différence au carré pour obtenir des nombres exclusivement positifs.
- Dans notre exemple :
(x je (\displaystyle x_(i)) - μ) 2 (\ style d'affichage ^ (2)) pour chaque valeur de population (de i = 1 à i = 6) :
(-5,5)2 (\ style d'affichage ^ (2)) = 30,25
(-5,5)2 (\ style d'affichage ^ (2)), où x n (\displaystyle x_(n)) est la dernière valeur de la population. - Pour calculer la valeur moyenne des résultats obtenus, il faut trouver leur somme et la diviser par n : (( x 1 (\displaystyle x_(1)) - μ) 2 (\ style d'affichage ^ (2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\ style d'affichage ^ (2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\ style d'affichage ^ (2))) / n
- Écrivons maintenant l'explication ci-dessus en utilisant des variables : (∑( x je (\displaystyle x_(i)) - μ) 2 (\ style d'affichage ^ (2))) / n et obtenir une formule pour calculer la variance de la population.
- Dans notre exemple :
Cette page décrit exemple standard trouver la variance, vous pouvez également consulter d'autres tâches pour la trouver
Exemple 1. Détermination de groupe, moyenne de groupe, inter-groupe et variance totale
Exemple 2. Recherche de la variance et du coefficient de variation dans un tableau de regroupement
Exemple 3. Trouver la variance dans une série discrète
Exemple 4. Nous avons les données suivantes pour un groupe de 20 étudiants par correspondance. Il est nécessaire de construire une série d'intervalles de la distribution des caractéristiques, de calculer la valeur moyenne de la caractéristique et d'étudier sa variance
Construisons un groupement d'intervalles. Déterminons la plage de l'intervalle par la formule :
![]()
où X max est la valeur maximale de la caractéristique de regroupement ;
X min est la valeur minimale de la caractéristique de regroupement ;
n est le nombre d'intervalles :
Nous acceptons n=5. Le pas est: h \u003d (192 - 159) / 5 \u003d 6,6
Faisons un regroupement par intervalle

Pour d'autres calculs, nous allons construire une table auxiliaire :

X "i - le milieu de l'intervalle. (par exemple, le milieu de l'intervalle 159 - 165,6 \u003d 162,3)
La croissance moyenne des étudiants est déterminée par la formule de la moyenne pondérée arithmétique:

Nous déterminons la dispersion par la formule :
La formule peut être convertie comme ceci :

De cette formule il résulte que l'écart est la différence entre la moyenne des carrés des options et le carré et la moyenne.
Écart dans les séries de variation avec des intervalles égaux selon la méthode des moments peut être calculé de la manière suivante en utilisant la deuxième propriété de dispersion (en divisant toutes les options par la valeur de l'intervalle). Définition de la variance, calculé par la méthode des moments, selon la formule suivante prend moins de temps :

où i est la valeur de l'intervalle ;
A - zéro conditionnel, ce qui est pratique pour utiliser le milieu de l'intervalle avec la fréquence la plus élevée;
m1 est le carré du moment du premier ordre ;
m2 - moment du second ordre
Écart de fonctionnalité (si dans la population statistique l'attribut change de telle manière qu'il n'y a que deux options mutuellement exclusives, alors cette variabilité est appelée alternative) peut être calculée par la formule :

En substituant dans cette formule de dispersion q = 1- p, on obtient :

Types de dispersion
Écart total mesure la variation d'un trait sur l'ensemble de la population dans son ensemble sous l'influence de tous les facteurs qui provoquent cette variation. Il est égal au carré moyen des écarts valeurs individuelles caractéristique x de la valeur moyenne globale de x et peut être définie comme une variance simple ou une variance pondérée.
Écart intragroupe caractérise la variation aléatoire, c'est-à-dire partie de la variation, qui est due à l'influence de facteurs non pris en compte et ne dépend pas du signe-facteur sous-jacent au regroupement. Cette variance est égale au carré moyen des écarts des valeurs individuelles de l'attribut au sein du groupe X par rapport à la moyenne arithmétique du groupe et peut être calculée comme une variance simple ou comme une variance pondérée.
De cette façon, mesures de variance intra-groupe variation d'un trait au sein d'un groupe et est déterminé par la formule :

où xi - moyenne du groupe ;
ni est le nombre d'unités dans le groupe.
Par exemple, les variances intra-groupe, qui doivent être déterminées dans le cadre de l'étude de l'influence des qualifications des travailleurs sur le niveau de productivité du travail dans l'atelier, montrent des variations de production dans chaque groupe causées par tous les facteurs possibles ( état techniqueéquipement, disponibilité des outils et des matériaux, âge des travailleurs, intensité de travail, etc.), à l'exception des différences de catégorie de qualification(au sein d'un groupe, tous les travailleurs ont les mêmes qualifications).
Calculons enMMEEXCELLERvariance et écart-type de l'échantillon. On calcule aussi la variance d'une variable aléatoire si sa distribution est connue.
Considérez d'abord dispersion, alors écart-type.
Écart d'échantillon
Écart d'échantillon (écart d'échantillon,goûtervariance) caractérise la répartition des valeurs dans le tableau par rapport à .
Les 3 formules sont mathématiquement équivalentes.
Il ressort de la première formule que écart d'échantillon est la somme des écarts au carré de chaque valeur du tableau de la moyenne divisé par la taille de l'échantillon moins 1.
dispersion échantillons la fonction DISP() est utilisée, eng. le nom du VAR, c'est-à-dire Variance. Depuis MS EXCEL 2010, il est recommandé d'utiliser son DISP.V() analogique, eng. le nom VARS, c'est-à-dire Variance de l'échantillon. De plus, à partir de la version de MS EXCEL 2010, il existe une fonction DISP.G (), eng. Nom VARP, c'est-à-dire Population VARIance qui calcule dispersion pour population. Toute la différence se résume au dénominateur : au lieu de n-1 comme DISP.V() , DISP.G() a juste n au dénominateur. Avant MS EXCEL 2010, la fonction VARP() était utilisée pour calculer la variance de la population.
Écart d'échantillon
=CARRÉ(Échantillon)/(COMPTE(Échantillon)-1)
=(SUMSQ(Échantillon)-COUNT(Échantillon)*MOYENNE(Échantillon)^2)/ (COUNT(Échantillon)-1)- la formule habituelle
=SOMME((Échantillon -MOYENNE(Échantillon))^2)/ (COMPTE(Échantillon)-1) –
Écart d'échantillon est égal à 0 uniquement si toutes les valeurs sont égales les unes aux autres et, par conséquent, sont égales valeur moyenne. Habituellement que plus de valeur dispersion, plus la dispersion des valeurs dans le tableau est grande.
Écart d'échantillon est une estimation ponctuelle dispersion distribution de la variable aléatoire à partir de laquelle goûter. À propos de la construction intervalles de confiance lors de l'évaluation dispersion peut être lu dans l'article.
Variance d'une variable aléatoire
Calculer dispersion variable aléatoire, vous devez la connaître.
Pour dispersion la variable aléatoire X utilise souvent la notation Var(X). Dispersion est égal au carré de l'écart à la moyenne E(X) : Var(X)=E[(X-E(X)) 2 ]
dispersion calculé par la formule :

où x i est la valeur que peut prendre la variable aléatoire, et μ est la valeur moyenne (), p(x) est la probabilité que la variable aléatoire prenne la valeur x.
Si la variable aléatoire a , alors dispersion calculé par la formule :

Dimension dispersion correspond au carré de l'unité de mesure des valeurs d'origine. Par exemple, si les valeurs de l'échantillon sont des mesures du poids de la pièce (en kg), alors la dimension de la variance serait kg 2 . Cela peut être difficile à interpréter, donc, pour caractériser la dispersion des valeurs, une valeur égale à la racine carrée de dispersion – écart-type.
Quelques propriétés dispersion:
Var(X+a)=Var(X), où X est une variable aléatoire et a une constante.
Var(aå)=a 2 Var(X)
Var(X)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2=E(X 2)- 2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2
Cette propriété de dispersion est utilisée dans article sur la régression linéaire.
Var(X+Y)=Var(X) + Var(Y) + 2*Cov(X;Y), où X et Y sont des variables aléatoires, Cov(X;Y) est la covariance de ces variables aléatoires.
Si les variables aléatoires sont indépendantes, alors leur covariance est 0, et donc Var(X+Y)=Var(X)+Var(Y). Cette propriété de la variance est utilisée dans la sortie.
Montrons que pour des grandeurs indépendantes Var(X-Y)=Var(X+Y). En effet, Var(X-Y)= Var(X-Y)= Var(X+(-Y))= Var(X)+Var(-Y)= Var(X)+Var(-Y)= Var( X)+(- 1) 2 Var(Y)= Var(X)+Var(Y)= Var(X+Y). Cette propriété de la variance est utilisée pour tracer .
Écart-type de l'échantillon
Écart-type de l'échantillon est une mesure de la dispersion des valeurs dans l'échantillon par rapport à leur .
Par définition, écart-type est égal à la racine carrée de dispersion:

Écart-type ne tient pas compte de l'ampleur des valeurs dans échantillonnage, mais seulement le degré de dispersion des valeurs autour d'eux milieu. Prenons un exemple pour illustrer cela.
Calculons l'écart type pour 2 échantillons : (1 ; 5 ; 9) et (1001 ; 1005 ; 1009). Dans les deux cas, s=4. Il est évident que le rapport de l'écart type aux valeurs du tableau est significativement différent pour les échantillons. Pour de tels cas, utilisez Le coefficient de variation(Coefficient de variation, CV) - ratio écart-typeà la moyenne arithmétique, exprimé en pourcentage.
Dans MS EXCEL 2007 et versions antérieures pour le calcul Écart-type de l'échantillon la fonction =STDEV() est utilisée, eng. le nom STDEV, c'est-à-dire écart-type. Depuis MS EXCEL 2010, il est recommandé d'utiliser son analogue = STDEV.B () , eng. nom STDEV.S, c'est-à-dire Exemple d'écart-type.
De plus, à partir de la version de MS EXCEL 2010, il existe une fonction STDEV.G () , eng. nom STDEV.P, c'est-à-dire Population STandard DEViation qui calcule écart-type pour population. Toute la différence se résume au dénominateur : au lieu de n-1 comme STDEV.V() , STDEV.G() a juste n au dénominateur.
Écart-type peut également être calculé directement à partir des formules ci-dessous (voir fichier exemple)
=SQRT(SQUADROTIV(Échantillon)/(COMPTE(Échantillon)-1))
=SQRT((SUMSQ(Échantillon)-COUNT(Échantillon)*MOYENNE(Échantillon)^2)/(COUNT(Échantillon)-1))
Autres mesures de dispersion
La fonction SQUADRIVE() calcule avec umm d'écarts au carré des valeurs par rapport à leur milieu. Cette fonction renverra le même résultat que la formule =VAR.G( Goûter)*CHÈQUE( Goûter) , où Goûter- une référence à une plage contenant un tableau d'exemples de valeurs(). Les calculs dans la fonction QUADROTIV() se font selon la formule :

La fonction SROOT() est également une mesure de la dispersion d'un ensemble de données. La fonction AVERAGE() calcule la moyenne valeurs absoluesécarts par rapport à milieu. Cette fonction renverra le même résultat que la formule =SOMMEPROD(ABS(Échantillon-MOYENNE(Échantillon)))/COMPTE(Échantillon), où Goûter- une référence à une plage contenant un tableau d'exemples de valeurs.
Les calculs dans la fonction SROOTKL () sont effectués selon la formule :

Dispersion je
Dispersion (du latin dispersio - dispersion)
dans statistiques mathématiques et la théorie des probabilités, la mesure de dispersion la plus couramment utilisée, c'est-à-dire les écarts par rapport à la moyenne. Au sens statistique, D. est la moyenne arithmétique des écarts au carré des valeurs x je de leur moyenne arithmétique Dans la théorie des probabilités, la distribution d'une variable aléatoire X est appelée Espérance E ( X - mx) 2 écart au carré X d'elle espérance mathématique mx= E ( X). D. variable aléatoire X noté D ( X) ou par σ 2X. La racine carrée de D. (c'est-à-dire σ, si D. est σ 2) est appelée l'écart type (voir Écart carré). Pour une variable aléatoire X avec une distribution de probabilité continue caractérisée par une densité de probabilité (Voir Densité de probabilité) R(X), D. est calculé par la formule En théorie des probabilités grande importance a un théorème: D. la somme des termes indépendants est égale à la somme de leur D. Non moins importante est l'inégalité de Chebyshev, qui permet d'estimer la probabilité de grands écarts d'une variable aléatoire X de son espérance mathématique. La présence d'ondes D. entraîne une distorsion de la forme des signaux lors de leur propagation dans le milieu. Cela est dû au fait que des ondes harmoniques de fréquences différentes, en lesquelles le signal peut être décomposé, se propagent à des vitesses différentes (pour plus de détails, voir Ondes, Vitesse de groupe). D. la lumière lorsqu'elle se propage dans un prisme transparent conduit à la décomposition lumière blanche dans le spectre (voir Dispersion de la lumière).![]()
![]()
Grande Encyclopédie soviétique. - M. : Encyclopédie soviétique. 1969-1978 .
Synonymes:Voyez ce que "Dispersion" est dans d'autres dictionnaires :
dispersion- Diffuser quelque chose. En mathématiques, la variance mesure l'écart des valeurs par rapport à la moyenne. La dispersion de la lumière blanche entraîne sa décomposition en composants. La dispersion du son est la cause de sa propagation. Dispersion des données stockées sur… … Manuel du traducteur technique
Encyclopédie moderne
- (variance) Une mesure de la dispersion des données. La variance d'un ensemble de N termes est trouvée en additionnant les carrés de leurs écarts par rapport à la moyenne et en divisant par N. Par conséquent, si les termes sont xi à i = 1, 2, ..., N, et leur moyenne est m , la variance ... ... Dictionnaire économique
Dispersion- (du latin dispersio scattering) ondes, la dépendance de la vitesse de propagation des ondes dans une substance à la longueur d'onde (fréquence). La dispersion est déterminée propriétés physiques milieu dans lequel se propagent les ondes. Par exemple, dans le vide ... ... Illustré Dictionnaire encyclopédique
- (du lat. dispersio scattering) dans les statistiques mathématiques et la théorie des probabilités, une mesure de la dispersion (écart par rapport à la moyenne). En statistique, la variance est la moyenne arithmétique des écarts au carré des valeurs observées (x1, x2,...,xn) d'un aléatoire ... ... Grand dictionnaire encyclopédique
En théorie des probabilités, la mesure la plus couramment utilisée de l'écart par rapport à la moyenne (mesure de diffusion). En anglais : Dispersion Synonymes : Statistical dispersion Synonymes anglais : Statistical dispersion Voir aussi : Sample populations Financial ... ... Vocabulaire financier
- [lat. dispersus dispersé, dispersé] 1) diffusion; 2) chim., physique. décomposer une substance en très petites particules. D. décomposition lumineuse de la lumière blanche à l'aide d'un prisme en un spectre; 3) tapis. écart par rapport à la moyenne. Dictionnaire des mots étrangers. Komlev N.G.,… … Dictionnaire des mots étrangers de la langue russe
dispersion- (variance) indicateur de dispersion des données, correspondant au carré moyen de l'écart de ces données à la moyenne arithmétique. Égal au carré de l'écart type. Dictionnaire psychologue pratique. Moscou : AST, Harvest. S. Yu. Golovine. 1998 ... Grande Encyclopédie Psychologique
Scattering, scattering Dictionnaire des synonymes russes. nom dispersion, nombre de synonymes : 6 nanodispersion (1) … Dictionnaire des synonymes
Dispersion est la dispersion caractéristique des valeurs d'une variable aléatoire, mesurée par le carré de leurs écarts à la valeur moyenne (notée d2). D. diffère théorique (continu ou discret) et empirique (également continu et ... ... Dictionnaire économique et mathématique
Dispersion- * dispersion * dispersion 1. Diffusion ; dispersion; variante (voir). 2. Un concept théoriquement probabiliste qui caractérise le degré d'écart d'une variable aléatoire par rapport à son espérance mathématique. Dans la pratique biométrique, la variance d'échantillon s2 ... La génétique. Dictionnaire encyclopédique
Livres
- Dispersion anormale dans de larges bandes d'absorption, D.S. Noël. Reproduit dans l'orthographe originale de l'auteur de l'édition de 1934 (maison d'édition "Actes de l'Académie des sciences de l'URSS"). À…
Plage de variation (ou plage de variation) - est la différence entre les valeurs maximale et minimale de la fonctionnalité :
Dans notre exemple, la plage de variation du rendement posté des ouvriers est : dans la première brigade R=105-95=10 enfants, dans la deuxième brigade R=125-75=50 enfants. (5 fois plus). Cela suggère que la production de la 1ère brigade est plus "stable", mais la deuxième brigade a plus de réserves pour la croissance de la production, car. si tous les ouvriers atteignent la production maximale pour cette brigade, elle peut produire 3 * 125 = 375 pièces, et dans la 1ère brigade seulement 105 * 3 = 315 pièces.
Si les valeurs extrêmes de l'attribut ne sont pas typiques de la population, des plages de quartile ou de décile sont utilisées. La tranche quartile RQ= Q3-Q1 couvre 50% de la population, la tranche premier décile RD1=D9-D1 couvre 80% des données, la tranche second décile RD2=D8-D2 couvre 60%.
L'inconvénient de l'indicateur de plage de variation est que sa valeur ne reflète pas toutes les fluctuations du trait.
L'indicateur de généralisation le plus simple qui reflète toutes les fluctuations d'un trait est écart linéaire moyen, qui est la moyenne arithmétique des écarts absolus des options individuelles par rapport à leur valeur moyenne :
,
pour les données groupées ![]() ,
,
où хi est la valeur de l'attribut dans une série discrète ou le milieu de l'intervalle dans la distribution d'intervalle.
Dans les formules ci-dessus, les différences au numérateur sont prises modulo, sinon, selon la propriété de la moyenne arithmétique, le numérateur sera toujours égal à zéro. Par conséquent, l'écart linéaire moyen dans la pratique statistique est rarement utilisé, uniquement dans les cas où la sommation des indicateurs sans tenir compte du signe a sens économique. Avec son aide, par exemple, la composition des employés, la rentabilité de la production et le chiffre d'affaires du commerce extérieur sont analysés.
Écart de fonctionnalité est le carré moyen des écarts du variant à leur valeur moyenne :
écart simple ![]() ,
,
variance pondérée  .
.
La formule de calcul de la variance peut être simplifiée :
Ainsi, la variance est égale à la différence entre la moyenne des carrés de la variante et le carré de la moyenne de la variante de la population :  .
.
Cependant, en raison de la somme des écarts au carré, la variance donne une idée déformée des écarts, de sorte que la moyenne est calculée à partir de celle-ci. écart-type, qui indique dans quelle mesure les variantes spécifiques de l'attribut s'écartent en moyenne de leur valeur moyenne. Calculé en extrayant racine carrée de dispersion :
pour les données non groupées  ,
,
pour la série de variations 
Comment moins de valeur dispersion et écart-type, plus la population est homogène, plus fiable (typique) sera valeur moyenne.
L'écart moyen linéaire et l'écart quadratique moyen sont des nombres nommés, c'est-à-dire qu'ils sont exprimés en unités de mesure de la caractéristique, sont identiques en contenu et proches en valeur.
Il est recommandé de calculer les indicateurs absolus de variation à l'aide de tableaux.
Tableau 3 - Calcul des caractéristiques de variation (sur l'exemple de la période de données sur le rendement posté des équipes de travail)
Nombre de travailleurs |
Le milieu de l'intervalle |
Valeurs estimées |
|||||
Total: |
|||||||
Rendement moyen d'un quart de travail : ![]()
Déviation linéaire moyenne : ![]()
Dispersion de sortie : 
L'écart type de la production des travailleurs individuels par rapport à la production moyenne :
.
1 Calcul de la dispersion par la méthode des moments
Le calcul des variances est associé à des calculs lourds (surtout si la moyenne est exprimée par un grand nombre avec plusieurs décimales). Les calculs peuvent être simplifiés en utilisant une formule simplifiée et des propriétés de dispersion.
La dispersion a les propriétés suivantes :
- si toutes les valeurs de l'attribut sont réduites ou augmentées de la même valeur A, la variance ne diminuera pas à partir de cela :
 ,
,
 , puis ou
, puis ou 
En utilisant les propriétés de la variance et en réduisant d'abord toutes les variantes de la population par la valeur A, puis en divisant par la valeur de l'intervalle h, nous obtenons une formule de calcul de la variance dans des séries variationnelles à intervalles égaux chemin des instants : ,
,
où est la dispersion calculée par la méthode des moments ;
h est la valeur de l'intervalle de la série de variation ;
– nouvelles valeurs de variantes (transformées);
MAIS- constant, qui est utilisé comme milieu de l'intervalle avec la fréquence la plus élevée ; ou la variante avec la fréquence la plus élevée ;  est le carré du moment du premier ordre;
est le carré du moment du premier ordre;
est un moment du second ordre.
Calculons la variance par la méthode des moments basée sur les données sur la sortie de l'équipe de travail.
Tableau 4 - Calcul de la dispersion par la méthode des moments
Groupes de travailleurs de la production, pc. |
Nombre de travailleurs |
Le milieu de l'intervalle |
Valeurs estimées |
||
Procédure de calcul :


- calculer l'écart :
2 Calcul de la variance d'une caractéristique alternative
Parmi les signes étudiés par la statistique, il y a ceux qui n'ont que deux sens qui s'excluent mutuellement. Ce sont des signes alternatifs. Deux valeurs quantitatives leur sont respectivement attribuées : les options 1 et 0. La fréquence des options 1, notée p, est la proportion d'unités qui présentent cette caractéristique. La différence 1-p=q est la fréquence des options 0. Ainsi,
xii |
|
Moyenne arithmétique de la caractéristique alternative ![]() , puisque p+q=1.
, puisque p+q=1.
Écart de fonctionnalité
, car 1-p=q
Ainsi, la variance d'un attribut alternatif est égale au produit de la proportion d'unités qui ont cet attribut et de la proportion d'unités qui n'ont pas cet attribut.
Si les valeurs 1 et 0 sont également fréquentes, c'est-à-dire p=q, la variance atteint son maximum pq=0,25.
La variable de variance est utilisée dans les enquêtes par sondage, par exemple, la qualité des produits.
3 Dispersion intergroupes. Règle d'addition de variance
La dispersion, contrairement à d'autres caractéristiques de variation, est une quantité additive. C'est-à-dire dans l'agrégat, qui est divisé en groupes selon le critère du facteur X , écart résultant y peut être décomposée en variance au sein de chaque groupe (intra groupe) et en variance entre groupes (entre groupe). Ensuite, parallèlement à l'étude de la variation du trait dans l'ensemble de la population, il devient possible d'étudier la variation dans chaque groupe, ainsi qu'entre ces groupes.
Écart total mesure la variation d'un trait à sur l'ensemble de la population sous l'influence de tous les facteurs qui ont provoqué cette variation (écarts). Il est égal au carré moyen des écarts des valeurs individuelles de la caractéristique à de la moyenne globale et peut être calculée comme une variance simple ou pondérée.
Écart intergroupe caractérise la variation de la caractéristique effective à, causée par l'influence du signe-facteur X sous-jacent au regroupement. Il caractérise la variation des moyennes de groupe et est égal au carré moyen des écarts des moyennes de groupe à la moyenne totale :  ,
,
où est la moyenne arithmétique du i-ème groupe ;
– nombre d'unités dans le i-ème groupe (fréquence du i-ème groupe);
est la moyenne totale de la population.
Écart intragroupe reflète la variation aléatoire, c'est-à-dire la partie de la variation qui est causée par l'influence de facteurs non pris en compte et qui ne dépend pas de l'attribut-facteur sous-jacent au regroupement. Il caractérise la variation des valeurs individuelles par rapport aux moyennes de groupe, il est égal au carré moyen des écarts des valeurs individuelles du trait à au sein d'un groupe à partir de la moyenne arithmétique de ce groupe (moyenne du groupe) et se calcule comme une variance simple ou pondérée pour chaque groupe : ![]() ou
ou ![]() ,
,
où est le nombre d'unités dans le groupe.
Sur la base des variances intra-groupe pour chaque groupe, il est possible de déterminer la moyenne globale des variances intra-groupe:
.
La relation entre les trois variances est appelée règles d'ajout d'écart, selon laquelle la variance totale est égale à la somme de la variance intergroupe et de la moyenne des variances intragroupe :
Exemple. Lors de l'étude de l'influence catégorie tarifaire(qualification) des travailleurs sur le niveau de productivité de leur travail, les données suivantes ont été obtenues.
Tableau 5 - Répartition des travailleurs selon le rendement horaire moyen.
№ p/n |
Travailleurs de la 4ème catégorie |
Travailleurs de la 5ème catégorie |
|||||
S'entraîner |
S'entraîner |
||||||
1 |
7 |
7-10=-3 |
9 |
1 |
14 |
14-15=-1 |
1 |
À cet exemple les travailleurs sont divisés en deux groupes selon un critère factoriel X- les diplômes, caractérisés par leur rang. Le trait effectif - la production - varie à la fois sous son influence (variation intergroupe) et en raison d'autres facteurs aléatoires (variation intragroupe). Le défi consiste à mesurer ces variations à l'aide de trois variances : totale, inter-groupe et intra-groupe. Le coefficient de détermination empirique montre la proportion de la variation de la caractéristique résultante à sous l'influence d'un signe facteur X. Le reste de la variation totale à causés par des changements dans d'autres facteurs.
Dans l'exemple, le coefficient de détermination empirique est : ![]() soit 66,7%,
soit 66,7%,
Cela signifie que 66,7 % de la variation de la productivité du travail des travailleurs est due à des différences de qualification et 33,3 % à l'influence d'autres facteurs.
Relation de corrélation empirique montre l'étroitesse de la relation entre le regroupement et les caractéristiques effectives. Il est calculé comme la racine carrée du coefficient de détermination empirique :
Le rapport de corrélation empirique , ainsi que , peut prendre des valeurs de 0 à 1.
S'il n'y a pas de connexion, alors =0. Dans ce cas, =0, c'est-à-dire que les moyennes des groupes sont égales et qu'il n'y a pas de variation intergroupes. Cela signifie que le signe de regroupement - le facteur n'affecte pas la formation de la variation générale.
Si la relation est fonctionnelle, alors =1. Dans ce cas, la variance des moyennes de groupe est égale à la variance totale (), c'est-à-dire qu'il n'y a pas de variation intragroupe. Cela signifie que la caractéristique de regroupement détermine complètement la variation de la caractéristique résultante étudiée.
Plus la valeur de la relation de corrélation est proche de un, plus proche, proche de la dépendance fonctionnelle, la relation entre les caractéristiques.
Pour une évaluation qualitative de la proximité de la connexion entre les signes, les relations de Chaddock sont utilisées.
Dans l'exemple ![]() , ce qui indique fermer la connexion entre la productivité des travailleurs et leurs qualifications.
, ce qui indique fermer la connexion entre la productivité des travailleurs et leurs qualifications.