L'angle entre deux lignes droites. Angle entre des lignes droites dans l'espace

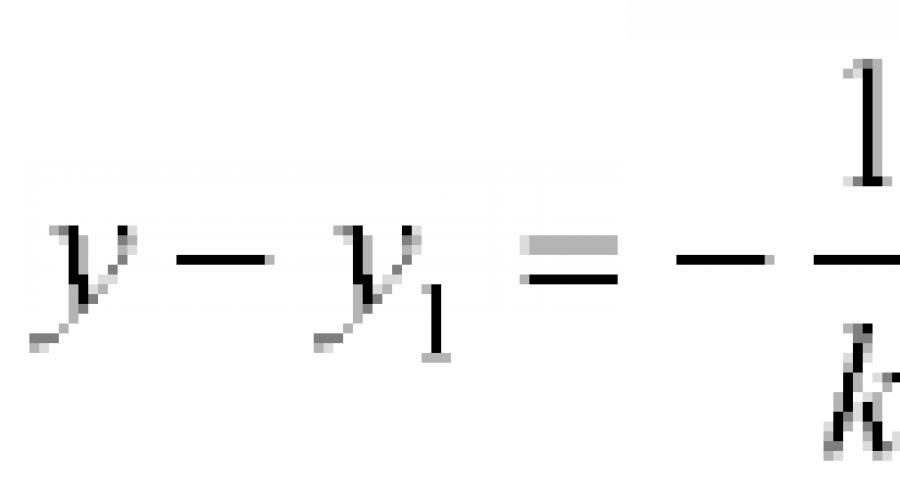
Il sera utile à chaque étudiant qui se prépare à l'examen d'État unifié de mathématiques de répéter le sujet « Trouver un angle entre des lignes droites ». Comme le montrent les statistiques, lors de la réussite du test de certification, les tâches de cette section de stéréométrie posent des difficultés pour grande quantitéétudiants. Dans le même temps, les tâches qui nécessitent de trouver l'angle entre des lignes droites se trouvent dans l'examen d'État unifié de base et niveau de profil. Cela signifie que tout le monde devrait pouvoir les résoudre.

Moments de base

Il existe 4 types de positions relatives des lignes dans l'espace. Ils peuvent coïncider, se croiser, être parallèles ou se croiser. L'angle entre eux peut être aigu ou droit.

Pour trouver l'angle entre les lignes dans l'examen d'État unifié ou, par exemple, pour résoudre, les écoliers de Moscou et d'autres villes peuvent utiliser plusieurs méthodes pour résoudre les problèmes de cette section de stéréométrie. Vous pouvez terminer la tâche en utilisant des constructions classiques. Pour ce faire, il vaut la peine d'apprendre les axiomes et théorèmes de base de la stéréométrie. L'élève doit être capable de raisonner logiquement et de créer des dessins afin d'amener la tâche à un problème planimétrique.

Vous pouvez également utiliser la méthode des vecteurs de coordonnées en utilisant des formules, des règles et des algorithmes simples. L'essentiel dans ce cas est d'effectuer correctement tous les calculs. Le projet éducatif Shkolkovo vous aidera à perfectionner vos compétences en résolution de problèmes en stéréométrie et dans d'autres sections du cours scolaire.

Définition. Si deux lignes sont données y = k 1 x + b 1, y = k 2 x + b 2, alors angle vif entre ces lignes droites sera défini comme

Deux droites sont parallèles si k 1 = k 2. Deux droites sont perpendiculaires si k 1 = -1/ k 2.

Théorème. Les droites Ax + Bу + C = 0 et A 1 x + B 1 y + C 1 = 0 sont parallèles lorsque les coefficients A 1 = λA, B 1 = λB sont proportionnels. Si aussi C 1 = λC, alors les droites coïncident. Les coordonnées du point d'intersection de deux droites sont trouvées comme solution du système d'équations de ces droites.

Équation d'une droite passant par ce point

Perpendiculaire à une ligne donnée

Définition. Une droite passant par le point M 1 (x 1, y 1) et perpendiculaire à la droite y = kx + b est représentée par l'équation :

Distance d'un point à une ligne

Théorème. Si un point M(x 0, y 0) est donné, alors la distance à la ligne Ax + Bу + C = 0 est déterminée comme

.

Preuve. Soit le point M 1 (x 1, y 1) la base de la perpendiculaire tombant du point M à une droite donnée. Puis la distance entre les points M et M 1 :

(1)

Les coordonnées x 1 et y 1 peuvent être trouvées en résolvant le système d'équations :

La deuxième équation du système est l'équation de la droite passant par point donné M 0 est perpendiculaire à une droite donnée. Si l'on transforme la première équation du système sous la forme :

A(x – x 0) + B(y – y 0) + Ax 0 + Par 0 + C = 0,

alors, en résolvant, on obtient :

En substituant ces expressions dans l'équation (1), nous trouvons :

Le théorème a été prouvé.

Exemple. Déterminez l'angle entre les lignes : y = -3 x + 7 ; y = 2 x + 1.

k 1 = -3 ; k2 = 2 ; tgφ = ; φ = p /4.

Exemple. Montrer que les droites 3x – 5y + 7 = 0 et 10x + 6y – 3 = 0 sont perpendiculaires.

Solution. On trouve : k 1 = 3/5, k 2 = -5/3, k 1* k 2 = -1, donc les droites sont perpendiculaires.

Exemple. Sont donnés les sommets du triangle A(0; 1), B (6; 5), C (12; -1). Trouvez l'équation de la hauteur tirée du sommet C.

Solution. On retrouve l’équation du côté AB : ; 4 x = 6 oui – 6 ;

2 x – 3 oui + 3 = 0 ;

L'équation de hauteur requise a la forme : Ax + By + C = 0 ou y = kx + b. k = . Alors y = . Parce que la hauteur passe par le point C, alors ses coordonnées satisfont à cette équation : d'où b = 17. Total : .

Réponse : 3 x + 2 y – 34 = 0.

L'équation d'une droite passant par un point donné dans une direction donnée. Équation d'une droite passant par deux points donnés. L'angle entre deux lignes droites. La condition de parallélisme et de perpendiculaire de deux lignes droites. Déterminer le point d'intersection de deux lignes

1. Équation d'une droite passant par un point donné UN(X 1 , oui 1) dans une direction donnée, déterminée par la pente k,

oui - oui 1 = k(X - X 1). (1)

Cette équation définit un crayon de lignes passant par un point UN(X 1 , oui 1), appelé centre du faisceau.

2. Équation d'une droite passant par deux points : UN(X 1 , oui 1) et B(X 2 , oui 2), écrit ainsi :

Le coefficient angulaire d'une droite passant par deux points donnés est déterminé par la formule

3. Angle entre les lignes droites UN Et B est l'angle dont la première ligne droite doit être tournée UN autour du point d'intersection de ces lignes dans le sens inverse des aiguilles d'une montre jusqu'à ce qu'il coïncide avec la deuxième ligne B. Si deux droites sont données par des équations avec une pente

oui = k 1 X + B 1 ,

oui = k 2 X + B 2 , (4)

alors l'angle entre eux est déterminé par la formule

Il est à noter qu'au numérateur de la fraction, la pente de la première droite est soustraite de la pente de la deuxième droite.

Si les équations d'une droite sont données dans vue générale

UN 1 X + B 1 oui + C 1 = 0,

UN 2 X + B 2 oui + C 2 = 0, (6)

l'angle entre eux est déterminé par la formule

4. Conditions de parallélisme de deux droites :

a) Si les droites sont données par les équations (4) avec un coefficient angulaire, alors la condition nécessaire et suffisante de leur parallélisme est l'égalité de leurs coefficients angulaires :

k 1 = k 2 . (8)

b) Pour le cas où les droites sont données par des équations sous la forme générale (6), une condition nécessaire et suffisante pour leur parallélisme est que les coefficients des coordonnées actuelles correspondantes dans leurs équations soient proportionnels, c'est-à-dire

5. Conditions de perpendiculaire de deux droites :

a) Dans le cas où les droites sont données par les équations (4) à coefficient angulaire, une condition nécessaire et suffisante pour leur circularité est qu'elles pistes sont inverses en grandeur et opposés en signe, c'est-à-dire

Cette condition peut aussi s’écrire sous la forme

k 1 k 2 = -1. (11)

b) Si les équations des droites sont données sous la forme générale (6), alors la condition de leur circularité (nécessaire et suffisante) est de satisfaire l'égalité

UN 1 UN 2 + B 1 B 2 = 0. (12)

6. Les coordonnées du point d'intersection de deux droites sont trouvées en résolvant le système d'équations (6). Les lignes (6) se coupent si et seulement si

1. Écrivez les équations des droites passant par le point M, dont l'une est parallèle et l'autre perpendiculaire à la droite donnée l.

Oh-oh-oh-oh-oh... eh bien, c'est dur, comme s'il se lisait une phrase =) Cependant, la relaxation aidera plus tard, d'autant plus qu'aujourd'hui j'ai acheté les accessoires appropriés. Par conséquent, passons à la première section, j'espère qu'à la fin de l'article je maintiendrai une humeur joyeuse.

La position relative de deux lignes droites

C'est le cas lorsque le public chante en chœur. Deux lignes droites peuvent:

1) correspondre ;

2) être parallèle : ;

3) ou se croisent en un seul point : .

Aide pour les nuls : s'il te plaît, souviens-toi signe mathématique aux intersections, cela se produira très souvent. La notation signifie que la ligne coupe la ligne au point .

Comment déterminer la position relative de deux lignes ?

Commençons par le premier cas :

Deux droites coïncident si et seulement si leurs coefficients correspondants sont proportionnels, c’est-à-dire qu’il existe un nombre « lambda » tel que les égalités soient satisfaites

Considérons les droites et créons trois équations à partir des coefficients correspondants : . De chaque équation, il s’ensuit que ces lignes coïncident.

En effet, si tous les coefficients de l'équation multipliez par –1 (changez de signe), et réduisez tous les coefficients de l'équation par 2, vous obtenez la même équation : .

Le deuxième cas, lorsque les droites sont parallèles :

Deux droites sont parallèles si et seulement si leurs coefficients des variables sont proportionnels : , Mais.

A titre d'exemple, considérons deux lignes droites. On vérifie la proportionnalité des coefficients correspondants pour les variables :

Cependant, cela est bien évident.

Et le troisième cas, lorsque les lignes se croisent :

Deux droites se coupent si et seulement si leurs coefficients des variables ne sont PAS proportionnels, c'est-à-dire qu'il n'existe AUCUNE valeur de « lambda » telle que les égalités soient satisfaites

Ainsi, pour les lignes droites nous allons créer un système :

De la première équation il résulte que , et de la deuxième équation : , ce qui signifie le système est incohérent(pas de solutions). Ainsi, les coefficients des variables ne sont pas proportionnels.

Conclusion : les lignes se croisent

Dans des problèmes pratiques, vous pouvez utiliser le schéma de solution que nous venons de décrire. D'ailleurs, cela rappelle beaucoup l'algorithme de vérification de la colinéarité des vecteurs, que nous avons examiné en classe Le concept d’(in)dépendance linéaire des vecteurs. Base des vecteurs. Mais il existe un packaging plus civilisé :

Exemple 1

Se rendre compte arrangement mutuel direct:

Solution basé sur l'étude des vecteurs directeurs de droites :

a) A partir des équations on trouve les vecteurs directeurs des droites : .

, ce qui signifie que les vecteurs ne sont pas colinéaires et que les droites se coupent.

Au cas où, je mettrai une pierre avec des panneaux au carrefour :

Les autres sautent par-dessus la pierre et suivent plus loin, directement jusqu'à Kashchei l'Immortel =)

b) Trouver les vecteurs directeurs des droites :

Les lignes ont le même vecteur directeur, ce qui signifie qu’elles sont soit parallèles, soit coïncidentes. Il n'est pas nécessaire de compter le déterminant ici.

Il est évident que les coefficients des inconnues sont proportionnels, et .

Voyons si l'égalité est vraie :

Ainsi,

c) Trouver les vecteurs directeurs des droites :

Calculons le déterminant constitué des coordonnées de ces vecteurs :
, donc les vecteurs directeurs sont colinéaires. Les lignes sont soit parallèles, soit coïncidentes.

Le coefficient de proportionnalité « lambda » est facile à voir directement à partir du rapport des vecteurs de direction colinéaires. Cependant, cela peut également être trouvé à travers les coefficients des équations elles-mêmes : .

Voyons maintenant si l'égalité est vraie. Les deux termes gratuits sont nuls, donc :

La valeur résultante satisfait cette équation (n'importe quel nombre en général la satisfait).

Les lignes coïncident donc.

Répondre:

Très vite, vous apprendrez (ou même avez déjà appris) à résoudre littéralement le problème discuté verbalement en quelques secondes. À cet égard, je ne vois pas l'intérêt d'offrir quoi que ce soit pour décision indépendante, il est préférable de poser une autre brique importante dans la fondation géométrique :

Comment construire une droite parallèle à une droite donnée ?

Par ignorance de cela tâche la plus simple Nightingale le voleur punit sévèrement.

Exemple 2

La droite est donnée par l'équation. Écrivez une équation pour une droite parallèle qui passe par ce point.

Solution: Désignons la ligne inconnue par la lettre . Que dit son état à son sujet ? La droite passe par le point. Et si les droites sont parallèles, alors il est évident que le vecteur directeur de la droite « tse » convient également pour construire la droite « de ».

Nous retirons le vecteur direction de l'équation :

Répondre:

L'exemple de géométrie semble simple :

Les tests analytiques comprennent les étapes suivantes :

1) On vérifie que les droites ont le même vecteur directeur (si l'équation de la droite n'est pas correctement simplifiée, alors les vecteurs seront colinéaires).

2) Vérifiez si le point satisfait à l’équation résultante.

Dans la plupart des cas, les tests analytiques peuvent être facilement effectués oralement. Regardez les deux équations, et beaucoup d’entre vous détermineront rapidement le parallélisme des droites sans aucun dessin.

Les exemples de solutions indépendantes d'aujourd'hui seront créatifs. Parce que vous devrez encore rivaliser avec Baba Yaga, et elle, vous le savez, est une amoureuse de toutes sortes d'énigmes.

Exemple 3

Écrire une équation pour une droite passant par un point parallèle à la droite si

Il existe une manière rationnelle et une manière moins rationnelle de résoudre ce problème. La plupart raccourci- à la fin du cours.

Nous avons travaillé un peu avec des lignes parallèles et y reviendrons plus tard. Le cas des lignes coïncidentes n’a que peu d’intérêt, considérons donc un problème qui vous est très familier grâce au programme scolaire :

Comment trouver le point d’intersection de deux droites ?

Si droit se croisent au point , alors ses coordonnées sont la solution systèmes d'équations linéaires

Comment trouver le point d’intersection des lignes ? Résolvez le système.

Voici signification géométrique du système de deux équations linéaires avec deux inconnues- ce sont deux lignes qui se croisent (le plus souvent) sur un plan.

Exemple 4

Trouver le point d'intersection des lignes

Solution: Il existe deux manières de résoudre : graphique et analytique.

La méthode graphique consiste simplement à tracer les lignes données et à connaître le point d'intersection directement à partir du dessin :

Voici notre point : . Pour vérifier, vous devez substituer ses coordonnées dans chaque équation de la droite, elles doivent s'adapter à la fois là et là. En d’autres termes, les coordonnées d’un point sont une solution du système. Essentiellement, nous avons examiné une solution graphique systèmes d'équations linéaires avec deux équations, deux inconnues.

La méthode graphique n'est bien sûr pas mauvaise, mais présente des inconvénients notables. Non, le fait n'est pas que les élèves de septième année décident de cette façon, le fait est qu'il faudra du temps pour créer un dessin correct et PRÉCIS. De plus, certaines lignes droites ne sont pas si faciles à construire, et le point d'intersection lui-même peut être situé quelque part dans le trentième royaume en dehors de la feuille du cahier.

Par conséquent, il est plus judicieux de rechercher le point d'intersection à l'aide de la méthode analytique. Résolvons le système :

Pour résoudre le système, la méthode d’addition d’équations terme par terme a été utilisée. Pour développer des compétences pertinentes, suivez une leçon Comment résoudre un système d'équations ?

Répondre:

La vérification est triviale : les coordonnées du point d'intersection doivent satisfaire chaque équation du système.

Exemple 5

Trouvez le point d'intersection des lignes si elles se croisent.

Ceci est un exemple à résoudre par vous-même. Il est pratique de diviser la tâche en plusieurs étapes. L'analyse de l'état suggère qu'il est nécessaire :
1) Écrivez l’équation de la droite.
2) Écrivez l’équation de la droite.
3) Découvrez la position relative des lignes.
4) Si les lignes se coupent, trouvez le point d'intersection.

Le développement d'un algorithme d'action est typique de nombreux problèmes géométriques, et je me concentrerai sur ce sujet à plusieurs reprises.

Solution complète et la réponse à la fin de la leçon :

Même une paire de chaussures n’était pas usée avant d’arriver à la deuxième partie de la leçon :

Les lignes perpendiculaire. Distance d'un point à une ligne.
Angle entre les lignes droites

Commençons par un exemple typique et très tâche importante. Dans la première partie, nous avons appris à construire une ligne droite parallèle à celle-ci, et maintenant la cabane sur cuisses de poulet va tourner de 90 degrés :

Comment construire une droite perpendiculaire à une droite donnée ?

Exemple 6

La droite est donnée par l'équation. Écrivez une équation perpendiculaire à la droite passant par ce point.

Solution: Par condition, on sait que . Ce serait bien de trouver le vecteur directeur de la ligne. Puisque les lignes sont perpendiculaires, l’astuce est simple :

De l'équation on "supprime" le vecteur normal : , qui sera le vecteur directeur de la droite.

Composons l'équation d'une droite à l'aide d'un point et d'un vecteur directeur :

Répondre:

Développons l'esquisse géométrique :

Hmmm... Ciel orange, mer orange, chameau orange.

Vérification analytique de la solution :

1) On sort les vecteurs directeurs des équations et avec l'aide produit scalaire de vecteurs on arrive à la conclusion que les droites sont bien perpendiculaires : .

D'ailleurs, vous pouvez utiliser des vecteurs normaux, c'est encore plus simple.

2) Vérifiez si le point satisfait à l'équation résultante .

Le test, là encore, est facile à réaliser oralement.

Exemple 7

Trouver le point d'intersection des droites perpendiculaires si l'équation est connue et période.

Ceci est un exemple à résoudre par vous-même. Il y a plusieurs actions dans le problème, il est donc pratique de formuler la solution point par point.

Notre voyage passionnant continue :

Distance d'un point à une ligne

Devant nous se trouve une bande droite de la rivière et notre tâche est d'y accéder par le chemin le plus court. Il n'y a pas d'obstacles et l'itinéraire le plus optimal sera de se déplacer le long de la perpendiculaire. Autrement dit, la distance d’un point à une ligne est la longueur du segment perpendiculaire.

La distance en géométrie est traditionnellement désignée par la lettre grecque « rho », par exemple : – la distance du point « em » à la droite « de ».

Distance d'un point à une ligne exprimé par la formule

Exemple 8

Trouver la distance d'un point à une ligne

Solution: il suffit de substituer soigneusement les nombres dans la formule et d'effectuer les calculs :

Répondre:

Faisons le dessin :

La distance trouvée entre le point et la ligne est exactement la longueur du segment rouge. Si vous faites un dessin sur papier quadrillé à l'échelle 1 unité. = 1 cm (2 cellules), alors la distance peut être mesurée avec une règle ordinaire.

Considérons une autre tâche basée sur le même dessin :

La tâche consiste à trouver les coordonnées d'un point symétrique au point par rapport à la droite . Je suggère d'effectuer les étapes vous-même, mais je vais décrire l'algorithme de solution avec des résultats intermédiaires :

1) Trouvez une droite perpendiculaire à la droite.

2) Trouvez le point d'intersection des lignes : .

Les deux actions sont discutées en détail dans cette leçon.

3) Le point est le milieu du segment. On connaît les coordonnées du milieu et de l'une des extrémités. Par formules pour les coordonnées du milieu d'un segment nous trouvons .

Ce serait une bonne idée de vérifier que la distance est également de 2,2 unités.

Des difficultés de calcul peuvent survenir ici, mais une microcalculatrice est d'une grande aide dans la tour, vous permettant de compter fractions communes. Je vous ai conseillé à plusieurs reprises et je vous recommanderai à nouveau.

Comment trouver la distance entre deux droites parallèles ?

Exemple 9

Trouver la distance entre deux lignes parallèles

Ceci est un autre exemple que vous pourrez décider vous-même. Je vais vous donner un petit indice : il existe une infinité de façons de résoudre ce problème. Débriefing à la fin du cours, mais il vaut mieux essayer de deviner par vous-même, je pense que votre ingéniosité était bien développée.

Angle entre deux droites

Chaque coin est un montant :


En géométrie, l'angle entre deux lignes droites est considéré comme le PLUS PETIT angle, d'où il s'ensuit automatiquement qu'il ne peut pas être obtus. Sur la figure, l'angle indiqué par l'arc rouge n'est pas considéré comme l'angle entre les lignes qui se croisent. Et son voisin « vert » ou orientation opposée coin "framboise".

Si les lignes sont perpendiculaires, alors n’importe lequel des 4 angles peut être pris comme angle entre eux.

En quoi les angles sont-ils différents ? Orientation. Premièrement, la direction dans laquelle l’angle « défile » est d’une importance fondamentale. Deuxièmement, un angle orienté négativement s'écrit avec un signe moins, par exemple si .

Pourquoi je t'ai dit ça ? Il semble que nous puissions nous contenter du concept habituel d’angle. Le fait est que les formules par lesquelles nous trouverons les angles peuvent facilement donner un résultat négatif, et cela ne devrait pas vous surprendre. Un angle avec un signe moins n'est pas pire et a une signification géométrique très précise. Sur le dessin, pour un angle négatif, veillez à indiquer son orientation avec une flèche (dans le sens des aiguilles d'une montre).

Comment trouver l’angle entre deux droites ? Il existe deux formules de travail :

Exemple 10

Trouver l'angle entre les lignes

Solution Et Première méthode

Considérons deux lignes droites, donné par des équations en général:

Si droit pas perpendiculaire, Que orienté L'angle entre eux peut être calculé à l'aide de la formule :

Faisons très attention au dénominateur - c'est exactement produit scalaire vecteurs directeurs de droites :

Si , alors le dénominateur de la formule devient zéro, les vecteurs seront orthogonaux et les lignes seront perpendiculaires. C'est pourquoi une réserve a été émise sur la non-perpendiculaire des droites dans la formulation.

Sur la base de ce qui précède, il convient de formaliser la solution en deux étapes :

1) Calculons produit scalaire vecteurs directeurs de droites :
, ce qui signifie que les lignes ne sont pas perpendiculaires.

2) Trouvez l'angle entre les lignes droites à l'aide de la formule :

En utilisant fonction inverse Il est facile de trouver le coin lui-même. Dans ce cas, nous utilisons l'étrangeté de l'arctangente (voir. Graphiques et propriétés des fonctions élémentaires):

Répondre:

Dans la réponse, nous indiquons valeur exacte, ainsi qu'une valeur approximative (de préférence en degrés et en radians), calculée à l'aide d'une calculatrice.

Eh bien, moins, moins, ce n'est pas grave. Voici une illustration géométrique :

Il n'est pas surprenant que l'angle se soit avéré être d'orientation négative, car dans l'énoncé du problème, le premier nombre est une ligne droite et le « dévissage » de l'angle a commencé précisément par lui.

Si vous voulez vraiment obtenir un angle positif, vous devez échanger les droites, c'est-à-dire prendre les coefficients de la deuxième équation , et prenons les coefficients de la première équation. Bref, il faut commencer par un direct .

Je serai bref. Angle entre deux droites égal à l'angle entre leurs vecteurs directeurs. Ainsi, si vous parvenez à trouver les coordonnées des vecteurs directeurs a = (x 1 ; y 1 ; z 1) et b = (x 2 ; y 2 ​​​​​​; z 2), vous pouvez trouver l'angle. Plus précisément, le cosinus de l'angle selon la formule :

Voyons comment cette formule fonctionne à l'aide d'exemples spécifiques :

Tâche. Dans le cube ABCDA 1 B 1 C 1 D 1, les points E et F sont marqués - les milieux des arêtes A 1 B 1 et B 1 C 1, respectivement. Trouvez l'angle entre les lignes AE et BF.

Puisque l'arête du cube n'est pas précisée, posons AB = 1. Nous introduisons un système de coordonnées standard : l'origine est au point A, les axes x, y, z sont dirigés selon AB, AD et AA 1, respectivement. Le segment unitaire est égal à AB = 1. Trouvons maintenant les coordonnées des vecteurs directeurs de nos droites.

Trouvons les coordonnées du vecteur AE. Pour cela nous avons besoin des points A = (0 ; 0 ; 0) et E = (0,5 ; 0 ; 1). Puisque le point E est le milieu du segment A 1 B 1, ses coordonnées sont égales à la moyenne arithmétique des coordonnées des extrémités. Notez que l'origine du vecteur AE coïncide avec l'origine des coordonnées, donc AE = (0,5 ; 0 ; 1).

Regardons maintenant le vecteur BF. De même, on analyse les points B = (1 ; 0 ; 0) et F = (1 ; 0,5 ; 1), car F est le milieu du segment B 1 C 1. Nous avons:
BF = (1 − 1 ; 0,5 − 0 ; 1 − 0) = (0 ; 0,5 ; 1).

Les vecteurs directeurs sont donc prêts. Le cosinus de l'angle entre droites est le cosinus de l'angle entre les vecteurs directeurs, on a donc :

Tâche. Dans un prisme triangulaire régulier ABCA 1 B 1 C 1, dont toutes les arêtes sont égales à 1, les points D et E sont marqués - les milieux des arêtes A 1 B 1 et B 1 C 1, respectivement. Trouvez l'angle entre les lignes AD et BE.

Introduisons un système de coordonnées standard : l'origine est au point A, l'axe x est dirigé selon AB, z - selon AA 1. Dirigons l'axe y pour que le plan OXY coïncide avec le plan ABC. Le segment unitaire est égal à AB = 1. Trouvons les coordonnées des vecteurs directeurs des droites recherchées.

Commençons par trouver les coordonnées du vecteur AD. Considérons les points : A = (0 ; 0 ; 0) et D = (0,5 ; 0 ; 1), car D - le milieu du segment A 1 B 1. Puisque le début du vecteur AD coïncide avec l'origine des coordonnées, on obtient AD = (0,5 ; 0 ; 1).

Trouvons maintenant les coordonnées du vecteur BE. Le point B = (1 ; 0 ; 0) est facile à calculer. Avec le point E - le milieu du segment C 1 B 1 - c'est un peu plus compliqué. Nous avons:

Reste à trouver le cosinus de l'angle :

Tâche. Dans un prisme hexagonal régulier ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , dont toutes les arêtes sont égales à 1, les points K et L sont marqués - les milieux des arêtes A 1 B 1 et B 1 C 1, respectivement . Trouvez l'angle entre les lignes AK et BL.

Introduisons un système de coordonnées standard pour un prisme : on place l'origine des coordonnées au centre de la base inférieure, l'axe x est dirigé selon FC, l'axe y est dirigé par les milieux des segments AB et DE, et le z l’axe est dirigé verticalement vers le haut. Le segment unitaire est à nouveau égal à AB = 1. Notons les coordonnées des points qui nous intéressent :

Les points K et L sont respectivement les milieux des segments A 1 B 1 et B 1 C 1, leurs coordonnées sont donc trouvées par la moyenne arithmétique. Connaissant les points, on retrouve les coordonnées des vecteurs directeurs AK et BL :

Trouvons maintenant le cosinus de l'angle :

Tâche. Dans le droit pyramide quadrangulaire SABCD, dont toutes les arêtes sont égales à 1, les points E et F sont marqués - les milieux des côtés SB et SC, respectivement. Trouvez l'angle entre les lignes AE et BF.

Introduisons un système de coordonnées standard : l'origine est au point A, les axes x et y sont dirigés respectivement le long de AB et AD, et l'axe z est dirigé verticalement vers le haut. Le segment unitaire est égal à AB = 1.

Les points E et F sont respectivement les milieux des segments SB et SC, leurs coordonnées sont donc trouvées comme moyenne arithmétique des extrémités. Notons les coordonnées des points d'intérêt qui nous intéressent :
UNE = (0 ; 0 ; 0); B = (1 ; 0 ; 0)

Connaissant les points, on retrouve les coordonnées des vecteurs directeurs AE et BF :

Les coordonnées du vecteur AE coïncident avec les coordonnées du point E, puisque le point A est l'origine. Reste à trouver le cosinus de l'angle :