Étant donné les coordonnées des points pour trouver l'angle entre les vecteurs. Produit scalaire de vecteurs
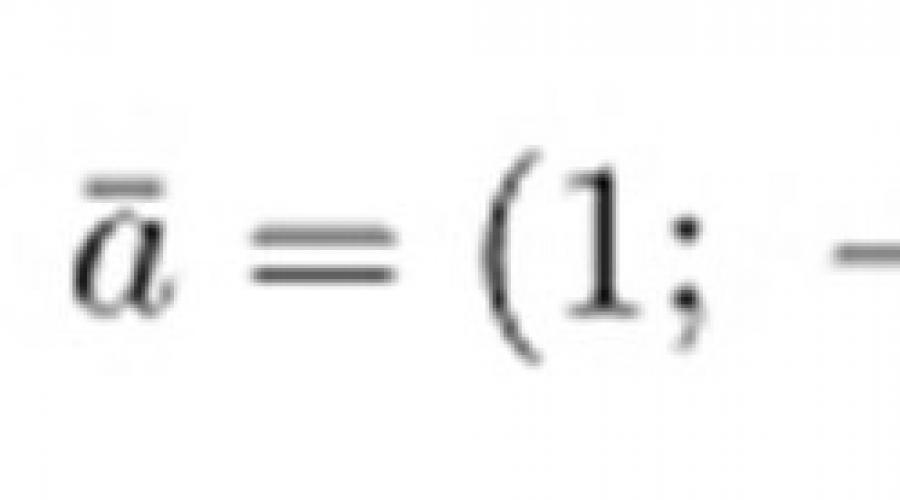
Lire aussi
Lors de l'étude de la géométrie, de nombreuses questions se posent sur le thème des vecteurs. L'élève éprouve des difficultés particulières lorsqu'il s'agit de trouver les angles entre les vecteurs.
Termes de base
Avant de considérer les angles entre vecteurs, il est nécessaire de se familiariser avec la définition d'un vecteur et la notion d'angle entre vecteurs.
Un vecteur est un segment qui a une direction, c'est-à-dire un segment dont le début et la fin sont définis.
L'angle entre deux vecteurs sur un plan qui ont une origine commune est le plus petit des angles, par lequel il est nécessaire de déplacer l'un des vecteurs autour d'un point commun, jusqu'à une position où leurs directions coïncident.
Formule de solution
Une fois que vous comprenez ce qu'est un vecteur et comment son angle est déterminé, vous pouvez calculer l'angle entre les vecteurs. La formule de solution pour cela est assez simple et le résultat de son application sera la valeur du cosinus de l'angle. Par définition, il est égal au quotient du produit scalaire des vecteurs et du produit de leurs longueurs.
Le produit scalaire des vecteurs est considéré comme la somme des coordonnées correspondantes des vecteurs multiplicateurs multipliées les unes par les autres. La longueur d'un vecteur, ou son module, est calculé comme la racine carrée de la somme des carrés de ses coordonnées.
Après avoir reçu la valeur du cosinus de l'angle, vous pouvez calculer la valeur de l'angle lui-même à l'aide d'une calculatrice ou à l'aide de table trigonométrique.
Exemple
Une fois que vous avez compris comment calculer l'angle entre les vecteurs, la solution au problème correspondant devient simple et directe. A titre d'exemple, considérons le problème simple de trouver la grandeur d'un angle.

Tout d'abord, il sera plus commode de calculer les valeurs des longueurs des vecteurs et de leur produit scalaire nécessaires à la résolution. En utilisant la description ci-dessus, nous obtenons :

En remplaçant les valeurs obtenues dans la formule, nous calculons la valeur du cosinus de l'angle souhaité:

Ce nombre n'est pas l'une des cinq valeurs de cosinus communes, donc pour obtenir la valeur de l'angle, vous devrez utiliser une calculatrice ou la table trigonométrique Bradis. Mais avant d'obtenir l'angle entre les vecteurs, la formule peut être simplifiée pour se débarrasser du signe négatif supplémentaire :

La réponse finale peut être laissée sous cette forme pour maintenir la précision, ou vous pouvez calculer la valeur de l'angle en degrés. Selon la table Bradis, sa valeur sera d'environ 116 degrés et 70 minutes, et la calculatrice affichera une valeur de 116,57 degrés.
Calcul d'angle dans un espace à n dimensions
Lorsque l'on considère deux vecteurs dans un espace tridimensionnel, il est beaucoup plus difficile de comprendre de quel angle on parle s'ils ne se trouvent pas dans le même plan. Pour simplifier la perception, vous pouvez dessiner deux segments qui se croisent qui forment le plus petit angle entre eux, et ce sera celui souhaité. Malgré la présence d'une troisième coordonnée dans le vecteur, le processus de calcul des angles entre les vecteurs ne changera pas. Calculez le produit scalaire et les modules de vecteurs, l'arc cosinus de leur quotient et sera la réponse à ce problème.
En géométrie, des problèmes surviennent souvent avec des espaces qui ont plus de trois dimensions. Mais pour eux, l'algorithme pour trouver la réponse semble similaire.
Différence entre 0 et 180 degrés
L'une des erreurs courantes lors de la rédaction d'une réponse à un problème conçu pour calculer l'angle entre les vecteurs est la décision d'écrire que les vecteurs sont parallèles, c'est-à-dire que l'angle souhaité s'est avéré être de 0 ou 180 degrés. Cette réponse est incorrecte.
Ayant reçu une valeur d'angle de 0 degré à la suite de la solution, la bonne réponse serait de désigner les vecteurs comme co-directionnels, c'est-à-dire que les vecteurs auront la même direction. Dans le cas de l'obtention de 180 degrés, les vecteurs seront de nature à directions opposées.
Vecteurs spécifiques
En trouvant les angles entre les vecteurs, l'un des types spéciaux peut être trouvé, en plus de ceux co-dirigés et dirigés de manière opposée décrits ci-dessus.
- Plusieurs vecteurs parallèles à un même plan sont dits coplanaires.
- Les vecteurs qui ont la même longueur et la même direction sont dits égaux.
- Les vecteurs qui se trouvent sur la même ligne droite, quelle que soit leur direction, sont appelés colinéaires.
- Si la longueur du vecteur est nulle, c'est-à-dire que son début et sa fin coïncident, alors il est appelé zéro, et s'il est un, alors il est appelé un.
Produit scalaire de vecteurs
Nous continuons à traiter les vecteurs. A la première leçon Des vecteurs pour les nuls nous avons considéré le concept de vecteur, les actions avec des vecteurs, les coordonnées vectorielles et les problèmes les plus simples avec des vecteurs. Si vous êtes venu sur cette page pour la première fois à partir d'un moteur de recherche, je vous recommande fortement de lire l'article d'introduction ci-dessus, car pour assimiler le matériel, vous devez être guidé dans les termes et la notation que j'utilise, avoir une connaissance de base des vecteurs et être capable de résoudre des problèmes élémentaires. Cette leçon est une suite logique du sujet, et j'y analyserai en détail les tâches typiques qui utilisent le produit scalaire de vecteurs. C'est un travail TRÈS IMPORTANT.. Essayez de ne pas sauter les exemples, ils viennent avec un bonus utile - la pratique vous aidera à consolider le matériel couvert et à "mettre la main" sur la résolution de problèmes courants de géométrie analytique.
Ajouter des vecteurs, multiplier un vecteur par un nombre…. Il serait naïf de penser que les mathématiciens n'ont rien trouvé d'autre. En plus des actions déjà envisagées, il existe un certain nombre d'autres opérations avec des vecteurs, à savoir : produit scalaire de vecteurs, produit croisé de vecteurs Et produit mixte de vecteurs. Le produit scalaire des vecteurs nous est familier dès l'école, les deux autres produits sont traditionnellement liés au cours de mathématiques supérieures. Les sujets sont simples, l'algorithme de résolution de nombreux problèmes est stéréotypé et compréhensible. La seule chose. Il y a une quantité décente d'informations, il n'est donc pas souhaitable d'essayer de maîtriser et de résoudre TOUT ET EN MÊME TEMPS. C'est particulièrement vrai pour les nuls, croyez-moi, l'auteur ne veut absolument pas se sentir comme Chikatilo des mathématiques. Eh bien, pas des mathématiques, bien sûr, non plus =) Les étudiants plus préparés peuvent utiliser le matériel de manière sélective, dans un certain sens, pour "acquérir" les connaissances manquantes, pour vous je serai un comte Dracula inoffensif =)
Enfin, ouvrons un peu la porte et regardons ce qui se passe lorsque deux vecteurs se rencontrent….
Définition du produit scalaire de vecteurs.
Propriétés du produit scalaire. Tâches typiques
Le concept de produit scalaire
D'abord sur angle entre les vecteurs. Je pense que tout le monde comprend intuitivement quel est l'angle entre les vecteurs, mais juste au cas où, un peu plus. Considérez les vecteurs libres non nuls et . Si nous reportons ces vecteurs d'un point arbitraire, nous obtenons une image que beaucoup ont déjà présentée mentalement : 
J'avoue, ici je n'ai décrit la situation qu'au niveau de la compréhension. Si vous avez besoin d'une définition stricte de l'angle entre les vecteurs, veuillez vous référer au manuel, mais pour les tâches pratiques, nous n'en avons en principe pas besoin. Aussi ICI ET PLUS LOIN, j'ignorerai parfois les vecteurs nuls en raison de leur faible signification pratique. J'ai effectué une réservation spécifiquement pour les visiteurs avertis du site, qui peuvent me reprocher l'incomplétude théorique de certains des énoncés suivants.
peut prendre des valeurs de 0 à 180 degrés (de 0 à radians) inclus. Analytiquement, ce fait s'écrit comme une double inégalité :Dans la littérature, l'icône d'angle est souvent omise et écrite simplement.
Définition: Le produit scalaire de deux vecteurs est un NOMBRE égal au produit des longueurs de ces vecteurs et du cosinus de l'angle entre eux : ![]()
Voilà une définition assez stricte.
Nous nous concentrons sur les informations essentielles :
Désignation: le produit scalaire est noté par ou simplement .
Le résultat de l'opération est un NOMBRE: Multiplier un vecteur par un vecteur pour obtenir un nombre. En effet, si les longueurs des vecteurs sont des nombres, le cosinus de l'angle est un nombre, alors leur produit ![]() sera également un nombre.
sera également un nombre.
Juste quelques exemples d'échauffement :
Exemple 1
![]()
Solution: Nous utilisons la formule ![]() . Dans ce cas:
. Dans ce cas:
Répondre:
Les valeurs de cosinus peuvent être trouvées dans table trigonométrique. Je recommande de l'imprimer - il sera nécessaire dans presque toutes les sections de la tour et sera nécessaire plusieurs fois.
D'un point de vue purement mathématique, le produit scalaire est sans dimension, c'est-à-dire que le résultat, dans ce cas, n'est qu'un nombre et c'est tout. Du point de vue des problèmes de physique, le produit scalaire a toujours un certain signification physique, c'est-à-dire qu'après le résultat, l'une ou l'autre unité physique doit être indiquée. L'exemple canonique du calcul du travail d'une force peut être trouvé dans n'importe quel manuel (la formule est exactement un produit scalaire). Le travail d'une force est mesuré en Joules, par conséquent, la réponse sera écrite de manière assez spécifique, par exemple,.
Exemple 2
Trouver si ![]() , et l'angle entre les vecteurs est .
, et l'angle entre les vecteurs est .
Ceci est un exemple pour décision indépendante, la réponse est à la fin de la leçon.
Angle entre les vecteurs et la valeur du produit scalaire
Dans l'exemple 1, le produit scalaire s'est avéré être positif, et dans l'exemple 2, il s'est avéré être négatif. Voyons de quoi dépend le signe du produit scalaire. Regardons notre formule : ![]() . Les longueurs des vecteurs non nuls sont toujours positives : , donc le signe ne peut dépendre que de la valeur du cosinus.
. Les longueurs des vecteurs non nuls sont toujours positives : , donc le signe ne peut dépendre que de la valeur du cosinus.
Note: Pour une meilleure compréhension des informations ci-dessous, il est préférable d'étudier le graphique cosinus dans le manuel Graphes et propriétés des fonctions. Voyez comment le cosinus se comporte sur le segment.
Comme déjà noté, l'angle entre les vecteurs peut varier dans ![]() , et les cas suivants sont possibles :
, et les cas suivants sont possibles :
1) Si coin entre vecteurs épicé: ![]() (de 0 à 90 degrés), puis
(de 0 à 90 degrés), puis ![]() , Et le produit scalaire sera positif co-dirigé, alors l'angle entre eux est considéré comme nul et le produit scalaire sera également positif. Puisque , alors la formule est simplifiée : .
, Et le produit scalaire sera positif co-dirigé, alors l'angle entre eux est considéré comme nul et le produit scalaire sera également positif. Puisque , alors la formule est simplifiée : .
2) Si coin entre vecteurs émoussé: ![]() (de 90 à 180 degrés), puis
(de 90 à 180 degrés), puis ![]() , et en conséquence, le produit scalaire est négatif: . Cas particulier : si les vecteurs dirigé à l'opposé, alors l'angle entre eux est considéré déployé: (180 degrés). Le produit scalaire est également négatif puisque
, et en conséquence, le produit scalaire est négatif: . Cas particulier : si les vecteurs dirigé à l'opposé, alors l'angle entre eux est considéré déployé: (180 degrés). Le produit scalaire est également négatif puisque
Les affirmations inverses sont également vraies :
1) Si , alors l'angle entre ces vecteurs est aigu. En variante, les vecteurs sont codirectionnels.
2) Si , alors l'angle entre ces vecteurs est obtus. Alternativement, les vecteurs sont dirigés de manière opposée.
Mais le troisième cas est particulièrement intéressant :
3) Si coin entre vecteurs droit: (90 degrés) puis et le produit scalaire est nul: . L'inverse est également vrai : si , alors . L'énoncé compact est formulé comme suit : Le produit scalaire de deux vecteurs est nul si et seulement si les vecteurs donnés sont orthogonaux. Notation mathématique courte : ![]()
! Note
: répéter fondements de la logique mathématique: l'icône de conséquence logique double face se lit généralement "si et seulement alors", "si et seulement si". Comme vous pouvez le voir, les flèches sont dirigées dans les deux sens - "de ceci suit ceci, et vice versa - de ceci suit ceci". Au fait, quelle est la différence avec l'icône de suivi à sens unique ? Revendications d'icônes seulement ça que "de ceci découle ceci", et non le fait que l'inverse soit vrai. Par exemple : , mais tous les animaux ne sont pas des panthères, l'icône ne peut donc pas être utilisée dans ce cas. En même temps, au lieu de l'icône Peut utiliser une icône unilatérale. Par exemple, en résolvant le problème, nous avons découvert que nous avions conclu que les vecteurs sont orthogonaux : ![]() - un tel enregistrement sera correct, et même plus approprié que
- un tel enregistrement sera correct, et même plus approprié que ![]() .
.
Le troisième cas est d'une grande importance pratique., puisqu'il permet de vérifier si les vecteurs sont orthogonaux ou non. Nous allons résoudre ce problème dans la deuxième partie de la leçon.
Propriétés du produit scalaire
Revenons à la situation où deux vecteurs co-dirigé. Dans ce cas, l'angle entre eux est nul, , et la formule du produit scalaire prend la forme : .
Que se passe-t-il si un vecteur est multiplié par lui-même ? Il est clair que le vecteur est co-orienté avec lui-même, nous utilisons donc la formule simplifiée ci-dessus :
Le numéro s'appelle carré scalaire vecteur , et sont notés .
Ainsi, le carré scalaire d'un vecteur est égal au carré de la longueur du vecteur donné :
A partir de cette égalité, on peut obtenir une formule pour calculer la longueur d'un vecteur :
Certes cela paraît obscur, mais les tâches de la leçon remettront tout à sa place. Pour résoudre des problèmes, nous avons également besoin propriétés du produit scalaire.
Pour les vecteurs arbitraires et n'importe quel nombre, les propriétés suivantes sont vraies :
1) - déplaçable ou commutatif loi du produit scalaire.
2) ![]() - distribution ou distributif loi du produit scalaire. Autrement dit, vous pouvez ouvrir des parenthèses.
- distribution ou distributif loi du produit scalaire. Autrement dit, vous pouvez ouvrir des parenthèses.
3) ![]() - combinaison ou associatif loi du produit scalaire. La constante peut être extraite du produit scalaire.
- combinaison ou associatif loi du produit scalaire. La constante peut être extraite du produit scalaire.
Souvent, toutes sortes de propriétés (qu'il faut aussi prouver !) sont perçues par les étudiants comme jonque, qu'il suffit de mémoriser et d'oublier en toute sécurité immédiatement après l'examen. Il semblerait que ce qui est important ici, tout le monde sait déjà dès le premier grade que le produit ne change pas d'une permutation des facteurs :. Je dois vous avertir, en mathématiques supérieures avec une telle approche, il est facile de tout gâcher. Ainsi, par exemple, la propriété commutative n'est pas valide pour matrices algébriques. Ce n'est pas vrai pour produit croisé de vecteurs. Par conséquent, il est au moins préférable de se plonger dans toutes les propriétés que vous rencontrerez au cours des mathématiques supérieures afin de comprendre ce qui peut et ne peut pas être fait.
Exemple 3
![]() .
.
Solution: Tout d'abord, clarifions la situation avec le vecteur. C'est à propos de quoi? La somme des vecteurs et est un vecteur bien défini, noté . L'interprétation géométrique des actions avec des vecteurs peut être trouvée dans l'article Des vecteurs pour les nuls. Le même persil avec un vecteur est la somme des vecteurs et .
Ainsi, selon la condition, il est nécessaire de trouver le produit scalaire. En théorie, vous devez appliquer la formule de travail ![]() , mais le problème est que nous ne connaissons pas les longueurs des vecteurs et l'angle entre eux. Mais dans la condition, des paramètres similaires sont donnés pour les vecteurs, nous irons donc dans l'autre sens :
, mais le problème est que nous ne connaissons pas les longueurs des vecteurs et l'angle entre eux. Mais dans la condition, des paramètres similaires sont donnés pour les vecteurs, nous irons donc dans l'autre sens :

(1) Nous substituons des expressions de vecteurs .
(2) On ouvre les parenthèses selon la règle de multiplication des polynômes, un virelangue vulgaire se trouve dans l'article Nombres complexes ou Intégration d'une fonction fractionnaire-rationnelle. Je ne vais pas me répéter =) D'ailleurs, la propriété distributive du produit scalaire permet d'ouvrir les parenthèses. Nous avons le droit.
(3) Dans les premier et dernier termes, on écrit de manière compacte les carrés scalaires des vecteurs : ![]() . Dans le second terme, on utilise la commutabilité du produit scalaire : .
. Dans le second terme, on utilise la commutabilité du produit scalaire : .
(4) Voici des termes similaires : .
(5) Dans le premier terme, nous utilisons la formule du carré scalaire, qui a été mentionnée il n'y a pas si longtemps. Dans le dernier terme, respectivement, la même chose fonctionne : . Le deuxième terme est développé selon la formule standard ![]() .
.
(6) Remplacer ces conditions ![]() , et effectuer SOIGNEUSEMENT les calculs finaux.
, et effectuer SOIGNEUSEMENT les calculs finaux.
Répondre:
Sens négatif produit scalaire indique le fait que l'angle entre les vecteurs est obtus.
La tâche est typique, voici un exemple de solution indépendante :
Exemple 4
Trouver le produit scalaire des vecteurs et , si l'on sait que ![]() .
.
Maintenant, une autre tâche courante, juste pour la nouvelle formule de longueur de vecteur. Les désignations ici se chevaucheront un peu, donc pour plus de clarté, je vais le réécrire avec une lettre différente :
Exemple 5
Trouver la longueur du vecteur si ![]() .
.
Solution sera comme suit :
(1) Nous fournissons l'expression vectorielle .
(2) Nous utilisons la formule de longueur : , alors que nous avons une expression entière comme vecteur "ve".
(3) Utilisation formule scolaire somme au carré. Faites attention à la façon dont cela fonctionne curieusement ici: - en fait, c'est le carré de la différence, et, en fait, c'est ainsi. Ceux qui le souhaitent peuvent réarranger les vecteurs par endroits : - il s'est avéré la même chose jusqu'à un réarrangement des termes.
(4) Ce qui suit est déjà familier des deux problèmes précédents.
Répondre: ![]()
Puisque nous parlons de longueur, n'oubliez pas d'indiquer la dimension - "unités".
Exemple 6
Trouver la longueur du vecteur si ![]() .
.
Ceci est un exemple à faire soi-même. Solution complète et la réponse à la fin de la leçon.
Nous continuons à extraire des éléments utiles du produit scalaire. Reprenons notre formule ![]() . Par la règle de proportion, on remet les longueurs des vecteurs au dénominateur du côté gauche :
. Par la règle de proportion, on remet les longueurs des vecteurs au dénominateur du côté gauche : 
Échangeons les pièces : 
Quelle est la signification de cette formule ? Si les longueurs de deux vecteurs et leur produit scalaire sont connus, alors le cosinus de l'angle entre ces vecteurs peut être calculé et, par conséquent, l'angle lui-même.
Le produit scalaire est-il un nombre ? Nombre. Les longueurs de vecteurs sont-elles des nombres ? Nombres. Donc une fraction est aussi un nombre. Et si le cosinus de l'angle est connu : ![]() , puis en utilisant fonction inverse il est facile de trouver le coin lui-même :
, puis en utilisant fonction inverse il est facile de trouver le coin lui-même : ![]() .
.
Exemple 7
Trouver l'angle entre les vecteurs et , s'il est connu que .
Solution: Nous utilisons la formule :
Au stade final des calculs, une technique a été utilisée - l'élimination de l'irrationalité dans le dénominateur. Afin d'éliminer l'irrationalité, j'ai multiplié le numérateur et le dénominateur par .
Donc si ![]() , Ce:
, Ce: ![]()
Valeurs inverses fonctions trigonométriques peut être trouvé par table trigonométrique. Bien que cela arrive rarement. Dans les problèmes de géométrie analytique, certains ours maladroits apparaissent beaucoup plus souvent, et la valeur de l'angle doit être trouvée approximativement à l'aide d'une calculatrice. En fait, nous reverrons cette image encore et encore.
Répondre: ![]()
Encore une fois, n'oubliez pas de spécifier la dimension - radians et degrés. Personnellement, afin de délibérément "supprimer toutes les questions", je préfère indiquer les deux (à moins, bien sûr, par condition, qu'il soit nécessaire de ne présenter la réponse qu'en radians ou qu'en degrés).
Vous pourrez désormais faire face à une tâche plus difficile par vous-même :
Exemple 7*
Donnés sont les longueurs des vecteurs, et l'angle entre eux. Trouver l'angle entre les vecteurs , .
La tâche n'est pas tellement difficile que multi-voies.
Analysons l'algorithme de solution :
1) Selon la condition, il est nécessaire de trouver l'angle entre les vecteurs et , vous devez donc utiliser la formule  .
.
2) On trouve le produit scalaire (voir exemples n°3, 4).
3) Trouvez la longueur du vecteur et la longueur du vecteur (voir exemples n ° 5, 6).
4) La fin de la solution coïncide avec l'exemple n ° 7 - nous connaissons le nombre , ce qui signifie qu'il est facile de trouver l'angle lui-même : 
Solution rapide et la réponse à la fin de la leçon.
La deuxième partie de la leçon est consacrée au même produit scalaire. Coordonnées. Ce sera encore plus facile que dans la première partie.
Produit scalaire de vecteurs,
donné par des coordonnées dans une base orthonormée
Répondre:
Inutile de dire que traiter les coordonnées est beaucoup plus agréable.
Exemple 14
Trouver le produit scalaire des vecteurs et si
Ceci est un exemple à faire soi-même. Ici, vous pouvez utiliser l'associativité de l'opération, c'est-à-dire ne pas compter, mais retirer immédiatement le triple du produit scalaire et le multiplier en dernier. Solution et réponse à la fin de la leçon.
A la fin du paragraphe, un exemple provocateur de calcul de la longueur d'un vecteur :
Exemple 15
Trouver des longueurs de vecteurs ![]() , Si
, Si
Solution: encore une fois la méthode de la section précédente se suggère : mais il y a un autre moyen :
Trouvons le vecteur :
Et sa longueur selon la formule triviale ![]() :
:
Le produit scalaire n'est pas du tout pertinent ici !
À quel point c'est hors d'affaire lors du calcul de la longueur d'un vecteur:
Arrêt. Pourquoi ne pas profiter de la propriété de longueur évidente d'un vecteur ? Que peut-on dire de la longueur d'un vecteur ? Ce vecteur est 5 fois plus long que le vecteur. La direction est opposée, mais peu importe, car nous parlons de longueur. Évidemment, la longueur du vecteur est égale au produit module nombres par longueur de vecteur :
- le signe du module "mange" le moins possible du nombre.
Ainsi:
Répondre:
La formule du cosinus de l'angle entre les vecteurs qui sont donnés par des coordonnées
Nous avons maintenant des informations complètes pour que la formule précédemment dérivée pour le cosinus de l'angle entre les vecteurs ![]() exprimer en termes de coordonnées vectorielles :
exprimer en termes de coordonnées vectorielles :
Cosinus de l'angle entre les vecteurs plans et , donné dans la base orthonormée , s'exprime par la formule:![]() .
.
Cosinus de l'angle entre les vecteurs spatiaux, donné dans la base orthonormée , s'exprime par la formule: ![]()
Exemple 16
Trois sommets d'un triangle sont donnés. Trouver (angle au sommet ).
Solution: Par condition, le dessin n'est pas obligatoire, mais quand même : 
L'angle requis est marqué d'un arc vert. Rappelez immédiatement la désignation scolaire de l'angle: - Attention particulière sur milieu lettre - c'est le sommet de l'angle dont nous avons besoin. Par souci de concision, il pourrait également être écrit simplement.
D'après le dessin, il est tout à fait évident que l'angle du triangle coïncide avec l'angle entre les vecteurs et , en d'autres termes : ![]() .
.
Il est souhaitable d'apprendre à effectuer l'analyse effectuée mentalement.
Trouvons les vecteurs : 
Calculons le produit scalaire :
Et les longueurs des vecteurs : 
Cosinus d'un angle :
C'est cet ordre de la tâche que je recommande aux nuls. Les lecteurs plus avancés peuvent écrire les calculs "sur une seule ligne": 
Voici un exemple de "mauvaise" valeur de cosinus. La valeur résultante n'est pas définitive, il n'y a donc pas grand intérêt à se débarrasser de l'irrationalité du dénominateur.
Trouvons l'angle :
Si vous regardez le dessin, le résultat est tout à fait plausible. Pour vérifier l'angle peut également être mesuré avec un rapporteur. N'endommagez pas le revêtement du moniteur =)
Répondre: ![]()
Dans la réponse, n'oubliez pas que interrogé sur l'angle du triangle(et non sur l'angle entre les vecteurs), n'oubliez pas d'indiquer la réponse exacte : et la valeur approximative de l'angle : ![]() trouvé avec une calculatrice.
trouvé avec une calculatrice.
Ceux qui ont apprécié le processus peuvent calculer les angles et s'assurer que l'égalité canonique est vraie
Exemple 17
Un triangle est donné dans l'espace par les coordonnées de ses sommets. Trouver l'angle entre les côtés et
Ceci est un exemple à faire soi-même. Solution complète et réponse à la fin de la leçon
Une petite section finale sera consacrée aux projections, dans lesquelles le produit scalaire est également "impliqué":
Projection d'un vecteur sur un vecteur. Projection vectorielle sur des axes de coordonnées.
Cosinus de direction vectorielle
Considérons les vecteurs et : 
Nous projetons le vecteur sur le vecteur , pour cela nous omettons le début et la fin du vecteur perpendiculaires par vecteur (lignes pointillées vertes). Imaginez que des rayons de lumière tombent perpendiculairement sur un vecteur. Ensuite, le segment (ligne rouge) sera "l'ombre" du vecteur. Dans ce cas, la projection d'un vecteur sur un vecteur est la LONGUEUR du segment. Autrement dit, LA PROJECTION EST UN NOMBRE.
Ce NUMERO est marqué de la manière suivante: , "grand vecteur" désigne le vecteur QUI projet, "petit vecteur en indice" désigne le vecteur SUR qui est projeté.
L'entrée elle-même se lit comme suit : "la projection du vecteur "a" sur le vecteur "be"".
Que se passe-t-il si le vecteur "be" est "trop court" ? Nous traçons une ligne droite contenant le vecteur "être". Et le vecteur "a" sera déjà projeté à la direction du vecteur "be", simplement - sur une ligne droite contenant le vecteur "be". La même chose se produira si le vecteur "a" est mis de côté dans le trentième règne - il sera toujours facilement projeté sur la ligne contenant le vecteur "be".
Si l'angle entre vecteurs épicé(comme sur la photo), puis
Si les vecteurs orthogonal, alors (la projection est un point dont les dimensions sont supposées nulles).
Si l'angle entre vecteurs émoussé(sur la figure, réarrangez mentalement la flèche du vecteur), puis (de même longueur, mais prise avec un signe moins).
Mettez de côté ces vecteurs à partir d'un point : 
Évidemment, lors du déplacement d'un vecteur, sa projection ne change pas
Instruction
Soit deux vecteurs non nuls donnés sur le plan, tracés à partir d'un point : vecteur A de coordonnées (x1, y1) B de coordonnées (x2, y2). Coin entre eux est noté θ. Pour trouver la mesure en degrés de l'angle θ, vous devez utiliser la définition du produit scalaire.
Le produit scalaire de deux vecteurs non nuls est un nombre égal au produit des longueurs de ces vecteurs et du cosinus de l'angle entre eux, c'est-à-dire (A,B)=|A|*|B|*cos( θ). Maintenant, vous devez exprimer le cosinus de l'angle à partir de ceci : cos(θ)=(A,B)/(|A|*|B|).
Le produit scalaire peut également être trouvé à l'aide de la formule (A,B)=x1*x2+y1*y2, puisque le produit de deux vecteurs non nuls est égal à la somme des produits des vecteurs correspondants. Si le produit scalaire de vecteurs non nuls est égal à zéro, alors les vecteurs sont perpendiculaires (l'angle entre eux est de 90 degrés) et d'autres calculs peuvent être omis. Si le produit scalaire de deux vecteurs est positif, alors l'angle entre ces vecteurs aigu, et s'il est négatif, alors l'angle est obtus.
Calculez maintenant les longueurs des vecteurs A et B à l'aide des formules : |A|=√(x1²+y1²), |B|=√(x2²+y2²). La longueur du vecteur est calculée comme Racine carrée de la somme des carrés de ses coordonnées.
Remplacez les valeurs trouvées du produit scalaire et les longueurs des vecteurs dans la formule de l'angle obtenu à l'étape 2, c'est-à-dire cos(θ)=(x1*x2+y1*y2)/(√(x1²+ y1²)+√(x2²+y2²)). Maintenant, connaissant la valeur de , pour trouver la mesure en degrés de l'angle entre vecteurs vous devez utiliser la table Bradis ou en tirer : θ=arccos(cos(θ)).
Si les vecteurs A et B sont donnés dans un espace tridimensionnel et ont respectivement les coordonnées (x1, y1, z1) et (x2, y2, z2), une coordonnée supplémentaire est ajoutée lors de la recherche du cosinus de l'angle. Dans ce cas cosinus : cos(θ)=(x1*x2+y1*y2+z1*z2)/(√(x1²+y1²+z1²)+√(x2²+y2²+z2²)).
Si deux vecteurs ne sont pas tracés à partir d'un point, alors pour trouver l'angle entre eux par translation parallèle, vous devez combiner les débuts de ces vecteurs.
L'angle entre deux vecteurs ne peut pas être supérieur à 180 degrés.
Sources:
- comment calculer l'angle entre les vecteurs
- Angle entre droite et plan
Pour résoudre de nombreux problèmes, tant appliqués que théoriques, en physique et en algèbre linéaire, il est nécessaire de calculer l'angle entre les vecteurs. Cette tâche apparemment simple peut entraîner de nombreuses difficultés si vous ne comprenez pas clairement l'essence du produit scalaire et quelle valeur apparaît à la suite de ce produit.
Instruction
L'angle entre les vecteurs dans un espace vectoriel linéaire est l'angle minimum à , auquel la codirection des vecteurs est atteinte. L'un des vecteurs est entraîné autour de son point de départ. À partir de la définition, il devient évident que la valeur de l'angle ne peut pas dépasser 180 degrés (voir l'étape).
Dans ce cas, on suppose à juste titre que dans un espace linéaire, lorsque les vecteurs sont transférés en parallèle, l'angle entre eux ne change pas. Par conséquent, pour le calcul analytique de l'angle, l'orientation spatiale des vecteurs n'a pas d'importance.
Le résultat du produit scalaire est un nombre, sinon un scalaire. Rappelez-vous (ceci est important à savoir) afin d'éviter des erreurs dans les calculs ultérieurs. La formule du produit scalaire, situé sur un plan ou dans l'espace des vecteurs, a la forme (voir la figure pour l'étape).
Si les vecteurs sont situés dans l'espace, effectuez le calcul de la même manière. La seule chose sera l'apparition du terme dans le dividende - c'est le terme pour la demande, c'est-à-dire la troisième composante du vecteur. En conséquence, lors du calcul du module des vecteurs, la composante z doit également être prise en compte, puis pour les vecteurs situés dans l'espace, la dernière expression est transformée comme suit (voir la figure 6 à l'étape).
Un vecteur est un segment de droite avec une direction donnée. L'angle entre les vecteurs a une signification physique, par exemple, lors de la recherche de la longueur de la projection d'un vecteur sur un axe.

Instruction
Angle entre deux vecteurs non nuls à l'aide du calcul du produit scalaire. Par définition, le produit est égal au produit des longueurs et de l'angle entre elles. D'autre part, le produit scalaire pour deux vecteurs a de coordonnées (x1 ; y1) et b de coordonnées (x2 ; y2) est calculé : ab = x1x2 + y1y2. De ces deux manières, le produit scalaire est facile à incliner entre les vecteurs.
Trouvez les longueurs ou les modules des vecteurs. Pour nos vecteurs a et b : |a| = (x1² + y1²)^1/2, |b| = (x2² + y2²)^1/2.
Trouvez le produit interne des vecteurs en multipliant leurs coordonnées par paires : ab = x1x2 + y1y2. D'après la définition du produit scalaire ab = |a|*|b|*cos α, où α est l'angle entre les vecteurs. Alors nous obtenons que x1x2 + y1y2 = |a|*|b|*cos α. Alors cos α = (x1x2 + y1y2)/(|a|*|b|) = (x1x2 + y1y2)/((x1² + y1²)(x2² + y2²))^1/2.
Trouvez l'angle α à l'aide des tables de Bradys.
Vidéos connexes
note
Le produit scalaire est une caractéristique scalaire des longueurs des vecteurs et de l'angle entre eux.
Le plan est l'un des concepts de base en géométrie. Un plan est une surface pour laquelle l'énoncé est vrai - toute droite reliant deux de ses points appartient entièrement à cette surface. Les plans sont généralement désignés par les lettres grecques α, β, γ, etc. Deux plans se coupent toujours en une ligne droite appartenant aux deux plans.

Instruction
Considérons les demi-plans α et β formés à l'intersection de . Angle formé par une droite a et deux demi-plans α et β par un angle dièdre. Dans ce cas, les demi-plans formant un angle dièdre par faces, la ligne a le long de laquelle les plans se coupent est appelée arête angle dièdre.

Angle dièdre, comme un angle plat, en degrés. Pour faire un angle dièdre, il faut choisir un point arbitraire sur sa face O. Dans les deux cas, deux rayons a sont tracés par le point O. L'angle résultant AOB est appelé l'angle linéaire de l'angle dièdre a.
Soit donc le vecteur V = (a, b, c) et le plan A x + B y + C z = 0, où A, B et C sont les coordonnées de la normale N. Alors le cosinus de l'angle α entre les vecteurs V et N est: cos α \u003d (a A + b B + c C) / (√ (a² + b² + c²) √ (A² + B² + C²)).
Pour calculer la valeur de l'angle en degrés ou en radians, vous devez calculer la fonction inverse du cosinus à partir de l'expression résultante, c'est-à-dire arccosinus: α \u003d arscos ((a A + b B + c C) / (√ (a² + b² + c²) √ (A² + B² + C²))).
Exemple : trouver coin entre vecteur(5, -3, 8) et avion, donné équation générale 2 x - 5 y + 3 z = 0. Solution : notez les coordonnées du vecteur normal du plan N = (2, -5, 3). Remplacez toutes les valeurs connues dans la formule ci-dessus : cos α = (10 + 15 + 24)/√3724 ≈ 0,8 → α = 36,87°.
Vidéos connexes
Écrivez une équation et isolez-en le cosinus. Selon une formule, le produit scalaire des vecteurs est égal à leurs longueurs multipliées entre elles et par le cosinus angle, et d'autre part - la somme des produits de coordonnées le long de chacun des axes. En assimilant les deux formules, nous pouvons conclure que le cosinus angle doit être égal au rapport de la somme des produits des coordonnées au produit des longueurs des vecteurs.
Écrivez l'équation résultante. Pour ce faire, nous devons désigner les deux vecteurs. Disons qu'ils sont donnés dans un système cartésien 3D et que leurs points de départ sont dans une grille. La direction et la grandeur du premier vecteur seront données par le point (X₁,Y₁,Z₁), le second - (X₂,Y₂,Z₂), et l'angle sera désigné par la lettre γ. Alors les longueurs de chacun des vecteurs peuvent être, par exemple, selon le théorème de Pythagore pour formées par leurs projections sur chacun des axes de coordonnées : √(X₁² + Y₁² + Z₁²) et √(X₂² + Y₂² + Z₂²). Remplacez ces expressions dans la formule formulée à l'étape précédente et vous obtenez l'égalité : cos(γ) = (X₁*X₂ + Y₁*Y₂ + Z₁*Z₂) / (√(X₁² + Y₁² + Z₁²) * √(X₂² + Y₂² + Z₂² )).
Utiliser le fait que la somme des carrés sinus et Cie sinus depuis angle une valeur en donne toujours un. Par conséquent, en augmentant ce qui a été obtenu à l'étape précédente pour co sinus au carré et soustrait de l'unité, puis
Angle entre deux vecteurs , :
Si l'angle entre deux vecteurs est aigu, alors leur produit scalaire est positif ; si l'angle entre les vecteurs est obtus, alors le produit scalaire de ces vecteurs est négatif. Le produit scalaire de deux vecteurs non nuls est nul si et seulement si ces vecteurs sont orthogonaux.
Exercer. Trouver l'angle entre les vecteurs et
Solution. Cosinus de l'angle souhaité

![]()
16. Calculer l'angle entre des droites, une droite et un plan
Angle entre droite et plan coupant cette ligne et non perpendiculaire à elle est l'angle entre la ligne et sa projection sur ce plan.
La détermination de l'angle entre une droite et un plan permet de conclure que l'angle entre une droite et un plan est l'angle entre deux droites sécantes : la droite elle-même et sa projection sur le plan. Par conséquent, l'angle entre une droite et un plan est un angle aigu.

L'angle entre une ligne perpendiculaire et un plan est considéré comme égal, et l'angle entre une ligne parallèle et un plan n'est pas déterminé du tout ou est considéré comme égal à .
§ 69. Calcul de l'angle entre droites.
Le problème du calcul de l'angle entre deux droites dans l'espace se résout de la même manière que dans le plan (§ 32). Notons φ l'angle entre les lignes je 1 et je 2 , et par ψ - l'angle entre les vecteurs directeurs UN Et b ces droites.

Puis si
ψ 90° (Fig. 206.6), alors φ = 180° - ψ. Il est évident que dans les deux cas l'égalité cos φ = |cos ψ| est vraie. Par la formule (1) § 20 nous avons
![]()
ainsi, ![]()
Soit les droites données par leurs équations canoniques
Ensuite, l'angle φ entre les lignes est déterminé à l'aide de la formule
Si l'une des lignes (ou les deux) est donnée par des équations non canoniques, alors pour calculer l'angle, vous devez trouver les coordonnées des vecteurs de direction de ces lignes, puis utiliser la formule (1).
17. Droites parallèles, Théorèmes sur les droites parallèles
Définition. Deux droites dans un plan s'appellent parallèle s'ils n'ont pas de points communs.

Deux lignes en trois dimensions sont appelées parallèle s'ils se trouvent dans le même plan et n'ont pas de points communs.

Angle entre deux vecteurs.
De la définition du produit scalaire :
 .
.
Condition d'orthogonalité de deux vecteurs:
Condition de colinéarité pour deux vecteurs :
![]() .
.
Découle de la définition 5 - . En effet, de la définition du produit d'un vecteur par un nombre, il découle. Par conséquent, sur la base de la règle d'égalité des vecteurs, nous écrivons , , , ce qui implique ![]() . Mais le vecteur résultant de la multiplication d'un vecteur par un nombre est colinéaire au vecteur .
. Mais le vecteur résultant de la multiplication d'un vecteur par un nombre est colinéaire au vecteur .
Projection vecteur à vecteur :
 .
.
Exemple 4. Points donnés , , , .
Trouvez le produit scalaire.
Solution. on trouve par la formule du produit scalaire de vecteurs donnés par leurs coordonnées. Parce que le
, ![]() ,
,
Exemple 5 Points donnés , , , .
Trouver projection.
Solution. Parce que le
, ![]() ,
,
Sur la base de la formule de projection, nous avons
 .
.
Exemple 6 Points donnés , , , .
Trouvez l'angle entre les vecteurs et .
Solution. A noter que les vecteurs
, ![]() ,
,
ne sont pas colinéaires, puisque leurs coordonnées ne sont pas proportionnelles :
![]() .
.
Ces vecteurs ne sont pas non plus perpendiculaires, puisque leur produit scalaire est .
Allons trouver,
Coin ![]() trouver à partir de la formule :
trouver à partir de la formule :
 .
.
Exemple 7 Déterminez pour quels vecteurs et ![]() colinéaire.
colinéaire.
Solution. En cas de colinéarité, les coordonnées correspondantes des vecteurs ![]() et doit être proportionnel, c'est-à-dire :
et doit être proportionnel, c'est-à-dire :
![]() .
.
D'ici et .
Exemple 8. Déterminer à quelle valeur du vecteur ![]() Et
Et ![]() sont perpendiculaires.
sont perpendiculaires.
Solution. Vecteur ![]() et sont perpendiculaires si leur produit scalaire est nul. De cette condition on obtient : . C'est, .
et sont perpendiculaires si leur produit scalaire est nul. De cette condition on obtient : . C'est, .
Exemple 9. Trouver ![]() , Si , , .
, Si , , .
Solution. En raison des propriétés du produit scalaire, nous avons :
Exemple 10. Trouver l'angle entre les vecteurs et , où et - vecteurs unitaires et l'angle entre les vecteurs et est égal à 120o.
Solution. Nous avons:  , ,
, ,
Enfin nous avons : ![]() .
.
5B. produit vectoriel.
Définition 21.art vectoriel vecteur à vecteur est appelé vecteur , ou , défini par les trois conditions suivantes :
1) Le module du vecteur est , où est l'angle entre les vecteurs et , c'est-à-dire ![]() .
.
Il s'ensuit que le module d'un produit croisé est numériquement égal à l'aire d'un parallélogramme construit sur des vecteurs et comme sur des côtés.
2) Le vecteur est perpendiculaire à chacun des vecteurs et ( ; ), c'est-à-dire perpendiculaire au plan du parallélogramme construit sur les vecteurs et .
3) Le vecteur est dirigé de telle manière que s'il est vu de son extrémité, le virage le plus court de vecteur à vecteur serait dans le sens antihoraire (les vecteurs , , forment un triplet droit).
Comment calculer les angles entre vecteurs ?
Lors de l'étude de la géométrie, de nombreuses questions se posent sur le thème des vecteurs. L'élève éprouve des difficultés particulières lorsqu'il s'agit de trouver les angles entre les vecteurs.
Termes de base
Avant de considérer les angles entre vecteurs, il est nécessaire de se familiariser avec la définition d'un vecteur et la notion d'angle entre vecteurs.

Un vecteur est un segment qui a une direction, c'est-à-dire un segment dont le début et la fin sont définis.
L'angle entre deux vecteurs sur un plan qui ont une origine commune est le plus petit des angles, par lequel il est nécessaire de déplacer l'un des vecteurs autour d'un point commun, jusqu'à une position où leurs directions coïncident.
Formule de solution
Une fois que vous comprenez ce qu'est un vecteur et comment son angle est déterminé, vous pouvez calculer l'angle entre les vecteurs. La formule de solution pour cela est assez simple et le résultat de son application sera la valeur du cosinus de l'angle. Par définition, il est égal au quotient du produit scalaire des vecteurs et du produit de leurs longueurs.
Le produit scalaire des vecteurs est considéré comme la somme des coordonnées correspondantes des vecteurs multiplicateurs multipliées les unes par les autres. La longueur d'un vecteur, ou son module, est calculé comme la racine carrée de la somme des carrés de ses coordonnées.
Après avoir reçu la valeur du cosinus de l'angle, vous pouvez calculer la valeur de l'angle lui-même à l'aide d'une calculatrice ou d'une table trigonométrique.
Exemple
Une fois que vous avez compris comment calculer l'angle entre les vecteurs, la solution au problème correspondant devient simple et directe. A titre d'exemple, considérons le problème simple de trouver la grandeur d'un angle.

Tout d'abord, il sera plus commode de calculer les valeurs des longueurs des vecteurs et de leur produit scalaire nécessaires à la résolution. En utilisant la description ci-dessus, nous obtenons :

En remplaçant les valeurs obtenues dans la formule, nous calculons la valeur du cosinus de l'angle souhaité:

Ce nombre n'est pas l'une des cinq valeurs de cosinus communes, donc pour obtenir la valeur de l'angle, vous devrez utiliser une calculatrice ou la table trigonométrique Bradis. Mais avant d'obtenir l'angle entre les vecteurs, la formule peut être simplifiée pour se débarrasser du signe négatif supplémentaire :

La réponse finale peut être laissée sous cette forme pour maintenir la précision, ou vous pouvez calculer la valeur de l'angle en degrés. Selon la table Bradis, sa valeur sera d'environ 116 degrés et 70 minutes, et la calculatrice affichera une valeur de 116,57 degrés.
Calcul d'angle dans un espace à n dimensions
Lorsque l'on considère deux vecteurs dans un espace tridimensionnel, il est beaucoup plus difficile de comprendre de quel angle on parle s'ils ne se trouvent pas dans le même plan. Pour simplifier la perception, vous pouvez dessiner deux segments qui se croisent qui forment le plus petit angle entre eux, et ce sera celui souhaité. Malgré la présence d'une troisième coordonnée dans le vecteur, le processus de calcul des angles entre les vecteurs ne changera pas. Calculez le produit scalaire et les modules de vecteurs, l'arc cosinus de leur quotient et sera la réponse à ce problème.
En géométrie, des problèmes surviennent souvent avec des espaces qui ont plus de trois dimensions. Mais pour eux, l'algorithme pour trouver la réponse semble similaire.
Différence entre 0 et 180 degrés
L'une des erreurs courantes lors de la rédaction d'une réponse à un problème conçu pour calculer l'angle entre les vecteurs est la décision d'écrire que les vecteurs sont parallèles, c'est-à-dire que l'angle souhaité s'est avéré être de 0 ou 180 degrés. Cette réponse est incorrecte.
Ayant reçu une valeur d'angle de 0 degré à la suite de la solution, la bonne réponse serait de désigner les vecteurs comme co-directionnels, c'est-à-dire que les vecteurs auront la même direction. Dans le cas de l'obtention de 180 degrés, les vecteurs seront de nature à directions opposées.
Vecteurs spécifiques
En trouvant les angles entre les vecteurs, l'un des types spéciaux peut être trouvé, en plus de ceux co-dirigés et dirigés de manière opposée décrits ci-dessus.
- Plusieurs vecteurs parallèles à un même plan sont dits coplanaires.
- Les vecteurs qui ont la même longueur et la même direction sont dits égaux.
- Les vecteurs qui se trouvent sur la même ligne droite, quelle que soit leur direction, sont appelés colinéaires.
- Si la longueur du vecteur est nulle, c'est-à-dire que son début et sa fin coïncident, alors il est appelé zéro, et s'il est un, alors il est appelé un.
Comment trouver l'angle entre les vecteurs ?
aidez moi s'il vous plait ! je connais la formule mais je n'y arrive pas
vecteur a (8 ; 10 ; 4) vecteur b (5 ; -20 ; -10)
Alexandre Titov
L'angle entre les vecteurs donné par leurs coordonnées est trouvé selon l'algorithme standard. Vous devez d'abord trouver le produit scalaire des vecteurs a et b : (a, b) = x1x2 + y1y2 + z1z2. Nous substituons ici les coordonnées de ces vecteurs et considérons :
(a,b) = 8*5 + 10*(-20) = 4*(-10) = 40 - 200 - 40 = -200.
Ensuite, nous déterminons les longueurs de chacun des vecteurs. La longueur ou module d'un vecteur est la racine carrée de la somme des carrés de ses coordonnées :
|a| = racine de (x1^2 + y1^2 + z1^2) = racine de (8^2 + 10^2 + 4^2) = racine de (64 + 100 + 16) = racine de 180 = 6 racines de 5
|b| = racine carrée de (x2^2 + y2^2 + z2^2) = racine carrée de (5^2 + (-20)^2 + (-10)^2) = racine carrée de (25 + 400 + 100 ) = racine carrée sur 525 = 5 racines sur 21.
Nous multiplions ces longueurs. Nous obtenons 30 racines sur 105.
Et enfin, on divise le produit scalaire des vecteurs par le produit des longueurs de ces vecteurs. On obtient -200 / (30 racines sur 105) soit
- (4 racines de 105) / 63. C'est le cosinus de l'angle entre les vecteurs. Et l'angle lui-même est égal à l'arc cosinus de ce nombre
f \u003d arccos (-4 racines de 105) / 63.
Si j'ai bien compté.
Comment calculer le sinus d'un angle entre des vecteurs à partir des coordonnées des vecteurs
Mikhaïl Tkatchev
Nous multiplions ces vecteurs. Leur produit scalaire est égal au produit des longueurs de ces vecteurs et du cosinus de l'angle entre eux.
L'angle nous est inconnu, mais les coordonnées sont connues.
Écrivons-le mathématiquement comme ceci.
Soit, étant donnés les vecteurs a(x1;y1) et b(x2;y2)
Alors
A*b=|a|*|b|*cosA
CosA=a*b/|a|*|b|
Nous nous disputons.
a*b-produit scalaire des vecteurs est égal à la somme des produits des coordonnées correspondantes des coordonnées de ces vecteurs, c'est-à-dire égal à x1*x2+y1*y2
|a|*|b|-produit des longueurs vectorielles est égal à √((x1)^2+(y1)^2)*√((x2)^2+(y2)^2).
Donc le cosinus de l'angle entre les vecteurs est :
CosA=(x1*x2+y1*y2)/√((x1)^2+(y1)^2)*√((x2)^2+(y2)^2)
Connaissant le cosinus d'un angle, on peut calculer son sinus. Discutons de la façon de le faire :
Si le cosinus d'un angle est positif, alors cet angle est compris entre 1 ou 4 quarts, donc son sinus est soit positif, soit négatif. Mais puisque l'angle entre les vecteurs est inférieur ou égal à 180 degrés, alors son sinus est positif. Nous raisonnons de la même manière si le cosinus est négatif.
SinA=√(1-cos^2A)=√(1-((x1*x2+y1*y2)/√((x1)^2+(y1)^2)*√((x2)^2+( y2)^2))^2)
C'est tout)))) bonne chance pour comprendre)))
Dmitri Levichtchev
Le fait qu'il soit impossible de sinusoïder directement n'est pas vrai.
En plus de la formule :
(a,b)=|a|*|b|*cos A
Il y a aussi celui-ci :
||=|a|*|b|*sin A
Autrement dit, au lieu du produit scalaire, vous pouvez prendre le module du produit vectoriel.
"Produit scalaire vectoriel" - Le produit scalaire des vecteurs. Dans un triangle équilatéral ABC de côté 1, la hauteur BD est tracée. Par définition, caractériser un angle ? entre les vecteurs et si : a) b) c) d). A quelle valeur de t est le vecteur perpendiculaire au vecteur si (2, -1), (4, 3). Le produit scalaire des vecteurs et est noté.
"Géométrie 9 classe "Vecteurs"" - La distance entre deux points. Les problèmes les plus simples en coordonnées. Vérifie toi-même! Coordonnées vectorielles. En 1903, O. Henrichi a proposé que le produit scalaire soit désigné par le symbole (a, c). Un vecteur est un segment orienté. Décomposition d'un vecteur en vecteurs de coordonnées. Le concept de vecteur. Décomposition d'un vecteur sur un plan en deux vecteurs non colinéaires.
"Vecteur de résolution de problèmes" - Exprimez les vecteurs AM, DA, CA, MB, CD en termes de vecteur a et de vecteur b. № 2 Exprimer les vecteurs DP, DM, AC à travers les vecteurs a et b. SR : PD=2:3 ; AK : KD = 1 : 2. Exprimez les vecteurs CK, RK par les vecteurs a et b. BE : EC = 3 : 1. K est le milieu de DC. VK : KС = 3 : 4. Exprimez les vecteurs AK, DK à travers les vecteurs a et b. Application des vecteurs à la résolution de problèmes (partie 1).
"Problèmes sur les vecteurs" - Théorème. Trouvez les coordonnées. Trois points sont accordés. Sommets du triangle. Trouvez les coordonnées des vecteurs. Trouver les coordonnées du point. Trouvez les coordonnées et la longueur du vecteur. Exprimer la longueur du vecteur. Coordonnées vectorielles. Coordonnées vectorielles. Trouvez les coordonnées du vecteur. Les vecteurs sont donnés. Nommez les coordonnées des vecteurs. Le vecteur a des coordonnées.
"Méthode des coordonnées sur un plan" - Un cercle est dessiné. Perpendiculaires. Axe de coordonnées. La valeur du sinus. Système de coordonnées rectangulaire sur le plan. Trouvez les coordonnées du sommet. Prenons un exemple. La solution à ce problème. Les points sont attribués dans l'avion. Sommets d'un parallélogramme. Développez les vecteurs. Calculer. Beaucoup de points. Résoudre graphiquement le système d'équations.
"Addition et soustraction de vecteurs" - 1. Objectifs de la leçon. 2. La partie principale. Votre très, plus meilleur ami Somnambule! Apprenez à soustraire des vecteurs. 2. Spécifiez le vecteur de la somme des vecteurs a et b. Mon ami!! Voyons ce que nous avons ici. Nos objectifs : Conclusion. 3. Examen de la tête. 4. Liste de références. Voyager avec Lunatic. A partir du point A, on reporte les deux vecteurs.
Au total, il y a 29 présentations dans le sujet