Quel est l'angle inscrit d'un arc ? Propriétés des angles inscrits
Lire aussi
L'angle ABC est un angle inscrit. Il repose sur l'arc AC, enfermé entre ses côtés (fig. 330).
Théorème. Un angle inscrit se mesure par la moitié de l'arc sur lequel il sous-tend.
Il faut comprendre cela ainsi : un angle inscrit contient autant de degrés angulaires, de minutes et de secondes qu'il y a de degrés d'arc, de minutes et de secondes contenus dans la moitié de l'arc sur laquelle il repose.
Pour prouver ce théorème, trois cas doivent être considérés.
Premier cas. Le centre du cercle se trouve du côté de l'angle inscrit (Fig. 331).
Soit ∠ABC un angle inscrit et le centre du cercle O se trouve du côté BC. Il faut prouver qu'il se mesure par un demi-arc AC.
Relions le point A au centre du cercle. On obtient un \(\Delta\)AOB isocèle, dans lequel AO = OB, comme les rayons du même cercle. Par conséquent, ∠A = ∠B.
∠AOC est externe au triangle AOB, donc ∠AOC = ∠A + ∠B, et puisque les angles A et B sont égaux, alors ∠B est 1/2 ∠AOC.
Mais ∠AOC est mesuré par l'arc AC, donc ∠B est mesuré par la moitié de l'arc AC.
Par exemple, si \(\breve(AC)\) contient 60°18', alors ∠B contient 30°9'.
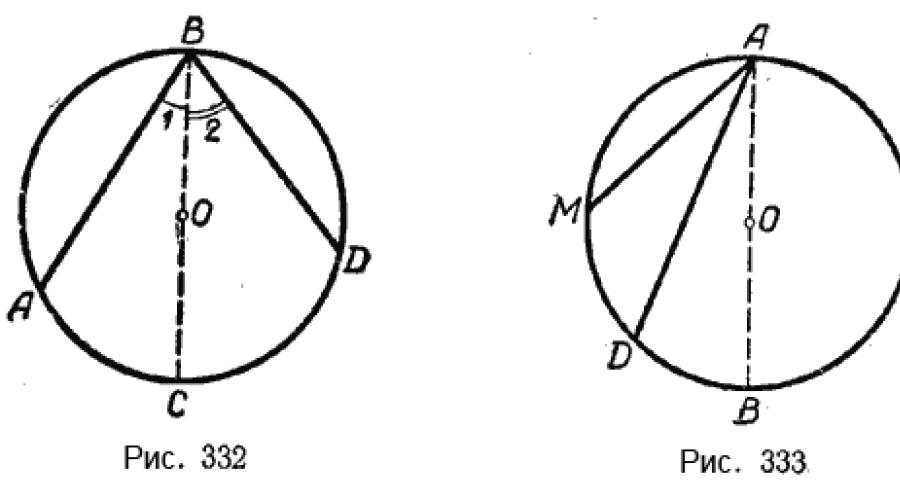
Deuxième cas. Le centre du cercle se situe entre les côtés de l'angle inscrit (Fig. 332).
Soit ∠ABD un angle inscrit. Le centre du cercle O se situe entre ses côtés. Nous devons prouver que ∠ABD est mesuré par la moitié de l’arc AD.
Pour le prouver, dessinons le diamètre BC. L'angle ABD est divisé en deux angles : ∠1 et ∠2.
∠1 est mesuré par un demi-arc AC, et ∠2 est mesuré par un demi-arc CD, donc l'ensemble ∠ABD est mesuré par 1 / 2 \(\breve(AC)\) + 1 / 2 \(\breve (CD)\), soit . demi-arc AD.
Par exemple, si \(\breve(AD)\) contient 124°, alors ∠B contient 62°.

Troisième cas. Le centre du cercle se trouve en dehors de l'angle inscrit (Fig. 333).
Soit ∠MAD un angle inscrit. Le centre du cercle O est à l’extérieur du coin. Nous devons prouver que ∠MAD est mesuré par la moitié de l’arc MD.
Pour le prouver, dessinons le diamètre AB. ∠MAD = ∠MAB - ∠DAB. Mais ∠MAB mesure 1 / 2 \(\breve(MB)\), et ∠DAB mesure 1 / 2 \(\breve(DB)\).
Par conséquent, ∠MAD mesure 1 / 2 (\(\breve(MB) - \breve(DB))\), soit 1 / 2 \(\breve(MD)\).
Par exemple, si \(\breve(MD)\) contient 48° 38", alors ∠MAD contient 24° 19' 8".
Conséquences
1.
Tous les angles inscrits sous-tendant le même arc sont égaux entre eux, puisqu'ils sont mesurés par la moitié du même arc.
(Fig. 334, a).

2. Un angle inscrit sous-tendu par un diamètre est un angle droit, puisqu'il sous-tend un demi-cercle. Un demi-cercle contient 180 degrés d'arc, ce qui signifie que l'angle basé sur le diamètre contient 90 degrés d'arc (Fig. 334, b).
Le plus souvent, le processus de préparation à l'examen d'État unifié de mathématiques commence par une répétition de définitions, de formules et de théorèmes de base, notamment sur le thème « Angles centraux et inscrits dans un cercle ». En règle générale, cette section de planimétrie est étudiée en lycée. Il n'est pas surprenant que de nombreux étudiants soient confrontés à la nécessité de revoir les concepts et théorèmes de base sur le thème « Angle central d'un cercle ». Ayant compris l'algorithme permettant de résoudre de tels problèmes, les écoliers peuvent compter sur des scores compétitifs basés sur les résultats de la réussite de l'examen d'État unifié.
Comment se préparer facilement et efficacement à la réussite du test de certification ?
Lorsqu'ils étudient avant de réussir l'examen d'État unifié, de nombreux lycéens sont confrontés au problème de trouver les informations nécessaires sur le thème « Angles centraux et inscrits dans un cercle ». Il n’est pas toujours possible de disposer d’un manuel scolaire. Et chercher des formules sur Internet prend parfois beaucoup de temps.
Notre équipe vous aidera à « gonfler » vos compétences et à améliorer vos connaissances dans une section de géométrie aussi difficile que la planimétrie. portail éducatif. « Shkolkovo » offre aux lycéens et à leurs professeurs une nouvelle façon de construire le processus de préparation à l'examen d'État unifié. Tout le matériel de base est présenté par nos spécialistes sous la forme la plus accessible. Après avoir lu les informations de la section « Contexte théorique », les élèves apprendront quelles sont les propriétés de l'angle central d'un cercle, comment trouver sa valeur, etc.
Ensuite, pour consolider les connaissances acquises et les compétences pratiques, nous recommandons de réaliser des exercices appropriés. Grand choix les tâches permettant de trouver la valeur d'un angle inscrit dans un cercle et d'autres paramètres sont présentées dans la section « Catalogue ». Pour chaque exercice, nos experts ont rédigé une solution détaillée et indiqué la bonne réponse. La liste des tâches sur le site est constamment complétée et mise à jour.
Les lycéens peuvent se préparer à l'examen d'État unifié en pratiquant des exercices, par exemple pour déterminer la grandeur d'un angle central et la longueur d'un arc de cercle, en ligne, dans n'importe quelle région de Russie.
Si nécessaire, la tâche réalisée peut être sauvegardée dans la rubrique « Favoris » afin d'y revenir ultérieurement et d'analyser à nouveau le principe de sa solution.
Angle inscrit, théorie du problème. Amis! Dans cet article, nous parlerons des tâches pour lesquelles vous devez connaître les propriétés d'un angle inscrit. Il s'agit de tout un groupe de tâches, elles sont incluses dans l'examen d'État unifié. La plupart d’entre eux peuvent être résolus très simplement, en une seule action.
Il existe des problèmes plus difficiles, mais ils ne vous poseront pas beaucoup de difficultés ; vous devez connaître les propriétés d’un angle inscrit. Petit à petit nous analyserons tous les prototypes de tâches, je vous invite sur le blog !
Maintenant la théorie nécessaire. Rappelons ce que sont un angle central et inscrit, une corde, un arc, sur lesquels reposent ces angles :
L'angle au centre d'un cercle est un angle plan avecsommet en son centre.
La partie d'un cercle située à l'intérieur d'un angle planappelé arc de cercle.
La mesure en degrés d’un arc de cercle est appelée mesure en degrésl'angle au centre correspondant.
Un angle est dit inscrit dans un cercle si son sommet est situésur un cercle, et les côtés de l'angle coupent ce cercle.
Un segment reliant deux points sur un cercle s'appelleaccord. La plus grande corde passe par le centre du cercle et s'appellediamètre.

Pour résoudre des problèmes impliquant des angles inscrits dans un cercle,vous devez connaître les propriétés suivantes :
1. L’angle inscrit est égal à la moitié de l’angle au centre, basé sur le même arc.


2. Tous les angles inscrits sous-tendant le même arc sont égaux.

3. Tous les angles inscrits basés sur la même corde et dont les sommets se trouvent du même côté de cette corde sont égaux.

4. Toute paire d'angles basés sur la même corde, dont les sommets se trouvent sur des côtés opposés de la corde, totalisent 180°.

Corollaire : les angles opposés d’un quadrilatère inscrit dans un cercle totalisent 180 degrés.
5. Tous les angles inscrits sous-tendus par un diamètre sont des angles droits.

En général, cette propriété est une conséquence de la propriété (1) ; c'est son cas particulier. Regardez - l'angle au centre est égal à 180 degrés (et cet angle déplié n'est rien de plus qu'un diamètre), ce qui signifie, selon la première propriété, l'angle inscrit C est égal à la moitié de celui-ci, c'est-à-dire 90 degrés.
Connaître cette propriété aide à résoudre de nombreux problèmes et permet souvent d'éviter des calculs inutiles. L'ayant bien maîtrisé, vous pourrez résoudre oralement plus de la moitié des problèmes de ce type. Deux conclusions peuvent être tirées :
Corollaire 1 : si un triangle est inscrit dans un cercle et qu'un de ses côtés coïncide avec le diamètre de ce cercle, alors le triangle est rectangle (sommet angle droit se trouve sur le cercle).
Corollaire 2 : le centre du décrit à propos triangle rectangle le cercle coïncide avec le milieu de son hypoténuse.
De nombreux prototypes de problèmes stéréométriques sont également résolus en utilisant cette propriété et ces conséquences. Rappelez-vous le fait lui-même : si le diamètre d'un cercle est un côté d'un triangle inscrit, alors ce triangle est rectangle (l'angle opposé au diamètre est de 90 degrés). Vous pouvez tirer toutes les autres conclusions et conséquences vous-même ; vous n’avez pas besoin de les enseigner.
En règle générale, la moitié des problèmes sur les angles inscrits sont présentés avec un croquis, mais sans symboles. Pour comprendre le processus de raisonnement lors de la résolution de problèmes (ci-dessous dans l'article), des notations pour les sommets (angles) sont introduites. Vous n'êtes pas obligé de le faire lors de l'examen d'État unifié.Considérons les tâches :
Quelle est la valeur d’un angle aigu inscrit sous-tendu par une corde égale au rayon du cercle ? Donnez votre réponse en degrés.

Construisons un angle central pour un angle inscrit donné et désignons les sommets :

D'après la propriété d'un angle inscrit dans un cercle :
![]()
L'angle AOB est égal à 60 0, puisque le triangle AOB est équilatéral, et dans un triangle équilatéral tous les angles sont égaux à 60 0. Les côtés du triangle sont égaux, puisque la condition dit que la corde est égale au rayon.
Ainsi, l'angle inscrit ACB est égal à 30 0.
Réponse : 30
Trouver la corde supportée par un angle de 30 0 inscrit dans un cercle de rayon 3.

Il s'agit essentiellement du problème inverse (du précédent). Construisons l'angle central.

Il est deux fois plus grand que celui inscrit, c'est-à-dire que l'angle AOB est égal à 60 0. De là, nous pouvons conclure que le triangle AOB est équilatéral. Ainsi, la corde est égale au rayon, soit trois.
Réponse : 3
Le rayon du cercle est 1. Trouvez la grandeur de l'angle inscrit obtus sous-tendu par la corde égale à la racine de deux. Donnez votre réponse en degrés.

Construisons l'angle central :

Connaissant le rayon et la corde, on peut trouver l'angle au centre ASV. Cela peut être fait en utilisant le théorème du cosinus. Connaissant l’angle au centre, on peut facilement trouver l’angle inscrit ACB.
Théorème du cosinus : le carré de n'importe quel côté d'un triangle est égal à la somme des carrés des deux autres côtés, sans le double du produit de ces côtés par le cosinus de l'angle qui les sépare.

Le deuxième angle au centre est donc 360 0 – 90 0 = 270 0 .
L'angle ACB, par la propriété d'un angle inscrit, est égal à la moitié de celui-ci, soit 135 degrés.
Réponse : 135
Trouvez la corde sous-tendue par un angle de 120 degrés inscrit dans un cercle de rayon racine de trois.

Reliez les points A et B au centre du cercle. Notons-le par O :

On connaît le rayon et l'angle inscrit ASV. On peut trouver l'angle au centre AOB (supérieur à 180 degrés), puis trouver l'angle AOB dans le triangle AOB. Et puis, en utilisant le théorème du cosinus, calculez AB.
Selon la propriété de l'angle inscrit, l'angle au centre AOB (qui est supérieur à 180 degrés) sera égal au double de l'angle inscrit, soit 240 degrés. Cela signifie que l'angle AOB dans le triangle AOB est égal à 360 0 – 240 0 = 120 0.
D'après le théorème du cosinus :

Réponse : 3
Trouvez l'angle inscrit sous-tendu par un arc qui représente 20 % du cercle. Donnez votre réponse en degrés.

Selon la propriété d'un angle inscrit, il est la moitié de la taille de l'angle au centre basé sur le même arc, dans ce cas nous parlons de l'arc AB.
On dit que l’arc AB représente 20 pour cent de la circonférence. Cela signifie que l'angle central AOB est également égal à 20 pour cent de 360 0.*Un cercle est un angle de 360 degrés. Moyens,

Ainsi, l'angle inscrit ACB est de 36 degrés.
Réponse : 36
Arc de cercle A.C., ne contenant pas de point B, fait 200 degrés. Et l'arc de cercle BC, ne contenant pas de point UN, fait 80 degrés. Trouvez l’angle inscrit ACB. Donnez votre réponse en degrés.

Pour plus de clarté, désignons les arcs dont les mesures angulaires sont données. Arc correspondant à 200 degrés – Couleur bleue, l'arc correspondant à 80 degrés est rouge, la partie restante du cercle est jaune.

Ainsi, la mesure en degré de l'arc AB (jaune), et donc de l'angle au centre AOB est : 360 0 – 200 0 – 80 0 = 80 0 .
L'angle inscrit ACB est la moitié de la taille de l'angle au centre AOB, c'est-à-dire égal à 40 degrés.
Réponse : 40
Quel est l’angle inscrit sous-tendu par le diamètre du cercle ? Donnez votre réponse en degrés.
Il faut connaître la propriété d'un angle inscrit ; comprendre quand et comment utiliser le théorème du cosinus, apprenez-en davantage à ce sujet.
C'est tout! Je te souhaite du succès!
Cordialement, Alexandre Krutitskikh
Professeur de mathématiques à l'école en troisième année :
- Les enfants, dites-moi, combien font 6*6 ?
Les enfants répondent à l'unisson :
- Soixante seize!
- Eh bien, qu'est-ce que vous dites, les enfants ! Six par six feront trente-six... enfin, peut-être encore 37, 38, 39... enfin, maximum 40... mais pas soixante-seize !
P.S : je vous serais reconnaissant de me parler du site sur les réseaux sociaux.
Dans cet article, je vais vous expliquer comment résoudre les problèmes liés à l'utilisation de .
Tout d'abord, comme d'habitude, rappelons les définitions et les théorèmes que vous devez connaître pour réussir à résoudre les problèmes de .
1.Angle inscrit est un angle dont le sommet se trouve sur un cercle et dont les côtés coupent le cercle :
2.Angle central est l'angle dont le sommet coïncide avec le centre du cercle :

Valeur en degrés d'un arc de cercle mesuré par la grandeur de l'angle central qui repose sur lui.
Dans ce cas, la valeur en degré de l'arc AC est égale à la valeur de l'angle AOS.
3. Si les angles inscrit et central sont basés sur le même arc, alors l'angle inscrit est la moitié de la taille de l'angle central:
 4. Tous les angles inscrits qui reposent sur un arc sont égaux les uns aux autres :
4. Tous les angles inscrits qui reposent sur un arc sont égaux les uns aux autres :

5. L'angle inscrit sous-tendu par le diamètre est de 90° :

Résolvons plusieurs problèmes.
1 . Tâche B7 (n° 27887)
Trouvons la valeur de l'angle au centre qui repose sur le même arc :
Évidemment, l’angle AOC est égal à 90°, donc l’angle ABC est égal à 45°
Réponse : 45°
2.Tâche B7 (n° 27888)
Trouvez la taille de l'angle ABC. Donnez votre réponse en degrés.
Évidemment, l’angle AOC est de 270°, alors l’angle ABC est de 135°.
Réponse : 135°
3. Tâche B7 (n° 27890)
Trouvez la valeur en degré de l’arc AC du cercle sous-tendu par l’angle ABC. Donnez votre réponse en degrés.
Trouvons la valeur de l'angle au centre qui repose sur l'arc AC :
La grandeur de l'angle AOS est de 45°, donc la mesure en degré de l'arc AC est de 45°.
Réponse : 45°.
4 . Tâche B7 (n° 27885)
Trouvez l'angle ACB si les angles inscrits ADB et DAE reposent sur des arcs de cercle dont les valeurs en degrés sont respectivement égales à et. Donnez votre réponse en degrés.
L'angle ADB repose sur l'arc AB, donc la valeur de l'angle au centre AOB est égale à 118°, donc l'angle BDA est égal à 59°, et l'angle adjacent ADC est égal à 180°-59° = 121° 
De même, l'angle DOE est de 38° et l'angle inscrit correspondant DAE est de 19°.
Considérons le triangle ADC :
La somme des angles d'un triangle est de 180°.
L'angle ACB est égal à 180°- (121°+19°)=40°
Réponse : 40°
5 . Tâche B7 (n° 27872)
Les côtés du quadrilatère ABCD AB, BC, CD et AD sous-tendent des arcs de cercle circonscrits dont les valeurs de degré sont respectivement égales à , , et . Trouvez l'angle B de ce quadrilatère. Donnez votre réponse en degrés.
 L'angle B repose sur l'arc ADC dont la valeur est égale à la somme des valeurs des arcs AD et CD, soit 71°+145°=216°
L'angle B repose sur l'arc ADC dont la valeur est égale à la somme des valeurs des arcs AD et CD, soit 71°+145°=216°
L'angle inscrit B est égal à la moitié de l'amplitude de l'arc ADC, soit 108°
Réponse : 108°
6. Tâche B7 (n° 27873)
Les points A, B, C, D, situés sur un cercle, divisent ce cercle en quatre arcs AB, BC, CD et AD dont les degrés sont respectivement dans le rapport 4:2:3:6. Trouvez l'angle A du quadrilatère ABCD. Donnez votre réponse en degrés.
(voir dessin de la tâche précédente)
Puisque nous avons donné le rapport des grandeurs des arcs, nous introduisons l’élément unitaire x. Alors la grandeur de chaque arc sera exprimée par le rapport suivant :
AB=4x, BC=2x, CD=3x, AD=6x. Tous les arcs forment un cercle, c'est-à-dire que leur somme est de 360°.
4x+2x+3x+6x=360°, donc x=24°.
L'angle A est supporté par les arcs BC et CD qui valent ensemble 5x=120°.
L’angle A est donc de 60°
Réponse : 60°
7. Tâche B7 (n° 27874)
Quadrilatère A B C D inscrit dans un cercle. Coin abcégal à , angle GOUJAT
Instructions
Si le rayon (R) du cercle et la longueur de l'arc (L) correspondant à l'angle au centre (θ) souhaité sont connus, il peut être calculé aussi bien en degrés qu'en radians. Le total est déterminé par la formule 2*π*R et correspond à un angle au centre de 360° ou à deux nombres Pi, si l'on utilise des radians au lieu de degrés. Par conséquent, partez de la proportion 2*π*R/L = 360°/θ = 2*π/θ. Exprimez-en l'angle central en radians θ = 2*π/(2*π*R/L) = L/R ou en degrés θ = 360°/(2*π*R/L) = 180*L/(π * R) et calculez en utilisant la formule résultante.
A partir de la longueur de la corde (m) reliant les points qui déterminent l'angle au centre (θ), sa valeur peut également être calculée si le rayon (R) du cercle est connu. Pour ce faire, considérons un triangle formé de deux rayons et . Ce triangle isocèle, tout le monde est connu, mais il faut trouver l'angle opposé à la base. Le sinus de sa moitié est égal au rapport de la longueur de la base - la corde - à deux fois la longueur du côté - le rayon. Par conséquent, utilisez la fonction sinus inverse pour les calculs - arc sinus : θ = 2*arcsin(½*m/R).
L'angle central peut être spécifié en fractions de tour ou à partir d'un angle de rotation. Par exemple, si vous devez trouver l'angle au centre correspondant à un quart de tour complet, divisez 360° par quatre : θ = 360°/4 = 90°. La même valeur en radians devrait être 2*π/4 ≈ 3,14/2 ≈ 1,57. L'angle déplié est égal à un demi-tour complet, donc, par exemple, l'angle au centre correspondant à un quart de celui-ci sera la moitié des valeurs calculées ci-dessus en degrés et en radians.
L'inverse du sinus est appelé fonction trigonométrique arc sinus. Il peut prendre des valeurs inférieures à la moitié du nombre Pi, à la fois positives et négatives. côté négatif lorsqu'il est mesuré en radians. Mesurées en degrés, ces valeurs seront respectivement comprises entre -90° et +90°.
Instructions
Certaines valeurs « rondes » n’ont pas besoin d’être calculées ; elles sont plus faciles à retenir. Par exemple : - si l'argument de la fonction est nul, alors son arc sinus est également nul ; - de 1/2 est égal à 30° ou 1/6 Pi, s'il est mesuré - l'arc sinus de -1/2 est -30° ; ou -1/ 6 du nombre Pi in ; - l'arc sinus de 1 est égal à 90° ou 1/2 du nombre Pi en radians - l'arc sinus de -1 est égal à -90° ou -1/2 de ; le nombre Pi en radians ;
Pour mesurer les valeurs de cette fonction à partir d'autres arguments, le plus simple est d'utiliser une calculatrice Windows standard, si vous en avez une sous la main. Pour commencer, ouvrez le menu principal sur le bouton « Démarrer » (ou en appuyant sur la touche WIN), allez dans la section « Tous les programmes », puis dans la sous-section « Accessoires » et cliquez sur « Calculatrice ».
Basculez l'interface de la calculatrice sur le mode de fonctionnement qui vous permet de calculer fonctions trigonométriques. Pour ce faire, ouvrez la section « Affichage » dans son menu et sélectionnez « Ingénierie » ou « Scientifique » (selon le type de système opérateur).
Entrez la valeur de l'argument à partir duquel l'arctangente doit être calculée. Cela peut être fait en cliquant sur les boutons de l'interface de la calculatrice avec la souris, ou en appuyant sur les touches de , ou en copiant la valeur (CTRL + C) puis en la collant (CTRL + V) dans le champ de saisie de la calculatrice.
Sélectionnez les unités de mesure dans lesquelles vous devez obtenir le résultat du calcul de la fonction. Sous le champ de saisie, il y a trois options parmi lesquelles vous devez en sélectionner (en cliquant dessus avec la souris) une - , radians ou rads.
Cochez la case qui inverse les fonctions indiquées sur les boutons de l'interface de la calculatrice. A côté se trouve une courte inscription Inv.
Cliquez sur le bouton péché. La calculatrice inversera la fonction qui lui est associée, effectuera le calcul et vous présentera le résultat dans les unités spécifiées.
Vidéo sur le sujet
L'un des problèmes géométriques courants consiste à calculer l'aire d'un segment circulaire - la partie du cercle délimitée par une corde et la corde correspondante par un arc de cercle.

L'aire d'un segment circulaire est égale à la différence entre l'aire du secteur circulaire correspondant et l'aire du triangle formé par les rayons du secteur correspondant au segment et la corde limitant le segment.
Exemple 1
La longueur de la corde qui sous-tend le cercle est égale à la valeur a. La mesure en degrés de l'arc correspondant à la corde est de 60°. Trouvez l'aire du segment circulaire.
Solution
Un triangle formé de deux rayons et d'une corde est isocèle, donc la hauteur tirée du sommet de l'angle central jusqu'au côté du triangle formé par la corde sera également la bissectrice de l'angle central, le divisant en deux, et le médiane, divisant la corde en deux. Sachant que le sinus de l'angle est égal au rapport de la jambe opposée à l'hypoténuse, on peut calculer le rayon :
Péché 30°= a/2 :R = 1/2 ;
Sc = πR²/360°*60° = πa²/6
L'aire du triangle correspondant au secteur est calculée comme suit :
S▲=1/2*ah, où h est la hauteur tirée du sommet de l'angle central à la corde. D'après le théorème de Pythagore h=√(R²-a²/4)= √3*a/2.
En conséquence, S▲=√3/4*a².
L'aire du segment, calculée comme Sreg = Sc - S▲, est égale à :
Sreg = πa²/6 - √3/4*a²
En remplaçant la valeur de a par une valeur numérique, vous pouvez facilement calculer la valeur numérique de l'aire du segment.
Exemple 2
Rayon du cercle égale à la valeur UN. La mesure en degrés de l'arc correspondant au segment est de 60°. Trouvez l'aire du segment circulaire.
Solution:
Superficie du secteur correspondant angle donné peut être calculé à l’aide de la formule suivante :