Transformations d'expressions littérales irrationnelles. Équations irrationnelles
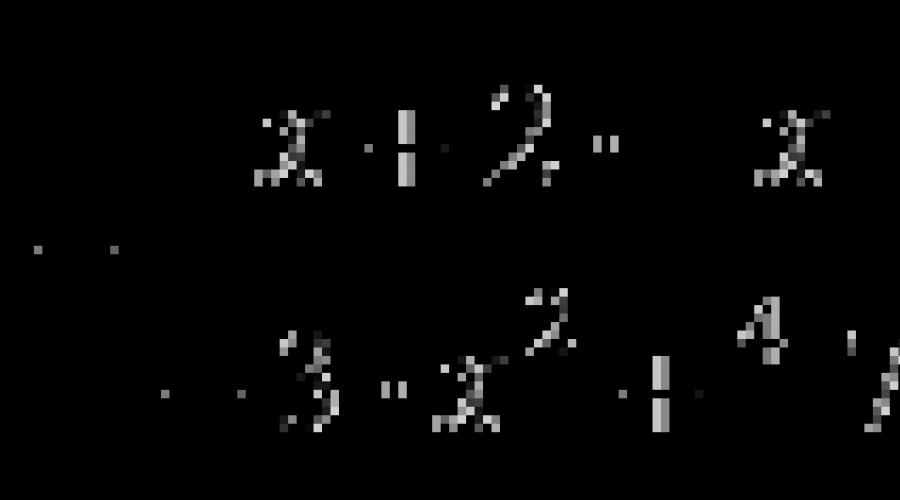
Lire aussi
Lors de la conversion des racines arithmétiques, leurs propriétés sont utilisées (voir point 35).
Considérons plusieurs exemples d'application des propriétés des racines arithmétiques pour les transformations les plus simples de radicaux. Dans ce cas, toutes les variables seront considérées comme ne prenant que des valeurs non négatives.
Exemple 1. Extraire la racine du produit Décision. En appliquant la propriété 1°, on obtient :
Exemple 2. Sortez le facteur sous le signe racine
La solution.
Une telle transformation est appelée factorisation sous le signe racine. Le but de la transformation est de simplifier l'expression radicale.
Exemple 3 : Simplifier
La solution. D'après la propriété 3°, on essaie généralement de simplifier l'expression radicale, pour laquelle on supprime les facteurs au-delà du signe de la racine. Nous avons
Exemple 4 : Simplifier
La solution. On transforme l'expression en introduisant un facteur sous le signe de la racine : Par la propriété 4° on a
Exemple 5 : Simplifier
La solution. Par la propriété 5°, on a le droit de diviser l'exposant de la racine et l'exposant de l'expression de la racine en le même entier naturel. Si dans l'exemple considéré nous divisons les indicateurs indiqués par 3, alors nous obtenons
Exemple 6. Simplifiez les expressions : a)
Solution, a) Par la propriété 1°, on obtient que pour multiplier des racines de même degré, il suffit de multiplier les expressions de racine et d'extraire la racine de même degré du résultat obtenu. Moyens,
b) Tout d'abord, il faut réduire les radicaux à un seul indice. D'après la propriété 5°, on peut multiplier l'exposant de la racine et l'exposant de l'expression de la racine par le même entier naturel. Par conséquent, Plus loin nous avons Et maintenant dans le résultat obtenu en divisant les indicateurs de la racine et le degré de l'expression radicale par 3, nous obtenons
Les propriétés des racines sous-tendent les deux transformations suivantes, appelées mise sous le signe de la racine et sortie sous le signe de la racine, sur lesquelles nous nous tournons maintenant.
Entrer un facteur sous le signe de la racine
Entrer un facteur sous le signe signifie remplacer l'expression , où B et C sont des nombres ou des expressions, et n est un nombre naturel supérieur à un, par une expression identiquement égale de la forme ou .
Par exemple, une expression irrationnelle après avoir ajouté le facteur 2 sous le signe racine prend la forme .
Base théorique cette transformation, les règles de sa mise en œuvre, ainsi que des solutions à toutes sortes d'exemples typiques sont données dans l'article introduisant un facteur sous le signe racine.
Sortir le multiplicateur sous le signe de la racine
La transformation, dans un certain sens, inverse de l'introduction du facteur sous le signe racine, est la suppression du facteur sous le signe racine. Elle consiste à représenter la racine comme un produit pour n impair ou comme un produit pour n pair, où B et C sont des nombres ou des expressions.
Pour un exemple, revenons au paragraphe précédent : après avoir retiré le facteur sous le signe racine, l'expression irrationnelle prend la forme . Autre exemple : retirer le facteur sous le signe racine dans l'expression donne un produit qui peut être réécrit sous la forme .
Sur quoi cette transformation est basée et selon quelles règles elle est effectuée, nous analyserons dans un article séparé la suppression d'un facteur sous le signe racine. Au même endroit, nous donnons des solutions à des exemples et énumérons des façons d'amener l'expression radicale à une forme commode pour sortir un multiplicateur.
Conversion de fractions contenant des racines
Les expressions irrationnelles peuvent contenir des fractions, au numérateur et au dénominateur desquelles il y a des racines. Avec de telles fractions, vous pouvez effectuer l'une des principales transformations identiques fractions.
Tout d'abord, rien ne vous empêche de travailler avec des expressions au numérateur et au dénominateur. Prenons une fraction comme exemple. L'expression irrationnelle au numérateur est évidemment identiquement égale à , et, se référant aux propriétés des racines, l'expression au dénominateur peut être remplacée par la racine. En conséquence, la fraction d'origine est convertie sous la forme .
Deuxièmement, vous pouvez changer le signe avant la fraction en changeant le signe du numérateur ou du dénominateur. Par exemple, il existe de telles transformations d'une expression irrationnelle :  .
.
Troisièmement, il est parfois possible et opportun de réduire la fraction. Par exemple, comment se priver du plaisir de réduire une fraction  à une expression irrationnelle, on obtient ainsi
à une expression irrationnelle, on obtient ainsi  .
.
Il est clair que dans de nombreux cas, avant d'effectuer la réduction d'une fraction, les expressions de son numérateur et de son dénominateur doivent être factorisées, ce qui, dans des cas simples, peut être réalisé par des formules de multiplication abrégées. Et parfois, la substitution d'une variable aide à réduire la fraction, vous permettant de passer de la fraction d'origine avec irrationalité à une fraction rationnelle, avec laquelle il est plus confortable et familier de travailler.
Prenons une expression comme exemple. Introduisons de nouvelles variables et , dans ces variables l'expression originale a la forme . Jouer au numérateur
Les expressions irrationnelles et leurs transformations
La dernière fois que nous nous sommes souvenus (ou découvert - comment quelqu'un l'aime) ce qui est , a appris à extraire de telles racines, a démonté les principales propriétés des racines pièce par pièce et a décidé de ne pas exemples complexes avec des racines.
Cette leçon sera la suite de la précédente et sera consacrée à la transformation d'une grande variété d'expressions contenant toutes sortes de racines. De telles expressions sont appelées irrationnel. Ici, il y aura des expressions avec des lettres et des conditions supplémentaires, et la suppression de l'irrationalité dans les fractions, et quelques astuces avancées pour travailler avec les racines. Les techniques qui seront considérées dans cette leçon deviendront une bonne base pour résoudre les problèmes de l'examen d'État unifié (et pas seulement) de presque tous les niveaux de complexité. Alors, commençons.
Tout d'abord, je vais dupliquer ici les formules de base et les propriétés des racines. Pour ne pas sauter de sujet en sujet. Les voici:
![]()
![]() à
à
![]()
Ces formules doivent être connues et pouvoir s'appliquer. Et dans les deux sens - à la fois de gauche à droite et de droite à gauche. C'est sur eux que repose la solution de la plupart des tâches avec des racines de tout degré de complexité. Commençons par le plus simple - avec l'application directe de formules ou de leurs combinaisons.
Application facile des formules
Dans cette partie, des exemples simples et inoffensifs seront considérés - sans lettres, conditions supplémentaires et autres astuces. Cependant, même en eux, en règle générale, il existe des options. Et plus l'exemple est fantaisiste, plus ces options sont nombreuses. Et pour un étudiant inexpérimenté, le principal problème se pose - par où commencer? La réponse ici est simple - tu ne sais pas quoi faire, fais ce que tu peux. Si seulement vos actions allaient en paix et en harmonie avec les règles des mathématiques et ne les contredisaient pas.) Par exemple, une telle tâche:
Calculer:
Même dans un exemple aussi simple, plusieurs voies de réponse sont possibles.
La première consiste simplement à multiplier les racines par la première propriété et à extraire la racine du résultat :
La deuxième option est celle-ci : ne touchez pas, travaillez avec . Nous retirons le facteur sous le signe de la racine, puis - selon la première propriété. Comme ça:
Vous pouvez décider ce que vous voulez. Dans l'une des options, la réponse est un - huit. Par exemple, il m'est plus facile de multiplier 4 et 128 et d'obtenir 512, et la racine cubique est parfaitement extraite de ce nombre. Si quelqu'un ne se souvient pas que 512 est 8 au cube, alors ce n'est pas grave : vous pouvez écrire 512 comme 2 9 (les 10 premières puissances de deux, j'espère que vous vous en souvenez ?) Et en utilisant la formule de la racine du degré :
Un autre exemple.
Calculez : .
Si vous travaillez sur la première propriété (conduisez tout sous une seule racine), vous obtenez un nombre élevé, à partir duquel la racine est ensuite extraite - également pas de sucre. Et ce n'est pas un fait qu'il sera extrait uniformément.) Par conséquent, il est utile ici de retirer les facteurs sous la racine du nombre. Et poussez-le au maximum :
Et maintenant tout va bien :
Il reste à écrire le huit et le deux sous une même racine (selon la première propriété) et - l'affaire est prête. :)
Ajoutons maintenant quelques fractions.
Calculer:
L'exemple est assez primitif, mais il a aussi des options. Vous pouvez utiliser le multiplicateur pour convertir le numérateur et réduire avec le dénominateur :

Et vous pouvez immédiatement utiliser la formule pour diviser les racines :

Comme vous pouvez le voir, de cette façon et de cela - tout va bien.) Si vous ne trébuchez pas à mi-chemin et faites une erreur. Mais où est l'erreur ici...
Considérons maintenant l'exemple le plus récent de devoirs dernière leçon:
Simplifier:
![]()
Un ensemble de racines complètement impensable, et même imbriquées. Comment être? L'essentiel est de ne pas avoir peur ! Ici, nous remarquons d'abord sous les racines des nombres 2, 4 et 32 - puissances de deux. La première chose à faire est de ramener tous les nombres à deux : après tout, plus mêmes numéros dans l'exemple, et moins il y en a de différents, plus c'est facile.) Commençons séparément avec le premier multiplicateur :
![]()
Le nombre peut être simplifié en réduisant les deux sous la racine avec les quatre dans l'exposant racine :
Maintenant, selon la racine du produit :
![]() .
.
Dans le nombre on enlève le deux pour le signe de la racine :
Et nous traitons l'expression selon la formule de la racine à partir de la racine:
Ainsi, le premier facteur s'écrira ainsi :
Les racines imbriquées ont disparu, les nombres sont devenus plus petits, ce qui fait déjà plaisir. C'est juste que les racines sont différentes, mais pour l'instant nous allons en rester là. Ce sera nécessaire - nous convertirons au même. Nous prenons le deuxième facteur.)
Nous transformons le deuxième facteur de la même manière, selon la formule de la racine du produit et de la racine de la racine. Si nécessaire, nous réduisons les indicateurs selon la cinquième formule :
Nous collons tout dans l'exemple original et obtenons :
Nous avons obtenu le produit de tout un tas de racines complètement différentes. Ce serait bien de les ramener tous à un seul indicateur, et ensuite nous verrons. Eh bien, c'est tout à fait possible. Le plus grand des indices racine est 12, et tous les autres - 2, 3, 4, 6 - sont des diviseurs du nombre 12. Par conséquent, nous amènerons toutes les racines selon la cinquième propriété à un indicateur - à 12:
![]()
On compte et on obtient :
Nous n'avons pas obtenu un bon chiffre, mais ça va. On nous a demandé simplifier expression, non compter. Simplifié? Bien sûr! Et le type de réponse (entier ou non) ne joue ici aucun rôle.
Quelques formules d'addition/soustraction et de multiplication abrégée
Malheureusement, formules générales pour ajouter et soustraire des racines pas en mathématiques. Cependant, dans les tâches, très souvent, ces actions se retrouvent avec des racines. Ici, il est nécessaire de comprendre que toutes les racines sont exactement les mêmes icônes mathématiques que les lettres en algèbre.) Et les mêmes techniques et règles s'appliquent aux racines qu'aux lettres - ouvrant des parenthèses, en apportant des similaires, des formules de multiplication abrégées, etc. P.
Par exemple, il est clair pour tout le monde que . Similaire le même Les racines peuvent être facilement ajoutées/soustraites entre elles :
![]()
![]()
Si les racines sont différentes, alors nous cherchons un moyen de les rendre identiques - en ajoutant / supprimant un facteur ou par la cinquième propriété. Si bien, cela ne simplifie en rien, alors, peut-être, les transformations sont plus délicates.
Regardons le premier exemple.
Trouvez la valeur de l'expression : .
Les trois racines, bien que cubiques, sont différent Nombres. Ils ne sont pas purement extraits et s'additionnent/se soustraient les uns des autres. Par conséquent, l'application de formules générales ne fonctionne pas ici. Comment être? Et supprimons les facteurs de chaque racine. En tout cas, ce ne sera pas pire.) De plus, il n'y a, en fait, pas d'autres options :
C'est-à-dire, .
C'est toute la solution. Ici, nous sommes passés de différentes racines aux mêmes avec l'aide de retirer le multiplicateur sous la racine. Et puis ils ont juste apporté des similaires.) Nous décidons plus loin.
Trouver la valeur d'une expression:
Avec une racine de dix-sept ans, vous ne pouvez certainement rien y faire. Nous travaillons selon la première propriété - nous créons une racine à partir du produit de deux racines :
Maintenant regardons de plus près. Qu'avons-nous sous le grand racine cubique? La différence est kva.. Eh bien, bien sûr ! Différence carrée :
Il ne reste plus qu'à extraire la racine : .
Calculer:
Ici, vous devez faire preuve d'ingéniosité mathématique.) Nous pensons approximativement de la manière suivante: « Donc, dans l'exemple, le produit des racines. Sous une racine se trouve la différence et sous l'autre se trouve la somme. Très similaire à la formule de la différence des carrés. Mais… Les racines sont différentes ! Le premier est carré, et le second est du quatrième degré... Ce serait bien de les rendre identiques. Selon la cinquième propriété, on peut facilement faire une racine du quatrième degré à partir d'une racine carrée. Pour ce faire, il suffit d'élever au carré l'expression racine.
Si vous pensiez à la même chose, alors vous êtes à mi-chemin du succès. Tout à fait exact ! Transformons le premier facteur en quatrième racine. Comme ça:
![]()
Maintenant, rien ne peut être fait, mais vous devez vous souvenir de la formule du carré de la différence. Uniquement lorsqu'il est appliqué sur les racines. Et alors? Pourquoi les racines sont-elles pires que les autres nombres ou expressions ? ! Nous construisons :
"Hmm, eh bien, ils l'ont construit, et alors ? Le radis raifort n'est pas plus sucré. Arrêt! Et si vous retiriez les quatre sous la racine ? Ensuite, la même expression apparaîtra comme sous la deuxième racine, seulement avec un moins, et c'est exactement ce que nous essayons de réaliser !
Droit! Prenons-en quatre :
![]() .
.
Et maintenant - une question de technologie :
C'est ainsi que les exemples complexes se déroulent.) Il est maintenant temps de s'entraîner avec les fractions.
Calculer:
Il est clair qu'il faut transformer le numérateur. Comment? Selon la formule du carré de la somme, bien sûr. Avons-nous d'autres options ? :) Mise au carré, suppression des multiplicateurs, réduction des indicateurs (si nécessaire) :
Comment! Nous avons obtenu exactement le dénominateur de notre fraction.) Ainsi, la fraction entière, évidemment, est égale à un :

Un autre exemple. Passons maintenant à une autre formule de multiplication abrégée.)
Calculer:
Il est clair que le carré de la différence doit être appliqué en entreprise. Nous écrivons le dénominateur séparément et - allons-y!
Nous sortons les multiplicateurs sous les racines:
![]()
Par conséquent,
Maintenant, tout ce qui est mauvais est superbement réduit et il s'avère:

Eh bien, passons au niveau suivant. :)
Lettres et conditions supplémentaires
Les expressions de lettres avec des racines sont une chose plus délicate que expressions numériques, et est une source intarissable d'erreurs ennuyeuses et très grossières. Bloquons cette source.) Des erreurs apparaissent en raison du fait que des nombres et des expressions négatifs apparaissent souvent dans de telles tâches. Ils nous sont soit donnés directement dans la tâche, soit cachés dans lettres et conditions supplémentaires. Et dans le processus de travail avec les racines, nous devons constamment nous rappeler que dans les racines degré pairà la fois sous la racine elle-même et à la suite de l'extraction de la racine doit être expression non négative. La formule clé dans les tâches de ce paragraphe sera la quatrième formule :
Avec des racines d'un degré impair, il n'y a pas de questions - tout y est toujours extrait avec un plus, avec un moins. Et moins, le cas échéant, est avancé. Nous allons immédiatement nous occuper des racines même degrés.) Par exemple, une tâche aussi courte.
Simplifier: , si .
Il semblerait que tout soit simple. Il se révélera juste x.) Mais pourquoi alors condition supplémentaire ? Dans de tels cas, il est utile d'estimer par des nombres. Purement pour moi.) Si, alors x est un nombre négatif. Moins trois, par exemple. Ou moins quarante. Laisser . Pouvez-vous relancer moins trois à la puissance quatre ? Bien sûr! Il s'avère 81. Est-il possible d'extraire la racine du quatrième degré de 81 ? Pourquoi pas? Boîte! Obtenez trois. Analysons maintenant toute notre chaîne :
Que voyons-nous ? L'entrée était négative et la sortie était positive. C'était moins trois, maintenant c'est plus trois.) Revenons aux lettres. Sans aucun doute, modulo ce sera exactement X, mais seul X lui-même est avec un moins (par condition!), Et le résultat de l'extraction (dû à la racine arithmétique!) Devrait être avec un plus. Comment obtenir un plus ? Très simple! Pour ce faire, il suffit de mettre un moins devant un nombre évidemment négatif.) Et la bonne décision Ressemble à ça:
Soit dit en passant, si nous utilisions la formule, alors, en nous souvenant de la définition du module, nous obtiendrions immédiatement la bonne réponse. Parce que le
|x| = -x à x<0.
Retirez le facteur du signe racine : , où .
Le premier regard porte sur l'expression racine. Tout va bien ici. Dans tous les cas, il sera non négatif. Nous commençons l'extraction. Selon la formule de la racine du produit, on extrait la racine de chaque facteur :
D'où viennent les modules, je pense, il n'est plus nécessaire d'expliquer.) Et maintenant, nous analysons chacun des modules.
Multiplicateur | un | donc nous la laissons inchangée : nous n'avons aucune condition sur la lettreun. On ne sait pas si c'est positif ou négatif. Module suivant |b 2 | peut être omise en toute sécurité : dans tous les cas, l'expressionb 2 non négatif. Et qu'en est-il |c 3 | - c'est déjà un problème.) Si, puis et c 3 <0. Стало быть, модуль надо раскрыть avec un moins: | c 3 | = - c 3 . Donc la bonne solution serait :
Et maintenant - la tâche inverse. Pas des plus faciles, je vous préviens tout de suite !
Entrez un facteur sous le signe de la racine: .
Si vous écrivez immédiatement la solution comme ceci
alors vous tombé dans un piège. ce mauvaise décision! Quel est le problème?
Examinons l'expression sous la racine. Sous la racine du quatrième degré, comme nous le savons, devrait être non négatif expression. Sinon, la racine n'a pas de sens.) Par conséquent, Et ceci, à son tour, signifie que et, par conséquent, est lui-même non positif : .
Et l'erreur ici est que nous apportons sous la racine non positif Numéro: la quatrième puissance le transforme en non négatif et un résultat incorrect est obtenu - un moins délibéré à gauche et déjà un plus à droite. Et amener sous la racine même degré nous n'avons droit qu'à non négatif nombres ou expressions. Et laissez le moins, le cas échéant, devant la racine.) Comment pouvons-nous sélectionner un facteur non négatif dans le nombre, sachant qu'il est lui-même négatif ? Oui exactement pareil ! Mettez un moins.) Et pour que rien n'ait changé, compensez-le avec un autre moins. Comme ça:
![]()
Et maintenant non négatif le nombre (-b) est entré calmement sous la racine selon toutes les règles :
Cet exemple montre clairement que, contrairement à d'autres branches des mathématiques, la bonne réponse dans les racines ne découle pas toujours automatiquement des formules. Vous devez réfléchir et prendre personnellement la bonne décision.) Vous devez surtout être plus prudent avec les signes dans équations et inégalités irrationnelles.
Nous traitons de la technique importante suivante dans le travail avec les racines - se débarrasser de l'irrationalité.
Se débarrasser de l'irrationalité dans les fractions
S'il y a des racines dans l'expression, alors, permettez-moi de vous rappeler, une telle expression s'appelle expression avec irrationalité. Dans certains cas, il est utile de se débarrasser de cette irrationalité même (c'est-à-dire des racines). Comment pouvez-vous éliminer la racine? Notre racine disparaît quand... s'élevant à une puissance. Avec un exposant soit égal à l'exposant de la racine, soit un multiple de celui-ci. Mais, si nous élevons la racine à une puissance (c'est-à-dire, multiplions la racine par elle-même le nombre de fois requis), alors l'expression changera à partir de cela. Pas bon.) Cependant, en mathématiques, il y a des sujets où la multiplication est assez indolore. En fractions, par exemple. Selon la propriété de base d'une fraction, si le numérateur et le dénominateur sont multipliés (divisés) par le même nombre, la valeur de la fraction ne changera pas.
Supposons qu'on nous donne la fraction suivante :
Est-il possible de supprimer la racine du dénominateur ? Boîte! Pour ce faire, la racine doit être cubée. Qu'est-ce qui nous manque dans le dénominateur pour le cube complet ? Il nous manque le multiplicateur , c'est-à-dire. Nous multiplions donc le numérateur et le dénominateur de la fraction par

La racine du dénominateur a disparu. Mais… il est apparu au numérateur. Il n'y a rien à faire, tel est le destin.) Cela n'a plus d'importance pour nous : on nous a demandé de libérer le dénominateur des racines. Publié? Indubitablement.)
Soit dit en passant, ceux qui sont déjà en désaccord avec la trigonométrie ont peut-être fait attention au fait que dans certains manuels et tableaux, par exemple, ils dénotent différemment : quelque part, mais quelque part. La question est qu'est-ce qui est juste? Réponse : tout est correct !) Si vous devinez queest simplement le résultat de la libération de l'irrationalité dans le dénominateur de la fraction. :)
Pourquoi devrions-nous nous libérer de l'irrationalité dans les fractions ? Quelle différence cela fait-il que la racine soit au numérateur ou au dénominateur ? La calculatrice calculera tout de toute façon.) Eh bien, pour ceux qui ne se séparent pas de la calculatrice, il n'y a pratiquement aucune différence ... Mais, même en comptant sur la calculatrice, vous pouvez faire attention au fait que diviser sur le ensemble numéro est toujours plus pratique et plus rapide que irrationnel. Et je garderai le silence sur la division dans une colonne.)
L'exemple suivant ne fera que confirmer mes propos.
Comment éliminer la racine carrée du dénominateur ici ? Si le numérateur et le dénominateur sont multipliés par l'expression, alors le dénominateur sera le carré de la somme. La somme des carrés des premier et deuxième nombres nous donnera juste des nombres sans aucune racine, ce qui est très agréable. Cependant ... il apparaîtra double produit le premier nombre au second, où la racine de trois restera toujours. Ne canalise pas. Comment être? Rappelez-vous une autre merveilleuse formule de multiplication abrégée ! Où il n'y a pas de produits doubles, mais seulement des carrés :
Une telle expression, qui, multipliée par une somme (ou une différence), conduit à différence de carrés, aussi appelé expression conjuguée. Dans notre exemple, l'expression adjointe sera la différence . On multiplie donc le numérateur et le dénominateur par cette différence :
Que peut-on dire ici ? À la suite de nos manipulations, non seulement la racine du dénominateur a disparu, mais la fraction a disparu en général ! :) Même avec une calculatrice, soustraire la racine de trois de trois est plus facile que de compter une fraction avec une racine au dénominateur. Un autre exemple.
Débarrassez-vous de l'irrationalité dans le dénominateur d'une fraction :
Comment sortir d'ici ? Les formules de multiplication abrégée avec des carrés ne fonctionnent pas tout de suite - il ne sera pas possible d'éliminer complètement les racines car cette fois notre racine n'est pas carrée, mais cubique. Il est nécessaire que la racine soit en quelque sorte élevée dans un cube. Par conséquent, il est nécessaire d'appliquer certaines des formules avec des cubes. Quoi? Réfléchissons. Le dénominateur est la somme. Comment obtient-on la racine cubique ? Multiplier par différence au carré incomplète! Nous appliquerons donc la formule sommes de cubes. Celui-ci:
Comme un nous en avons trois, et comme b est la racine cubique de cinq :
Et encore une fois la fraction a disparu.) De telles situations, où, une fois libérée de l'irrationalité dans le dénominateur de la fraction, la fraction elle-même disparaît complètement avec les racines, sont très courantes. Comment aimez-vous cet exemple!
Calculer:
![]()
Essayez simplement d'additionner ces trois fractions ! Sans fautes ! :) Un dénominateur commun vaut quelque chose. Mais que se passe-t-il si nous essayons de nous débarrasser de l'irrationalité dans le dénominateur de chaque fraction ? Bon, essayons :
Waouh, comme c'est intéressant ! Toutes les fractions ont disparu ! Totalement. Et maintenant l'exemple est résolu en deux temps :
Simple et élégant. Et sans calculs longs et fastidieux. :)
C'est pourquoi l'opération de libération de l'irrationalité dans les fractions doit pouvoir se faire. Dans des exemples aussi fantaisistes, seule elle sauve, oui.) Bien sûr, personne n'a annulé l'attention. Il y a des tâches où on leur demande de se débarrasser de l'irrationalité dans numérateur. Ces tâches ne sont pas différentes de celles considérées, seul le numérateur est débarrassé des racines.)
Exemples plus complexes
Il reste à considérer certaines techniques spéciales de travail avec les racines et à s'entraîner à ne pas démêler les exemples les plus simples. Et puis les informations reçues seront déjà suffisantes pour résoudre des tâches avec des racines de n'importe quel niveau de complexité. Alors - allez-y.) Tout d'abord, voyons ce qu'il faut faire avec les racines imbriquées lorsque la formule racine de la racine ne fonctionne pas. Par exemple, voici un exemple.
Calculer:
La racine sous la racine... De plus, sous les racines se trouve la somme ou la différence. Par conséquent, la formule de la racine à partir de la racine (avec multiplication des indicateurs) est ici Ça ne marche pas. Il faut donc faire quelque chose pour expressions radicales R : Nous n'avons tout simplement pas d'autres options. Dans de tels exemples, le plus souvent sous une grande racine est chiffré carré plein un certain montant. Ou des différences. Et la racine du carré est déjà parfaitement extraite ! Et maintenant, notre tâche est de le déchiffrer.) Un tel décryptage est magnifiquement fait à travers système d'équations. Maintenant, vous pouvez voir par vous-même.)
Ainsi, sous la première racine, nous avons cette expression :
Et si vous n'aviez pas deviné ? Allons vérifier! Équarrissage à l'aide de la formule de la somme au carré :
C'est vrai.) Mais... D'où ai-je tiré cette expression ? Depuis le ciel?
Non.) Nous l'obtiendrons un peu plus bas honnêtement. En utilisant simplement cette expression, je montre exactement comment les compilateurs de tâches chiffrent de tels carrés. :) Qu'est-ce que 54 ? ce la somme des carrés des premier et deuxième nombres. Et, attention, déjà sans racines ! Mais la racine reste double produit, qui dans notre cas est égal à . Par conséquent, démêler de tels exemples commence par la recherche d'un produit double. Si vous vous démêlez avec la sélection habituelle. Et au fait, sur les signes. Tout est simple ici. Si avant doublé plus, alors le carré de la somme. Si moins, alors la différence.) Nous avons un plus - ce qui signifie le carré de la somme.) Et maintenant - la méthode analytique de décodage promise. via le système.)
Donc, sous notre racine, l'expression traîne clairement (a+b) 2, et notre tâche est de trouver un et b. Dans notre cas, la somme des carrés donne 54. On écrit donc :
![]()
Doubler maintenant le produit. Nous l'avons. Alors on écrit :
Nous avons obtenu le système suivant :
![]()
Nous résolvons par la méthode de substitution habituelle. Nous exprimons à partir de la deuxième équation, par exemple, et substituons à la première :

Résolvons la première équation :
A obtenu bi-carrééquation pourun . On considère le discriminant :
Moyens,
Nous avons obtenu jusqu'à quatre valeurs possiblesun. Nous n'avons pas peur. Maintenant, nous allons éliminer tout ce qui est superflu.) Si nous calculons maintenant les valeurs correspondantes pour chacune des quatre valeurs trouvées, nous obtiendrons quatre solutions à notre système. Les voici:
Et puis la question est - laquelle des solutions nous convient? Réfléchissons. Les solutions négatives peuvent être immédiatement rejetées: lors de la quadrature, les moins «s'épuiseront» et toute l'expression radicale ne changera pas dans son ensemble.) Les deux premières options restent. Vous pouvez les choisir de manière totalement arbitraire : la somme ne change de toute façon pas à partir du réarrangement des termes.) Soit, par exemple, , et .
Au total, nous avons obtenu le carré du montant suivant sous la racine :
Tout est clair.)
Ce n'est pas pour rien que je décris le cours de la solution avec tant de détails. Pour préciser comment le décryptage a lieu.) Mais il y a un problème. La méthode analytique de déchiffrement, bien que fiable, est très longue et lourde : il faut résoudre une équation biquadratique, obtenir quatre solutions au système, puis réfléchir à celles qu'il faut choisir... Gênant ? Je suis d'accord, c'est dur. Cette méthode fonctionne parfaitement dans la plupart de ces exemples. Cependant, il est souvent bon de réduire votre travail et de trouver les deux chiffres de manière créative. Sélection.) Oui, oui ! Maintenant, en utilisant l'exemple du deuxième terme (la deuxième racine), je vais montrer un moyen plus simple et plus rapide de sélectionner le carré complet sous la racine.
Alors maintenant, nous avons cette racine: ![]() .
.
Nous pensons ainsi : « Sous la racine se trouve très probablement un carré complet crypté. Les temps devant un moins doublé signifient le carré de la différence. La somme des carrés des premier et deuxième nombres nous donne le nombre 54. Mais que sont ces carrés ? 1 et 53 ? 49 et 5 ? Trop d'options... Non, il vaut mieux commencer à démêler avec un double produit. Notrepeut être écrit comme . Une fois une œuvre double, alors nous rejetons immédiatement le deux. Ensuite, les candidats au rôle a et b restent 7 et . Et soudain, il est 14h et/2 ? Pas exclu. Mais on commence toujours par un simple ! Alors, laissez , a . Vérifions-les pour la somme des carrés:
Passé! Donc, notre expression racine est en fait le carré de la différence :
Voici une telle voie-lumière, afin de ne pas jouer avec le système. Cela ne fonctionne pas toujours, mais dans de nombreux exemples, cela suffit amplement. Ainsi, sous les racines se trouvent des carrés pleins. Il ne reste plus qu'à extraire correctement les racines, et compter l'exemple :
Et maintenant, analysons une tâche encore plus non standard dans les racines.)
Démontrer que le nombre Aest un entier si .
Rien n'est extrait directement, les racines sont imbriquées, et même à des degrés divers... Cauchemar ! Cependant, la tâche a du sens.) Par conséquent, il y a une clé à sa solution.) Et voici la clé. Considérez notre égalité
comment équation pour UN. Oui oui! Ce serait bien de se débarrasser des racines. Nos racines sont cubiques, donc élevons les deux côtés de l'équation à un cube. Selon la formule cube somme:

Les cubes et les racines cubiques se compensent, et sous chaque grande racine, nous prenons une parenthèse du carré et transformons le produit de la différence et de la somme en la différence des carrés :
Séparément, nous calculons la différence des carrés sous les racines:
Les transformations d'expressions à l'identique constituent l'un des axes du contenu du cours de mathématiques scolaires. Les transformations d'identité sont largement utilisées pour résoudre des équations, des inégalités, des systèmes d'équations et des inégalités. De plus, des transformations identiques d'expressions contribuent au développement de l'ingéniosité, de la souplesse et de la rationalité de la pensée.
Le matériel proposé s'adresse aux élèves de 8e année et comprend les fondements théoriques de transformations identiques de rationnel et expressions irrationnelles, les types de tâches pour la transformation de ces expressions et le texte du test.
1. Fondements théoriques des transformations identiques
Les expressions en algèbre sont des enregistrements constitués de chiffres et de lettres reliés par des signes d'action.
https://pandia.ru/text/80/197/images/image002_92.gif" width="77" height="21 src=">.gif" width="20" height="21 src="> – expressions algébriques.
Selon les opérations, on distingue les expressions rationnelles et irrationnelles.
Les expressions algébriques sont dites rationnelles si, par rapport aux lettres qu'elles contiennent un, b, Avec, … aucune autre opération n'est effectuée à l'exception de l'addition, de la multiplication, de la soustraction, de la division et de l'élévation à une puissance entière.
Les expressions algébriques contenant les opérations d'extraction d'une racine d'une variable ou d'élévation d'une variable à une puissance rationnelle qui n'est pas un entier sont dites irrationnelles par rapport à cette variable.
La transformation d'identité d'une expression donnée est le remplacement d'une expression par une autre, identiquement égale à elle sur un ensemble.
Les faits théoriques suivants sous-tendent les transformations identiques des expressions rationnelles et irrationnelles.
1. Propriétés des degrés avec un exposant entier :
![]() , n SUR; un 1=un;
, n SUR; un 1=un;
, n SUR, un¹0; un 0=1, un¹0;
![]() , un¹0;
, un¹0;
, un¹0;
, un¹0;
, un¹0, b¹0;
![]() , un¹0, b¹0.
, un¹0, b¹0.
2. Formules de multiplication abrégées :
où un, b, Avec- tous les nombres réels ;
Où un¹0, X 1 et X 2 - les racines de l'équation ![]() .
.
3. La propriété principale d'une fraction et les actions sur les fractions :
![]() , où b¹0, Avec¹0;
, où b¹0, Avec¹0;
; ![]() ;
;
4. Définition de la racine arithmétique et de ses propriétés :
![]() ; , b¹0 ; https://pandia.ru/text/80/197/images/image026_24.gif" width="84" height="32">; ;
; , b¹0 ; https://pandia.ru/text/80/197/images/image026_24.gif" width="84" height="32">; ; ![]() ,
,
où un, b sont des nombres non négatifs n SUR, n³2, m SUR, m³2.
1. Types d'exercices de transformation d'expression
Exister différents types exercices sur les transformations identiques d'expressions. Premier type: spécifie explicitement la conversion à effectuer.
Par exemple.
1. Présenter sous forme de polynôme.
Lors de l'exécution de cette transformation, les règles de multiplication et de soustraction de polynômes, la formule de multiplication abrégée et la réduction de termes similaires ont été utilisées.
2. Factoriser : ![]() .
.
Lors de la transformation, la règle consistant à retirer le facteur commun de la parenthèse et 2 formules de multiplication abrégées ont été utilisées.
3. Réduisez la fraction :
![]() .
.

Lors de la transformation, nous avons utilisé la mise entre parenthèses du facteur commun, les lois de déplacement et de contraction, 2 formules de multiplication abrégée et des actions sur les puissances.
4. Retirez le facteur sous le signe racine si un³0, b³0, Avec³0 : https://pandia.ru/text/80/197/images/image036_17.gif" width="432" height="27">
Nous avons utilisé les règles des opérations sur les racines et la définition du module d'un nombre.
5. Débarrassez-vous de l'irrationalité dans le dénominateur d'une fraction ![]() .
.
Deuxième type les exercices sont des exercices dans lesquels la principale transformation à effectuer est explicitement indiquée. Dans de tels exercices, l'exigence est généralement formulée sous l'une des formes suivantes : simplifier l'expression, calculer. Lors de l'exécution de tels exercices, il est tout d'abord nécessaire d'identifier quelles transformations et dans quel ordre doivent être effectuées pour que l'expression prenne une forme plus compacte que celle donnée, ou qu'un résultat numérique soit obtenu.
Par exemple
6. Simplifiez l'expression :
La solution:
![]() .
.
Utilisé les règles d'action sur fractions algébriques et formules de multiplication abrégées.
7. Simplifiez l'expression :
 .
.
Si un un³0, b³0, un¹ b.
Nous avons utilisé des formules de multiplication abrégées, des règles pour additionner des fractions et multiplier des expressions irrationnelles, identité https://pandia.ru/text/80/197/images/image049_15.gif" width="203" height="29">.
Nous avons utilisé l'opération de sélection carrée complète, l'identité https://pandia.ru/text/80/197/images/image053_11.gif" width="132 height=21" height="21">, si .
Preuve:
Depuis , puis et ou ou ou , c'est-à-dire .
Nous avons utilisé la condition et la formule de la somme des cubes.
Rappelons que les conditions liant les variables peuvent également être précisées dans les exercices des deux premiers types.
Par exemple.
10. Trouvez si .
Formateur numéro 1
Sujet : Conversion de puissance et expressions irrationnelles
Programme de cours au choix en mathématiques pour les élèves de 10e année
ProgrammeApplication. Application des formules trigonométriques de base à transformation expressions. Sujet 4. Fonctions trigonométriques et leurs cartes. Résumer... . 16.01-20.01 18 transformation Puissance et irrationnel expressions. 23.01-27.01 19 ...
Calendrier-planification thématique de l'algèbre du matériel pédagogique et début de l'analyse, 11e année
Calendrier-planification thématiqueEt un indicateur rationnel. transformation Puissance et irrationnel expressions. 2 2 2 septembre Propriétés des logarithmes. transformation logarithmique expressions. 1 1 1 ... entièrement traité ceuxétudiants qui aspirent à des études supérieures...
Sujet de la leçon Type de leçon (4)
Leçon... transformations numérique et alphabétique expressions contenant diplôme ... degrés Savoir : notion diplôme avec un exposant irrationnel ; propriétés de base degrés. Être capable de : trouver le sens diplôme Avec irrationnel... 3 par sujet « Diplôme nombre positif...
Thème Fondements culturels et historiques du développement des connaissances psychologiques du travail Thème Le travail comme réalité socio-psychologique
DocumentEt etc.) sujet le travail est étroitement lié à la situation socio-économique transformations. Par exemple, ... la restructuration de la conscience, des instincts, irrationnel tendances, c'est-à-dire conflits internes... connaître la disponibilité et diplôme expressivité une personne a certains...
Conversion d'expressions contenant des racines carrées (1)
LeçonEdité par S.A. Téliakovsky. Sujet leçon: transformation expressions contenant carré...) transformations racines du produit, fractions et diplôme, multiplication ... (formation de l'habileté de transformations irrationnel expressions). N° 421. (au tableau noir...