Le concept d'une fonction impaire et sa propriété. Fonctions élémentaires de base et leurs propriétés

14.10.2019

Comment construire correctement les axes de coordonnées ?

En pratique, les épreuves sont presque toujours rédigées par les élèves dans des cahiers séparés, alignés dans une cage. Pourquoi avez-vous besoin de marquages à carreaux ? Après tout, le travail peut en principe être effectué sur des feuilles A4. Et la cage est nécessaire uniquement pour la conception précise et de haute qualité des dessins.

Tout dessin d'un graphe de fonction commence par des axes de coordonnées.

Les dessins sont en deux dimensions et en trois dimensions.

Considérons d'abord le cas bidimensionnel système de coordonnées cartésiennes:

1) Nous dessinons des axes de coordonnées. L'axe s'appelle axe x , et l'axe axe y . Nous essayons toujours de les dessiner soigné et non tordu. Les flèches ne doivent pas non plus ressembler à la barbe de Papa Carlo.

2) Nous signons les axes avec les majuscules "x" et "y". N'oubliez pas de signer les haches.

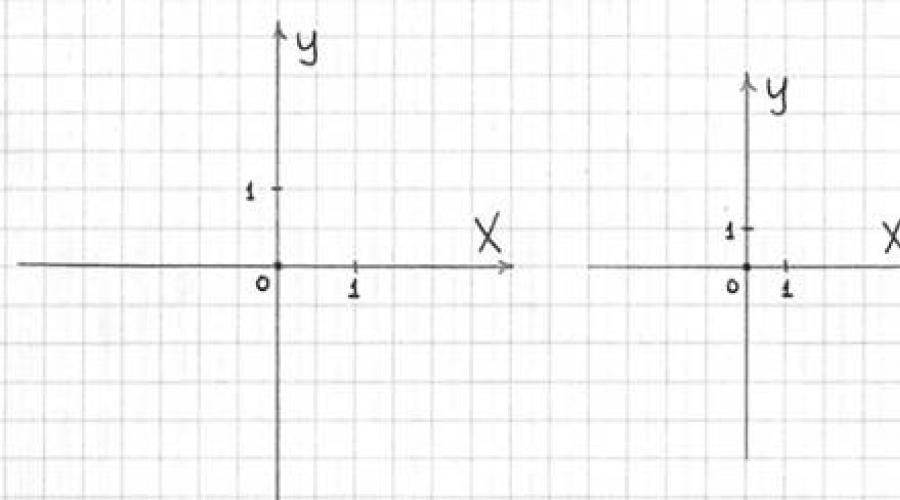
3) Réglez l'échelle le long des axes : tirer zéro et deux uns. Lors de la réalisation d'un dessin, l'échelle la plus pratique et la plus courante est : 1 unité = 2 cellules (dessin de gauche) - respectez-la si possible. Cependant, il arrive de temps en temps que le dessin ne tienne pas sur une feuille de cahier - alors on réduit l'échelle : 1 unité = 1 cellule (dessin de droite). Rarement, mais il arrive que l'échelle du dessin doive encore être réduite (ou augmentée)

NE PAS griffonner avec une mitrailleuse ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... Car le plan de coordonnées n'est pas un monument à Descartes, et l'étudiant n'est pas une colombe. nous mettons zéro et deux unités le long des axes. quelquefois à la place de unités, il est pratique de "détecter" d'autres valeurs, par exemple, "deux" sur l'axe des abscisses et "trois" sur l'axe des ordonnées - et ce système (0, 2 et 3) définira également de manière unique la grille de coordonnées.

Il est préférable d'estimer les dimensions estimées du dessin AVANT que le dessin ne soit dessiné.. Ainsi, par exemple, si la tâche nécessite de dessiner un triangle avec des sommets , , , alors il est tout à fait clair que l'échelle populaire 1 unité = 2 cellules ne fonctionnera pas. Pourquoi? Voyons le point - ici, vous devez mesurer quinze centimètres de profondeur et, évidemment, le dessin ne tiendra pas (ou à peine) sur une feuille de cahier. Par conséquent, nous sélectionnons immédiatement une échelle plus petite 1 unité = 1 cellule.

Soit dit en passant, environ des centimètres et des cellules de cahier. Est-il vrai qu'il y a 15 centimètres dans 30 cellules de cahier ? Mesurez dans un cahier d'intérêt 15 centimètres avec une règle. En URSS, c'était peut-être vrai... Il est intéressant de noter que si vous mesurez ces mêmes centimètres horizontalement et verticalement, alors les résultats (en cellules) seront différents ! À proprement parler, les cahiers modernes ne sont pas à carreaux, mais rectangulaires. Cela peut sembler absurde, mais dessiner, par exemple, un cercle avec une boussole dans de telles situations est très gênant. Pour être honnête, à de tels moments, vous commencez à penser à l'exactitude du camarade Staline, qui a été envoyé dans des camps pour travailler dans la production, sans parler de l'industrie automobile nationale, de la chute d'avions ou de l'explosion de centrales électriques.

En parlant de qualité, ou une brève recommandation sur la papeterie. A ce jour, la plupart des carnets sont en solde, gros mots sans parler, merde complète. Pour la raison qu'ils se mouillent, et pas seulement avec les stylos gel, mais aussi avec les stylos à bille ! Économisez sur le papier. Pour le dédouanement travaux de contrôle Je recommande d'utiliser les cahiers de l'usine de pâtes et papiers d'Arkhangelsk (18 feuilles, cage) ou Pyaterochka, bien que ce soit plus cher. Il est conseillé de choisir un stylo gel, même la recharge de gel chinoise la moins chère est bien meilleure qu'un stylo à bille, qui tache ou déchire le papier. Le seul stylo à bille "compétitif" dans ma mémoire est le Erich Krause. Elle écrit clairement, magnifiquement et de manière stable - soit avec une tige pleine, soit avec une tige presque vide.

En outre: la vision d'un système de coordonnées rectangulaires à travers les yeux de la géométrie analytique est couverte dans l'article (non) dépendance linéaire des vecteurs. Base vectorielle, des informations détaillées sur les quarts de coordonnées peuvent être trouvées dans le deuxième paragraphe de la leçon Inégalités linéaires.

cas 3D

C'est presque pareil ici.

1) Nous dessinons des axes de coordonnées. Standard: appliquer l'axe – dirigé vers le haut, axe – dirigé vers la droite, axe – vers le bas vers la gauche strictementà un angle de 45 degrés.

2) Nous signons les axes.

3) Réglez l'échelle le long des axes. Échelle le long de l'axe - deux fois plus petite que l'échelle le long des autres axes. Notez également que dans le dessin de droite, j'ai utilisé un "serif" non standard le long de l'axe (cette possibilité a déjà été mentionnée ci-dessus). De mon point de vue, c'est plus précis, plus rapide et plus esthétique - vous n'avez pas besoin de chercher le milieu de la cellule sous un microscope et de "sculpter" l'unité jusqu'à l'origine.

Lorsque vous refaites un dessin 3D - donnez la priorité à l'échelle
1 unité = 2 cellules (dessin de gauche).

A quoi servent toutes ces règles ? Les règles sont là pour être enfreintes. Qu'est-ce que je vais faire maintenant. Le fait est que les dessins ultérieurs de l'article seront réalisés par moi dans Excel, et les axes de coordonnées sembleront incorrects du point de vue conception correcte. Je pourrais dessiner tous les graphiques à la main, mais c'est vraiment effrayant de les dessiner, car Excel hésite à les dessiner avec beaucoup plus de précision.

Graphiques et propriétés de base des fonctions élémentaires

La fonction linéaire est donnée par l'équation . Le graphique de la fonction linéaire est direct. Pour construire une droite, il suffit de connaître deux points.

Exemple 1

Tracez la fonction. Trouvons deux points. Il est avantageux de choisir zéro comme l'un des points.

Si donc

Prenons un autre point, par exemple, 1.

Si donc

Lors de la préparation des tâches, les coordonnées des points sont généralement résumées dans un tableau :

Et les valeurs elles-mêmes sont calculées oralement ou sur un brouillon, calculatrice.

Deux points sont trouvés, dessinons:

Lors de l'élaboration d'un dessin, nous signons toujours les graphiques.

Il ne sera pas superflu de rappeler des cas particuliers d'une fonction linéaire :

Remarquez comment j'ai placé les légendes, les signatures ne doivent pas être ambiguës lors de l'étude du dessin. Dans ce cas, il était hautement indésirable de mettre une signature à côté du point d'intersection des lignes, ou en bas à droite entre les graphiques.

1) Une fonction linéaire de la forme () est appelée proportionnalité directe. Par exemple, . Le graphe de proportionnalité directe passe toujours par l'origine. Ainsi, la construction d'une droite est simplifiée - il suffit de trouver un seul point.

2) Une équation de la forme définit une droite parallèle à l'axe, en particulier, l'axe lui-même est donné par l'équation. Le graphe de la fonction est construit immédiatement, sans trouver de points. C'est-à-dire que l'entrée doit être comprise comme suit : "y est toujours égal à -4, pour toute valeur de x".

3) Une équation de la forme définit une droite parallèle à l'axe, en particulier, l'axe lui-même est donné par l'équation. Le graphe de la fonction est également construit immédiatement. L'entrée doit être comprise comme suit : "x est toujours, pour toute valeur de y, égal à 1."

Certains se demanderont, eh bien, pourquoi se souvenir de la 6e année ?! C'est ainsi, peut-être, seulement pendant les années de pratique j'ai rencontré une bonne douzaine d'étudiants déconcertés par la tâche de construire un graphe comme ou .

Dessiner une ligne droite est l'action la plus courante lors de la réalisation de dessins.

La droite est discutée en détail dans le cours de géométrie analytique, et ceux qui le souhaitent peuvent se reporter à l'article Équation d'une droite sur un plan.

Graphique de fonction quadratique, graphique de fonction cubique, graphique polynomial

Parabole. Programme fonction quadratique () est une parabole. Prenons le fameux cas :

Rappelons quelques propriétés de la fonction.

Donc, la solution de notre équation : - c'est en ce point que se situe le sommet de la parabole. Pourquoi il en est ainsi peut être appris de l'article théorique sur la dérivée et de la leçon sur les extrema de la fonction. En attendant, nous calculons la valeur correspondante de "y":

Donc le sommet est au point

Maintenant, nous trouvons d'autres points, tout en utilisant effrontément la symétrie de la parabole. Il est à noter que la fonction – n'est même pas, mais, néanmoins, personne n'a annulé la symétrie de la parabole.

Dans quel ordre trouver les points restants, je pense que cela ressortira clairement du tableau final :

Cet algorithme de construction peut être appelé au sens figuré une "navette" ou le principe du "va-et-vient" avec Anfisa Chekhova.

Faisons un dessin :

D'après les graphiques considérés, une autre fonctionnalité utile vient à l'esprit :

Pour une fonction quadratique () ce qui suit est vrai :

Si , alors les branches de la parabole sont dirigées vers le haut.

Si , alors les branches de la parabole sont dirigées vers le bas.

Une connaissance approfondie de la courbe peut être obtenue dans la leçon Hyperbole et parabole.

La parabole cubique est donnée par la fonction . Voici un dessin familier de l'école :

On liste les principales propriétés de la fonction

Graphique de fonction

Il représente l'une des branches de la parabole. Faisons un dessin :

Les principales propriétés de la fonction :

Dans ce cas, l'axe est asymptote verticale pour le graphique hyperbole à .

Ce sera une GROSSE erreur si, lors de l'élaboration d'un dessin, par négligence, vous laissez le graphe se croiser avec l'asymptote.

Aussi limites unilatérales, dites-nous qu'une hyperbole pas limité d'en haut et non limité par le bas.

Explorons la fonction à l'infini: , c'est-à-dire que si nous commençons à nous déplacer le long de l'axe vers la gauche (ou la droite) jusqu'à l'infini, alors les «jeux» seront un pas élancé infiniment proche s'approchent de zéro, et, par conséquent, les branches de l'hyperbole infiniment proche se rapprocher de l'axe.

Donc l'axe est asymptote horizontale pour le graphique de la fonction, si "x" tend vers plus ou moins l'infini.

La fonction est étrange, ce qui signifie que l'hyperbole est symétrique par rapport à l'origine. Ce fait ressort clairement du dessin, de plus, il peut être facilement vérifié analytiquement: .

Le graphe d'une fonction de la forme () représente deux branches d'une hyperbole.

Si , alors l'hyperbole est située dans les premier et troisième quadrants de coordonnées(voir photo ci-dessus).

Si , alors l'hyperbole est située dans les deuxième et quatrième quadrants de coordonnées.

Il n'est pas difficile d'analyser la régularité spécifiée du lieu de résidence de l'hyperbole du point de vue des transformations géométriques des graphiques.

Exemple 3

Construire la branche droite de l'hyperbole

Nous utilisons la méthode de construction ponctuelle, alors qu'il est avantageux de sélectionner les valeurs pour qu'elles se divisent complètement :

Faisons un dessin :

Il ne sera pas difficile de construire la branche gauche de l'hyperbole, ici l'étrangeté de la fonction aidera juste. En gros, dans le tableau de construction point par point, ajoutez mentalement un moins à chaque nombre, placez les points correspondants et dessinez la deuxième branche.

Des informations géométriques détaillées sur la ligne considérée peuvent être trouvées dans l'article Hyperbole et parabole.

Graphique d'une fonction exponentielle

Dans ce paragraphe, je vais immédiatement considérer la fonction exponentielle, puisque dans les problèmes de mathématiques supérieures dans 95% des cas, c'est l'exposant qui se produit.

Je vous rappelle que - c'est un nombre irrationnel : , cela sera nécessaire lors de la construction d'un graphe, que, en fait, je construirai sans cérémonie. Trois points probablement assez :

Laissons le graphique de la fonction seul pour l'instant, à ce sujet plus tard.

Les principales propriétés de la fonction :

Fondamentalement, les graphiques des fonctions se ressemblent, etc.

Je dois dire que le deuxième cas est moins courant dans la pratique, mais il se produit, j'ai donc jugé nécessaire de l'inclure dans cet article.

Graphique d'une fonction logarithmique

Considérons une fonction avec un logarithme naturel.
Faisons un dessin au trait:

Si vous avez oublié ce qu'est un logarithme, veuillez vous référer aux manuels scolaires.

Les principales propriétés de la fonction :

Domaine:

Plage de valeurs : .

La fonction n'est pas limitée par le haut : , bien que lentement, mais la branche du logarithme monte à l'infini.
Examinons le comportement de la fonction proche de zéro à droite : . Donc l'axe est asymptote verticale pour le graphique de la fonction avec "x" tendant vers zéro à droite.

Assurez-vous de connaître et de vous souvenir de la valeur typique du logarithme: .

Fondamentalement, le graphique du logarithme à la base est le même : , , ( logarithme décimal en base 10), etc. Dans le même temps, plus la base est large, plus le graphique sera plat.

Nous ne considérerons pas le cas, je ne me souviens pas quand dernière fois construit un graphe avec une telle base. Oui, et le logarithme semble être un invité très rare dans les problèmes de mathématiques supérieures.

En conclusion du paragraphe, je dirai un fait de plus: Fonction exponentielle et fonction logarithmiquesont deux fonctions mutuellement inverses. Si vous regardez attentivement le graphique du logarithme, vous pouvez voir qu'il s'agit du même exposant, juste qu'il est situé un peu différemment.

Graphiques de fonctions trigonométriques

Comment commence le tourment trigonométrique à l'école ? Correctement. Du sinus

Traçons la fonction

Cette ligne s'appelle sinusoïde.

Je vous rappelle que "pi" est un nombre irrationnel :, et en trigonométrie il éblouit les yeux.

Les principales propriétés de la fonction :

Cette fonction est périodique avec une période. Qu'est-ce que ça veut dire? Regardons la coupe. À gauche et à droite de celui-ci, exactement le même morceau du graphique se répète à l'infini.

Domaine: , c'est-à-dire que pour toute valeur de "x", il existe une valeur sinusoïdale.

Plage de valeurs : . La fonction est limité: , c'est-à-dire que tous les "jeux" se situent strictement dans le segment .
Cela ne se produit pas : ou, plus précisément, cela se produit, mais ces équations n'ont pas de solution.

Limites et continuité

Ensembles

En dessous de de nombreux est compris comme un ensemble d'objets homogènes. Les objets qui forment un ensemble sont appelés éléments ou des points cet ensemble. Les ensembles dénotent majuscules, et leurs éléments sont en ligne. Si un un est un élément de l'ensemble UN, alors la notation unÎ UN. Si un b n'est pas un élément de l'ensemble UN, alors il s'écrit comme ceci : b Ï UN. Un ensemble qui ne contient pas un seul élément est appelé un ensemble vide et est noté comme suit : Ø.

Si l'ensemble B est constitué d'une partie des éléments de l'ensemble UN ou coïncide avec lui, alors l'ensemble B appelé sous-ensemble définit et dénote BÌ UN.

Les deux ensembles sont appelés égal s'ils sont constitués des mêmes éléments.

Association deux jeux UN et B est appelé un ensemble C, constitué de tous les éléments appartenant à au moins un des ensembles : C=UNÈ B.

traversée deux jeux UN et B est appelé un ensemble C, composé de tous les éléments appartenant à chacun des ensembles donnés : C=UNÇ B.

différence ensembles UN et B est appelé un ensemble E UN, qui n'appartiennent pas à l'ensemble B: .

Supplément ensembles UNÌ B est appelé un ensemble C, composé de tous les éléments de l'ensemble B, n'appartenant pas UN.

Les ensembles dont les éléments sont des nombres réels sont appelés numérique:

Où NÌ ZÌ QÌ R, jeÌ R et R=jeÈ Q.

Beaucoup de X, dont les éléments satisfont l'inégalité est appelé segment(segment) et noté [ un; b] ; inégalité un<X<b – intervalle et est noté () ; inégalités et - demi-intervalles et sont désignés par et , respectivement. Vous devez également souvent gérer des intervalles infinis et des demi-intervalles : , , , et . Il est commode de les appeler tous à intervalles .

Intervalle, c'est-à-dire l'ensemble des points satisfaisant l'inégalité (où ), est appelé -voisinage du point un.

La notion de fonction. Principales propriétés de la fonction

Si chaque élément X ensembles X un seul élément correspond y ensembles Oui, alors on dit que sur le plateau X donné fonction y=F(X). Où X appelé variable indépendante ou dispute, un y – variable dépendante ou fonction, un F représente la loi de la correspondance. Beaucoup de X appelé domaine de définition fonctions, mais l'ensemble Oui – intervalle les fonctions.

Il existe plusieurs façons de définir des fonctions.

1) Méthode analytique - la fonction est donnée par une formule de la forme y=F(X).

2) Méthode tabulaire - la fonction est définie par un tableau contenant les valeurs de l'argument et les valeurs de fonction correspondantes y=F(X).

3) Méthode graphique - l'image du graphique de la fonction, c'est-à-dire ensemble de points ( X; y) du plan de coordonnées, dont les abscisses représentent les valeurs de l'argument , et les ordonnées sont les valeurs correspondantes de la fonction y=F(X).

4) Méthode verbale - la fonction est décrite par la règle de sa compilation. Par exemple, la fonction de Dirichlet prend la valeur 1 si X est un nombre rationnel et 0 si X est un nombre irrationnel.

Les principales propriétés suivantes des fonctions sont distinguées.

1 pair et impair Fonction y=F(X) est appelé même, si pour toutes les valeurs X du domaine de sa définition, F(–X)=F(X), et étrange, si F(–X)=–F(X). Si aucune des équations ci-dessus ne tient, alors y=F(X) est appelé fonction générale. Le graphe d'une fonction paire est symétrique par rapport à l'axe Oy, et le graphe d'une fonction impaire est symétrique par rapport à l'origine.

2 Monotonie Fonction y=F(X) est appelé en augmentant (déclin) sur l'intervalle X, si plus grande valeur un argument de cet intervalle correspond à une valeur plus grande (plus petite) de la fonction. Laisser X 1 ,X 2 О X, X 2 >X une . Alors la fonction croît sur l'intervalle X, si F(X 2)>F(X 1) et diminue si F(X 2)<F(X 1).

En plus des fonctions croissantes et décroissantes, des fonctions non décroissantes et non croissantes sont prises en compte. La fonction s'appelle non décroissant (non croissant), si X 1 ,X 2 О X, X 2 >X 1 l'inégalité F(X 2)≥F(X 1) (F(X 2)≤F(X 1)).

Les fonctions croissantes et décroissantes, ainsi que les fonctions non croissantes et non décroissantes, sont dites monotones.

3 Limité Fonction y=F(X) est dit borné sur l'intervalle X s'il existe un tel nombre positif M>0, quoi | F(X)|≤M pour tout le monde XÎ X. Sinon, la fonction est dite illimitée sur X.

4 Périodicité Fonction y=F(X) est dit périodique de période J≠0 si pour tout X hors de portée de la fonction F(X+J)=F(X). Dans ce qui suit, une période sera comprise comme la plus petite période positive d'une fonction.

La fonction s'appelle explicite, s'il est donné par une formule de la forme y=F(X). Si la fonction est donnée par l'équation F(X, y)=0 non autorisé par rapport à la variable dépendante y, alors il s'appelle implicite.

Laisser y=F(X) est une fonction de la variable indépendante définie sur l'ensemble X avec gamme Oui. Associons chacun yÎ Oui sens unique XÎ X, auquel F(X)=y.Puis la fonction résultante X=φ (y) défini sur l'ensemble Oui avec gamme X, est appelé inverse et noté y=F –1 (X). Graphiques mutuellement fonctions inverses sont symétriques par rapport à la bissectrice des premier et troisième quarts de coordonnées.

Laissez la fonction y=F(tu) est une fonction de la variable tu défini sur le plateau tu avec gamme Oui, et la variable tu est à son tour une fonction tu=φ (X) défini sur l'ensemble X avec gamme tu. Puis donné sur le plateau X fonction y=F(φ (X)) est appelé fonction complexe (composition de fonctions, superposition de fonctions, fonction d'une fonction).

Fonctions élémentaires

Les principales fonctions élémentaires comprennent :

fonction de puissance y=x n; y=x-n et y=X 1/ n;
fonction exponentielle y=un x;
fonction logarithmique y=journal un x;
fonctions trigonométriques y= péché X, y= cos X, y=tg X et y=ctg X;
fonctions trigonométriques inverses y= arcsin X, y= arccos X, y=arctg X et y=arctg X.

A partir des fonctions élémentaires de base, de nouvelles fonctions peuvent être obtenues à l'aide d'opérations algébriques et de superposition de fonctions.

Les fonctions construites à partir de fonctions élémentaires de base utilisant un nombre fini d'opérations algébriques et un nombre fini d'opérations de superposition sont appelées élémentaire.

Algébrique est une fonction dans laquelle un nombre fini d'opérations algébriques sont effectuées sur l'argument. Les fonctions algébriques comprennent :

fonction rationnelle entière (polynôme ou polynôme)

fonction rationnelle fractionnaire (rapport de deux polynômes)

fonction irrationnelle (si les opérations sur l'argument incluent l'extraction de la racine).

Toute fonction non algébrique est appelée transcendant. Les fonctions transcendantales comprennent les fonctions exponentielles, logarithmiques, trigonométriques et trigonométriques inverses.

Pour comprendre ce sujet, considérons la fonction affichée sur le graphique // Montrons comment le graphique de la fonction vous permet de déterminer ses propriétés.

Nous analysons les propriétés d'une fonction à l'aide d'un exemple

La portée de la fonction est yavl. intervalle [ 3,5 ; 5.5].

La plage de la fonction yavl. intervalle [ 1; 3].

1. À x = -3, x = - 1, x = 1,5, x = 4,5, la valeur de la fonction est zéro.

La valeur de l'argument, à laquelle la valeur de la fonction est zéro, est appelée le zéro de la fonction.

//ceux. pour cette fonction les nombres -3;-1;1.5; 4,5 sont des zéros.

2. Sur les intervalles [ 4,5 ; 3) et (1 ; 1.5) et (4.5 ; 5.5] le graphe de la fonction f est situé au-dessus de l'axe des abscisses, et aux intervalles (-3 ; -1) et (1.5 ; 4.5) sous l'axe des abscisses, c'est expliqué comme suit - à intervalles[4,5 ; 3) et (1 ; 1.5) et (4.5 ; 5.5] la fonction prend valeurs positives, et sur les intervalles (-3 ; -1) et (1,5 ; 4,5) ils sont négatifs.

Chacun des intervalles indiqués (où la fonction prend des valeurs de même signe) est appelé l'intervalle de signe constant de la fonction f.//i.e. par exemple, si nous prenons l'intervalle (0; 3), alors ce n'est pas un intervalle de signe constant de la fonction donnée.

En mathématiques, lors de la recherche d'intervalles de signe constant d'une fonction, il est d'usage d'indiquer des intervalles de longueur maximale. //Ceux. l'intervalle (2 ; 3) est intervalle de constance fonction f, mais la réponse doit inclure l'intervalle [ 4,5 ; 3) contenant l'intervalle (2 ; 3).

3. Si vous vous déplacez le long de l'axe des x de 4,5 à 2, vous remarquerez que le graphique de la fonction diminue, c'est-à-dire que les valeurs de la fonction diminuent. //En mathématiques, il est d'usage de dire que sur l'intervalle [ 4,5; 2] la fonction est décroissante.

Lorsque x augmente de 2 à 0, le graphique de la fonction augmente, c'est-à-dire les valeurs de la fonction augmentent. //En mathématiques, il est d'usage de dire que sur l'intervalle [ 2; 0] la fonction est croissante.

La fonction f est appelée si pour deux valeurs quelconques de l'argument x1 et x2 de cet intervalle telles que x2 > x1, l'inégalité f (x2) > f (x1) est satisfaite. // ou La fonction est appelée augmentant sur un certain intervalle, si pour toutes les valeurs de l'argument de cet intervalle, la plus grande valeur de l'argument correspond à la plus grande valeur de la fonction.//c'est-à-dire plus il y a de x, plus il y a de y.

La fonction f est appelée décroissant sur un certain intervalle, si pour deux valeurs quelconques de l'argument x1 et x2 de cet intervalle tel que x2 > x1, l'inégalité f(x2) décroissante sur un certain intervalle est satisfaite, si pour toutes valeurs de l'argument de cet intervalle un plus grand valeur de l'argument correspond à une plus petite valeur de la fonction. //ceux. plus il y a de x, moins il y a de y.

Si une fonction est croissante sur tout le domaine de définition, alors on l'appelle en augmentant.

Si une fonction est décroissante sur tout le domaine de définition, alors on l'appelle déclin.

Exemple 1 graphique des fonctions croissantes et décroissantes, respectivement.

Exemple 2

Définir yavl. qu'il s'agisse fonction linéaire f(x) = 3x + 5 croissant ou décroissant ?

Preuve. Utilisons les définitions. Soient x1 et x2 des valeurs arbitraires de l'argument, et x1< x2., например х1=1, х2=7

Définition: Une fonction numérique est une correspondance qui correspond à chaque nombre x d'un ensemble donné singulier y.

La désignation:

où x est une variable indépendante (argument), y est une variable dépendante (fonction). L'ensemble des valeurs x est appelé le domaine de la fonction (noté D(f)). L'ensemble des valeurs y est appelé la plage de la fonction (notée E(f)). Le graphe d'une fonction est l'ensemble des points du plan de coordonnées (x, f(x))

Façons de définir une fonction.

méthode analytique (utilisant une formule mathématique);
méthode tabulaire (utilisant un tableau);
méthode descriptive (utilisant une description verbale);
méthode graphique (à l'aide d'un graphe).

Propriétés de base de la fonction.

1. Pair et impair

Une fonction est appelée même si
– le domaine de définition de la fonction est symétrique par rapport à zéro
f(-x) = f(x)

Le graphe d'une fonction paire est symétrique par rapport à l'axe 0a

Une fonction est dite impaire si
– le domaine de définition de la fonction est symétrique par rapport à zéro
– pour tout x du domaine de définition f(-x) = -f(x)

Le graphe d'une fonction impaire est symétrique par rapport à l'origine.

2. Périodicité

La fonction f(x) est dite périodique de période si pour tout x du domaine de définition f(x) = f(x+T) = f(x-T) .

Le graphe d'une fonction périodique consiste à répéter à l'infini des fragments identiques.

3. Monotonie (augmenter, diminuer)

La fonction f(x) est croissante sur l'ensemble P si pour tout x 1 et x 2 de cet ensemble, tel que x 1

La fonction f(x) est décroissante sur l'ensemble P si pour tous x 1 et x 2 de cet ensemble, tels que x 1 f(x 2) .

4. Extrêmes

Le point X max est appelé le point maximum de la fonction f (x) si pour tout x d'un certain voisinage X max , l'inégalité f (x) f (X max) est satisfaite.

La valeur Y max = f(X max) est appelée le maximum de cette fonction.

X max - point maximum
Max a un maximum

Le point X min est appelé point minimum de la fonction f (x) si pour tout x d'un voisinage X min, l'inégalité f (x) f (X min) est satisfaite.

La valeur de Y min = f(X min) est appelée le minimum de cette fonction.

X min - point minimum
Y min - minimum

X min , X max - points extrêmes
Y min , Y max - extrêmes.

5. Fonction zéros

Le zéro de la fonction y = f(x) est la valeur de l'argument x à laquelle la fonction s'annule : f(x) = 0.

X 1, X 2, X 3 sont des zéros de la fonction y = f(x).

Tâches et tests sur le thème "Propriétés de base d'une fonction"

Propriétés de la fonction - Fonctions numériques 9e année
Leçons : 2 Devoirs : 11 Tests : 1
Propriétés des logarithmes - Fonctions exponentielles et logarithmiques 11e année
Leçons : 2 Devoirs : 14 Tests : 1
Fonction racine carrée, ses propriétés et son graphique - Fonction racine carrée. Propriétés de la racine carrée 8e année
Leçons : 1 Devoirs : 9 Tests : 1
Fonctions puissance, leurs propriétés et graphiques - Degrés et racines. Fonctions de puissance 11e année
Leçons : 4 Devoirs : 14 Tests : 1
Les fonctions - Sujets importants pour répéter l'examen en mathématiques
Tâches : 24

Après avoir étudié ce sujet, vous devriez être en mesure de trouver le domaine de définition de diverses fonctions, de déterminer les intervalles de monotonie d'une fonction à l'aide de graphiques et d'examiner les fonctions paires et impaires. Considérez la solution de tels problèmes sur les exemples suivants.

Exemples.

1. Trouvez le domaine de la fonction.

La solution: la portée de la fonction est trouvée à partir de la condition

Le concept d'une fonction impaire et sa propriété. Fonctions élémentaires de base et leurs propriétés

Lire aussi

Comment construire correctement les axes de coordonnées ?

Graphiques et propriétés de base des fonctions élémentaires

Graphique de fonction quadratique, graphique de fonction cubique, graphique polynomial

Graphique de fonction

Graphique d'une fonction exponentielle

Graphique d'une fonction logarithmique

Graphiques de fonctions trigonométriques

Nous analysons les propriétés d'une fonction à l'aide d'un exemple

Tâches et tests sur le thème "Propriétés de base d'une fonction"