Ecuație cuadratică și teorema lui Pitagora. Istoria teoremei lui Pitagora

Potrivit lui van der Waerden, este foarte probabil ca raportul în vedere generala era cunoscut în Babilon deja în jurul secolului al XVIII-lea î.Hr. e.

Aproximativ 400 î.Hr. e., conform lui Proclu, Platon a dat o metodă de găsire a triplelor pitagoreice, combinând algebra și geometria. În jurul anului 300 î.Hr. e. în „Elementele” lui Euclid a apărut cea mai veche demonstrație axiomatică a teoremei lui Pitagora.

Cuvântare

Formularea principală conține operații algebrice - într-un triunghi dreptunghic, ale căror lungimi ale catetelor sunt egale a (\displaystyle a)Și b (\displaystyle b), iar lungimea ipotenuzei este c (\displaystyle c), relația este îndeplinită:

Este posibilă și o formulare geometrică echivalentă, recurgând la conceptul de zonă figura: într-un triunghi dreptunghic, aria pătratului construit pe ipotenuză este egală cu suma ariilor pătratelor construite pe catete. În această formă, teorema este formulată în Principia lui Euclid.

Teorema inversă a lui Pitagora- afirmația despre dreptunghiularea oricărui triunghi, ale cărui lungimi ale laturilor sunt legate prin relație a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). În consecință, pentru orice triplu de numere pozitive a (\displaystyle a), b (\displaystyle b)Și c (\displaystyle c), astfel încât a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), există un triunghi dreptunghic cu catete a (\displaystyle a)Și b (\displaystyle b) si ipotenuza c (\displaystyle c).

Dovada

În literatura științifică au fost înregistrate cel puțin 400 de dovezi ale teoremei lui Pitagora, ceea ce se explică atât prin valoarea fundamentală pentru geometrie, cât și prin caracterul elementar al rezultatului. Principalele direcții ale demonstrațiilor sunt: ​​utilizarea algebrică a rapoartelor elementelor triunghi (cum ar fi, de exemplu, metoda populară a similitudinii), metoda zonei, există și diverse dovezi exotice (de exemplu, folosind ecuatii diferentiale).

Prin triunghiuri asemănătoare

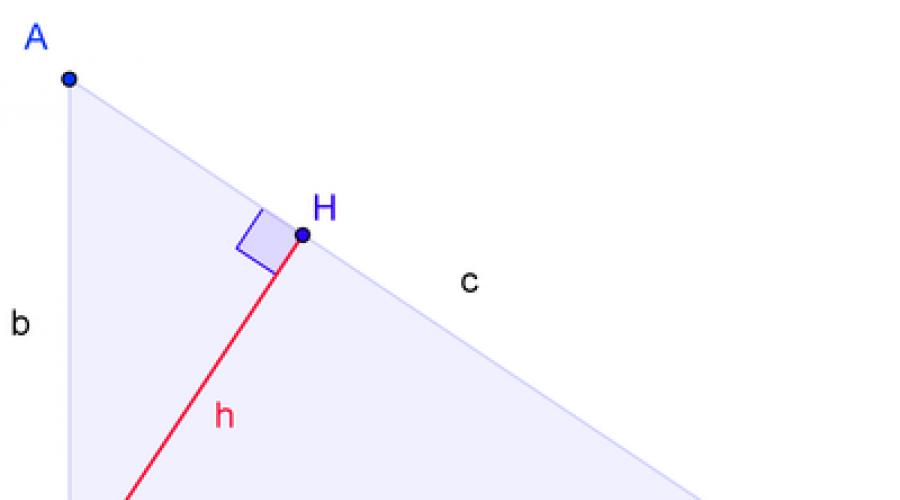
Demonstrația clasică a lui Euclid își propune să stabilească egalitatea ariilor dintre dreptunghiurile formate prin disecția pătratului de deasupra ipotenuzei cu înălțimea din unghiul drept cu pătratele de deasupra catetelor.

Construcția folosită pentru demonstrație este următoarea: pentru un triunghi dreptunghic cu unghi drept C (\displaystyle C), pătrate peste catete și și pătrate peste ipotenuză A B I K (\displaystyle ABIK) se construiește înălțimea CH H (\displaystyle CH)și fasciculul care o continuă s (\displaystyle s), împărțind pătratul de deasupra ipotenuzei în două dreptunghiuri și . Dovada are ca scop stabilirea egalității ariilor dreptunghiului A H J K (\displaystyle AHJK) cu un pătrat peste picior A C (\displaystyle AC); egalitatea ariilor celui de-al doilea dreptunghi, care este un pătrat deasupra ipotenuzei, și dreptunghiul de deasupra celuilalt catet se stabilește în mod similar.

Egalitatea ariilor unui dreptunghi A H J K (\displaystyle AHJK)Și A C E D (\displaystyle ACED) stabilit prin congruenţa triunghiurilor △ A C K ​​​​(\displaystyle \triangle ACK)Și △ A B D (\displaystyle \triunghi ABD), a căror suprafață este egală cu jumătate din suprafața pătratelor A H J K (\displaystyle AHJK)Și A C E D (\displaystyle ACED) respectiv, în legătură cu următoarea proprietate: aria unui triunghi este egală cu jumătate din aria unui dreptunghi dacă figurile au o latură comună, iar înălțimea triunghiului față de latura comună este cealaltă latură a dreptunghiul. Congruența triunghiurilor rezultă din egalitatea a două laturi (laturile pătratelor) și unghiul dintre ele (compus dintr-un unghi drept și un unghi la A (\displaystyle A).

Astfel, dovada stabilește că aria pătratului de deasupra ipotenuzei, compusă din dreptunghiuri A H J K (\displaystyle AHJK)Și B H J I (\displaystyle BHJI), este egală cu suma ariilor pătratelor de deasupra catetelor.

Dovada lui Leonardo da Vinci

Metoda zonei include și dovada găsită de Leonardo da Vinci. Să fie un triunghi dreptunghic △ A B C (\displaystyle \triunghi ABC) unghi drept C (\displaystyle C)și pătrate A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG)Și A B H J (\displaystyle ABHJ)(Vezi poza). În această dovadă în lateral H J (\displaystyle HJ) ultimul in afara se construiește un triunghi, congruent △ A B C (\displaystyle \triunghi ABC)în plus, reflectată atât în ​​raport cu ipotenuză, cât și în raport cu înălțimea acesteia (adică J I = B C (\displaystyle JI=BC)Și H I = A C (\displaystyle HI=AC)). Drept C I (\displaystyle CI)împarte pătratul construit pe ipotenuză în două părți egale, deoarece triunghiuri △ A B C (\displaystyle \triunghi ABC)Și △ J H I (\displaystyle \triunghi JHI) sunt egale în construcție. Demonstrarea stabilește congruența patrulaterelor C A J I (\displaystyle CAJI)Și D A B G (\displaystyle DABG), aria fiecăruia dintre ele, pe de o parte, este egală cu suma jumătate din ariile pătratelor de pe picioare și aria triunghiului inițial, pe de altă parte, cu jumătate din suprafața pătratul ipotenuzei plus aria triunghiului inițial. În total, jumătate din suma ariilor pătratelor peste catete este egală cu jumătate din aria pătratului peste ipotenuză, ceea ce este echivalent cu formularea geometrică a teoremei lui Pitagora.

Dovada prin metoda infinitezimală

Există mai multe dovezi folosind tehnica ecuațiilor diferențiale. În special, lui Hardy i se atribuie o dovadă folosind incremente infinitezimale ale piciorului a (\displaystyle a)Și b (\displaystyle b) si ipotenuza c (\displaystyle c), și păstrând asemănarea cu dreptunghiul inițial, adică asigurând îndeplinirea următoarelor relații diferențiale:

Prin metoda separării variabilelor, din acestea se derivă o ecuație diferențială c d c = a re a + b d b (\displaystyle c\ dc=a\,da+b\,db), a cărui integrare dă relația c 2 = a 2 + b 2 + C o n s t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). Aplicarea condițiilor inițiale a = b = c = 0 (\displaystyle a=b=c=0) definește o constantă ca 0, ceea ce are ca rezultat afirmarea teoremei.

Dependența pătratică în formula finală apare datorită proporționalității liniare dintre laturile triunghiului și incremente, în timp ce suma se datorează contribuțiilor independente din incrementul diferitelor catete.

Variații și generalizări

Forme geometrice similare pe trei laturi

O importantă generalizare geometrică a teoremei lui Pitagora a fost dată de Euclid în Elemente, trecând de la ariile pătratelor de pe laturi la ariile de similare arbitrare. forme geometrice: suma ariilor unor astfel de figuri construite pe picioare va fi egală cu aria unei figuri asemănătoare acestora, construită pe ipotenuză.

Ideea principală a acestei generalizări este că aria unei astfel de figuri geometrice este proporțională cu pătratul oricăreia dintre dimensiunile sale liniare și, în special, cu pătratul lungimii oricărei laturi. Prin urmare, pentru cifre similare cu zone A (\displaystyle A), B (\displaystyle B)Și C (\displaystyle C) construit pe picioare cu lungimi a (\displaystyle a)Și b (\displaystyle b) si ipotenuza c (\displaystyle c)în consecință, există o relație:

Deoarece conform teoremei lui Pitagora a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), atunci este gata.

În plus, dacă este posibil să se demonstreze fără a folosi teorema lui Pitagora că pentru Trei figuri geometrice asemănătoare pe laturile unui triunghi dreptunghic A + B = C (\displaystyle A+B=C), apoi folosind reversul dovezii generalizării lui Euclid, putem deriva demonstrația teoremei lui Pitagora. De exemplu, dacă pe ipotenuză construim un triunghi dreptunghic congruent cu cel inițial cu aria C (\displaystyle C), iar pe picioare - două asemănătoare cu el triunghi dreptunghic cu zone A (\displaystyle A)Și B (\displaystyle B), atunci se dovedește că triunghiurile de pe picioare sunt formate ca urmare a împărțirii triunghiului inițial la înălțimea sa, adică suma a două suprafețe mai mici ale triunghiurilor este egală cu aria celui de-al treilea, astfel A + B = C (\displaystyle A+B=C)și, aplicând relația pentru figuri similare, se derivă teorema lui Pitagora.

Teorema cosinusului

Teorema lui Pitagora este un caz special al teoremei cosinusului mai generală care raportează lungimile laturilor dintr-un triunghi arbitrar:

unde este unghiul dintre laturi a (\displaystyle a)Și b (\displaystyle b). Dacă unghiul este de 90°, atunci cos ⁡ θ = 0 (\displaystyle \cos \theta =0), iar formula se simplifică la teorema obișnuită a lui Pitagora.

Triunghi arbitrar

Există o generalizare a teoremei lui Pitagora la un triunghi arbitrar, care operează numai pe raportul lungimilor laturilor, se crede că a fost stabilită pentru prima dată de astronomul sabian Sabit ibn Kurra. În el, pentru un triunghi arbitrar cu laturi, un triunghi isoscel cu o bază pe latură c (\displaystyle c), vârful care coincide cu vârful triunghiului original, opus laturii c (\displaystyle c)și colțuri la bază, egal cu unghiul θ (\displaystyle \theta ) partea opusă c (\displaystyle c). Ca urmare, se formează două triunghiuri asemănătoare cu cel original: primul cu laturi a (\displaystyle a), latura laterală a triunghiului isoscel înscris departe de acesta și r (\displaystyle r)- părți laterale c (\displaystyle c); al doilea este simetric cu acesta din lateral b (\displaystyle b) cu o petrecere s (\displaystyle s)- partea relevantă a laturii c (\displaystyle c). Ca urmare, relația este îndeplinită:

care degenerează în teorema lui Pitagora la θ = π / 2 (\displaystyle \theta =\pi /2). Raportul este o consecință a asemănării triunghiurilor formate:

Teorema zonei Pappus

Geometrie non-euclidiană

Teorema lui Pitagora este derivată din axiomele geometriei euclidiene și este invalidă pentru geometria non-euclidiană - îndeplinirea teoremei lui Pitagora este echivalentă cu postulatul paralelismului euclidian.

În geometria non-euclidiană, relația dintre laturile unui triunghi dreptunghic va fi în mod necesar într-o formă diferită de teorema lui Pitagora. De exemplu, în geometria sferică, toate cele trei laturi ale unui triunghi dreptunghic, care delimitează octantul sferei unității, au lungime π / 2 (\displaystyle \pi /2), care contrazice teorema lui Pitagora.

Mai mult, teorema lui Pitagora este valabilă în geometria hiperbolică și eliptică, dacă cerința ca triunghiul să fie dreptunghiular este înlocuită cu condiția ca suma a două unghiuri ale triunghiului să fie egală cu al treilea.

geometrie sferică

Pentru orice triunghi dreptunghic pe o sferă cu rază R (\displaystyle R)(de exemplu, dacă unghiul din triunghi este drept) cu laturile a , b , c (\displaystyle a,b,c) relația dintre părți este:

Această egalitate poate fi derivată ca un caz special al teoremei cosinusului sferic, care este valabilă pentru toate triunghiurile sferice:

Unde ch (\displaystyle \operatorname (ch) )- cosinus hiperbolic. Această formulă este un caz special al teoremei cosinusului hiperbolic, care este valabilă pentru toate triunghiurile:

Unde γ (\displaystyle \gamma )- un unghi al cărui vârf este opus unei laturi c (\displaystyle c).

Folosind seria Taylor pentru cosinusul hiperbolic ( ch ⁡ x ≈ 1 + x 2 / 2 (\displaystyle \operatorname (ch) x\aprox 1+x^(2)/2)) se poate arăta că dacă triunghiul hiperbolic scade (adică când a (\displaystyle a), b (\displaystyle b)Și c (\displaystyle c) tind spre zero), atunci relațiile hiperbolice dintr-un triunghi dreptunghic se apropie de relația teoremei lui Pitagora clasice.

Aplicație

Distanța în sisteme dreptunghiulare bidimensionale

Cea mai importantă aplicație a teoremei lui Pitagora este determinarea distanței dintre două puncte dintr-un sistem de coordonate dreptunghiular: distanța s (\displaystyle s)între punctele cu coordonate (a, b) (\displaystyle (a,b))Și (c, d) (\displaystyle (c,d)) este egal cu:

Pentru numere complexe teorema lui Pitagora oferă o formulă naturală pentru găsirea numărului complex modul - pt. z = x + y i (\displaystyle z=x+yi) este egal cu lungimea

teorema lui Pitagora: Suma ariilor pătratelor susținute de picioare ( AȘi b), este egală cu aria pătratului construit pe ipotenuză ( c).

Formulare geometrică:

Teorema a fost formulată inițial în felul următor:

Formulare algebrică:

Adică indicând lungimea ipotenuzei triunghiului prin c, iar lungimile picioarelor prin AȘi b :

Ambele formulări ale teoremei sunt echivalente, dar a doua formulare este mai elementară, nu necesită conceptul de zonă. Adică, a doua afirmație poate fi verificată fără a ști nimic despre zonă și măsurând doar lungimile laturilor unui triunghi dreptunghic.

Teorema inversă a lui Pitagora:

Dovada

Pe acest moment 367 de dovezi ale acestei teoreme sunt consemnate în literatura științifică. Probabil, teorema lui Pitagora este singura teoremă cu un număr atât de impresionant de demonstrații. O astfel de varietate poate fi explicată doar prin semnificația fundamentală a teoremei pentru geometrie.

Desigur, din punct de vedere conceptual, toate pot fi împărțite într-un număr mic de clase. Cele mai cunoscute dintre ele: dovezi prin metoda zonei, dovezi axiomatice și exotice (de exemplu, folosind ecuații diferențiale).

Prin triunghiuri asemănătoare

Următoarea demonstrație a formulării algebrice este cea mai simplă dintre dovezile construite direct din axiome. În special, nu folosește conceptul de zonă a figurii.

Lăsa ABC există un triunghi dreptunghic C. Să desenăm o înălțime de la Cși notează-i baza prin H. Triunghi ACH asemănător cu un triunghi ABC la două colţuri. La fel, triunghiul CBH asemănătoare ABC. Introducerea notației

primim

Ce este echivalent

Adăugând, primim

Dovezi de zonă

Următoarele dovezi, în ciuda aparentei lor simplități, nu sunt deloc atât de simple. Toate folosesc proprietățile zonei, a cărei demonstrație este mai complicată decât demonstrarea teoremei lui Pitagora în sine.

Dovada prin echivalență

1. Aranjați patru triunghiuri dreptunghiulare egale așa cum se arată în figura 1.
2. Cadrilater cu laturi c este un pătrat deoarece suma a doi colțuri ascuțite 90° și unghiul drept este de 180°.
3. Aria întregii figuri este egală, pe de o parte, cu aria unui pătrat cu o latură (a + b), iar pe de altă parte, suma ariilor a patru triunghiuri și două interioare pătrate.

Q.E.D.

Dovezi prin echivalență

O dovadă elegantă a permutării

Un exemplu de una dintre aceste dovezi este prezentat în desenul din dreapta, unde pătratul construit pe ipotenuză este convertit prin permutare în două pătrate construite pe catete.

Dovada lui Euclid

Desen pentru demonstrația lui Euclid

Ilustrație pentru demonstrația lui Euclid

Ideea demonstrației lui Euclid este următoarea: să încercăm să demonstrăm că jumătate din aria pătratului construit pe ipotenuză este egală cu suma jumătăților ariilor pătratelor construite pe catete și apoi ariile lui pătratele mari și cele două pătrate mici sunt egale.

Luați în considerare desenul din stânga. Am construit pe el pătrate pe laturile unui triunghi dreptunghic și am desenat o rază s din vârful unghiului drept C perpendicular pe ipotenuza AB, ea taie pătratul ABIK, construit pe ipotenuză, în două dreptunghiuri - BHJI și HAKJ , respectiv. Se pare că ariile acestor dreptunghiuri sunt exact egale cu ariile pătratelor construite pe picioarele corespunzătoare.

Să încercăm să demonstrăm că aria pătratului DECA este egală cu aria dreptunghiului AHJK Pentru a face acest lucru, folosim o observație auxiliară: aria unui triunghi cu aceeași înălțime și bază ca și cea dată. dreptunghiul este egal cu jumătate din aria dreptunghiului dat. Aceasta este o consecință a definirii ariei unui triunghi ca jumătate din produsul bazei și înălțimii. Din această observație rezultă că aria triunghiului ACK este egală cu aria triunghiului AHK (neprezentată), care, la rândul său, este egală cu jumătate din aria dreptunghiului AHJK.

Să demonstrăm acum că aria triunghiului ACK este, de asemenea, egală cu jumătate din aria pătratului DECA. Singurul lucru care trebuie făcut pentru aceasta este să demonstrați egalitatea triunghiurilor ACK și BDA (deoarece aria triunghiului BDA este egală cu jumătate din aria pătratului cu proprietatea de mai sus). Această egalitate este evidentă, triunghiurile sunt egale în două laturi și unghiul dintre ele. Și anume - AB=AK,AD=AC - egalitatea unghiurilor CAK și BAD este ușor de demonstrat prin metoda mișcării: să rotim triunghiul CAK cu 90 ° în sens invers acelor de ceasornic, atunci este evident că laturile corespunzătoare ale celor două triunghiuri luate în considerare vor coincid (datorită faptului că unghiul la vârful pătratului este de 90°).

Argumentul despre egalitatea ariilor pătratului BCFG și dreptunghiului BHJI este complet analog.

Astfel, am demonstrat că aria pătratului construit pe ipotenuză este suma ariilor pătratelor construite pe catete. Ideea din spatele acestei dovezi este ilustrată în continuare cu animația de mai sus.

Dovada lui Leonardo da Vinci

Dovada lui Leonardo da Vinci

Elementele principale ale demonstrației sunt simetria și mișcarea.

Luați în considerare desenul, așa cum se poate vedea din simetrie, segmentul Ceu disecă pătratul ABHJ în două părți identice (deoarece triunghiuri ABCȘi JHeu sunt egale în construcție). Folosind o rotație de 90 de grade în sens invers acelor de ceasornic, vedem egalitatea figurilor umbrite CAJeu Și GDAB . Acum este clar că aria figurii umbrite de noi este egală cu suma a jumătate din suprafețele pătratelor construite pe picioare și aria triunghiului original. Pe de altă parte, este egal cu jumătate din aria pătratului construit pe ipotenuză, plus aria triunghiului original. Ultimul pas în demonstrație este lăsat cititorului.

Dovada prin metoda infinitezimală

Următoarea demonstrație folosind ecuații diferențiale este adesea atribuită celebrului matematician englez Hardy, care a trăit în prima jumătate a secolului al XX-lea.

Luând în considerare desenul prezentat în figură și observând schimbarea laturii A, putem scrie următoarea relație pentru incremente infinitezimale CuȘi A(folosind triunghiuri similare):

Dovada prin metoda infinitezimală

Folosind metoda separării variabilelor, găsim

O expresie mai generală pentru modificarea ipotenuzei în cazul creșterilor ambelor catete

Integrarea ecuația datăși folosind condițiile inițiale, obținem

Astfel, ajungem la răspunsul dorit

După cum este ușor de observat, dependența pătratică în formula finală apare datorită proporționalității liniare dintre laturile triunghiului și incremente, în timp ce suma se datorează contribuțiilor independente din incrementul diferitelor catete.

O dovadă mai simplă poate fi obținută dacă presupunem că unul dintre picioare nu experimentează o creștere (în acest caz, piciorul b). Apoi pentru constanta de integrare obținem

Variații și generalizări

• Dacă, în loc de pătrate, alte figuri similare sunt construite pe picioare, atunci următoarea generalizare a teoremei lui Pitagora este adevărată: Într-un triunghi dreptunghic, suma ariilor figurilor similare construite pe catete este egală cu aria figurii construite pe ipotenuză.În special:
  • Suma ariilor triunghiurilor regulate construite pe catete este egală cu aria unui triunghi regulat construit pe ipotenuză.
  • Suma ariilor semicercurilor construite pe picioare (ca și pe diametru) este egală cu aria semicercului construit pe ipotenuză. Acest exemplu este folosit pentru a demonstra proprietățile figurilor delimitate de arce de două cercuri și care poartă denumirea de lunula hipocratică.

Poveste

Chu-pei 500–200 î.Hr. În stânga este inscripția: suma pătratelor lungimii înălțimii și baza este pătratul lungimii ipotenuzei.

Vechea carte chineză despre care vorbește Chu-pei Triunghiul lui Pitagora cu fețele 3, 4 și 5: În aceeași carte este propus un desen care coincide cu unul dintre desenele geometriei hinduse a lui Bashara.

Kantor (cel mai mare istoric german al matematicii) crede că egalitatea 3² + 4² = 5² era deja cunoscută egiptenilor în jurul anului 2300 î.Hr. e., pe vremea regelui Amenemhet I (conform papirusului 6619 al Muzeului din Berlin). Potrivit lui Cantor, harpedonapții, sau „stringers”, construiau unghiuri drepte folosind triunghiuri dreptunghiulare cu laturile 3, 4 și 5.

Este foarte ușor să reproduci metoda lor de construcție. Luați o frânghie de 12 m lungime și legați-o de ea de-a lungul unei benzi colorate la o distanță de 3 m. de la un capăt și la 4 metri de celălalt. Un unghi drept va fi închis între laturile de 3 și 4 metri lungime. S-ar putea obiecta Harpedonapților că modul lor de a construi devine de prisos dacă se folosește, de exemplu, pătratul de lemn folosit de toți dulgherii. Într-adevăr, se cunosc desene egiptene în care se găsește un astfel de instrument, de exemplu, desene care înfățișează un atelier de tâmplărie.

Se cunosc ceva mai multe despre teorema lui Pitagora la babilonieni. Într-un text datând din timpul lui Hammurabi, adică din anul 2000 î.Hr. e., se dă un calcul aproximativ al ipotenuzei unui triunghi dreptunghic. Din aceasta putem concluziona că în Mesopotamia au fost capabili să efectueze calcule cu triunghiuri dreptunghiulare, cel puțin în unele cazuri. Bazându-se, pe de o parte, pe nivelul actual de cunoaștere a matematicii egiptene și babiloniene, iar pe de altă parte, pe un studiu critic al surselor grecești, Van der Waerden (un matematician olandez) a concluzionat următoarele:

Literatură

In rusa

• Skopets Z. A. Miniaturi geometrice. M., 1990
• Yelensky Sh. Pe urmele lui Pitagora. M., 1961
• Van der Waerden B.L. Trezirea Științei. Matematică Egiptul antic, Babilonul și Grecia. M., 1959
• Glazer G.I. Istoria matematicii la scoala. M., 1982
• W. Litzman, „Teorema lui Pitagora” M., 1960.
  • Un site despre teorema lui Pitagora cu un număr mare de dovezi, materialul este preluat din cartea lui V. Litzman, număr mare desenele sunt prezentate ca fișiere grafice separate.
• Teorema lui Pitagora și capitolul triplelor lui Pitagora din cartea lui D. V. Anosov „O privire asupra matematicii și ceva din ea”
• Despre teorema lui Pitagora și metodele demonstrației sale G. Glaser, academician al Academiei Ruse de Educație, Moscova

În limba engleză

• Teorema lui Pitagora la WolframMathWorld
• Cut-The-Knot, secțiune despre teorema lui Pitagora, aproximativ 70 de dovezi și informații suplimentare extinse (ing.)

Fundația Wikimedia. 2010 .

Pitagora este un om de știință grec care a trăit acum aproximativ 2500 de ani (564-473 î.Hr.).

Să fie dat un triunghi dreptunghic ale cărui laturi A, bȘi Cu(Fig. 267).

Să construim pătrate pe laturile sale. Suprafețele acestor pătrate sunt, respectiv A 2 , b 2 și Cu 2. Să demonstrăm asta Cu 2 = a 2 +b 2 .

Să construim două pătrate MKOR și M'K'O'R' (Fig. 268, 269), luând pentru latura fiecăruia dintre ele un segment egal cu suma catetelor triunghiului dreptunghic ABC.

După finalizarea construcțiilor prezentate în figurile 268 și 269 în aceste pătrate, vom vedea că pătratul MKOR este împărțit în două pătrate cu zone A 2 și b 2 și patru triunghiuri dreptunghiulare egale, fiecare dintre ele egal cu triunghiul dreptunghic ABC. Pătratul M'K'O'R' este împărțit într-un patrulater (este umbrit în Figura 269) și patru triunghiuri dreptunghiulare, fiecare dintre ele egal cu triunghiul ABC. Patrulaterul umbrit este un pătrat, deoarece laturile sale sunt egale (fiecare este egală cu ipotenuza triunghiului ABC, adică. Cu), iar unghiurile sunt drepte ∠1 + ∠2 = 90°, de unde ∠3 = 90°).

Astfel, suma ariilor pătratelor construite pe picioare (în Figura 268 aceste pătrate sunt umbrite) este egală cu aria pătratului MKOR fără suma ariilor a patru triunghiuri egale și aria lui ​pătratul construit pe ipotenuză (în Figura 269 acest pătrat este și umbrit) este egal cu aria pătratului M'K'O'R', egal cu pătratul lui MKOR, fără suma ariilor lui patru triunghiuri asemănătoare. Prin urmare, aria pătratului construit pe ipotenuza unui triunghi dreptunghic este egală cu suma ariilor pătratelor construite pe catete.

Primim formula Cu 2 = a 2 +b 2, unde Cu- ipotenuza, AȘi b- catetele unui triunghi dreptunghic.

Teorema lui Pitagora poate fi rezumată după cum urmează:

Pătratul ipotenuzei unui triunghi dreptunghic este egal cu suma pătratelor catetelor.

Din formula Cu 2 = a 2 +b 2 puteți obține următoarele formule:

A 2 = Cu 2 - b 2 ;

b 2 = Cu 2 - A 2 .

Aceste formule pot fi folosite pentru a găsi latura necunoscută a unui triunghi dreptunghic având în vedere două dintre laturile sale.

De exemplu:

a) dacă sunt date picioare A= 4 cm, b\u003d 3 cm, atunci puteți găsi ipotenuza ( Cu):

Cu 2 = a 2 +b 2, adică Cu 2 = 4 2 + 3 2 ; cu 2 = 25, de unde Cu= √25 = 5(cm);

b) dacă este dată ipotenuza Cu= 17 cm și picior A= 8 cm, apoi puteți găsi un alt picior ( b):

b 2 = Cu 2 - A 2, adică b 2 = 17 2 - 8 2 ; b 2 = 225, de unde b= √225 = 15 (cm).

Corolar: Dacă în două triunghiuri dreptunghice ABC și A 1 B 1 C 1 ipotenuza CuȘi Cu 1 sunt egale, iar piciorul b triunghiul ABC este mai mare decât catetul b 1 triunghi A 1 B 1 C 1,

apoi piciorul A triunghiul ABC este mai mic decât catetul A 1 triunghi A 1 B 1 C 1 .

Într-adevăr, pe baza teoremei lui Pitagora, obținem:

A 2 = Cu 2 - b 2 ,

A 1 2 = Cu 1 2 - b 1 2

În formulele scrise, minuendurile sunt egale, iar subtraendul din prima formulă este mai mare decât subtrahendul din a doua formulă, prin urmare, prima diferență mai puțin de o secundă,

adică A 2 a 1 2 . Unde A a 1 .

Textul lucrării este plasat fără imagini și formule.
Versiunea completă a lucrării este disponibilă în fila „Fișiere de locuri de muncă” în format PDF

Introducere

La cursul școlar de geometrie, folosind teorema lui Pitagora, se rezolvă doar probleme de matematică. Din păcate, problema aplicării practice a teoremei lui Pitagora nu este luată în considerare.

În acest sens, scopul lucrării mele a fost acela de a afla domeniul de aplicare al teoremei lui Pitagora.

În prezent, este general recunoscut că succesul dezvoltării multor domenii ale științei și tehnologiei depinde de dezvoltarea diferitelor domenii ale matematicii. O condiție importantăîmbunătățirea eficienței producției este introducerea pe scară largă metode matematiceîn tehnologie şi economie nationala care presupune crearea de noi metode eficiente cercetări calitative și cantitative, care ne permit să rezolvăm problemele prezentate de practică.

Voi lua în considerare exemple de aplicare practică a teoremei lui Pitagora. Nu voi încerca să dau toate exemplele de utilizare a teoremei - cu greu ar fi posibil. Aria de aplicare a teoremei este destul de extinsă și, în general, nu poate fi indicată cu suficientă completitate.

Ipoteză:

Folosind teorema lui Pitagora, puteți rezolva nu numai probleme matematice.

Conform cu aceasta muncă de cercetare se definește următorul scop:

Aflați domeniul de aplicare al teoremei lui Pitagora.

Pe baza obiectivului de mai sus, au fost identificate următoarele sarcini:

Colectați informații despre aplicarea practică a teoremei lui Pitagora în diverse surseși determinați domeniul de aplicare al teoremei.

Aflați câteva informații istorice despre Pitagora și teorema sa.

Arată aplicarea teoremei în rezolvarea problemelor istorice.

Procesați datele colectate pe subiect.

Am fost implicat în căutarea și colectarea de informații - am studiat materiale tipărite, am lucrat cu materiale pe Internet și am procesat datele colectate.

Metodologia de cercetare:

Studiul materialului teoretic.

Studiul metodelor de cercetare.

Implementare practică cercetare.

Comunicativ (metoda de măsurare, chestionare).

Tip proiect: cercetarea informaţiei. Lucrarea a fost făcută în timpul meu liber.

Despre Pitagora.

Pitagora este un filozof, matematician și astronom grec antic. Fundamentate multe proprietăți ale formelor geometrice, dezvoltate teorie matematică numerele și proporțiile acestora. El a adus o contribuție semnificativă la dezvoltarea astronomiei și acusticii. Autor al „Versurilor de aur”, fondator al școlii pitagoreice din Croton.

Potrivit legendei, Pitagora s-a născut în jurul anului 580 î.Hr. e. pe insula Samos într-o familie bogată de negustori. Mama lui, Pythasis, și-a primit numele în onoarea Pythiei, preoteasa lui Apollo. Pythia a prezis lui Mnesarchus și soției sale nașterea unui fiu, fiul fiind numit și după Pythia. Potrivit multor mărturii străvechi, băiatul era fabulos de frumos și și-a arătat curând abilitățile remarcabile. Primele cunoștințe le-a primit de la tatăl său Mnesarchus, un bijutier, sculptor pietre pretioase care a visat că fiul său va deveni succesorul operei sale. Dar viața a judecat altfel. Viitorul filozof a dat dovadă de o mare aptitudine pentru științe. Printre profesorii lui Pitagora s-au numărat Pherekides din Syros și bătrânul Germodamant. Primul a insuflat băiatului dragostea pentru știință, iar al doilea pentru muzică, pictură și poezie. Ulterior, Pitagora s-a întâlnit filosof celebru- matematicianul Thales din Milet și, la sfatul lui, a plecat în Egipt - centrul științificului și activitati de cercetare. După ce a trăit 22 de ani în Egipt și 12 ani în Babilon, s-a întors pe insula Samos, apoi a părăsit-o din motive necunoscute și s-a mutat în orașul Croton, din sudul Italiei. Aici a creat școala (uniunea) pitagoreică, care a studiat diverse probleme de filozofie și matematică. La vârsta de aproximativ 60 de ani, Pitagora s-a căsătorit cu Theano, unul dintre elevii săi. Au trei copii și toți devin urmași ai tatălui lor. Condițiile istorice ale vremii sunt caracterizate de o mișcare largă a demosului împotriva puterii aristocraților. Fugând de valurile furiei populare, Pitagora și studenții săi s-au mutat în orașul Tarentum. Potrivit unei versiuni: Kilon, un om bogat și rău, a venit la el, dorind să se alăture frăției în stare de ebrietate. După ce a fost refuzat, Cylon a început o luptă cu Pitagora. În timpul incendiului, elevii pe cheltuiala lor au salvat viața profesorului. Pitagora a devenit dor de casă și în curând s-a sinucis.

Trebuie remarcat faptul că aceasta este una dintre variantele biografiei sale. Datele exacte ale nașterii și morții sale nu au fost stabilite, multe fapte din viața lui sunt contradictorii. Dar un lucru este clar: acest om a trăit și a lăsat urmașilor săi o mare moștenire filozofică și matematică.

Teorema lui Pitagora.

Teorema lui Pitagora este cea mai importantă afirmație a geometriei. Teorema se formulează astfel: aria unui pătrat construit pe ipotenuza unui triunghi dreptunghic este egală cu suma ariilor pătratelor construite pe catetele sale.

Descoperirea acestei afirmații este atribuită lui Pitagora din Samos (secolul XII î.Hr.)

Studiul tăblițelor cuneiforme babiloniene și al manuscriselor chinezești antice (copii ale manuscriselor chiar mai vechi) a arătat că celebra teoremă era cunoscută cu mult înaintea lui Pitagora, poate cu câteva milenii înaintea lui.

(Dar există o presupunere că Pitagora i-a dat o dovadă completă)

Dar există o altă părere: în școala pitagoreică era un obicei minunat să-i atribuie lui Pitagora toate meritele și oarecum să nu-și însuşească gloria descoperitorilor, decât poate în câteva cazuri.

(Iamblichus-scriitor siriac vorbitor de greacă, autor al tratatului „Viața lui Pitagora.” (secolul II d.Hr.)

Deci istoricul german de matematică Kantor crede că egalitatea 3 2 + 4 2= 5 2 a fost

cunoscută egiptenilor în jurul anului 2300 î.Hr. e. pe vremea regelui Amenechmet (conform papirusului 6619 al Muzeului din Berlin). Unii cred că Pitagora a dat teoremei o dovadă completă, în timp ce alții îi neagă acest merit.

Unii îi atribuie lui Pitagora dovada dată de Euclid în Elementele sale. Pe de altă parte, Proclus (matematician, secolul al V-lea) susține că proba din „Principii” i-a aparținut lui Euclid însuși, adică istoria matematicii nu are aproape date sigure despre activitatea matematică a lui Pitagora. În matematică, poate, nu există altă teoremă care să merite tot felul de comparații.

În unele liste ale „Începuturilor” lui Euclid, această teoremă a fost numită „teorema nimfei” pentru asemănarea desenului cu o albină, fluture („teorema fluturelui”), care în greacă era numită nimfă. Grecii au numit acest cuvânt și alte zeițe, precum și tinere și mirese. Traducătorul arabă nu a acordat atenție desenului și a tradus cuvântul „nimfă” ca „mireasă”. Așa a apărut numele afectuos „teorema miresei”. Există o legendă că atunci când Pitagora din Samos și-a dovedit teorema, el a mulțumit zeilor sacrificând 100 de tauri. De aici un alt nume - „teorema unei sute de tauri”.

În țările vorbitoare de engleză, se numea: „ moara de vant”, „coada de păun”, „scaunul miresei”, „podul măgarului” (dacă elevul nu putea „trece” prin ea, atunci era un adevărat „măgar”)

În Rusia prerevoluționară, desenul teoremei lui Pitagora pentru cazul unui triunghi isoscel a fost numit „pantaloni pitagoreici”.

Acești „pantaloni” apar atunci când, pe fiecare parte a unui triunghi dreptunghic, construiesc pătrate spre exterior.

Câte dovezi diferite ale teoremei lui Pitagora există?

Din vremea lui Pitagora au apărut peste 350. Teorema a fost inclusă în Cartea Recordurilor Guinness. Dacă analizăm dovezile teoremei, atunci în principiu diverse idei putin se foloseste in ele.

Domenii de aplicare a teoremei.

Este utilizat pe scară largă în rezolvare geometric sarcini.

Cu ajutorul acestuia puteți găsi geometric valorile rădăcinilor pătrate ale numerelor întregi:

Pentru a face acest lucru, construim un triunghi dreptunghic AOB (unghiul A este de 90 °) cu catete unități. Atunci ipotenuza sa este √2. Apoi construim un singur segment BC, BC este perpendicular pe OB, lungimea ipotenuzei OS=√3 etc.

(această metodă se găsește la Euclid și F. Kirensky).

Sarcini în curs fizică liceul necesită cunoașterea teoremei lui Pitagora.

Acestea sunt sarcini legate de adăugarea vitezelor.

Atenție la diapozitiv: o sarcină dintr-un manual de fizică de clasa a IX-a. ÎN sens practic poate fi formulat astfel: în ce unghi față de curgerea râului ar trebui să se deplaseze o ambarcațiune care transportă pasageri între debarcadere pentru a respecta programul? (digurile sunt situate pe malurile opuse ale râului)

Când un biatlet trage la o țintă, el face o „corecție de vânt”. Dacă vântul bate din dreapta, iar sportivul trage în linie dreaptă, atunci glonțul va merge spre stânga. Pentru a lovi ținta, trebuie să mutați vizorul spre dreapta cu distanța de deplasare a glonțului. Pentru ei au fost întocmite tabele speciale (pe baza consecințelor tovarășului Pitagora). Biatletul știe în ce unghi să schimbe vederea la o viteză cunoscută a vântului.

Astronomie - de asemenea, o zonă largă de aplicare a teoremei calea fasciculului de lumină. Figura arată traseul unui fascicul de lumină de la A la B și înapoi. Calea fasciculului este afișată cu o săgeată curbă pentru claritate, de fapt, fasciculul de lumină este drept.

Care este calea fasciculului? Lumina se deplasează înainte și înapoi în același mod. Care este jumătate din drumul pe care îl parcurge raza? Dacă marcam segmentul AB simbol l, jumătate din timp ca t, și, de asemenea, indicând viteza luminii prin literă c, atunci ecuația noastră va lua forma

c*t=l

Acesta este produsul timpului petrecut cu viteza!

Acum să încercăm să privim același fenomen dintr-un alt cadru de referință, de exemplu, de la o navă spațială care zboară pe lângă un fascicul care călătorește cu o viteză v. Cu o astfel de observație, vitezele tuturor corpurilor se vor schimba, iar corpurile staționare vor începe să se miște cu o viteză. vîn sens invers. Să presupunem că nava se mișcă spre stânga. Apoi cele două puncte între care aleargă iepurașul se vor deplasa spre dreapta cu aceeași viteză. Mai mult, în timp ce iepurașul își aleargă drumul, punctul de plecare A se deplasează și fasciculul revine la un nou punct C.

Întrebare: cât timp se va mișca punctul (pentru a se transforma în punctul C) în timp ce se deplasează fasciculul de lumină? Mai precis: cu ce este egală jumătate din această compensare? Dacă notăm jumătate din timpul de călătorie al fasciculului cu literă t", și jumătate din distanță AC scrisoare d, atunci obținem ecuația noastră sub forma:

v * t" = d

scrisoare v indică viteza navei spațiale.

O altă întrebare: ce cale va parcurge raza de lumină în acest caz?(Mai precis, care este jumătate din această cale? Care este distanța până la obiectul necunoscut?)

Dacă notăm jumătate din lungimea căii luminii cu litera s, atunci obținem ecuația:

c * t" = s

Aici c este viteza luminii și t" este același timp cu cel discutat mai sus.

Acum luați în considerare triunghiul ABC. Este un triunghi isoscel a cărui înălțime este l, pe care l-am introdus atunci când luăm în considerare procesul dintr-un punct de vedere fix. Deoarece mișcarea este perpendiculară l, atunci nu putea să o afecteze.

Triunghi ABC compus din două jumătăți - triunghiuri dreptunghiulare identice, ale căror ipotenuze ABȘi î.Hr trebuie conectat cu picioarele conform teoremei lui Pitagora. Unul dintre picioare este d, pe care tocmai l-am calculat, iar al doilea picior este s, prin care trece lumina și pe care l-am calculat și noi. Obținem ecuația:

s 2 = l 2 +d 2

Aceasta este teorema lui Pitagora!

Fenomen aberație stelară, descoperit în 1729, constă în faptul că toate stelele pe sfera celestiala descrie elipsele. Semi-axa majoră a acestor elipse este observată de pe Pământ la un unghi de 20,5 grade. Acest unghi este asociat cu mișcarea Pământului în jurul Soarelui cu o viteză de 29,8 km pe oră. Pentru a observa o stea de pe un Pământ în mișcare, este necesar să înclinați tubul telescopului înainte de-a lungul mișcării stelei, deoarece în timp ce lumina străbate lungimea telescopului, ocularul se deplasează înainte împreună cu pământul. Adunarea vitezelor luminii și a Pământului se face vectorial, folosind așa-numitele.

Pitagora. U 2 \u003d C 2 + V 2

C este viteza luminii

Viteza la sol în V

tubul telescopului

La sfârșitul secolului al XIX-lea, s-au făcut diverse presupuneri cu privire la existența unor locuitori de pe Marte asemănători oamenilor, acesta a fost rezultatul descoperirilor astronomului italian Schiaparelli (a deschis canale pe Marte care au fost considerate artificiale multă vreme) . Desigur, întrebarea dacă este posibil să comunici cu aceste creaturi ipotetice cu ajutorul semnalelor luminoase a provocat o discuție plină de viață. Academia de Științe din Paris a stabilit chiar un premiu de 100.000 de franci pentru prima persoană care a stabilit contact cu vreun locuitor al altui corp ceresc; acest premiu îl așteaptă încă pe norocos. Ca o glumă, deși nu complet nerezonabilă, s-a decis să se trimită un semnal locuitorilor de pe Marte sub forma teoremei lui Pitagora.

Nu se știe cum să facă asta; dar este evident pentru toată lumea că faptul matematic exprimat de teorema lui Pitagora are loc peste tot și, prin urmare, locuitorii unei alte lumi ca noi ar trebui să înțeleagă un astfel de semnal.

conexiune mobilă

Cine în lumea de astăzi nu folosește un telefon mobil? Fiecare abonat mobil este interesat de calitatea acestuia. Iar calitatea, la rândul ei, depinde de înălțimea antenei operatorului de telefonie mobilă. Pentru a calcula în ce rază poate fi recepționată o transmisie, folosim teorema lui Pitagora.

Ce cea mai mare altitudine trebuie sa aiba o antena de operator de telefonie mobila astfel incat transmisia sa poata fi primita pe o raza de R = 200 km? (Raza Pământului este de 6380 km.)

Soluţie:

Lăsa AB= x , BC=R=200 km , OC= r = 6380 km.

OB=OA+ABOB=r+x.

Folosind teorema lui Pitagora, obținem Raspuns: 2,3 km.

Când construiți case și cabane, apare adesea întrebarea cu privire la lungimea căpriorii pentru acoperiș, dacă grinzile au fost deja făcute. De exemplu: se intenționează construirea unui acoperiș în două frontoane într-o casă (formă secțională). Ce lungime ar trebui să aibă căpriorii dacă grinzile sunt realizate AC=8 m. și AB=BF.

Soluţie:

Triunghiul ADC este isoscel AB=BC=4 m., BF=4 m. Dacă presupunem că FD=1,5 m., atunci:

A) Din triunghiul DBC: DB=2,5 m.

B) Din triunghiul ABF:

Fereastră

În clădiri Stil gotic și romanic părțile superioare ale ferestrelor sunt împărțite de nervuri de piatră, care nu numai că joacă rolul unui ornament, dar contribuie și la rezistența ferestrelor. Figura prezintă un exemplu simplu de astfel de fereastră în stil gotic. Metoda de construire este foarte simplă: din figură este ușor să găsiți centrele a șase arce de cerc, ale căror raze sunt egale cu

lăţimea ferestrei (b) pentru arcade exterioare

jumătate de lățime, (b/2) pentru arcuri interne

Există încă un cerc complet care atinge cele patru arce. Deoarece este închis între două cercuri concentrice, diametrul său este egal cu distanța dintre aceste cercuri, adică b / 2 și, prin urmare, raza este egală cu b / 4. Și atunci devine clar

poziţia centrului său.

ÎN Arhitectura romanica motivul prezentat în figură este adesea găsit. Dacă b tot desemnează lățimea ferestrei, atunci razele semicercurilor vor fi egale cu R = b / 2 și r = b / 4. Raza p a cercului interior poate fi calculată din triunghiul dreptunghic prezentat în fig. linie punctata. Ipotenuza acestui triunghi, care trece prin punctul tangent al cercurilor, este egală cu b/4+p, un catet este egal cu b/4, iar celălalt este b/2-p. După teorema lui Pitagora avem:

(b/4+p) 2 =(b/4) 2 +(b/4-p) 2

b 2 /16+ bp / 2 + p 2 \u003d b 2 / 16 + b 2 / 4 - bp / 2 + p 2,

Împărțind cu b și aducând termeni similari, obținem:

(3/2)p=b/4, p=b/6.

În industria forestieră: pentru nevoile de construcție, buștenii sunt tăiați în cherestea, în timp ce sarcina principală este de a obține cât mai puține deșeuri. Cea mai mică cantitate de deșeuri va fi atunci când fasciculul are cel mai mare volum. Ce ar trebui să fie în secțiune? După cum se poate vedea din soluție, secțiunea transversală trebuie să fie pătrată și teorema lui Pitagora iar alte considerente permit tragerea unei asemenea concluzii.

Bar cu cel mai mare volum

Sarcină

Dintr-un buștean cilindric este necesar să tăiați un fascicul dreptunghiular de cel mai mare volum. Ce formă ar trebui să aibă secțiunea sa transversală (Fig. 23)?

Soluţie

Dacă laturile unei secțiuni dreptunghiulare sunt x și y, atunci după teorema lui Pitagora

x 2 + y 2 \u003d d 2,

unde d este diametrul buștenului. Volumul lemnului este cel mai mare atunci când aria sa transversală este cea mai mare, adică atunci când xy atinge valoarea sa cea mai mare. Dar dacă xy este cel mai mare, atunci produsul x 2 y 2 va fi și cel mai mare. Deoarece suma x 2 + y 2 este neschimbată, atunci, conform celor dovedite mai devreme, produsul x 2 y 2 este cel mai mare atunci când

x 2 \u003d y 2 sau x \u003d y.

Deci, secțiunea transversală a fasciculului ar trebui să fie pătrată.

Sarcini de transport(așa-numitele sarcini de optimizare; sarcini, a căror soluție permite răspunsul la întrebarea: cum să dispuneți de fonduri pentru a obține beneficii mari)

La prima vedere, nimic deosebit: măsurați înălțimea de la podea la tavan în mai multe puncte, scădeți câțiva centimetri pentru ca dulapul să nu se sprijine de tavan. După ce a făcut acest lucru, în procesul de asamblare a mobilierului, pot apărea dificultăți. La urma urmei, producătorii de mobilier asamblează cadrul prin plasarea dulapului într-o poziție orizontală, iar atunci când cadrul este asamblat, îl ridică într-o poziție verticală. Luați în considerare peretele lateral al dulapului. Înălțimea dulapului trebuie să fie cu 10 cm mai mică decât distanța de la podea la tavan, cu condiția ca această distanță să nu depășească 2500 mm. Și adâncimea dulapului este de 700 mm. De ce 10 cm, și nu 5 cm sau 7, și ce legătură are teorema lui Pitagora cu ea?

Deci: perete lateral 2500-100=2400(mm) - inaltimea maxima a structurii.

Peretele lateral în procesul de ridicare a cadrului trebuie să treacă liber atât în ​​înălțime, cât și în diagonală. De teorema lui Pitagora

AC \u003d √ AB 2 + BC 2

AC= √ 2400 2 + 700 2 = 2500 (mm)

Ce se întâmplă dacă înălțimea dulapului este redusă cu 50 mm?

AC= √ 2450 2 + 700 2 = 2548 (mm)

Diagonala 2548 mm. Deci, nu poți pune un dulap (poți strica tavanul).

Paratrăsnet.

Se știe că un paratrăsnet protejează toate obiectele de trăsnet, a căror distanță de la bază nu depășește înălțimea sa dublată. Este necesar să se determine poziția optimă a paratrăsnetului pe un acoperiș cu fronton, oferind cea mai mică înălțime disponibilă.

Conform teoremei lui Pitagora h 2 ≥ a 2 +b 2 înseamnă h≥(a 2 +b 2) 1/2

urgent pentru zona suburbana trebuie să faceți o seră pentru răsaduri.

Din scânduri a doborât un pătrat de 1m1m. Există rămășițe de peliculă care măsoară 1,5 m1,5 m. La ce înălțime în centrul pătratului ar trebui să fie fixată șina astfel încât filmul să o acopere complet?

1) Diagonala serei d == 1,4; 0,7

2) Diagonala filmului d 1= 2,12 1,06

3) Înălțimea șinei x= 0,7

Concluzie

În urma cercetărilor, am aflat câteva domenii de aplicare a teoremei lui Pitagora. Am adunat și prelucrat o mulțime de materiale din surse literare și de pe Internet pe această temă. Am studiat câteva informații istorice despre Pitagora și teorema lui. Da, într-adevăr, folosind teorema lui Pitagora, poți rezolva nu numai probleme matematice. Teorema lui Pitagora și-a găsit aplicația în construcții și arhitectură, comunicații mobile și literatură.

Studiul și analiza surselor de informații despre teorema lui Pitagora

a aratat ca:

A) atenția exclusivă a matematicienilor și a matematicienilor asupra teoremei se bazează pe simplitatea, frumusețea și semnificația acesteia;

b) teorema lui Pitagora de multe secole servește drept imbold pentru descoperiri matematice interesante și importante (teorema lui Fermat, teoria relativității a lui Einstein);

V) teorema lui Pitagora - este întruchiparea limbajului universal al matematicii, valabil în întreaga lume;

G) domeniul de aplicare al teoremei este destul de extins și, în general, nu poate fi indicat cu suficientă completitudine;

d) secretele teoremei lui Pitagora continuă să excite umanitatea și, prin urmare, fiecăruia dintre noi i se oferă șansa de a fi implicat în dezvăluirea lor.

Bibliografie

Uspekhi matematicheskikh nauk, 1962, vol. 17, nr. 6 (108).

Alexander Danilovici Alexandrov (la 50 de ani de la zi de nastere),

Alexandrov A.D., Werner A.L., Ryzhik V.I. Geometrie, 10 - 11 celule. - M.: Iluminismul, 1992.

Atanasyan L.S. etc Geometrie, 10 - 11 celule. - M.: Iluminismul, 1992.

Vladimirov Yu.S. Spațiu - timp: dimensiuni explicite și ascunse. - M.: „Nauka”, 1989.

Voloshin A.V. Pitagora. - M.: Iluminismul, 1993.

Ziarul „Matematică”, nr. 21, 2006.

Ziarul „Matematică”, nr. 28, 1995.

Geometrie: Proc. Pentru 7 - 11 celule. gimnaziu / G.P. Bevz, V.G. Bevz, N.G. Vladimirova. - M.: Iluminismul, 1992.

Geometrie: manual pentru 7 - 9 celule. educatie generala Institutii/ L.S. Atanasyan, V.F. Butozov, S.B. Kadomtsev și alții - ed. a VI-a. - M.: Iluminismul, 1996.

Glazer G.I. Istoria matematicii la scoala: IX - Xcl. Un ghid pentru profesori. - M.: Iluminismul, 1983.

Capitole suplimentare la manualul școlar clasa a VIII-a: Manual pentru elevi. si cursuri cu aprofundare. studiu matematică /L.S. Atanasyan, V.F. Butozov, S.B. Kadomtsev și alții - M .: Educație, 1996.

Yelensky Sh. Pe urmele lui Pitagora. M., 1961.

Kiselev A.P., Rybkin N.A. Geometrie: Planimetrie: 7 - 9 celule: Manual și carte de probleme. - M.: Dropia, 1995.

Kline M. Matematică. Caută adevăr: traducere din engleză. / Ed. și prefață. IN SI. Arshinova, Yu.V. Sachkov. - M.: Mir, 1998.

Liturman V. Teorema lui Pitagora. - M., 1960.

Matematică: Manualul școlarilor și elevilor / B. Frank și alții; Traducere de la el. - Ed. a III-a, stereotip. - M.: Dropia, 2003.

Peltwer A. Cine ești tu Pitagora? - M.: Cunoașterea este putere, nr. 12, 1994.

Perelman Ya. I. Matematică distractivă. - M.: „Știință”, 1976.

Ponomareva T.D. Mari oameni de știință. - M .: SRL Editura Astrel, 2002.

Sveshnikova A. Călătorie în istoria matematicii. - M., 1995.

Semyonov E.E. Studiem geometria: Cartea. Pentru elevi 6 - 8 celule. gimnaziu - M.: Iluminismul, 1987.

Smyshlyaev V.K. Despre matematică și matematicieni. - Editura Carte Mari, 1977.

Tuchnin N.P. Cum să pui o întrebare. - M.: Iluminismul, 1993.

Cherkasov O.Yu. Planimetrie la examenul de admitere. - M.: Liceul din Moscova, 1996.

Dicţionar enciclopedic tânăr matematician. Comp. A.P. Savin. - M.: Pedagogie, 1985.

Enciclopedie pentru copii. T. 11. Matematică. /Ch. Ed. M.D. Aksenova. - M.: Avanta +, 2001.

Într-un singur lucru, poți fi sută la sută sigur că atunci când este întrebat care este pătratul ipotenuzei, orice adult va răspunde cu îndrăzneală: „Suma pătratelor picioarelor”. Această teorie este ferm plantată în mintea tuturor. persoană educată, dar este suficient doar să ceri cuiva să o dovedească și atunci pot apărea dificultăți. Prin urmare, să ne amintim și să luăm în considerare diferite moduri de a demonstra teorema lui Pitagora.

Scurtă prezentare a biografiei

Teorema lui Pitagora este familiară aproape tuturor, dar din anumite motive biografia persoanei care a produs-o nu este atât de populară. O vom repara. Prin urmare, înainte de a studia diferitele modalități de demonstrare a teoremei lui Pitagora, trebuie să vă familiarizați pe scurt cu personalitatea sa.

Pitagora - un filozof, matematician, gânditor, originar din Astăzi este foarte greu să-i deosebești biografia de legendele care s-au dezvoltat în memoria acestui mare om. Dar, după cum reiese din scrierile adepților săi, Pitagora din Samos s-a născut pe insula Samos. Tatăl său era un tăietor de pietre obișnuit, dar mama lui provenea dintr-o familie nobilă.

Potrivit legendei, nașterea lui Pitagora a fost prezisă de o femeie pe nume Pythia, în cinstea căreia băiatul a fost numit. Potrivit predicției ei, un băiat născut avea să aducă multe beneficii și bine omenirii. Ceea ce a făcut de fapt.

Nașterea unei teoreme

În tinerețe, Pitagora s-a mutat în Egipt pentru a-i întâlni pe celebrii înțelepți egipteni de acolo. După întâlnirea cu ei, a fost admis la studii, unde a învățat toate marile realizări ale filosofiei, matematicii și medicinei egiptene.

Probabil, în Egipt, Pitagora a fost inspirat de măreția și frumusețea piramidelor și a creat marea sa teorie. Acest lucru poate șoca cititorii, dar istoricii moderni cred că Pitagora nu și-a dovedit teoria. Dar el a transmis cunoștințele sale doar adepților săi, care ulterior au finalizat toate calculele matematice necesare.

Oricum ar fi, astăzi nu se cunoaște o tehnică de demonstrare a acestei teoreme, ci mai multe deodată. Astăzi putem doar ghici cum exact grecii antici și-au făcut calculele, așa că aici vom lua în considerare diferite moduri de a demonstra teorema lui Pitagora.

teorema lui Pitagora

Înainte de a începe orice calcul, trebuie să vă dați seama ce teorie să dovediți. Teorema lui Pitagora sună astfel: „Într-un triunghi în care unul dintre unghiuri este de 90 o, suma pătratelor catetelor este egală cu pătratul ipotenuzei”.

Există 15 moduri diferite de a demonstra teorema lui Pitagora în total. Acesta este un număr destul de mare, așa că să acordăm atenție celor mai populare dintre ele.

Metoda unu

Să definim mai întâi ce avem. Aceste date se vor aplica și altor modalități de demonstrare a teoremei lui Pitagora, așa că ar trebui să vă amintiți imediat toată notația disponibilă.

Să presupunem că este dat un triunghi dreptunghic, cu catetele a, b și ipotenuza egală cu c. Prima metodă de demonstrare se bazează pe faptul că un pătrat trebuie trasat dintr-un triunghi dreptunghic.

Pentru a face acest lucru, trebuie să desenați un segment egal cu piciorul în lungimea piciorului a și invers. Deci ar trebui să iasă două laturi egale ale pătratului. Rămâne doar să desenați două linii paralele, iar pătratul este gata.

În interiorul figurii rezultate, trebuie să desenați un alt pătrat cu o latură egal cu ipotenuza triunghiul original. Pentru a face acest lucru, din vârfurile ac și sv, trebuie să desenați două segmente paralele egale cu c. Astfel, obținem trei laturi ale pătratului, dintre care una este ipotenuza triunghiului dreptunghic inițial. Rămâne doar să desenăm al patrulea segment.

Pe baza cifrei rezultate, putem concluziona că aria pătratului exterior este (a + b) 2. Dacă te uiți în interiorul figurii, poți vedea că, pe lângă pătratul interior, are patru triunghiuri dreptunghiulare. Suprafața fiecăruia este de 0,5 av.

Prin urmare, aria este: 4 * 0,5av + s 2 \u003d 2av + s 2

Prin urmare (a + c) 2 \u003d 2av + c 2

Și, prin urmare, cu 2 \u003d a 2 + în 2

Teorema a fost demonstrată.

Metoda a doua: triunghiuri similare

Această formulă pentru demonstrarea teoremei lui Pitagora a fost derivată pe baza unei afirmații din secțiunea de geometrie despre triunghiuri asemănătoare. Se spune că catetul unui triunghi dreptunghic este media proporțională cu ipotenuza sa și segmentul de ipotenuză care provine din vârful unui unghi de 90 o.

Datele inițiale rămân aceleași, așa că să începem imediat cu dovada. Să desenăm un segment CD perpendicular pe latura AB. Pe baza afirmației de mai sus, catetele triunghiurilor sunt egale:

AC=√AB*AD, SW=√AB*DV.

Pentru a răspunde la întrebarea cum să demonstrăm teorema lui Pitagora, demonstrația trebuie făcută prin pătrarea ambelor inegalități.

AC 2 \u003d AB * IAD și SV 2 \u003d AB * DV

Acum trebuie să adăugăm inegalitățile rezultate.

AC 2 + SV 2 \u003d AB * (AD * DV), unde AD + DV \u003d AB

Se pare că:

AC 2 + CB 2 \u003d AB * AB

Prin urmare:

AC 2 + CB 2 \u003d AB 2

Demonstrarea teoremei lui Pitagora și diferite căi soluțiile sale necesită o abordare cu mai multe fațete a acestei probleme. Cu toate acestea, această opțiune este una dintre cele mai simple.

O altă metodă de calcul

Descrierea diferitelor moduri de a demonstra teorema lui Pitagora poate să nu spună nimic, până când nu începeți să exersați pe cont propriu. Multe metode implică nu numai calcule matematice, ci și construcția de noi figuri din triunghiul original.

În acest caz, este necesar să completați un alt triunghi dreptunghic VSD de la piciorul aeronavei. Astfel, acum există două triunghiuri cu catetă comună BC.

Știind că ariile figurilor similare au un raport ca pătratele dimensiunilor lor liniare similare, atunci:

S avs * s 2 - S avd * în 2 \u003d S avd * a 2 - S vd * a 2

S avs * (de la 2 la 2) \u003d a 2 * (S avd -S vvd)

de la 2 la 2 \u003d un 2

c 2 \u003d a 2 + în 2

Deoarece această opțiune nu este potrivită din diferite metode de demonstrare a teoremei lui Pitagora pentru clasa a 8-a, puteți utiliza următoarea tehnică.

Cel mai simplu mod de a demonstra teorema lui Pitagora. Recenzii

Istoricii cred că această metodă a fost folosită pentru prima dată pentru a demonstra teorema Grecia antică. Este cel mai simplu, deoarece nu necesită absolut niciun calcul. Dacă desenați corect o imagine, atunci dovada afirmației că a 2 + b 2 \u003d c 2 va fi clar vizibilă.

Conditii pentru aceasta metoda va fi ușor diferită de cea precedentă. Pentru a demonstra teorema, presupunem că triunghiul dreptunghic ABC este isoscel.

Luăm ipotenuza AC ca latură a pătratului și desenăm cele trei laturi ale acestuia. În plus, este necesar să desenați două linii diagonale în pătratul rezultat. Astfel încât în ​​interiorul ei să obții patru triunghiuri isoscele.

Pentru picioarele AB și CB, trebuie, de asemenea, să desenați un pătrat și să desenați o linie diagonală în fiecare dintre ele. Desenăm prima linie de la vârful A, a doua - de la C.

Acum trebuie să vă uitați cu atenție la imaginea rezultată. Deoarece există patru triunghiuri pe ipotenuza AC, egale cu cea inițială, și două pe catete, acest lucru indică veridicitatea acestei teoreme.

Apropo, datorită acestei metode de demonstrare a teoremei lui Pitagora s-a născut celebra frază: „Pantalonii pitagoreici sunt egali în toate direcțiile”.

Dovada de J. Garfield

James Garfield este al 20-lea președinte al Statelor Unite ale Americii. Pe lângă faptul că și-a lăsat amprenta asupra istoriei ca conducător al Statelor Unite, a fost și un autodidact talentat.

La începutul carierei, a fost profesor obișnuit la o școală populară, dar în curând a devenit directorul uneia dintre instituțiile de învățământ superior. Dorința de auto-dezvoltare i-a permis să ofere o nouă teorie a demonstrației teoremei lui Pitagora. Teorema și un exemplu de soluție sunt după cum urmează.

Mai întâi trebuie să desenați două triunghiuri dreptunghiulare pe o bucată de hârtie, astfel încât piciorul unuia dintre ele să fie o continuare a celui de-al doilea. Vârfurile acestor triunghiuri trebuie să fie conectate pentru a ajunge la un trapez.

După cum știți, aria unui trapez este egală cu produsul dintre jumătate din suma bazelor sale și înălțimea.

S=a+b/2 * (a+b)

Dacă luăm în considerare trapezul rezultat ca o figură formată din trei triunghiuri, atunci aria sa poate fi găsită după cum urmează:

S \u003d av / 2 * 2 + s 2 / 2

Acum trebuie să egalăm cele două expresii originale

2av / 2 + s / 2 \u003d (a + c) 2 / 2

c 2 \u003d a 2 + în 2

Se pot scrie mai mult de un volum despre teorema lui Pitagora și despre cum se demonstrează ghid de studiu. Dar are sens atunci când aceste cunoștințe nu pot fi puse în practică?

Aplicarea practică a teoremei lui Pitagora

Din păcate, programele școlare moderne prevăd utilizarea acestei teoreme doar în problemele geometrice. Absolvenții vor pleca în curând zidurile școlii fără să știe cum își pot aplica cunoștințele și abilitățile în practică.

De fapt, utilizați teorema lui Pitagora în dvs Viata de zi cu zi toată lumea poate. Și nu numai în activități profesionale, ci și în treburile casnice obișnuite. Să luăm în considerare câteva cazuri în care teorema lui Pitagora și metodele de demonstrare a acesteia pot fi extrem de necesare.

Legătura dintre teoremă și astronomie

S-ar părea cum stelele și triunghiurile pot fi conectate pe hârtie. De fapt, astronomia este un domeniu științific în care teorema lui Pitagora este utilizată pe scară largă.

De exemplu, luați în considerare mișcarea unui fascicul de lumină în spațiu. Știm că lumina se deplasează în ambele direcții cu aceeași viteză. Numim traiectoria AB de-a lungul căreia se mișcă raza de lumină l. Și jumătate din timpul necesar pentru ca lumina să ajungă din punctul A în punctul B, să sunăm t. Și viteza fasciculului - c. Se pare că: c*t=l

Dacă te uiți la același fascicul dintr-un alt plan, de exemplu, de la o căptușeală spațială care se mișcă cu o viteză v, atunci cu o astfel de observare a corpurilor, viteza lor se va schimba. În acest caz, chiar și elementele staționare se vor deplasa cu o viteză v în direcția opusă.

Să presupunem că linia de benzi desenate navighează spre dreapta. Apoi punctele A și B, între care raza se repezi, se vor deplasa spre stânga. Mai mult, atunci când fasciculul se deplasează din punctul A în punctul B, punctul A are timp să se miște și, în consecință, lumina va ajunge deja într-un nou punct C. Pentru a găsi jumătate din distanța la care punctul A s-a deplasat, trebuie să înmulțiți viteza căptușelii cu jumătate din timpul de călătorie al fasciculului (t ").

Și pentru a afla cât de departe ar putea călători o rază de lumină în acest timp, trebuie să desemnați jumătate din calea noului fag și să obțineți următoarea expresie:

Dacă ne imaginăm că punctele de lumină C și B, precum și linia spațială, sunt vârfurile unui triunghi isoscel, atunci segmentul de la punctul A la căptușeală îl va împărți în două triunghiuri dreptunghiulare. Prin urmare, datorită teoremei lui Pitagora, puteți afla distanța pe care o poate parcurge o rază de lumină.

Acest exemplu, desigur, nu este cel mai de succes, deoarece doar câțiva pot fi destul de norocoși să-l încerce în practică. Prin urmare, luăm în considerare aplicații mai banale ale acestei teoreme.

Raza de transmisie a semnalului mobil

Viața modernă nu mai poate fi imaginată fără existența smartphone-urilor. Dar cât de mult le-ar fi de folos dacă nu ar putea conecta abonații prin comunicații mobile?!

Calitatea comunicațiilor mobile depinde direct de înălțimea la care se află antena operatorului de telefonie mobilă. Pentru a calcula cât de departe de un turn mobil un telefon poate primi un semnal, puteți aplica teorema lui Pitagora.

Să presupunem că trebuie să găsiți înălțimea aproximativă a unui turn staționar, astfel încât să poată propaga un semnal pe o rază de 200 de kilometri.

AB (înălțimea turnului) = x;

BC (raza de transmisie a semnalului) = 200 km;

OS (raza globului) = 6380 km;

OB=OA+ABOB=r+x

Aplicând teorema lui Pitagora, aflăm că înălțimea minimă a turnului ar trebui să fie de 2,3 kilometri.

Teorema lui Pitagora în viața de zi cu zi

În mod ciudat, teorema lui Pitagora poate fi utilă chiar și în chestiuni de zi cu zi, cum ar fi determinarea înălțimii unui dulap, de exemplu. La prima vedere, nu este nevoie să folosiți astfel de calcule complexe, deoarece puteți efectua pur și simplu măsurători cu o bandă de măsurare. Dar mulți sunt surprinși de ce apar anumite probleme în timpul procesului de asamblare dacă toate măsurătorile au fost luate mai mult decât exact.

Faptul este că dulapul este asamblat în poziție orizontală și abia apoi se ridică și este instalat pe perete. Prin urmare, peretele lateral al dulapului în procesul de ridicare a structurii trebuie să treacă liber atât de-a lungul înălțimii, cât și în diagonală a încăperii.

Să presupunem că există un dulap cu o adâncime de 800 mm. Distanța de la podea la tavan - 2600 mm. Un producător de mobilier cu experiență va spune că înălțimea dulapului ar trebui să fie cu 126 mm mai mică decât înălțimea camerei. Dar de ce exact 126 mm? Să ne uităm la un exemplu.

Cu dimensiunile ideale ale dulapului, să verificăm funcționarea teoremei lui Pitagora:

AC \u003d √AB 2 + √BC 2

AC \u003d √ 2474 2 +800 2 \u003d 2600 mm - totul converge.

Să presupunem că înălțimea dulapului nu este de 2474 mm, ci de 2505 mm. Apoi:

AC \u003d √2505 2 + √800 2 \u003d 2629 mm.

Prin urmare, acest dulap nu este potrivit pentru instalarea în această cameră. Deoarece atunci când îl ridicați într-o poziție verticală, poate fi cauzată deteriorarea corpului.

Poate, având în vedere diferite moduri de a demonstra teorema lui Pitagora de către diferiți oameni de știință, putem concluziona că este mai mult decât adevărată. Acum puteți utiliza informațiile primite în viața de zi cu zi și puteți fi complet sigur că toate calculele vor fi nu numai utile, ci și corecte.