Triunghiul este o figură binecunoscută. Și asta, în ciuda varietății bogate a formelor sale. Dreptunghiular, echilateral, acut, isoscel, obtuz. Fiecare dintre ele este oarecum diferit. Dar pentru orice este necesar să cunoașteți aria triunghiului.

Formule comune pentru toate triunghiurile care folosesc lungimile laturilor sau înălțimii

Denumirile adoptate în ele: laturile - a, b, c; înălțimi pe părțile relevante n a, n c, n s.

1. Aria unui triunghi se calculează ca produsul dintre ½, latura și înălțimea coborâte pe acesta. S = ½ * a * n a. În mod similar, ar trebui să scrieți formule pentru celelalte două părți.

2. Formula lui Heron, în care apare semiperimetrul (se obișnuiește să-l notăm cu litera p mică, în contrast cu întregul perimetru). Semi-perimetrul trebuie calculat după cum urmează: se adună toate laturile și se împart la 2. Formula semi-perimetru: p \u003d (a + b + c) / 2. Apoi egalitatea pentru aria de \ u200b\u200bfigura arată astfel: S \u003d √ (p * (p - a) * ( p - c) * (p - c)).

3. Dacă nu doriți să utilizați un semi-perimetru, atunci o astfel de formulă va fi utilă, în care sunt prezente doar lungimile laturilor: S \u003d ¼ * √ ((a + b + c) * ( b + c - a) * (a + c - c) * (a + b - c)). Este oarecum mai lung decât precedentul, dar vă va ajuta dacă ați uitat cum să găsiți semi-perimetrul.

Formule generale în care apar unghiurile unui triunghi

Notația care este necesară pentru a citi formulele: α, β, γ - unghiuri. Ele se află laturi opuse a, b, c, respectiv.

1. Potrivit acestuia, jumătate din produsul a două laturi și sinusul unghiului dintre ele este egal cu aria triunghiului. Adică: S = ½ a * b * sin γ. Formulele pentru celelalte două cazuri ar trebui scrise într-un mod similar.

2. Aria unui triunghi poate fi calculată dintr-o latură și trei unghiuri cunoscute. S \u003d (a 2 * sin β * sin γ) / (2 sin α).

3. Există și o formulă cu o latură cunoscută și două unghiuri adiacente acesteia. Arata astfel: S = c 2 / (2 (ctg α + ctg β)).

Ultimele două formule nu sunt cele mai simple. E destul de greu să-i amintești.

Formule generale pentru situația în care se cunosc razele cercurilor înscrise sau circumscrise

Denumiri suplimentare: r, R — razele. Primul este folosit pentru raza cercului înscris. Al doilea este pentru cel descris.

1. Prima formulă prin care se calculează aria unui triunghi este legată de semiperimetrul. S = r * r. Într-un alt mod, poate fi scris după cum urmează: S \u003d ½ r * (a + b + c).

2. În al doilea caz, va trebui să înmulțiți toate laturile triunghiului și să le împărțiți la raza cvadruplă a cercului circumscris. ÎN expresie literală arată astfel: S = (a * b * c) / (4R).

3. A treia situație vă permite să faceți fără a cunoaște laturile, dar aveți nevoie de valorile tuturor celor trei unghiuri. S \u003d 2 R 2 * sin α * sin β * sin γ.

Caz special: triunghi dreptunghic

Aceasta este cea mai simplă situație, deoarece este necesară doar lungimea ambelor picioare. Ele sunt notate cu literele latine a și b. Pătrat triunghi dreptunghic egal cu jumătate din suprafața dreptunghiului adăugat la acesta.

Matematic, arată astfel: S = ½ a * b. Ea este cel mai ușor de reținut. Deoarece arată ca formula pentru aria unui dreptunghi, apare doar o fracție, denotă jumătate.

Caz special: triunghi isoscel

Deoarece cele două laturi ale sale sunt egale, unele formule pentru zona sa par oarecum simplificate. De exemplu, formula lui Heron, care calculează aria unui triunghi isoscel, ia următoarea formă:

S = ½ in √((a + ½ in)*(a - ½ in)).

Dacă îl converti, va deveni mai scurt. În acest caz, formula lui Heron pentru un triunghi isoscel este scrisă după cum urmează:

S = ¼ în √(4 * a 2 - b 2).

Formula ariei pare oarecum mai simplă decât pentru un triunghi arbitrar dacă laturile și unghiul dintre ele sunt cunoscute. S \u003d ½ a 2 * sin β.

Caz special: triunghi echilateral

De obicei, în problemele despre el, latura este cunoscută sau poate fi cumva recunoscută. Apoi arată formula pentru găsirea ariei unui astfel de triunghi în felul următor:

S = (a 2 √3) / 4.

Sarcini pentru găsirea zonei dacă triunghiul este reprezentat pe hârtie în carouri

Cea mai simplă situație este atunci când un triunghi dreptunghic este desenat astfel încât picioarele acestuia să coincidă cu liniile hârtiei. Apoi trebuie doar să numărați numărul de celule care se potrivesc în picioare. Apoi înmulțiți-le și împărțiți-le la doi.

Când triunghiul este acut sau obtuz, trebuie să fie desenat într-un dreptunghi. Apoi, în figura rezultată vor fi 3 triunghiuri. Unul este cel dat în sarcină. Iar celelalte două sunt auxiliare și dreptunghiulare. Zonele ultimelor două trebuie determinate prin metoda descrisă mai sus. Apoi calculați aria dreptunghiului și scădeți din el cele calculate pentru cele auxiliare. Se determină aria triunghiului.

Mult mai dificilă este situația în care niciuna dintre laturile triunghiului nu coincide cu liniile hârtiei. Apoi trebuie să fie înscris într-un dreptunghi, astfel încât vârfurile figurii originale să se afle pe laturile sale. În acest caz, vor exista trei triunghiuri dreptunghiulare auxiliare.

Un exemplu de problemă cu formula lui Heron

Condiție. Unele triunghiuri au laturi. Ele sunt egale cu 3, 5 și 6 cm. Trebuie să-i aflați aria.

Acum puteți calcula aria unui triunghi folosind formula de mai sus. Sub rădăcina pătrată se află produsul a patru numere: 7, 4, 2 și 1. Adică, aria este √ (4 * 14) = 2 √ (14).

Dacă nu aveți nevoie de mai multă precizie, atunci puteți lua rădăcina pătrată a lui 14. Este 3,74. Atunci aria va fi egală cu 7,48.

Răspuns. S \u003d 2 √14 cm 2 sau 7,48 cm 2.

Un exemplu de problemă cu un triunghi dreptunghic

Condiție. Un picior al unui triunghi dreptunghic este cu 31 cm mai lung decât al doilea. Este necesar să aflați lungimile lor dacă aria triunghiului este de 180 cm 2.
Soluţie. Trebuie să rezolvi un sistem de două ecuații. Primul are legătură cu zona. Al doilea este cu raportul picioarelor, care este dat în problemă.
180 \u003d ½ a * b;

a \u003d b + 31.
În primul rând, valoarea lui „a” trebuie înlocuită în prima ecuație. Se dovedește: 180 \u003d ½ (in + 31) * in. Are o singură cantitate necunoscută, deci este ușor de rezolvat. După ce deschidem parantezele, obținem ecuație pătratică: în 2 + 31 in - 360 = 0. Oferă două valori pentru „în”: 9 și - 40. Al doilea număr nu este potrivit ca răspuns, deoarece lungimea laturii triunghiului nu poate fi negativă valoare.

Rămâne de calculat al doilea etapă: la numărul rezultat se adaugă 31. Rezultă 40. Acestea sunt cantitățile căutate în problemă.

Răspuns. Lamele triunghiului au 9 și 40 cm.

Sarcina de a găsi latura prin zona, latura și unghiul unui triunghi

Condiție. Aria unui triunghi este de 60 cm2. Este necesar să se calculeze una dintre laturile sale dacă a doua latură este de 15 cm, iar unghiul dintre ele este de 30º.

Soluţie. Pe baza denumirilor acceptate, partea dorită „a”, cunoscutul „b”, unghi prestabilit„γ”. Apoi formula zonei poate fi rescrisă după cum urmează:

60 \u003d ½ a * 15 * sin 30º. Aici sinusul de 30 de grade este 0,5.

După transformări, „a” se dovedește a fi egal cu 60 / (0,5 * 0,5 * 15). Adică 16.

Răspuns. Latura dorită este de 16 cm.

Problema unui pătrat înscris într-un triunghi dreptunghic

Condiție. Vârful unui pătrat cu latura de 24 cm coincide cu unghiul drept al triunghiului. Ceilalți doi se întind pe picioare. Al treilea aparține ipotenuzei. Lungimea unuia dintre picioare este de 42 cm Care este aria unui triunghi dreptunghic?

Soluţie. Luați în considerare două triunghiuri dreptunghiulare. Primul este specificat în sarcină. Al doilea se bazează pe picior celebru triunghiul original. Sunt asemănătoare deoarece au un unghi comun și sunt formate din linii paralele.

Atunci rapoartele picioarelor lor sunt egale. Picioarele triunghiului mai mic sunt de 24 cm (latura pătratului) și 18 cm (cu piciorul dat 42 cm minus latura pătratului de 24 cm). Picioarele corespunzătoare triunghi mare- 42 cm și x cm. Acest „x” este necesar pentru a calcula aria triunghiului.

18/42 \u003d 24 / x, adică x \u003d 24 * 42 / 18 \u003d 56 (cm).

Atunci aria este egală cu produsul dintre 56 și 42, împărțit la doi, adică 1176 cm 2.

Răspuns. Suprafața dorită este de 1176 cm 2.

Conceptul de zonă

Conceptul de zonă a oricărei figuri geometrice, în special un triunghi, va fi asociat cu o astfel de figură precum un pătrat. Pentru o unitate de suprafață a oricărei figuri geometrice, vom lua aria unui pătrat, a cărui latură este egală cu unu. Pentru a fi complet, amintim două proprietăți de bază pentru conceptul de zone forme geometrice.

Proprietatea 1: Dacă figurile geometrice sunt egale, atunci și zonele lor sunt egale.

Proprietatea 2: Orice figură poate fi împărțită în mai multe figuri. Mai mult, aria figurii originale este egală cu suma valorilor ariilor tuturor figurilor care o alcătuiesc.

Luați în considerare un exemplu.

Exemplul 1

Este evident că una dintre laturile triunghiului este diagonala dreptunghiului, care are o latură de lungime $5$ (din moment ce $5$ celule) și cealaltă $6$ (din moment ce $6$ celule). Prin urmare, aria acestui triunghi va fi egală cu jumătate dintr-un astfel de dreptunghi. Aria dreptunghiului este

Atunci aria triunghiului este

Răspuns: $15$.

În continuare, luați în considerare mai multe metode pentru găsirea ariilor triunghiurilor, și anume folosind înălțimea și baza, folosind formula Heron și aria unui triunghi echilateral.

Cum să găsiți aria unui triunghi folosind înălțimea și baza

Teorema 1

Aria unui triunghi poate fi găsită ca jumătate din produsul lungimii unei laturi cu înălțimea trasă de acea latură.

Matematic arată așa

$S=\frac(1)(2)αh$

unde $a$ este lungimea laturii, $h$ este înălțimea trasă la ea.

Dovada.

Considerăm triunghiul $ABC$ unde $AC=α$. Înălțimea $BH$ este trasă în această parte și este egală cu $h$. Să-l construim până la pătratul $AXYC$ ca în Figura 2.

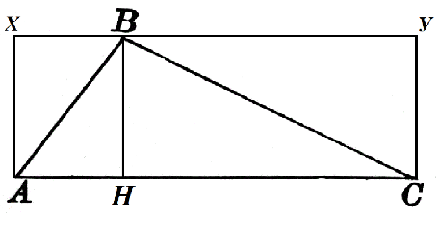
Aria dreptunghiului $AXBH$ este $h\cdot AH$, iar cea a dreptunghiului $HBYC$ este $h\cdot HC$. Apoi

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Prin urmare, aria dorită a triunghiului, conform proprietății 2, este egală cu

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

Teorema a fost demonstrată.

Exemplul 2

Găsiți aria triunghiului din figura de mai jos, dacă celula are o zonă egală cu unu

Baza acestui triunghi este $9$ (deoarece $9$ este $9$ celule). Înălțimea este de asemenea de 9 USD. Apoi, prin teorema 1, obținem

$S=\frac(1)(2)\cdot 9\cdot 9=40.5$

Răspuns: 40,5 USD.

Formula lui Heron

Teorema 2

Dacă ni se dau trei laturi ale unui triunghi $α$, $β$ și $γ$, atunci aria acestuia poate fi găsită după cum urmează

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

aici $ρ$ înseamnă jumătate de perimetru al acestui triunghi.

Dovada.

Luați în considerare următoarea figură:

Prin teorema lui Pitagora, din triunghiul $ABH$ obtinem

Din triunghiul $CBH$, după teorema lui Pitagora, avem

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Din aceste două relații obținem egalitatea

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Deoarece $ρ=\frac(α+β+γ)(2)$, atunci $α+β+γ=2ρ$, deci

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Prin teorema 1, obținem

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Instruire

Petreceri iar colțurile sunt considerate elemente de bază A. Un triunghi este complet definit de oricare dintre următoarele elemente de bază: fie trei laturi, fie o latură și două unghiuri, fie două laturi și un unghi între ele. Pentru existență triunghi definit de trei laturi a, b, c, este necesar și suficient ca inegalitățile, numite inegalități triunghi:
a+b > c
a+c > b
b+c > a.

Pentru constructie triunghi pe trei laturi a, b, c, este necesar din punctul C al segmentului CB=a sa se deseneze cu compasul un cerc de raza b. Apoi, în mod similar, desenați un cerc din punctul B cu o rază egală cu latura c. Punctul lor de intersecție A este al treilea vârf al celui dorit triunghi ABC, unde AB=c, CB=a, CA=b - laturile triunghi. Problema are , dacă laturile a, b, c satisfac inegalitățile triunghi specificat la pasul 1.

Zona lui S construită în acest fel triunghi ABC cu laturile cunoscute a, b, c, se calculează prin formula lui Heron:
S=v(p(p-a)(p-b)(p-c)),
unde a, b, c sunt laturi triunghi, p este semiperimetrul.
p = (a+b+c)/2

Dacă triunghiul este echilateral, adică toate laturile lui sunt egale (a=b=c).Aria triunghi calculat prin formula:
S=(a^2 v3)/4

Dacă triunghiul este dreptunghic, adică unul dintre unghiurile sale este de 90 °, iar laturile care îl formează sunt catete, a treia latură este ipotenuza. În acest caz pătrat este egal cu produsul catetelor împărțit la doi.
S=ab/2

A găsi pătrat triunghi, puteți folosi una dintre numeroasele formule. Alegeți formula în funcție de ce date sunt deja cunoscute.

Vei avea nevoie

• cunoașterea formulelor pentru găsirea ariei unui triunghi

Instruire

Dacă știți valoarea uneia dintre laturi și valoarea înălțimii coborâte în această latură din colțul opus, atunci puteți găsi aria folosind următoarele: S = a*h/2, unde S este aria lui ​triunghiul, a este una dintre laturile triunghiului, iar h - înălțimea, la latura a.

Există o modalitate cunoscută de a determina aria unui triunghi dacă trei dintre laturile sale sunt cunoscute. Ea este formula lui Heron. Pentru a simplifica înregistrarea acesteia, se introduce o valoare intermediară - un semiperimetru: p \u003d (a + b + c) / 2, unde a, b, c - . Atunci formula lui Heron este următoarea: S = (p(p-a)(p-b)(p-c))^1, ^ exponentiație.

Să presupunem că cunoști una dintre laturile unui triunghi și trei unghiuri. Atunci este ușor să găsiți aria triunghiului: S = a²sinα sinγ / (2sinβ), unde β este unghiul opus laturii a, iar α și γ sunt unghiuri adiacente laturii.

Videoclipuri asemănătoare

Notă

Cel mai formula generala, care este potrivit pentru toate cazurile - aceasta este formula lui Heron.

Surse:

Sfat 3: Cum să găsiți aria unui triunghi având trei laturi

Găsirea ariei unui triunghi este una dintre cele mai comune sarcini în planimetria școlară. Cunoașterea celor trei laturi ale unui triunghi este suficientă pentru a determina aria oricărui triunghi. În cazuri speciale și triunghiuri echilaterale, este suficient să cunoaștem lungimile a două și, respectiv, a unei laturi.

Vei avea nevoie

• lungimile laturilor triunghiurilor, formula lui Heron, teorema cosinusului

Instruire

Formula lui Heron pentru aria unui triunghi este următoarea: S = sqrt(p(p-a)(p-b)(p-c)). Dacă pictați semiperimetrul p, atunci obțineți: S = sqrt(((a+b+c)/2)((b+c-a)/2)((a+c-b)/2)((a+b-c) /2) ) = (sqrt((a+b+c)(a+b-c)(a+c-b)(b+c-a)))/4.

De asemenea, puteți obține o formulă pentru aria unui triunghi din considerații, de exemplu, prin aplicarea teoremei cosinusului.

După legea cosinusurilor, AC^2 = (AB^2)+(BC^2)-2*AB*BC*cos(ABC). Folosind notația introdusă, acestea pot fi și sub forma: b^2 = (a^2)+(c^2)-2a*c*cos(ABC). Prin urmare, cos(ABC) = ((a^2)+(c^2)-(b^2))/(2*a*c)

Aria unui triunghi se găsește și prin formula S = a*c*sin(ABC)/2 prin două laturi și unghiul dintre ele. Sinusul unghiului ABC poate fi exprimat în termenii lui folosind identitatea trigonometrică de bază: sin (ABC) = sqrt (1- ((cos (ABC)) ^ 2) Înlocuind sinusul în formula zonei și pictând-o, puteți veniți la formula pentru aria unui triunghi ABC.

Videoclipuri asemănătoare

Pentru lucrări de reparații poate fi necesar să fie măsurat pătrat ziduri. Este mai ușor de calculat suma necesară vopsea sau tapet. Pentru măsurători, cel mai bine este să folosiți o bandă de măsurare sau o bandă de centimetri. Măsurătorile trebuie luate după ziduri au fost aliniate.

Vei avea nevoie

• -ruletă;
• -scară.

Instruire

A număra pătrat pereți, trebuie să cunoașteți înălțimea exactă a tavanelor, precum și să măsurați lungimea de-a lungul podelei. Acest lucru se face după cum urmează: luați un centimetru, așezați-l peste soclu. De obicei, un centimetru nu este suficient pentru toată lungimea, așa că fixează-l în colț, apoi derulează-l la lungimea maximă. În acest moment, puneți un semn cu un creion, notați rezultatul și efectuați măsurarea ulterioară în același mod, începând de la ultimul punct de măsurare.

Plafoane standard în tipic - 2 metri 80 centimetri, 3 metri și 3 metri 20 centimetri, în funcție de casă. Dacă casa a fost construită înainte de anii 50, atunci cel mai probabil înălțimea reală este puțin mai mică decât cea indicată. Dacă calculezi pătrat pentru lucrări de reparații, atunci o marjă mică nu va strica - luați în considerare pe baza standardului. Dacă mai trebuie să știți înălțimea reală - luați măsurători. Principiul este similar cu măsurarea lungimii, dar veți avea nevoie de o scară.

Înmulțiți cifrele rezultate - aceasta este pătrat ta ziduri. Adevărat, pentru lucrări de pictură sau pentru este necesar să se scadă pătrat usa si deschideri ale ferestrelor. Pentru a face acest lucru, așezați un centimetru de-a lungul deschiderii. Dacă vorbim despre o ușă pe care o veți schimba mai târziu, atunci executați-o cu cadru de ușă, luând în considerare numai pătrat deschiderea în sine. Suprafața ferestrei este calculată de-a lungul perimetrului cadrului său. După pătrat fereastră și ușă calculate, scădeți rezultatul din suprafața totală a încăperii obținută.

Vă rugăm să rețineți că măsurătorile lungimii și lățimii camerei sunt efectuate împreună, este mai ușor să fixați un centimetru sau o bandă de măsură și, în consecință, să obțineți un rezultat mai precis. Faceți aceeași măsurătoare de mai multe ori pentru a vă asigura că numerele pe care le obțineți sunt corecte.

Videoclipuri asemănătoare

Găsirea volumului unui triunghi este într-adevăr o sarcină non-trivială. Faptul este că un triunghi este o figură bidimensională, adică. se află în întregime într-un singur plan, ceea ce înseamnă că pur și simplu nu are volum. Desigur, nu poți găsi ceva care nu există. Dar să nu renunțăm! Putem face următoarea presupunere - volumul unei figuri bidimensionale, aceasta este aria sa. Căutăm aria triunghiului.

Vei avea nevoie

• coală de hârtie, creion, riglă, calculator

Instruire

Desenați pe o foaie de hârtie cu o riglă și un creion. Examinând cu atenție triunghiul, vă puteți asigura că într-adevăr nu are, deoarece este desenat pe un plan. Etichetați laturile triunghiului: o latură să fie latura „a”, cealaltă parte „b”, iar a treia latură „c”. Etichetați vârfurile triunghiului cu literele „A”, „B” și „C”.

Măsurați orice latură a triunghiului cu o riglă și notați rezultatul. După aceea, restabiliți perpendiculara pe latura măsurată de la vârful opus, o astfel de perpendiculară va fi înălțimea triunghiului. În cazul prezentat în figură, perpendiculara „h” este restabilită pe latura „c” de la vârful „A”. Măsurați înălțimea rezultată cu o riglă și înregistrați rezultatul măsurării.

Se poate întâmpla să vi se pare dificil să restabiliți perpendiculara exactă. În acest caz, ar trebui să utilizați o formulă diferită. Măsurați toate laturile triunghiului cu o riglă. După aceea, calculați jumătate de perimetru al triunghiului „p” adunând lungimile rezultate ale laturilor și împărțind suma lor la jumătate. Avand la dispozitie valoarea semiperimetrului, puteti folosi formula Heron. Pentru a face acest lucru, trebuie să extrageți Rădăcină pătrată din următoarele: p(p-a)(p-b)(p-c).

Ați obținut aria dorită a triunghiului. Problema găsirii volumului unui triunghi nu a fost rezolvată, dar după cum am menționat mai sus, volumul nu este . Puteți găsi volum care este în esență un triunghi în lumea 3D. Dacă ne imaginăm că triunghiul nostru inițial a devenit o piramidă tridimensională, atunci volumul unei astfel de piramide va fi produsul lungimii bazei sale și aria triunghiului pe care l-am primit.

Notă

Calculele vor fi mai precise cu cât efectuați măsurătorile cu mai multă atenție.

Surse:

• Calculator All-to-All - Portal de referință
• volumul triunghiului în 2019

Cele trei puncte care definesc unic un triunghi în sistemul de coordonate carteziene sunt vârfurile acestuia. Cunoscând poziția lor față de fiecare axă de coordonate, puteți calcula orice parametri ai acestei figuri plate, inclusiv cel limitat de perimetrul său pătrat. Acest lucru se poate face în mai multe moduri.

Instruire

Utilizați formula lui Heron pentru a calcula suprafața triunghi. Implică dimensiunile celor trei laturi ale figurii, așa că începeți calculele cu. Lungimea fiecărei laturi trebuie să fie egală cu rădăcina sumei pătratelor lungimilor proiecțiilor sale pe axele de coordonate. Dacă notăm coordonatele A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) și C(X₃,Y₃,Z₃), lungimile laturilor lor pot fi exprimate astfel: AB = √((X₁- X₂)² + (Y₁ -Y₂)² + (Z₁-Z₂)²), BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²), AC = √(( X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).

Pentru a simplifica calculele, introduceți o variabilă auxiliară - semiperimetrul (P). De aici, aceasta este jumătate din suma lungimilor tuturor laturilor: P \u003d ½ * (AB + BC + AC) \u003d ½ * (√ ((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-) Z₂)²) + √ ((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) + √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃) ²).

Aria unui triunghi - formule și exemple de rezolvare a problemelor

Mai jos sunt formule pentru găsirea ariei unui triunghi arbitrar care sunt potrivite pentru găsirea ariei oricărui triunghi, indiferent de proprietățile, unghiurile sau dimensiunile acestuia. Formulele sunt prezentate sub forma unei imagini, aici sunt explicații pentru aplicarea sau justificarea corectitudinii lor. Tot într-o figură separată sunt corespondențele scrisoriîn formule şi simboluri grafice pe desen.

Notă . Dacă triunghiul are proprietăți speciale (izoscel, dreptunghiular, echilateral), puteți utiliza formulele de mai jos, precum și formule speciale care sunt valabile numai pentru triunghiuri cu aceste proprietăți:

• „Formulele pentru aria unui triunghi echilateral”

Formulele ariei triunghiulare

Explicații pentru formule:
a, b, c- lungimile laturilor triunghiului a cărui arie dorim să aflăm
r- raza cercului înscris în triunghi
R- raza cercului circumscris în jurul triunghiului
h- inaltimea triunghiului, coborat in lateral
p- semiperimetrul unui triunghi, 1/2 din suma laturilor acestuia (perimetrul)
α - unghiul opus laturii a a triunghiului
β - unghiul opus laturii b a triunghiului
γ - unghiul opus laturii c a triunghiului
h A, h b , h c- înălțimea triunghiului, coborâtă pe latura a, b, c

Vă rugăm să rețineți că notația dată corespunde figurii de mai sus, astfel încât atunci când rezolvați o problemă reală de geometrie, vă va fi mai ușor din punct de vedere vizual să înlocuiți valorile corecte în locurile potrivite din formulă.

• Aria triunghiului este jumătate din produsul înălțimii unui triunghi și lungimea laturii pe care se coboară această înălțime(Formula 1). Corectitudinea acestei formule poate fi înțeleasă logic. Înălțimea coborâtă la bază va împărți un triunghi arbitrar în două dreptunghiulare. Dacă completăm fiecare dintre ele într-un dreptunghi cu dimensiunile b și h, atunci, evident, aria acestor triunghiuri va fi egală cu exact jumătate din aria dreptunghiului (Spr = bh)
• Aria triunghiului este jumătate din produsul celor două laturi ale sale și sinusul unghiului dintre ele(Formula 2) (vezi un exemplu de rezolvare a unei probleme folosind această formulă mai jos). În ciuda faptului că pare diferit de precedentul, poate fi ușor transformat în el. Dacă coborâm înălțimea de la unghiul B la latura b, rezultă că produsul laturii a și sinusul unghiului γ, conform proprietăților sinusului într-un triunghi dreptunghic, este egal cu înălțimea triunghiului desenat de noi, care ne va da formula anterioară
• Aria unui triunghi arbitrar poate fi găsită prin muncă jumătate din raza unui cerc înscris în el prin suma lungimilor tuturor laturilor sale(Formula 3), cu alte cuvinte, trebuie să înmulțiți jumătatea perimetrului triunghiului cu raza cercului înscris (este mai ușor de reținut în acest fel)
• Aria unui triunghi arbitrar poate fi găsită prin împărțirea produsului tuturor laturilor sale la 4 raze ale cercului circumscris în jurul lui (Formula 4)
• Formula 5 este găsirea aria unui triunghi în funcție de lungimile laturilor și semiperimetrului său (jumătate din suma tuturor laturilor sale)
• Formula lui Heron(6) este o reprezentare a aceleiași formule fără a utiliza conceptul de semiperimetru, doar prin lungimile laturilor
• Aria unui triunghi arbitrar este egală cu produsul dintre pătratul laturii triunghiului și sinusurile unghiurilor adiacente acestei laturi împărțit la sinusul dublu al unghiului opus acestei laturi (Formula 7)
• Aria unui triunghi arbitrar poate fi găsită ca produsul a două pătrate ale unui cerc circumscris în jurul lui și sinusurile fiecăruia dintre unghiurile sale. (Formula 8)
• Dacă lungimea unei laturi și mărimea celor două unghiuri adiacente acesteia sunt cunoscute, atunci aria triunghiului poate fi găsită ca pătratul acestei laturi, împărțit la suma dublă a cotangentelor acestora. unghiuri (Formula 9)
• Dacă se cunoaște doar lungimea fiecăreia dintre înălțimile unui triunghi (Formula 10), atunci aria unui astfel de triunghi este invers proporțională cu lungimile acestor înălțimi, așa cum este formula lui Heron
• Formula 11 vă permite să calculați aria unui triunghi în funcție de coordonatele vârfurilor sale, care sunt date ca valori (x;y) pentru fiecare dintre vârfuri. Vă rugăm să rețineți că valoarea rezultată trebuie luată modulo, deoarece coordonatele vârfurilor individuale (sau chiar ale tuturor) pot fi în zona valorilor negative

Notă. Următoarele sunt exemple de rezolvare a problemelor de geometrie pentru a găsi aria unui triunghi. Dacă trebuie să rezolvați o problemă de geometrie, similară cu care nu este aici - scrieți despre ea pe forum. În soluții, funcția sqrt() poate fi folosită în locul simbolului „rădăcină pătrată”, în care sqrt este simbolul rădăcinii pătrate, iar expresia radicalului este indicată între paranteze.Uneori simbolul poate fi folosit pentru expresii radicale simple √

Sarcină. Aflați aria dată celor două laturi și unghiul dintre ele

Laturile triunghiului sunt de 5 si 6 cm.Unghiul dintre ele este de 60 de grade. Găsiți aria unui triunghi.

Soluţie.

Pentru a rezolva această problemă, folosim formula numărul doi din partea teoretică a lecției.
Aria unui triunghi poate fi găsită prin lungimile a două laturi și sinusul unghiului dintre ele și va fi egală cu
S=1/2 ab sin γ

Deoarece avem toate datele necesare pentru soluție (conform formulei), putem înlocui doar valorile din enunțul problemei în formula:
S=1/2*5*6*sin60

În tabelul de valori funcții trigonometrice găsiți și înlocuiți în expresie valoarea sinusului 60 de grade. Va fi egal cu rădăcina lui trei câte doi.
S = 15 √3 / 2

Răspuns: 7,5 √3 (în funcție de cerințele profesorului, probabil că este posibil să lăsați 15 √3/2)

Sarcină. Aflați aria unui triunghi echilateral

Aflați aria unui triunghi echilateral cu latura de 3 cm.

Soluție.

Aria unui triunghi poate fi găsită folosind formula lui Heron:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))

Deoarece a \u003d b \u003d c, formula pentru aria unui triunghi echilateral va lua forma:

S = √3 / 4 * a2

S = √3 / 4 * 3 2

Răspuns: 9 √3 / 4.

Sarcină. Schimbarea suprafeței la modificarea lungimii laturilor

De câte ori va crește aria unui triunghi dacă laturile sunt de patru ori?

Soluţie.

Deoarece dimensiunile laturilor triunghiului ne sunt necunoscute, pentru a rezolva problema vom presupune că lungimile laturilor sunt, respectiv, egale cu numerele arbitrare a, b, c. Apoi, pentru a răspunde la întrebarea problemei, găsim zona triunghi datși apoi găsiți aria unui triunghi ale cărui laturi sunt de patru ori mai mari. Raportul dintre ariile acestor triunghiuri ne va oferi răspunsul la problemă.

În continuare, oferim o explicație textuală a soluției problemei în pași. Cu toate acestea, la sfârșit, aceeași soluție este prezentată într-o formă grafică care este mai convenabilă pentru percepție. Cei care doresc pot retrage imediat soluția.

Pentru a rezolva, folosim formula Heron (vezi mai sus în partea teoretică a lecției). Arata cam asa:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(vezi prima linie a imaginii de mai jos)

Lungimile laturilor unui triunghi arbitrar sunt date de variabilele a, b, c.
Dacă laturile sunt mărite de 4 ori, atunci aria noului triunghi c va fi:

S 2 = 1/4 pătrat((4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c))
(vezi a doua linie din imaginea de mai jos)

După cum puteți vedea, 4 este un factor comun care poate fi scos din paranteze din toate cele patru expresii conform reguli generale matematică.
Apoi

S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - pe a treia linie a imaginii
S 2 = 1/4 sqrt(256 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - a patra linie

Din numărul 256 se extrage perfect rădăcina pătrată, așa că o vom scoate de sub rădăcină
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(vezi a cincea linie a figurii de mai jos)

Pentru a răspunde la întrebarea pusă în problemă, este suficient să împărțim aria triunghiului rezultat cu aria celui original.
Determinăm rapoartele ariei împărțind expresiile unele în altele și reducând fracția rezultată.

Triunghiul este una dintre cele mai comune forme geometrice, cu care suntem deja familiarizați școală primară. Întrebarea cum să găsești aria unui triunghi se confruntă de fiecare student la lecțiile de geometrie. Deci, care sunt caracteristicile găsirii zonei unei cifre date care pot fi distinse? În acest articol, vom lua în considerare formulele de bază necesare pentru a finaliza o astfel de sarcină și, de asemenea, vom analiza tipurile de triunghiuri.

Tipuri de triunghiuri

Puteți găsi cu siguranță aria unui triunghi căi diferite, deoarece în geometrie există mai mult de un tip de figură care conține trei unghiuri. Aceste tipuri includ:

• obtuz.
• Echilateral (corect).
• Triunghi dreptunghic.
• Isoscel.

Să aruncăm o privire mai atentă la fiecare dintre ele tipurile existente triunghiuri.

O astfel de figură geometrică este considerată cea mai comună în rezolvarea problemelor geometrice. Când devine necesar să desenați un triunghi arbitrar, această opțiune vine în ajutor.

Într-un triunghi ascuțit, după cum sugerează și numele, toate unghiurile sunt acute și se adună până la 180°.

Un astfel de triunghi este, de asemenea, foarte comun, dar este oarecum mai puțin comun decât unul cu unghi ascuțit. De exemplu, atunci când rezolvați triunghiuri (adică știți mai multe dintre laturile și unghiurile sale și trebuie să găsiți elementele rămase), uneori trebuie să determinați dacă unghiul este obtuz sau nu. Cosinusul este un număr negativ.

În valoarea unuia dintre unghiuri depășește 90°, astfel încât celelalte două unghiuri pot lua valori mici (de exemplu, 15° sau chiar 3°).

Pentru a găsi aria unui triunghi de acest tip, trebuie să cunoașteți câteva dintre nuanțe, despre care vom vorbi în continuare.

Triunghiuri regulate și isoscele

poligon regulat O figură se numește o figură care include n unghiuri, în care toate laturile și unghiurile sunt egale. Acesta este triunghiul dreptunghic. Deoarece suma tuturor unghiurilor unui triunghi este de 180°, fiecare dintre cele trei unghiuri este de 60°.

Triunghiul dreptunghic, datorită proprietății sale, este numit și figură echilaterală.

De asemenea, este de remarcat faptul că un singur cerc poate fi înscris într-un triunghi obișnuit și un singur cerc poate fi circumscris în jurul lui, iar centrele lor sunt situate într-un punct.

Pe lângă tipul echilateral, se poate distinge și un triunghi isoscel, care diferă ușor de acesta. Într-un astfel de triunghi, două laturi și două unghiuri sunt egale între ele, iar a treia latură (la care unghiuri egale) este baza.

Figura prezintă un triunghi isoscel DEF, ale cărui unghiuri D și F sunt egale, iar DF ​​este baza.

Triunghi dreptunghic

Un triunghi dreptunghic este numit astfel deoarece unul dintre unghiurile sale este un unghi drept, adică egal cu 90°. Celelalte două unghiuri se adună până la 90°.

Cea mai mare latură a unui astfel de triunghi, care se află opus unui unghi de 90 °, este ipotenuza, în timp ce celelalte două laturi ale sale sunt catetele. Pentru acest tip de triunghiuri se aplică teorema lui Pitagora:

Suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei.

Figura prezintă un triunghi dreptunghic BAC cu ipotenuza AC și catetele AB și BC.

Pentru a găsi aria unui triunghi cu unghi drept, trebuie să cunoașteți valorile numerice ale catetelor sale.

Să trecem la formulele pentru găsirea ariei unei figuri date.

Formule de bază pentru găsirea zonei

În geometrie, se pot distinge două formule care sunt potrivite pentru a găsi aria celor mai multe tipuri de triunghiuri, și anume pentru unghi ascuți, unghi obtuz, regulat și triunghiuri isoscele. Să analizăm fiecare dintre ele.

După lateral și înălțime

Această formulă este universală pentru găsirea zonei figurii pe care o luăm în considerare. Pentru a face acest lucru, este suficient să cunoașteți lungimea laturii și lungimea înălțimii trasate pe ea. Formula în sine (jumătate din produsul bazei și înălțimea) este următoarea:

unde A este latura triunghiului dat și H este înălțimea triunghiului.

De exemplu, pentru a găsi aria unui triunghi cu unghi ascuțit ACB, trebuie să înmulțiți latura AB cu înălțimea CD și să împărțiți valoarea rezultată la două.

Cu toate acestea, nu este întotdeauna ușor să găsiți aria unui triunghi în acest fel. De exemplu, pentru a utiliza această formulă pentru un triunghi obtuz în unghi, trebuie să continuați una dintre laturile sale și abia apoi să desenați o înălțime la ea.

În practică, această formulă este folosită mai des decât altele.

Două laturi și un colț

Această formulă, ca și cea anterioară, este potrivită pentru majoritatea triunghiurilor și, în sensul ei, este o consecință a formulei de găsire a ariei de latura și înălțimea unui triunghi. Adică formula luată în considerare poate fi derivată cu ușurință din cea anterioară. Formularea lui arată astfel:

S = ½*sinO*A*B,

unde A și B sunt laturile triunghiului și O este unghiul dintre laturile A și B.

Amintiți-vă că sinusul unui unghi poate fi vizualizat într-un tabel special numit după remarcabilul matematician sovietic V. M. Bradis.

Și acum să trecem la alte formule care sunt potrivite doar pentru tipuri excepționale de triunghiuri.

Aria unui triunghi dreptunghic

Pe lângă formula universală, care include necesitatea de a desena o înălțime într-un triunghi, aria unui triunghi care conține un unghi drept poate fi găsită din picioarele sale.

Deci, aria unui triunghi care conține un unghi drept este jumătate din produsul catetelor sale sau:

unde a și b sunt catetele unui triunghi dreptunghic.

triunghi dreptunghic

Acest tip de figuri geometrice se distinge prin faptul că aria sa poate fi găsită cu valoarea specificată doar a uneia dintre laturile sale (deoarece toate laturile unui triunghi obișnuit sunt egale). Deci, după ce ați îndeplinit sarcina de a „găsi aria unui triunghi când laturile sunt egale”, trebuie să utilizați următoarea formulă:

S = A 2 *√3 / 4,

unde A este latura unui triunghi echilateral.

Formula lui Heron

Ultima opțiune pentru găsirea ariei unui triunghi este formula lui Heron. Pentru a-l folosi, trebuie să cunoașteți lungimile celor trei laturi ale figurii. Formula lui Heron arată astfel:

S = √p (p - a) (p - b) (p - c),

unde a, b și c sunt laturile triunghiului dat.

Uneori, sarcina este dată: „aria unui triunghi obișnuit este de a găsi lungimea laturii sale”. În acest caz, trebuie să utilizați formula deja cunoscută de noi pentru a găsi aria unui triunghi obișnuit și să obțineți din aceasta valoarea laturii (sau pătratul său):

A 2 \u003d 4S / √3.

Probleme de examen

Există multe formule în sarcinile GIA în matematică. În plus, destul de des este necesar să găsiți aria unui triunghi pe hârtie în carouri.

În acest caz, cel mai convenabil este să desenați înălțimea pe una dintre laturile figurii, să determinați lungimea acesteia prin celule și să utilizați formula universală pentru găsirea zonei:

Deci, după ce ați studiat formulele prezentate în articol, nu veți avea probleme în a găsi aria unui triunghi de orice fel.