Ce este o funcție și formula ei generală. Concepte de bază și proprietăți ale funcțiilor

Confidențialitatea dumneavoastră este importantă pentru noi. Din acest motiv, am dezvoltat o Politică de confidențialitate care descrie modul în care folosim și stocăm informațiile dumneavoastră. Vă rugăm să citiți politica noastră de confidențialitate și să ne spuneți dacă aveți întrebări.

Colectarea și utilizarea informațiilor personale

Informațiile personale se referă la date care pot fi folosite pentru a identifica sau contacta o anumită persoană.

Vi se poate cere să furnizați informațiile dumneavoastră personale în orice moment când ne contactați.

Următoarele sunt câteva exemple de tipuri de informații personale pe care le putem colecta și modul în care putem folosi aceste informații.

Ce informații personale colectăm:

• Când trimiteți o cerere pe site, este posibil să colectăm diverse informații, inclusiv numele dvs., numărul de telefon, adresa de e-mail etc.

Cum folosim informațiile dumneavoastră personale:

• Informațiile personale pe care le colectăm ne permit să vă contactăm și să vă informăm despre oferte unice, promoții și alte evenimente și evenimente viitoare.
• Din când în când, putem folosi informațiile dumneavoastră personale pentru a vă trimite notificări și comunicări importante.
• De asemenea, putem folosi informații personale în scopuri interne, cum ar fi efectuarea de audituri, analize de date și diverse cercetări pentru a îmbunătăți serviciile pe care le oferim și pentru a vă oferi recomandări cu privire la serviciile noastre.
• Dacă participați la o extragere cu premii, un concurs sau un stimulent similar, este posibil să folosim informațiile pe care le furnizați pentru a administra astfel de programe.

Dezvăluirea către terți

Nu dezvăluim informațiile primite de la dumneavoastră către terți.

Excepții:

• Dacă este necesar - în conformitate cu legea, ordin judiciar, în proceduri judiciare și/sau pe baza unor solicitări publice sau solicitări din partea organelor de stat de pe teritoriul Federației Ruse - de a vă dezvălui informațiile personale. De asemenea, putem dezvălui informații despre dumneavoastră dacă stabilim că o astfel de dezvăluire este necesară sau adecvată pentru securitate, aplicarea legii sau alte scopuri de interes public.
• În cazul unei reorganizări, fuziuni sau vânzări, putem transfera informațiile personale pe care le colectăm către succesorul terț relevant.

Protecția informațiilor personale

Luăm măsuri de precauție - inclusiv administrative, tehnice și fizice - pentru a vă proteja informațiile personale împotriva pierderii, furtului și utilizării greșite, precum și împotriva accesului, dezvăluirii, modificării și distrugerii neautorizate.

Menținerea confidențialității la nivel de companie

Pentru a ne asigura că informațiile dumneavoastră personale sunt în siguranță, comunicăm angajaților noștri practicile de confidențialitate și securitate și aplicăm strict practicile de confidențialitate.

Secțiunea conține materiale de referință despre funcțiile elementare de bază și proprietățile acestora. Se da clasificarea functii elementare. Mai jos sunt legături către subsecțiuni care discută proprietățile funcțiilor specifice - grafice, formule, derivate, antiderivate (integrale), expansiuni în serie, expresii în termeni de variabile complexe.

Pagini de referință pentru funcții elementare

Clasificarea funcţiilor elementare

Funcția algebrică este o funcție care satisface ecuația:
,
unde este un polinom în variabila dependentă y și variabila independentă x . Se poate scrie ca:
,
unde sunt polinoame.

Funcțiile algebrice sunt împărțite în polinoame (funcții raționale întregi), funcții raționale și funcții iraționale.

Întreaga funcție rațională, care se mai numește polinom sau polinom, se obține din variabila x și un număr finit de numere folosind operatii aritmetice adunarea (scăderea) și înmulțirea. După deschiderea parantezelor, polinomul se reduce la forma canonică:
.

Funcție rațională fracțională, sau pur și simplu functie rationala, se obține din variabila x și un număr finit de numere folosind operațiile aritmetice de adunare (scădere), înmulțire și împărțire. Funcția rațională poate fi redusă la forma
,
unde și sunt polinoame.

Funcția irațională este o funcție algebrică care nu este rațională. De regulă, o funcție irațională este înțeleasă ca rădăcini și compozițiile lor cu funcții raționale. O rădăcină de grad n este definită ca o soluție a ecuației
.
Este marcat astfel:
.

Funcții transcendente se numesc funcţii non-algebrice. Acestea sunt funcții exponențiale, trigonometrice, hiperbolice și inverse.

Prezentare generală a funcțiilor elementare de bază

Toate funcțiile elementare pot fi reprezentate ca un număr finit de operații de adunare, scădere, înmulțire și împărțire efectuate pe o expresie de forma:
z t .
Funcțiile inverse pot fi exprimate și în termeni de logaritmi. Principalele funcții elementare sunt enumerate mai jos.

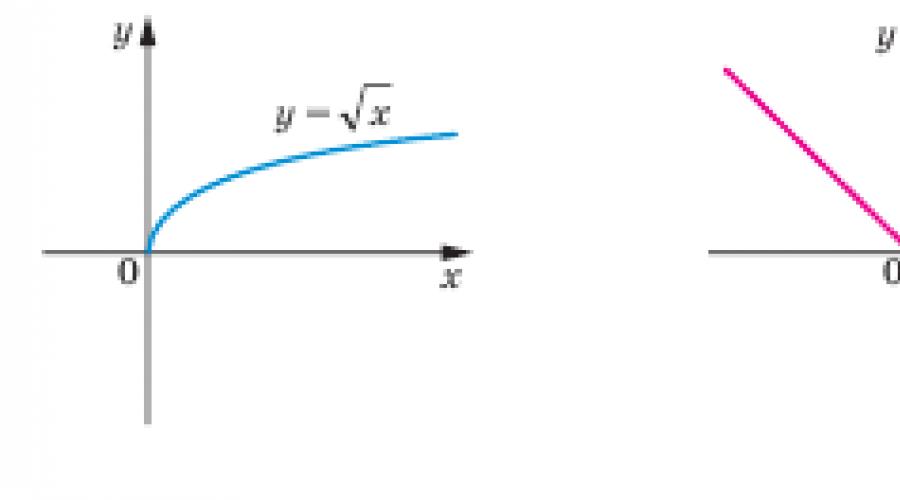
Funcția de putere:
y(x) = x p ,
unde p este exponentul. Depinde de baza lui x.
Inversa unei funcții de putere este, de asemenea, o funcție de putere:
.
Pentru o valoare întreagă nenegativă a exponentului p, este un polinom. Pentru o valoare întreagă p este o funcție rațională. Cu o valoare rațională - o funcție irațională.

Funcții transcendente

Functie exponentiala :
y(x) = a x ,
unde a este baza gradului. Depinde de exponentul x.
Funcția inversă este logaritmul la baza a:
x= log a y.

Exponent, e la puterea lui x:
y(x) = e x ,
Aceasta este o funcție exponențială a cărei derivată este egală cu funcția în sine:
.
Baza exponentului este numărul e:
≈ 2,718281828459045... .
Funcție inversă - logaritm natural - logaritm la baza lui e :
x= ln y ≡ log e y.

Funcții trigonometrice:
Sinus : ;
Cosinus : ;
Tangenta : ;
Cotangent : ;
Aici i este o unitate imaginară, i 2 = -1.

Funcții trigonometrice inverse:
Arcsin: x = arcsin y, ;
Arccozin: x = arc cos y, ;
Arctangent: x = arctg y, ;
Arc tangentă: x = arcctg y, .

Pentru a înțelege acest subiect, luați în considerare funcția afișată pe grafic // Să arătăm cum graficul funcției vă permite să determinați proprietățile sale.

Analizăm proprietățile unei funcții folosind un exemplu

Domeniul de aplicare al funcției este yavl. interval [ 3,5; 5.5].

Domeniul funcției yavl. interval [ 1; 3].

1. La x = -3, x = - 1, x = 1,5, x = 4,5, valoarea funcției este zero.

Valoarea argumentului, la care valoarea funcției este zero, se numește zero al funcției.

//acestea. pentru aceasta functie numerele -3;-1;1,5; 4,5 sunt zerouri.

2. Pe intervalele [ 4,5; 3) și (1; 1.5) și (4.5; 5.5] graficul funcției f este situat deasupra axei absciselor, iar la intervale (-3; -1) și (1.5; 4.5) sub axa absciselor, aceasta este explicat după cum urmează - la intervale[4,5; 3) și (1; 1.5) și (4.5; 5.5] funcția ia valori pozitive, iar pe intervalele (-3; -1) și (1,5; 4,5) sunt negative.

Fiecare dintre intervalele indicate (unde funcția ia valori de același semn) se numește interval de semn constant al funcției f.//i.e. de exemplu, dacă luăm intervalul (0; 3), atunci nu este un interval cu semn constant al funcției date.

În matematică, când se caută intervale cu semn constant al unei funcții, se obișnuiește să se indice intervale de lungime maximă. //Acestea. intervalul (2; 3) este interval de constanță funcția f, dar răspunsul trebuie să includă intervalul [ 4,5; 3) conţinând intervalul (2; 3).

3. Dacă vă deplasați de-a lungul axei x de la 4,5 la 2, veți observa că graficul funcției scade, adică valorile funcției scad. //La matematică, se obișnuiește să se spună că pe intervalul [ 4,5; 2] funcția este în scădere.

Pe măsură ce x crește de la 2 la 0, graficul funcției crește, adică. valorile funcției cresc. //La matematică, se obișnuiește să se spună că pe intervalul [ 2; 0] funcția este în creștere.

Funcția f este numită dacă pentru oricare două valori ale argumentului x1 și x2 din acest interval astfel încât x2 > x1, inegalitatea f (x2) > f (x1) este satisfăcută. // sau Funcția este apelată crescând într-un anumit interval, dacă pentru orice valori ale argumentului din acest interval valoare mai mare argument corespunde valorii mai mari a funcției.//i.e. cu cât mai mult x, cu atât mai mult y.

Se apelează funcția f scăzând într-un anumit interval, dacă pentru oricare două valori ale argumentului x1 și x2 din acest interval astfel încât x2 > x1, inegalitatea f(x2) descrescătoare pe un anumit interval este satisfăcută, dacă pentru orice valoare a argumentului din acest interval este satisfăcută o mai mare valoarea argumentului corespunde unei valori mai mici a funcției. //acestea. cu cât mai mult x, cu atât mai puțin y.

Dacă o funcție crește pe întregul domeniu de definiție, atunci este numită crescând.

Dacă o funcție este în scădere pe întregul domeniu de definiție, atunci este numită în scădere.

Exemplul 1 grafic al funcțiilor crescătoare și, respectiv, descrescătoare.

Exemplul 2

Definiți yavl. dacă funcție liniară f(x) = 3x + 5 crescător sau descrescător?

Dovada. Să folosim definițiile. Fie x1 și x2 valori arbitrare ale argumentului și x1< x2., например х1=1, х2=7

1) Domeniul de aplicare și domeniul de funcționare.

Sfera unei funcții este setul tuturor valorilor valide valide ale argumentului X(variabil X) pentru care funcţia y = f(x) definit. Domeniul unei funcții este mulțimea tuturor valorilor reale y pe care funcția le acceptă.

În matematica elementară, funcțiile sunt studiate numai pe mulțimea numerelor reale.

2) Zerourile funcției.

Zero al funcției este valoarea argumentului la care valoarea funcției este egală cu zero.

3) Intervale de constanță a semnului unei funcții.

Intervalele de semn constant ale unei funcții sunt astfel de seturi de valori argument pe care valorile funcției sunt doar pozitive sau numai negative.

4) Monotonitatea funcției.

O funcție crescătoare (într-un anumit interval) este o funcție în care o valoare mai mare a argumentului din acest interval îi corespunde unei valori mai mari a funcției.

Funcție descrescătoare (într-un anumit interval) - o funcție în care o valoare mai mare a argumentului din acest interval corespunde unei valori mai mici a funcției.

5) Funcții pare (impare)..

O funcție pară este o funcție al cărei domeniu de definiție este simetric față de origine și pentru oricare X din domeniul definirii egalitatea f(-x) = f(x). Graficul unei funcții pare este simetric față de axa y.

O funcție impară este o funcție al cărei domeniu de definiție este simetric față de origine și pentru oricare X din domeniul definirii egalitatea f(-x) = - f(x). Graficul unei funcții impare este simetric față de origine.

6) Funcții limitate și nelimitate.

O funcție se numește mărginită dacă există un număr pozitiv M astfel încât |f(x)| ≤ M pentru toate valorile lui x. Dacă nu există un astfel de număr, atunci funcția este nelimitată.

7) Periodicitatea funcției.

O funcție f(x) este periodică dacă există un număr T diferit de zero, astfel încât pentru orice x din domeniul funcției, f(x+T) = f(x). Acest număr cel mai mic se numește perioada funcției. Toate funcțiile trigonometrice sunt periodice. (Formulele trigonometrice).

19. Funcții elementare de bază, proprietățile și graficele lor. Aplicarea funcțiilor în economie.

Funcții elementare de bază. Proprietățile și graficele lor

1. Funcția liniară.

Funcție liniară se numește funcție de forma , unde x este o variabilă și b sunt numere reale.

Număr A numit factor de pantă drept, el egal cu tangenta unghiul de înclinare al acestei drepte față de direcția pozitivă a axei x. Graficul unei funcții liniare este o linie dreaptă. Este definit de două puncte.

Proprietățile funcției liniare

1. Domeniul definiției - mulțimea tuturor numerelor reale: D (y) \u003d R

2. Mulțimea valorilor este mulțimea tuturor numerelor reale: E(y)=R

3. Funcția ia o valoare zero pentru sau.

4. Funcția crește (descrește) pe întregul domeniu de definire.

5. Funcția liniară este continuă pe întregul domeniu al definiției, diferențiabilă și .

2. Funcția pătratică.

O funcție de forma, unde x este o variabilă, coeficienții a, b, c sunt numere reale, se numește pătratică.

Limite și continuitate

Seturi

Sub mulți este înțeles ca un ansamblu de obiecte omogene. Obiectele care formează o mulțime sunt numite elemente sau puncte acest set. Seturile denotă litere mari, iar elementele lor sunt inline. Dacă A este un element al ansamblului A, apoi notația AÎ A. Dacă b nu este un element al setului A, atunci se scrie asa: b Ï A. O mulţime care nu conţine un singur element se numeşte mulţime goală şi se notează astfel: Ø.

Dacă setul B este format dintr-o parte din elementele multimii A sau coincide cu ea, apoi setul B numit subset mulţimi şi denotă BÌ A.

Cele două seturi sunt numite egal dacă sunt formate din aceleaşi elemente.

Asociere doua seturi AȘi B se numeste multime C, constând din toate elementele aparținând cel puțin unuia dintre mulțimile: C=AÈ B.

trecere doua seturi AȘi B se numeste multime C, constând din toate elementele aparținând fiecăruia dintre mulțimile date: C=AÇ B.

diferență seturi AȘi B se numeste multime E A, care nu aparțin setului B: .

Supliment seturi AÌ B se numeste multime C, format din toate elementele setului B, neaparținând A.

Se numesc multimi ale caror elemente sunt numere reale numeric:

în care NÌ ZÌ QÌ R, euÌ RȘi R=euÈ Q.

O multime de X, ale cărui elemente satisfac inegalitatea se numește segment(segment) și notat cu [ A; b]; inegalitate A<X<b – intervalși se notează cu () ; inegalități și - semiintervaleși sunt notate cu și, respectiv. De asemenea, de multe ori trebuie să vă ocupați de intervale infinite și semiintervale: , , , și . Este convenabil să le sunați pe toate la intervale .

Interval, adică setul de puncte care satisfac inegalitatea (unde), se numeste -vecinatatea punctului A.

Conceptul de funcție. Principalele proprietăți ale funcției

Dacă fiecare element X seturi X un singur element este potrivit y seturi Y, apoi spunem asta pe platou X dat funcţie y=f(X). în care X numit variabila independenta sau argument, A y – variabilă dependentă sau funcţie, A f reprezintă legea corespondenței. O multime de X numit domeniul definirii funcții, ci setul Y – gamă funcții.

Există mai multe moduri de a defini funcțiile.

1) Metoda analitica - functia este data printr-o formula a formei y=f(X).

2) Metoda tabulară - funcția este definită de un tabel care conține valorile argumentului și valorile funcției corespunzătoare y=f(X).

3) Metoda grafica - imaginea graficului functiei, i.e. set de puncte ( X; y) din planul de coordonate, ale cărui abscise reprezintă valorile argumentului, iar ordonatele sunt valorile corespunzătoare ale funcției y=f(X).

4) Metoda verbală - funcția este descrisă de regula compilării ei. De exemplu, funcția Dirichlet ia valoarea 1 dacă X este un număr rațional și 0 dacă X este un număr irațional.

Se disting următoarele proprietăți principale ale funcțiilor.

1 Par și impar Funcţie y=f(X) se numește chiar, dacă pentru orice valoare X din domeniul definirii sale, f(–X)=f(X), Și ciudat, Dacă f(–X)=–f(X). Dacă niciuna dintre ecuațiile de mai sus nu este valabilă, atunci y=f(X) se numește functia generala. Graficul unei funcții pare este simetric față de axă Oi, iar graficul unei funcții impare este simetric față de origine.

2 Monotonie Funcţie y=f(X) se numește crescând (în scădere) pe interval X, dacă valoarea mai mare a argumentului din acest interval corespunde valorii mai mari (mai mici) a funcției. Lăsa X 1 ,X 2 О X, X 2 >X 1 . Apoi funcția crește pe interval X, Dacă f(X 2)>f(X 1) și scade dacă f(X 2)<f(X 1).

Alături de funcțiile crescătoare și descrescătoare, sunt luate în considerare funcțiile nedescrescătoare și necrescătoare. Funcția este numită nedescrescătoare (necrescătoare), dacă X 1 ,X 2 О X, X 2 >X 1 inegalitatea f(X 2)≥f(X 1) (f(X 2)≤f(X 1)).

Funcțiile crescătoare și descrescătoare, precum și funcțiile necrescătoare și nedescrescătoare, se numesc monotone.

3 Limitat Funcţie y=f(X) se numește mărginit pe interval X dacă există un număr atât de pozitiv M>0, ce | f(X)|≤M pentru oricine XÎ X. În caz contrar, funcția se numește nelimitată pe X.

4 Periodicitatea Funcţie y=f(X) se numește periodic cu punct T≠0 dacă pentru oricare Xîn afara domeniului de aplicare f(X+T)=f(X). În cele ce urmează, o perioadă va fi înțeleasă ca fiind cea mai mică perioadă pozitivă a unei funcții.

Funcția este numită explicit, dacă este dat de o formulă de formă y=f(X). Dacă funcția este dată de ecuație F(X, y)=0 nu este permis în raport cu variabila dependentă y, atunci se numește implicit.

Lăsa y=f(X) este o funcție a variabilei independente definite pe mulțime X cu raza de actiune Y. Să potrivim fiecare yÎ Y sens unic XÎ X, la care f(X)=y.Apoi functia rezultata X=φ (y) definite pe platou Y cu raza de actiune X, se numește versoși notat y=f –1 (X). Grafice reciproc funcții inverse sunt simetrice față de bisectoarea primului și al treilea sferturi de coordonate.

Lasă funcția y=f(u) este o funcție a variabilei u definite pe platou U cu raza de actiune Y, și variabila u la rândul său este o funcție u=φ (X) definite pe platou X cu raza de actiune U. Apoi dat pe platou X funcţie y=f(φ (X)) se numește functie complexa (compunerea funcțiilor, suprapunerea funcțiilor, funcția unei funcții).

Funcții elementare

Principalele funcții elementare includ:

• functie de putere y=x n; y=x-nȘi y=X 1/ n;
• functie exponentiala y=un x;
• funcţie logaritmică y=log un x;
• funcții trigonometrice y=păcat X, y= cos X, y=tg XȘi y=ctg X;
• funcții trigonometrice inverse y= arcsin X, y= arccos X, y=arctg XȘi y=arctg X.

Din funcțiile elementare de bază se pot obține funcții noi folosind operații algebrice și suprapunerea funcțiilor.

Funcțiile construite din funcții elementare de bază folosind un număr finit de operații algebrice și un număr finit de operații de suprapunere se numesc elementar.

Algebric este o funcție în care se efectuează un număr finit de operații algebrice asupra argumentului. Funcțiile algebrice includ:

întreaga funcție rațională (polinom sau polinom)

funcție rațională fracțională (raportul a două polinoame)

funcție irațională (dacă operațiunile pe argument includ extragerea rădăcinilor).

Se numește orice funcție non-algebrică transcendent. Funcțiile transcendentale includ funcții exponențiale, logaritmice, trigonometrice, trigonometrice inverse.