Lineare Gleichungen. Der komplette Leitfaden (2019)
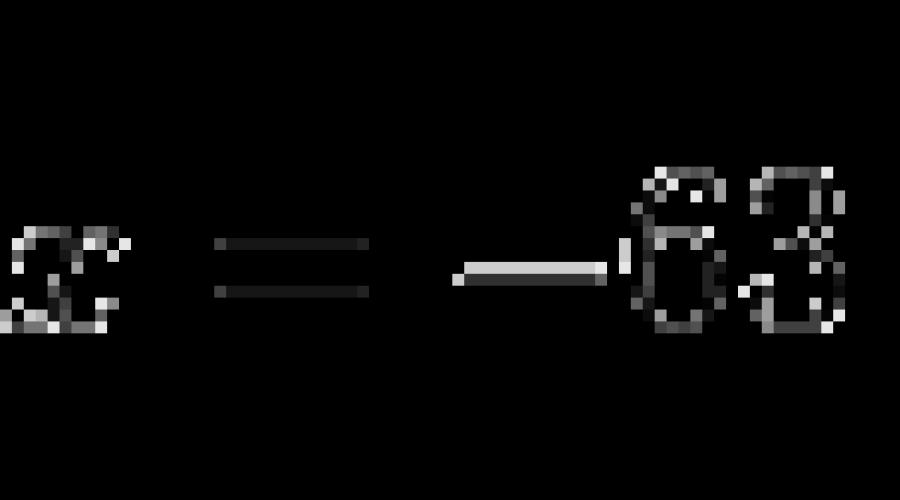
Lesen Sie auch
Gleichungen. Anders ausgedrückt: Die Lösung aller Gleichungen beginnt mit diesen Transformationen. Bei der Entscheidung lineare Gleichungen, es (die Lösung) basiert auf Identitätstransformationen und endet mit der endgültigen Antwort.
Der Fall eines Koeffizienten ungleich Null für eine unbekannte Variable.
ax+b=0, a ≠ 0
Wir verschieben Terme mit X auf die eine Seite und Zahlen auf die andere Seite. Denken Sie unbedingt daran, dass Sie beim Verschieben von Termen auf die entgegengesetzte Seite der Gleichung das Vorzeichen ändern müssen:
ax:(a)=-b:(a)
Lassen Sie uns abkürzen A bei X und wir bekommen:
x=-b:(a)
Das ist die Antwort. Wenn Sie überprüfen müssen, ob eine Nummer vorhanden ist -b:(a) Wurzel unserer Gleichung, dann müssen wir stattdessen die ursprüngliche Gleichung einsetzen X das ist die Nummer:
a(-b:(a))+b=0 ( diese. 0=0)
Weil Diese Gleichheit ist also richtig -b:(a) und die Wahrheit ist die Wurzel der Gleichung.
Antwort: x=-b:(a), a ≠ 0.
Erstes Beispiel:
5x+2=7x-6
Wir verschieben Mitglieder mit auf eine Seite X, und auf der anderen Seite die Zahlen:
5x-7x=-6-2
-2x:(-2)=-8:(-2)
Für einen unbekannten Faktor haben wir den Koeffizienten reduziert und die Antwort erhalten:
Das ist die Antwort. Wenn Sie überprüfen müssen, ob die Zahl 4 wirklich die Wurzel unserer Gleichung ist, ersetzen wir diese Zahl anstelle von X in der ursprünglichen Gleichung:
5*4+2=7*4-6 ( diese. 22=22)
Weil Wenn diese Gleichheit wahr ist, dann ist 4 die Wurzel der Gleichung.
Zweites Beispiel:
Löse die Gleichung:
5x+14=x-49
Indem wir die Unbekannten und Zahlen in verschiedene Richtungen verschieben, erhalten wir:
Teilen Sie die Teile der Gleichung durch den Koeffizienten bei X(durch 4) und wir erhalten:
![]()
Drittes Beispiel:
Löse die Gleichung:
![]()
Zuerst beseitigen wir die Irrationalität im Koeffizienten für die Unbekannte, indem wir alle Terme mit multiplizieren:
![]()
![]()
Dieses Formular gilt als vereinfacht, weil Die Zahl hat die Wurzel der Zahl im Nenner. Wir müssen die Antwort vereinfachen, indem wir Zähler und Nenner mit multiplizieren selbe Nummer, wir haben das:
![]()
Der Fall, dass es keine Lösungen gibt.
Löse die Gleichung:
2x+3=2x+7
Vor allen X unsere Gleichung wird keine echte Gleichheit werden. Das heißt, unsere Gleichung hat keine Wurzeln.
Antwort: Es gibt keine Lösungen.
Ein Sonderfall sind unendlich viele Lösungen.
Löse die Gleichung:
2x+3=2x+3
Wenn wir die xs und Zahlen in verschiedene Richtungen verschieben und ähnliche Terme hinzufügen, erhalten wir die Gleichung:
Auch hier ist es nicht möglich, beide Teile durch 0 zu dividieren, weil es ist verboten. Allerdings an Ort und Stelle setzen X jede Zahl, wir erhalten die richtige Gleichheit. Das heißt, jede Zahl ist eine Lösung einer solchen Gleichung. Es gibt also unendlich viele Lösungen.
Antwort: unendlich viele Lösungen.
Der Fall der Gleichheit zweier vollständiger Formen.
ax+b=cx+d
ax-cx=d-b
(a-c)x=d-b
x=(d-b):(a-c)
Antwort: x=(d-b):(a-c), Wenn d≠b und a≠c, sonst gibt es unendlich viele Lösungen, aber wenn a=c, A d≠b, dann gibt es keine Lösungen.
Das Lösen von Gleichungen zu lernen ist eine der Hauptaufgaben der Algebra für Studierende. Beginnend mit dem Einfachsten, wenn es aus einer Unbekannten besteht, bis hin zu immer komplexeren. Wenn Sie die Aktionen, die mit den Gleichungen der ersten Gruppe ausgeführt werden müssen, nicht beherrschen, wird es schwierig sein, die anderen zu verstehen.
Um das Gespräch fortzusetzen, müssen Sie sich auf die Schreibweise einigen.
Allgemeine Form einer linearen Gleichung mit einer Unbekannten und das Prinzip ihrer Lösung
Jede Gleichung, die so geschrieben werden kann:
a * x = b,
angerufen linear. Das allgemeine Formel. Aber oft werden lineare Gleichungen in Aufgaben in impliziter Form geschrieben. Dann müssen Sie es tun Identitätstransformationen um den allgemein akzeptierten Eintrag zu erhalten. Zu diesen Aktionen gehören:
- öffnende Klammern;
- alle Begriffe verschieben mit Variable auf der linken Seite der Gleichung und der Rest auf der rechten Seite;
- Reduzierung ähnlicher Begriffe.
Für den Fall, dass im Nenner eines Bruchs eine unbekannte Größe steht, müssen Sie deren Werte bestimmen, bei denen der Ausdruck keinen Sinn ergibt. Mit anderen Worten: Sie müssen den Definitionsbereich der Gleichung kennen.
Das Prinzip, nach dem alle linearen Gleichungen gelöst werden, besteht darin, den Wert auf der rechten Seite der Gleichung durch den Koeffizienten vor der Variablen zu dividieren. Das heißt, „x“ ist gleich b/a.
Spezialfälle linearer Gleichungen und ihre Lösungen
Beim Denken können Momente auftreten, in denen lineare Gleichungen eine der Sonderformen annehmen. Jeder von ihnen hat eine spezifische Lösung.
In der ersten Situation:
a * x = 0 und a ≠ 0.
Die Lösung einer solchen Gleichung wird immer x = 0 sein.
Im zweiten Fall nimmt „a“ den Wert Null an:
0 * x = 0.
Die Antwort auf eine solche Gleichung wird eine beliebige Zahl sein. Das heißt, es hat unendlich viele Wurzeln.
Die dritte Situation sieht so aus:
0 * x = Zoll, wobei in ≠ 0.
Diese Gleichung ergibt keinen Sinn. Weil es keine Wurzeln gibt, die es befriedigen.

Gesamtansicht einer linearen Gleichung mit zwei Variablen
Aus seinem Namen wird deutlich, dass darin bereits zwei unbekannte Größen enthalten sind. Lineare Gleichungen in zwei Variablen sieht aus wie das:
a * x + b * y = c.
Da der Datensatz zwei Unbekannte enthält, sieht die Antwort wie ein Zahlenpaar aus. Das heißt, es reicht nicht aus, nur einen Wert anzugeben. Dies wird eine unvollständige Antwort sein. Ein Größenpaar, für das die Gleichung eine Identität wird, ist eine Lösung der Gleichung. Darüber hinaus wird in der Antwort immer die Variable zuerst notiert, die im Alphabet an erster Stelle steht. Manchmal heißt es, dass ihn diese Zahlen befriedigen. Darüber hinaus kann es unendlich viele solcher Paare geben.
Wie löst man eine lineare Gleichung mit zwei Unbekannten?
Dazu müssen Sie lediglich ein beliebiges Zahlenpaar auswählen, das sich als richtig herausstellt. Der Einfachheit halber können Sie eine der Unbekannten nehmen, die einer Primzahl entspricht, und dann die zweite ermitteln.
Beim Lösen müssen Sie häufig Schritte ausführen, um die Gleichung zu vereinfachen. Sie werden Identitätstransformationen genannt. Darüber hinaus gelten für Gleichungen immer die folgenden Eigenschaften:
- Jeder Begriff kann in den entgegengesetzten Teil der Gleichheit verschoben werden, indem sein Vorzeichen durch das entgegengesetzte ersetzt wird.
- Die linke und rechte Seite jeder Gleichung dürfen durch dieselbe Zahl geteilt werden, solange diese nicht gleich Null ist.

Beispiele für Aufgaben mit linearen Gleichungen
Erste Aufgabe. Lösen Sie lineare Gleichungen: 4x = 20, 8(x - 1) + 2x = 2(4 - 2x); (5x + 15) / (x + 4) = 4; (5x + 15) / (x + 3) = 4.
Teilen Sie in der Gleichung, die in dieser Liste an erster Stelle steht, einfach 20 durch 4. Das Ergebnis ist 5. Das ist die Antwort: x = 5.
Die dritte Gleichung erfordert, dass eine Identitätstransformation durchgeführt wird. Es besteht darin, die Klammern zu öffnen und ähnliche Begriffe einzufügen. Nach dem ersten Schritt nimmt die Gleichung die Form an: 8x - 8 + 2x = 8 - 4x. Dann müssen Sie alle Unbekannten auf die linke Seite der Gleichung verschieben und den Rest auf die rechte Seite. Die Gleichung sieht folgendermaßen aus: 8x + 2x + 4x = 8 + 8. Nach dem Hinzufügen ähnlicher Terme: 14x = 16. Jetzt sieht sie genauso aus wie die erste und ihre Lösung ist leicht zu finden. Die Antwort lautet x=8/7. Aber in der Mathematik soll man den ganzen Teil aus einem unechten Bruch isolieren. Dann wird das Ergebnis transformiert und „x“ entspricht einem Ganzen und einem Siebtel.
In den übrigen Beispielen stehen die Variablen im Nenner. Das bedeutet, dass Sie zunächst herausfinden müssen, bei welchen Werten die Gleichungen definiert sind. Dazu müssen Sie Zahlen ausschließen, deren Nenner gegen Null gehen. Im ersten Beispiel ist es „-4“, im zweiten „-3“. Das heißt, diese Werte müssen aus der Antwort ausgeschlossen werden. Danach müssen Sie beide Seiten der Gleichheit mit den Ausdrücken im Nenner multiplizieren.
Wenn wir die Klammern öffnen und ähnliche Terme angeben, erhalten wir in der ersten dieser Gleichungen: 5x + 15 = 4x + 16 und in der zweiten 5x + 15 = 4x + 12. Nach Transformationen lautet die Lösung der ersten Gleichung x = -1. Der zweite Wert ist gleich „-3“, was bedeutet, dass letzterer keine Lösungen hat.
Zweite Aufgabe. Lösen Sie die Gleichung: -7x + 2y = 5.
Angenommen, die erste Unbekannte x = 1, dann nimmt die Gleichung die Form -7 * 1 + 2y = 5 an. Wenn man den Faktor „-7“ auf die rechte Seite der Gleichung verschiebt und sein Vorzeichen in Plus ändert, stellt sich heraus, dass dies der Fall ist 2y = 12. Das bedeutet y =6. Antwort: eine der Lösungen der Gleichung x = 1, y = 6.

Allgemeine Form der Ungleichung mit einer Variablen
Alle möglichen Situationen für Ungleichheiten werden hier dargestellt:
- a * x > b;
- ein * x< в;
- a * x ≥b;
- a * x ≤в.
Im Allgemeinen sieht es aus wie eine einfache lineare Gleichung, nur das Gleichheitszeichen wird durch eine Ungleichung ersetzt.
Regeln für Identitätstransformationen von Ungleichheiten
Ebenso wie lineare Gleichungen können Ungleichungen nach bestimmten Gesetzen modifiziert werden. Sie laufen auf Folgendes hinaus:
- Auf der linken und rechten Seite der Ungleichung können Sie einen beliebigen Buchstaben oder hinzufügen numerischer Ausdruck, und das Ungleichheitszeichen bleibt gleich;
- Sie können auch mit derselben positiven Zahl multiplizieren oder dividieren, auch hier ändert sich das Vorzeichen nicht;
- Bei der Multiplikation oder Division mit derselben negativen Zahl bleibt die Gleichheit wahr, sofern das Ungleichheitszeichen umgekehrt wird.

Allgemeine Sicht auf doppelte Ungleichungen
Die folgenden Ungleichungen können in Problemen dargestellt werden:
- V< а * х < с;
- c ≤ a * x< с;
- V< а * х ≤ с;
- c ≤ a * x ≤ c.
Es wird doppelt genannt, weil es auf beiden Seiten durch Ungleichheitszeichen begrenzt ist. Die Lösung erfolgt nach den gleichen Regeln wie bei gewöhnlichen Ungleichungen. Und um die Antwort zu finden, kommt es auf eine Reihe identischer Transformationen an. Bis das Einfachste erreicht ist.
Merkmale der Lösung doppelter Ungleichungen
Das erste davon ist sein Bild auf der Koordinatenachse. Für einfache Ungleichungen ist diese Methode nicht erforderlich. Aber in schwierigen Fällen kann es einfach notwendig sein.
Um eine Ungleichung darzustellen, müssen Sie auf der Achse alle Punkte markieren, die während der Argumentation ermittelt wurden. Dies sind ungültige Werte, die durch punktierte Punkte gekennzeichnet sind, und Werte aus Ungleichungen, die nach Transformationen erhalten werden. Auch hier ist es wichtig, die Punkte richtig zu zeichnen. Das heißt, wenn die Ungleichung streng ist< или >, dann werden diese Werte ausgestanzt. Bei nichtstrikten Ungleichungen müssen die Punkte schattiert werden.
Dann ist es notwendig, die Bedeutung der Ungleichungen anzugeben. Dies kann durch Schattierungen oder Bögen erfolgen. Ihr Schnittpunkt gibt die Antwort an.
Das zweite Merkmal hängt mit der Aufnahme zusammen. Hier werden zwei Möglichkeiten angeboten. Die erste ist die ultimative Ungleichheit. Die zweite hat die Form von Intervallen. Bei ihm kommt es vor, dass Schwierigkeiten auftauchen. Die Antwort in Leerzeichen sieht immer wie eine Variable mit einem Zugehörigkeitszeichen und Klammern mit Zahlen aus. Manchmal gibt es mehrere Leerzeichen, dann müssen Sie das „und“-Symbol zwischen die Klammern schreiben. Diese Zeichen sehen so aus: ∈ und ∩. Auch Abstandshalter spielen eine Rolle. Der runde Punkt wird platziert, wenn der Punkt aus der Antwort ausgeschlossen wird, und der rechteckige enthält diesen Wert. Das Unendlichkeitszeichen steht immer in Klammern.

Beispiele für die Lösung von Ungleichungen
1. Lösen Sie die Ungleichung 7 - 5x ≥ 37.
Nach einfachen Transformationen erhalten wir: -5x ≥ 30. Durch Division durch „-5“ erhalten wir den folgenden Ausdruck: x ≤ -6. Dies ist bereits die Antwort, kann aber auch anders geschrieben werden: x ∈ (-∞; -6].
2. Lösen Sie die doppelte Ungleichung -4< 2x + 6 ≤ 8.
Zuerst müssen Sie überall 6 subtrahieren. Sie erhalten: -10< 2x ≤ 2. Теперь нужно разделить на 2. Неравенство примет вид: -5 < x ≤ 1. Изобразив ответ на числовой оси, сразу можно понять, что результатом будет промежуток от -5 до 1. Причем первая точка исключена, а вторая включена. То есть ответ у неравенства такой: х ∈ (-5; 1].
In diesem Video analysieren wir eine ganze Reihe linearer Gleichungen, die mit demselben Algorithmus gelöst werden – deshalb werden sie als die einfachsten bezeichnet.
Definieren wir zunächst: Was ist eine lineare Gleichung und welche wird als die einfachste bezeichnet?
Eine lineare Gleichung ist eine Gleichung, in der es nur eine Variable gibt, und zwar nur im ersten Grad.
Die einfachste Gleichung bedeutet die Konstruktion:
Alle anderen linearen Gleichungen werden mit dem Algorithmus auf die einfachste reduziert:
- Erweitern Sie ggf. Klammern.
- Verschieben Sie Begriffe, die eine Variable enthalten, auf eine Seite des Gleichheitszeichens und Begriffe ohne Variable auf die andere.
- Geben Sie links und rechts vom Gleichheitszeichen ähnliche Begriffe an;
- Teilen Sie die resultierende Gleichung durch den Koeffizienten der Variablen $x$.
Natürlich hilft dieser Algorithmus nicht immer. Tatsache ist, dass sich nach all diesen Machenschaften manchmal herausstellt, dass der Koeffizient der Variablen $x$ gleich Null ist. In diesem Fall sind zwei Optionen möglich:
- Die Gleichung hat überhaupt keine Lösungen. Wenn zum Beispiel so etwas wie $0\cdot x=8$ herauskommt, d.h. links ist Null und rechts ist eine Zahl ungleich Null. Im folgenden Video werden wir uns mehrere Gründe ansehen, warum diese Situation möglich ist.
- Die Lösung sind alle Zahlen. Dies ist nur dann möglich, wenn die Gleichung auf die Konstruktion $0\cdot x=0$ reduziert wurde. Es ist ganz logisch, dass, egal welches $x$ wir ersetzen, immer noch herauskommt: „Null ist gleich Null“, d. h. Korrekte numerische Gleichheit.
Sehen wir uns nun anhand von Beispielen aus der Praxis an, wie das alles funktioniert.
Beispiele zum Lösen von Gleichungen
Heute haben wir es mit linearen Gleichungen zu tun, und zwar nur mit den einfachsten. Im Allgemeinen bedeutet eine lineare Gleichung jede Gleichheit, die genau eine Variable enthält und nur bis zum ersten Grad reicht.
Solche Konstruktionen werden ungefähr auf die gleiche Weise gelöst:
- Zunächst müssen Sie die Klammern erweitern, falls vorhanden (wie in unserem letzten Beispiel);
- Dann ähnlich kombinieren
- Isolieren Sie abschließend die Variable, d. h. Bewegen Sie alles, was mit der Variablen zusammenhängt – die Begriffe, in denen sie enthalten ist – auf eine Seite und alles, was ohne sie übrig bleibt, auf die andere Seite.
Dann müssen Sie in der Regel auf jeder Seite der resultierenden Gleichheit ähnliche Werte angeben, und danach müssen Sie nur noch durch den Koeffizienten „x“ dividieren, und wir erhalten das endgültige Ergebnis.
In der Theorie sieht das schön und einfach aus, aber in der Praxis können sogar erfahrene Oberstufenschüler bei relativ einfachen linearen Gleichungen beleidigende Fehler machen. Typischerweise werden entweder beim Öffnen von Klammern oder bei der Berechnung der „Pluspunkte“ und „Minuspunkte“ Fehler gemacht.
Darüber hinaus kommt es vor, dass eine lineare Gleichung überhaupt keine Lösungen hat oder dass die Lösung der gesamte Zahlenstrahl ist, d. h. irgendeine Nummer. Wir werden uns diese Feinheiten in der heutigen Lektion ansehen. Aber wir beginnen, wie Sie bereits verstanden haben, mit dem Ganzen einfache Aufgaben.
Schema zur Lösung einfacher linearer Gleichungen
Lassen Sie mich zunächst noch einmal das gesamte Schema zur Lösung der einfachsten linearen Gleichungen schreiben:
- Erweitern Sie ggf. die Klammern.
- Wir isolieren die Variablen, d.h. Wir verschieben alles, was „X“ enthält, auf eine Seite und alles ohne „X“ auf die andere.
- Wir präsentieren ähnliche Begriffe.
- Wir dividieren alles durch den Koeffizienten „x“.
Natürlich funktioniert dieses Schema nicht immer; es enthält gewisse Feinheiten und Tricks, und jetzt werden wir sie kennenlernen.
Lösen realer Beispiele einfacher linearer Gleichungen
Aufgabe Nr. 1
Im ersten Schritt müssen wir die Klammern öffnen. Da sie in diesem Beispiel nicht vorhanden sind, überspringen wir diesen Schritt. Im zweiten Schritt müssen wir die Variablen isolieren. Bitte beachten Sie: Es handelt sich hierbei ausschließlich um einzelne Begriffe. Schreiben wir es auf:
Wir präsentieren links und rechts ähnliche Begriffe, dies wurde hier jedoch bereits getan. Daher gehen wir zum vierten Schritt über: Division durch den Koeffizienten:
\[\frac(6x)(6)=-\frac(72)(6)\]
Also haben wir die Antwort bekommen.
Aufgabe Nr. 2
Wir können die Klammern in diesem Problem sehen, also erweitern wir sie:
Sowohl links als auch rechts sehen wir ungefähr das gleiche Design, aber wir handeln nach dem Algorithmus, d.h. Trennen der Variablen:
Hier sind einige ähnliche:
An welchen Wurzeln funktioniert das? Antwort: für jeden. Daher können wir schreiben, dass $x$ eine beliebige Zahl ist.
Aufgabe Nr. 3
Interessanter ist die dritte lineare Gleichung:
\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]
Hier gibt es mehrere Klammern, die jedoch nicht mit irgendetwas multipliziert werden, sondern lediglich unterschiedliche Vorzeichen vorangestellt werden. Lassen Sie uns sie aufschlüsseln:
Wir führen den uns bereits bekannten zweiten Schritt durch:
\[-x+x+2x=15-6-12+3\]
Lass uns rechnen:
Wir führen den letzten Schritt aus – dividieren Sie alles durch den Koeffizienten „x“:
\[\frac(2x)(x)=\frac(0)(2)\]
Dinge, die Sie beim Lösen linearer Gleichungen beachten sollten
Wenn wir allzu einfache Aufgaben außer Acht lassen, möchte ich Folgendes sagen:
- Wie ich oben sagte, hat nicht jede lineare Gleichung eine Lösung – manchmal gibt es einfach keine Wurzeln;
- Selbst wenn es Wurzeln gibt, kann es sein, dass es null darunter gibt – daran ist nichts auszusetzen.
Null ist die gleiche Zahl wie die anderen; Sie sollten sie in keiner Weise diskriminieren oder davon ausgehen, dass Sie etwas falsch gemacht haben, wenn Sie Null erhalten.
Eine weitere Funktion betrifft das Öffnen von Klammern. Bitte beachten Sie: Wenn davor ein „Minus“ steht, entfernen wir es, aber in Klammern ändern wir die Vorzeichen in Gegenteil. Und dann können wir es mit Standardalgorithmen öffnen: Wir erhalten das, was wir in den obigen Berechnungen gesehen haben.
Das verstehen einfache Tatsache wird Ihnen dabei helfen, dumme und beleidigende Fehler in der High School zu vermeiden ähnliche Aktionen selbstverständlich.
Komplexe lineare Gleichungen lösen
Kommen wir zu mehr komplexe Gleichungen. Jetzt werden die Konstruktionen komplexer und bei der Durchführung verschiedener Transformationen erscheint eine quadratische Funktion. Wir sollten jedoch keine Angst davor haben, denn wenn wir nach dem Plan des Autors eine lineare Gleichung lösen, werden sich während des Transformationsprozesses alle Monome, die eine quadratische Funktion enthalten, mit Sicherheit aufheben.
Beispiel Nr. 1
Der erste Schritt besteht natürlich darin, die Klammern zu öffnen. Gehen wir dabei ganz vorsichtig vor:
Werfen wir nun einen Blick auf den Datenschutz:
\[-x+6((x)^(2))-6((x)^(2))+x=-12\]
Hier sind einige ähnliche:
Offensichtlich hat diese Gleichung keine Lösungen, daher schreiben wir Folgendes in die Antwort:
\[\varnothing\]
oder es gibt keine Wurzeln.
Beispiel Nr. 2
Wir führen die gleichen Aktionen aus. Erster Schritt:
Verschieben wir alles mit einer Variablen nach links und ohne sie nach rechts:
Hier sind einige ähnliche:
Offensichtlich hat diese lineare Gleichung keine Lösung, deshalb schreiben wir sie so:
\[\varnothing\],
oder es gibt keine Wurzeln.
Nuancen der Lösung
Beide Gleichungen sind vollständig gelöst. Am Beispiel dieser beiden Ausdrücke waren wir erneut davon überzeugt, dass selbst in den einfachsten linearen Gleichungen möglicherweise nicht alles so einfach ist: Es kann entweder eine oder keine oder unendlich viele Wurzeln geben. In unserem Fall haben wir zwei Gleichungen betrachtet, beide haben einfach keine Wurzeln.
Aber ich möchte Ihre Aufmerksamkeit auf eine andere Tatsache lenken: wie man mit Klammern umgeht und wie man sie öffnet, wenn ein Minuszeichen davor steht. Betrachten Sie diesen Ausdruck:
Vor dem Öffnen müssen Sie alles mit „X“ multiplizieren. Bitte beachten: multipliziert jeder einzelne Begriff. Darin befinden sich zwei Terme – bzw. zwei Terme und multipliziert.
Und erst nachdem diese scheinbar elementaren, aber sehr wichtigen und gefährlichen Transformationen abgeschlossen sind, können Sie die Klammer unter dem Gesichtspunkt öffnen, dass dahinter ein Minuszeichen steht. Ja, ja: Erst jetzt, wenn die Transformationen abgeschlossen sind, erinnern wir uns daran, dass vor den Klammern ein Minuszeichen steht, was bedeutet, dass alles darunter einfach das Vorzeichen wechselt. Gleichzeitig verschwinden die Klammern selbst und vor allem auch das vordere „Minus“.
Das Gleiche machen wir mit der zweiten Gleichung:
Es ist kein Zufall, dass ich auf diese kleinen, scheinbar unbedeutenden Tatsachen achte. Denn das Lösen von Gleichungen ist immer eine Abfolge elementarer Transformationen, bei denen die Unfähigkeit, einfache Handlungen klar und kompetent auszuführen, dazu führt, dass Gymnasiasten zu mir kommen und erneut lernen, solche einfachen Gleichungen zu lösen.
Natürlich wird der Tag kommen, an dem Sie diese Fähigkeiten bis zur Automatisierung verfeinern werden. Sie müssen nicht mehr jedes Mal so viele Transformationen durchführen, sondern schreiben alles in eine Zeile. Aber während Sie gerade erst lernen, müssen Sie jede Aktion separat schreiben.
Lösen noch komplexerer linearer Gleichungen
Was wir jetzt lösen werden, kann kaum als die einfachste Aufgabe bezeichnet werden, aber die Bedeutung bleibt dieselbe.
Aufgabe Nr. 1
\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]
Lassen Sie uns alle Elemente im ersten Teil multiplizieren:
Lassen Sie uns etwas Privatsphäre schaffen:
Hier sind einige ähnliche:
Lassen Sie uns den letzten Schritt abschließen:
\[\frac(-4x)(4)=\frac(4)(-4)\]
Hier ist unsere endgültige Antwort. Und trotz der Tatsache, dass wir im Lösungsprozess Koeffizienten mit einer quadratischen Funktion hatten, löschten sie sich gegenseitig aus, was die Gleichung linear und nicht quadratisch machte.
Aufgabe Nr. 2
\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]
Führen wir den ersten Schritt sorgfältig aus: Multiplizieren Sie jedes Element aus der ersten Klammer mit jedem Element aus der zweiten. Nach den Transformationen soll es insgesamt vier neue Begriffe geben:
Lassen Sie uns nun die Multiplikation in jedem Term sorgfältig durchführen:
Verschieben wir die Begriffe mit „X“ nach links und die ohne „X“ nach rechts:
\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]
Hier sind ähnliche Begriffe:
Wieder einmal haben wir die endgültige Antwort erhalten.
Nuancen der Lösung
Der wichtigste Hinweis zu diesen beiden Gleichungen ist der folgende: Sobald wir beginnen, Klammern zu multiplizieren, die mehr als einen Term enthalten, geschieht dies nach der folgenden Regel: Wir nehmen den ersten Term aus dem ersten und multiplizieren mit jedem Element aus der Zweite; dann nehmen wir das zweite Element vom ersten und multiplizieren auf ähnliche Weise mit jedem Element vom zweiten. Infolgedessen werden wir vier Amtszeiten haben.
Über die algebraische Summe
Mit diesem letzten Beispiel möchte ich die Schüler daran erinnern, was eine algebraische Summe ist. In der klassischen Mathematik meinen wir mit 1-7$ einfaches Design: subtrahiere sieben von eins. In der Algebra meinen wir damit Folgendes: Zur Zahl „eins“ addieren wir eine weitere Zahl, nämlich „minus sieben“. Darin unterscheidet sich eine algebraische Summe von einer gewöhnlichen arithmetischen Summe.
Sobald Sie bei der Durchführung aller Transformationen, jeder Addition und Multiplikation ähnliche Konstruktionen wie die oben beschriebenen sehen, werden Sie bei der Arbeit mit Polynomen und Gleichungen in der Algebra einfach keine Probleme mehr haben.
Schauen wir uns abschließend noch ein paar weitere Beispiele an, die noch komplexer sein werden als die, die wir gerade betrachtet haben. Um sie zu lösen, müssen wir unseren Standardalgorithmus leicht erweitern.
Gleichungen mit Brüchen lösen
Um solche Aufgaben zu lösen, müssen wir unserem Algorithmus einen weiteren Schritt hinzufügen. Aber zunächst möchte ich Sie an unseren Algorithmus erinnern:
- Öffne die Klammern.
- Separate Variablen.
- Bringen Sie ähnliche mit.
- Teilen Sie durch das Verhältnis.
Leider erweist sich dieser wunderbare Algorithmus trotz seiner Wirksamkeit als nicht ganz geeignet, wenn wir Brüche vor uns haben. Und in dem, was wir weiter unten sehen werden, haben wir in beiden Gleichungen sowohl links als auch rechts einen Bruch.
Wie geht man in diesem Fall vor? Ja, es ist ganz einfach! Dazu müssen Sie dem Algorithmus einen weiteren Schritt hinzufügen, der sowohl vor als auch nach der ersten Aktion durchgeführt werden kann, nämlich das Entfernen von Brüchen. Der Algorithmus sieht also wie folgt aus:
- Beseitigen Sie Brüche.
- Öffne die Klammern.
- Separate Variablen.
- Bringen Sie ähnliche mit.
- Teilen Sie durch das Verhältnis.
Was bedeutet es, „Brüche loszuwerden“? Und warum kann dies sowohl nach als auch vor dem ersten Standardschritt erfolgen? Tatsächlich sind in unserem Fall alle Brüche im Nenner numerisch, d.h. Überall ist der Nenner nur eine Zahl. Wenn wir also beide Seiten der Gleichung mit dieser Zahl multiplizieren, werden wir Brüche los.
Beispiel Nr. 1
\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]
Lassen Sie uns die Brüche in dieser Gleichung loswerden:
\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]
Bitte beachten Sie: Alles wird einmal mit „vier“ multipliziert, d. h. Nur weil Sie zwei Klammern haben, heißt das nicht, dass Sie jede mit „vier“ multiplizieren müssen. Schreiben wir auf:
\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]
Lassen Sie uns nun erweitern:
Wir schließen die Variable ab:
Wir führen die Reduktion ähnlicher Begriffe durch:
\[-4x=-1\left| :\left(-4 \right) \right.\]
\[\frac(-4x)(-4)=\frac(-1)(-4)\]
Wir haben die endgültige Lösung erhalten, fahren wir mit der zweiten Gleichung fort.
Beispiel Nr. 2
\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]
Hier führen wir alle gleichen Aktionen aus:
\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]
\[\frac(4x)(4)=\frac(4)(4)\]
Das Problem ist behoben.
Das ist eigentlich alles, was ich Ihnen heute sagen wollte.
Wichtige Punkte
Die wichtigsten Erkenntnisse sind:
- Kennen Sie den Algorithmus zum Lösen linearer Gleichungen.
- Möglichkeit, Klammern zu öffnen.
- Machen Sie sich keine Sorgen, wenn Sie es sehen quadratische Funktionen Höchstwahrscheinlich werden sie im Zuge weiterer Transformationen abnehmen.
- Es gibt drei Arten von Wurzeln in linearen Gleichungen, selbst in den einfachsten: eine einzelne Wurzel, die gesamte Zahlenlinie ist eine Wurzel und überhaupt keine Wurzeln.
Ich hoffe, dass diese Lektion Ihnen dabei hilft, ein einfaches, aber sehr wichtiges Thema für ein besseres Verständnis der gesamten Mathematik zu meistern. Wenn etwas nicht klar ist, gehen Sie auf die Website und lösen Sie die dort vorgestellten Beispiele. Bleiben Sie dran, es erwarten Sie noch viele weitere interessante Dinge!
In dieser Lektion werden wir uns mit Methoden zur Lösung eines linearen Gleichungssystems befassen. In einem Kurs der höheren Mathematik müssen lineare Gleichungssysteme sowohl in Form separater Aufgaben, zum Beispiel „Löse das System mit den Cramer-Formeln“, als auch im Zuge der Lösung anderer Probleme gelöst werden. Systeme linearer Gleichungen müssen in fast allen Teilgebieten der höheren Mathematik behandelt werden.
Zunächst eine kleine Theorie. Was bedeutet in diesem Fall das mathematische Wort „linear“? Dies bedeutet, dass die Gleichungen des Systems Alle Variablen enthalten im ersten Grad: ohne irgendwelche ausgefallenen Sachen wie ![]() usw., über die sich nur Teilnehmer an Mathematikolympiaden freuen.
usw., über die sich nur Teilnehmer an Mathematikolympiaden freuen.
In der höheren Mathematik werden zur Bezeichnung von Variablen nicht nur aus der Kindheit bekannte Buchstaben verwendet.
Eine ziemlich beliebte Option sind Variablen mit Indizes: .
Oder die Anfangsbuchstaben des lateinischen Alphabets, klein und groß:
Es ist nicht so selten, griechische Buchstaben zu finden: – vielen bekannt als „Alpha, Beta, Gamma“. Und auch eine Menge mit Indizes, sagen wir, mit dem Buchstaben „mu“:
Die Verwendung des einen oder anderen Buchstabensatzes hängt von dem Abschnitt der höheren Mathematik ab, in dem wir mit einem System linearer Gleichungen konfrontiert sind. So zum Beispiel in Systemen linearer Gleichungen, die man bei der Lösung von Integralen antrifft, Differentialgleichung Es ist traditionell, die Notation zu verwenden
Aber egal wie die Variablen bezeichnet werden, die Prinzipien, Methoden und Methoden zur Lösung eines linearen Gleichungssystems ändern sich nicht. Wenn Sie also auf etwas Unheimliches stoßen, wie z. B. , beeilen Sie sich nicht, das Aufgabenbuch aus Angst zu schließen, schließlich können Sie stattdessen die Sonne, stattdessen einen Vogel und stattdessen ein Gesicht (den Lehrer) zeichnen. Und so komisch es auch klingen mag, ein System linearer Gleichungen kann mit diesen Notationen auch gelöst werden.
Ich habe das Gefühl, dass der Artikel ziemlich lang werden wird, daher ein kleines Inhaltsverzeichnis. Die sequentielle „Nachbesprechung“ sieht also wie folgt aus:
– Lösen eines linearen Gleichungssystems mit der Substitutionsmethode („ Schulmethode»)
;
– Lösen des Systems durch termweise Addition (Subtraktion) der Systemgleichungen;
– Lösung des Systems mit Cramers Formeln;
– Lösen des Systems mithilfe einer inversen Matrix;
– Lösung des Systems mit der Gaußschen Methode.
Lineare Gleichungssysteme kennt jeder aus dem Mathematikunterricht der Schule. Im Wesentlichen beginnen wir mit der Wiederholung.
Lösen eines linearen Gleichungssystems mit der Substitutionsmethode
Diese Methode kann auch als „Schulmethode“ oder Methode zur Eliminierung von Unbekannten bezeichnet werden. Im übertragenen Sinne kann man es auch als „eine unvollendete Gaußsche Methode“ bezeichnen.
Beispiel 1
![]()
Hier erhalten wir ein System aus zwei Gleichungen mit zwei Unbekannten. Beachten Sie, dass sich die freien Terme (Nummern 5 und 7) auf der linken Seite der Gleichung befinden. Im Allgemeinen spielt es keine Rolle, wo sie sich befinden, links oder rechts, nur sind sie bei Problemen in der höheren Mathematik oft so angeordnet. Und eine solche Aufzeichnung sollte nicht zu Verwirrung führen; bei Bedarf kann das System immer „wie gewohnt“ geschrieben werden: . Vergessen Sie nicht, dass beim Verschieben eines Begriffs von Teil zu Teil das Vorzeichen geändert werden muss.
Was bedeutet es, ein System linearer Gleichungen zu lösen? Das Lösen eines Gleichungssystems bedeutet, viele seiner Lösungen zu finden. Die Lösung eines Systems ist eine Menge von Werten aller darin enthaltenen Variablen, was JEDE Gleichung des Systems in eine echte Gleichheit verwandelt. Darüber hinaus kann das System sein nicht gelenkig (habe keine Lösungen).Keine Sorge, das ist es allgemeine Definition=) Wir werden nur einen Wert „x“ und einen Wert „y“ haben, die jede Gleichung c-we erfüllen.
Existiert grafische Methode Lösung des Systems, die im Unterricht gefunden werden kann Die einfachsten Probleme mit einer Linie. Da habe ich darüber gesprochen geometrischer Sinn Systeme aus zwei linearen Gleichungen mit zwei Unbekannten. Aber jetzt ist die Ära der Algebra und der Zahlen-Zahlen, Aktionen-Aktionen.
Lass uns entscheiden: Aus der ersten Gleichung drücken wir aus:
Den resultierenden Ausdruck setzen wir in die zweite Gleichung ein:
Wir öffnen die Klammern, fügen ähnliche Begriffe hinzu und finden den Wert: 
Als nächstes erinnern wir uns daran, wofür wir getanzt haben:
Wir kennen den Wert bereits, es bleibt nur noch Folgendes zu finden:
Antwort:
Nachdem JEDES Gleichungssystem auf IRGENDEINE Weise gelöst wurde, empfehle ich dringend, es zu überprüfen (mündlich, auf einem Entwurf oder auf einem Taschenrechner). Zum Glück geht das einfach und schnell.
1) Setzen Sie die gefundene Antwort in die erste Gleichung ein:
– die richtige Gleichheit erreicht wird.
2) Setzen Sie die gefundene Antwort in die zweite Gleichung ein: ![]()
– die richtige Gleichheit erreicht wird.
Oder einfacher ausgedrückt: „Alles passte zusammen“
Die betrachtete Lösungsmethode ist nicht die einzige; aus der ersten Gleichung konnte man ausdrücken, und nicht.
Sie können das Gegenteil tun – etwas aus der zweiten Gleichung ausdrücken und es in die erste Gleichung einsetzen. Beachten Sie übrigens, dass die nachteiligste der vier Methoden darin besteht, aus der zweiten Gleichung Folgendes auszudrücken:
Das Ergebnis sind Brüche, aber warum? Es gibt eine rationalere Lösung.
Allerdings kommt man in manchen Fällen trotzdem nicht ohne Brüche aus. In diesem Zusammenhang möchte ich Sie darauf aufmerksam machen, WIE ich den Ausdruck niedergeschrieben habe. Nicht so: und auf keinen Fall so: ![]() .
.
Wenn Sie es in der höheren Mathematik mit Bruchzahlen zu tun haben, versuchen Sie, alle Berechnungen in gewöhnlichen unechten Brüchen durchzuführen.
Genau, und nicht oder!
Ein Komma kann nur manchmal verwendet werden, insbesondere wenn es die endgültige Antwort auf ein Problem darstellt und mit dieser Zahl keine weiteren Aktionen durchgeführt werden müssen.
Viele Leser dachten wahrscheinlich: „Warum eine so ausführliche Erklärung wie für einen Korrekturkurs, alles ist klar.“ Nichts dergleichen, es scheint so einfach Schulbeispiel, und wie viele SEHR wichtige Schlussfolgerungen! Hier ist ein anderes:
Sie sollten sich bemühen, jede Aufgabe auf möglichst rationale Weise zu erledigen. Schon allein deshalb, weil es Zeit und Nerven spart und zudem die Fehlerwahrscheinlichkeit verringert.
Wenn Sie bei einer Aufgabe in der höheren Mathematik auf ein System aus zwei linearen Gleichungen mit zwei Unbekannten stoßen, können Sie jederzeit die Substitutionsmethode verwenden (es sei denn, es wird angegeben, dass das System mit einer anderen Methode gelöst werden muss). Kein einziger Lehrer wird dies tun Denken Sie, dass Sie ein Trottel sind und Ihre Note herabsetzen werden, weil Sie die „Schulmethode“ anwenden.
Darüber hinaus empfiehlt es sich in manchen Fällen, die Substitutionsmethode bei einer größeren Anzahl von Variablen anzuwenden.
Beispiel 2
Lösen Sie ein lineares Gleichungssystem mit drei Unbekannten

Ein ähnliches Gleichungssystem entsteht häufig bei der sogenannten Methode der unbestimmten Koeffizienten, wenn wir das Integral einer gebrochenen rationalen Funktion ermitteln. Das betreffende System wurde von mir von dort übernommen.
Beim Finden des Integrals ist das Ziel schnell Finden Sie die Werte der Koeffizienten und greifen Sie nicht auf Cramers Formeln zurück, die Methode inverse Matrix usw. Daher ist in diesem Fall die Substitutionsmethode geeignet.
Wenn ein Gleichungssystem angegeben ist, ist es zunächst wünschenswert herauszufinden, ob es SOFORT möglich ist, es irgendwie zu vereinfachen. Bei der Analyse der Gleichungen des Systems stellen wir fest, dass die zweite Gleichung des Systems durch 2 geteilt werden kann, was wir tun:

Referenz: mathematisches Zeichen bedeutet „daraus folgt dies“ und wird häufig bei der Problemlösung verwendet.
Lassen Sie uns nun die Gleichungen analysieren. Wir müssen eine Variable durch die anderen ausdrücken. Welche Gleichung soll ich wählen? Sie haben wahrscheinlich bereits vermutet, dass der einfachste Weg zu diesem Zweck darin besteht, die erste Gleichung des Systems zu verwenden:

Hier kann man, egal welche Variable ausgedrückt werden soll, genauso gut oder ausdrücken.
Als nächstes setzen wir den Ausdruck für in die zweite und dritte Gleichung des Systems ein: 
Wir öffnen die Klammern und präsentieren ähnliche Begriffe: 
Teilen Sie die dritte Gleichung durch 2: 
Aus der zweiten Gleichung drücken wir Folgendes aus und ersetzen es in die dritte Gleichung:

Fast alles ist fertig, aus der dritten Gleichung finden wir:
Aus der zweiten Gleichung: ![]()
Aus der ersten Gleichung:
Überprüfen: Setzen Sie die gefundenen Werte der Variablen in die linke Seite jeder Gleichung des Systems ein:
1)
2)
3)
Man erhält die entsprechenden rechten Seiten der Gleichungen und somit ist die Lösung korrekt gefunden.
Beispiel 3
Lösen Sie ein lineares Gleichungssystem mit 4 Unbekannten

Dies ist ein Beispiel dafür unabhängige Entscheidung(Antwort am Ende der Lektion).
Lösen des Systems durch termweise Addition (Subtraktion) der Systemgleichungen
Beim Lösen linearer Gleichungssysteme sollten Sie versuchen, nicht die „Schulmethode“, sondern die Methode der Term-für-Term-Addition (Subtraktion) der Gleichungen des Systems zu verwenden. Warum? Das spart Zeit und vereinfacht die Berechnungen, aber jetzt wird alles klarer.
Beispiel 4
Lösen Sie ein lineares Gleichungssystem: ![]()
Ich habe das gleiche System wie im ersten Beispiel genommen.
Bei der Analyse des Gleichungssystems stellen wir fest, dass die Koeffizienten der Variablen in ihrer Größe identisch und im Vorzeichen entgegengesetzt sind (–1 und 1). In einer solchen Situation können die Gleichungen Term für Term hinzugefügt werden: 
Rot eingekreiste Aktionen werden GEISTLICH ausgeführt.
Wie Sie sehen können, ist uns durch die Term-für-Term-Addition die Variable verloren gegangen. Das ist es tatsächlich Der Kern der Methode besteht darin, eine der Variablen zu entfernen.
Erste Ebene
Lineare Gleichungen. Vollständiger Leitfaden (2019)
Was sind „lineare Gleichungen“?
oder mündlich – drei Freunde bekamen jeweils Äpfel, weil Vasya alle Äpfel hatte, die er hatte.
Und jetzt haben Sie sich bereits entschieden Lineargleichung
Geben wir diesem Begriff nun eine mathematische Definition.
Lineare Gleichung - ist eine algebraische Gleichung, deren Gesamtgrad der sie bildenden Polynome gleich ist. Es sieht aus wie das:
Wo und sind irgendwelche Zahlen und
Für unseren Fall mit Vasya und Äpfeln schreiben wir:
- „Wenn Vasya allen drei Freunden die gleiche Anzahl Äpfel gibt, hat er keine Äpfel mehr“
„Versteckte“ lineare Gleichungen oder die Bedeutung von Identitätstransformationen
Obwohl auf den ersten Blick alles äußerst einfach ist, muss man beim Lösen von Gleichungen vorsichtig sein, denn als lineare Gleichungen werden nicht nur Gleichungen dieser Art bezeichnet, sondern auch alle Gleichungen, die durch Transformationen und Vereinfachungen auf diese Art reduziert werden können. Zum Beispiel:
Wir sehen, was rechts steht, was theoretisch bereits darauf hindeutet, dass die Gleichung nicht linear ist. Wenn wir außerdem die Klammern öffnen, erhalten wir zwei weitere Begriffe, in denen es heißt: Aber ziehen Sie keine voreiligen Schlüsse! Bevor beurteilt werden kann, ob eine Gleichung linear ist, müssen alle Transformationen durchgeführt und so das ursprüngliche Beispiel vereinfacht werden. In diesem Fall können sich Transformationen ändern Aussehen, aber nicht das eigentliche Wesen der Gleichung.
Mit anderen Worten: Die Transformationsdaten müssen vorhanden sein identisch oder Äquivalent. Es gibt nur zwei solcher Transformationen, aber sie spielen sehr, SEHR wichtige Rolle beim Lösen von Problemen. Schauen wir uns beide Transformationen anhand konkreter Beispiele an.
Übertragen von links nach rechts.
Nehmen wir an, wir müssen die folgende Gleichung lösen:
Auch in Grundschule Uns wurde gesagt: „Mit X – nach links, ohne X – nach rechts.“ Welcher Ausdruck mit einem X steht rechts? Das ist richtig, aber nicht wie nicht. Und das ist wichtig, denn wenn dies missverstanden wird, scheint es so einfache Frage, die Antwort ist falsch. Welcher Ausdruck mit einem X steht links? Rechts, .
Nachdem wir das nun herausgefunden haben, übertragen wir alle Begriffe mit Unbekannten auf linke Seite, und alles, was bekannt ist - auf der rechten Seite. Denken Sie daran, dass, wenn beispielsweise kein Zeichen vor der Zahl steht, die Zahl positiv ist, d. h., davor steht ein „ “-Zeichen.
Übertragen? Was hast du bekommen?
Es bleibt nur noch, ähnliche Begriffe einzuführen. Wir präsentieren:
Wir haben also die erste identische Transformation erfolgreich analysiert, obwohl ich sicher bin, dass Sie sie wussten und ohne mich aktiv nutzten. Die Hauptsache ist, die Vorzeichen von Zahlen nicht zu vergessen und sie bei der Übertragung durch das Gleichheitszeichen in die entgegengesetzten zu ändern!
Multiplikation-Division.
Beginnen wir gleich mit einem Beispiel
Schauen wir mal hin und überlegen: Was gefällt uns an diesem Beispiel nicht? Das Unbekannte ist alles in einem Teil, das Bekannte ist in einem anderen, aber etwas hält uns auf ... Und dieses Etwas ist eine Vier, denn wenn es nicht existierte, wäre alles perfekt – x ist gleich einer Zahl – genau wie wir es brauchen!
Wie kann man es loswerden? Wir können es nicht nach rechts verschieben, weil wir dann den gesamten Multiplikator verschieben müssen (wir können ihn nicht nehmen und wegreißen), und es macht auch keinen Sinn, den gesamten Multiplikator zu verschieben ...
Es ist Zeit, sich an die Division zu erinnern, also teilen wir alles durch! Alles – also sowohl die linke als auch die rechte Seite. So und nur so! Was machen wir?
Hier ist die Antwort.
Schauen wir uns nun ein weiteres Beispiel an:
Können Sie erraten, was in diesem Fall zu tun ist? Das ist richtig, multiplizieren Sie die linke und rechte Seite mit! Welche Antwort haben Sie erhalten? Rechts. .
Sicherlich wussten Sie bereits alles über Identitätstransformationen. Bedenken Sie, dass wir dieses Wissen einfach in Ihrem Gedächtnis aufgefrischt haben und es Zeit für etwas mehr ist – zum Beispiel für die Lösung unseres großen Beispiels:
Wie wir bereits sagten, kann man das nicht sagen, wenn man ihn ansieht gegebene Gleichung ist linear, aber wir müssen die Klammern öffnen und identische Transformationen durchführen. Also lasst uns anfangen!
Zunächst erinnern wir uns an die Formeln der abgekürzten Multiplikation, insbesondere an das Quadrat der Summe und das Quadrat der Differenz. Wenn Sie sich nicht erinnern, was es ist und wie die Klammern geöffnet werden, empfehle ich Ihnen dringend, das Thema zu lesen, da Ihnen diese Fähigkeiten bei der Lösung fast aller in der Prüfung vorkommenden Beispiele nützlich sein werden.
Enthüllt? Lass uns vergleichen:
Jetzt ist es an der Zeit, ähnliche Begriffe einzuführen. Erinnern Sie sich, wie wir im selben Jahr waren? Grundschule Haben sie gesagt: „Wir stecken keine Fliegen in Koteletts“? Hier möchte ich Sie daran erinnern. Wir addieren alles separat – die Faktoren, die haben, die Faktoren, die haben, und die übrigen Faktoren, die keine Unbekannten haben. Wenn Sie ähnliche Begriffe verwenden, verschieben Sie alle Unbekannten nach links und alles Bekannte nach rechts. Was hast du bekommen?
Wie Sie sehen können, sind die X im Quadrat verschwunden und wir sehen etwas völlig Normales. Lineargleichung. Es bleibt nur noch, es zu finden!
Und zum Schluss möchte ich noch etwas sehr Wichtiges über Identitätstransformationen sagen: Identitätstransformationen sind nicht nur auf lineare Gleichungen anwendbar, sondern auch auf quadratische, gebrochenrationale Gleichungen und andere. Sie müssen sich nur daran erinnern, dass wir bei der Übertragung von Faktoren durch das Gleichheitszeichen das Vorzeichen in das Gegenteil ändern, und wenn wir mit einer Zahl dividieren oder multiplizieren, multiplizieren/dividieren wir beide Seiten der Gleichung mit der GLEICHEN Zahl.
Was haben Sie aus diesem Beispiel noch mitgenommen? Dass es durch die Betrachtung einer Gleichung nicht immer möglich ist, direkt und genau zu bestimmen, ob sie linear ist oder nicht. Es ist notwendig, den Ausdruck zunächst vollständig zu vereinfachen und erst dann zu beurteilen, was er ist.
Lineare Gleichungen. Beispiele.
Hier sind ein paar weitere Beispiele, die Sie selbst üben können: Bestimmen Sie, ob die Gleichung linear ist, und wenn ja, finden Sie ihre Wurzeln:
Antworten:
1. Ist.
2. Ist nicht.
Öffnen wir die Klammern und präsentieren wir ähnliche Begriffe:
Führen wir eine identische Transformation durch – teilen Sie die linke und rechte Seite in:
Wir sehen, dass die Gleichung nicht linear ist und daher nicht nach ihren Wurzeln gesucht werden muss.
3. Ist.
Führen wir eine identische Transformation durch – multiplizieren Sie die linke und rechte Seite mit, um den Nenner loszuwerden.
Denken Sie darüber nach, warum das so wichtig ist? Wenn Sie die Antwort auf diese Frage kennen, fahren Sie mit der weiteren Lösung der Gleichung fort. Wenn nicht, sollten Sie sich unbedingt mit dem Thema befassen, um keine weiteren Fehler zu machen komplexe Beispiele. Wie Sie sehen, ist die Situation übrigens unmöglich. Warum?
Lassen Sie uns also fortfahren und die Gleichung neu ordnen:
Wenn Sie alles problemlos geschafft haben, sprechen wir über lineare Gleichungen mit zwei Variablen.
Lineare Gleichungen in zwei Variablen
Kommen wir nun zu etwas komplexeren linearen Gleichungen mit zwei Variablen.
Lineare Gleichungen mit zwei Variablen haben die Form:
Wo und - beliebige Zahlen und.
Wie Sie sehen, besteht der einzige Unterschied darin, dass der Gleichung eine weitere Variable hinzugefügt wird. Und so ist alles gleich – es gibt kein x-Quadrat, keine Division durch eine Variable usw. usw.
Was für ein Lebensbeispiel kann ich Ihnen geben ... Nehmen wir denselben Vasya. Nehmen wir an, er hat beschlossen, jedem seiner drei Freunde die gleiche Anzahl Äpfel zu geben und die Äpfel für sich zu behalten. Wie viele Äpfel muss Vasya kaufen, wenn er jedem Freund einen Apfel gibt? Wie wäre es mit? Was wäre, wenn bis?
Das Verhältnis zwischen der Anzahl der Äpfel, die jede Person erhält, und der Gesamtzahl der Äpfel, die gekauft werden müssen, wird durch die Gleichung ausgedrückt:
- - die Anzahl der Äpfel, die eine Person erhält (, oder, oder);
- - die Anzahl der Äpfel, die Vasya für sich nehmen wird;
- - Wie viele Äpfel muss Vasya kaufen, wenn man die Anzahl der Äpfel pro Person berücksichtigt?
Bei der Lösung dieses Problems stellen wir fest, dass Vasya, wenn er einem Freund einen Apfel gibt, Stücke kaufen muss, wenn er Äpfel gibt usw.
Und überhaupt. Wir haben zwei Variablen. Warum nicht diesen Zusammenhang grafisch darstellen? Wir bauen und markieren unseren Wert, also Punkte, mit Koordinaten und!
Wie Sie sehen, sind sie voneinander abhängig linear, daher der Name der Gleichungen – „ linear».
Lassen Sie uns von Äpfeln abstrahieren und verschiedene Gleichungen grafisch betrachten. Schauen Sie sich die beiden konstruierten Graphen – eine Gerade und eine Parabel, die durch beliebige Funktionen angegeben werden – genau an:

Suchen und markieren Sie die entsprechenden Punkte in beiden Bildern.
Was hast du bekommen?

Das sehen Sie im Diagramm der ersten Funktion allein entspricht eins, das heißt, sie hängen auch linear voneinander ab, was man von der zweiten Funktion nicht sagen kann. Natürlich kann man argumentieren, dass im zweiten Diagramm auch das x – entspricht, aber das ist nur ein Punkt, also ein Sonderfall, da man immer noch einen finden kann, der mehr als nur einem entspricht. Und der konstruierte Graph ähnelt in keiner Weise einer Linie, sondern ist eine Parabel.
Ich wiederhole noch einmal: Der Graph einer linearen Gleichung muss eine GERADE sein.
Mit der Tatsache, dass die Gleichung nicht linear sein wird, wenn wir bis zu irgendeinem Grad gehen – das wird am Beispiel einer Parabel deutlich, obwohl Sie zum Beispiel noch ein paar einfachere Diagramme für sich selbst erstellen können oder. Aber ich versichere Ihnen – keines davon wird eine GERADE LINIE sein.
Glaubst du nicht? Bauen Sie es und vergleichen Sie es dann mit dem, was ich habe:

Was passiert, wenn wir etwas beispielsweise durch eine Zahl dividieren? Wird es einen linearen Zusammenhang geben und? Lasst uns nicht streiten, sondern lasst uns aufbauen! Lassen Sie uns zum Beispiel einen Graphen einer Funktion erstellen.

Irgendwie sieht es nicht so aus, als wäre es eine Gerade konstruiert... dementsprechend ist die Gleichung auch nicht linear.
Fassen wir zusammen:
- Lineare Gleichung - ist eine algebraische Gleichung, in der der Gesamtgrad der Polynome, aus denen sie besteht, gleich ist.
- Lineare Gleichung mit einer Variablen hat die Form:
, wo und sind beliebige Zahlen;
Lineare Gleichung mit zwei Variablen:
, wo und sind beliebige Zahlen. - Es ist nicht immer möglich, sofort zu bestimmen, ob eine Gleichung linear ist oder nicht. Um dies zu verstehen, ist es manchmal notwendig, identische Transformationen durchzuführen, ähnliche Terme nach links/rechts zu verschieben, nicht zu vergessen, das Vorzeichen zu ändern, oder beide Seiten der Gleichung mit derselben Zahl zu multiplizieren/dividieren.
LINEARE GLEICHUNGEN. KURZ ÜBER DAS WICHTIGSTE
1. Lineare Gleichung
Dies ist eine algebraische Gleichung, in der der Gesamtgrad der Polynome, aus denen sie besteht, gleich ist.
2. Lineare Gleichung mit einer Variablen hat die Form:
Wo und sind irgendwelche Zahlen;
3. Lineare Gleichung mit zwei Variablen hat die Form:
Wo und - beliebige Zahlen.
4. Identitätstransformationen
Um festzustellen, ob eine Gleichung linear ist oder nicht, müssen identische Transformationen durchgeführt werden:
- Verschieben Sie ähnliche Begriffe nach links/rechts und vergessen Sie nicht, das Vorzeichen zu ändern.
- Beide Seiten der Gleichung mit derselben Zahl multiplizieren/dividieren.