Finden Sie online Teillösungen für Differentialgleichungen. Lösen der einfachsten Differentialgleichungen erster Ordnung

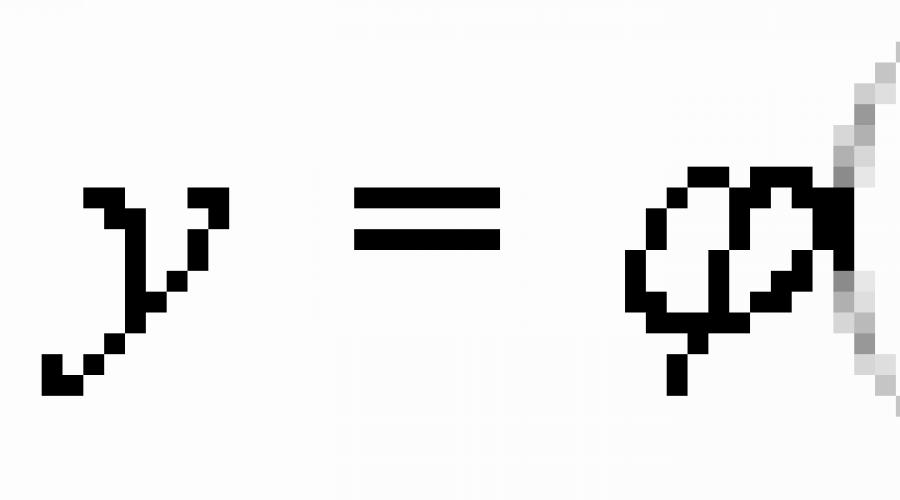
I. Gewöhnliche Differentialgleichungen

1.1. Grundlegende Konzepte und Definitionen

Eine Differentialgleichung ist eine Gleichung, die eine unabhängige Variable in Beziehung setzt X, die erforderliche Funktion j und seine Ableitungen oder Differentiale.

Symbolisch wird die Differentialgleichung wie folgt geschrieben:

F(x,y,y")=0, F(x,y,y")=0, F(x,y,y",y",.., y (n))=0

Eine Differentialgleichung heißt gewöhnlich, wenn die gesuchte Funktion von einer unabhängigen Variablen abhängt.

Lösen einer Differentialgleichung heißt eine Funktion, die diese Gleichung in eine Identität umwandelt.

Die Ordnung der Differentialgleichung ist die Ordnung der höchsten in dieser Gleichung enthaltenen Ableitung

Beispiele.

1. Betrachten Sie eine Differentialgleichung erster Ordnung

Die Lösung dieser Gleichung ist die Funktion y = 5 ln x. In der Tat, ersetzen y" In die Gleichung erhalten wir die Identität.

Und das bedeutet, dass die Funktion y = 5 ln x– eine Lösung dieser Differentialgleichung ist.

2. Betrachten Sie die Differentialgleichung zweiter Ordnung y" - 5y" +6y = 0. Die Funktion ist die Lösung dieser Gleichung.

Wirklich, .

Wenn wir diese Ausdrücke in die Gleichung einsetzen, erhalten wir: , – Identität.

Und das bedeutet, dass die Funktion die Lösung dieser Differentialgleichung ist.

Integrieren von Differentialgleichungen ist der Prozess, Lösungen für Differentialgleichungen zu finden.

Allgemeine Lösung der Differentialgleichung eine Funktion der Form genannt , die so viele unabhängige beliebige Konstanten enthält, wie die Ordnung der Gleichung.

Teillösung der Differentialgleichung ist eine Lösung, die aus einer allgemeinen Lösung für verschiedene numerische Werte beliebiger Konstanten erhalten wird. Die Werte beliebiger Konstanten liegen bei bestimmten Anfangswerten des Arguments und der Funktion.

Der Graph einer bestimmten Lösung einer Differentialgleichung heißt Integralkurve.

Beispiele

1. Finden Sie eine bestimmte Lösung für eine Differentialgleichung erster Ordnung

xdx + ydy = 0, Wenn j= 4 bei X = 3.

Lösung. Wenn wir beide Seiten der Gleichung integrieren, erhalten wir

Kommentar. Eine durch Integration erhaltene beliebige Konstante C kann in jeder für weitere Transformationen geeigneten Form dargestellt werden. In diesem Fall ist es unter Berücksichtigung der kanonischen Kreisgleichung zweckmäßig, eine beliebige Konstante C in der Form darzustellen.

- gemeinsame Entscheidung Differentialgleichung.

Bestimmte Lösung der Gleichung, die die Anfangsbedingungen erfüllt j = 4 bei X = 3 ergibt sich aus der allgemeinen Lösung durch Einsetzen der Anfangsbedingungen in die allgemeine Lösung: 3 2 + 4 2 = C 2 ; C=5.

Wenn wir C=5 in die allgemeine Lösung einsetzen, erhalten wir x 2 +y 2 = 5 2 .

Dies ist eine spezielle Lösung einer Differentialgleichung, die aus einer allgemeinen Lösung unter gegebenen Anfangsbedingungen erhalten wird.

2. Finden Sie die allgemeine Lösung der Differentialgleichung

Die Lösung dieser Gleichung ist eine beliebige Funktion der Form, wobei C eine beliebige Konstante ist. Tatsächlich erhalten wir beim Einsetzen in die Gleichungen: , .

Folglich hat diese Differentialgleichung unendlich viele Lösungen, da für unterschiedliche Werte der Konstante C die Gleichheit unterschiedliche Lösungen der Gleichung bestimmt.

Durch direkte Substitution können Sie beispielsweise überprüfen, ob die Funktionen funktionieren sind Lösungen der Gleichung.

Ein Problem, bei dem Sie eine bestimmte Lösung für die Gleichung finden müssen y" = f(x,y) Erfüllung der Anfangsbedingung y(x 0) = y 0, wird Cauchy-Problem genannt.

Lösung der Gleichung y" = f(x,y), die Anfangsbedingung erfüllend, y(x 0) = y 0, wird als Lösung des Cauchy-Problems bezeichnet.

Die Lösung des Cauchy-Problems hat eine einfache geometrische Bedeutung. Tatsächlich, nach diesen Definitionen, um das Cauchy-Problem zu lösen y" = f(x,y) angesichts dessen y(x 0) = y 0 bedeutet, die Integralkurve der Gleichung zu finden y" = f(x,y) was durchgeht angegebenen Punkt M 0 (x 0,y 0).

II. Differentialgleichungen erster Ordnung

2.1. Grundlegendes Konzept

Eine Differentialgleichung erster Ordnung ist eine Gleichung der Form F(x,y,y") = 0.

Eine Differentialgleichung erster Ordnung umfasst die erste Ableitung und keine Ableitungen höherer Ordnung.

Die gleichung y" = f(x,y) heißt eine nach der Ableitung gelöste Gleichung erster Ordnung.

Die allgemeine Lösung einer Differentialgleichung erster Ordnung ist eine Funktion der Form, die eine beliebige Konstante enthält.

Beispiel. Betrachten Sie eine Differentialgleichung erster Ordnung.

Die Lösung dieser Gleichung ist die Funktion.

Tatsächlich erhalten wir, wenn wir diese Gleichung durch ihren Wert ersetzen

also 3x=3x

Daher ist die Funktion eine allgemeine Lösung der Gleichung für jede Konstante C.

Finden Sie eine bestimmte Lösung dieser Gleichung, die die Anfangsbedingung erfüllt y(1)=1 Anfangsbedingungen ersetzen x = 1, y =1 In die allgemeine Lösung der Gleichung kommen wir von wo C=0.

Somit erhalten wir eine bestimmte Lösung aus der allgemeinen Lösung, indem wir den resultierenden Wert in diese Gleichung einsetzen C=0– private Lösung.

2.2. Differentialgleichungen mit separierbaren Variablen

Eine Differentialgleichung mit separierbaren Variablen ist eine Gleichung der Form: y"=f(x)g(y) oder durch Differentiale, wo f(x) Und g(y)– spezifizierte Funktionen.

Für diejenigen j, für die die Gleichung y"=f(x)g(y) ist äquivalent zur Gleichung, in dem die Variable j ist nur auf der linken Seite vorhanden und die Variable x ist nur auf der rechten Seite vorhanden. Sie sagen: „In Gl. y"=f(x)g(y Trennen wir die Variablen.“

Gleichung des Formulars wird als Gleichung mit getrennten Variablen bezeichnet.

Integration beider Seiten der Gleichung Von X, wir bekommen G(y) = F(x) + C ist die allgemeine Lösung der Gleichung, wobei G(y) Und F(x)– einige Stammfunktionen jeweils von Funktionen und f(x), C Willkürliche Konstante.

Algorithmus zur Lösung einer Differentialgleichung erster Ordnung mit separierbaren Variablen

Beispiel 1

Löse die Gleichung y" = xy

Lösung. Ableitung einer Funktion y" Ersetzen Sie es durch

Trennen wir die Variablen

Integrieren wir beide Seiten der Gleichheit:

Beispiel 2

2yy" = 1- 3x 2, Wenn y 0 = 3 bei x 0 = 1

Dies ist eine Gleichung mit getrennten Variablen. Stellen wir es uns in Differentialen vor. Dazu schreiben wir diese Gleichung in der Form um Von hier

Wir finden, dass wir beide Seiten der letzten Gleichheit integrieren

Ersetzen der Anfangswerte x 0 = 1, y 0 = 3 wir werden finden MIT 9=1-1+C, d.h. C = 9.

Daher wird das erforderliche Teilintegral sein oder

Beispiel 3

Schreiben Sie eine Gleichung für eine Kurve, die durch einen Punkt verläuft M(2;-3) und eine Tangente mit einem Winkelkoeffizienten haben

Lösung. Je nach Zustand

Dies ist eine Gleichung mit trennbaren Variablen. Durch Division der Variablen erhalten wir:

Wenn wir beide Seiten der Gleichung integrieren, erhalten wir:

Unter Verwendung der Anfangsbedingungen x = 2 Und y = - 3 wir werden finden C:

Daher hat die erforderliche Gleichung die Form

2.3. Linear Differentialgleichung erste Bestellung

Eine lineare Differentialgleichung erster Ordnung ist eine Gleichung der Form y" = f(x)y + g(x)

Wo f(x) Und g(x)- einige spezifizierte Funktionen.

Wenn g(x)=0 dann heißt die lineare Differentialgleichung homogen und hat die Form: y" = f(x)y

Wenn dann die Gleichung y" = f(x)y + g(x) als heterogen bezeichnet.

Allgemeine Lösung einer linearen homogenen Differentialgleichung y" = f(x)y wird durch die Formel gegeben: wo MIT- Willkürliche Konstante.

Insbesondere, wenn C = 0, dann ist die Lösung y = 0 Wenn linear homogene Gleichung sieht aus wie y" = ky Wo k eine Konstante ist, dann hat ihre allgemeine Lösung die Form: .

Allgemeine Lösung einer linearen inhomogenen Differentialgleichung y" = f(x)y + g(x) ergibt sich aus der Formel ,

diese. ist gleich der Summe der allgemeinen Lösung der entsprechenden linearen homogenen Gleichung und der besonderen Lösung dieser Gleichung.

Für eine lineare inhomogene Gleichung der Form y" = kx + b,

Wo k Und B- Einige Zahlen und eine bestimmte Lösung sind eine konstante Funktion. Daher hat die allgemeine Lösung die Form.

Beispiel. Löse die Gleichung y" + 2y +3 = 0

Lösung. Stellen wir die Gleichung im Formular dar y" = -2y - 3 Wo k = -2, b= -3 Die allgemeine Lösung ergibt sich aus der Formel.

Daher ist C eine beliebige Konstante.

2.4. Lösung linearer Differentialgleichungen erster Ordnung nach der Bernoulli-Methode

Finden einer allgemeinen Lösung für eine lineare Differentialgleichung erster Ordnung y" = f(x)y + g(x) reduziert sich auf die Lösung zweier Differentialgleichungen mit getrennten Variablen mittels Substitution y=uv, Wo u Und v- unbekannte Funktionen von X. Diese Lösungsmethode wird Bernoulli-Methode genannt.

Algorithmus zur Lösung einer linearen Differentialgleichung erster Ordnung

y" = f(x)y + g(x)

1. Geben Sie die Vertretung ein y=uv.

2. Differenzieren Sie diese Gleichheit y" = u"v + uv"

3. Ersatz j Und y" V gegebene Gleichung: u"v + uv" =f(x)uv + g(x) oder u"v + uv" + f(x)uv = g(x).

4. Gruppieren Sie die Terme der Gleichung so u nimm es aus der Klammer:

5. Suchen Sie aus der Klammer, indem Sie sie mit Null gleichsetzen, die Funktion

Dies ist eine trennbare Gleichung:

Teilen wir die Variablen und erhalten:

Wo . .

6. Ersetzen Sie den resultierenden Wert v in die Gleichung ein (aus Schritt 4):

und finden Sie die Funktion Dies ist eine Gleichung mit trennbaren Variablen:

7. Schreiben Sie die allgemeine Lösung in das Formular: , d.h. .

Beispiel 1

Finden Sie eine bestimmte Lösung der Gleichung y" = -2y +3 = 0 Wenn y =1 bei x = 0

Lösung. Lassen Sie es uns durch Substitution lösen y=uv,.y" = u"v + uv"

Ersetzen j Und y" in diese Gleichung erhalten wir

Indem wir den zweiten und dritten Term auf der linken Seite der Gleichung gruppieren, entfernen wir den gemeinsamen Faktor u außerhalb der Klammern

Wir setzen den Ausdruck in Klammern mit Null gleich und finden nach Lösung der resultierenden Gleichung die Funktion v = v(x)

Wir erhalten eine Gleichung mit getrennten Variablen. Integrieren wir beide Seiten dieser Gleichung: Finden Sie die Funktion v:

Ersetzen wir den resultierenden Wert v in die Gleichung erhalten wir:

Dies ist eine Gleichung mit getrennten Variablen. Integrieren wir beide Seiten der Gleichung: Finden wir die Funktion u = u(x,c) Lassen Sie uns eine allgemeine Lösung finden: Lassen Sie uns eine bestimmte Lösung der Gleichung finden, die die Anfangsbedingungen erfüllt y = 1 bei x = 0:

III. Differentialgleichungen höherer Ordnung

3.1. Grundlegende Konzepte und Definitionen

Eine Differentialgleichung zweiter Ordnung ist eine Gleichung, die Ableitungen nicht höherer als zweiter Ordnung enthält. Im allgemeinen Fall wird eine Differentialgleichung zweiter Ordnung wie folgt geschrieben: F(x,y,y",y") = 0

Die allgemeine Lösung einer Differentialgleichung zweiter Ordnung ist eine Funktion der Form, die zwei beliebige Konstanten enthält C 1 Und C 2.

Eine besondere Lösung einer Differentialgleichung zweiter Ordnung ist eine Lösung, die aus einer allgemeinen Lösung für bestimmte Werte beliebiger Konstanten erhalten wird C 1 Und C 2.

3.2. Lineare homogene Differentialgleichungen zweiter Ordnung mit konstante Koeffizienten.

Lineare homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten wird als Gleichung der Form bezeichnet y" + py" +qy = 0, Wo P Und Q- konstante Werte.

Algorithmus zur Lösung homogener Differentialgleichungen zweiter Ordnung mit konstanten Koeffizienten

1. Schreiben Sie die Differentialgleichung in der Form: y" + py" +qy = 0.

2. Erstellen Sie die charakteristische Gleichung und bezeichnen Sie sie y" durch r 2, y" durch R, j in 1: r 2 + pr +q = 0

Differentialgleichungen lösen. Vielen Dank an unsere Onlineservice Sie können Differentialgleichungen jeder Art und Komplexität lösen: inhomogen, homogen, nichtlinear, linear, erster, zweiter Ordnung, mit trennbaren oder nicht trennbaren Variablen usw. Eine Lösung von Differentialgleichungen erhalten Sie in analytischer Form mit detaillierte Beschreibung. Viele Menschen interessieren sich für die Frage: Warum ist es notwendig, Differentialgleichungen online zu lösen? Diese Art von Gleichung ist in der Mathematik und Physik weit verbreitet, wo es unmöglich sein wird, viele Probleme zu lösen, ohne die Differentialgleichung zu berechnen. Differentialgleichungen sind auch in den Wirtschaftswissenschaften, der Medizin, der Biologie, der Chemie und anderen Wissenschaften weit verbreitet. Das Online-Lösen einer solchen Gleichung vereinfacht Ihre Aufgaben erheblich und gibt Ihnen die Möglichkeit, den Stoff besser zu verstehen und sich selbst zu testen. Vorteile der Online-Lösung von Differentialgleichungen. Eine moderne mathematische Serviceseite ermöglicht Ihnen die Lösung von Differentialgleichungen online irgendwelche Schwierigkeiten. Wie Sie wissen, gibt es das große Menge Arten von Differentialgleichungen und jede von ihnen hat ihre eigenen Lösungsmethoden. Auf unserem Service können Sie online Lösungen für Differentialgleichungen jeglicher Ordnung und Art finden. Um eine Lösung zu erhalten, empfehlen wir Ihnen, die Ausgangsdaten einzugeben und auf die Schaltfläche „Lösung“ zu klicken. Fehler bei der Bedienung des Dienstes sind ausgeschlossen, sodass Sie zu 100 % sicher sein können, dass Sie die richtige Antwort erhalten haben. Lösen Sie Differentialgleichungen mit unserem Service. Differentialgleichungen online lösen. Standardmäßig ist in einer solchen Gleichung die Funktion y eine Funktion der x-Variablen. Sie können aber auch eine eigene Variablenbezeichnung angeben. Wenn Sie beispielsweise y(t) in einer Differentialgleichung angeben, ermittelt unser Dienst automatisch, dass y eine Funktion der Variablen t ist. Die Ordnung der gesamten Differentialgleichung hängt von der maximalen Ordnung der Ableitung der in der Gleichung vorhandenen Funktion ab. Das Lösen einer solchen Gleichung bedeutet, die gewünschte Funktion zu finden. Unser Service hilft Ihnen, Differentialgleichungen online zu lösen. Es erfordert von Ihrer Seite keinen großen Aufwand, die Gleichung zu lösen. Sie müssen lediglich die linke und rechte Seite Ihrer Gleichung in die erforderlichen Felder eingeben und auf die Schaltfläche „Lösung“ klicken. Bei der Eingabe muss die Ableitung einer Funktion durch einen Apostroph gekennzeichnet werden. In Sekundenschnelle erhalten Sie das fertige Produkt detaillierte Lösung Differentialgleichung. Unser Service ist absolut kostenlos. Differentialgleichungen mit separierbaren Variablen. Wenn in einer Differentialgleichung auf der linken Seite ein Ausdruck steht, der von y abhängt, und auf der rechten Seite ein Ausdruck, der von x abhängt, dann heißt eine solche Differentialgleichung mit separierbaren Variablen. Die linke Seite kann eine Ableitung von y enthalten; die Lösung für Differentialgleichungen dieser Art wird in Form einer Funktion von y vorliegen, ausgedrückt durch das Integral der rechten Seite der Gleichung. Liegt auf der linken Seite ein Differential der Funktion von y vor, so werden in diesem Fall beide Seiten der Gleichung integriert. Wenn die Variablen in einer Differentialgleichung nicht getrennt sind, müssen sie getrennt werden, um eine getrennte Differentialgleichung zu erhalten. Lineare Differentialgleichung. Eine Differentialgleichung, deren Funktion und alle ihre Ableitungen ersten Grades sind, heißt linear. Generelle Form Gleichungen: y’+a1(x)y=f(x). f(x) und a1(x) sind kontinuierliche Funktionen von x. Die Lösung derartiger Differentialgleichungen reduziert sich auf die Integration zweier Differentialgleichungen mit getrennten Variablen. Ordnung der Differentialgleichung. Eine Differentialgleichung kann erster, zweiter und n-ter Ordnung sein. Die Ordnung einer Differentialgleichung bestimmt die Ordnung der höchsten darin enthaltenen Ableitung. In unserem Service können Sie Differentialgleichungen lösen zuerst online, zweiter, dritter usw. Befehl. Die Lösung der Gleichung ist eine beliebige Funktion y=f(x). Wenn Sie sie in die Gleichung einsetzen, erhalten Sie eine Identität. Der Prozess, eine Lösung für eine Differentialgleichung zu finden, wird Integration genannt. Cauchy-Problem. Ist zusätzlich zur Differentialgleichung selbst die Anfangsbedingung y(x0)=y0 gegeben, so spricht man vom Cauchy-Problem. Die Indikatoren y0 und x0 werden zur Lösung der Gleichung addiert und der Wert einer beliebigen Konstante C bestimmt, und dann wird eine bestimmte Lösung der Gleichung bei diesem Wert von C bestimmt. Dies ist die Lösung des Cauchy-Problems. Das Cauchy-Problem wird auch als Problem mit Randbedingungen bezeichnet, was in der Physik und Mechanik sehr verbreitet ist. Sie haben auch die Möglichkeit, das Cauchy-Problem festzulegen, also von allen mögliche Lösungen Wählen Sie in der Gleichung den Quotienten aus, der die gegebenen Anfangsbedingungen erfüllt.

Differentialgleichung (DE) - das ist die Gleichung,
Wo sind die unabhängigen Variablen, y ist die Funktion und sind die partiellen Ableitungen.

Gewöhnliche Differentialgleichung ist eine Differentialgleichung, die nur eine unabhängige Variable hat, .

Partielle Differentialgleichung ist eine Differentialgleichung mit zwei oder mehr unabhängigen Variablen.

Die Wörter „gewöhnliche“ und „partielle Ableitungen“ können weggelassen werden, wenn klar ist, welche Gleichung berücksichtigt wird. Im Folgenden werden gewöhnliche Differentialgleichungen betrachtet.

Ordnung der Differentialgleichung ist die Ordnung der höchsten Ableitung.

Hier ist ein Beispiel für eine Gleichung erster Ordnung:

Hier ist ein Beispiel für eine Gleichung vierter Ordnung:

Manchmal wird eine Differentialgleichung erster Ordnung als Differentialgleichung geschrieben:

In diesem Fall sind die Variablen x und y gleich. Das heißt, die unabhängige Variable kann entweder x oder y sein. Im ersten Fall ist y eine Funktion von x. Im zweiten Fall ist x eine Funktion von y. Bei Bedarf können wir diese Gleichung auf eine Form reduzieren, die explizit die Ableitung y′ einschließt.
Wenn wir diese Gleichung durch dx dividieren, erhalten wir:
.
Da und folgt daraus
.

Differentialgleichungen lösen

Derivate von elementare Funktionen werden durch Elementarfunktionen ausgedrückt. Integrale elementarer Funktionen werden oft nicht durch elementare Funktionen ausgedrückt. Bei Differentialgleichungen ist die Situation noch schlimmer. Als Ergebnis der Lösung erhalten Sie:

• explizite Abhängigkeit einer Funktion von einer Variablen;

  Lösen einer Differentialgleichung ist die Funktion y = u (X), die definiert ist, n-mal differenzierbar, und .

• implizite Abhängigkeit in Form einer Gleichung vom Typ Φ (x, y) = 0 oder Gleichungssysteme;

  Integral einer Differentialgleichung ist eine Lösung einer Differentialgleichung, die eine implizite Form hat.

• Abhängigkeit, ausgedrückt durch Elementarfunktionen und Integrale von ihnen;

  Lösen einer Differentialgleichung in Quadraturen - Dies bedeutet, eine Lösung in Form einer Kombination von Elementarfunktionen und deren Integralen zu finden.

• Die Lösung darf nicht durch Elementarfunktionen ausgedrückt werden.

Da es beim Lösen von Differentialgleichungen auf die Berechnung von Integralen ankommt, enthält die Lösung einen Satz von Konstanten C 1, C 2, C 3, ... C n. Die Anzahl der Konstanten entspricht der Ordnung der Gleichung. Partielles Integral einer Differentialgleichung ist das allgemeine Integral für gegebene Werte der Konstanten C 1, C 2, C 3, ..., C n.

Verweise:
V.V. Stepanov, Kurs über Differentialgleichungen, „LKI“, 2015.
N.M. Gunter, R.O. Kuzmin, Sammlung von Problemen der höheren Mathematik, „Lan“, 2003.

6.1. GRUNDLEGENDE KONZEPTE UND DEFINITIONEN

Bei der Entscheidung mehrere Aufgaben Mathematik und Physik, Biologie und Medizin, oft ist es nicht möglich, sofort einen funktionalen Zusammenhang in Form einer Verbindungsformel herzustellen Variablen, die den untersuchten Prozess beschreiben. Normalerweise müssen Sie Gleichungen verwenden, die neben der unabhängigen Variablen und der unbekannten Funktion auch deren Ableitungen enthalten.

Definition. Eine Gleichung, die eine unabhängige Variable, eine unbekannte Funktion und ihre Ableitungen verschiedener Ordnungen verbindet, wird aufgerufen Differential.

Normalerweise wird eine unbekannte Funktion bezeichnet y(x) oder einfach ja, und seine Derivate - y", y" usw.

Auch andere Bezeichnungen sind möglich, zum Beispiel: if j= x(t), dann x"(t), x""(t)- seine Derivate und T- unabhängige Variable.

Definition. Wenn eine Funktion von einer Variablen abhängt, heißt die Differentialgleichung gewöhnlich. Generelle Form gewöhnliche Differentialgleichung:

oder

Funktionen F Und F Möglicherweise sind einige Argumente nicht enthalten, aber damit die Gleichungen Differentialgleichungen sind, ist das Vorhandensein einer Ableitung unerlässlich.

Definition.Die Ordnung der Differentialgleichung heißt die Ordnung der höchsten darin enthaltenen Ableitung.

Zum Beispiel, x 2 y"- j= 0, y" + sin X= 0 sind Gleichungen erster Ordnung und y"+ 2 y"+ 5 j= X- Gleichung zweiter Ordnung.

Bei der Lösung von Differentialgleichungen wird die Integrationsoperation verwendet, die mit dem Auftreten einer beliebigen Konstante verbunden ist. Wenn die Integrationsaktion angewendet wird N mal, dann wird die Lösung natürlich enthalten N beliebige Konstanten.

6.2. DIFFERENZGLEICHUNGEN ERSTER ORDNUNG

Generelle Form Differentialgleichung erster Ordnung wird durch den Ausdruck bestimmt

Die Gleichung darf nicht explizit enthalten X Und ja, enthält aber notwendigerweise y".

Wenn die Gleichung geschrieben werden kann als

dann erhalten wir eine nach der Ableitung aufgelöste Differentialgleichung erster Ordnung.

Definition. Die allgemeine Lösung der Differentialgleichung erster Ordnung (6.3) (oder (6.4)) ist die Menge der Lösungen , Wo MIT- Willkürliche Konstante.

Der Graph der Lösung einer Differentialgleichung heißt Integralkurve.

Angabe einer beliebigen Konstante MIT Bei unterschiedlichen Werten können Teillösungen erhalten werden. Auf der Oberfläche xOy Die allgemeine Lösung ist eine Familie von Integralkurven, die jeder einzelnen Lösung entsprechen.

Wenn Sie einen Punkt setzen A (x 0 , y 0), durch die die Integralkurve verlaufen muss, also in der Regel aus einer Menge von Funktionen Eines kann man herausgreifen – eine private Lösung.

Definition.Private Entscheidung einer Differentialgleichung ist ihre Lösung, die keine beliebigen Konstanten enthält.

Wenn ist eine allgemeine Lösung, dann aus der Bedingung

Sie können eine Konstante finden MIT. Die Bedingung wird aufgerufen ausgangsbedingung.

Das Problem, eine bestimmte Lösung für die Differentialgleichung (6.3) oder (6.4) zu finden, die die Anfangsbedingung erfüllt bei angerufen Cauchy-Problem. Gibt es für dieses Problem immer eine Lösung? Die Antwort ist im folgenden Satz enthalten.

Satz von Cauchy(Theorem der Existenz und Einzigartigkeit einer Lösung). Lassen Sie die Differentialgleichung ein y"= f(x,y) Funktion f(x,y) und sie

partielle Ableitung in einigen Fällen definiert und kontinuierlich

Region D, einen Punkt enthalten Dann in der Gegend D existiert

einzige Entscheidung Gleichung, die die Anfangsbedingung erfüllt bei

Der Satz von Cauchy besagt, dass es unter bestimmten Bedingungen eine eindeutige Integralkurve gibt j= f(x), durch einen Punkt gehen Punkte, an denen die Bedingungen des Satzes nicht erfüllt sind

Cauchies werden genannt besonders. An diesen Stellen bricht es F(x, y) oder.

Entweder verlaufen mehrere Integralkurven oder keine durch einen singulären Punkt.

Definition. Wenn die Lösung (6.3), (6.4) in der Form gefunden wird F(x, y, C)= 0, relativ zu y nicht erlaubt, dann heißt es allgemeines Integral Differentialgleichung.

Der Satz von Cauchy garantiert nur, dass eine Lösung existiert. Da es keine einheitliche Methode zum Finden einer Lösung gibt, betrachten wir nur einige Arten von Differentialgleichungen erster Ordnung, in die integriert werden kann Quadraturen

Definition. Die Differentialgleichung heißt in Quadraturen integrierbar, wenn es bei der Lösungsfindung auf die Integration von Funktionen ankommt.

6.2.1. Differentialgleichungen erster Ordnung mit separierbaren Variablen

Definition. Eine Differentialgleichung erster Ordnung heißt Gleichung mit trennbare Variablen,

Die rechte Seite der Gleichung (6.5) ist das Produkt zweier Funktionen, die jeweils nur von einer Variablen abhängen.

Zum Beispiel die Gleichung ist eine Gleichung mit Trennfunktion

gemischt mit Variablen
und die Gleichung

kann nicht in der Form (6.5) dargestellt werden.

Bedenkt, dass , schreiben wir (6.5) in der Form um

Aus dieser Gleichung erhalten wir eine Differentialgleichung mit getrennten Variablen, in der die Differentiale Funktionen sind, die nur von der entsprechenden Variablen abhängen:

Wir haben Begriff für Begriff integriert

wobei C = C 2 - C 1 - beliebige Konstante. Ausdruck (6.6) ist das allgemeine Integral von Gleichung (6.5).

Indem wir beide Seiten der Gleichung (6.5) durch dividieren, können wir diejenigen Lösungen verlieren, für die In der Tat, wenn bei

Das ist offensichtlich eine Lösung für Gleichung (6.5).

Beispiel 1. Finden Sie eine Lösung der Gleichung, die erfüllt

Zustand: j= 6 at X= 2 (j(2) = 6).

Lösung. Wir werden ersetzen y" Dann . Multiplizieren Sie beide Seiten mit

dx, denn während der weiteren Integration ist ein Weggehen nicht möglich dx im Nenner:

und dann beide Teile durch dividieren wir erhalten die Gleichung,

die integriert werden können. Integrieren wir:

Dann ; Potenzierend erhalten wir y = C. (x + 1) - ob-

Allgemeine Lösung.

Anhand der Ausgangsdaten bestimmen wir eine beliebige Konstante und setzen sie in die allgemeine Lösung ein

Endlich bekommen wir j= 2(x + 1) ist eine bestimmte Lösung. Schauen wir uns noch ein paar Beispiele für die Lösung von Gleichungen mit trennbaren Variablen an.

Beispiel 2. Finden Sie die Lösung der Gleichung

Lösung. Bedenkt, dass , wir bekommen .

Wenn wir beide Seiten der Gleichung integrieren, haben wir

Wo

Beispiel 3. Finden Sie die Lösung der Gleichung Lösung. Wir unterteilen beide Seiten der Gleichung in diejenigen Faktoren, die von einer Variablen abhängen, die nicht mit der Variablen unter dem Differentialvorzeichen übereinstimmt, d.h. und integrieren. Dann bekommen wir

und endlich,

Beispiel 4. Finden Sie die Lösung der Gleichung

Lösung. Wissen, was wir bekommen werden. Abschnitt

Lim-Variablen. Dann

Integrieren, verstehen wir

Kommentar. In den Beispielen 1 und 2 lautet die erforderliche Funktion j explizit ausgedrückt (allgemeine Lösung). In den Beispielen 3 und 4 - implizit (allgemeines Integral). Die Form der Entscheidung wird künftig nicht präzisiert.

Beispiel 5. Finden Sie die Lösung der Gleichung Lösung.

Beispiel 6. Finden Sie die Lösung der Gleichung , befriedigend

Zustand Ihr)= 1.

Lösung. Schreiben wir die Gleichung in das Formular

Beide Seiten der Gleichung mit multiplizieren dx und weiter, wir bekommen

Wenn wir beide Seiten der Gleichung integrieren (das Integral auf der rechten Seite wird in Teile genommen), erhalten wir

Aber je nach Zustand j= 1 bei X= e. Dann

Ersetzen wir die gefundenen Werte MIT zur allgemeinen Lösung:

Der resultierende Ausdruck wird Teillösung der Differentialgleichung genannt.

6.2.2. Homogene Differentialgleichungen erster Ordnung

Definition. Die Differentialgleichung erster Ordnung heißt homogen, wenn es in der Form dargestellt werden kann

Stellen wir einen Algorithmus zur Lösung einer homogenen Gleichung vor.

1.Stattdessen j Lassen Sie uns eine neue Funktion einführenDann und deshalb

2. In Bezug auf die Funktion u Gleichung (6.7) nimmt die Form an

das heißt, die Ersetzung reduziert eine homogene Gleichung auf eine Gleichung mit trennbaren Variablen.

3. Wenn wir Gleichung (6.8) lösen, finden wir zuerst u und dann j= ux.

Beispiel 1. Löse die Gleichung Lösung. Schreiben wir die Gleichung in das Formular

Wir führen die Substitution durch:
Dann

Wir werden ersetzen

Mit dx multiplizieren: Teilen durch X und weiter Dann

Nachdem wir beide Seiten der Gleichung über die entsprechenden Variablen integriert haben, haben wir

oder wenn wir zu den alten Variablen zurückkehren, erhalten wir endlich

Beispiel 2.Löse die Gleichung Lösung.Lassen Dann

Teilen wir beide Seiten der Gleichung durch x2: Öffnen wir die Klammern und ordnen wir die Begriffe neu an:

Wenn wir zu den alten Variablen übergehen, kommen wir zum Endergebnis:

Beispiel 3.Finden Sie die Lösung der Gleichung angesichts dessen

Lösung.Durchführen eines Standardaustauschs wir bekommen

oder

oder

Dies bedeutet, dass die jeweilige Lösung die Form hat Beispiel 4. Finden Sie die Lösung der Gleichung

Lösung.

Beispiel 5.Finden Sie die Lösung der Gleichung Lösung.

Selbstständige Arbeit

Finden Sie Lösungen für Differentialgleichungen mit separierbaren Variablen (1-9).

Finden Sie eine Lösung für homogene Differentialgleichungen (9-18).

6.2.3. Einige Anwendungen von Differentialgleichungen erster Ordnung

Problem des radioaktiven Zerfalls

Die Zerfallsrate von Ra (Radium) ist zu jedem Zeitpunkt proportional zu seiner verfügbaren Masse. Finden Sie das Gesetz des radioaktiven Zerfalls von Ra, wenn bekannt ist, dass es im ersten Moment Ra gab und die Halbwertszeit von Ra 1590 Jahre beträgt.

Lösung. Sei im Moment die Masse Ra X= x(t) g, und Dann ist die Abklingrate Ra gleich

Je nach den Bedingungen des Problems

Wo k

Wenn wir die Variablen in der letzten Gleichung trennen und integrieren, erhalten wir

Wo

Zur Bestimmung C Wir verwenden die Anfangsbedingung: wann .

Dann und deshalb,

Proportionalitätsfaktor k ermittelt aus Zusätzlicher Zustand:

Wir haben

Von hier und die erforderliche Formel

Problem mit der bakteriellen Reproduktionsrate

Die Vermehrungsrate der Bakterien ist proportional zu ihrer Anzahl. Am Anfang waren es 100 Bakterien. Innerhalb von 3 Stunden verdoppelte sich ihre Zahl. Finden Sie die Abhängigkeit der Bakterienzahl von der Zeit. Wie oft wird die Anzahl der Bakterien innerhalb von 9 Stunden ansteigen?

Lösung. Lassen X- Anzahl der Bakterien gleichzeitig T. Dann, je nach Bedingung,

Wo k- Proportionalitätskoeffizient.

Von hier Aus der Bedingung ist das bekannt . Bedeutet,

Aus der Zusatzbedingung . Dann

Die Funktion, die Sie suchen:

Also, wann T= 9 X= 800, d.h. innerhalb von 9 Stunden erhöhte sich die Bakterienzahl um das 8-fache.

Das Problem der Erhöhung der Enzymmenge

In einer Bierhefekultur ist die Wachstumsrate des aktiven Enzyms proportional zu seiner Anfangsmenge X. Anfangsmenge an Enzym A innerhalb einer Stunde verdoppelt. Abhängigkeit finden

x(t).

Lösung. Unter der Bedingung hat die Differentialgleichung des Prozesses die Form

von hier

Aber . Bedeutet, C= A und dann

Das ist auch bekannt

Somit,

6.3. DIFFERENZGLEICHUNGEN ZWEITER ORDNUNG

6.3.1. Grundlegendes Konzept

Definition.Differentialgleichung zweiter Ordnung wird eine Beziehung genannt, die die unabhängige Variable, die gewünschte Funktion und ihre ersten und zweiten Ableitungen verbindet.

In besonderen Fällen kann x in der Gleichung fehlen, bei oder y". Allerdings muss eine Gleichung zweiter Ordnung notwendigerweise y enthalten." Im allgemeinen Fall wird eine Differentialgleichung zweiter Ordnung wie folgt geschrieben:

oder, wenn möglich, in der bezüglich der zweiten Ableitung aufgelösten Form:

Wie bei einer Gleichung erster Ordnung kann es auch bei einer Gleichung zweiter Ordnung allgemeine und besondere Lösungen geben. Die allgemeine Lösung lautet:

Eine bestimmte Lösung finden

unter Anfangsbedingungen - gegeben

Zahlen) aufgerufen wird Cauchy-Problem. Geometrisch bedeutet das, dass wir die Integralkurve finden müssen bei= y(x), Durchqueren eines bestimmten Punktes und an diesem Punkt eine Tangente haben, die ist

richtet sich nach der positiven Achsenrichtung Ochse angegebenen Winkel. e. (Abb. 6.1). Das Cauchy-Problem hat eine eindeutige Lösung, wenn die rechte Seite der Gleichung (6.10) unaufhörlich

ist diskontinuierlich und hat stetige partielle Ableitungen nach äh, äh" in einer Gegend des Ausgangspunkts

Konstanten finden In einer privaten Lösung enthalten, muss das System aufgelöst werden

Reis. 6.1. Integralkurve

Entweder wurden sie bereits bezüglich der Ableitung gelöst, oder sie können bezüglich der Ableitung gelöst werden .

Allgemeine Lösung von Differentialgleichungen vom Typ auf dem Intervall X, die gegeben ist, kann gefunden werden, indem man das Integral beider Seiten dieser Gleichheit bildet.

Wir bekommen .

Wenn man sich die Eigenschaften anschaut unbestimmtes Integral, dann finden wir die gewünschte allgemeine Lösung:

y = F(x) + C,

Wo F(x)- eine der primitiven Funktionen f(x) zwischen X, A MIT- Willkürliche Konstante.

Bitte beachten Sie, dass bei den meisten Problemen das Intervall X nicht angeben. Das bedeutet, dass für alle eine Lösung gefunden werden muss. X, wofür und die gewünschte Funktion j und die ursprüngliche Gleichung machen Sinn.

Wenn Sie eine bestimmte Lösung einer Differentialgleichung berechnen müssen, die die Anfangsbedingung erfüllt y(x 0) = y 0, dann nach der Berechnung allgemeines Integral y = F(x) + C, ist es noch notwendig, den Wert der Konstante zu bestimmen C = C 0, unter Verwendung der Anfangsbedingung. Das heißt, eine Konstante C = C 0 aus der Gleichung ermittelt F(x 0) + C = y 0, und die gewünschte Teillösung der Differentialgleichung wird die Form annehmen:

y = F(x) + C 0.

Schauen wir uns ein Beispiel an:

Lassen Sie uns eine allgemeine Lösung der Differentialgleichung finden und die Richtigkeit des Ergebnisses überprüfen. Lassen Sie uns eine bestimmte Lösung für diese Gleichung finden, die die Anfangsbedingung erfüllen würde.

Lösung:

Nachdem wir die gegebene Differentialgleichung integriert haben, erhalten wir:

.

Nehmen wir dieses Integral mit der Methode der partiellen Integration:

Das., ist eine allgemeine Lösung der Differentialgleichung.

Um sicherzustellen, dass das Ergebnis korrekt ist, führen wir eine Überprüfung durch. Dazu setzen wir die gefundene Lösung in die gegebene Gleichung ein:

.

Das ist wenn aus der ursprünglichen Gleichung wird eine Identität:

Daher wurde die allgemeine Lösung der Differentialgleichung korrekt bestimmt.

Die von uns gefundene Lösung ist eine allgemeine Lösung der Differentialgleichung für jeden reellen Wert des Arguments X.

Es bleibt noch eine bestimmte Lösung der ODE zu berechnen, die die Anfangsbedingung erfüllen würde. Mit anderen Worten: Es ist notwendig, den Wert der Konstante zu berechnen MIT, bei dem die Gleichheit wahr sein wird:

.

.

Dann ersetzen C = 2 In die allgemeine Lösung der ODE erhalten wir eine bestimmte Lösung der Differentialgleichung, die die Anfangsbedingung erfüllt:

.

Gewöhnliche Differentialgleichung kann nach der Ableitung gelöst werden, indem man die beiden Seiten der Gleichung durch dividiert f(x). Diese Transformation ist äquivalent, wenn f(x) geht unter keinen Umständen auf Null X aus dem Integrationsintervall der Differentialgleichung X.

Es gibt wahrscheinliche Situationen, in denen für einige Werte das Argument gilt X ∈ X Funktionen f(x) Und g(x) werden gleichzeitig Null. Für ähnliche Werte X Die allgemeine Lösung einer Differentialgleichung ist eine beliebige Funktion j, was in ihnen definiert ist, weil .

Wenn für einige Argumentwerte X ∈ X die Bedingung ist erfüllt, was bedeutet, dass die ODE in diesem Fall keine Lösungen hat.

Für alle anderen X aus dem Intervall X Aus der transformierten Gleichung wird die allgemeine Lösung der Differentialgleichung ermittelt.

Schauen wir uns Beispiele an:

Beispiel 1.

Lassen Sie uns eine allgemeine Lösung für die ODE finden: .

Lösung.

Aus den Eigenschaften der grundlegenden Elementarfunktionen geht hervor, dass die natürliche Logarithmusfunktion für nichtnegative Werte des Arguments definiert ist, daher der Definitionsbereich des Ausdrucks ln(x+3) es gibt ein Intervall X > -3 . Dies bedeutet, dass die gegebene Differentialgleichung sinnvoll ist X > -3 . Für diese Argumentwerte ist der Ausdruck x+3 verschwindet nicht, daher können Sie die ODE für die Ableitung lösen, indem Sie die beiden Teile durch dividieren x + 3.

Wir bekommen .

Als nächstes integrieren wir die resultierende Differentialgleichung, gelöst nach der Ableitung: . Um dieses Integral zu bilden, verwenden wir die Methode, es unter dem Differentialzeichen zu subsumieren.