Was ist eine Funktion und ihre allgemeine Formel? Grundlegende Konzepte und Eigenschaften von Funktionen

Die Wahrung Ihrer Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Daten verwenden und speichern. Bitte lesen Sie unsere Datenschutzpraktiken durch und teilen Sie uns mit, wenn Sie Fragen haben.

Erhebung und Nutzung personenbezogener Daten

Unter personenbezogenen Daten versteht man Daten, die dazu genutzt werden können, eine bestimmte Person zu identifizieren oder mit ihr in Kontakt zu treten.

Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie mit uns Kontakt aufnehmen.

Nachfolgend finden Sie einige Beispiele für die Arten personenbezogener Daten, die wir möglicherweise sammeln, und wie wir diese Informationen verwenden können.

Welche personenbezogenen Daten erfassen wir:

• Wenn Sie auf der Website eine Bewerbung einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer, Ihrer E-Mail-Adresse usw.

Wie wir Ihre persönlichen Daten verwenden:

• Die von uns erfassten personenbezogenen Daten ermöglichen es uns, Sie mit einzigartigen Angeboten, Werbeaktionen und anderen Veranstaltungen sowie bevorstehenden Veranstaltungen zu kontaktieren.
• Von Zeit zu Zeit können wir Ihre persönlichen Daten verwenden, um wichtige Mitteilungen und Mitteilungen zu versenden.
• Wir können personenbezogene Daten auch für interne Zwecke verwenden, beispielsweise zur Durchführung von Audits, Datenanalysen und verschiedenen Forschungsarbeiten, um die von uns bereitgestellten Dienste zu verbessern und Ihnen Empfehlungen zu unseren Diensten zu geben.
• Wenn Sie an einer Verlosung, einem Wettbewerb oder einer ähnlichen Aktion teilnehmen, können wir die von Ihnen bereitgestellten Informationen zur Verwaltung solcher Programme verwenden.

Weitergabe von Informationen an Dritte

Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.

Ausnahmen:

• Falls erforderlich, in Übereinstimmung mit dem Gesetz, Gerichtsverfahren, in Gerichtsverfahren und/oder auf der Grundlage öffentlicher Anfragen oder Anfragen von Regierungsbehörden in der Russischen Föderation – um Ihre personenbezogenen Daten offenzulegen. Wir können auch Informationen über Sie offenlegen, wenn wir zu dem Schluss kommen, dass eine solche Offenlegung aus Sicherheits-, Strafverfolgungs- oder anderen Gründen von öffentlicher Bedeutung notwendig oder angemessen ist.
• Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den jeweiligen Nachfolger-Dritten weitergeben.

Schutz personenbezogener Daten

Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer –, um Ihre persönlichen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung zu schützen.

Respektieren Sie Ihre Privatsphäre auf Unternehmensebene

Um sicherzustellen, dass Ihre persönlichen Daten sicher sind, kommunizieren wir Datenschutz- und Sicherheitsstandards an unsere Mitarbeiter und setzen Datenschutzpraktiken strikt durch.

Der Abschnitt enthält Referenzmaterial zu den wichtigsten Elementarfunktionen und ihren Eigenschaften. Die Klassifizierung ist angegeben elementare Funktionen. Unten finden Sie Links zu Unterabschnitten, in denen die Eigenschaften bestimmter Funktionen besprochen werden – Graphen, Formeln, Ableitungen, Stammfunktionen (Integrale), Reihenentwicklungen, Ausdrücke durch komplexe Variablen.

Referenzseiten für Grundfunktionen

Klassifizierung elementarer Funktionen

Algebraische Funktion ist eine Funktion, die die Gleichung erfüllt:
,
wobei ein Polynom in der abhängigen Variablen y und der unabhängigen Variablen x ist. Es kann wie folgt geschrieben werden:
,
Wo sind Polynome?

Algebraische Funktionen werden in Polynome (vollständige rationale Funktionen), rationale Funktionen und irrationale Funktionen unterteilt.

Vollständige rationale Funktion, was auch genannt wird Polynom oder Polynom, wird aus der Variablen x und einer endlichen Anzahl von Zahlen mit erhalten Rechenoperationen Addition (Subtraktion) und Multiplikation. Nach dem Öffnen der Klammern wird das Polynom auf die kanonische Form reduziert:
.

Bruchrationale Funktion, oder einfach rationale Funktion, wird aus der Variablen x und einer endlichen Anzahl von Zahlen durch die Rechenoperationen Addition (Subtraktion), Multiplikation und Division gewonnen. Die rationale Funktion lässt sich auf die Form reduzieren
,
wobei und Polynome sind.

Irrationale Funktion ist eine algebraische Funktion, die nicht rational ist. Unter einer irrationalen Funktion werden in der Regel Wurzeln und deren Zusammensetzungen mit rationalen Funktionen verstanden. Als Lösung der Gleichung wird eine Wurzel vom Grad n definiert
.
Es wird wie folgt bezeichnet:
.

Transzendentale Funktionen werden nichtalgebraische Funktionen genannt. Dies sind exponentielle, trigonometrische, hyperbolische und ihre Umkehrfunktionen.

Übersicht über grundlegende Elementarfunktionen

Alle Elementarfunktionen können als endliche Anzahl von Additions-, Subtraktions-, Multiplikations- und Divisionsoperationen dargestellt werden, die an einem Ausdruck der Form ausgeführt werden:
z t .
Umkehrfunktionen können auch durch Logarithmen ausgedrückt werden. Nachfolgend sind die grundlegenden Elementarfunktionen aufgeführt.

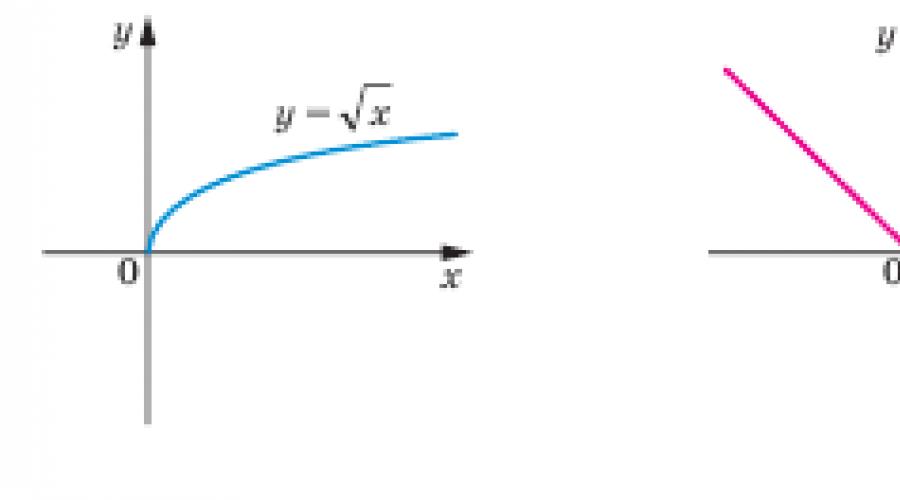
Leistungsfunktion:
y(x) = x p ,
wobei p der Exponent ist. Es kommt auf die Basis des Grades x an.
Die Umkehrung der Potenzfunktion ist auch die Potenzfunktion:
.
Für einen ganzzahligen, nicht negativen Wert des Exponenten p handelt es sich um ein Polynom. Für einen ganzzahligen Wert p - eine rationale Funktion. Mit einer rationalen Bedeutung – einer irrationalen Funktion.

Transzendentale Funktionen

Exponentialfunktion :
y(x) = a x ,
wobei a die Basis des Grades ist. Es kommt auf den Exponenten x an.
Die Umkehrfunktion ist der Logarithmus zur Basis von a:
x = log ein y.

Exponent, e hoch x:
y(x) = e x ,
Dies ist eine Exponentialfunktion, deren Ableitung gleich der Funktion selbst ist:
.
Die Basis des Exponenten ist die Zahl e:
≈ 2,718281828459045... .
Die Umkehrfunktion ist der natürliche Logarithmus – der Logarithmus zur Basis der Zahl e:
x = ln y ≡ log e y.

Trigonometrische Funktionen:
Sinus: ;
Kosinus: ;
Tangente: ;
Kotangens: ;
Hier ist i die imaginäre Einheit, i 2 = -1.

Inverse trigonometrische Funktionen:
Arkussinus: x = arcsin y, ;
Arkuskosinus: x = arccos y, ;
Arkustangens: x = arctan y, ;
Arcustangens: x = arcctg y, .

Um dieses Thema zu verstehen, betrachten wir eine in einem Diagramm dargestellte Funktion. // Zeigen wir, wie ein Diagramm einer Funktion es Ihnen ermöglicht, ihre Eigenschaften zu bestimmen.

Schauen wir uns die Eigenschaften einer Funktion anhand eines Beispiels an

Der Definitionsbereich der Funktion ist Spanne [ 3,5; 5.5].

Der Wertebereich der Funktion ist Spanne [ 1; 3].

1. Bei x = -3, x = - 1, x = 1,5, x = 4,5 ist der Wert der Funktion Null.

Der Argumentwert, bei dem der Funktionswert Null ist, wird Funktion Null genannt.

//diese. Für diese Funktion sind die Zahlen -3;-1;1,5; 4,5 sind Nullen.

2. In Abständen [ 4,5; 3) und (1; 1,5) und (4,5; 5,5] der Graph der Funktion f liegt oberhalb der Abszissenachse und in den Intervallen (-3; -1) und (1,5; 4,5) unterhalb der Abszissenachse wird so erklärt -in Intervallen[ 4,5; 3) und (1; 1.5) und (4.5;5.5] nimmt die Funktion an positive Werte, und auf den Intervallen (-3; -1) und (1,5; 4,5) sind negativ.

Jedes der angegebenen Intervalle (wobei die Funktion Werte mit demselben Vorzeichen annimmt) wird als Intervall mit konstantem Vorzeichen der Funktion f.//d.h. bezeichnet. Nehmen wir zum Beispiel das Intervall (0; 3), dann ist es kein Intervall mit konstantem Vorzeichen dieser Funktion.

In der Mathematik ist es bei der Suche nach Intervallen mit konstantem Vorzeichen einer Funktion üblich, Intervalle mit maximaler Länge anzugeben. //Diese. das Intervall (2; 3) ist Intervall der Vorzeichenkonstanz Funktion f, aber die Antwort sollte das Intervall [ 4,5; 3) enthält das Intervall (2; 3).

3. Wenn Sie sich entlang der x-Achse von 4,5 auf 2 bewegen, werden Sie feststellen, dass der Funktionsgraph nach unten geht, das heißt, die Funktionswerte sinken. //In der Mathematik ist es üblich zu sagen, dass auf dem Intervall [ 4,5; 2] nimmt die Funktion ab.

Wenn x von 2 auf 0 steigt, steigt der Graph der Funktion, d. h. die Funktionswerte steigen. //In der Mathematik ist es üblich zu sagen, dass auf dem Intervall [ 2; 0] erhöht sich die Funktion.

Eine Funktion f heißt, wenn für zwei beliebige Werte des Arguments x1 und x2 aus diesem Intervall mit x2 > x1 die Ungleichung f (x2) > f (x1) gilt. // oder die Funktion wird aufgerufen über einen gewissen Zeitraum ansteigend, falls für irgendwelche Werte des Arguments aus diesem Intervall höherer Wert Argument entspricht einem größeren Wert der Funktion.//d.h. je mehr x, desto mehr y.

Die Funktion f wird aufgerufen über einen gewissen Zeitraum abnehmend, wenn für zwei beliebige Werte des Arguments x1 und x2 aus diesem Intervall, so dass x2 > x1, die Ungleichung f(x2) in einem bestimmten Intervall abnimmt, wenn für beliebige Werte des Arguments aus diesem Intervall der größere Wert des Arguments dem kleineren Wert der Funktion entspricht. //diese. je mehr x, desto weniger y.

Wenn eine Funktion über den gesamten Definitionsbereich zunimmt, wird sie aufgerufen zunehmend.

Wenn eine Funktion über den gesamten Definitionsbereich abnimmt, wird sie aufgerufen abnehmend.

Beispiel 1. Diagramm der steigenden bzw. fallenden Funktionen.

Beispiel 2.

Definieren Sie das Phänomen. ob lineare Funktion f (x) = 3x + 5 steigend oder fallend?

Nachweisen. Lassen Sie uns die Definitionen verwenden. Seien x1 und x2 beliebige Werte des Arguments und x1< x2., например х1=1, х2=7

1) Funktionsbereich und Funktionsumfang.

Der Definitionsbereich einer Funktion ist die Menge aller gültigen Argumentwerte X(Variable X), für die die Funktion y = f(x) bestimmt. Der Bereich einer Funktion ist die Menge aller reellen Werte j, was die Funktion akzeptiert.

In der Elementarmathematik werden Funktionen nur auf der Menge der reellen Zahlen untersucht.

2) Funktionsnullstellen.

Funktionsnull ist der Wert des Arguments, bei dem der Wert der Funktion gleich Null ist.

3) Intervalle mit konstantem Vorzeichen einer Funktion.

Intervalle mit konstantem Vorzeichen einer Funktion sind Mengen von Argumentwerten, bei denen die Funktionswerte nur positiv oder nur negativ sind.

4) Monotonie der Funktion.

Eine steigende Funktion (in einem bestimmten Intervall) ist eine Funktion, bei der ein größerer Wert des Arguments aus diesem Intervall einem größeren Wert der Funktion entspricht.

Eine abnehmende Funktion (in einem bestimmten Intervall) ist eine Funktion, bei der ein größerer Wert des Arguments aus diesem Intervall einem kleineren Wert der Funktion entspricht.

5) Gerade (ungerade) Funktion.

Eine gerade Funktion ist eine Funktion, deren Definitionsbereich bezüglich des Ursprungs und für jeden symmetrisch ist X aus dem Definitionsbereich die Gleichheit f(-x) = f(x). Der Graph einer geraden Funktion ist symmetrisch zur Ordinate.

Eine ungerade Funktion ist eine Funktion, deren Definitionsbereich bezüglich des Ursprungs und für jeden symmetrisch ist X Aus dem Definitionsbereich ist die Gleichheit wahr f(-x) = - f(x). Der Graph einer ungeraden Funktion ist symmetrisch zum Ursprung.

6) Begrenzte und unbegrenzte Funktionen.

Eine Funktion heißt beschränkt, wenn es eine positive Zahl M mit |f(x)| gibt ≤ M für alle Werte von x. Existiert eine solche Zahl nicht, ist die Funktion unbegrenzt.

7) Periodizität der Funktion.

Eine Funktion f(x) ist periodisch, wenn es eine Zahl T ungleich Null gibt, so dass für jedes x aus dem Definitionsbereich der Funktion gilt: f(x+T) = f(x). Diese kleinste Zahl wird als Periode der Funktion bezeichnet. Alle trigonometrischen Funktionen sind periodisch. (Trigonometrische Formeln).

19. Grundlegende Elementarfunktionen, ihre Eigenschaften und Graphen. Anwendung von Funktionen in der Wirtschaftswissenschaft.

Grundlegende Elementarfunktionen. Ihre Eigenschaften und Diagramme

1. Lineare Funktion.

Lineare Funktion heißt eine Funktion der Form , wobei x eine Variable ist, a und b reelle Zahlen sind.

Nummer A angerufen Neigung gerade, er gleich Tangente der Neigungswinkel dieser Geraden zur positiven Richtung der x-Achse. Der Graph einer linearen Funktion ist eine Gerade. Es wird durch zwei Punkte definiert.

Eigenschaften einer linearen Funktion

1. Definitionsbereich – die Menge aller reellen Zahlen: D(y)=R

2. Die Wertemenge ist die Menge aller reellen Zahlen: E(y)=R

3. Die Funktion nimmt einen Nullwert an, wenn oder.

4. Die Funktion nimmt über den gesamten Definitionsbereich zu (ab).

5. Eine lineare Funktion ist über den gesamten Definitionsbereich stetig, differenzierbar und .

2. Quadratische Funktion.

Eine Funktion der Form, wobei x eine Variable ist, Koeffizienten a, b, c reelle Zahlen sind, heißt quadratisch

Grenzen und Kontinuität

Sets

Unter viele wird als eine Ansammlung homogener Objekte verstanden. Objekte, die eine Menge bilden, werden aufgerufen Elemente oder Punkte dieser Menge. Mengen bezeichnen in Großbuchstaben, und ihre Elemente sind Kleinbuchstaben. Wenn A ist ein Element der Menge A, dann wird der Eintrag verwendet AÎ A. Wenn B ist kein Element der Menge A, dann schreibt man es so: B Ï A. Eine Menge, die kein einzelnes Element enthält, heißt leere Menge und wird wie folgt bezeichnet: Ø.

Wenn das Set B besteht aus einem Teil der Elemente der Menge A oder damit übereinstimmt, dann die Menge B angerufen Teilmenge setzt und bezeichnet BÌ A.

Die beiden Mengen werden aufgerufen gleich, wenn sie aus den gleichen Elementen bestehen.

Verband zwei Sets A Und B eine Menge genannt C, bestehend aus allen Elementen, die zu mindestens einer der Mengen gehören: C=AÈ B.

Durch Überqueren zwei Sets A Und B eine Menge genannt C, bestehend aus allen Elementen, die zu jeder dieser Mengen gehören: C=AÇ B.

Durch Differenz Sätze A Und B eine Menge genannt E A, die nicht zur Menge gehören B: .

Ergänzung Sätze AÌ B eine Menge genannt C, bestehend aus allen Elementen der Menge B, nicht dazugehörend A.

Mengen, deren Elemente reelle Zahlen sind, werden aufgerufen numerisch:

Dabei NÌ ZÌ QÌ R, ICHÌ R Und R=ICHÈ Q.

Ein Haufen X, deren Elemente die Ungleichung erfüllen, heißt Segment(Segment) und wird mit [ A; B]; Ungleichheit A<X<B – Intervall und wird mit () bezeichnet; Ungleichheiten und - Halbintervalle und werden jeweils mit und bezeichnet. Oft muss man sich auch mit unendlichen Intervallen und Halbintervallen befassen: , , , und . Es ist praktisch, sie alle anzurufen in Intervallen .

Intervall, d.h. Menge von Punkten, die die Ungleichung erfüllen (wobei ), heißt die -Nachbarschaft des Punktes A.

Der Funktionsbegriff. Grundlegende Eigenschaften einer Funktion

Wenn jedes Element X Sätze X ein einzelnes Element wird abgeglichen j Sätze Y, dann sagen sie das am Set X gegeben Funktion j=F(X). Dabei X angerufen unabhängige Variable oder Streit, A j – abhängige Variable oder Funktion, A F bezeichnet das Gesetz der Korrespondenz. Ein Haufen X angerufen Definitionsbereich Funktionen und eine Menge Y – Wertebereich Funktionen.

Es gibt mehrere Möglichkeiten, Funktionen anzugeben.

1) Analytische Methode – die Funktion wird durch eine Formel der Form gegeben j=F(X).

2) Tabellarische Methode – die Funktion wird durch eine Tabelle spezifiziert, die die Argumentwerte und die entsprechenden Funktionswerte enthält j=F(X).

3) Grafische Methode – Darstellung eines Graphen einer Funktion, d.h. Menge von Punkten ( X; j) Koordinatenebene, deren Abszissen die Werte des Arguments und deren Ordinaten die entsprechenden Werte der Funktion darstellen j=F(X).

4) Verbale Methode – eine Funktion wird durch die Regel für ihre Zusammensetzung beschrieben. Beispielsweise nimmt die Dirichlet-Funktion den Wert 1 an, wenn X ist eine rationale Zahl und 0, wenn X- irrationale Zahl.

Folgende Haupteigenschaften von Funktionen werden unterschieden.

1 Gerade und ungerade Funktion j=F(X) wird genannt sogar, wenn für irgendwelche Werte X aus seinem Definitionsbereich erfüllt ist F(–X)=F(X), Und seltsam, Wenn F(–X)=–F(X). Wenn keine der aufgeführten Gleichheiten erfüllt ist, dann j=F(X) wird genannt allgemeine Funktion. Der Graph einer geraden Funktion ist symmetrisch zur Achse Oy, und der Graph der ungeraden Funktion ist symmetrisch zum Ursprung.

2 Monotonie Funktion j=F(X) wird genannt zunehmend (abnehmend) auf dem Intervall X, wenn einem größeren Argumentwert aus diesem Intervall ein größerer (kleinerer) Funktionswert entspricht. Lassen X 1 ,X 2 Î X, X 2 >X 1 . Dann nimmt die Funktion im Intervall zu X, Wenn F(X 2)>F(X 1) und verringert sich, wenn F(X 2)<F(X 1).

Neben steigenden und fallenden Funktionen werden auch nicht fallende und nicht steigende Funktionen berücksichtigt. Die Funktion wird aufgerufen nicht abnehmend (nicht zunehmend), wenn bei X 1 ,X 2 Î X, X 2 >X 1 Ungleichung gilt F(X 2)≥F(X 1) (F(X 2)≤F(X 1)).

Steigende und fallende Funktionen sowie nicht steigende und nicht fallende Funktionen werden als monoton bezeichnet.

3 Begrenzt Funktion j=F(X) heißt auf dem Intervall beschränkt X, wenn es eine solche positive Zahl gibt M>0, was | F(X)|≤M für jeden XÎ X. Andernfalls heißt die Funktion unbeschränkt X.

4 Frequenz Funktion j=F(X) heißt periodisch mit Punkt T≠0, falls vorhanden X aus dem Bereich der Funktion F(X+T)=F(X). Unter Periode verstehen wir im Folgenden die kleinste positive Periode einer Funktion.

Die Funktion wird aufgerufen explizit, wenn es durch eine Formel der Form gegeben ist j=F(X). Wenn die Funktion durch die Gleichung gegeben ist F(X, j)=0, relativ zur abhängigen Variablen nicht zulässig j, dann heißt es implizit.

Lassen j=F(X) ist eine Funktion der auf der Menge definierten unabhängigen Variablen X mit Reichweite Y. Lassen Sie uns jeden einzelnen zuordnen jÎ Y einzige Bedeutung XÎ X, bei welchem F(X)=j.Dann die resultierende Funktion X=φ (j), auf dem Set definiert Y mit Reichweite X, angerufen umkehren und ist bezeichnet j=F –1 (X). Diagramme gegenseitig Umkehrfunktionen symmetrisch relativ zur Winkelhalbierenden des ersten und dritten Koordinatenviertels.

Lassen Sie die Funktion j=F(u) ist eine Funktion einer Variablen u, am Set definiert U mit Reichweite Y, und die Variable u wiederum ist eine Funktion u=φ (X), auf dem Set definiert X mit Reichweite U. Dann am Set gegeben X Funktion j=F(φ (X)) wird genannt komplexe Funktion (Zusammensetzung von Funktionen, Überlagerung von Funktionen, Funktion einer Funktion).

Elementare Funktionen

Zu den wichtigsten Elementarfunktionen gehören:

• Power-Funktion j=x n; j=x–n Und j=X 1/ N;
• Exponentialfunktion j=ein x;
• logarithmische Funktion j=log ein x;
• trigonometrische Funktionen j=Sünde X, j=cos X, j=tg X Und j=ctg X;
• inverse trigonometrische Funktionen j= Arcsin X, j=arccos X, j=arctg X Und j=arcctg X.

Aus den Grundelementarfunktionen können durch algebraische Operationen und Überlagerung von Funktionen neue Funktionen gewonnen werden.

Es werden Funktionen aufgerufen, die aus grundlegenden Elementarfunktionen unter Verwendung einer endlichen Anzahl algebraischer Operationen und einer endlichen Anzahl von Superpositionsoperationen aufgebaut sind elementar.

Algebraisch ist eine Funktion, bei der eine endliche Anzahl algebraischer Operationen für das Argument ausgeführt wird. Zu den algebraischen Funktionen gehören:

· eine ganze rationale Funktion (Polynom oder Polynom)

· gebrochenrationale Funktion (Verhältnis zweier Polynome)

· Irrationale Funktion (wenn die Operationen am Argument das Extrahieren der Wurzel beinhalten).

Jede nicht-algebraische Funktion wird aufgerufen transzendental. Zu den transzendenten Funktionen gehören exponentielle, logarithmische, trigonometrische und inverse trigonometrische Funktionen.