Quadratwurzel von 12000. Berechnung der Wurzel durch lange Division
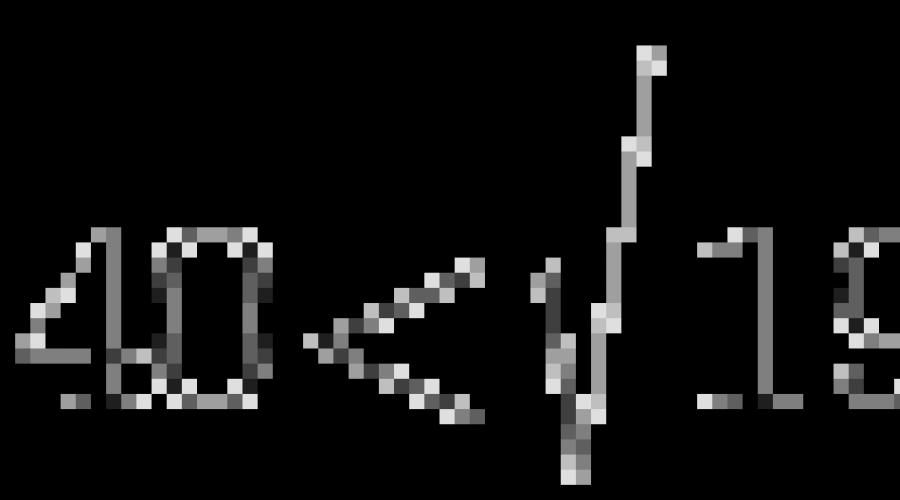
Lesen Sie auch
Vorzugsweise eine technische Version – eine mit einem Knopf mit dem Grundzeichen „√“. Um die Wurzel zu extrahieren, reicht es normalerweise aus, die Zahl selbst einzugeben und dann die Taste „√“ zu drücken.
In den meisten modernen Mobiltelefone Es gibt eine „Rechner“-Anwendung mit einer Root-Extraktionsfunktion. Das Verfahren zum Ermitteln der Wurzel einer Zahl mit einem Telefonrechner ähnelt dem oben beschriebenen.
Beispiel.
Finden Sie ab 2.
Schalten Sie den Rechner ein (falls er ausgeschaltet ist) und drücken Sie nacheinander die Tasten mit dem Bild von Zwei und Wurzel („2“, „√“). In der Regel ist es nicht erforderlich, die Taste „=“ zu drücken. Als Ergebnis erhalten wir eine Zahl wie 1,4142 (die Anzahl der Stellen und die „Rundheit“ hängen von der Bittiefe und den Rechnereinstellungen ab).
Hinweis: Beim Versuch, die Wurzel zu finden, gibt der Rechner normalerweise eine Fehlermeldung aus.
Wenn Sie Zugang zu einem Computer haben, ist es sehr einfach, die Wurzel einer Zahl zu finden.
1. Sie können die Rechneranwendung verwenden, die auf fast jedem Computer verfügbar ist. Für Windows XP kann dieses Programm ausgeführt werden auf die folgende Weise:
„Start“ – „Alle Programme“ – „Zubehör“ – „Rechner“.
Besser ist es, die Ansicht auf „normal“ zu stellen. Im Gegensatz zu einem echten Taschenrechner ist die Schaltfläche zum Ziehen der Wurzel übrigens mit „sqrt“ und nicht mit „√“ gekennzeichnet.
Wenn Sie mit der angegebenen Methode nicht zum Rechner gelangen, können Sie den Standardrechner „manuell“ ausführen:
„Start“ – „Ausführen“ – „Berechnen“.
2. Um die Wurzel einer Zahl zu finden, können Sie auch einige auf Ihrem Computer installierte Programme verwenden. Darüber hinaus verfügt das Programm über einen eigenen integrierten Taschenrechner.
Für die MS Excel-Anwendung können Sie beispielsweise die folgende Abfolge von Aktionen ausführen:
Starten Sie MS Excel.
Wir schreiben in eine beliebige Zelle die Zahl, aus der wir die Wurzel ziehen müssen.
Bewegen Sie den Zellzeiger an eine andere Position
Drücken Sie die Funktionsauswahltaste (fx)
Wählen Sie die Funktion „ROOT“.
Wir geben eine Zelle mit einer Zahl als Argument für die Funktion an
Klicken Sie auf „OK“ oder „Enter“
Vorteil diese Methode ist, dass es jetzt ausreicht, einen beliebigen Wert in die Zelle mit der Zahl einzugeben, wie in der Funktion .
Notiz.
Es gibt mehrere andere, exotischere Möglichkeiten, die Wurzel einer Zahl zu finden. Zum Beispiel in einer „Ecke“, mit einem Rechenschieber oder Bradis-Tischen. Aufgrund ihrer Komplexität und praktischen Nutzlosigkeit werden diese Methoden in diesem Artikel jedoch nicht besprochen.
Video zum Thema
Quellen:
- wie man die Wurzel einer Zahl findet
Manchmal treten Situationen auf, in denen Sie mathematische Berechnungen durchführen müssen, einschließlich der Extraktion von Quadratwurzeln und größeren Wurzeln einer Zahl. Die „n“-Wurzel von „a“ ist die Zahl n. Grad Das ist die Zahl „a“.
Anweisungen
Gehen Sie wie folgt vor, um die Wurzel „n“ von zu finden.
Klicken Sie auf Ihrem Computer auf „Start“ – „Alle Programme“ – „Zubehör“. Gehen Sie dann zum Unterabschnitt „Service“ und wählen Sie „Rechner“. Sie können dies manuell tun: Klicken Sie auf Start, geben Sie „calk“ in das Feld „Ausführen“ ein und drücken Sie die Eingabetaste. Wird Öffnen. Um die Quadratwurzel einer Zahl zu ziehen, geben Sie sie in den Taschenrechner ein und drücken Sie die Taste mit der Bezeichnung „sqrt“. Der Rechner zieht aus der eingegebenen Zahl die Wurzel zweiten Grades, die so genannte Quadratwurzel.
Um eine Wurzel zu ziehen, deren Grad höher als der zweite ist, müssen Sie einen anderen Rechnertyp verwenden. Klicken Sie dazu in der Rechneroberfläche auf die Schaltfläche „Ansicht“ und wählen Sie im Menü die Zeile „Ingenieurwesen“ oder „Wissenschaftlich“ aus. Diese Art von Rechner verfügt über die notwendigen Funktionen zur Berechnung der Wurzel n. Grad Funktion.
Um die Wurzel des dritten Grades () zu extrahieren, geben Sie auf einem „Ingenieur“-Rechner die gewünschte Zahl ein und drücken Sie die Taste „3√“. Um eine Wurzel zu erhalten, deren Grad höher als 3 ist, geben Sie die gewünschte Zahl ein, drücken Sie die Schaltfläche mit dem Symbol „y√x“ und geben Sie dann die Zahl ein – den Exponenten. Drücken Sie anschließend das Gleichheitszeichen (die Schaltfläche „=“) und Sie erhalten die gewünschte Wurzel.
Wenn Ihr Rechner nicht über die Funktion „y√x“ verfügt, gilt Folgendes.
Extrahieren Kubikwurzel Geben Sie den radikalen Ausdruck ein und markieren Sie dann das Kontrollkästchen neben der Aufschrift „Inv“. Mit dieser Aktion kehren Sie die Funktionen der Rechnerschaltflächen um, d. h. durch Klicken auf die Würfelschaltfläche ziehen Sie die Kubikwurzel. Auf den Knopf, den Sie
So extrahieren Sie die Wurzel aus der Nummer. In diesem Artikel lernen wir, wie man die Quadratwurzel aus vier- und fünfstelligen Zahlen zieht.
Nehmen wir als Beispiel die Quadratwurzel von 1936.
Somit, ![]() .
.
Die letzte Ziffer in der Zahl 1936 ist die Zahl 6. Das Quadrat der Zahl 4 und der Zahl 6 endet bei 6. Daher kann 1936 das Quadrat der Zahl 44 oder der Zahl 46 sein. Es bleibt die Überprüfung durch Multiplikation.
Bedeutet,
Ziehen wir die Quadratwurzel aus der Zahl 15129.
Somit, ![]() .
.
Die letzte Ziffer in der Zahl 15129 ist die Zahl 9. Das Quadrat der Zahl 3 und der Zahl 7 endet bei 9. Daher kann 15129 das Quadrat der Zahl 123 oder der Zahl 127 sein. Überprüfen wir dies mithilfe der Multiplikation.
Bedeutet, ![]()
So extrahieren Sie das Root-Video
Und jetzt schlage ich vor, dass Sie sich das Video von Anna Denisova ansehen – „Wie man die Wurzel extrahiert ", Autor der Seite" Einfache Physik", in dem sie erklärt, wie man Quadrat- und Kubikwurzeln ohne Taschenrechner findet.
Das Video bespricht verschiedene Möglichkeiten, Wurzeln zu extrahieren:
1. Der einfachste Weg zum Extrahieren Quadratwurzel.
2. Durch Auswahl anhand des Quadrats der Summe.
3. Babylonische Methode.
4. Methode zum Extrahieren der Quadratwurzel einer Spalte.
5. Der schnelle Weg Ziehen der Kubikwurzel.
6. Methode zum Extrahieren der Kubikwurzel in einer Spalte.
Möchten Sie beim Einheitlichen Staatsexamen in Mathematik gut abschneiden? Dann müssen Sie schnell, richtig und ohne Taschenrechner zählen können. Schließlich Hauptgrund Punkteverlust beim Einheitlichen Staatsexamen in Mathematik - Rechenfehler.
Nach den Regeln des Einheitlichen Staatsexamens ist die Verwendung eines Taschenrechners während der Mathematikprüfung verboten. Möglicherweise ist der Preis zu hoch – Ausschluss von der Prüfung.
Tatsächlich benötigen Sie für das Einheitliche Staatsexamen in Mathematik keinen Taschenrechner. Alle Probleme sind ohne sie gelöst. Das Wichtigste sind Aufmerksamkeit, Genauigkeit und einige geheime Techniken, die wir Ihnen verraten.
Beginnen wir mit der Hauptregel. Wenn eine Berechnung vereinfacht werden kann, vereinfachen Sie sie.
Hier ist zum Beispiel die „teuflische Gleichung“:

Siebzig Prozent der Absolventen lösen es frontal. Sie berechnen die Diskriminante mit der Formel und sagen dann, dass die Wurzel nicht ohne Taschenrechner gezogen werden kann. Sie können jedoch die linke und rechte Seite der Gleichung durch dividieren. Es klappt
Welcher Weg ist einfacher? :-)
Viele Schulkinder mögen die Spaltenmultiplikation nicht. In der vierten Klasse löste niemand gerne langweilige „Beispiele“. In vielen Fällen ist es jedoch möglich, Zahlen ohne „Spalte“ hintereinander zu multiplizieren. Es ist viel schneller.
Bitte beachten Sie, dass wir nicht mit kleineren, sondern mit größeren Ziffern beginnen. Das ist bequem.
Jetzt - Teilung. Es ist nicht einfach, „in einer Spalte“ durch zu dividieren. Aber denken Sie daran, dass das Divisionszeichen: und der Bruchstrich dasselbe sind. Schreiben wir es als Bruch und reduzieren den Bruch:
Ein anderes Beispiel.
Wie kann man eine zweistellige Zahl schnell und ohne Spalten quadrieren? Wir wenden abgekürzte Multiplikationsformeln an:
Manchmal ist es praktisch, eine andere Formel zu verwenden:
Zahlen, die auf , enden, werden sofort quadriert.
Nehmen wir an, wir müssen das Quadrat einer Zahl finden (- nicht unbedingt eine Zahl, sondern eine beliebige natürliche Zahl). Wir multiplizieren mit und addieren zum Ergebnis. Alle!
Zum Beispiel: (und zugeschrieben).
(und zugeschrieben).
(und zugeschrieben).
Diese Methode eignet sich nicht nur zum Quadrieren, sondern auch zum Ziehen der Quadratwurzel aus Zahlen, die auf enden.
Wie kann man ohne Taschenrechner überhaupt die Quadratwurzel ziehen? Wir zeigen Ihnen zwei Möglichkeiten.
Die erste Methode besteht darin, den Wurzelausdruck zu faktorisieren.
Lassen Sie uns zum Beispiel finden
Eine Zahl ist durch teilbar (da die Summe ihrer Ziffern durch teilbar ist). Lassen Sie uns faktorisieren:
Finden wir es. Diese Zahl ist durch teilbar. Es wird auch geteilt durch. Lassen Sie es uns ausklammern.
Ein anderes Beispiel.
Es gibt einen zweiten Weg. Dies ist praktisch, wenn die Zahl, aus der Sie die Wurzel ziehen müssen, nicht faktorisiert werden kann.
Beispielsweise müssen Sie finden. Die Zahl unter der Wurzel ist ungerade, sie ist nicht teilbar, ist nicht teilbar durch, ist nicht teilbar durch... Sie können weiter suchen, durch was sie teilbar ist, oder Sie können es einfacher machen – finden Sie diese Wurzel durch Auswahl .
Offensichtlich wurde eine zweistellige Zahl quadriert, die zwischen den Zahlen und liegt, da , und die Zahl zwischen ihnen liegt. Die erste Ziffer der Antwort kennen wir bereits, sie lautet .
Die letzte Ziffer der Nummer ist . Da , ist die letzte Ziffer in der Antwort entweder , oder . Lass uns das Prüfen:
. Passiert!
Finden wir es.
Das bedeutet, dass die erste Ziffer der Antwort eine Fünf ist.
Die letzte Ziffer der Zahl ist neun. , . Das bedeutet, dass die letzte Ziffer der Antwort entweder , oder ist.
Lass uns das Prüfen:
Wenn die Zahl, aus der Sie die Quadratwurzel ziehen müssen, auf oder endet, ist die Quadratwurzel daraus eine irrationale Zahl. Weil kein ganzzahliges Quadrat auf or endet. Denken Sie daran im Aufgabenteil Optionen für das einheitliche Staatsexamen In der Mathematik muss die Antwort als ganze Zahl oder endliche Zahl geschrieben werden Dezimal, das heißt, es muss eine rationale Zahl sein.
Quadratische Gleichungen begegnen uns in Aufgaben und Varianten des Einheitlichen Staatsexamens sowie in Teilen. Sie müssen die Diskriminante zählen und dann die Wurzel daraus ziehen. Und es ist überhaupt nicht notwendig, Wurzeln aus fünfstelligen Zahlen zu suchen. In vielen Fällen kann die Diskriminante faktorisiert werden.
Beispielsweise in Gl.
Eine andere Situation, in der der Ausdruck unter der Wurzel faktorisiert werden kann, ist dem Problem entnommen.
Hypotenuse rechtwinkliges Dreieck ist gleich, eines der Beine ist gleich, finde das zweite Bein.
Nach dem Satz des Pythagoras ist es gleich. Sie können in einer Spalte lange zählen, es ist jedoch einfacher, die abgekürzte Multiplikationsformel zu verwenden.
Und jetzt erzählen wir Ihnen das Interessanteste – warum Absolventen beim Einheitlichen Staatsexamen wertvolle Punkte verlieren. Denn Rechenfehler passieren nicht einfach so.
 1
. Richtiger Weg Punkte verlieren - schlampige Berechnungen, bei denen etwas korrigiert, durchgestrichen, eine Zahl über eine andere geschrieben wird. Schauen Sie sich Ihre Entwürfe an. Vielleicht sehen sie gleich aus? :-)
1
. Richtiger Weg Punkte verlieren - schlampige Berechnungen, bei denen etwas korrigiert, durchgestrichen, eine Zahl über eine andere geschrieben wird. Schauen Sie sich Ihre Entwürfe an. Vielleicht sehen sie gleich aus? :-)
Schreiben Sie leserlich! Sparen Sie nicht am Papier. Wenn etwas nicht stimmt, korrigieren Sie nicht eine Zahl durch eine andere, sondern schreiben Sie sie lieber noch einmal.
2. Aus irgendeinem Grund versuchen viele Schulkinder, wenn sie in einer Spalte zählen, dies 1) sehr, sehr schnell, 2) in sehr kleinen Zahlen in der Ecke ihres Notizbuchs und 3) mit einem Bleistift zu tun. Das Ergebnis ist folgendes:


Es ist unmöglich, etwas zu erkennen. Ist es also verwunderlich, dass die Punktzahl beim Einheitlichen Staatsexamen niedriger ausfällt als erwartet?
3. Viele Schulkinder sind es gewohnt, Klammern in Ausdrücken zu ignorieren. Manchmal passiert Folgendes:
Denken Sie daran, dass das Gleichheitszeichen nicht irgendwo platziert wird, sondern nur dazwischen Gleiche Beträge. Schreiben Sie richtig, auch in Entwurfsform.
 4 . Bei einer großen Zahl von Rechenfehlern handelt es sich um Brüche. Wenn Sie einen Bruch durch einen Bruch dividieren, verwenden Sie what
4 . Bei einer großen Zahl von Rechenfehlern handelt es sich um Brüche. Wenn Sie einen Bruch durch einen Bruch dividieren, verwenden Sie what
Gezeichnet ist hier ein „Hamburger“, also ein mehrstöckiger Bruch. Mit dieser Methode ist es äußerst schwierig, die richtige Antwort zu erhalten.
Fassen wir zusammen.
Überprüfung der Aufgaben des ersten Teils Profil Einheitliches Staatsexamen in Mathematik - automatisch. Eine „fast richtige“ Antwort gibt es hier nicht. Entweder hat er Recht oder nicht. Ein Rechenfehler – und hallo, die Aufgabe zählt nicht. Daher liegt es in Ihrem Interesse, schnell, richtig und ohne Taschenrechner zählen zu lernen.
Die Aufgaben des zweiten Teils des Profils Einheitliche Staatsprüfung in Mathematik werden von einem Experten überprüft. Pass auf ihn auf! Lassen Sie ihn sowohl Ihre Handschrift als auch die Logik der Entscheidung verstehen.
Fakt 1.
\(\bullet\) Nehmen wir eine nichtnegative Zahl \(a\) (das heißt \(a\geqslant 0\) ). Dann (Arithmetik) Quadratwurzel aus der Zahl \(a\) nennt man eine solche nichtnegative Zahl \(b\), quadriert erhalten wir die Zahl \(a\) : \[\sqrt a=b\quad \text(same as )\quad a=b^2\] Aus der Definition ergibt sich das \(a\geqslant 0, b\geqslant 0\). Diese Einschränkungen sind eine wichtige Voraussetzung die Existenz einer Quadratwurzel und sie sollten im Gedächtnis behalten werden!
Denken Sie daran, dass jede quadrierte Zahl ein nicht negatives Ergebnis ergibt. Das heißt, \(100^2=10000\geqslant 0\) und \((-100)^2=10000\geqslant 0\) .
\(\bullet\) Was ist \(\sqrt(25)\) gleich? Wir wissen, dass \(5^2=25\) und \((-5)^2=25\) . Da wir per Definition eine nichtnegative Zahl finden müssen, ist \(-5\) nicht geeignet, daher gilt \(\sqrt(25)=5\) (da \(25=5^2\) ).
Den Wert von \(\sqrt a\) zu ermitteln, nennt man Ziehen der Quadratwurzel aus der Zahl \(a\) und die Zahl \(a\) nennt man Wurzelausdruck.
\(\bullet\) Basierend auf der Definition, dem Ausdruck \(\sqrt(-25)\), \(\sqrt(-4)\) usw. ergibt keinen Sinn.
Fakt 2.
Für schnelle Berechnungen ist es hilfreich, die Quadrattabelle zu lernen natürliche Zahlen von \(1\) bis \(20\) : \[\begin(array)(|ll|) \hline 1^2=1 & \quad11^2=121 \\ 2^2=4 & \quad12^2=144\\ 3^2=9 & \quad13 ^2=169\\ 4^2=16 & \quad14^2=196\\ 5^2=25 & \quad15^2=225\\ 6^2=36 & \quad16^2=256\\ 7^ 2=49 & \quad17^2=289\\ 8^2=64 & \quad18^2=324\\ 9^2=81 & \quad19^2=361\\ 10^2=100& \quad20^2= 400\\ \hline \end(array)\]
Fakt 3.
Welche Operationen können Sie mit Quadratwurzeln durchführen?
\(\Kugel\) Die Summe oder Differenz der Quadratwurzeln ist NICHT GLEICH der Quadratwurzel der Summe oder Differenz \[\sqrt a\pm\sqrt b\ne \sqrt(a\pm b)\] Wenn Sie also beispielsweise \(\sqrt(25)+\sqrt(49)\) berechnen müssen, müssen Sie zunächst die Werte von \(\sqrt(25)\) und \(\ sqrt(49)\ ) und falten Sie sie dann. Somit, \[\sqrt(25)+\sqrt(49)=5+7=12\] Können bei der Addition von \(\sqrt a+\sqrt b\) die Werte \(\sqrt a\) oder \(\sqrt b\) nicht gefunden werden, dann wird ein solcher Ausdruck nicht weiter transformiert und bleibt so wie er ist. Beispielsweise können wir in der Summe \(\sqrt 2+ \sqrt (49)\) feststellen, dass \(\sqrt(49)\) \(7\) ist, aber \(\sqrt 2\) kann nicht in umgewandelt werden Wie auch immer, Deshalb \(\sqrt 2+\sqrt(49)=\sqrt 2+7\). Leider kann dieser Ausdruck nicht weiter vereinfacht werden\(\bullet\) Das Produkt/Quotient der Quadratwurzeln ist gleich der Quadratwurzel des Produkts/Quotienten, d. h \[\sqrt a\cdot \sqrt b=\sqrt(ab)\quad \text(s)\quad \sqrt a:\sqrt b=\sqrt(a:b)\] (vorausgesetzt, dass beide Seiten der Gleichheiten Sinn ergeben)
Beispiel: \(\sqrt(32)\cdot \sqrt 2=\sqrt(32\cdot 2)=\sqrt(64)=8\);
\(\sqrt(768):\sqrt3=\sqrt(768:3)=\sqrt(256)=16\);
\(\sqrt((-25)\cdot (-64))=\sqrt(25\cdot 64)=\sqrt(25)\cdot \sqrt(64)= 5\cdot 8=40\). \(\bullet\) Mit diesen Eigenschaften ist es praktisch, Quadratwurzeln großer Zahlen zu finden, indem man sie faktorisiert.
Schauen wir uns ein Beispiel an. Finden wir \(\sqrt(44100)\) . Da \(44100:100=441\) , dann \(44100=100\cdot 441\) . Gemäß dem Kriterium der Teilbarkeit ist die Zahl \(441\) durch \(9\) teilbar (da die Summe ihrer Ziffern 9 ist und durch 9 teilbar ist), also \(441:9=49\), das heißt, \(441=9\ cdot 49\) .
So bekamen wir: \[\sqrt(44100)=\sqrt(9\cdot 49\cdot 100)= \sqrt9\cdot \sqrt(49)\cdot \sqrt(100)=3\cdot 7\cdot 10=210\] Schauen wir uns ein anderes Beispiel an: \[\sqrt(\dfrac(32\cdot 294)(27))= \sqrt(\dfrac(16\cdot 2\cdot 3\cdot 49\cdot 2)(9\cdot 3))= \sqrt( \ dfrac(16\cdot4\cdot49)(9))=\dfrac(\sqrt(16)\cdot \sqrt4 \cdot \sqrt(49))(\sqrt9)=\dfrac(4\cdot 2\cdot 7)3 =\dfrac(56)3\]
\(\bullet\) Lassen Sie uns am Beispiel des Ausdrucks \(5\sqrt2\) zeigen, wie man Zahlen unter dem Quadratwurzelzeichen eingibt (Kurzschreibweise für den Ausdruck \(5\cdot \sqrt2\)). Da \(5=\sqrt(25)\) , dann \
Beachten Sie auch, dass z. B.
1) \(\sqrt2+3\sqrt2=4\sqrt2\) ,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\) .
Warum so? Erklären wir es anhand von Beispiel 1). Wie Sie bereits verstehen, können wir die Zahl \(\sqrt2\) nicht irgendwie umwandeln. Stellen wir uns vor, dass \(\sqrt2\) eine Zahl \(a\) ist. Dementsprechend ist der Ausdruck \(\sqrt2+3\sqrt2\) nichts anderes als \(a+3a\) (eine Zahl \(a\) plus drei weitere gleiche Zahlen \(a\)). Und wir wissen, dass dies vier solchen Zahlen \(a\) entspricht, also \(4\sqrt2\) .
Fakt 4.
\(\bullet\) Sie sagen oft „Sie können die Wurzel nicht extrahieren“, wenn Sie das Vorzeichen \(\sqrt () \ \) der Wurzel (Radikal) nicht entfernen können, wenn Sie den Wert einer Zahl ermitteln . Beispielsweise können Sie die Wurzel der Zahl \(16\) ziehen, weil \(16=4^2\) , also \(\sqrt(16)=4\) . Es ist jedoch unmöglich, die Wurzel der Zahl \(3\) zu ziehen, also \(\sqrt3\) zu finden, da es keine Zahl gibt, die quadriert \(3\) ergibt.
Solche Zahlen (oder Ausdrücke mit solchen Zahlen) sind irrational. Zum Beispiel Zahlen \(\sqrt3, \ 1+\sqrt2, \ \sqrt(15)\) usw. sind irrational.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\) ), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\) ) usw.
\(\bullet\) Bitte beachten Sie, dass jede Zahl entweder rational oder irrational sein kann. Und alle rationalen und alle irrationalen Zahlen bilden zusammen eine Menge namens eine Menge reeller Zahlen. Diese Menge wird mit dem Buchstaben \(\mathbb(R)\) bezeichnet.
Dies bedeutet, dass alle Nummern, die eingeschaltet sind dieser Moment wir wissen, werden reelle Zahlen genannt.
Fakt 5.
\(\bullet\) Der Modul einer reellen Zahl \(a\) ist eine nicht negative Zahl \(|a|\) gleich dem Abstand vom Punkt \(a\) zu \(0\) auf der echte Linie. Zum Beispiel sind \(|3|\) und \(|-3|\) gleich 3, da die Abstände von den Punkten \(3\) und \(-3\) zu \(0\) sind gleich und gleich \(3 \) .
\(\bullet\) Wenn \(a\) eine nicht negative Zahl ist, dann ist \(|a|=a\) .
Beispiel: \(|5|=5\) ; \(\qquad |\sqrt2|=\sqrt2\) . \(\bullet\) Wenn \(a\) eine negative Zahl ist, dann \(|a|=-a\) .
Beispiel: \(|-5|=-(-5)=5\) ; \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\).
Sie sagen, dass bei negativen Zahlen der Modul das Minus „frisst“, während positive Zahlen sowie die Zahl \(0\) vom Modul unverändert bleiben.
ABER Diese Regel gilt nur für Zahlen. Если у вас под знаком модуля находится неизвестная \(x\) (или какая-то другая неизвестная), например, \(|x|\) , про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля wir können nicht. In diesem Fall bleibt dieser Ausdruck derselbe: \(|x|\) . \(\bullet\) Es gelten die folgenden Formeln: \[(\large(\sqrt(a^2)=|a|))\] \[(\large((\sqrt(a))^2=a)), \text( vorausgesetzt ) a\geqslant 0\] Sehr oft wird der folgende Fehler gemacht: Man sagt, dass \(\sqrt(a^2)\) und \((\sqrt a)^2\) ein und dasselbe seien. Dies gilt nur, wenn \(a\) eine positive Zahl oder Null ist. Aber wenn \(a\) eine negative Zahl ist, dann ist dies falsch. Es genügt, dieses Beispiel zu betrachten. Nehmen wir statt \(a\) die Zahl \(-1\) . Dann ist \(\sqrt((-1)^2)=\sqrt(1)=1\) , aber der Ausdruck \((\sqrt (-1))^2\) existiert überhaupt nicht (schließlich Es ist unmöglich, das Wurzelzeichen für negative Zahlen zu verwenden!).
Deshalb machen wir Sie darauf aufmerksam, dass \(\sqrt(a^2)\) nicht gleich \((\sqrt a)^2\) ist! Beispiel 1) \(\sqrt(\left(-\sqrt2\right)^2)=|-\sqrt2|=\sqrt2\), Weil \(-\sqrt2<0\)
;
\(\phantom(00000)\) 2) \((\sqrt(2))^2=2\) . \(\bullet\) Da \(\sqrt(a^2)=|a|\) , dann ist \[\sqrt(a^(2n))=|a^n|\] (Der Ausdruck \(2n\) bezeichnet eine gerade Zahl)
Das heißt, wenn man aus einer Zahl, die bis zu einem gewissen Grad die Wurzel zieht, diesen Grad halbiert.
Beispiel:
1) \(\sqrt(4^6)=|4^3|=4^3=64\)
2) \(\sqrt((-25)^2)=|-25|=25\) (Beachten Sie, dass sich herausstellt, dass die Wurzel der Zahl gleich \(-25\) ist, wenn das Modul nicht angegeben wird. ) ; aber wir erinnern uns, dass dies per Definition einer Wurzel nicht passieren kann: Wenn wir eine Wurzel ziehen, sollten wir immer eine positive Zahl oder Null erhalten)
3) \(\sqrt(x^(16))=|x^8|=x^8\) (da jede Zahl zu einer geraden Potenz nicht negativ ist)
Fakt 6.
Wie vergleiche ich zwei Quadratwurzeln?
\(\bullet\) Für Quadratwurzeln gilt: if \(\sqrt a<\sqrt b\)
, то \(a
1) Vergleiche \(\sqrt(50)\) und \(6\sqrt2\) . Lassen Sie uns zunächst den zweiten Ausdruck in umwandeln \(\sqrt(36)\cdot \sqrt2=\sqrt(36\cdot 2)=\sqrt(72)\). Da \(50<72\)
, то и \(\sqrt{50}<\sqrt{72}\)
. Следовательно, \(\sqrt{50}<6\sqrt2\)
.
2) Zwischen welchen ganzen Zahlen liegt \(\sqrt(50)\)?
Da \(\sqrt(49)=7\) , \(\sqrt(64)=8\) und \(49<50<64\)
, то \(7<\sqrt{50}<8\)
, то есть число \(\sqrt{50}\)
находится между числами \(7\)
и \(8\)
.
3) Vergleichen wir \(\sqrt 2-1\) und \(0.5\) . Nehmen wir an, dass \(\sqrt2-1>0.5\) : \[\begin(aligned) &\sqrt 2-1>0.5 \ \big| +1\quad \text((einen auf beiden Seiten hinzufügen))\\ &\sqrt2>0.5+1 \ \big| \ ^2 \quad\text((beide Seiten quadrieren))\\ &2>1.5^2\\ &2>2.25 \end(aligned)\] Wir sehen, dass wir eine falsche Ungleichung erhalten haben. Daher war unsere Annahme falsch und \(\sqrt 2-1<0,5\)
.
Beachten Sie, dass das Hinzufügen einer bestimmten Zahl zu beiden Seiten der Ungleichung das Vorzeichen nicht beeinflusst. Das Multiplizieren/Dividieren beider Seiten einer Ungleichung mit einer positiven Zahl hat ebenfalls keinen Einfluss auf deren Vorzeichen, aber das Multiplizieren/Dividieren mit einer negativen Zahl kehrt das Vorzeichen der Ungleichung um!
Sie können beide Seiten einer Gleichung/Ungleichung NUR dann quadrieren, wenn beide Seiten nicht negativ sind. Beispielsweise kann man in der Ungleichung aus dem vorherigen Beispiel beide Seiten quadrieren, in der Ungleichung \(-3<\sqrt2\)
нельзя (убедитесь в этом сами)!
\(\bullet\) Daran sollte man sich erinnern \[\begin(aligned) &\sqrt 2\ca. 1,4\\ &\sqrt 3\ca. 1,7 \end(aligned)\] Die ungefähre Bedeutung dieser Zahlen zu kennen, wird Ihnen beim Zahlenvergleich helfen! \(\bullet\) Um die Wurzel (sofern sie extrahiert werden kann) aus einer großen Zahl zu ziehen, die nicht in der Quadrattabelle enthalten ist, müssen Sie zunächst bestimmen, zwischen welchen „Hundertern“ sie liegt, und dann – zwischen denen „ Zehner“ und bestimmen Sie dann die letzte Ziffer dieser Zahl. Lassen Sie uns anhand eines Beispiels zeigen, wie das funktioniert.
Nehmen wir \(\sqrt(28224)\) . Wir wissen, dass \(100^2=10\.000\), \(200^2=40\.000\) usw. Beachten Sie, dass \(28224\) zwischen \(10\,000\) und \(40\,000\) liegt. Daher liegt \(\sqrt(28224)\) zwischen \(100\) und \(200\) .
Nun bestimmen wir, zwischen welchen „Zehnern“ unsere Zahl liegt (also zum Beispiel zwischen \(120\) und \(130\)). Aus der Quadrattabelle wissen wir auch, dass \(11^2=121\) , \(12^2=144\) usw., dann \(110^2=12100\) , \(120^2=14400 \ ) , \(130^2=16900\) , \(140^2=19600\) , \(150^2=22500\) , \(160^2=25600\) , \(170^2=28900 \ ). Wir sehen also, dass \(28224\) zwischen \(160^2\) und \(170^2\) liegt. Daher liegt die Zahl \(\sqrt(28224)\) zwischen \(160\) und \(170\) .
Versuchen wir, die letzte Ziffer zu bestimmen. Erinnern wir uns, welche einstelligen Zahlen quadriert am Ende \(4\) ergeben? Dies sind \(2^2\) und \(8^2\) . Daher endet \(\sqrt(28224)\) entweder mit 2 oder 8. Lassen Sie uns dies überprüfen. Finden wir \(162^2\) und \(168^2\) :
\(162^2=162\cdot 162=26224\)
\(168^2=168\cdot 168=28224\) .
Daher ist \(\sqrt(28224)=168\) . Voila!
Um das Einheitliche Staatsexamen in Mathematik adäquat zu lösen, müssen Sie zunächst theoretisches Material studieren, das Sie in zahlreiche Theoreme, Formeln, Algorithmen usw. einführt. Auf den ersten Blick scheint dies recht einfach zu sein. Tatsächlich ist es jedoch eine ziemlich schwierige Aufgabe, eine Quelle zu finden, in der die Theorie für das Einheitliche Staatsexamen in Mathematik für Studierende jeden Ausbildungsniveaus einfach und verständlich dargestellt wird. Schulbücher können nicht immer griffbereit sein. Und selbst im Internet kann es schwierig sein, Grundformeln für das Einheitliche Staatsexamen in Mathematik zu finden.
Warum ist das Studium der Mathematiktheorie nicht nur für Absolventen des Einheitlichen Staatsexamens so wichtig?
- Weil es Ihren Horizont erweitert. Das Studium theoretischer Materialien in der Mathematik ist für jeden nützlich, der Antworten auf eine Vielzahl von Fragen im Zusammenhang mit dem Wissen über die Welt um ihn herum erhalten möchte. Alles in der Natur ist geordnet und hat eine klare Logik. Genau das spiegelt sich in der Wissenschaft wider, durch die es möglich ist, die Welt zu verstehen.
- Weil es Intelligenz entwickelt. Durch das Studium von Referenzmaterialien für das Einheitliche Staatsexamen in Mathematik sowie das Lösen verschiedener Probleme lernt eine Person, logisch zu denken und zu argumentieren, Gedanken kompetent und klar zu formulieren. Er entwickelt die Fähigkeit zu analysieren, zu verallgemeinern und Schlussfolgerungen zu ziehen.
Wir laden Sie ein, alle Vorteile unseres Ansatzes zur Systematisierung und Präsentation von Lehrmaterialien persönlich zu bewerten.
Es ist Zeit, das zu klären Wurzelextraktionsmethoden. Sie basieren auf den Eigenschaften von Wurzeln, insbesondere auf der Gleichheit, die für jede nichtnegative Zahl b gilt.
Im Folgenden werden wir uns die wichtigsten Methoden zum Extrahieren von Wurzeln einzeln ansehen.
Beginnen wir mit dem einfachsten Fall – dem Ziehen von Wurzeln aus natürlichen Zahlen mithilfe einer Quadrattabelle, einer Kubiktabelle usw.
Wenn Tabellen mit Quadraten, Würfeln usw. Wenn Sie es nicht zur Hand haben, ist es logisch, die Methode des Wurzelziehens zu verwenden, bei der die Wurzelzahl in Primfaktoren zerlegt wird.
Besonders hervorzuheben ist, was für Wurzeln mit ungeraden Exponenten möglich ist.
Betrachten wir abschließend eine Methode, mit der wir nacheinander die Ziffern des Wurzelwerts ermitteln können.
Lass uns anfangen.
Verwendung einer Quadrattabelle, einer Würfeltabelle usw.
Im einfachsten Fall ermöglichen Tabellen mit Quadraten, Würfeln usw. das Ziehen von Wurzeln. Was sind das für Tabellen?
Die Tabelle der Quadrate ganzer Zahlen von 0 bis einschließlich 99 (siehe unten) besteht aus zwei Zonen. Der erste Bereich der Tabelle befindet sich auf einem grauen Hintergrund; durch Auswahl einer bestimmten Zeile und einer bestimmten Spalte können Sie eine Zahl von 0 bis 99 zusammenstellen. Wählen wir zum Beispiel eine Reihe mit 8 Zehnern und eine Spalte mit 3 Einern aus. Damit haben wir die Zahl 83 festgelegt. Die zweite Zone belegt den Rest der Tabelle. Jede Zelle befindet sich am Schnittpunkt einer bestimmten Zeile und einer bestimmten Spalte und enthält das Quadrat der entsprechenden Zahl von 0 bis 99. Am Schnittpunkt der von uns gewählten Zehnerreihe und der Einer-Spalte 3 befindet sich eine Zelle mit der Zahl 6.889, die dem Quadrat der Zahl 83 entspricht.

Würfeltabellen, Tabellen der vierten Potenzen von Zahlen von 0 bis 99 usw. ähneln der Quadrattabelle, nur dass sie in der zweiten Zone Würfel, vierte Potenzen usw. enthalten. entsprechende Nummern.
Tabellen mit Quadraten, Würfeln, vierten Potenzen usw. Ermöglicht das Extrahieren von Quadratwurzeln, Kubikwurzeln, vierten Wurzeln usw. entsprechend aus den Zahlen in diesen Tabellen. Lassen Sie uns das Prinzip ihrer Verwendung bei der Wurzelextraktion erklären.
Nehmen wir an, wir müssen die n-te Wurzel der Zahl a ziehen, während die Zahl a in der Tabelle der n-ten Potenzen enthalten ist. Mithilfe dieser Tabelle finden wir die Zahl b mit a=b n. Dann ![]() , daher ist die Zahl b die gesuchte Wurzel n-ten Grades.
, daher ist die Zahl b die gesuchte Wurzel n-ten Grades.
Lassen Sie uns als Beispiel zeigen, wie Sie mithilfe einer Würfeltabelle die Kubikwurzel von 19.683 extrahieren. Wir finden die Zahl 19.683 in der Würfeltabelle, daraus finden wir, dass diese Zahl die Kubikzahl der Zahl 27 ist, also ![]() .
.

Es ist klar, dass Tabellen mit n-ten Potenzen sehr praktisch sind, um Wurzeln zu ziehen. Allerdings sind sie oft nicht zur Hand und ihre Zusammenstellung nimmt einige Zeit in Anspruch. Darüber hinaus ist es oft notwendig, Wurzeln aus Zahlen zu ziehen, die nicht in den entsprechenden Tabellen enthalten sind. In diesen Fällen müssen Sie auf andere Methoden der Wurzelextraktion zurückgreifen.
Zerlegen einer Wurzelzahl in Primfaktoren
Eine ziemlich bequeme Möglichkeit, die Wurzel einer natürlichen Zahl zu ziehen (sofern die Wurzel natürlich gezogen wird), besteht darin, die Wurzelzahl in Primfaktoren zu zerlegen. Sein Der Punkt ist dieser: Danach ist es ganz einfach, sie als Potenz mit dem gewünschten Exponenten darzustellen, wodurch Sie den Wert der Wurzel erhalten können. Lassen Sie uns diesen Punkt klären.
Nehmen wir die n-te Wurzel einer natürlichen Zahl a und ihr Wert ist gleich b. In diesem Fall gilt die Gleichung a=b n. Die Zahl b kann wie jede natürliche Zahl als Produkt aller ihrer Primfaktoren p 1 , p 2 , …, p m in der Form p 1 ·p 2 ·…·p m dargestellt werden, und in diesem Fall als Wurzelzahl a wird dargestellt als (p 1 ·p 2 ·…·p m) n . Da die Zerlegung einer Zahl in Primfaktoren eindeutig ist, hat die Zerlegung der Grundzahl a in Primfaktoren die Form (p 1 ·p 2 ·…·p m) n, was die Berechnung des Wertes der Wurzel ermöglicht als .
Beachten Sie, dass, wenn die Zerlegung einer Wurzelzahl a in Primfaktoren nicht in der Form (p 1 ·p 2 ·…·p m) n dargestellt werden kann, die n-te Wurzel einer solchen Zahl a nicht vollständig extrahiert wird.
Lassen Sie uns dies beim Lösen von Beispielen herausfinden.
Beispiel.
Ziehe die Quadratwurzel aus 144.
Lösung.
Wenn Sie sich die im vorherigen Absatz angegebene Quadrattabelle ansehen, können Sie deutlich erkennen, dass 144 = 12 · 2, woraus klar hervorgeht, dass die Quadratwurzel von 144 gleich 12 ist.
Vor diesem Hintergrund interessiert uns jedoch, wie die Wurzel gezogen wird, indem die Grundzahl 144 in Primfaktoren zerlegt wird. Schauen wir uns diese Lösung an.
Lasst uns zerlegen 144 zu Primfaktoren:
Das heißt, 144=2·2·2·2·3·3. Basierend auf der resultierenden Zerlegung können folgende Transformationen durchgeführt werden: 144=2·2·2·2·3·3=(2·2) 2·3 2 =(2·2·3) 2 =12 2. Somit, ![]() .
.
Unter Verwendung der Eigenschaften des Grades und der Eigenschaften der Wurzeln könnte die Lösung etwas anders formuliert werden: .
Antwort:
Um das Material zu festigen, betrachten Sie die Lösungen zu zwei weiteren Beispielen.
Beispiel.
Berechnen Sie den Wert der Wurzel.
Lösung.
Die Primfaktorzerlegung der Wurzelzahl 243 hat die Form 243=3 5 . Auf diese Weise, ![]() .
.
Antwort:
Beispiel.
Ist der Wurzelwert eine ganze Zahl?
Lösung.
Um diese Frage zu beantworten, zerlegen wir die Wurzelzahl in Primfaktoren und prüfen, ob sie als Kubikzahl einer ganzen Zahl dargestellt werden kann.
Wir haben 285 768=2 3 ·3 6 ·7 2. Die resultierende Entwicklung kann nicht als Kubikzahl einer ganzen Zahl dargestellt werden, da die Potenz des Primfaktors 7 kein Vielfaches von drei ist. Daher kann die Kubikwurzel von 285.768 nicht vollständig gezogen werden.
Antwort:
Nein.
Wurzeln aus Bruchzahlen ziehen
Es ist an der Zeit herauszufinden, wie man die Wurzel einer Bruchzahl zieht. Die gebrochene Wurzelzahl sei als p/q geschrieben. Gemäß der Eigenschaft der Wurzel eines Quotienten gilt die folgende Gleichheit. Aus dieser Gleichheit folgt Regel zum Ziehen der Wurzel eines Bruchs: Die Wurzel eines Bruchs ist gleich dem Quotienten aus der Wurzel des Zählers dividiert durch die Wurzel des Nenners.
Schauen wir uns ein Beispiel für das Ziehen einer Wurzel aus einem Bruch an.
Beispiel.
Was ist die Quadratwurzel des gemeinsamen Bruchs 25/169?
Lösung.
Mithilfe der Quadrattabelle finden wir, dass die Quadratwurzel des Zählers des ursprünglichen Bruchs gleich 5 und die Quadratwurzel des Nenners gleich 13 ist. Dann  . Damit ist die Extraktion der Wurzel des gemeinsamen Bruchs 25/169 abgeschlossen.
. Damit ist die Extraktion der Wurzel des gemeinsamen Bruchs 25/169 abgeschlossen.
Antwort:
Die Wurzel eines Dezimalbruchs oder einer gemischten Zahl wird extrahiert, nachdem die Grundzahlen durch gewöhnliche Brüche ersetzt wurden.
Beispiel.
Ziehen Sie die Kubikwurzel aus dem Dezimalbruch 474,552.
Lösung.
Stellen wir uns den ursprünglichen Dezimalbruch als gewöhnlichen Bruch vor: 474,552=474552/1000. Dann  . Es müssen noch die Kubikwurzeln gezogen werden, die im Zähler und Nenner des resultierenden Bruchs stehen. Als 474 552=2·2·2·3·3·3·13·13·13=(2 3 13) 3 =78 3 und 1 000 = 10 3, dann
. Es müssen noch die Kubikwurzeln gezogen werden, die im Zähler und Nenner des resultierenden Bruchs stehen. Als 474 552=2·2·2·3·3·3·13·13·13=(2 3 13) 3 =78 3 und 1 000 = 10 3, dann ![]() Und
Und ![]() . Jetzt müssen nur noch die Berechnungen abgeschlossen werden
. Jetzt müssen nur noch die Berechnungen abgeschlossen werden  .
.
Antwort:
![]() .
.
Ziehen Sie die Wurzel einer negativen Zahl
Es lohnt sich, näher auf das Ziehen von Wurzeln aus negativen Zahlen einzugehen. Bei der Untersuchung von Wurzeln haben wir gesagt, dass, wenn der Wurzelexponent eine ungerade Zahl ist, unter dem Wurzelzeichen eine negative Zahl stehen kann. Wir haben diesen Einträgen folgende Bedeutung gegeben: Für eine negative Zahl −a und einen ungeraden Exponenten der Wurzel 2 n−1, ![]() . Diese Gleichheit gibt Regel zum Ziehen ungerader Wurzeln aus negativen Zahlen: Um die Wurzel einer negativen Zahl zu ziehen, müssen Sie die Wurzel der entgegengesetzten positiven Zahl ziehen und dem Ergebnis ein Minuszeichen voranstellen.
. Diese Gleichheit gibt Regel zum Ziehen ungerader Wurzeln aus negativen Zahlen: Um die Wurzel einer negativen Zahl zu ziehen, müssen Sie die Wurzel der entgegengesetzten positiven Zahl ziehen und dem Ergebnis ein Minuszeichen voranstellen.
Schauen wir uns die Beispiellösung an.
Beispiel.
Finden Sie den Wert der Wurzel.
Lösung.
Lassen Sie uns den ursprünglichen Ausdruck so umwandeln, dass unter dem Wurzelzeichen eine positive Zahl steht:  . Ersetzen Sie nun die gemischte Zahl durch einen gewöhnlichen Bruch:
. Ersetzen Sie nun die gemischte Zahl durch einen gewöhnlichen Bruch:  . Wir wenden die Regel zum Ziehen der Wurzel eines gewöhnlichen Bruchs an:
. Wir wenden die Regel zum Ziehen der Wurzel eines gewöhnlichen Bruchs an:  . Es müssen noch die Wurzeln im Zähler und Nenner des resultierenden Bruchs berechnet werden:
. Es müssen noch die Wurzeln im Zähler und Nenner des resultierenden Bruchs berechnet werden:  .
.
Hier eine kurze Zusammenfassung der Lösung:  .
.
Antwort:
 .
.
Bitweise Bestimmung des Wurzelwerts
Im allgemeinen Fall steht unter der Wurzel eine Zahl, die mit den oben besprochenen Techniken nicht als n-te Potenz einer Zahl dargestellt werden kann. In diesem Fall besteht jedoch die Notwendigkeit, die Bedeutung einer bestimmten Wurzel zumindest bis zu einem bestimmten Zeichen zu kennen. In diesem Fall können Sie zum Extrahieren der Wurzel einen Algorithmus verwenden, der es Ihnen ermöglicht, nacheinander eine ausreichende Anzahl von Ziffernwerten der gewünschten Zahl zu erhalten.
Der erste Schritt dieses Algorithmus besteht darin, herauszufinden, welches das höchstwertige Bit des Wurzelwerts ist. Dazu werden die Zahlen 0, 10, 100, ... nacheinander so lange mit n potenziert, bis der Zeitpunkt erreicht ist, an dem eine Zahl die Wurzelzahl überschreitet. Dann gibt die Zahl, die wir im vorherigen Schritt zur Potenz n erhoben haben, die entsprechende höchstwertige Ziffer an.
Betrachten Sie diesen Schritt des Algorithmus beispielsweise beim Extrahieren der Quadratwurzel aus fünf. Nehmen Sie die Zahlen 0, 10, 100, ... und quadrieren Sie sie, bis wir eine Zahl größer als 5 erhalten. Wir haben 0 2 =0<5 , 10 2 =100>5, was bedeutet, dass die Einerstelle die höchstwertige Ziffer ist. Der Wert dieses Bits sowie der niedrigeren Werte wird in den nächsten Schritten des Root-Extraktionsalgorithmus ermittelt.
Alle nachfolgenden Schritte des Algorithmus zielen darauf ab, den Wert der Wurzel nacheinander zu klären, indem die Werte der nächsten Bits des gewünschten Wertes der Wurzel ermittelt werden, beginnend mit dem höchsten bis hin zu den niedrigsten. Beispielsweise stellt sich heraus, dass der Wert der Wurzel beim ersten Schritt 2 ist, beim zweiten – 2,2, beim dritten – 2,23 und so weiter 2,236067977…. Beschreiben wir, wie die Werte der Ziffern ermittelt werden.
Die Ziffern werden durch Durchsuchen ihrer möglichen Werte 0, 1, 2, ..., 9 gefunden. Dabei werden parallel die n-ten Potenzen der entsprechenden Zahlen berechnet und mit der Wurzelzahl verglichen. Wenn der Wert des Grades irgendwann die Wurzelzahl überschreitet, gilt der Wert der Ziffer, die dem vorherigen Wert entspricht, als gefunden und es erfolgt ein Übergang zum nächsten Schritt des Wurzelextraktionsalgorithmus. Geschieht dies nicht, dann ist der Wert dieser Ziffer 9.
Lassen Sie uns diese Punkte anhand des gleichen Beispiels des Ziehens der Quadratwurzel aus fünf erläutern.
Zuerst ermitteln wir den Wert der Einerstelle. Wir gehen die Werte 0, 1, 2, ..., 9 durch und berechnen jeweils 0 2, 1 2, ..., 9 2, bis wir einen Wert erhalten, der größer als die Grundzahl 5 ist. Es ist zweckmäßig, alle diese Berechnungen in tabellarischer Form darzustellen: 
Der Wert der Einerstelle ist also 2 (da 2 2<5
, а 2 3 >5 ). Kommen wir nun dazu, den Wert des Zehntelplatzes zu ermitteln. In diesem Fall quadrieren wir die Zahlen 2,0, 2,1, 2,2, ..., 2,9 und vergleichen die resultierenden Werte mit der Grundzahl 5: 
Seit 2.2 2<5
, а 2,3 2 >5, dann ist der Wert der Zehntelstelle 2. Sie können mit der Ermittlung des Werts der Hundertstelstelle fortfahren: 
So wurde der nächste Wert der Wurzel aus fünf gefunden, er ist gleich 2,23. Und so finden Sie weiterhin Werte: 2,236, 2,2360, 2,23606, 2,236067, … .
Um das Material zu konsolidieren, analysieren wir die Extraktion der Wurzel mit einer Genauigkeit von Hundertstel mit dem betrachteten Algorithmus.
Zuerst ermitteln wir die höchstwertige Ziffer. Dazu würfeln wir die Zahlen 0, 10, 100 usw. bis wir eine Zahl größer als 2.151.186 erhalten. Wir haben 0 3 =0<2 151,186 , 10 3 =1 000<2151,186 , 100 3 =1 000 000>2 151.186, die höchstwertige Ziffer ist also die Zehnerstelle.
Lassen Sie uns seinen Wert bestimmen. 
Seit 10 3<2 151,186
, а 20 3 >2 151,186, dann ist der Wert der Zehnerstelle 1. Kommen wir zu den Einheiten. 
Somit ist der Wert der Einerstelle 2. Kommen wir zu den Zehnteln. 
Da sogar 12,9 3 kleiner als die Grundzahl 2 · 151,186 ist, beträgt der Wert der Zehntelstelle 9. Es bleibt noch der letzte Schritt des Algorithmus auszuführen; er wird uns den Wert der Wurzel mit der erforderlichen Genauigkeit liefern. 
In diesem Stadium wird der Wert der Wurzel auf Hundertstel genau ermittelt: ![]() .
.
Zum Abschluss dieses Artikels möchte ich sagen, dass es viele andere Möglichkeiten gibt, Wurzeln zu ziehen. Aber für die meisten Aufgaben reichen die oben untersuchten aus.
Referenzliste.
- Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: Lehrbuch für die 8. Klasse. Bildungsinstitutionen.
- Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. und andere. Algebra und die Anfänge der Analysis: Lehrbuch für die Klassen 10 - 11 allgemeinbildender Bildungseinrichtungen.
- Gusev V.A., Mordkovich A.G. Mathematik (ein Handbuch für Berufsanfänger).