Das Dreieck ist eine Figur, die jeder kennt. Und das trotz der großen Formenvielfalt. Rechteckig, gleichseitig, spitz, gleichschenklig, stumpf. Jeder von ihnen ist in irgendeiner Weise anders. Aber für jeden muss man die Fläche eines Dreiecks herausfinden.

Für alle Dreiecke gemeinsame Formeln, die Seitenlängen oder Höhen verwenden

Die in ihnen übernommenen Bezeichnungen: Seiten - a, b, c; Höhen bei relevanten Parteien n a, n v, n s.

1. Die Fläche eines Dreiecks wird als Produkt aus ½, einer Seite und der davon subtrahierten Höhe berechnet. S = ½ * a * n a. Die Formeln für die anderen beiden Seiten sollten ähnlich geschrieben werden.

2. Herons Formel, in der der Halbumfang vorkommt (im Gegensatz zum Vollumfang wird er normalerweise mit dem kleinen Buchstaben p bezeichnet). Der Halbumfang muss wie folgt berechnet werden: Addieren Sie alle Seiten und teilen Sie sie durch 2. Die Formel für den Halbumfang lautet: p = (a+b+c) / 2. Dann gilt die Gleichheit für die Fläche von ​​Die Abbildung sieht so aus: S = √ (p * (p - a) * ( ð - в) * (ð - с)).

3. Wenn Sie keinen Halbumfang verwenden möchten, ist eine Formel nützlich, die nur die Längen der Seiten enthält: S = ¼ * √ ((a + b + c) * (b + c – a ) * (a + c – c) * (a + b – c)). Es ist etwas länger als das vorherige, hilft aber, wenn Sie vergessen haben, den Halbumfang zu finden.

Allgemeine Formeln für die Winkel eines Dreiecks

Zum Lesen der Formeln erforderliche Notationen: α, β, γ – Winkel. Sie liegen jeweils auf den gegenüberliegenden Seiten a, b, c.

1. Demnach ist das halbe Produkt zweier Seiten und der Sinus des Winkels zwischen ihnen gleich der Fläche des Dreiecks. Das heißt: S = ½ a * b * sin γ. Die Formeln für die anderen beiden Fälle sollten auf ähnliche Weise geschrieben werden.

2. Die Fläche eines Dreiecks kann aus einer Seite und drei bekannten Winkeln berechnet werden. S = (a 2 * sin β * sin γ) / (2 sin α).

3. Es gibt auch eine Formel mit einer bekannten Seite und zwei benachbarten Winkeln. Es sieht so aus: S = c 2 / (2 (ctg α + ctg β)).

Die letzten beiden Formeln sind nicht die einfachsten. Es ist ziemlich schwierig, sich an sie zu erinnern.

Allgemeine Formeln für den Fall, dass die Radien eingeschriebener oder umschriebener Kreise bekannt sind

Zusätzliche Bezeichnungen: r, R - Radien. Der erste wird für den Radius des eingeschriebenen Kreises verwendet. Der zweite ist für den beschriebenen.

1. Die erste Formel, nach der die Fläche eines Dreiecks berechnet wird, bezieht sich auf den Halbumfang. S = r * r. Eine andere Schreibweise ist: S = ½ r * (a + b + c).

2. Im zweiten Fall müssen Sie alle Seiten des Dreiecks multiplizieren und durch das Vierfache des Radius des umschriebenen Kreises dividieren. IN wörtlicher Ausdruck es sieht so aus: S = (a * b * c) / (4R).

3. In der dritten Situation können Sie auf die Kenntnis der Seiten verzichten, benötigen jedoch die Werte aller drei Winkel. S = 2 R 2 * sin α * sin β * sin γ.

Sonderfall: rechtwinkliges Dreieck

Dies ist die einfachste Situation, da nur die Länge beider Beine benötigt wird. Sie werden mit den lateinischen Buchstaben a und b bezeichnet. Quadrat rechtwinkliges Dreieck gleich der Hälfte der Fläche des hinzugefügten Rechtecks.

Mathematisch sieht es so aus: S = ½ a * b. Es ist am einfachsten, sich daran zu erinnern. Da es wie die Formel für die Fläche eines Rechtecks ​​​​aussieht, erscheint nur ein Bruchteil, der die Hälfte angibt.

Sonderfall: gleichschenkliges Dreieck

Da es zwei gleiche Seiten hat, sehen einige Formeln für seine Fläche etwas vereinfacht aus. Die Formel von Heron, die die Fläche eines gleichschenkligen Dreiecks berechnet, sieht beispielsweise wie folgt aus:

S = ½ in √((a + ½ in)*(a - ½ in)).

Wenn Sie es umwandeln, wird es kürzer. In diesem Fall lautet Herons Formel für ein gleichschenkliges Dreieck wie folgt:

S = ¼ in √(4 * a 2 - b 2).

Die Flächenformel sieht etwas einfacher aus als für ein beliebiges Dreieck, wenn die Seiten und der Winkel zwischen ihnen bekannt sind. S = ½ a 2 * sin β.

Sonderfall: gleichseitiges Dreieck

Normalerweise ist bei Problemen die Seite darüber bekannt oder kann auf irgendeine Weise herausgefunden werden. Dann sieht die Formel zum Ermitteln der Fläche eines solchen Dreiecks so aus wie folgt:

S = (a 2 √3) / 4.

Probleme beim Finden der Fläche, wenn das Dreieck auf kariertem Papier abgebildet ist

Die einfachste Situation ist, wenn ein rechtwinkliges Dreieck so gezeichnet wird, dass seine Schenkel mit den Linien des Papiers übereinstimmen. Dann müssen Sie nur noch die Anzahl der Zellen zählen, die in die Beine passen. Dann multipliziere sie und dividiere durch zwei.

Wenn das Dreieck spitz oder stumpf ist, muss es zu einem Rechteck gezeichnet werden. Dann wird die resultierende Figur 3 Dreiecke haben. Eine davon ist die in der Aufgabe angegebene. Und die anderen beiden sind Hilfs- und rechteckig. Die Flächen der letzten beiden müssen mit der oben beschriebenen Methode bestimmt werden. Berechnen Sie dann die Fläche des Rechtecks ​​und subtrahieren Sie davon die für die Hilfsflächen berechneten. Die Fläche des Dreiecks wird bestimmt.

Als wesentlich komplizierter erweist sich die Situation, in der keine der Seiten des Dreiecks mit den Linien des Papiers übereinstimmt. Dann muss es in ein Rechteck eingeschrieben werden, sodass die Eckpunkte der Originalfigur auf seinen Seiten liegen. In diesem Fall gibt es drei rechtwinklige Hilfsdreiecke.

Beispiel für ein Problem mit der Heron-Formel

Zustand. Manche Dreiecke haben bekannte Seiten. Sie betragen 3, 5 und 6 cm. Sie müssen die Fläche ermitteln.

Jetzt können Sie die Fläche des Dreiecks mit der obigen Formel berechnen. Unter der Quadratwurzel steht das Produkt aus vier Zahlen: 7, 4, 2 und 1. Das heißt, die Fläche ist √(4 * 14) = 2 √(14).

Wenn keine größere Genauigkeit erforderlich ist, können Sie die Quadratwurzel aus 14 ziehen. Sie entspricht 3,74. Dann beträgt die Fläche 7,48.

Antwort. S = 2 √14 cm 2 oder 7,48 cm 2.

Beispielproblem mit einem rechtwinkligen Dreieck

Zustand. Ein Bein eines rechtwinkligen Dreiecks ist 31 cm größer als das zweite. Sie müssen ihre Länge ermitteln, wenn die Fläche des Dreiecks 180 cm 2 beträgt.
Lösung. Wir müssen ein System aus zwei Gleichungen lösen. Die erste bezieht sich auf die Fläche. Die zweite betrifft das Verhältnis der Beine, das in der Aufgabe angegeben ist.
180 = ½ a * b;

a = b + 31.
Zunächst muss der Wert von „a“ in die erste Gleichung eingesetzt werden. Es stellt sich heraus: 180 = ½ (in + 31) * in. Es gibt nur eine unbekannte Größe und ist daher leicht zu lösen. Nach dem Öffnen der Klammern erhalten wir quadratische Gleichung: in 2 + 31 in - 360 = 0. Es gibt zwei Werte für „in“: 9 und – 40. Die zweite Zahl eignet sich nicht als Antwort, da die Seitenlänge eines Dreiecks nicht negativ sein kann Wert.

Es bleibt noch das zweite Bein zu berechnen: Addiere 31 zur resultierenden Zahl. Es ergibt sich 40. Dies sind die in der Aufgabe gesuchten Größen.

Antwort. Die Beine des Dreiecks sind 9 und 40 cm lang.

Problem, eine Seite durch Fläche, Seite und Winkel eines Dreiecks zu finden

Zustand. Die Fläche eines bestimmten Dreiecks beträgt 60 cm 2. Es ist notwendig, eine seiner Seiten zu berechnen, wenn die zweite Seite 15 cm beträgt und der Winkel zwischen ihnen 30 ° beträgt.

Lösung. Basierend auf der akzeptierten Notation sind die gewünschte Seite „a“, die bekannte Seite „b“, angegebenen Winkel„γ“. Dann kann die Flächenformel wie folgt umgeschrieben werden:

60 = ½ a * 15 * sin 30º. Hier beträgt der Sinus von 30 Grad 0,5.

Nach den Transformationen ergibt sich, dass „a“ gleich 60 / (0,5 * 0,5 * 15) ist. Das sind 16.

Antwort. Die erforderliche Seitenlänge beträgt 16 cm.

Problem mit einem Quadrat, das in ein rechtwinkliges Dreieck eingeschrieben ist

Zustand. Der Scheitelpunkt eines Quadrats mit einer Seitenlänge von 24 cm fällt mit dem rechten Winkel des Dreiecks zusammen. Die anderen beiden liegen an den Seiten. Die dritte gehört zur Hypotenuse. Die Länge eines der Beine beträgt 42 cm. Wie groß ist die Fläche des rechtwinkligen Dreiecks?

Lösung. Betrachten Sie zwei rechtwinklige Dreiecke. Der erste ist der in der Aufgabe angegebene. Der zweite basiert auf berühmtes Bein das ursprüngliche Dreieck. Sie sind ähnlich, weil sie einen gemeinsamen Winkel haben und durch parallele Linien gebildet werden.

Dann sind die Verhältnisse ihrer Beine gleich. Die Beine des kleineren Dreiecks sind gleich 24 cm (Seite des Quadrats) und 18 cm (bei gegebenem Bein 42 cm abzüglich der Seite des Quadrats 24 cm). Entsprechende Beine großes Dreieck- 42 cm und x cm. Dieses „x“ wird benötigt, um die Fläche des Dreiecks zu berechnen.

18/42 = 24/x, also x = 24 * 42 / 18 = 56 (cm).

Dann ist die Fläche gleich dem Produkt aus 56 und 42 dividiert durch zwei, also 1176 cm 2.

Antwort. Die benötigte Fläche beträgt 1176 cm 2.

Konzept der Fläche

Der Begriff der Fläche einer beliebigen geometrischen Figur, insbesondere eines Dreiecks, wird mit einer Figur wie einem Quadrat in Verbindung gebracht. Für die Flächeneinheit einer beliebigen geometrischen Figur nehmen wir die Fläche eines Quadrats, dessen Seite gleich eins ist. Der Vollständigkeit halber erinnern wir uns an zwei Grundeigenschaften des Flächenkonzepts geometrische Formen.

Eigenschaft 1: Wenn geometrische Figuren gleich sind, dann sind auch ihre Flächen gleich.

Eigenschaft 2: Jede Figur kann in mehrere Figuren unterteilt werden. Darüber hinaus ist die Fläche der Originalfigur gleich der Summe der Flächen aller ihrer Bestandteile.

Schauen wir uns ein Beispiel an.

Beispiel 1

Offensichtlich ist eine der Seiten des Dreiecks eine Diagonale eines Rechtecks, dessen eine Seite eine Länge von 5 $ hat (da es 5 $-Zellen gibt) und die andere 6 $ hat (da es 6 $-Zellen gibt). Daher entspricht die Fläche dieses Dreiecks der Hälfte eines solchen Rechtecks. Die Fläche des Rechtecks ​​beträgt

Dann ist die Fläche des Dreiecks gleich

Antwort: 15 $.

Als nächstes betrachten wir mehrere Methoden zum Ermitteln der Flächen von Dreiecken, nämlich die Verwendung der Höhe und der Basis, die Verwendung der Heron-Formel und die Fläche eines gleichseitigen Dreiecks.

So ermitteln Sie die Fläche eines Dreiecks anhand seiner Höhe und Basis

Satz 1

Die Fläche eines Dreiecks kann als halbes Produkt aus der Länge einer Seite und der Höhe zu dieser Seite ermittelt werden.

Mathematisch sieht es so aus

$S=\frac(1)(2)αh$

Dabei ist $a$ die Länge der Seite und $h$ die dorthin gezogene Höhe.

Nachweisen.

Betrachten Sie ein Dreieck $ABC$, in dem $AC=α$. Auf dieser Seite wird die Höhe $BH$ eingezeichnet, die gleich $h$ ist. Bauen wir es wie in Abbildung 2 zum Quadrat $AXYC$ auf.

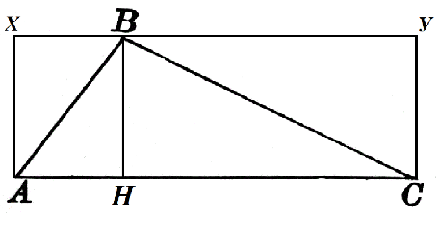
Die Fläche des Rechtecks ​​$AXBH$ ist $h\cdot AH$, und die Fläche des Rechtecks ​​$HBYC$ ist $h\cdot HC$. Dann

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Daher ist die erforderliche Fläche des Dreiecks gemäß Eigenschaft 2 gleich

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

Der Satz ist bewiesen.

Beispiel 2

Finden Sie die Fläche des Dreiecks in der Abbildung unten, wenn die Zelle eine Fläche von eins hat

Die Basis dieses Dreiecks ist gleich 9 $ (da 9 $ aus 9 $ Quadraten besteht). Die Höhe beträgt ebenfalls 9$. Dann erhalten wir nach Satz 1

$S=\frac(1)(2)\cdot 9\cdot 9=40,5$

Antwort: 40,5 $.

Herons Formel

Satz 2

Wenn wir drei Seiten eines Dreiecks $α$, $β$ und $γ$ erhalten, dann kann seine Fläche wie folgt ermittelt werden

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

hier bedeutet $ρ$ den Halbumfang dieses Dreiecks.

Nachweisen.

Betrachten Sie die folgende Abbildung:

Nach dem Satz des Pythagoras erhalten wir aus dem Dreieck $ABH$

Aus dem Dreieck $CBH$ gilt nach dem Satz des Pythagoras

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Aus diesen beiden Beziehungen erhalten wir die Gleichheit

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Da $ρ=\frac(α+β+γ)(2)$, dann $α+β+γ=2ρ$, was bedeutet

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Nach Satz 1 erhalten wir

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Anweisungen

Partys und Winkel gelten als Grundelemente A. Ein Dreieck wird vollständig durch eines seiner folgenden Grundelemente definiert: entweder drei Seiten oder eine Seite und zwei Winkel oder zwei Seiten und einen Winkel zwischen ihnen. Für die Existenz Dreieck gegeben durch drei Seiten a, b, c, ist es notwendig und ausreichend, die Ungleichungen zu erfüllen, die Ungleichungen genannt werden Dreieck:
a+b > c,
a+c > b,
b+c > a.

Zum Bauen Dreieck Auf drei Seiten a, b, c ist es notwendig, vom Punkt C des Segments CB = a aus mit einem Zirkel einen Kreis mit Radius b zu zeichnen. Zeichnen Sie dann auf die gleiche Weise einen Kreis vom Punkt B aus mit einem Radius gleich der Seite c. Ihr Schnittpunkt A ist der dritte Scheitelpunkt des Gewünschten Dreieck ABC, wobei AB=c, CB=a, CA=b – Seiten Dreieck. Das Problem gilt, wenn die Seiten a, b, c die Ungleichungen erfüllen Dreieck in Schritt 1 angegeben.

Auf diese Weise konstruierter Bereich S Dreieck ABC mit bekannten Seiten a, b, c wird mit der Formel von Heron berechnet:
S=v(p(p-a)(p-b)(p-c)),
wobei a, b, c Seiten sind Dreieck, p – Halbumfang.
p = (a+b+c)/2

Wenn ein Dreieck gleichseitig ist, d. h. alle seine Seiten gleich sind (a=b=c).Fläche Dreieck berechnet nach der Formel:
S=(a^2 v3)/4

Wenn das Dreieck rechtwinklig ist, das heißt, einer seiner Winkel gleich 90° ist und die Seiten, die es bilden, Schenkel sind, ist die dritte Seite die Hypotenuse. In diesem Fall Quadrat entspricht dem Produkt der Beine dividiert durch zwei.
S=ab/2

Zu finden Quadrat Dreieck, können Sie eine der vielen Formeln verwenden. Wählen Sie eine Formel abhängig davon, welche Daten bereits bekannt sind.

Sie werden brauchen

• Kenntnis der Formeln zur Bestimmung der Fläche eines Dreiecks

Anweisungen

Wenn Sie die Größe einer der Seiten und den Wert der zu dieser Seite abgesenkten Höhe aus dem gegenüberliegenden Winkel kennen, können Sie die Fläche wie folgt ermitteln: S = a*h/2, wobei S die Fläche ist des Dreiecks ist a eine der Seiten des Dreiecks und h die Höhe zur Seite a.

Es gibt eine bekannte Methode zur Bestimmung der Fläche eines Dreiecks, wenn seine drei Seiten bekannt sind. Es ist Herons Formel. Um die Aufzeichnung zu vereinfachen, wird ein Zwischenwert eingeführt – Halbumfang: p = (a+b+c)/2, wobei a, b, c – . Dann lautet Herons Formel wie folgt: S = (p(p-a)(p-b)(p-c))^½, ^ Potenzierung.

Nehmen wir an, Sie kennen eine Seite eines Dreiecks und drei Winkel. Dann ist es leicht, die Fläche des Dreiecks zu ermitteln: S = a²sinα sinγ / (2sinβ), wobei β der Winkel gegenüber der Seite a und α und γ die zur Seite benachbarten Winkel sind.

Video zum Thema

bitte beachten Sie

Am meisten allgemeine Formel, die für alle Fälle geeignet ist, ist Herons Formel.

Quellen:

Tipp 3: So ermitteln Sie die Fläche eines Dreiecks anhand von drei Seiten

Das Ermitteln der Fläche eines Dreiecks ist eines der häufigsten Probleme in der Schulplanimetrie. Die Kenntnis der drei Seiten eines Dreiecks reicht aus, um die Fläche eines Dreiecks zu bestimmen. In besonderen Fällen gleichseitiger Dreiecke reicht es aus, die Längen von zwei bzw. einer Seite zu kennen.

Sie werden brauchen

• Seitenlängen von Dreiecken, Heronsche Formel, Kosinussatz

Anweisungen

Herons Formel für die Fläche eines Dreiecks lautet wie folgt: S = sqrt(p(p-a)(p-b)(p-c)). Wenn wir den Halbumfang p schreiben, erhalten wir: S = sqrt(((a+b+c)/2)((b+c-a)/2)((a+c-b)/2)((a+b-c )/2) ) = (sqrt((a+b+c)(a+b-c)(a+c-b)(b+c-a)))/4.

Eine Formel für die Fläche eines Dreiecks kann man aus Überlegungen beispielsweise durch Anwendung des Kosinussatzes ableiten.

Nach dem Kosinussatz gilt AC^2 = (AB^2)+(BC^2)-2*AB*BC*cos(ABC). Mit den eingeführten Notationen können diese auch in der Form geschrieben werden: b^2 = (a^2)+(c^2)-2a*c*cos(ABC). Daher ist cos(ABC) = ((a^2)+(c^2)-(b^2))/(2*a*c)

Die Fläche eines Dreiecks wird auch durch die Formel S = a*c*sin(ABC)/2 unter Verwendung zweier Seiten und des Winkels zwischen ihnen ermittelt. Der Sinus des Winkels ABC kann dadurch ausgedrückt werden, indem man die grundlegende trigonometrische Identität verwendet: sin(ABC) = sqrt(1-((cos(ABC))^2). Indem man den Sinus in die Formel für die Fläche einsetzt und ausschreibt , können Sie die Formel für die Fläche des Dreiecks ABC ermitteln.

Video zum Thema

Zur Durchführung Reparaturarbeiten Möglicherweise ist eine Messung erforderlich Quadrat Wände Es ist einfacher zu berechnen benötigte Menge Farbe oder Tapete. Für Messungen verwenden Sie am besten ein Maßband oder Maßband. Anschließend sollten Messungen vorgenommen werden Wände wurden eingeebnet.

Sie werden brauchen

• -Roulette;
• -Leiter.

Anweisungen

Zählen Quadrat Wände müssen Sie die genaue Höhe der Decken kennen und auch die Länge entlang des Bodens messen. Das geht wie folgt: Nehmen Sie einen Zentimeter und legen Sie ihn über die Fußleiste. Normalerweise reicht ein Zentimeter für die gesamte Länge nicht aus. Befestigen Sie es daher in der Ecke und wickeln Sie es dann auf die maximale Länge ab. Setzen Sie an dieser Stelle eine Markierung mit einem Bleistift, notieren Sie das erhaltene Ergebnis und führen Sie weitere Messungen auf die gleiche Weise, beginnend mit dem letzten Messpunkt, durch.

Die Standarddecken betragen je nach Haus 2 Meter 80 Zentimeter, 3 Meter und 3 Meter 20 Zentimeter. Wenn das Haus vor den 50er Jahren gebaut wurde, ist die tatsächliche Höhe höchstwahrscheinlich etwas niedriger als angegeben. Wenn Sie rechnen Quadrat Für Reparaturarbeiten kann ein kleiner Vorrat nicht schaden - berücksichtigen Sie dies anhand der Norm. Wenn Sie dennoch die tatsächliche Höhe wissen müssen, nehmen Sie Messungen vor. Das Prinzip ähnelt der Längenmessung, allerdings benötigen Sie eine Trittleiter.

Multiplizieren Sie die resultierenden Indikatoren – das ist Quadrat dein Wände. Es stimmt, beim Malen oder zum Malen ist es notwendig, etwas zu subtrahieren Quadrat Tür und Fensteröffnungen. Legen Sie dazu einen Zentimeter entlang der Öffnung. Wenn es sich um eine Tür handelt, die Sie später austauschen möchten, führen Sie dies mit der ausgebauten Tür durch Türrahmen, nur unter Berücksichtigung Quadrat direkt zur Öffnung selbst. Die Fläche des Fensters wird entlang des Umfangs seines Rahmens berechnet. Nach Quadrat Wenn Sie Fenster und Türöffnung berechnet haben, subtrahieren Sie das Ergebnis von der resultierenden Gesamtfläche des Raums.

Bitte beachten Sie, dass die Messung der Raumlänge und -breite von zwei Personen durchgeführt wird, dies erleichtert die Fixierung des Zentimeter- oder Maßbandes und dementsprechend ein genaueres Ergebnis. Führen Sie die gleiche Messung mehrmals durch, um sicherzustellen, dass die erhaltenen Zahlen korrekt sind.

Video zum Thema

Das Volumen eines Dreiecks zu ermitteln ist in der Tat keine triviale Aufgabe. Tatsache ist, dass ein Dreieck eine zweidimensionale Figur ist, d.h. es liegt vollständig in einer Ebene, was bedeutet, dass es einfach kein Volumen hat. Natürlich kann man nichts finden, was es nicht gibt. Aber lasst uns nicht aufgeben! Wir können die folgende Annahme akzeptieren: Das Volumen einer zweidimensionalen Figur ist ihre Fläche. Wir werden nach der Fläche des Dreiecks suchen.

Sie werden brauchen

• Blatt Papier, Bleistift, Lineal, Taschenrechner

Anweisungen

Zeichnen Sie mit Lineal und Bleistift auf ein Blatt Papier. Durch sorgfältige Untersuchung des Dreiecks können Sie sicherstellen, dass es sich tatsächlich nicht um ein Dreieck handelt, da es auf einer Ebene gezeichnet ist. Beschriften Sie die Seiten des Dreiecks: Eine Seite sei „a“, die andere Seite „b“ und die dritte Seite „c“. Beschriften Sie die Eckpunkte des Dreiecks mit den Buchstaben „A“, „B“ und „C“.

Messen Sie eine beliebige Seite des Dreiecks mit einem Lineal und notieren Sie das Ergebnis. Stellen Sie anschließend vom gegenüberliegenden Scheitelpunkt aus eine Senkrechte zur gemessenen Seite her. Diese Senkrechte entspricht der Höhe des Dreiecks. Im in der Abbildung gezeigten Fall wird die Senkrechte „h“ vom Scheitelpunkt „A“ zur Seite „c“ wiederhergestellt. Messen Sie die resultierende Höhe mit einem Lineal und notieren Sie das Messergebnis.

Es kann für Sie schwierig sein, die exakte Senkrechte wiederherzustellen. In diesem Fall sollten Sie eine andere Formel verwenden. Messen Sie alle Seiten des Dreiecks mit einem Lineal. Berechnen Sie anschließend den Halbumfang des Dreiecks „p“, indem Sie die resultierenden Längen der Seiten addieren und ihre Summe in zwei Hälften teilen. Wenn Sie über den Wert des Halbumfangs verfügen, können Sie die Formel von Heron verwenden. Dazu müssen Sie extrahieren Quadratwurzel aus dem Folgenden: p(p-a)(p-b)(p-c).

Sie haben die erforderliche Fläche des Dreiecks erhalten. Das Problem, das Volumen eines Dreiecks zu ermitteln, wurde nicht gelöst, aber wie oben erwähnt, ist das Volumen nicht . In der dreidimensionalen Welt kann man ein Volumen finden, das im Wesentlichen ein Dreieck ist. Wenn wir uns vorstellen, dass unser ursprüngliches Dreieck zu einer dreidimensionalen Pyramide geworden ist, dann ist das Volumen einer solchen Pyramide das Produkt der Länge ihrer Basis und der Fläche des Dreiecks, die wir erhalten haben.

bitte beachten Sie

Je sorgfältiger Sie messen, desto genauer werden Ihre Berechnungen.

Quellen:

• Rechner „Alles zu allem“ – ein Portal für Richtwerte
• Dreiecksvolumen im Jahr 2019

Die drei Punkte, die ein Dreieck im kartesischen Koordinatensystem eindeutig definieren, sind seine Eckpunkte. Wenn Sie ihre Position relativ zu jeder der Koordinatenachsen kennen, können Sie alle Parameter dieser flachen Figur berechnen, einschließlich der durch ihren Umfang begrenzten Quadrat. Dies kann auf verschiedene Arten erfolgen.

Anweisungen

Verwenden Sie die Formel von Heron, um die Fläche zu berechnen Dreieck. Dabei geht es um die Abmessungen der drei Seiten der Figur. Beginnen Sie Ihre Berechnungen also mit . Die Länge jeder Seite muss gleich der Wurzel der Summe der Quadrate der Längen ihrer Projektionen auf die Koordinatenachsen sein. Wenn wir die Koordinaten A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) und C(X₃,Y₃,Z₃) bezeichnen, können die Längen ihrer Seiten wie folgt ausgedrückt werden: AB = √((X₁- X₂)² + (Y₁ -Y₂)² + (Z₁-Z₂)²), BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²), AC = √(( X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).

Um die Berechnungen zu vereinfachen, führen Sie eine Hilfsvariable ein – den Halbumfang (P). Aus der Tatsache, dass dies die Hälfte der Summe der Längen aller Seiten ist: P = ½*(AB+BC+AC) = ½*(√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁- Z₂)²) + √ ((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) + √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃) ²).

Fläche eines Dreiecks – Formeln und Beispiele zur Problemlösung

Unten sind Formeln zum Ermitteln der Fläche eines beliebigen Dreiecks die geeignet sind, die Fläche jedes Dreiecks zu ermitteln, unabhängig von seinen Eigenschaften, Winkeln oder Größen. Die Formeln werden in Form eines Bildes dargestellt, mit Erläuterungen zu ihrer Anwendung bzw. Begründung ihrer Richtigkeit. Korrespondenzen sind ebenfalls in einer separaten Abbildung angegeben Buchstabenbezeichnungen in Formeln und grafische Symbole auf der Zeichnung.

Notiz . Wenn das Dreieck besondere Eigenschaften hat (gleichschenklig, rechtwinklig, gleichseitig), können Sie die unten angegebenen Formeln sowie zusätzliche Sonderformeln verwenden, die nur für Dreiecke mit diesen Eigenschaften gültig sind:

• „Formel für die Fläche eines gleichseitigen Dreiecks“

Dreiecksflächenformeln

Erläuterungen zu Formeln:
a, b, c- die Längen der Seiten des Dreiecks, dessen Fläche wir ermitteln möchten
R- Radius des in das Dreieck eingeschriebenen Kreises
R- Radius des um das Dreieck umschriebenen Kreises
H- Höhe des seitlich abgesenkten Dreiecks
P- Halbumfang eines Dreiecks, 1/2 der Summe seiner Seiten (Umfang)
α - Winkel gegenüber der Seite a des Dreiecks
β - Winkel gegenüber der Seite b des Dreiecks
γ - Winkel gegenüber der Seite c des Dreiecks
H A, H B , H C- Höhe des Dreiecks abgesenkt zu den Seiten a, b, c

Bitte beachten Sie, dass die angegebenen Notationen der obigen Abbildung entsprechen, sodass es Ihnen bei der Lösung eines realen Geometrieproblems optisch leichter fällt, die richtigen Werte an den richtigen Stellen in der Formel einzusetzen.

• Die Fläche des Dreiecks beträgt das halbe Produkt aus der Höhe des Dreiecks und der Länge der Seite, um die diese Höhe abgesenkt wird(Formel 1). Die Richtigkeit dieser Formel kann logisch verstanden werden. Die auf die Basis abgesenkte Höhe teilt ein beliebiges Dreieck in zwei rechteckige. Wenn Sie jedes von ihnen zu einem Rechteck mit den Abmessungen b und h zusammenbauen, dann entspricht die Fläche dieser Dreiecke offensichtlich genau der Hälfte der Fläche des Rechtecks ​​(Spr = bh).
• Die Fläche des Dreiecks beträgt das halbe Produkt seiner beiden Seiten und der Sinus des Winkels zwischen ihnen(Formel 2) (siehe unten ein Beispiel für die Lösung eines Problems mit dieser Formel). Trotz der Tatsache, dass es anders aussieht als das vorherige, kann es leicht in dieses umgewandelt werden. Wenn wir die Höhe vom Winkel B zur Seite b verringern, stellt sich heraus, dass das Produkt aus Seite a und dem Sinus des Winkels γ gemäß den Eigenschaften des Sinus in einem rechtwinkligen Dreieck gleich der Höhe des von uns gezeichneten Dreiecks ist , was uns die vorherige Formel liefert
• Die Fläche eines beliebigen Dreiecks kann ermittelt werden durch arbeiten der halbe Radius des darin eingeschriebenen Kreises durch die Summe der Längen aller seiner Seiten(Formel 3), einfach ausgedrückt, Sie müssen den Halbumfang des Dreiecks mit dem Radius des eingeschriebenen Kreises multiplizieren (das ist leichter zu merken)
• Die Fläche eines beliebigen Dreiecks kann ermittelt werden, indem das Produkt aller seiner Seiten durch 4 Radien des umschriebenen Kreises geteilt wird (Formel 4)
• Formel 5 ermittelt die Fläche eines Dreiecks durch die Länge seiner Seiten und seinen Halbumfang (die Hälfte der Summe aller seiner Seiten).
• Herons Formel(6) ist eine Darstellung derselben Formel ohne Verwendung des Konzepts des Halbumfangs, nur durch die Längen der Seiten
• Die Fläche eines beliebigen Dreiecks ist gleich dem Produkt aus dem Quadrat der Seite des Dreiecks und den Sinuswerten der an diese Seite angrenzenden Winkel geteilt durch den doppelten Sinus des dieser Seite gegenüberliegenden Winkels (Formel 7)
• Die Fläche eines beliebigen Dreiecks kann als Produkt zweier Quadrate des Kreises ermittelt werden, der von den Sinuswerten jedes seiner Winkel umschrieben wird. (Formel 8)
• Wenn die Länge einer Seite und die Werte zweier benachbarter Winkel bekannt sind, kann die Fläche des Dreiecks als Quadrat dieser Seite dividiert durch die doppelte Summe der Kotangenten dieser Winkel ermittelt werden (Formel 9).
• Wenn nur die Länge jeder der Höhen des Dreiecks bekannt ist (Formel 10), dann ist die Fläche eines solchen Dreiecks umgekehrt proportional zu den Längen dieser Höhen, wie nach der Heron-Formel
• Mit der Formel 11 können Sie rechnen Fläche eines Dreiecks basierend auf den Koordinaten seiner Eckpunkte, die als (x;y)-Werte für jeden der Eckpunkte angegeben werden. Bitte beachten Sie, dass der resultierende Wert modulo genommen werden muss, da die Koordinaten einzelner (oder sogar aller) Eckpunkte im Bereich negativer Werte liegen können

Notiz. Im Folgenden finden Sie Beispiele für die Lösung von Geometrieproblemen, um die Fläche eines Dreiecks zu ermitteln. Wenn Sie ein Geometrieproblem lösen müssen, das hier nicht ähnlich ist, schreiben Sie im Forum darüber. In Lösungen kann anstelle des „Quadratwurzel“-Symbols die Funktion sqrt() verwendet werden, wobei sqrt das Quadratwurzelsymbol ist und der Radikandenausdruck in Klammern angegeben wird.Manchmal kann für einfache radikale Ausdrücke das Symbol verwendet werden √

Aufgabe. Ermitteln Sie die Fläche zweier Seiten und den Winkel zwischen ihnen

Die Seiten des Dreiecks betragen 5 und 6 cm. Der Winkel zwischen ihnen beträgt 60 Grad. Finden Sie die Fläche des Dreiecks.

Lösung.

Um dieses Problem zu lösen, verwenden wir Formel Nummer zwei aus dem theoretischen Teil der Lektion.
Die Fläche eines Dreiecks ergibt sich aus den Längen zweier Seiten und dem Sinus des Winkels zwischen ihnen und ist gleich
S=1/2 ab sin γ

Da wir alle notwendigen Daten für die Lösung haben (laut Formel), können wir nur die Werte aus den Problembedingungen in die Formel einsetzen:
S = 1/2 * 5 * 6 * Sünde 60

In der Wertetabelle trigonometrische Funktionen Lassen Sie uns den Wert von Sinus 60 Grad finden und in den Ausdruck einsetzen. Es entspricht der Wurzel aus drei mal zwei.
S = 15 √3 / 2

Antwort: 7,5 √3 (abhängig von den Anforderungen des Lehrers können Sie wahrscheinlich 15 √3/2 belassen)

Aufgabe. Finden Sie die Fläche eines gleichseitigen Dreiecks

Finden Sie die Fläche eines gleichseitigen Dreiecks mit einer Seitenlänge von 3 cm.

Lösung .

Die Fläche eines Dreiecks kann mit der Formel von Heron ermittelt werden:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))

Da a = b = c ist, hat die Formel für die Fläche eines gleichseitigen Dreiecks die Form:

S = √3 / 4 * a 2

S = √3 / 4 * 3 2

Antwort: 9 √3 / 4.

Aufgabe. Flächenänderung bei Änderung der Seitenlänge

Wie oft vergrößert sich die Fläche des Dreiecks, wenn die Seiten um das Vierfache vergrößert werden?

Lösung.

Da uns die Abmessungen der Seiten des Dreiecks unbekannt sind, gehen wir zur Lösung des Problems davon aus, dass die Längen der Seiten jeweils gleich den beliebigen Zahlen a, b, c sind. Um die Frage nach dem Problem zu beantworten, ermitteln wir dann den Bereich gegebenes Dreieck, und ermitteln Sie dann die Fläche eines Dreiecks, dessen Seiten viermal größer sind. Das Flächenverhältnis dieser Dreiecke gibt uns die Antwort auf das Problem.

Im Folgenden erklären wir Ihnen Schritt für Schritt die Lösung des Problems in Textform. Ganz am Ende wird dieselbe Lösung jedoch in einer praktischeren grafischen Form präsentiert. Interessierte können sich die Lösungen gleich durchlesen.

Zur Lösung verwenden wir die Formel von Heron (siehe oben im theoretischen Teil der Lektion). Es sieht so aus:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(siehe erste Bildzeile unten)

Die Längen der Seiten eines beliebigen Dreiecks werden durch die Variablen a, b, c angegeben.
Wenn die Seiten um das Vierfache vergrößert werden, beträgt die Fläche des neuen Dreiecks c:

S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c))
(siehe zweite Zeile im Bild unten)

Wie Sie sehen, ist 4 ein gemeinsamer Faktor, der aus allen vier Ausdrücken gemäß aus Klammern genommen werden kann allgemeine Regeln Mathematik.
Dann

S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - in der dritten Zeile des Bildes
S 2 = 1/4 sqrt(256 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - vierte Zeile

Die Quadratwurzel der Zahl 256 ist perfekt extrahiert, also ziehen wir sie unter der Wurzel heraus
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(siehe fünfte Zeile des Bildes unten)

Um die im Problem gestellte Frage zu beantworten, müssen wir lediglich die Fläche des resultierenden Dreiecks durch die Fläche des ursprünglichen Dreiecks dividieren.
Bestimmen wir die Flächenverhältnisse, indem wir die Ausdrücke durcheinander dividieren und den resultierenden Bruch reduzieren.

Dreieck ist eine der häufigsten geometrischen Formen, die wir bereits kennen lernen Grundschule. Jeder Schüler steht im Geometrieunterricht vor der Frage, wie man die Fläche eines Dreiecks ermittelt. Welche Merkmale beim Finden der Fläche einer bestimmten Figur können also identifiziert werden? In diesem Artikel werden wir uns die Grundformeln ansehen, die zur Lösung einer solchen Aufgabe erforderlich sind, und auch die Arten von Dreiecken analysieren.

Arten von Dreiecken

Sie können die Fläche eines Dreiecks absolut ermitteln auf unterschiedliche Weise, weil es in der Geometrie mehr als eine Art von Figuren gibt, die drei Winkel enthalten. Zu diesen Typen gehören:

• Stumpf.
• Gleichseitig (richtig).
• Rechtwinkliges Dreieck.
• Gleichschenklige.

Schauen wir uns jeden einzelnen genauer an vorhandene Typen Dreiecke.

Diese geometrische Figur gilt als die häufigste bei der Lösung geometrischer Probleme. Wenn die Notwendigkeit besteht, ein beliebiges Dreieck zu zeichnen, ist diese Option hilfreich.

In einem spitzen Dreieck sind, wie der Name schon sagt, alle Winkel spitz und ergeben zusammen 180°.

Dieser Dreieckstyp kommt ebenfalls sehr häufig vor, ist aber etwas seltener als ein spitzes Dreieck. Wenn Sie beispielsweise Dreiecke lösen (d. h. mehrere ihrer Seiten und Winkel sind bekannt und Sie müssen die verbleibenden Elemente finden), müssen Sie manchmal feststellen, ob der Winkel stumpf ist oder nicht. Kosinus ist eine negative Zahl.

B, der Wert eines der Winkel übersteigt 90°, sodass die verbleibenden zwei Winkel kleine Werte annehmen können (z. B. 15° oder sogar 3°).

Um die Fläche eines solchen Dreiecks zu ermitteln, müssen Sie einige Nuancen kennen, über die wir später sprechen werden.

Regelmäßige und gleichschenklige Dreiecke

Regelmäßiges Polygon ist eine Figur, die n Winkel einschließt und deren Seiten und Winkel alle gleich sind. Das ist ein regelmäßiges Dreieck. Da die Summe aller Winkel eines Dreiecks 180° beträgt, beträgt jeder der drei Winkel 60°.

Ein regelmäßiges Dreieck wird aufgrund seiner Eigenschaft auch gleichseitige Figur genannt.

Es ist auch erwähnenswert, dass in ein regelmäßiges Dreieck nur ein Kreis eingeschrieben werden kann und dass nur ein Kreis darum herum beschrieben werden kann und dass ihre Mittelpunkte im selben Punkt liegen.

Neben dem gleichseitigen Typ kann man auch ein gleichschenkliges Dreieck unterscheiden, das sich davon geringfügig unterscheidet. In einem solchen Dreieck sind zwei Seiten und zwei Winkel einander gleich und die dritte Seite (an die die angrenzende Seite angrenzt). gleiche Winkel) ist die Basis.

Die Abbildung zeigt ein gleichschenkliges Dreieck DEF, dessen Winkel D und F gleich sind und DF die Basis ist.

Rechtwinkliges Dreieck

Ein rechtwinkliges Dreieck wird so genannt, weil einer seiner Winkel gerade ist, also 90° beträgt. Die beiden anderen Winkel ergeben zusammen 90°.

Die größte Seite eines solchen Dreiecks, die dem 90°-Winkel gegenüberliegt, ist die Hypotenuse, während die restlichen beiden Seiten die Schenkel sind. Für diese Art von Dreiecken gilt der Satz des Pythagoras:

Die Summe der Quadrate der Längen der Beine ist gleich dem Quadrat der Länge der Hypotenuse.

Die Abbildung zeigt ein rechtwinkliges Dreieck BAC mit Hypotenuse AC und den Schenkeln AB und BC.

Um die Fläche eines Dreiecks mit rechtem Winkel zu ermitteln, müssen Sie die Zahlenwerte seiner Schenkel kennen.

Kommen wir zu den Formeln zum Ermitteln der Fläche einer bestimmten Figur.

Grundformeln zum Finden von Flächen

In der Geometrie lassen sich zwei Formeln unterscheiden, die geeignet sind, die Fläche der meisten Dreiecksarten zu ermitteln, nämlich für spitze, stumpfe, regelmäßige und gleichschenklige Dreiecke. Schauen wir uns jeden von ihnen an.

Nach Seite und Höhe

Diese Formel ist universell, um die Fläche der betrachteten Figur zu ermitteln. Dazu reicht es aus, die Länge der Seite und die Länge der darauf gezeichneten Höhe zu kennen. Die Formel selbst (halbes Produkt aus Grundfläche und Höhe) lautet wie folgt:

Dabei ist A die Seite eines gegebenen Dreiecks und H die Höhe des Dreiecks.

Um beispielsweise die Fläche eines spitzen Dreiecks ACB zu ermitteln, müssen Sie seine Seite AB mit der Höhe CD multiplizieren und den resultierenden Wert durch zwei teilen.

Allerdings ist es nicht immer einfach, auf diese Weise die Fläche eines Dreiecks zu ermitteln. Um diese Formel beispielsweise für ein stumpfes Dreieck zu verwenden, müssen Sie eine seiner Seiten verlängern und erst dann eine Höhe dazu zeichnen.

In der Praxis wird diese Formel häufiger verwendet als andere.

Auf beiden Seiten und an der Ecke

Diese Formel ist wie die vorherige für die meisten Dreiecke geeignet und ist in ihrer Bedeutung eine Folge der Formel zur Ermittlung der Seitenfläche und Höhe eines Dreiecks. Das heißt, die betreffende Formel kann leicht aus der vorherigen abgeleitet werden. Seine Formulierung sieht so aus:

S = ½*sinO*A*B,

Dabei sind A und B die Seiten des Dreiecks und O der Winkel zwischen den Seiten A und B.

Erinnern wir uns daran, dass der Sinus eines Winkels in einer speziellen Tabelle angezeigt werden kann, die nach dem herausragenden sowjetischen Mathematiker V. M. Bradis benannt ist.

Kommen wir nun zu anderen Formeln, die nur für außergewöhnliche Dreieckstypen geeignet sind.

Fläche eines rechtwinkligen Dreiecks

Zusätzlich zur universellen Formel, die die Notwendigkeit beinhaltet, die Höhe in einem Dreieck zu ermitteln, kann die Fläche eines Dreiecks, das einen rechten Winkel enthält, anhand seiner Schenkel ermittelt werden.

Somit ist die Fläche eines Dreiecks, das einen rechten Winkel enthält, die Hälfte des Produkts seiner Schenkel, oder:

wobei a und b die Schenkel eines rechtwinkligen Dreiecks sind.

Regelmäßiges Dreieck

Diese Art von geometrischer Figur zeichnet sich dadurch aus, dass ihre Fläche mit dem angegebenen Wert nur einer ihrer Seiten ermittelt werden kann (da alle Seiten eines regelmäßigen Dreiecks gleich sind). Wenn Sie also vor der Aufgabe stehen, „die Fläche eines Dreiecks bei gleichen Seiten zu ermitteln“, müssen Sie die folgende Formel verwenden:

S = A 2 *√3 / 4,

wobei A die Seite des gleichseitigen Dreiecks ist.

Herons Formel

Die letzte Möglichkeit, die Fläche eines Dreiecks zu ermitteln, ist die Heron-Formel. Um es verwenden zu können, müssen Sie die Länge der drei Seiten der Figur kennen. Herons Formel sieht so aus:

S = √p·(p - a)·(p - b)·(p - c),

wobei a, b und c die Seiten eines gegebenen Dreiecks sind.

Manchmal wird das Problem gestellt: „Die Fläche eines regelmäßigen Dreiecks besteht darin, die Länge seiner Seite zu ermitteln.“ In diesem Fall müssen wir die uns bereits bekannte Formel zum Ermitteln der Fläche eines regelmäßigen Dreiecks verwenden und daraus den Wert der Seite (oder ihres Quadrats) ableiten:

A 2 = 4S / √3.

Prüfungsaufgaben

Es gibt viele Formeln in GIA-Aufgaben in der Mathematik. Darüber hinaus ist es häufig erforderlich, die Fläche eines Dreiecks auf kariertem Papier zu ermitteln.

In diesem Fall ist es am bequemsten, die Höhe einer der Seiten der Figur zu zeichnen, ihre Länge aus den Zellen zu bestimmen und die universelle Formel zur Ermittlung der Fläche zu verwenden:

Nachdem Sie die im Artikel vorgestellten Formeln studiert haben, werden Sie also keine Probleme haben, die Fläche eines Dreiecks jeglicher Art zu finden.