Numerische trigonometrische Ausdrücke. Identische Transformationen trigonometrischer Ausdrücke

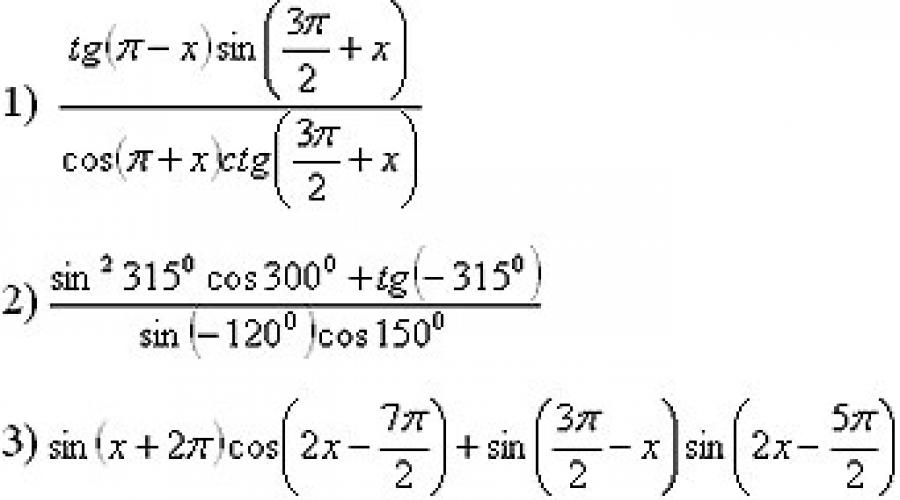
Abschnitte: Mathematik

Klasse: 11

Lektion 1

Thema: 11. Klasse (Vorbereitung auf das Einheitliche Staatsexamen)

Vereinfachung trigonometrischer Ausdrücke.

Einfache trigonometrische Gleichungen lösen. (2 Stunden)

Ziele:

• Systematisieren, verallgemeinern und erweitern Sie die Kenntnisse und Fähigkeiten der Schüler im Zusammenhang mit der Verwendung trigonometrischer Formeln und der Lösung einfacher trigonometrischer Gleichungen.

Ausrüstung für den Unterricht:

Unterrichtsaufbau:

1. Organisatorischer Moment
2. Testen auf Laptops. Die Diskussion der Ergebnisse.
3. Vereinfachung trigonometrischer Ausdrücke
4. Einfache trigonometrische Gleichungen lösen
5. Selbstständige Arbeit.
6. Zusammenfassung der Lektion. Erläuterung der Hausaufgabe.

1. Organisatorischer Moment. (2 Minuten.)

Der Lehrer begrüßt das Publikum, verkündet das Thema der Unterrichtsstunde, erinnert daran, dass ihm zuvor die Aufgabe übertragen wurde, trigonometrische Formeln zu wiederholen, und bereitet die Schüler auf die Prüfung vor.

2. Testen. (15 Min. + 3 Min. Diskussion)

Ziel ist es, das Wissen über trigonometrische Formeln und die Fähigkeit, diese anzuwenden, zu testen. Jeder Schüler hat auf seinem Schreibtisch einen Laptop mit einer Version des Tests.

Es kann eine beliebige Anzahl von Optionen geben, ich werde ein Beispiel für eine davon geben:

Ich wähle.

Ausdrücke vereinfachen:

a) grundlegende trigonometrische Identitäten

1. Sünde 2 3y + cos 2 3y + 1;

b) Additionsformeln

3. sin5x - sin3x;

c) Umwandeln eines Produkts in eine Summe

6. 2sin8y cos3y;

d) Doppelwinkelformeln

7. 2sin5x cos5x;

e) Formeln für Halbwinkel

f) Dreifachwinkelformeln

g) universelle Substitution

h) Reduzierung des Abschlusses

16. cos 2 (3x/7);

Die Schüler sehen ihre Antworten auf dem Laptop neben jeder Formel.

Die Arbeit wird sofort vom Computer überprüft. Die Ergebnisse werden auf einem großen Bildschirm angezeigt, damit jeder sie sehen kann.

Außerdem werden nach Abschluss der Arbeit die richtigen Antworten auf den Laptops der Schüler angezeigt. Jeder Schüler sieht, wo der Fehler gemacht wurde und welche Formeln er wiederholen muss.

3. Vereinfachung trigonometrischer Ausdrücke. (25 Min.)

Ziel ist es, die Anwendung grundlegender trigonometrischer Formeln zu wiederholen, zu üben und zu festigen. Lösung von Problemen B7 aus dem Einheitlichen Staatsexamen.

In dieser Phase ist es ratsam, die Klasse in Gruppen aus starken Schülern (unabhängiges Arbeiten mit anschließender Prüfung) und schwachen Schülern, die mit dem Lehrer zusammenarbeiten, aufzuteilen.

Aufgabe für starke Studierende (vorab in gedruckter Form vorbereitet). Der Schwerpunkt liegt auf den Formeln Reduktion und Doppelwinkel nach dem Einheitlichen Staatsexamen 2011.

Ausdrücke vereinfachen (für starke Schüler):

Gleichzeitig arbeitet der Lehrer mit schwachen Schülern, indem er Aufgaben am Bildschirm unter dem Diktat der Schüler bespricht und löst.

Berechnung:

5) sin(270º - α) + cos (270º + α)

6)

Vereinfachen:

Es war Zeit, die Ergebnisse der Arbeit der starken Gruppe zu besprechen.

Die Antworten erscheinen auf dem Bildschirm, außerdem wird mit einer Videokamera die Arbeit von 5 verschiedenen Schülern angezeigt (jeweils eine Aufgabe).

Die schwache Gruppe sieht die Bedingung und Methode der Lösung. Diskussion und Analyse sind im Gange. Durch den Einsatz technischer Mittel geschieht dies schnell.

4. Einfache trigonometrische Gleichungen lösen. (30 Minuten.)

Ziel ist es, die Lösung der einfachsten trigonometrischen Gleichungen zu wiederholen, zu systematisieren und zu verallgemeinern und ihre Wurzeln aufzuschreiben. Lösung für Problem B3.

Jede trigonometrische Gleichung, egal wie wir sie lösen, führt zur einfachsten.

Bei der Bearbeitung der Aufgabe sollten die Studierenden darauf achten, die Wurzeln von Gleichungen für Sonderfälle aufzuschreiben und Gesamtansicht und über die Auswahl der Wurzeln in der letzten Gleichung.

Gleichungen lösen:

Notieren Sie als Antwort die kleinste positive Wurzel.

5. Selbstständiges Arbeiten (10 Min.)

Ziel ist es, die erworbenen Fähigkeiten zu testen, Probleme, Fehler und Möglichkeiten zu deren Beseitigung zu identifizieren.

Es werden mehrstufige Arbeiten nach Wahl des Studierenden angeboten.

Option „3“

1) Finden Sie den Wert des Ausdrucks

2) Vereinfachen Sie den Ausdruck 1 - sin 2 3α - cos 2 3α

3) Lösen Sie die Gleichung

Option für „4“

1) Finden Sie den Wert des Ausdrucks

2) Lösen Sie die Gleichung Notieren Sie die kleinste positive Wurzel Ihrer Antwort.

Option „5“

1) Finden Sie tanα if

2) Finden Sie die Wurzel der Gleichung Notieren Sie als Antwort die kleinste positive Wurzel.

6. Zusammenfassung der Lektion (5 Min.)

Der Lehrer fasst die Tatsache zusammen, dass sie während des Unterrichts trigonometrische Formeln wiederholt und vertieft und die einfachsten trigonometrischen Gleichungen gelöst haben.

Die Hausaufgaben werden (im Voraus in gedruckter Form vorbereitet) mit stichprobenartiger Kontrolle in der nächsten Unterrichtsstunde verteilt.

Gleichungen lösen:

9)

10) Geben Sie in Ihrer Antwort die kleinste positive Wurzel an.

Lektion 2

Thema: 11. Klasse (Vorbereitung auf das Einheitliche Staatsexamen)

Methoden zur Lösung trigonometrischer Gleichungen. Wurzelauswahl. (2 Stunden)

Ziele:

• Verallgemeinern und systematisieren Sie das Wissen über die Lösung trigonometrischer Gleichungen verschiedener Art.
• Förderung der Entwicklung des mathematischen Denkens der Schüler sowie der Fähigkeit zum Beobachten, Vergleichen, Verallgemeinern und Klassifizieren.
• Ermutigen Sie die Schüler, dabei Schwierigkeiten zu überwinden geistige Aktivität, zur Selbstkontrolle, Selbstbeobachtung der eigenen Aktivitäten.

Ausrüstung für den Unterricht: KRMu, Laptops für jeden Schüler.

Unterrichtsaufbau:

1. Organisatorischer Moment
2. Diskussion von d/z und self. Arbeit aus der letzten Lektion
3. Überblick über Methoden zur Lösung trigonometrischer Gleichungen.
4. Trigonometrische Gleichungen lösen
5. Auswahl von Wurzeln in trigonometrischen Gleichungen.
6. Selbstständige Arbeit.
7. Zusammenfassung der Lektion. Hausaufgaben.

1. Organisatorischer Moment (2 Min.)

Der Lehrer begrüßt das Publikum, gibt das Unterrichtsthema und den Arbeitsplan bekannt.

2. a) Analyse Hausaufgaben(5 Minuten.)

Ziel ist es, die Ausführung zu überprüfen. Ein Werk wird per Videokamera auf dem Bildschirm angezeigt, der Rest wird gezielt zur Lehrerkontrolle eingesammelt.

b) Analyse unabhängige Arbeit(3 Minuten.)

Ziel ist es, Fehler zu analysieren und Wege zu deren Überwindung aufzuzeigen.

Antworten und Lösungen werden auf dem Bildschirm angezeigt, die Studierenden erhalten ihre Aufgaben vorab ausgeteilt. Die Analyse geht schnell vonstatten.

3. Überprüfung der Methoden zur Lösung trigonometrischer Gleichungen (5 Min.)

Ziel ist es, Methoden zur Lösung trigonometrischer Gleichungen in Erinnerung zu rufen.

Fragen Sie die Schüler, welche Methoden zum Lösen trigonometrischer Gleichungen sie kennen. Betonen Sie, dass es sogenannte grundlegende (häufig verwendete) Methoden gibt:

• Variablenersatz,
• Faktorisierung,
• homogene Gleichungen,

und es gibt angewandte Methoden:

• Verwendung der Formeln zur Umrechnung einer Summe in ein Produkt und eines Produkts in eine Summe,
• nach den Formeln zur Reduzierung des Grades,
• universelle trigonometrische Substitution
• Einführung eines Hilfswinkels,
• Multiplikation mit einigen Trigonometrische Funktion.

Es sollte auch daran erinnert werden, dass eine Gleichung auf unterschiedliche Weise gelöst werden kann.

4. Trigonometrische Gleichungen lösen (30 Min.)

Ziel ist es, Kenntnisse und Fähigkeiten zu diesem Thema zu verallgemeinern und zu festigen, um sich auf die C1-Lösung des Einheitlichen Staatsexamens vorzubereiten.

Ich halte es für ratsam, die Gleichungen für jede Methode gemeinsam mit den Studierenden zu lösen.

Der Schüler diktiert die Lösung, der Lehrer schreibt sie auf das Tablet und der gesamte Vorgang wird auf dem Bildschirm angezeigt. Auf diese Weise können Sie zuvor behandeltes Material in Ihrem Gedächtnis schnell und effektiv abrufen.

Gleichungen lösen:

1) Ersetzen der Variablen 6cos 2 x + 5sinx - 7 = 0

2) Faktorisierung 3cos(x/3) + 4cos 2 (x/3) = 0

3) homogene Gleichungen sin 2 x + 3cos 2 x - 2sin2x = 0

4) Umwandeln der Summe in ein Produkt cos5x + cos7x = cos(π + 6x)

5) Umrechnung des Produkts in die Summe 2sinx sin2x + cos3x = 0

6) Reduzierung des Grades sin2x - sin 2 2x + sin 2 3x = 0,5

7) Universelle trigonometrische Substitution sinx + 5cosx + 5 = 0.

Bei der Lösung dieser Gleichung ist zu beachten, dass mit diese Methode führt zu einer Einengung des Definitionsbereiches, da Sinus und Cosinus durch tg(x/2) ersetzt werden. Daher müssen Sie vor dem Ausschreiben der Antwort prüfen, ob die Zahlen aus der Menge π + 2πn, n Z Pferde dieser Gleichung sind.

8) Einführung eines Hilfswinkels √3sinx + cosx - √2 = 0

9) Multiplikation mit einer trigonometrischen Funktion cosx cos2x cos4x = 1/8.

5. Auswahl der Wurzeln trigonometrischer Gleichungen (20 Min.)

Da es im harten Wettbewerb beim Hochschulzugang allein nicht ausreicht, den ersten Teil der Prüfung zu lösen, sollten sich die meisten Studierenden auf die Aufgaben des zweiten Teils (C1, C2, C3) konzentrieren.

Daher besteht das Ziel dieser Unterrichtsphase darin, sich an zuvor gelerntes Material zu erinnern und sich auf die Lösung der Aufgabe C1 aus dem Einheitlichen Staatsexamen 2011 vorzubereiten.

Existieren trigonometrische Gleichungen, bei dem beim Ausschreiben der Antwort Wurzeln ausgewählt werden müssen. Dies liegt an einigen Einschränkungen, zum Beispiel: Der Nenner des Bruchs ist ungleich Null, der Ausdruck unter der geraden Wurzel ist nicht negativ, der Ausdruck unter dem Logarithmuszeichen ist positiv usw.

Solche Gleichungen gelten als Gleichungen erhöhter Komplexität und in Version des Einheitlichen Staatsexamens liegen im zweiten Teil, nämlich C1.

Löse die Gleichung:

Ein Bruch ist dann gleich Null Mithilfe des Einheitskreises wählen wir die Wurzeln aus (siehe Abbildung 1).

Bild 1.

wir erhalten x = π + 2πn, n Z

Antwort: π + 2πn, n Z

Auf dem Bildschirm wird die Auswahl der Wurzeln in einem Kreis in einem Farbbild dargestellt.

Das Produkt ist gleich Null, wenn mindestens einer der Faktoren gleich Null ist und der Bogen seine Bedeutung nicht verliert. Dann

Mithilfe des Einheitskreises wählen wir die Wurzeln aus (siehe Abbildung 2).

Figur 2.

5)

Kommen wir zum System:

In der ersten Gleichung des Systems machen wir den Ersatz log 2 (sinx) = y, wir erhalten dann die Gleichung , kehren wir zum System zurück

Mithilfe des Einheitskreises wählen wir die Wurzeln aus (siehe Abbildung 5).

Abbildung 5.

6. Selbstständiges Arbeiten (15 Min.)

Ziel ist es, die Aufnahme des Materials zu festigen und zu überprüfen, Fehler zu identifizieren und Möglichkeiten zu deren Korrektur aufzuzeigen.

Das Werk wird den Studierenden in drei vorab in gedruckter Form erstellten Fassungen zur Auswahl angeboten.

Sie können Gleichungen auf beliebige Weise lösen.

Option „3“

Gleichungen lösen:

1) 2sin 2 x + sinx - 1 = 0

2) sin2x = √3cosx

Option für „4“

Gleichungen lösen:

1) cos2x = 11sinx - 5

2) (2sinx + √3)log 8 (cosx) = 0

Option „5“

Gleichungen lösen:

1) 2sinx - 3cosx = 2

2)

7. Zusammenfassung der Lektion, Hausaufgaben (5 Min.)

Der Lehrer fasst die Lektion zusammen und macht noch einmal darauf aufmerksam, dass eine trigonometrische Gleichung auf verschiedene Arten gelöst werden kann. Am meisten Der beste Weg für Leistung schnelle Ergebnisse Es ist diejenige, die ein bestimmter Schüler am besten lernt.

Bei der Prüfungsvorbereitung müssen Sie Formeln und Methoden zur Lösung von Gleichungen systematisch wiederholen.

Hausaufgaben (vorab in gedruckter Form vorbereitet) werden verteilt und die Methoden zur Lösung einiger Gleichungen werden kommentiert.

Gleichungen lösen:

1) cosx + cos5x = cos3x + cos7x

2) 5sin(x/6) - cos(x/3) + 3 = 0

3) 4sin 2 x + sin2x = 3

4) Sünde 2 x + Sünde 2 2x - Sünde 2 3x - Sünde 2 4x = 0

5) cos3x cos6x = cos4x cos7x

6) 4sinx - 6cosx = 1

7) 3sin2x + 4 cos2x = 5

8)cosx cos2x cos4x cos8x = (1/8)cos15x

9) (2sin 2 x - sinx)log 3 (2cos 2 x + cosx) = 0

10) (2cos 2 x - √3cosx)log 7 (-tgx) = 0

11)

Woronkowa Olga Iwanowna

MBOU „Sekundarschule“

Nr. 18"

Engels, Region Saratow.

Mathematiklehrer.

„Trigonometrische Ausdrücke und ihre Transformationen“

Einleitung………………………………………………………………………………......3

Kapitel 1 Aufgabenklassifizierung zur Verwendung von Transformationen trigonometrischer Ausdrücke ………………………….…………………...5

1.1. Rechenaufgaben Werte trigonometrischer Ausdrücke……….5

1.2.Aufgaben zur Vereinfachung trigonometrischer Ausdrücke.... 7

1.3. Aufgaben zur Konvertierung numerischer trigonometrischer Ausdrücke.....7

1.4 Gemischte Aufgaben…………………………………………………….....9

Kapitel 2. Methodische Aspekte der Organisation der abschließenden Wiederholung des Themas „Transformation trigonometrischer Ausdrücke“……………………………11

2.1 Thematische Wiederholung in der 10. Klasse………………………………………………………...11

Test 1……………………………………………………………………………..12

Test 2……………………………………………………………………………..13

Test 3……………………………………………………………………………..14

2.2 Abschlusswiederholung in der 11. Klasse………………………………………………………...15

Test 1……………………………………………………………………………..17

Test 2……………………………………………………………………………..17

Test 3……………………………………………………………………………..18

Fazit.……………………………………………………………………………......19

Referenzliste………………………………………………………..…….20

Einführung.

Im heutigen Umfeld lautet die wichtigste Frage: „Wie können wir dazu beitragen, einige der Wissenslücken der Schüler zu schließen und ihnen vorzubeugen?“ mögliche Fehler für das Einheitliche Staatsexamen? Um dieses Problem zu lösen, ist es notwendig, von den Studierenden nicht eine formale Assimilation des Programmmaterials, sondern dessen tiefes und bewusstes Verständnis, die Entwicklung der Geschwindigkeit mündlicher Berechnungen und Transformationen sowie die Entwicklung von Fähigkeiten zur Lösung einfacher Probleme „in“ zu erreichen der Verstand." Es ist notwendig, die Schüler davon zu überzeugen, dass dies nur möglich ist aktive Position Wenn Sie im Mathematikstudium praktische Fähigkeiten und Fertigkeiten erwerben und diese anwenden, können Sie mit echtem Erfolg rechnen. Es ist notwendig, jede Gelegenheit zur Vorbereitung auf das Einheitliche Staatsexamen zu nutzen, einschließlich Wahlfächern in den Klassen 10-11, und komplexe Aufgaben regelmäßig mit den Schülern zu besprechen und die rationalste Lösung für sie im Unterricht und in Zusatzstunden zu wählen.Positives Ergebnis inLösungsbereiche typische Aufgaben kann erreicht werden, wenn Mathematiklehrer durch die Schaffunggute Grundausbildung der Studierenden, nach neuen Wegen zur Lösung der sich uns eröffnenden Probleme suchen, aktiv experimentieren, moderne pädagogische Technologien, Methoden, Techniken anwenden, die günstige Voraussetzungen für eine effektive Selbstverwirklichung und Selbstbestimmung der Studierenden in neuen sozialen Verhältnissen schaffen Bedingungen.

Trigonometrie – Komponente Schulmathematikkurs. Gute Kenntnisse und ausgeprägte Fähigkeiten in der Trigonometrie zeugen von einer ausreichenden mathematischen Bildung und sind eine unabdingbare Voraussetzung für ein erfolgreiches Studium der Mathematik, Physik und verschiedener technischer Fachgebiete an einer Universität. Disziplinen.

Relevanz der Arbeit. Ein erheblicher Anteil der Schulabsolventen zeigt von Jahr zu Jahr eine sehr schlechte Vorbereitung in diesem wichtigen Teil der Mathematik, wie die Ergebnisse der vergangenen Jahre (Abschlussquote 2011 – 48,41 %, 2012 – 51,05 %) seit der Analyse des Bestehens belegen Das Einheitliche Staatsexamen hat gezeigt, dass Studierende bei der Bearbeitung von Aufgaben in diesem Abschnitt viele Fehler machen oder solche Aufgaben überhaupt nicht übernehmen. In Eins Im Staatsexamen finden sich Fragen zur Trigonometrie in fast drei Aufgabentypen. Dazu gehören die Lösung einfachster trigonometrischer Gleichungen in Aufgabe B5 und die Arbeit mit trigonometrischen Ausdrücken in Aufgabe B7 sowie das Studium trigonometrischer Funktionen in Aufgabe B14 sowie Aufgaben B12, in denen es beschreibende Formeln gibt physikalische Phänomene und trigonometrische Funktionen enthalten. Und das ist nur ein Teil der Aufgaben B! Es gibt aber auch beliebte trigonometrische Gleichungen mit Auswahl von C1-Wurzeln und „nicht so beliebte“ geometrische Aufgaben C2 und C4.

Ziel der Arbeit. Analysieren Sie den Stoff der Aufgaben B7 des Einheitlichen Staatsexamens, die sich mit Transformationen trigonometrischer Ausdrücke befassen, und klassifizieren Sie die Aufgaben nach der Form ihrer Präsentation in Tests.

Die Arbeit besteht aus zwei Kapiteln, Einleitung und Schluss. Die Einleitung betont die Relevanz der Arbeit. Das erste Kapitel bietet eine Klassifizierung von Aufgaben zur Verwendung von Transformationen trigonometrischer Ausdrücke im Test Aufgaben zum Einheitlichen Staatsexamen(2012).

Im zweiten Kapitel wird die Organisation der Wiederholung des Themas „Transformation trigonometrischer Ausdrücke“ in den Klassen 10 und 11 besprochen und Tests zu diesem Thema entwickelt.

Das Literaturverzeichnis umfasst 17 Quellen.

Kapitel 1. Klassifizierung von Aufgaben mithilfe von Transformationen trigonometrischer Ausdrücke.

Entsprechend dem Standard der weiterführenden (vollständigen) Bildung und den Anforderungen an den Vorbereitungsstand der Studierenden umfasst der Anforderungskodifikator Aufgaben zur Kenntnis der Grundlagen der Trigonometrie.

Das Erlernen der Grundlagen der Trigonometrie ist am effektivsten, wenn:

Es wird eine positive Motivation für die Schüler geschaffen, zuvor gelerntes Material zu wiederholen.

im Bildungsprozess wird ein personenorientierter Ansatz umgesetzt;

Es wird ein Aufgabensystem eingesetzt, das dabei hilft, das Wissen der Studierenden zu erweitern, zu vertiefen und zu systematisieren.

Es werden fortschrittliche pädagogische Technologien eingesetzt.

Nach der Analyse der Literatur und Internetressourcen zur Vorbereitung auf das Einheitliche Staatsexamen haben wir eine der möglichen Klassifizierungen der Aufgaben B7 (KIM Einheitliches Staatsexamen 2012-Trigonometrie) vorgeschlagen: RechenaufgabenWerte trigonometrischer Ausdrücke; Aufgaben fürKonvertieren numerischer trigonometrischer Ausdrücke; Aufgaben zur Konvertierung wörtlicher trigonometrischer Ausdrücke; gemischte Aufgaben.

1.1. Rechenaufgaben Bedeutungen trigonometrischer Ausdrücke.

Eine der häufigsten Arten einfacher Trigonometrieprobleme ist die Berechnung der Werte trigonometrischer Funktionen aus dem Wert einer von ihnen:

a) Verwendung der grundlegenden trigonometrischen Identität und ihre Konsequenzen.

Beispiel 1 . Finden Sie, ob
Und
.

Lösung.
,
,

Weil , Das
.

Antwort.

Beispiel 2 . Finden
, Wenn
Und .

Lösung.
,
,
.

Weil , Das
.

Antwort. .

b) Verwendung von Doppelwinkelformeln.

Beispiel 3 . Finden
, Wenn
.

Lösung. , .

Antwort.
.

Beispiel 4 . Finden Sie die Bedeutung des Ausdrucks
.

Lösung. .

Antwort.
.

1. Finden , Wenn
Und
. Antwort. -0,2

2. Finden , Wenn
Und
. Antwort. 0,4

3. Finden
, Wenn . Antwort. -12,884. Finden
, Wenn
. Antwort. -0,845. Finden Sie die Bedeutung des Ausdrucks:
. Antwort. 66. Finden Sie die Bedeutung des Ausdrucks
.Antwort. -19

1.2.Aufgaben zur Vereinfachung trigonometrischer Ausdrücke. Reduktionsformeln sollten von Studierenden gut verstanden werden, da sie in der Geometrie, Physik und anderen verwandten Disziplinen weitere Anwendung finden.

Beispiel 5 . Ausdrücke vereinfachen
.

Lösung. .

Antwort.
.

Aufgaben zur eigenständigen Lösung:

1. Den Ausdruck vereinfachen
. Antwort. 0,62. Finden
, Wenn
Und. Antwort. 10.563. Finden Sie die Bedeutung des Ausdrucks
, Wenn
. Antwort. 2

1.3. Aufgaben zur Konvertierung numerischer trigonometrischer Ausdrücke.

Beim Üben der Aufgaben zur Umrechnung numerischer trigonometrischer Ausdrücke sollten Sie auf Kenntnisse der Wertetabelle trigonometrischer Funktionen, der Paritätseigenschaften und der Periodizität trigonometrischer Funktionen achten.

a) Verwendung genaue Werte trigonometrische Funktionen für einige Winkel.

Beispiel 6 . Berechnung
.

Lösung.
.

Antwort.
.

b) Verwendung von Paritätseigenschaften trigonometrische Funktionen.

Beispiel 7 . Berechnung
.

Lösung. .

Antwort.

V) Verwendung von Periodizitätseigenschaftentrigonometrische Funktionen.

Beispiel 8 . Finden Sie die Bedeutung des Ausdrucks
.

Lösung. .

Antwort.
.

Aufgaben zur eigenständigen Lösung:

1. Finden Sie die Bedeutung des Ausdrucks
. Antwort. -40,52. Finden Sie die Bedeutung des Ausdrucks
. Antwort. 17

3. Finden Sie die Bedeutung des Ausdrucks
. Antwort. 6

. Antwort. -24
Antwort. -64

1.4 Aufgaben gemischter Art.

Das Zertifizierungstestformular weist sehr wichtige Funktionen auf, daher ist es wichtig, auf Aufgaben im Zusammenhang mit der gleichzeitigen Verwendung mehrerer trigonometrischer Formeln zu achten.

Beispiel 9. Finden
, Wenn
.

Lösung.
.

Antwort.
.

Beispiel 10 . Finden
, Wenn
Und
.

Lösung. .

Weil , Das
.

Antwort.
.

Beispiel 11. Finden
, Wenn .

Lösung. , ,
,
,
,
,
.

Antwort.

Beispiel 12. Berechnung
.

Lösung. .

Antwort.
.

Beispiel 13. Finden Sie die Bedeutung des Ausdrucks
, Wenn
.

Lösung. .

Antwort.
.

Aufgaben zur eigenständigen Lösung:

1. Finden
, Wenn
. Antwort. -1,75
2. Finden
, Wenn
. Antwort. 33. Finden
, Wenn .Antwort. 0,254. Finden Sie die Bedeutung des Ausdrucks
, Wenn
. Antwort. 0,35. Finden Sie die Bedeutung des Ausdrucks
, Wenn
. Antwort. 5

Kapitel 2. Methodische Aspekte der Organisation der abschließenden Wiederholung des Themas „Transformation trigonometrischer Ausdrücke“.

Eine der wichtigsten Fragen, die zur weiteren Verbesserung der Studienleistungen und zum Erwerb tiefer und dauerhafter Kenntnisse der Studierenden beitragen, ist die Wiederholung bereits behandelter Inhalte. Die Praxis zeigt, dass es in der 10. Klasse sinnvoller ist, thematische Wiederholungen zu organisieren; in der 11. Klasse - Abschlusswiederholung.

2.1. Thematische Überarbeitung in der 10. Klasse.

Insbesondere bei der Arbeit an mathematischem Material sehr wichtig erwirbt die Wiederholung jedes abgeschlossenen Themas oder gesamten Abschnitts des Kurses.

Bei der thematischen Wiederholung wird das Wissen der Studierenden zu einem Thema im Endstadium seiner Bearbeitung oder nach einer gewissen Pause systematisiert.

Für die thematische Wiederholung sind Sonderstunden vorgesehen, in denen der Stoff eines bestimmten Themas konzentriert und verallgemeinert wird.

Die Wiederholung im Unterricht erfolgt durch Gespräche unter umfassender Beteiligung der Schüler an diesem Gespräch. Danach erhalten die Studierenden die Aufgabe, ein bestimmtes Thema zu wiederholen und werden darauf hingewiesen, dass eine Testarbeit durchgeführt wird.

Ein Test zu einem Thema sollte alle Hauptfragen umfassen. Nach Abschluss der Arbeit werden charakteristische Fehler analysiert und Wiederholungen zur Beseitigung dieser Fehler organisiert.

Für thematische Wiederholungsstunden bieten wir entwickelte Kurse an Beurteilungsarbeiten in Form von Tests zum Thema „Transformation trigonometrischer Ausdrücke“.

Test Nr. 1

Test Nr. 2

Test Nr. 3

Antworttabelle

Prüfen

2.2. Abschlussprüfung in der 11. Klasse.

Die abschließende Wiederholung erfolgt in der letzten Phase des Studiums der Hauptthemen des Mathematikstudiums und steht in logischem Zusammenhang mit dem Studium der Lehrmaterialien für diesen Abschnitt oder das gesamte Studium.

Die abschließende Wiederholung des Lehrstoffs verfolgt folgende Ziele:

1. Aktivierung des gesamten Materials Trainingskurs um seine logische Struktur zu klären und ein System innerhalb der Subjekt- und Intersubjektverbindungen aufzubauen.

2. Vertiefung und, wenn möglich, Erweiterung des Wissens der Studierenden zu den Hauptthemen der Lehrveranstaltung im Wiederholungsprozess.

Im Rahmen einer verpflichtenden Mathematikprüfung für alle Absolventen zwingt die sukzessive Einführung des Einheitlichen Staatsexamens die Lehrkräfte zu einem neuen Ansatz bei der Vorbereitung und Durchführung des Unterrichts unter Berücksichtigung der Notwendigkeit, sicherzustellen, dass alle Schüler den Unterrichtsstoff auf einem grundlegenden Niveau beherrschen Niveau sowie die Möglichkeit für motivierte Studierende, die an einer hohen Punktzahl für die Zulassung zu einer Universität interessiert sind, dynamische Fortschritte bei der Beherrschung des Stoffes auf fortgeschrittenem und hohem Niveau.

Im letzten Wiederholungsunterricht können Sie sich mit folgenden Aufgaben befassen:

Beispiel 1 . Berechnen Sie den Wert des Ausdrucks.Lösung. =
= =
=
=
=
=0,5. Antwort. 0,5. Beispiel 2. Geben Sie den größten ganzzahligen Wert an, den der Ausdruck akzeptieren kann
.

Lösung. Als
kann jeden Wert annehmen, der zum Segment [–1; 1] also
nimmt einen beliebigen Wert des Segments an [–0,4; 0,4], also . Der Ausdruck hat einen ganzzahligen Wert – die Zahl 4.

Antwort: 4 Beispiel 3 . Den Ausdruck vereinfachen
.

Lösung: Verwenden wir die Formel zum Faktorisieren der Würfelsumme: . Wir haben

Wir haben:
.

Antwort 1

Beispiel 4. Berechnung
.

Lösung. .

Antwort: 0,28

Für den abschließenden Wiederholungsunterricht bieten wir ausgereifte Tests zum Thema „Transformation trigonometrischer Ausdrücke“ an.

Geben Sie die größte Ganzzahl ein, die 1 nicht überschreitet

Abschluss.

Nach dem Studium der einschlägigen methodischen Literatur zu diesem Thema können wir den Schluss ziehen, dass die Fähigkeit und Fertigkeit zur Lösung von Problemen im Zusammenhang mit trigonometrischen Transformationen im schulischen Mathematikunterricht sehr wichtig ist.

Im Zuge der durchgeführten Arbeiten wurde eine Aufgabenklassifizierung B7 vorgenommen. Berücksichtigt werden die trigonometrischen Formeln, die 2012 in KMGs am häufigsten verwendet wurden. Beispiele für Aufgaben mit Lösungen werden gegeben. Zur Organisation der Wiederholung und Systematisierung des Wissens zur Vorbereitung auf das Einheitliche Staatsexamen wurden differenzierte Tests entwickelt.

Es empfiehlt sich, die begonnene Arbeit durch Nachdenken fortzusetzen Lösen der einfachsten trigonometrischen Gleichungen in Aufgabe B5, Studium trigonometrischer Funktionen in Aufgabe B14, Aufgaben B12, die Formeln enthalten, die physikalische Phänomene beschreiben und trigonometrische Funktionen enthalten.

Abschließend möchte ich darauf hinweisen, dass die Wirksamkeit des Bestehens des Einheitlichen Staatsexamens maßgeblich davon abhängt, wie effektiv der Vorbereitungsprozess auf allen Bildungsebenen und mit allen Kategorien von Studierenden organisiert ist. Und wenn es uns gelingt, den Schülern Selbstständigkeit, Verantwortungsbewusstsein und die Bereitschaft zum Weiterlernen ein Leben lang zu vermitteln, dann erfüllen wir nicht nur die Ordnung von Staat und Gesellschaft, sondern stärken auch unser eigenes Selbstwertgefühl.

Die Wiederholung des Unterrichtsstoffs erfordert den Lehrer kreative Arbeit. Er muss einen klaren Zusammenhang zwischen den Wiederholungsarten herstellen und ein durchdachtes Wiederholungssystem implementieren. Die Beherrschung der Kunst, Wiederholungen zu organisieren, ist die Aufgabe des Lehrers. Die Stärke des Wissens der Studierenden hängt weitgehend von seiner Lösung ab.

Literatur.

Vygodsky Ya.Ya., Handbuch der Elementarmathematik. -M.: Nauka, 1970.

Probleme mit erhöhtem Schwierigkeitsgrad in Algebra und Grundanalyse: Lehrbuch für die Klassen 10-11 weiterführende Schule/ B.M. Ivlev, A.M. Abramov, Yu.P. Dudnitsyn, S.I. Schwartzburd. – M.: Bildung, 1990.

Anwendung grundlegender trigonometrischer Formeln zur Transformation von Ausdrücken (10. Klasse) //Festival pädagogische Ideen. 2012-2013.

Korjanow A.G. , Prokofjew A.A. Wir bereiten gute und hervorragende Studierende auf das Einheitliche Staatsexamen vor. - M.: Pädagogische Universität „Erster September“, 2012.- 103 S.

Kuznetsova E.N. Vereinfachung trigonometrischer Ausdrücke. Trigonometrische Gleichungen lösen verschiedene Methoden(Vorbereitung auf das Einheitliche Staatsexamen). 11. Klasse. 2012-2013.

Kulanin E. D. 3000 Wettbewerbsprobleme in der Mathematik. 4. Auflage, richtig. und zusätzlich – M.: Rolf, 2000.

Mordkovich A.G. Methodische Probleme des Trigonometriestudiums an weiterführenden Schulen // Mathematik in der Schule. 2002. Nr. 6.

Pichurin L.F. Über Trigonometrie und nicht nur darüber: -M. Aufklärung, 1985

Reshetnikov N.N. Trigonometrie in der Schule: -M. : Pädagogische Universität „Erster September“, 2006, lx 1.

Shabunin M. I., Prokofjew A. A. Mathematik. Algebra. Anfänge der mathematischen Analyse. Profilniveau: Lehrbuch für Klasse 10 - M.: BINOM. Wissenslabor, 2007.

Bildungsportal zur Vorbereitung auf das Einheitliche Staatsexamen.

Vorbereitung auf das Einheitliche Staatsexamen in Mathematik „Oh, diese Trigonometrie! http://festival.1september.ru/articles/621971/

Projekt „Mathe? Einfach!!!“ http://www.resolventa.ru/

Die Videolektion „Trigonometrische Ausdrücke vereinfachen“ soll die Fähigkeiten der Schüler bei der Lösung trigonometrischer Probleme mithilfe grundlegender trigonometrischer Identitäten entwickeln. In der Videolektion werden Arten trigonometrischer Identitäten und Beispiele für die Lösung von Problemen mit ihnen besprochen. Durch den Einsatz visueller Hilfsmittel ist es für den Lehrer einfacher, die Unterrichtsziele zu erreichen. Die anschauliche Präsentation des Materials fördert das Auswendiglernen wichtige Punkte. Durch den Einsatz von Animationseffekten und Voice-Over können Sie den Lehrer bei der Erläuterung des Stoffes vollständig ersetzen. Somit kann der Lehrer durch den Einsatz dieser visuellen Hilfe im Mathematikunterricht die Effektivität des Unterrichts steigern.

Zu Beginn der Videolektion wird das Thema bekannt gegeben. Dann erinnern wir uns an die zuvor untersuchten trigonometrischen Identitäten. Der Bildschirm zeigt die Gleichungen sin 2 t+cos 2 t=1, tg t=sin t/cos t an, wobei t≠π/2+πk für kϵZ, ctg t=cos t/sin t, korrekt für t≠πk, wobei kϵZ, tg t· ctg t=1, für t≠πk/2, wobei kϵZ, die grundlegenden trigonometrischen Identitäten genannt. Es wird darauf hingewiesen, dass diese Identitäten häufig zur Lösung von Problemen verwendet werden, bei denen es notwendig ist, Gleichheit zu beweisen oder einen Ausdruck zu vereinfachen.

Im Folgenden betrachten wir Beispiele für die Anwendung dieser Identitäten bei der Lösung von Problemen. Zunächst wird vorgeschlagen, die Lösung von Problemen der Vereinfachung von Ausdrücken in Betracht zu ziehen. In Beispiel 1 ist es notwendig, den Ausdruck cos 2 t- cos 4 t+ sin 4 t zu vereinfachen. Um das Beispiel zu lösen, nehmen Sie zunächst den gemeinsamen Faktor cos 2 t aus der Klammer. Als Ergebnis dieser Transformation in Klammern erhält man den Ausdruck 1-cos 2 t, dessen Wert aus der Hauptidentität der Trigonometrie gleich sin 2 t ist. Nach der Transformation des Ausdrucks ist es offensichtlich, dass ein weiterer gemeinsamer Faktor sin 2 t aus den Klammern herausgenommen werden kann, wonach der Ausdruck die Form annimmt sin 2 t(sin 2 t+cos 2 t). Aus derselben Grundidentität leiten wir den Wert des Ausdrucks in Klammern gleich 1 ab. Durch Vereinfachung erhalten wir cos 2 t- cos 4 t+ sin 4 t= sin 2 t.

In Beispiel 2 muss der Ausdruck cost/(1- sint)+ cost/(1+ sint) vereinfacht werden. Da die Zähler beider Brüche den Ausdruck Kosten enthalten, kann dieser als gemeinsamer Faktor aus Klammern genommen werden. Dann werden die Brüche in Klammern durch Multiplikation von (1- sint)(1+ sint) auf einen gemeinsamen Nenner gebracht. Nach dem Zusammenführen ähnlicher Terme bleibt der Zähler 2 und der Nenner 1 - sin 2 t. Auf der rechten Seite des Bildschirms wird an die grundlegende trigonometrische Identität sin 2 t+cos 2 t=1 erinnert. Damit ermitteln wir den Nenner des Bruchs cos 2 t. Nachdem wir den Bruch reduziert haben, erhalten wir eine vereinfachte Form des Ausdrucks cost/(1- sint)+ cost/(1+ sint)=2/cost.

Als nächstes betrachten wir Beispiele für Identitätsbeweise, die das erworbene Wissen über die grundlegenden Identitäten der Trigonometrie nutzen. In Beispiel 3 muss die Identität (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t nachgewiesen werden. Auf der rechten Seite des Bildschirms werden drei Identitäten angezeigt, die für den Beweis benötigt werden: tg t·ctg t=1, ctg t=cos t/sin t und tg t=sin t/cos t mit Einschränkungen. Um die Identität zu beweisen, werden zunächst die Klammern geöffnet und anschließend ein Produkt gebildet, das den Ausdruck der trigonometrischen Hauptidentität tg t·ctg t=1 widerspiegelt. Dann wird gemäß der Identität aus der Definition des Kotangens ctg 2 t transformiert. Als Ergebnis der Transformationen erhält man den Ausdruck 1-cos 2 t. Anhand der Hauptidentität finden wir die Bedeutung des Ausdrucks. Somit wurde bewiesen, dass (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t.

In Beispiel 4 müssen Sie den Wert des Ausdrucks tg 2 t+ctg 2 t ermitteln, wenn tg t+ctg t=6. Um den Ausdruck zu berechnen, quadrieren Sie zunächst die rechte und linke Seite der Gleichung (tg t+ctg t) 2 =6 2. Die abgekürzte Multiplikationsformel wird auf der rechten Seite des Bildschirms angezeigt. Nach dem Öffnen der Klammern auf der linken Seite des Ausdrucks wird die Summe tg 2 t+2· tg t·ctg t+ctg 2 t gebildet, für deren Transformation Sie eine der trigonometrischen Identitäten tg t·ctg t=1 anwenden können , dessen Form auf der rechten Seite des Bildschirms angezeigt wird. Nach der Transformation erhält man die Gleichung tg 2 t+ctg 2 t=34. Die linke Seite der Gleichheit stimmt mit der Bedingung des Problems überein, daher lautet die Antwort 34. Das Problem ist gelöst.

Die Videolektion „Vereinfachung trigonometrischer Ausdrücke“ wird für den Einsatz im traditionellen Mathematikunterricht in der Schule empfohlen. Das Material wird auch für Lehrer nützlich sein, die Fernunterricht anbieten. Um Fähigkeiten zur Lösung trigonometrischer Probleme zu entwickeln.

TEXTDEKODIERUNG:

„Vereinfachung trigonometrischer Ausdrücke.“

Gleichheiten

1) sin 2 t + cos 2 t = 1 (Sinusquadrat te plus Kosinusquadrat te gleich eins)

2)tgt =, für t ≠ + πk, kϵZ (Tangens te ist gleich dem Verhältnis von Sinus te zu Kosinus te mit te ungleich pi um zwei plus pi ka, ka gehört zu zet)

3)ctgt = , für t ≠ πk, kϵZ (Kotangens te ist gleich dem Verhältnis von Kosinus te zu Sinus te mit te ungleich pi ka, ka gehört zu zet).

4) tgt ∙ ctgt = 1 für t ≠ , kϵZ (das Produkt von Tangente te und Kotangente te ist gleich eins, wenn te nicht gleich dem Peak ka ist, dividiert durch zwei, ka gehört zu zet)

werden grundlegende trigonometrische Identitäten genannt.

Sie werden häufig zur Vereinfachung und zum Beweis trigonometrischer Ausdrücke verwendet.

Schauen wir uns Beispiele für die Verwendung dieser Formeln zur Vereinfachung trigonometrischer Ausdrücke an.

BEISPIEL 1. Vereinfachen Sie den Ausdruck: cos 2 t - cos 4 t + sin 4 t. (Ausdruck a Kosinus zum Quadrat te minus Kosinus vierten Grades te plus Sinus vierten Grades te).

Lösung. cos 2 t - cos 4 t + sin 4 t = cos 2 t∙ (1 - cos 2 t) + sin 4 t =cos 2 t ∙ sin 2 t + sin 4 t = sin 2 t (cos 2 t + sin 2 t) = Sünde 2 t 1= Sünde 2 t

(Wir nehmen den gemeinsamen Faktor Cosinusquadrat te heraus, in Klammern erhalten wir die Differenz zwischen Eins und dem quadrierten Cosinus te, der gleich dem quadrierten Sinus te durch die erste Identität ist. Wir erhalten die Summe des Sinus te der vierten Potenz von Produkt Kosinusquadrat te und Sinusquadrat te. Wir nehmen den gemeinsamen Faktor Sinusquadrat te außerhalb der Klammern heraus, in Klammern erhalten wir die Summe der Quadrate von Kosinus und Sinus, die gemäß der grundlegenden trigonometrischen Identität gleich 1 ist . Als Ergebnis erhalten wir das Quadrat des Sinus te).

BEISPIEL 2. Vereinfachen Sie den Ausdruck: + .

(Ausdruck sei die Summe zweier Brüche im Zähler des ersten Kosinus te im Nenner eins minus Sinus te, im Zähler des zweiten Kosinus te im Nenner des zweiten eins plus Sinus te).

(Nehmen wir den gemeinsamen Faktor Kosinus te aus Klammern und bringen ihn in Klammern auf einen gemeinsamen Nenner, der das Produkt von eins minus Sinus te mal eins plus Sinus te ist.

Im Zähler erhalten wir: eins plus Sinus te plus eins minus Sinus te, wir geben ähnliche Einsen an, der Zähler ist gleich zwei, nachdem wir ähnliche Einsen gebracht haben.

Im Nenner können Sie die abgekürzte Multiplikationsformel (Quadratdifferenz) anwenden und erhalten die Differenz zwischen Eins und dem Quadrat des Sinus te, der gemäß der grundlegenden trigonometrischen Identität

gleich dem Quadrat des Kosinus te. Nach der Reduktion durch Kosinus te erhalten wir die endgültige Antwort: zwei dividiert durch Kosinus te).

Schauen wir uns Beispiele für die Verwendung dieser Formeln beim Beweis trigonometrischer Ausdrücke an.

BEISPIEL 3. Beweisen Sie die Identität (tg 2 t - sin 2 t) ∙ ctg 2 t = sin 2 t (das Produkt der Differenz zwischen den Quadraten des Tangens te und des Sinus te durch das Quadrat des Kotangens te ist gleich dem Quadrat von sinus te).

Nachweisen.

Lassen Sie uns die linke Seite der Gleichheit transformieren:

(tg 2 t - sin 2 t) ∙ ctg 2 t = tg 2 t ∙ ctg 2 t - sin 2 t ∙ ctg 2 t = 1 - sin 2 t ∙ ctg 2 t =1 - sin 2 t ∙ = 1 - cos 2 t = sin 2 t

(Öffnen wir die Klammern; aus der zuvor erhaltenen Beziehung ist bekannt, dass das Produkt der Quadrate von Tangens te und Kotangens te gleich eins ist. Erinnern wir uns, dass der Kotangens te gleich dem Verhältnis von Kosinus te zu Sinus te ist, was bedeutet, dass das Kotangensquadrat das Verhältnis des Kosinusquadrats te zum Sinusquadrat te ist.

Nach der Reduktion um das Sinusquadrat te erhalten wir die Differenz zwischen Eins und dem Kosinusquadrat te, die gleich dem Sinusquadrat te ist. Q.E.D.

BEISPIEL 4. Ermitteln Sie den Wert des Ausdrucks tg 2 t + ctg 2 t, wenn tgt + ctgt = 6.

(die Summe der Quadrate von Tangente te und Kotangens te, wenn die Summe von Tangente und Kotangens sechs beträgt).

Lösung. (tgt + ctgt) 2 = 6 2

tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36

tg 2 t + 2 + ctg 2 t = 36

tg 2 t + ctg 2 t = 36-2

tg 2 t + ctg 2 t = 34

Quadrieren wir beide Seiten der ursprünglichen Gleichheit:

(tgt + ctgt) 2 = 6 2 (das Quadrat der Summe aus Tangens te und Kotangens te ist gleich sechs zum Quadrat). Erinnern wir uns an die Formel für die abgekürzte Multiplikation: Das Quadrat der Summe zweier Größen ist gleich dem Quadrat der ersten plus dem doppelten Produkt der ersten mit der zweiten plus dem Quadrat der zweiten. (a+b) 2 =a 2 +2ab+b 2 Wir erhalten tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 (Tangens zum Quadrat te plus das Doppelte des Produkts aus Tangens te mal Kotangens te plus Kotangens zum Quadrat te gleich sechsunddreißig) .

Da das Produkt aus Tangente te und Kotangens te gleich eins ist, dann ist tg 2 t + 2 + ctg 2 t = 36 (die Summe der Quadrate aus Tangente te und Kotangens te und zwei ist gleich sechsunddreißig),

Abschnitte: Mathematik

Klasse: 11

Lektion 1

Thema: 11. Klasse (Vorbereitung auf das Einheitliche Staatsexamen)

Vereinfachung trigonometrischer Ausdrücke.

Einfache trigonometrische Gleichungen lösen. (2 Stunden)

Ziele:

• Systematisieren, verallgemeinern und erweitern Sie die Kenntnisse und Fähigkeiten der Schüler im Zusammenhang mit der Verwendung trigonometrischer Formeln und der Lösung einfacher trigonometrischer Gleichungen.

Ausrüstung für den Unterricht:

Unterrichtsaufbau:

1. Organisatorischer Moment
2. Testen auf Laptops. Die Diskussion der Ergebnisse.
3. Vereinfachung trigonometrischer Ausdrücke
4. Einfache trigonometrische Gleichungen lösen
5. Selbstständige Arbeit.
6. Zusammenfassung der Lektion. Erläuterung der Hausaufgabe.

1. Organisatorischer Moment. (2 Minuten.)

Der Lehrer begrüßt das Publikum, verkündet das Thema der Unterrichtsstunde, erinnert daran, dass ihm zuvor die Aufgabe übertragen wurde, trigonometrische Formeln zu wiederholen, und bereitet die Schüler auf die Prüfung vor.

2. Testen. (15 Min. + 3 Min. Diskussion)

Ziel ist es, das Wissen über trigonometrische Formeln und die Fähigkeit, diese anzuwenden, zu testen. Jeder Schüler hat auf seinem Schreibtisch einen Laptop mit einer Version des Tests.

Es kann eine beliebige Anzahl von Optionen geben, ich werde ein Beispiel für eine davon geben:

Ich wähle.

Ausdrücke vereinfachen:

a) grundlegende trigonometrische Identitäten

1. Sünde 2 3y + cos 2 3y + 1;

b) Additionsformeln

3. sin5x - sin3x;

c) Umwandeln eines Produkts in eine Summe

6. 2sin8y cos3y;

d) Doppelwinkelformeln

7. 2sin5x cos5x;

e) Formeln für Halbwinkel

f) Dreifachwinkelformeln

g) universelle Substitution

h) Reduzierung des Abschlusses

16. cos 2 (3x/7);

Die Schüler sehen ihre Antworten auf dem Laptop neben jeder Formel.

Die Arbeit wird sofort vom Computer überprüft. Die Ergebnisse werden auf einem großen Bildschirm angezeigt, damit jeder sie sehen kann.

Außerdem werden nach Abschluss der Arbeit die richtigen Antworten auf den Laptops der Schüler angezeigt. Jeder Schüler sieht, wo der Fehler gemacht wurde und welche Formeln er wiederholen muss.

3. Vereinfachung trigonometrischer Ausdrücke. (25 Min.)

Ziel ist es, die Anwendung grundlegender trigonometrischer Formeln zu wiederholen, zu üben und zu festigen. Lösung von Problemen B7 aus dem Einheitlichen Staatsexamen.

In dieser Phase ist es ratsam, die Klasse in Gruppen aus starken Schülern (unabhängiges Arbeiten mit anschließender Prüfung) und schwachen Schülern, die mit dem Lehrer zusammenarbeiten, aufzuteilen.

Aufgabe für starke Studierende (vorab in gedruckter Form vorbereitet). Der Schwerpunkt liegt auf den Formeln Reduktion und Doppelwinkel nach dem Einheitlichen Staatsexamen 2011.

Ausdrücke vereinfachen (für starke Schüler):

Gleichzeitig arbeitet der Lehrer mit schwachen Schülern, indem er Aufgaben am Bildschirm unter dem Diktat der Schüler bespricht und löst.

Berechnung:

5) sin(270º - α) + cos (270º + α)

6)

Vereinfachen:

Es war Zeit, die Ergebnisse der Arbeit der starken Gruppe zu besprechen.

Die Antworten erscheinen auf dem Bildschirm, außerdem wird mit einer Videokamera die Arbeit von 5 verschiedenen Schülern angezeigt (jeweils eine Aufgabe).

Die schwache Gruppe sieht die Bedingung und Methode der Lösung. Diskussion und Analyse sind im Gange. Durch den Einsatz technischer Mittel geschieht dies schnell.

4. Einfache trigonometrische Gleichungen lösen. (30 Minuten.)

Ziel ist es, die Lösung der einfachsten trigonometrischen Gleichungen zu wiederholen, zu systematisieren und zu verallgemeinern und ihre Wurzeln aufzuschreiben. Lösung für Problem B3.

Jede trigonometrische Gleichung, egal wie wir sie lösen, führt zur einfachsten.

Beim Lösen der Aufgabe sollten die Schüler darauf achten, die Wurzeln von Gleichungen in Sonderfällen und allgemeiner Form zu schreiben und die Wurzeln in der letzten Gleichung auszuwählen.

Gleichungen lösen:

Notieren Sie als Antwort die kleinste positive Wurzel.

5. Selbstständiges Arbeiten (10 Min.)

Ziel ist es, die erworbenen Fähigkeiten zu testen, Probleme, Fehler und Möglichkeiten zu deren Beseitigung zu identifizieren.

Es werden mehrstufige Arbeiten nach Wahl des Studierenden angeboten.

Option „3“

1) Finden Sie den Wert des Ausdrucks

2) Vereinfachen Sie den Ausdruck 1 - sin 2 3α - cos 2 3α

3) Lösen Sie die Gleichung

Option für „4“

1) Finden Sie den Wert des Ausdrucks

2) Lösen Sie die Gleichung Notieren Sie die kleinste positive Wurzel Ihrer Antwort.

Option „5“

1) Finden Sie tanα if

2) Finden Sie die Wurzel der Gleichung Notieren Sie als Antwort die kleinste positive Wurzel.

6. Zusammenfassung der Lektion (5 Min.)

Der Lehrer fasst die Tatsache zusammen, dass sie während des Unterrichts trigonometrische Formeln wiederholt und vertieft und die einfachsten trigonometrischen Gleichungen gelöst haben.

Die Hausaufgaben werden (im Voraus in gedruckter Form vorbereitet) mit stichprobenartiger Kontrolle in der nächsten Unterrichtsstunde verteilt.

Gleichungen lösen:

9)

10) Geben Sie in Ihrer Antwort die kleinste positive Wurzel an.

Lektion 2

Thema: 11. Klasse (Vorbereitung auf das Einheitliche Staatsexamen)

Methoden zur Lösung trigonometrischer Gleichungen. Wurzelauswahl. (2 Stunden)

Ziele:

• Verallgemeinern und systematisieren Sie das Wissen über die Lösung trigonometrischer Gleichungen verschiedener Art.
• Förderung der Entwicklung des mathematischen Denkens der Schüler sowie der Fähigkeit zum Beobachten, Vergleichen, Verallgemeinern und Klassifizieren.
• Ermutigen Sie die Schüler, Schwierigkeiten im Prozess der geistigen Aktivität zu überwinden, sich selbst zu kontrollieren und ihre Aktivitäten selbst zu prüfen.

Ausrüstung für den Unterricht: KRMu, Laptops für jeden Schüler.

Unterrichtsaufbau:

1. Organisatorischer Moment
2. Diskussion von d/z und self. Arbeit aus der letzten Lektion
3. Überblick über Methoden zur Lösung trigonometrischer Gleichungen.
4. Trigonometrische Gleichungen lösen
5. Auswahl von Wurzeln in trigonometrischen Gleichungen.
6. Selbstständige Arbeit.
7. Zusammenfassung der Lektion. Hausaufgaben.

1. Organisatorischer Moment (2 Min.)

Der Lehrer begrüßt das Publikum, gibt das Unterrichtsthema und den Arbeitsplan bekannt.

2. a) Analyse der Hausaufgaben (5 Min.)

Ziel ist es, die Ausführung zu überprüfen. Ein Werk wird per Videokamera auf dem Bildschirm angezeigt, der Rest wird gezielt zur Lehrerkontrolle eingesammelt.

b) Analyse der selbstständigen Arbeit (3 Min.)

Ziel ist es, Fehler zu analysieren und Wege zu deren Überwindung aufzuzeigen.

Antworten und Lösungen werden auf dem Bildschirm angezeigt, die Studierenden erhalten ihre Aufgaben vorab ausgeteilt. Die Analyse geht schnell vonstatten.

3. Überprüfung der Methoden zur Lösung trigonometrischer Gleichungen (5 Min.)

Ziel ist es, Methoden zur Lösung trigonometrischer Gleichungen in Erinnerung zu rufen.

Fragen Sie die Schüler, welche Methoden zum Lösen trigonometrischer Gleichungen sie kennen. Betonen Sie, dass es sogenannte grundlegende (häufig verwendete) Methoden gibt:

• Variablenersatz,
• Faktorisierung,
• homogene Gleichungen,

und es gibt angewandte Methoden:

• Verwendung der Formeln zur Umrechnung einer Summe in ein Produkt und eines Produkts in eine Summe,
• nach den Formeln zur Reduzierung des Grades,
• universelle trigonometrische Substitution
• Einführung eines Hilfswinkels,
• Multiplikation mit einer trigonometrischen Funktion.

Es sollte auch daran erinnert werden, dass eine Gleichung auf unterschiedliche Weise gelöst werden kann.

4. Trigonometrische Gleichungen lösen (30 Min.)

Ziel ist es, Kenntnisse und Fähigkeiten zu diesem Thema zu verallgemeinern und zu festigen, um sich auf die C1-Lösung des Einheitlichen Staatsexamens vorzubereiten.

Ich halte es für ratsam, die Gleichungen für jede Methode gemeinsam mit den Studierenden zu lösen.

Der Schüler diktiert die Lösung, der Lehrer schreibt sie auf das Tablet und der gesamte Vorgang wird auf dem Bildschirm angezeigt. Auf diese Weise können Sie zuvor behandeltes Material in Ihrem Gedächtnis schnell und effektiv abrufen.

Gleichungen lösen:

1) Ersetzen der Variablen 6cos 2 x + 5sinx - 7 = 0

2) Faktorisierung 3cos(x/3) + 4cos 2 (x/3) = 0

3) homogene Gleichungen sin 2 x + 3cos 2 x - 2sin2x = 0

4) Umwandeln der Summe in ein Produkt cos5x + cos7x = cos(π + 6x)

5) Umrechnung des Produkts in die Summe 2sinx sin2x + cos3x = 0

6) Reduzierung des Grades sin2x - sin 2 2x + sin 2 3x = 0,5

7) Universelle trigonometrische Substitution sinx + 5cosx + 5 = 0.

Bei der Lösung dieser Gleichung ist zu beachten, dass die Verwendung dieser Methode zu einer Einengung des Definitionsbereichs führt, da Sinus und Cosinus durch tg(x/2) ersetzt werden. Daher müssen Sie vor dem Ausschreiben der Antwort prüfen, ob die Zahlen aus der Menge π + 2πn, n Z Pferde dieser Gleichung sind.

8) Einführung eines Hilfswinkels √3sinx + cosx - √2 = 0

9) Multiplikation mit einer trigonometrischen Funktion cosx cos2x cos4x = 1/8.

5. Auswahl der Wurzeln trigonometrischer Gleichungen (20 Min.)

Da es im harten Wettbewerb beim Hochschulzugang allein nicht ausreicht, den ersten Teil der Prüfung zu lösen, sollten sich die meisten Studierenden auf die Aufgaben des zweiten Teils (C1, C2, C3) konzentrieren.

Daher besteht das Ziel dieser Unterrichtsphase darin, sich an zuvor gelerntes Material zu erinnern und sich auf die Lösung der Aufgabe C1 aus dem Einheitlichen Staatsexamen 2011 vorzubereiten.

Es gibt trigonometrische Gleichungen, bei denen Sie beim Ausschreiben der Antwort Wurzeln auswählen müssen. Dies liegt an einigen Einschränkungen, zum Beispiel: Der Nenner des Bruchs ist ungleich Null, der Ausdruck unter der geraden Wurzel ist nicht negativ, der Ausdruck unter dem Logarithmuszeichen ist positiv usw.

Solche Gleichungen gelten als Gleichungen mit erhöhter Komplexität und sind in der Version des Unified State Exam im zweiten Teil, nämlich C1, zu finden.

Löse die Gleichung:

Ein Bruch ist dann gleich Null Mithilfe des Einheitskreises wählen wir die Wurzeln aus (siehe Abbildung 1).

Bild 1.

wir erhalten x = π + 2πn, n Z

Antwort: π + 2πn, n Z

Auf dem Bildschirm wird die Auswahl der Wurzeln in einem Kreis in einem Farbbild dargestellt.

Das Produkt ist gleich Null, wenn mindestens einer der Faktoren gleich Null ist und der Bogen seine Bedeutung nicht verliert. Dann

Mithilfe des Einheitskreises wählen wir die Wurzeln aus (siehe Abbildung 2).