Eigenschaften von Sinus. Einfache trigonometrische Gleichungen lösen
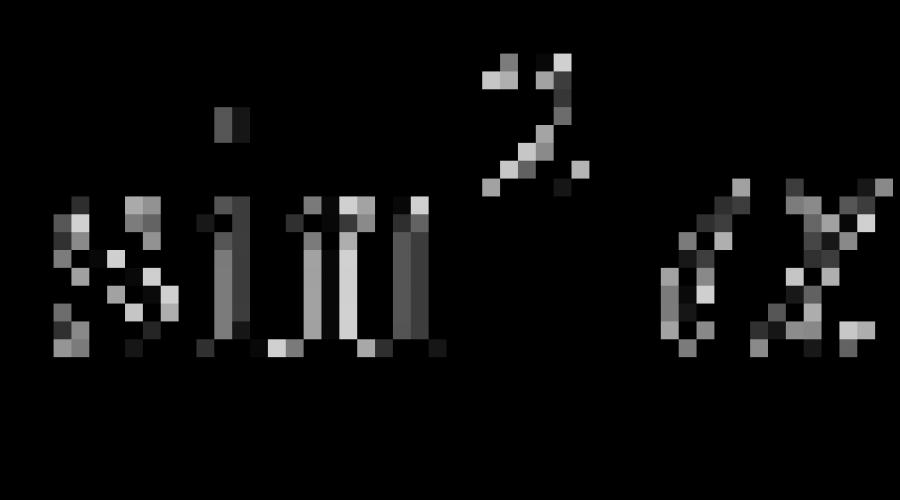
Lesen Sie auch
In diesem Artikel werfen wir einen umfassenden Blick darauf. Grundlegende trigonometrische Identitäten sind Gleichheiten, die die Beziehung zwischen Sinus, Cosinus, Tangens und Kotangens eines Winkels festlegen und es Ihnen ermöglichen, diese zu finden trigonometrische Funktionen durch einen bekannten Anderen.
Lassen Sie uns gleich die wichtigsten trigonometrischen Identitäten auflisten, die wir in diesem Artikel analysieren werden. Schreiben wir sie in eine Tabelle, und unten geben wir die Ergebnisse dieser Formeln an und geben die notwendigen Erklärungen.
Seitennavigation.
Beziehung zwischen Sinus und Cosinus eines Winkels
Manchmal geht es nicht um die in der obigen Tabelle aufgeführten wichtigsten trigonometrischen Identitäten, sondern um eine einzige grundlegende trigonometrische Identität Art ![]() . Die Erklärung für diese Tatsache ist recht einfach: Die Gleichheiten werden aus der trigonometrischen Hauptidentität erhalten, nachdem beide Teile durch und bzw. und die Gleichheiten dividiert wurden
. Die Erklärung für diese Tatsache ist recht einfach: Die Gleichheiten werden aus der trigonometrischen Hauptidentität erhalten, nachdem beide Teile durch und bzw. und die Gleichheiten dividiert wurden  Und
Und ![]() ergeben sich aus den Definitionen von Sinus, Cosinus, Tangens und Kotangens. Wir werden in den folgenden Abschnitten ausführlicher darauf eingehen.
ergeben sich aus den Definitionen von Sinus, Cosinus, Tangens und Kotangens. Wir werden in den folgenden Abschnitten ausführlicher darauf eingehen.
Das heißt, von besonderem Interesse ist die Gleichheit, die den Namen der wichtigsten trigonometrischen Identität erhielt.
Bevor wir die trigonometrische Hauptidentität beweisen, geben wir ihre Formulierung an: Die Summe der Quadrate von Sinus und Cosinus eines Winkels ist identisch gleich eins. Jetzt wollen wir es beweisen.
Die grundlegende trigonometrische Identität wird sehr oft verwendet, wenn Transformation trigonometrische Ausdrücke . Es ermöglicht, die Summe der Quadrate von Sinus und Cosinus eines Winkels durch eins zu ersetzen. Nicht seltener wird die grundlegende trigonometrische Identität in umgekehrter Reihenfolge verwendet: Die Einheit wird durch die Summe der Quadrate von Sinus und Cosinus eines beliebigen Winkels ersetzt.
Tangens und Kotangens durch Sinus und Cosinus
Identitäten, die Tangens und Kotangens mit Sinus und Cosinus eines Blickwinkels verbinden und ![]() ergeben sich unmittelbar aus den Definitionen von Sinus, Cosinus, Tangens und Kotangens. Tatsächlich ist der Sinus per Definition die Ordinate von y, der Kosinus die Abszisse von x und der Tangens das Verhältnis der Ordinate zur Abszisse, d. h.
ergeben sich unmittelbar aus den Definitionen von Sinus, Cosinus, Tangens und Kotangens. Tatsächlich ist der Sinus per Definition die Ordinate von y, der Kosinus die Abszisse von x und der Tangens das Verhältnis der Ordinate zur Abszisse, d. h. ![]() , und der Kotangens ist das Verhältnis der Abszisse zur Ordinate, d. h.
, und der Kotangens ist das Verhältnis der Abszisse zur Ordinate, d. h. ![]() .
.
Dank dieser Offensichtlichkeit der Identitäten und ![]() Tangens und Kotangens werden oft nicht durch das Verhältnis von Abszisse und Ordinate, sondern durch das Verhältnis von Sinus und Cosinus definiert. Der Tangens eines Winkels ist also das Verhältnis des Sinus zum Cosinus dieses Winkels, und der Kotangens ist das Verhältnis des Cosinus zum Sinus.
Tangens und Kotangens werden oft nicht durch das Verhältnis von Abszisse und Ordinate, sondern durch das Verhältnis von Sinus und Cosinus definiert. Der Tangens eines Winkels ist also das Verhältnis des Sinus zum Cosinus dieses Winkels, und der Kotangens ist das Verhältnis des Cosinus zum Sinus.
Zum Abschluss dieses Absatzes ist anzumerken, dass die Identitäten und ![]() finden für alle Winkel statt, bei denen die darin enthaltenen trigonometrischen Funktionen sinnvoll sind. Die Formel gilt also für alle außer (ansonsten hat der Nenner eine Null, und wir haben die Division durch Null nicht definiert) und die Formel
finden für alle Winkel statt, bei denen die darin enthaltenen trigonometrischen Funktionen sinnvoll sind. Die Formel gilt also für alle außer (ansonsten hat der Nenner eine Null, und wir haben die Division durch Null nicht definiert) und die Formel ![]() - für alle, anders als wenn z irgendein Wert ist.
- für alle, anders als wenn z irgendein Wert ist.
Beziehung zwischen Tangens und Kotangens
Eine noch offensichtlichere trigonometrische Identität als die beiden vorherigen ist die Identität, die Tangens und Kotangens eines Winkels der Form verbindet ![]() . Es ist klar, dass dies für alle anderen Winkel als gilt, da sonst entweder der Tangens oder der Kotangens nicht definiert sind.
. Es ist klar, dass dies für alle anderen Winkel als gilt, da sonst entweder der Tangens oder der Kotangens nicht definiert sind.
Beweis der Formel ![]() sehr einfach. Per Definition und von wo
sehr einfach. Per Definition und von wo  . Der Beweis hätte etwas anders erfolgen können. Seit
. Der Beweis hätte etwas anders erfolgen können. Seit ![]() , Das
, Das  .
.
Tangens und Kotangens des gleichen Winkels, bei dem sie einen Sinn ergeben, sind also .
– Es wird sicherlich Aufgaben zur Trigonometrie geben. Die Trigonometrie wird oft nicht gemocht, weil sie eine große Anzahl schwieriger Formeln vollstopfen muss, in denen es nur so von Sinus, Cosinus, Tangens und Kotangens wimmelt. Die Seite gab bereits einmal Ratschläge, wie man sich eine vergessene Formel merken kann, am Beispiel der Euler- und Peel-Formeln.
Und in diesem Artikel werden wir versuchen zu zeigen, dass es ausreicht, nur fünf einfache trigonometrische Formeln genau zu kennen und den Rest zu kennen Grund Idee und bring sie heraus, während du gehst. Es ist wie bei der DNA: Das Molekül speichert nicht die vollständigen Baupläne eines fertigen Lebewesens. Es enthält vielmehr Anweisungen zum Zusammenbau aus verfügbaren Aminosäuren. Also in der Trigonometrie, ich kenne einige allgemeine Grundsätze, wir werden alle notwendigen Formeln aus einer kleinen Menge derjenigen erhalten, die im Auge behalten werden müssen.
Wir werden uns auf die folgenden Formeln verlassen:
Aus den Formeln für Sinus- und Kosinussummen erhalten wir, wenn wir die Parität der Kosinusfunktion und die Ungeradheit der Sinusfunktion kennen und -b anstelle von b einsetzen, Formeln für Differenzen:
- Sinus der Differenz: Sünde(ab) = SündeAcos(-B)+cosASünde(-B) = SündeAcosB-cosASündeB
- Kosinus der Differenz: cos(ab) = cosAcos(-B)-SündeASünde(-B) = cosAcosB+SündeASündeB
Setzt man a = b in die gleichen Formeln ein, erhält man die Formeln für Sinus und Cosinus von Doppelwinkeln:
- Sinus des doppelten Winkels: Sünde2a = Sünde(a+a) = SündeAcosA+cosASündeA = 2SündeAcosA
- Kosinus des doppelten Winkels: cos2a = cos(a+a) = cosAcosA-SündeASündeA = cos2 a-Sünde2 a
Die Formeln für andere Mehrfachwinkel erhält man auf ähnliche Weise:
- Sinus eines Dreifachwinkels: Sünde3a = Sünde(2a+a) = Sünde2acosA+cos2aSündeA = (2SündeAcosA)cosA+(cos2 a-Sünde2 a)SündeA = 2SündeAcos2 a+SündeAcos2 a-Sünde 3 a = 3 SündeAcos2 a-Sünde 3 a = 3 SündeA(1-Sünde2 a)-Sünde 3 a = 3 SündeA-4Sünde 3a
- Kosinus des dreifachen Winkels: cos3a = cos(2a+a) = cos2acosA-Sünde2aSündeA = (cos2 a-Sünde2 a)cosA-(2SündeAcosA)SündeA = cos 3 a- Sünde2 acosA-2Sünde2 acosA = cos 3 a-3 Sünde2 acosA = cos 3 a-3(1- cos2 a)cosA = 4cos 3 a-3 cosA
Bevor wir fortfahren, schauen wir uns ein Problem an.
Gegeben: Der Winkel ist spitz.
Finden Sie seinen Kosinus, wenn
Lösung eines Studenten:
Weil , Das SündeA= 3,a cosA = 4.
(Aus Mathe-Humor)
Die Definition des Tangens bezieht diese Funktion also sowohl auf den Sinus als auch auf den Kosinus. Sie können jedoch eine Formel erhalten, die den Tangens nur mit dem Kosinus in Beziehung setzt. Um es abzuleiten, nehmen wir die trigonometrische Hauptidentität: Sünde 2 A+cos 2 A= 1 und teile es durch cos 2 A. Wir bekommen:
Die Lösung für dieses Problem wäre also:
(Da der Winkel spitz ist, wird beim Extrahieren der Wurzel das +-Zeichen verwendet)
Auch die Formel für den Tangens einer Summe ist schwer zu merken. Geben wir es so aus:
Sofort angezeigt und
Aus der Kosinusformel für einen doppelten Winkel können Sie die Sinus- und Kosinusformel für halbe Winkel erhalten. Gehen Sie dazu auf der linken Seite der Doppelwinkelkosinusformel wie folgt vor:
cos2
A = cos 2
A-Sünde 2
A
wir fügen eins hinzu und rechts - eine trigonometrische Einheit, d.h. die Summe der Quadrate von Sinus und Cosinus.
cos2a+1 = cos2 a-Sünde2 a+cos2 a+Sünde2 a
2cos 2
A = cos2
A+1
Ausdrücken cosA durch cos2
A und wenn wir eine Variablenänderung durchführen, erhalten wir:
Das Vorzeichen wird abhängig vom Quadranten genommen.
In ähnlicher Weise erhalten wir, wenn wir eins von der linken Seite der Gleichheit und die Summe der Quadrate von Sinus und Cosinus von der rechten Seite subtrahieren:
cos2a-1 = cos2 a-Sünde2 a-cos2 a-Sünde2 a
2Sünde 2
A = 1-cos2
A
Und schließlich verwenden wir die folgende Technik, um die Summe trigonometrischer Funktionen in ein Produkt umzuwandeln. Nehmen wir an, wir müssen die Summe der Sinuswerte als Produkt darstellen SündeA+SündeB. Lassen Sie uns die Variablen x und y einführen, sodass a = x+y, b+x-y. Dann
SündeA+SündeB = Sünde(x+y)+ Sünde(x-y) = Sünde X cos y+ cos X Sünde y+ Sünde X cos y- cos X Sünde y=2 Sünde X cos j. Lassen Sie uns nun x und y durch a und b ausdrücken.
Da a = x+y, b = x-y, dann . Deshalb
Sie können sofort zurücktreten
- Formel zur Partitionierung Produkte von Sinus und Cosinus V Menge: SündeAcosB = 0.5(Sünde(a+b)+Sünde(ab))
Wir empfehlen Ihnen, Formeln zur Umrechnung der Sinusdifferenz und der Summe und Differenz der Kosinuswerte in das Produkt sowie zur Division der Produkte aus Sinus und Kosinus in die Summe zu üben und selbst abzuleiten. Nach Abschluss dieser Übungen beherrschen Sie die Fähigkeit, trigonometrische Formeln abzuleiten, gründlich und verlieren sich auch bei der schwierigsten Prüfung, Olympiade oder Prüfung nicht.
Wenn wir einen Einheitskreis mit dem Mittelpunkt im Ursprung konstruieren und einen beliebigen Wert für das Argument festlegen x 0 und von der Achse aus zählen Ochse Ecke X 0, dann entspricht dieser Winkel auf dem Einheitskreis einem bestimmten Punkt A(Abb. 1) und seine Projektion auf die Achse Oh Es wird einen Punkt geben M. Abschnittslänge OM gleich Absolutwert Abszissenpunkte A. Dieser Wert Streit x 0 Funktionswert abgebildet j=cos X 0 wie Abszissenpunkte A. Dementsprechend Punkt IN(X 0 ;bei 0) gehört zum Graphen der Funktion bei=cos X(Abb. 2). Wenn der Punkt A liegt rechts von der Achse OU, Der Stromsinus ist positiv, links dagegen negativ. Aber egal, Punkt A kann den Kreis nicht verlassen. Daher liegt der Kosinus im Bereich von –1 bis 1:
–1 = cos X = 1.

Zusätzliche Drehung um jeden Winkel, Vielfaches von 2 P, gibt Punkt zurück A zum selben Ort. Daher die Funktion y = cos XP:
weil( X+ 2P) = cos X.
Wenn wir zwei Werte des Arguments nehmen, die im absoluten Wert gleich, aber im Vorzeichen entgegengesetzt sind, X Und - X, Finden Sie die entsprechenden Punkte auf dem Kreis Ein x Und A-x. Wie in Abb. zu sehen ist. 3 ihre Projektion auf die Achse Oh ist der gleiche Punkt M. Deshalb
cos(– X) = cos ( X),

diese. Kosinus ist eine gerade Funktion, F(–X) = F(X).
Das bedeutet, dass wir die Eigenschaften der Funktion untersuchen können j=cos X auf dem Segment , und dann seine Parität und Periodizität berücksichtigen.
Bei X= 0 Punkt A liegt auf der Achse Oh, seine Abszisse ist 1 und daher cos 0 = 1. Mit zunehmender X Punkt A bewegt sich um den Kreis nach oben und links, seine Projektion erfolgt natürlich nur nach links und bei x = P/2 Kosinus wird gleich 0. Punkt A In diesem Moment steigt es auf seine maximale Höhe und bewegt sich dann weiter nach links, jedoch bereits absteigend. Seine Abszisse nimmt immer weiter ab, bis sie erreicht niedrigster Wert, gleich –1 at X= P. Also auf dem Intervall die Funktion bei=cos X nimmt monoton von 1 auf –1 ab (Abb. 4, 5).

Aus der Parität des Kosinus folgt, dass auf dem Intervall [– P, 0] steigt die Funktion monoton von –1 auf 1 und nimmt bei an x =–P/2. Nimmt man mehrere Perioden, erhält man eine wellenförmige Kurve (Abb. 6).
Also die Funktion j=cos X nimmt an Punkten Nullwerte an X= P/2 + kp, Wo k – jede ganze Zahl. An Punkten werden Maxima gleich 1 erreicht X= 2kp, d.h. in 2er-Schritten P und Mindestwerte gleich –1 an Punkten X= P + 2kp.
Funktion y = sin x.
An der Ecke des Einheitskreises X 0 entspricht einem Punkt A(Abb. 7), und seine Projektion auf die Achse OU Es wird einen Punkt geben N.Z Funktionswert y 0 = Sünde x 0 definiert als die Ordinate eines Punktes A. Punkt IN(Ecke X 0 ,bei 0) gehört zum Graphen der Funktion j= Sünde X(Abb. 8). Es ist klar, dass die Funktion y = Sünde X periodisch, seine Periode ist 2 P:
Sünde( X+ 2P) = Sünde ( X).


Für zwei Argumentwerte gilt: X Und - , Projektionen ihrer entsprechenden Punkte Ein x Und A-x pro Achse OU symmetrisch zum Punkt angeordnet UM. Deshalb
Sünde(- X) = –sin ( X),
diese. Sinus ist eine ungerade Funktion, f(– X) = –f( X) (Abb. 9).

Wenn der Punkt A relativ zu einem Punkt drehen UM in einem Winkel P/2 gegen den Uhrzeigersinn (mit anderen Worten, wenn der Winkel X erhöhen um P/2), dann ist seine Ordinate in der neuen Position gleich der Abszisse in der alten. Was bedeutet
Sünde( X+ P/2) = cos X.
Ansonsten ist der Sinus ein „später“ Kosinus P/2, da sich jeder Kosinuswert im Sinus „wiederholt“, wenn das Argument um zunimmt P/2. Und um einen Sinusgraphen zu erstellen, reicht es aus, den Kosinusgraphen um zu verschieben P/2 nach rechts (Abb. 10). Eine äußerst wichtige Eigenschaft des Sinus wird durch die Gleichheit ausgedrückt

Die geometrische Bedeutung der Gleichheit ist aus Abb. ersichtlich. 11. Hier X - das ist ein halber Bogen AB, wie in X - die Hälfte des entsprechenden Akkords. Das ist offensichtlich, je näher die Punkte kommen A Und IN die Länge der Sehne nähert sich zunehmend der Länge des Bogens an. Aus derselben Abbildung lässt sich die Ungleichung leicht ableiten
|Sünde X| x|, wahr für alle X.

Mathematiker nennen die Formel (*) eine bemerkenswerte Grenze. Daraus folgt insbesondere diese Sünde X» X bei klein X.
Funktionen bei= tg x, y=ctg X. Die anderen beiden trigonometrischen Funktionen, Tangens und Kotangens, lassen sich am einfachsten als die uns bereits bekannten Verhältnisse von Sinus und Cosinus definieren:
Tangens und Kotangens sind wie Sinus und Cosinus periodische Funktionen, aber ihre Perioden sind gleich P, d.h. Sie sind halb so groß wie Sinus und Cosinus. Der Grund dafür ist klar: Wenn Sinus und Cosinus beide das Vorzeichen ändern, ändert sich ihr Verhältnis nicht.
Da der Nenner des Tangens einen Kosinus enthält, ist der Tangens an den Punkten nicht definiert, an denen der Kosinus 0 ist - wann X= P/2 +kp. An allen anderen Punkten steigt sie monoton an. Direkte X= P/2 + kp für Tangente sind vertikale Asymptoten. An Punkten kp Tangente und Neigung sind 0 bzw. 1 (Abb. 12).

Der Kotangens ist nicht definiert, wenn der Sinus 0 ist (wenn x = kp). An anderen Stellen nimmt sie monoton und geradlinig ab x = kp – seine vertikalen Asymptoten. An Punkten x = p/2 +kp der Kotangens wird 0 und die Steigung an diesen Punkten beträgt –1 (Abb. 13).

Parität und Periodizität.
Eine Funktion wird aufgerufen, auch wenn F(–X) = F(X). Die Kosinus- und Sekantenfunktionen sind gerade und die Sinus-, Tangens-, Kotangens- und Kosekansfunktionen sind ungerade:
| Sünde (–α) = – Sünde α | tan (–α) = – tan α |
| cos (–α) = cos α | ctg (–α) = – ctg α |
| Sek. (–α) = Sek. α | cosec (–α) = – cosec α |
Paritätseigenschaften ergeben sich aus der Symmetrie der Punkte P ein und R- A (Abb. 14) relativ zur Achse X. Bei einer solchen Symmetrie ändert die Ordinate des Punktes das Vorzeichen (( X;bei) geht zu ( X; –у)). Alle Funktionen – periodisch, Sinus, Kosinus, Sekanten und Kosekans – haben eine Periode von 2 P, und Tangens und Kotangens - P:

| Sünde (α + 2 kπ) = sin α | cos(α+2 kπ) = cos α |
| tg(α+ kπ) = tan α | Kinderbett(α+ kπ) = cotg α |
| Sek. (α + 2 kπ) = Sek. α | cosec(α+2 kπ) = cosec α |
Die Periodizität von Sinus und Cosinus ergibt sich aus der Tatsache, dass alle Punkte P a+2 kp, Wo k= 0, ±1, ±2,…, zusammenfallen, und die Periodizität von Tangens und Kotangens beruht auf der Tatsache, dass die Punkte P a+ kp fallen abwechselnd in zwei diametral gegenüberliegende Punkte des Kreises und ergeben denselben Punkt auf der Tangentenachse.
Die Haupteigenschaften trigonometrischer Funktionen lassen sich in einer Tabelle zusammenfassen:
| Funktion | Domain | Mehrere Bedeutungen | Parität | Bereiche der Monotonie ( k= 0, ± 1, ± 2,…) |
| Sünde X | –Ґ x Ґ | [–1, +1] | seltsam | steigt mit X O((4 k – 1) P /2, (4k + 1) P/2), nimmt um ab X O((4 k + 1) P /2, (4k + 3) P/2) |
| cos X | –Ґ x Ґ | [–1, +1] | sogar | Steigt mit X O((2 k – 1) P, 2kp), nimmt um ab X O(2 kp, (2k + 1) P) |
| tg X | X № P/2 + p k | (–Ґ , +Ґ ) | seltsam | steigt mit X O((2 k – 1) P /2, (2k + 1) P /2) |
| ctg X | X № p k | (–Ґ , +Ґ ) | seltsam | nimmt ab X UM ( kp, (k + 1) P) |
| Sek X | X № P/2 + p k | (–Ґ , –1] UND [+1, +Ґ ) | sogar | Steigt mit X O(2 kp, (2k + 1) P), nimmt um ab X O((2 k– 1) p , 2 kp) |
| cosec X | X № p k | (–Ґ , –1] UND [+1, +Ґ ) | seltsam | steigt mit X O((4 k + 1) P /2, (4k + 3) P/2), nimmt um ab X O((4 k – 1) P /2, (4k + 1) P /2) |
Reduktionsformeln.
Nach diesen Formeln ist der Wert der trigonometrischen Funktion des Arguments a, wo P/2 a p kann auf den Wert der Argumentfunktion a reduziert werden, wobei 0 a p /2 entweder gleich oder komplementär dazu ist.
| Argument b |  -A -A |
+a | P-A | P+a | +a | +a | 2P-A |
| Sünde b | weil a | weil a | Sünde a | –Sünde a | –cos a | –cos a | –Sünde a |
| cos b | Sünde a | –Sünde a | –cos a | –cos a | –Sünde a | Sünde a | weil a |
Daher werden in den Tabellen der trigonometrischen Funktionen Werte nur für spitze Winkel angegeben und es genügt, sich beispielsweise auf Sinus und Tangens zu beschränken. Die Tabelle zeigt nur die am häufigsten verwendeten Formeln für Sinus und Cosinus. Daraus lassen sich leicht Formeln für Tangens und Kotangens erhalten. Beim Umwandeln einer Funktion aus einem Argument der Form kp/2 ± a, wo k– eine ganze Zahl, zu einer Funktion des Arguments a:
1) Der Funktionsname wird gespeichert, wenn k gerade, und ändert sich in „komplementär“, wenn k seltsam;
2) Das Vorzeichen auf der rechten Seite stimmt mit dem Vorzeichen der reduzierbaren Funktion am Punkt überein kp/2 ± a, wenn der Winkel a spitz ist.
Zum Beispiel beim Gießen von ctg (a – P/2) Wir stellen sicher, dass ein – P/2 bei 0 a p /2 liegt im vierten Quadranten, wo der Kotangens negativ ist, und wir ändern gemäß Regel 1 den Namen der Funktion: ctg (a – P/2) = –tg a .
Additionsformeln.
Formeln für mehrere Winkel.
Diese Formeln leiten sich direkt aus den Additionsformeln ab:
sin 2a = 2 sin a cos a ;
cos 2a = cos 2 a – sin 2 a = 2 cos 2 a – 1 = 1 – 2 sin 2 a ;
Sünde 3a = 3 Sünde a – 4 Sünde 3 a ;
cos 3a = 4 cos 3 a – 3 cos a ;
Die Formel für cos 3a wurde von François Viète bei der Lösung der kubischen Gleichung verwendet. Er war der erste, der Ausdrücke für cos fand N a und Sünde N a , von denen später mehr erhalten wurden auf einfache Weise aus Moivres Formel.
Wenn Sie in Formeln mit doppelten Argumenten a durch /2 ersetzen, können diese in Halbwinkelformeln umgewandelt werden:
Universelle Substitutionsformeln.
Mit diesen Formeln kann ein Ausdruck, der verschiedene trigonometrische Funktionen desselben Arguments beinhaltet, in einen rationalen Ausdruck einer einzelnen Funktion tg (a /2) umgeschrieben werden. Dies kann bei der Lösung einiger Gleichungen nützlich sein:
 |
|
 |
 |
Formeln zur Umrechnung von Summen in Produkte und von Produkten in Summen.
Vor dem Aufkommen von Computern wurden diese Formeln zur Vereinfachung von Berechnungen verwendet. Berechnungen wurden mit logarithmischen Tabellen und später mit einem Rechenschieber durchgeführt, weil Logarithmen eignen sich am besten zum Multiplizieren von Zahlen, daher wurden alle ursprünglichen Ausdrücke in eine für die Logarithmisierung geeignete Form gebracht, d. h. zu Werken, zum Beispiel:
2 Sünde A sin b = cos ( a–b) – weil ( a+b);
2cos A cos B=cos( a–b) + cos ( a+b);
2 Sünde A cos B= Sünde ( a–b) + Sünde ( a+b).
Formeln für die Tangens- und Kotangensfunktionen können oben entnommen werden.
Formeln zur Gradreduzierung.
Aus den Mehrfachargumentformeln werden die folgenden Formeln abgeleitet:
| sin 2 a = (1 – cos 2a)/2; | cos 2 a = (1 + cos 2a )/2; |
| sin 3 a = (3 sin a – sin 3a)/4; | cos 3 a = (3 cos a + cos 3 a )/4. |
Mit diesen Formeln können trigonometrische Gleichungen auf Gleichungen niedrigeren Grades reduziert werden. Auf die gleiche Weise können wir Reduktionsformeln für mehr ableiten hohe Abschlüsse Sinus und Cosinus.
| Ableitungen und Integrale trigonometrischer Funktionen | |
| (Sünde X)` = cos X; | (weil X)` = –Sünde X; |
| (tg X)` = ; | (ctg X)` = – ; |
| Ich sündige nicht x dx= –cos X + C; | t weil x dx= Sünde X + C; |
| t tg x dx= –ln|cos X| + C; | t ctg x dx = ln|sin X| + C; |
Jede trigonometrische Funktion ist an jedem Punkt ihres Definitionsbereichs stetig und unendlich differenzierbar. Darüber hinaus sind die Ableitungen trigonometrischer Funktionen trigonometrische Funktionen, und wenn man sie integriert, erhält man auch trigonometrische Funktionen oder deren Logarithmen. Integrale rationaler Kombinationen trigonometrischer Funktionen sind immer Elementarfunktionen.
Darstellung trigonometrischer Funktionen in Form von Potenzreihen und unendlichen Produkten.
Alle trigonometrischen Funktionen können in Potenzreihen entwickelt werden. In diesem Fall sind die Funktionen sin X bcos X werden zeilenweise dargestellt. konvergent für alle Werte X:
Diese Reihen können verwendet werden, um Näherungsausdrücke für Sünde zu erhalten X und cos X bei kleinen Werten X:
bei | x| p/2;
bei 0 x| P
(B n – Bernoulli-Zahlen).
Sünde funktioniert X und cos X kann in Form unendlicher Produkte dargestellt werden:
Trigonometrisches System 1, cos X,Sünde X, weil 2 X, Sünde 2 X,¼,cos nx,Sünde nx, ¼, bildet sich auf dem Segment [– P, P] ein orthogonales Funktionensystem, das es ermöglicht, Funktionen in Form trigonometrischer Reihen darzustellen.
werden als analytische Fortsetzungen der entsprechenden trigonometrischen Funktionen des reellen Arguments in die komplexe Ebene definiert. Ja, Sünde z und cos z kann mithilfe von Reihen für Sünde definiert werden X und cos X, wenn stattdessen X setzen z:
Diese Reihen konvergieren über die gesamte Ebene, also Sünde z und cos z- ganze Funktionen.
Tangens und Kotangens werden durch die Formeln bestimmt:
tg-Funktionen z und ctg z– meromorphe Funktionen. TG-Stöcke z und Sek z– einfach (1. Ordnung) und an Punkten gelegen z = p/2 + pn, Pole ctg z und cosec z– ebenfalls einfach und punktuell angeordnet z = p n, n = 0, ±1, ±2,…
Alle Formeln, die für trigonometrische Funktionen eines reellen Arguments gelten, gelten auch für ein komplexes. Insbesondere,
Sünde(- z) = –Sünde z,
cos(– z) = cos z,
tg(– z) = –tg z,
ctg(– z) = –ctg z,
diese. Gerade und ungerade Parität bleiben erhalten. Formeln werden ebenfalls gespeichert
Sünde( z + 2P) = Sünde z, (z + 2P) = cos z, (z + P) = tg z, (z + P) = ctg z,
diese. Auch die Periodizität bleibt erhalten und die Perioden sind die gleichen wie bei Funktionen eines reellen Arguments.
Trigonometrische Funktionen können als Exponentialfunktion eines rein imaginären Arguments ausgedrückt werden:
Zurück, e iz ausgedrückt in cos z und Sünde z nach der Formel:
e iz=cos z + ich Sünde z
Diese Formeln werden Eulersche Formeln genannt. Leonhard Euler entwickelte sie 1743.
Trigonometrische Funktionen können auch als hyperbolische Funktionen ausgedrückt werden:
z = –ich Sch iz, cos z = ch iz, z = –i th iz.
wobei sh, ch und th hyperbolischer Sinus, Cosinus und Tangens sind.
Trigonometrische Funktionen komplexer Argumente z = x + iy, Wo X Und j– reelle Zahlen, können durch trigonometrische und hyperbolische Funktionen reeller Argumente ausgedrückt werden, zum Beispiel:
Sünde( x + iy) = Sünde X CH j + ich cos X Sch j;
weil( x + iy) = cos X CH j + ich Sünde X Sch j.
Sinus und Cosinus eines komplexen Arguments können reelle Werte annehmen, die im Absolutwert größer als 1 sind. Zum Beispiel:
Wenn ein unbekannter Winkel als Argument trigonometrischer Funktionen in eine Gleichung eingeht, heißt die Gleichung trigonometrisch. Solche Gleichungen sind so verbreitet, dass ihre Methoden Die Lösungen sind sehr detailliert und sorgfältig ausgearbeitet. MIT Mithilfe verschiedener Techniken und Formeln werden trigonometrische Gleichungen auf Gleichungen der Form reduziert F(X)= a, Wo F– eine der einfachsten trigonometrischen Funktionen: Sinus, Cosinus, Tangens oder Kotangens. Bringen Sie dann das Argument zum Ausdruck X diese Funktion durch ihren bekannten Wert A.
Da trigonometrische Funktionen periodisch sind, gilt das Gleiche A Aus dem Wertebereich gibt es unendlich viele Werte des Arguments, und die Lösungen der Gleichung können nicht als einzelne Funktion von geschrieben werden A. Daher wird im Definitionsbereich jeder der wichtigsten trigonometrischen Funktionen ein Abschnitt ausgewählt, in dem sie alle ihre Werte jeweils nur einmal annimmt, und in diesem Abschnitt befindet sich die dazu inverse Funktion. Solche Funktionen werden durch das Hinzufügen des Präfixes arc (arc) zum Namen der ursprünglichen Funktion gekennzeichnet und als inverse trigonometrisch bezeichnet Funktionen oder einfach Bogenfunktionen.
Inverse trigonometrische Funktionen.
Für die Sünde X, cos X, tg X und ctg X bestimmt werden kann Umkehrfunktionen. Sie werden entsprechend mit arcsin bezeichnet X(lesen Sie „Arkussinus“ X"), arcos X, arctan X und arcctg X. Per Definition Arcsin X es gibt so eine Nummer ja, Was
Sünde bei = X.
Ähnliches gilt für andere inverse trigonometrische Funktionen. Diese Definition weist jedoch einige Ungenauigkeiten auf.
Wenn Sie Sünde reflektieren X, cos X, tg X und ctg X relativ zur Winkelhalbierenden des ersten und dritten Quadranten der Koordinatenebene werden die Funktionen aufgrund ihrer Periodizität mehrdeutig: Unendlich viele Winkel entsprechen demselben Sinus (Kosinus, Tangens, Kotangens).
Um Mehrdeutigkeiten zu beseitigen, wird ein Abschnitt der Kurve mit einer Breite von P, in diesem Fall ist es notwendig, dass eine Eins-zu-eins-Entsprechung zwischen dem Argument und dem Wert der Funktion gewahrt bleibt. Bereiche in der Nähe des Koordinatenursprungs werden ausgewählt. Für Sinus in Als „Eins-zu-eins-Intervall“ nehmen wir das Segment [– P/2, P/2], auf dem der Sinus monoton von –1 auf 1 ansteigt, für den Kosinus – das Segment, für den Tangens bzw. Kotangens die Intervalle (– P/2, P/2) und (0, P). Jede Kurve im Intervall wird relativ zur Winkelhalbierenden gespiegelt und nun können inverse trigonometrische Funktionen bestimmt werden. Lassen Sie beispielsweise den Argumentwert angegeben x 0 , so dass 0 Ј X 0 Ј 1. Dann der Wert der Funktion j 0 = Arcsin X 0 es wird nur eine Bedeutung geben bei 0 , so dass - P/2 Ј bei 0 Ј P/2 und X 0 = Sünde j 0 .
Somit ist der Arkussinus eine Funktion des Arkussinus A, definiert auf dem Intervall [–1, 1] und für jeden gleich A auf einen solchen Wert, – P/2 a p /2 dass sin a = A. Es ist sehr praktisch, dies mithilfe eines Einheitskreises darzustellen (Abb. 15). Wann | a| 1 Auf einem Kreis gibt es zwei Punkte mit Ordinate A, symmetrisch um die Achse u. Einer davon entspricht dem Winkel A= Arcsin A, und das andere ist die Ecke p - a. MIT unter Berücksichtigung der Periodizität des Sinus die Gleichung sin lösen X= A wird wie folgt geschrieben:
x =(–1)N Arcsin A + 2p n,
Wo N= 0, ±1, ±2,...

Andere einfache trigonometrische Gleichungen können auf die gleiche Weise gelöst werden:
cos X = A, –1 =A= 1;
x =±arcos A + 2p n,
Wo P= 0, ±1, ±2,... (Abb. 16);

tg X = A;
X= arctan A + P N,
Wo n = 0, ±1, ±2,... (Abb. 17);

ctg X= A;
X= arcctg A + P N,
Wo n = 0, ±1, ±2,... (Abb. 18).

Grundlegende Eigenschaften inverser trigonometrischer Funktionen:
Arcsin X(Abb. 19): Definitionsbereich – Segment [–1, 1]; Reichweite - [- P/2, P/2], monoton steigende Funktion;

arccos X(Abb. 20): Definitionsbereich – Segment [–1, 1]; Reichweite - ; monoton fallende Funktion;

arctg X(Abb. 21): Definitionsbereich – alle reellen Zahlen; Wertebereich – Intervall (– P/2, P/2); monoton steigende Funktion; gerade bei= –P/2 und y = p /2 – horizontale Asymptoten;

arcctg X(Abb. 22): Definitionsbereich – alle reellen Zahlen; Wertebereich – Intervall (0, P); monoton fallende Funktion; gerade j= 0 und y = p– horizontale Asymptoten.

Für jeden z = x + iy, Wo X Und j sind reelle Zahlen, es gelten Ungleichungen
½| E\e y–E-y| ≤|sin z|≤½( e y +e-y),
½| Ey–E-y| ≤|cos z|≤½( e y +e -y),
davon bei j® Ґ asymptotische Formeln folgen (einheitlich bezüglich X)
|Sünde z| » 1/2 e |y| ,
|cos z| » 1/2 e |y| .
Trigonometrische Funktionen tauchten erstmals im Zusammenhang mit astronomischen und geometrischen Forschungen auf. Die Verhältnisse der Segmente in einem Dreieck und einem Kreis, die im Wesentlichen trigonometrische Funktionen sind, finden sich bereits im 3. Jahrhundert. Chr e. in den Werken der Mathematiker des antiken Griechenlands – Euklid, Archimedes, Apollonius von Perga und andere waren diese Beziehungen jedoch kein eigenständiger Untersuchungsgegenstand, sodass sie trigonometrische Funktionen als solche nicht untersuchten. Sie galten zunächst als Segmente und wurden in dieser Form von Aristarchos (spätes 4. – 2. Hälfte des 3. Jahrhunderts v. Chr.), Hipparchos (2. Jahrhundert v. Chr.), Menelaos (1. Jahrhundert n. Chr.) und Ptolemaios (2. Jahrhundert n. Chr.) verwendet sphärische Dreiecke lösen. Ptolemäus erstellte die erste Akkordtabelle für spitze Winkel alle 30 Zoll mit einer Genauigkeit von 10 –6. Dies war die erste Sinustabelle. Als Verhältnis findet sich die Funktion sin a bereits in Aryabhata (Ende des 5. Jahrhunderts). Die Funktionen tg a und ctg a finden sich bei al-Battani (2. Hälfte des 9. – frühen 10. Jahrhunderts) und Abul-Vefa (10. Jahrhundert), der auch sec a und cosec a verwendet... Aryabhata kannte die Formel bereits ( sin 2 a + cos 2 a) = 1, sowie Formeln für sin und cos eines halben Winkels, mit deren Hilfe ich Sinustabellen für Winkel bis 3°45" erstellt habe; basierend auf den bekannten Werten trigonometrischer Funktionen für die einfachsten Argumente. Bhaskara (12. Jahrhundert) gab eine Methode zum Erstellen von Tabellen in Form von 1 unter Verwendung von Additionsformeln an. Formeln zur Umwandlung der Summe und Differenz trigonometrischer Funktionen verschiedener Argumente in ein Produkt wurden von Regiomontanus (15. Jahrhundert) und J. Napier im Zusammenhang mit dessen Erfindung der Logarithmen (1614) abgeleitet. Regiomontan gab eine Tabelle mit Sinuswerten in 1". Die Entwicklung trigonometrischer Funktionen in Potenzreihen wurde von I. Newton (1669) erhalten. In moderne Form die Theorie der trigonometrischen Funktionen wurde von L. Euler (18. Jahrhundert) eingeführt. Er besitzt ihre Definition für reale und komplexe Argumente, die derzeit akzeptierte Symbolik, die Herstellung von Zusammenhängen mit Exponentialfunktion und Orthogonalität des Sinus- und Kosinussystems.
Trigonometrische Identitäten- Dies sind Gleichheiten, die eine Beziehung zwischen Sinus, Cosinus, Tangens und Kotangens eines Winkels herstellen, die es Ihnen ermöglicht, jede dieser Funktionen zu finden, sofern eine andere bekannt ist.
tg \alpha = \frac(\sin \alpha)(\cos \alpha), \enspace ctg \alpha = \frac(\cos \alpha)(\sin \alpha)
tg \alpha \cdot ctg \alpha = 1
Diese Identität besagt, dass die Summe des Quadrats des Sinus eines Winkels und des Quadrats des Kosinus eines Winkels gleich eins ist, was es in der Praxis ermöglicht, den Sinus eines Winkels zu berechnen, wenn sein Kosinus bekannt ist, und umgekehrt .
Bei der Konvertierung trigonometrischer Ausdrücke wird diese Identität sehr häufig verwendet, wodurch Sie die Summe der Quadrate von Kosinus und Sinus eines Winkels durch eins ersetzen und den Ersetzungsvorgang auch in umgekehrter Reihenfolge durchführen können.
Tangens und Kotangens mithilfe von Sinus und Cosinus ermitteln
tg \alpha = \frac(\sin \alpha)(\cos \alpha),\enspace
Diese Identitäten werden aus den Definitionen von Sinus, Cosinus, Tangens und Kotangens gebildet. Wenn man es sich genau ansieht, dann ist die Ordinate y per Definition ein Sinus und die Abszisse x ein Kosinus. Dann ist der Tangens gleich dem Verhältnis \frac(y)(x)=\frac(\sin \alpha)(\cos \alpha) und das Verhältnis \frac(x)(y)=\frac(\cos \alpha)(\sin \alpha)- wird ein Kotangens sein.
Fügen wir hinzu, dass die Identitäten nur für solche Winkel \alpha gelten, bei denen die darin enthaltenen trigonometrischen Funktionen einen Sinn ergeben, ctg \alpha=\frac(\cos \alpha)(\sin \alpha).
Zum Beispiel: tg \alpha = \frac(\sin \alpha)(\cos \alpha) gilt für andere Winkel \alpha als \frac(\pi)(2)+\pi z, A ctg \alpha=\frac(\cos \alpha)(\sin \alpha)- Für einen anderen Winkel \alpha als \pi z ist z eine ganze Zahl.
Beziehung zwischen Tangens und Kotangens
tg \alpha \cdot ctg \alpha=1
Diese Identität gilt nur für andere Winkel \alpha als \frac(\pi)(2) z. Andernfalls wird weder der Kotangens noch der Tangens bestimmt.
Basierend auf den oben genannten Punkten erhalten wir das tg \alpha = \frac(y)(x), A ctg \alpha=\frac(x)(y). Es folgt dem tg \alpha \cdot ctg \alpha = \frac(y)(x) \cdot \frac(x)(y)=1. Daher sind Tangens und Kotangens desselben Winkels, bei dem sie sinnvoll sind, zueinander inverse Zahlen.
Beziehungen zwischen Tangens und Cosinus, Kotangens und Sinus
tg^(2) \alpha + 1=\frac(1)(\cos^(2) \alpha)- Die Summe des Quadrats des Tangens des Winkels \alpha und 1 ist gleich dem Umkehrquadrat des Kosinus dieses Winkels. Diese Identität gilt für alle \alpha außer \frac(\pi)(2)+ \pi z.
1+ctg^(2) \alpha=\frac(1)(\sin^(2)\alpha)- Die Summe aus 1 und dem Quadrat des Kotangens des Winkels \alpha ist gleich dem Umkehrquadrat des Sinus angegebenen Winkel. Diese Identität gilt für jedes \alpha, das sich von \pi z unterscheidet.
Beispiele mit Lösungen für Probleme unter Verwendung trigonometrischer Identitäten
Beispiel 1
Finden Sie \sin \alpha und tg \alpha if \cos \alpha=-\frac12 Und \frac(\pi)(2)< \alpha < \pi ;
Lösung anzeigen
Lösung
Die Funktionen \sin\alpha und \cos\alpha hängen durch die Formel zusammen \sin^(2)\alpha + \cos^(2) \alpha = 1. Einsetzen in diese Formel \cos \alpha = -\frac12, wir bekommen:
\sin^(2)\alpha + \left (-\frac12 \right)^2 = 1
Diese Gleichung hat zwei Lösungen:
\sin \alpha = \pm \sqrt(1-\frac14) = \pm \frac(\sqrt 3)(2)
Nach Bedingung \frac(\pi)(2)< \alpha < \pi . Im zweiten Viertel ist der Sinus also positiv \sin \alpha = \frac(\sqrt 3)(2).
Um tan \alpha zu finden, verwenden wir die Formel tg \alpha = \frac(\sin \alpha)(\cos \alpha)
tg \alpha = \frac(\sqrt 3)(2) : \frac12 = \sqrt 3
Beispiel 2
Finden Sie \cos \alpha und ctg \alpha, wenn und \frac(\pi)(2)< \alpha < \pi .
Lösung anzeigen
Lösung
Einsetzen in die Formel \sin^(2)\alpha + \cos^(2) \alpha = 1 angegebene Nummer \sin \alpha=\frac(\sqrt3)(2), wir bekommen \left (\frac(\sqrt3)(2)\right)^(2) + \cos^(2) \alpha = 1. Diese Gleichung hat zwei Lösungen \cos \alpha = \pm \sqrt(1-\frac34)=\pm\sqrt\frac14.
Nach Bedingung \frac(\pi)(2)< \alpha < \pi . Im zweiten Viertel ist der Kosinus also negativ \cos \alpha = -\sqrt\frac14=-\frac12.
Um ctg \alpha zu finden, verwenden wir die Formel ctg \alpha = \frac(\cos \alpha)(\sin \alpha). Wir kennen die entsprechenden Werte.
ctg \alpha = -\frac12: \frac(\sqrt3)(2) = -\frac(1)(\sqrt 3).
Sinus und Cosinus entstanden ursprünglich aus der Notwendigkeit, Größen in rechtwinkligen Dreiecken zu berechnen. Es wurde festgestellt, dass das Seitenverhältnis immer gleich bleibt, unabhängig davon, wie stark sich die Länge dieser Seiten ändert, wenn das Gradmaß der Winkel in einem rechtwinkligen Dreieck nicht geändert wird.
So wurden die Konzepte Sinus und Cosinus eingeführt. Sinus spitzer Winkel in einem rechtwinkligen Dreieck ist das Verhältnis der gegenüberliegenden Seite zur Hypotenuse, und der Kosinus ist das Verhältnis der Seite neben der Hypotenuse.
Sätze von Kosinus und Sinus
Kosinus und Sinus können jedoch nicht nur für rechtwinklige Dreiecke verwendet werden. Um den Wert eines stumpfen oder spitzen Winkels oder einer Seite eines Dreiecks zu ermitteln, reicht es aus, den Satz von Kosinus und Sinus anzuwenden.
Der Kosinussatz ist ganz einfach: „Das Quadrat einer Seite eines Dreiecks ist gleich der Summe der Quadrate der anderen beiden Seiten minus dem doppelten Produkt dieser Seiten und dem Kosinus des Winkels zwischen ihnen.“
Es gibt zwei Interpretationen des Sinussatzes: klein und erweitert. Laut dem Minderjährigen: „In einem Dreieck sind die Winkel proportional zu den gegenüberliegenden Seiten.“ Dieser Satz wird aufgrund der Eigenschaft des umschriebenen Kreises eines Dreiecks oft erweitert: „In einem Dreieck sind die Winkel proportional zu den gegenüberliegenden Seiten und ihr Verhältnis ist gleich dem Durchmesser des umschriebenen Kreises.“
Derivate
Die Ableitung ist ein mathematisches Hilfsmittel, das zeigt, wie schnell sich eine Funktion relativ zu einer Änderung ihres Arguments ändert. Ableitungen werden in der Geometrie und in einer Reihe technischer Disziplinen verwendet.
Beim Lösen von Problemen müssen Sie die Tabellenwerte der Ableitungen trigonometrischer Funktionen kennen: Sinus und Cosinus. Die Ableitung eines Sinus ist ein Kosinus, und ein Kosinus ist ein Sinus, aber mit einem Minuszeichen.
Anwendung in der Mathematik
Beim Lösen werden besonders häufig Sinus und Cosinus verwendet rechtwinklige Dreiecke und damit verbundene Aufgaben.
Die Bequemlichkeit von Sinus und Cosinus spiegelt sich auch in der Technologie wider. Winkel und Seiten ließen sich mithilfe des Kosinus- und Sinussatzes leicht ermitteln, indem komplexe Formen und Objekte in „einfache“ Dreiecke zerlegt wurden. Ingenieure, die sich häufig mit der Berechnung von Seitenverhältnissen und Gradmaßen befassen, haben viel Zeit und Mühe in die Berechnung der Kosinus- und Sinuswerte von nicht tabellarischen Winkeln investiert.
Dann kamen Bradis-Tabellen zur Rettung, die Tausende von Werten für Sinus, Cosinus, Tangens und Kotangens verschiedener Winkel enthielten. IN Sowjetzeit Einige Lehrer zwangen ihre Schüler, Seiten von Bradis-Tabellen auswendig zu lernen.
Das Bogenmaß ist der Winkelwert eines Bogens, dessen Länge dem Radius oder 57,295779513° Grad entspricht.
Grad (in der Geometrie) – 1/360 Teil eines Kreises oder 1/90 Teil rechter Winkel.
π = 3,141592653589793238462… (ungefährer Wert von Pi).
Kosinustabelle für Winkel: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Winkel x (in Grad) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Winkel x (im Bogenmaß) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| weil x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |