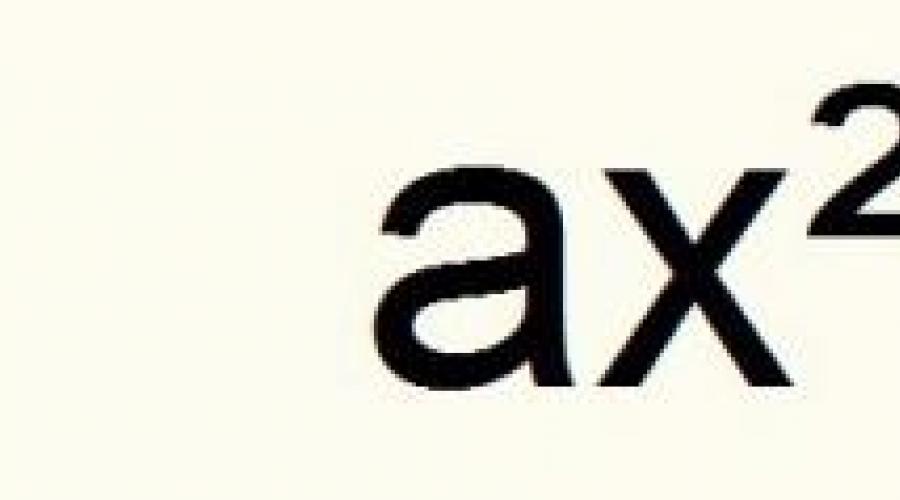
Acest subiect poate părea complicat la început din cauza numeroaselor formule nu atât de simple. Nu numai că ecuațiile pătratice în sine au notații lungi, dar rădăcinile se găsesc și prin discriminant. În total, se obțin trei formule noi. Nu foarte ușor de reținut. Acest lucru este posibil numai după rezolvarea frecventă a unor astfel de ecuații. Atunci toate formulele vor fi reținute de la sine.

Vedere generală a unei ecuații pătratice

Aici propunem înregistrarea lor explicită, când se scrie mai întâi gradul cel mai mare, apoi în ordine descrescătoare. Există adesea situații în care termenii sunt inconsecvenți. Atunci este mai bine să rescrieți ecuația în ordinea descrescătoare a gradului variabilei.

Să introducem o notație. Ele sunt prezentate în tabelul de mai jos.

Dacă acceptăm aceste notații, toate ecuațiile pătratice sunt reduse la următoarea notație.

Mai mult, coeficientul a ≠ 0. Fie ca această formulă să fie desemnată numărul unu.

Când este dată o ecuație, nu este clar câte rădăcini vor fi în răspuns. Pentru că una dintre cele trei opțiuni este întotdeauna posibilă:

• soluția va avea două rădăcini;
• răspunsul va fi un număr;
• ecuația nu va avea deloc rădăcini.

Și până la finalizarea deciziei, este greu de înțeles care opțiune va apărea într-un anumit caz.

Tipuri de înregistrări ale ecuațiilor pătratice

Pot exista diferite intrări în sarcini. Nu vor arăta întotdeauna ca formula generala ecuație pătratică. Uneori îi vor lipsi niște termeni. Ceea ce a fost scris mai sus este ecuația completă. Dacă eliminați al doilea sau al treilea termen din el, obțineți altceva. Aceste înregistrări sunt numite și ecuații pătratice, doar incomplete.

Mai mult, numai termenii cu coeficienții „b” și „c” pot dispărea. Numărul „a” nu poate fi egal cu zero în nicio circumstanță. Pentru că în acest caz formula devine ecuație liniară. Formulele pentru forma incompletă a ecuațiilor vor fi următoarele:

Deci, există doar două tipuri; pe lângă cele complete, există și ecuații pătratice incomplete. Prima formulă să fie numărul doi, iar a doua - trei.

Discriminarea și dependența numărului de rădăcini de valoarea acestuia

Trebuie să cunoașteți acest număr pentru a calcula rădăcinile ecuației. Poate fi întotdeauna calculată, indiferent de formula ecuației pătratice. Pentru a calcula discriminantul, trebuie să folosiți egalitatea scrisă mai jos, care va avea numărul patru.

După înlocuirea valorilor coeficientului în această formulă, puteți obține numere cu semne diferite. Dacă răspunsul este da, atunci răspunsul la ecuație va fi două rădăcini diferite. Dacă numărul este negativ, nu vor exista rădăcini ale ecuației pătratice. Dacă este egal cu zero, va exista un singur răspuns.

Cum se rezolvă o ecuație pătratică completă?

De fapt, luarea în considerare a acestei probleme a început deja. Pentru că mai întâi trebuie să găsești un discriminant. După ce se stabilește că există rădăcini ale ecuației pătratice și numărul acestora este cunoscut, trebuie să utilizați formule pentru variabile. Dacă există două rădăcini, atunci trebuie să aplicați următoarea formulă.

Deoarece conține un semn „±”, vor exista două valori. Expresie sub semn rădăcină pătrată este un discriminator. Prin urmare, formula poate fi rescrisă diferit.

Formula numărul cinci. Din aceeași înregistrare este clar că dacă discriminantul este egal cu zero, atunci ambele rădăcini vor lua aceleași valori.

Dacă rezolvarea ecuațiilor pătratice nu a fost încă elaborată, atunci este mai bine să notați valorile tuturor coeficienților înainte de a aplica formulele discriminante și variabile. Mai târziu, acest moment nu va crea dificultăți. Dar la început există confuzie.

Cum se rezolvă o ecuație pătratică incompletă?

Totul este mult mai simplu aici. Nici măcar nu este nevoie de formule suplimentare. Iar cele care au fost deja notate pentru discriminant și necunoscut nu vor fi necesare.

Mai întâi, să ne uităm la ecuația numărul doi incompletă. În această egalitate, este necesar să scoateți cantitatea necunoscută din paranteze și să rezolvați ecuația liniară, care va rămâne între paranteze. Răspunsul va avea două rădăcini. Prima este neapărat egală cu zero, deoarece există un multiplicator format din variabila însăși. Al doilea se va obține prin rezolvarea unei ecuații liniare.

Ecuația incompletă numărul trei este rezolvată prin mutarea numărului din partea stângă a egalității la dreapta. Apoi, trebuie să împărțiți cu coeficientul în fața necunoscutului. Tot ce rămâne este să extragi rădăcina pătrată și să nu uiți să o notezi de două ori cu semne opuse.

Mai jos sunt câțiva pași care vă vor ajuta să învățați cum să rezolvați tot felul de egalități care se transformă în ecuații pătratice. Ele vor ajuta elevul să evite greșelile din cauza neatenției. Aceste neajunsuri pot cauza note slabe atunci când studiezi un subiect amplu”. Ecuații cuadratice(clasa a 8-a)". Ulterior, aceste acțiuni nu vor trebui efectuate în mod constant. Pentru că va apărea o abilitate stabilă.

• Mai întâi trebuie să scrieți ecuația în formă standard. Adică, mai întâi termenul cu cel mai mare grad al variabilei, apoi - fără un grad, și ultimul - doar un număr.

• Dacă înaintea coeficientului „a apare un minus”, poate complica munca unui începător care studiază ecuațiile pătratice. Este mai bine să scapi de el. În acest scop, toată egalitatea trebuie înmulțită cu „-1”. Aceasta înseamnă că toți termenii vor schimba semnul invers.

• Se recomandă să scăpați de fracții în același mod. Pur și simplu înmulțiți ecuația cu factorul corespunzător, astfel încât numitorii să se anuleze.

Exemple

Este necesar să se rezolve următoarele ecuații pătratice:

x 2 − 7x = 0;

15 − 2x − x 2 = 0;

x 2 + 8 + 3x = 0;

12x + x 2 + 36 = 0;

(x+1) 2 + x + 1 = (x+1)(x+2).

Prima ecuație: x 2 − 7x = 0. Este incompletă, prin urmare se rezolvă așa cum este descris pentru formula numărul doi.

După ce o scoateți din paranteze, rezultă: x (x - 7) = 0.

Prima rădăcină ia valoarea: x 1 = 0. A doua va fi găsită din ecuația liniară: x - 7 = 0. Este ușor de observat că x 2 = 7.

A doua ecuație: 5x 2 + 30 = 0. Din nou incompletă. Doar că se rezolvă așa cum este descris pentru a treia formulă.

După ce mutați 30 în partea dreaptă a ecuației: 5x 2 = 30. Acum trebuie să împărțiți la 5. Rezultă: x 2 = 6. Răspunsurile vor fi numerele: x 1 = √6, x 2 = - √6.

A treia ecuație: 15 − 2x − x 2 = 0. Aici și mai departe, rezolvarea ecuațiilor pătratice va începe prin a le rescrie în forma standard: − x 2 − 2x + 15 = 0. Acum este timpul să folosiți a doua ecuație. sfat utilși înmulțiți totul cu minus unu. Se dovedește x 2 + 2x - 15 = 0. Folosind a patra formulă, trebuie să calculați discriminantul: D = 2 2 - 4 * (- 15) = 4 + 60 = 64. Este un număr pozitiv. Din cele spuse mai sus, reiese că ecuația are două rădăcini. Ele trebuie calculate folosind a cincea formulă. Rezultă că x = (-2 ± √64) / 2 = (-2 ± 8) / 2. Atunci x 1 = 3, x 2 = - 5.

A patra ecuație x 2 + 8 + 3x = 0 se transformă în aceasta: x 2 + 3x + 8 = 0. Discriminantul său este egal cu această valoare: -23. Deoarece acest număr este negativ, răspunsul la această sarcină va fi următoarea intrare: „Nu există rădăcini”.

A cincea ecuație 12x + x 2 + 36 = 0 ar trebui rescrisă după cum urmează: x 2 + 12x + 36 = 0. După aplicarea formulei discriminantului, se obține numărul zero. Aceasta înseamnă că va avea o singură rădăcină, și anume: x = -12/ (2 * 1) = -6.

A șasea ecuație (x+1) 2 + x + 1 = (x+1)(x+2) necesită transformări, care constau în faptul că trebuie să aduci termeni similari, deschizând mai întâi parantezele. În locul primei va exista următoarea expresie: x 2 + 2x + 1. După egalitate, va apărea această intrare: x 2 + 3x + 2. După ce se numără termeni similari, ecuația va lua forma: x 2 - x = 0. A devenit incomplet . Ceva similar cu asta a fost deja discutat puțin mai sus. Rădăcinile acestuia vor fi numerele 0 și 1.

Ecuația formei

Expresie D= b 2 - 4 ac numit discriminant ecuație pătratică. DacăD = 0, atunci ecuația are o rădăcină reală; daca D> 0, atunci ecuația are două rădăcini reale.
În cazul în care D = 0 , se spune uneori că o ecuație pătratică are două rădăcini identice.
Folosind notația D= b 2 - 4 ac, putem rescrie formula (2) sub forma

Dacă b= 2k, atunci formula (2) ia forma:

Unde k= b / 2 .
Ultima formulă este deosebit de convenabilă în cazurile în care b / 2 - un număr întreg, adică coeficient b- număr par.
Exemplul 1: Rezolvați ecuația 2 X 2 - 5 x + 2 = 0 . Aici a = 2, b = -5, c = 2. Avem D= b 2 - 4 ac = (-5) 2- 4*2*2 = 9 . Deoarece D > 0 , atunci ecuația are două rădăcini. Să le găsim folosind formula (2)

Asa de X 1 =(5 + 3) / 4 = 2, x 2 =(5 - 3) / 4 = 1 / 2 ,
acesta este X 1 = 2 Și X 2 = 1 / 2 - rădăcini ecuația dată.
Exemplul 2: Rezolvați ecuația 2 X 2 - 3 x + 5 = 0 . Aici a = 2, b = -3, c = 5. Găsirea discriminantului D= b 2 - 4 ac = (-3) 2- 4*2*5 = -31 . Deoarece D 0 , atunci ecuația nu are rădăcini reale.

Ecuații patratice incomplete. Dacă într-o ecuație pătratică topor 2 +bx+c =0 al doilea coeficient b sau membru gratuit c este egal cu zero, atunci se numește ecuația pătratică incomplet. Ecuațiile incomplete sunt evidențiate deoarece pentru a le găsi rădăcinile nu trebuie să utilizați formula pentru rădăcinile unei ecuații pătratice - este mai ușor să rezolvați ecuația prin factorizarea părții stângi.
Exemplul 1: rezolva ecuatia 2 X 2 - 5 x = 0 .
Avem X(2 x - 5) = 0 . Deci fie X = 0 , sau 2 X - 5 = 0 , acesta este X = 2.5 . Deci ecuația are două rădăcini: 0 Și 2.5
Exemplul 2: rezolva ecuatia 3 X 2 - 27 = 0 .
Avem 3 X 2 = 27 . Prin urmare, rădăcinile acestei ecuații sunt 3 Și -3 .

teorema lui Vieta. Dacă ecuaţia pătratică redusă X 2 +px+q =0 are rădăcini reale, atunci suma lor este egală cu - p, iar produsul este egal q, acesta este

x 1 + x 2 = -p,
x 1 x 2 = q

(suma rădăcinilor ecuației pătratice de mai sus este egală cu al doilea coeficient luat cu semnul opus, iar produsul rădăcinilor este egal cu termenul liber).

Primul nivel

Ecuații cuadratice. Ghid cuprinzător (2019)

În termenul „ecuație pătratică”, cuvântul cheie este „quadratic”. Aceasta înseamnă că ecuația trebuie să conțină în mod necesar o variabilă (același x) pătrat și nu ar trebui să existe x la cea de-a treia putere (sau mai mare).

Rezolvarea multor ecuații se reduce la rezolvarea ecuațiilor pătratice.

Să învățăm să determinăm că aceasta este o ecuație pătratică și nu o altă ecuație.

Exemplul 1.

Să scăpăm de numitor și să înmulțim fiecare termen al ecuației cu

Să mutăm totul în partea stângă și să aranjam termenii în ordinea descrescătoare a puterilor lui X

Acum putem spune cu încredere că ecuația dată este pătrat!

Exemplul 2.

Înmulțiți părțile din stânga și din dreapta cu:

Această ecuație, deși a fost inițial în ea, nu este pătratică!

Exemplul 3.

Să înmulțim totul cu:

Infricosator? Gradul al patrulea și al doilea... Totuși, dacă facem o înlocuire, vom vedea că avem o ecuație pătratică simplă:

Exemplul 4.

Se pare că este acolo, dar să aruncăm o privire mai atentă. Să mutăm totul în partea stângă:

Vezi, este redusă - și acum este o simplă ecuație liniară!

Acum încercați să determinați singuri care dintre următoarele ecuații sunt pătratice și care nu:

Exemple:

Raspunsuri:

1. pătrat;
2. pătrat;
3. nu pătrat;
4. nu pătrat;
5. nu pătrat;
6. pătrat;
7. nu pătrat;
8. pătrat.

În mod convențional, matematicienii împart toate ecuațiile pătratice în următoarele tipuri:

• Completează ecuațiile pătratice- ecuații în care coeficienții și, precum și termenul liber c, nu sunt egali cu zero (ca în exemplu). În plus, printre ecuațiile pătratice complete există dat- acestea sunt ecuații în care coeficientul (ecuația din exemplul unu este nu numai completă, ci și redusă!)

• Ecuații patratice incomplete- ecuații în care coeficientul și/sau termenul liber c sunt egali cu zero:

  Sunt incomplete pentru că le lipsește un element. Dar ecuația trebuie să conțină întotdeauna x pătrat!!! În caz contrar, nu va mai fi o ecuație pătratică, ci o altă ecuație.

De ce au venit cu o asemenea împărțire? S-ar părea că există un X pătrat și bine. Această împărțire este determinată de metodele de soluție. Să ne uităm la fiecare dintre ele mai detaliat.

Rezolvarea ecuațiilor pătratice incomplete

În primul rând, să ne concentrăm pe rezolvarea ecuațiilor pătratice incomplete - sunt mult mai simple!

Există tipuri de ecuații pătratice incomplete:

1. , în această ecuație coeficientul este egal.
2. , în această ecuație termenul liber este egal cu.
3. , în această ecuație coeficientul și termenul liber sunt egali.

1. i. Deoarece știm să luăm rădăcina pătrată, să exprimăm din această ecuație

Expresia poate fi fie negativă, fie pozitivă. Un număr pătrat nu poate fi negativ, deoarece la înmulțirea a două numere negative sau două pozitive, rezultatul va fi întotdeauna un număr pozitiv, deci: dacă, atunci ecuația nu are soluții.

Și dacă, atunci obținem două rădăcini. Nu este nevoie să memorezi aceste formule. Principalul lucru este că trebuie să știți și să vă amintiți întotdeauna că nu poate fi mai puțin.

Să încercăm să rezolvăm câteva exemple.

Exemplul 5:

Rezolvați ecuația

Acum tot ce rămâne este să extragi rădăcina din partea stângă și dreaptă. La urma urmei, îți amintești cum să extragi rădăcini?

Răspuns:

Nu uita niciodată de rădăcinile cu semn negativ!!!

Exemplul 6:

Rezolvați ecuația

Răspuns:

Exemplul 7:

Rezolvați ecuația

Oh! Pătratul unui număr nu poate fi negativ, ceea ce înseamnă că ecuația

fara radacini!

Pentru astfel de ecuații care nu au rădăcini, matematicienii au venit cu o pictogramă specială - (set gol). Și răspunsul poate fi scris astfel:

Răspuns:

Astfel, această ecuație pătratică are două rădăcini. Nu există restricții aici, deoarece nu am extras rădăcina.
Exemplul 8:

Rezolvați ecuația

Să scoatem factorul comun din paranteze:

Prin urmare,

Această ecuație are două rădăcini.

Răspuns:

Cel mai simplu tip de ecuații pătratice incomplete (deși toate sunt simple, nu?). Evident, această ecuație are întotdeauna o singură rădăcină:

Ne vom dispensa de exemple aici.

Rezolvarea ecuațiilor pătratice complete

Vă reamintim că o ecuație pătratică completă este o ecuație a ecuației de formă unde

Rezolvarea ecuațiilor pătratice complete este puțin mai dificilă (doar puțin) decât acestea.

Tine minte, Orice ecuație pătratică poate fi rezolvată folosind un discriminant! Chiar incomplet.

Celelalte metode te vor ajuta să o faci mai rapid, dar dacă ai probleme cu ecuațiile pătratice, mai întâi stăpânește soluția folosind discriminantul.

1. Rezolvarea ecuațiilor pătratice folosind un discriminant.

Rezolvarea ecuațiilor pătratice folosind această metodă este foarte simplă; principalul lucru este să vă amintiți succesiunea de acțiuni și câteva formule.

Dacă, atunci ecuația are rădăcină. Atentie speciala Fă un pas. Discriminantul () ne spune numărul de rădăcini ale ecuației.

• Dacă, atunci formula din pas se va reduce la. Astfel, ecuația va avea doar o rădăcină.
• Dacă, atunci nu vom putea extrage rădăcina discriminantului la pas. Aceasta indică faptul că ecuația nu are rădăcini.

Să ne întoarcem la ecuațiile noastre și să vedem câteva exemple.

Exemplul 9:

Rezolvați ecuația

Pasul 1 sărim.

Pasul 2.

Găsim discriminantul:

Aceasta înseamnă că ecuația are două rădăcini.

Pasul 3.

Răspuns:

Exemplul 10:

Rezolvați ecuația

Ecuația este prezentată în formă standard, deci Pasul 1 sărim.

Pasul 2.

Găsim discriminantul:

Aceasta înseamnă că ecuația are o singură rădăcină.

Răspuns:

Exemplul 11:

Rezolvați ecuația

Ecuația este prezentată în formă standard, deci Pasul 1 sărim.

Pasul 2.

Găsim discriminantul:

Aceasta înseamnă că nu vom putea extrage rădăcina discriminantului. Nu există rădăcini ale ecuației.

Acum știm cum să scriem corect astfel de răspunsuri.

Răspuns: fara radacini

2. Rezolvarea ecuațiilor pătratice folosind teorema lui Vieta.

Dacă vă amintiți, există un tip de ecuație care se numește redusă (când coeficientul a este egal cu):

Astfel de ecuații sunt foarte ușor de rezolvat folosind teorema lui Vieta:

Suma rădăcinilor dat ecuația pătratică este egală, iar produsul rădăcinilor este egal.

Exemplul 12:

Rezolvați ecuația

Această ecuație poate fi rezolvată folosind teorema lui Vieta deoarece .

Suma rădăcinilor ecuației este egală, adică. obținem prima ecuație:

Și produsul este egal cu:

Să compunem și să rezolvăm sistemul:

• Și. Suma este egală cu;
• Și. Suma este egală cu;
• Și. Suma este egală.

și sunt soluția pentru sistem:

Răspuns: ; .

Exemplul 13:

Rezolvați ecuația

Răspuns:

Exemplul 14:

Rezolvați ecuația

Ecuația este dată, ceea ce înseamnă:

Răspuns:

ECUAȚII CADRATICE. NIVEL MEDIU

Ce este o ecuație pătratică?

Cu alte cuvinte, o ecuație pătratică este o ecuație de forma, unde - necunoscutul, - unele numere și.

Numărul se numește cel mai mare sau primul coeficient ecuație pătratică, - al doilea coeficient, A - membru liber.

De ce? Pentru că dacă ecuația devine imediat liniară, pentru că va disparea.

În acest caz, și poate fi egal cu zero. În această ecuație de scaun se numește incompletă. Dacă toți termenii sunt la locul lor, adică, ecuația este completă.

Soluții la diferite tipuri de ecuații pătratice

Metode de rezolvare a ecuațiilor pătratice incomplete:

În primul rând, să ne uităm la metodele de rezolvare a ecuațiilor pătratice incomplete - sunt mai simple.

Putem distinge următoarele tipuri de ecuații:

I., în această ecuație coeficientul și termenul liber sunt egali.

II. , în această ecuație coeficientul este egal.

III. , în această ecuație termenul liber este egal cu.

Acum să ne uităm la soluția pentru fiecare dintre aceste subtipuri.

Evident, această ecuație are întotdeauna o singură rădăcină:

Un număr pătrat nu poate fi negativ, deoarece atunci când înmulțiți două numere negative sau două pozitive, rezultatul va fi întotdeauna un număr pozitiv. De aceea:

dacă, atunci ecuația nu are soluții;

dacă avem două rădăcini

Nu este nevoie să memorezi aceste formule. Principalul lucru de reținut este că nu poate fi mai puțin.

Exemple:

Solutii:

Răspuns:

Nu uita niciodată de rădăcinile cu semn negativ!

Pătratul unui număr nu poate fi negativ, ceea ce înseamnă că ecuația

fara radacini.

Pentru a nota pe scurt că o problemă nu are soluții, folosim pictograma set gol.

Răspuns:

Deci, această ecuație are două rădăcini: și.

Răspuns:

Să scoatem factorul comun din paranteze:

Produsul este egal cu zero dacă cel puțin unul dintre factori este egal cu zero. Aceasta înseamnă că ecuația are o soluție atunci când:

Deci, această ecuație pătratică are două rădăcini: și.

Exemplu:

Rezolvați ecuația.

Soluţie:

Să factorizăm partea stângă a ecuației și să găsim rădăcinile:

Răspuns:

Metode de rezolvare a ecuațiilor pătratice complete:

1. Discriminant

Rezolvarea ecuațiilor pătratice în acest fel este ușoară, principalul lucru este să vă amintiți succesiunea de acțiuni și câteva formule. Amintiți-vă, orice ecuație pătratică poate fi rezolvată folosind un discriminant! Chiar incomplet.

Ați observat rădăcina de la discriminant în formula pentru rădăcini? Dar discriminantul poate fi negativ. Ce să fac? Trebuie să acordăm o atenție deosebită pasului 2. Discriminantul ne spune numărul de rădăcini ale ecuației.

• Dacă, atunci ecuația are rădăcini:
• Dacă, atunci ecuația are aceleași rădăcini și, de fapt, o rădăcină:

  Astfel de rădăcini se numesc rădăcini duble.

• Dacă, atunci rădăcina discriminantului nu este extrasă. Aceasta indică faptul că ecuația nu are rădăcini.

De ce este posibil cantități diferite rădăcini? Să ne întoarcem la semnificația geometrică a ecuației pătratice. Graficul funcției este o parabolă:

Într-un caz special, care este o ecuație pătratică, . Aceasta înseamnă că rădăcinile unei ecuații pătratice sunt punctele de intersecție cu axa (axa) absciselor. O parabolă poate să nu intersecteze axa deloc sau o poate intersecta într-unul (când vârful parabolei se află pe axă) sau două puncte.

În plus, coeficientul este responsabil pentru direcția ramurilor parabolei. Dacă, atunci ramurile parabolei sunt îndreptate în sus, iar dacă, atunci în jos.

Exemple:

Solutii:

Răspuns:

Răspuns: .

Răspuns:

Asta înseamnă că nu există soluții.

Răspuns: .

2. Teorema lui Vieta

Este foarte ușor de folosit teorema lui Vieta: trebuie doar să alegeți o pereche de numere al căror produs este egal cu termenul liber al ecuației, iar suma este egală cu al doilea coeficient luat cu semnul opus.

Este important să ne amintim că teorema lui Vieta poate fi aplicată numai în ecuații pătratice reduse ().

Să ne uităm la câteva exemple:

Exemplul #1:

Rezolvați ecuația.

Soluţie:

Această ecuație poate fi rezolvată folosind teorema lui Vieta deoarece . Alți coeficienți: ; .

Suma rădăcinilor ecuației este:

Și produsul este egal cu:

Să selectăm perechi de numere al căror produs este egal și să verificăm dacă suma lor este egală:

• Și. Suma este egală cu;
• Și. Suma este egală cu;
• Și. Suma este egală.

și sunt soluția pentru sistem:

Astfel, și sunt rădăcinile ecuației noastre.

Răspuns: ; .

Exemplul #2:

Soluţie:

Să selectăm perechi de numere care dau în produs și apoi să verificăm dacă suma lor este egală:

si: dau in total.

si: dau in total. Pentru a obține, este suficient să schimbați pur și simplu semnele presupuselor rădăcini: și, la urma urmei, produsul.

Răspuns:

Exemplul #3:

Soluţie:

Termenul liber al ecuației este negativ și, prin urmare, produsul rădăcinilor este un număr negativ. Acest lucru este posibil numai dacă una dintre rădăcini este negativă, iar cealaltă este pozitivă. Prin urmare, suma rădăcinilor este egală cu diferențele modulelor lor.

Să selectăm astfel de perechi de numere care dau în produs și a căror diferență este egală cu:

și: diferența lor este egală - nu se potrivește;

și: - neadecvat;

și: - neadecvat;

şi: - potrivite. Tot ce rămâne este să ne amintim că una dintre rădăcini este negativă. Deoarece suma lor trebuie să fie egală, rădăcina cu modulul mai mic trebuie să fie negativă: . Verificăm:

Răspuns:

Exemplul #4:

Rezolvați ecuația.

Soluţie:

Ecuația este dată, ceea ce înseamnă:

Termenul liber este negativ și, prin urmare, produsul rădăcinilor este negativ. Și acest lucru este posibil numai atunci când o rădăcină a ecuației este negativă, iar cealaltă este pozitivă.

Să selectăm perechi de numere al căror produs este egal și apoi să determinăm care rădăcini ar trebui să aibă semn negativ:

Evident, doar rădăcinile și sunt potrivite pentru prima condiție:

Răspuns:

Exemplul #5:

Rezolvați ecuația.

Soluţie:

Ecuația este dată, ceea ce înseamnă:

Suma rădăcinilor este negativă, ceea ce înseamnă că cel puțin una dintre rădăcini este negativă. Dar, deoarece produsul lor este pozitiv, înseamnă că ambele rădăcini au semnul minus.

Să selectăm perechi de numere al căror produs este egal cu:

Evident, rădăcinile sunt numerele și.

Răspuns:

De acord, este foarte convenabil să veniți cu rădăcini oral, în loc să numărați acest discriminant urât. Încercați să utilizați teorema lui Vieta cât mai des posibil.

Dar teorema lui Vieta este necesară pentru a facilita și accelera găsirea rădăcinilor. Pentru a beneficia de pe urma folosirii lui, trebuie să aduci acțiunile la automatitate. Și pentru asta, rezolvă încă cinci exemple. Dar nu înșela: nu poți folosi un discriminant! Doar teorema lui Vieta:

Soluții la sarcini pentru munca independentă:

Sarcina 1. ((x)^(2))-8x+12=0

Conform teoremei lui Vieta:

Ca de obicei, începem selecția cu piesa:

Nu este potrivit pentru că suma;

: suma este exact ceea ce ai nevoie.

Răspuns: ; .

Sarcina 2.

Și din nou teorema noastră preferată Vieta: suma trebuie să fie egală, iar produsul trebuie să fie egal.

Dar din moment ce nu trebuie să fie, dar, schimbăm semnele rădăcinilor: și (în total).

Răspuns: ; .

Sarcina 3.

Hmm... Unde este asta?

Trebuie să mutați toți termenii într-o singură parte:

Suma rădăcinilor este egală cu produsul.

Bine, oprește-te! Ecuația nu este dată. Dar teorema lui Vieta este aplicabilă numai în ecuațiile date. Deci mai întâi trebuie să dați o ecuație. Dacă nu poți conduce, renunță la această idee și rezolvă-o într-un alt mod (de exemplu, printr-un discriminant). Permiteți-mi să vă reamintesc că a da o ecuație pătratică înseamnă a egaliza coeficientul principal:

Grozav. Apoi suma rădăcinilor este egală cu și produsul.

Aici este la fel de ușor ca decojirea perelor să alegi: la urma urmei, este un număr prim (scuze pentru tautologie).

Răspuns: ; .

Sarcina 4.

Membrul liber este negativ. Ce e special la asta? Și adevărul este că rădăcinile vor avea semne diferite. Și acum, în timpul selecției, verificăm nu suma rădăcinilor, ci diferența dintre modulele lor: această diferență este egală, dar un produs.

Deci, rădăcinile sunt egale cu și, dar una dintre ele este minus. Teorema lui Vieta ne spune că suma rădăcinilor este egală cu al doilea coeficient cu semnul opus, adică. Aceasta înseamnă că rădăcina mai mică va avea un minus: și, din moment ce.

Răspuns: ; .

Sarcina 5.

Ce ar trebui să faci mai întâi? Așa este, dați ecuația:

Din nou: selectăm factorii numărului, iar diferența lor ar trebui să fie egală cu:

Rădăcinile sunt egale cu și, dar una dintre ele este minus. Care? Suma lor ar trebui să fie egală, ceea ce înseamnă că minusul va avea o rădăcină mai mare.

Răspuns: ; .

Lasă-mă să rezum:

1. Teorema lui Vieta este folosită numai în ecuațiile pătratice date.
2. Folosind teorema lui Vieta, puteți găsi rădăcinile prin selecție, oral.
3. Dacă ecuația nu este dată sau nu se găsește o pereche adecvată de factori ai termenului liber, atunci nu există rădăcini întregi și trebuie să o rezolvați în alt mod (de exemplu, printr-un discriminant).

3. Metoda de selectare a unui pătrat complet

Dacă toți termenii care conțin necunoscutul sunt reprezentați sub formă de termeni din formule de înmulțire prescurtate - pătratul sumei sau al diferenței - atunci după înlocuirea variabilelor, ecuația poate fi prezentată sub forma unei ecuații pătratice incomplete de tip.

De exemplu:

Exemplul 1:

Rezolvați ecuația: .

Soluţie:

Răspuns:

Exemplul 2:

Rezolvați ecuația: .

Soluţie:

Răspuns:

ÎN vedere generala transformarea va arata astfel:

Asta implică: .

Nu-ți aduce aminte de nimic? Acesta este un lucru discriminatoriu! Exact așa am obținut formula discriminantă.

ECUAȚII CADRATICE. SCURT DESPRE LUCRURILE PRINCIPALE

Ecuație pătratică- aceasta este o ecuație de formă, unde - necunoscutul, - coeficienții ecuației pătratice, - termenul liber.

Ecuație pătratică completă- o ecuație în care coeficienții nu sunt egali cu zero.

Ecuație pătratică redusă- o ecuaţie în care coeficientul, adică: .

Ecuație pătratică incompletă- o ecuație în care coeficientul și/sau termenul liber c sunt egali cu zero:

• dacă coeficientul, ecuația arată astfel: ,
• dacă există un termen liber, ecuația are forma: ,
• dacă și, ecuația arată astfel: .

1. Algoritm pentru rezolvarea ecuațiilor pătratice incomplete

1.1. O ecuație pătratică incompletă de forma, unde:

1) Să exprimăm necunoscutul: ,

2) Verificați semnul expresiei:

• dacă, atunci ecuația nu are soluții,
• dacă, atunci ecuația are două rădăcini.

1.2. O ecuație pătratică incompletă de forma, unde:

1) Să scoatem factorul comun din paranteze: ,

2) Produsul este egal cu zero dacă cel puțin unul dintre factori este egal cu zero. Prin urmare, ecuația are două rădăcini:

1.3. O ecuație pătratică incompletă de forma, unde:

Această ecuație are întotdeauna o singură rădăcină: .

2. Algoritm pentru rezolvarea ecuaţiilor pătratice complete de forma unde

2.1. Soluție folosind discriminant

1) Să reducem ecuația la vedere standard: ,

2) Să calculăm discriminantul folosind formula: , care indică numărul de rădăcini ale ecuației:

3) Aflați rădăcinile ecuației:

• dacă, atunci ecuația are rădăcini, care se găsesc prin formula:
• dacă, atunci ecuația are o rădăcină, care se găsește prin formula:
• dacă, atunci ecuația nu are rădăcini.

2.2. Rezolvare folosind teorema lui Vieta

Suma rădăcinilor ecuației pătratice reduse (ecuația formei unde) este egală, iar produsul rădăcinilor este egal, i.e. , A.

2.3. Rezolvare prin metoda selectării unui pătrat complet

Continuăm să studiem subiectul " rezolvarea ecuatiilor" Ne-am familiarizat deja cu ecuațiile liniare și trecem la cunoștință ecuații pătratice.

În primul rând, ne vom uita la ce este o ecuație pătratică, cum este scrisă în formă generală și vom da definiții înrudite. După aceasta, vom folosi exemple pentru a examina în detaliu modul în care sunt rezolvate ecuațiile pătratice incomplete. Să trecem la soluție ecuații complete, vom obține formula rădăcinii, ne vom familiariza cu discriminantul unei ecuații pătratice și vom lua în considerare soluții la exemple tipice. În cele din urmă, să urmărim conexiunile dintre rădăcini și coeficienți.

Navigare în pagină.

Ce este o ecuație pătratică? Tipurile lor

Mai întâi trebuie să înțelegeți clar ce este o ecuație pătratică. Prin urmare, este logic să începem o conversație despre ecuațiile pătratice cu definiția unei ecuații pătratice, precum și definițiile aferente. După aceasta, puteți lua în considerare principalele tipuri de ecuații pătratice: reduse și nereduse, precum și ecuații complete și incomplete.

Definiție și exemple de ecuații pătratice

Definiție.

Ecuație pătratică este o ecuație a formei a x 2 +b x+c=0, unde x este o variabilă, a, b și c sunt unele numere, iar a este diferit de zero.

Să spunem imediat că ecuațiile pătratice sunt adesea numite ecuații de gradul doi. Acest lucru se datorează faptului că ecuația pătratică este ecuație algebrică gradul doi.

Definiția menționată ne permite să dăm exemple de ecuații pătratice. Deci 2 x 2 +6 x+1=0, 0,2 x 2 +2,5 x+0,03=0 etc. Acestea sunt ecuații pătratice.

Definiție.

Numerele a, b și c sunt numite coeficienții ecuației pătratice a·x 2 +b·x+c=0, iar coeficientul a se numește primul, sau cel mai mare, sau coeficientul lui x 2, b este al doilea coeficient sau coeficientul lui x și c este termenul liber .

De exemplu, să luăm o ecuație pătratică de forma 5 x 2 −2 x −3=0, aici coeficientul principal este 5, al doilea coeficient este egal cu −2, iar termenul liber este egal cu −3. Rețineți că atunci când coeficienții b și/sau c sunt negativi, ca în exemplul dat, atunci forma scurta scriind o ecuație pătratică de forma 5 x 2 −2 x−3=0, și nu 5 x 2 +(−2) x+(−3)=0.

Este demn de remarcat faptul că, atunci când coeficienții a și/sau b sunt egali cu 1 sau -1, atunci ei nu sunt de obicei prezenți în mod explicit în ecuația pătratică, ceea ce se datorează particularităților scrierii astfel de. De exemplu, în ecuația pătratică y 2 −y+3=0 coeficientul principal este unu, iar coeficientul lui y este egal cu −1.

Ecuații patratice reduse și nereduse

În funcție de valoarea coeficientului conducător, se disting ecuațiile pătratice reduse și nereduse. Să dăm definițiile corespunzătoare.

Definiție.

Se numește o ecuație pătratică în care coeficientul principal este 1 ecuație pătratică dată. În caz contrar, ecuația pătratică este neatins.

Conform această definiție, ecuații pătratice x 2 −3·x+1=0, x 2 −x−2/3=0 etc. – dat, în fiecare dintre ele primul coeficient este egal cu unu. A 5 x 2 −x−1=0 etc. - ecuații pătratice nereduse, coeficienții lor conducători sunt diferiți de 1.

Din orice ecuație pătratică neredusă, împărțind ambele părți la coeficientul principal, se poate trece la cea redusă. Această acțiune este o transformare echivalentă, adică ecuația pătratică redusă obținută în acest fel are aceleași rădăcini ca și ecuația pătratică neredusă inițială sau, ca ea, nu are rădăcini.

Să ne uităm la un exemplu despre cum se realizează tranziția de la o ecuație pătratică neredusă la una redusă.

Exemplu.

Din ecuația 3 x 2 +12 x−7=0, mergeți la ecuația pătratică redusă corespunzătoare.

Soluţie.

Trebuie doar să împărțim ambele părți ale ecuației inițiale la coeficientul principal 3, acesta este diferit de zero, astfel încât să putem efectua această acțiune. Avem (3 x 2 +12 x−7):3=0:3, care este același, (3 x 2):3+(12 x):3−7:3=0 și apoi (3: 3) x 2 +(12:3) x−7:3=0, de unde . Așa am obținut ecuația pătratică redusă, care este echivalentă cu cea inițială.

Răspuns:

Ecuații pătratice complete și incomplete

Definiția unei ecuații pătratice conține condiția a≠0. Această condiție este necesară pentru ca ecuația a x 2 + b x + c = 0 să fie pătratică, deoarece atunci când a = 0 devine de fapt o ecuație liniară de forma b x + c = 0.

În ceea ce privește coeficienții b și c, aceștia pot fi egali cu zero, atât individual, cât și împreună. În aceste cazuri, ecuația pătratică se numește incompletă.

Definiție.

Ecuația pătratică a x 2 +b x+c=0 se numește incomplet, dacă cel puțin unul dintre coeficienții b, c este egal cu zero.

La randul lui

Definiție.

Ecuație pătratică completă este o ecuație în care toți coeficienții sunt diferiți de zero.

Asemenea nume nu au fost date întâmplător. Acest lucru va deveni clar din discuțiile următoare.

Dacă coeficientul b este zero, atunci ecuația pătratică ia forma a·x 2 +0·x+c=0 și este echivalentă cu ecuația a·x 2 +c=0. Dacă c=0, adică ecuația pătratică are forma a·x 2 +b·x+0=0, atunci poate fi rescrisă ca a·x 2 +b·x=0. Și cu b=0 și c=0 obținem ecuația pătratică a·x 2 =0. Ecuațiile rezultate diferă de ecuația pătratică completă prin aceea că părțile lor din stânga nu conțin nici un termen cu variabila x, nici un termen liber sau ambele. De aici și numele lor - ecuații patratice incomplete.

Deci ecuațiile x 2 +x+1=0 și −2 x 2 −5 x+0,2=0 sunt exemple de ecuații patratice complete, iar x 2 =0, −2 x 2 =0, 5 x 2 +3=0 , −x 2 −5 x=0 sunt ecuații pătratice incomplete.

Rezolvarea ecuațiilor pătratice incomplete

Din informațiile din paragraful anterior rezultă că există trei tipuri de ecuații pătratice incomplete:

• a·x 2 =0, îi corespund coeficienții b=0 și c=0;
• a x 2 +c=0 când b=0;
• şi a·x 2 +b·x=0 când c=0.

Să examinăm în ordine modul în care sunt rezolvate ecuațiile pătratice incomplete ale fiecăruia dintre aceste tipuri.

a x 2 =0

Să începem cu rezolvarea ecuațiilor pătratice incomplete în care coeficienții b și c sunt egali cu zero, adică cu ecuații de forma a x 2 =0. Ecuația a·x 2 =0 este echivalentă cu ecuația x 2 =0, care se obține din original prin împărțirea ambelor părți la un număr diferit de zero a. Evident, rădăcina ecuației x 2 =0 este zero, deoarece 0 2 =0. Această ecuație nu are alte rădăcini, ceea ce se explică prin faptul că pentru orice număr p diferit de zero este valabilă inegalitatea p 2 >0, ceea ce înseamnă că pentru p≠0 egalitatea p 2 =0 nu este niciodată atinsă.

Deci, ecuația pătratică incompletă a·x 2 =0 are o singură rădăcină x=0.

Ca exemplu, dăm soluția ecuației pătratice incomplete −4 x 2 =0. Este echivalent cu ecuația x 2 =0, singura sa rădăcină este x=0, prin urmare, ecuația originală are o singură rădăcină zero.

O soluție scurtă în acest caz poate fi scrisă după cum urmează:
−4 x 2 =0 ,
x 2 =0,
x=0.

a x 2 +c=0

Acum să vedem cum se rezolvă ecuațiile pătratice incomplete în care coeficientul b este zero și c≠0, adică ecuații de forma a x 2 +c=0. Știm că mutarea unui termen dintr-o parte a ecuației în cealaltă cu semnul opus, precum și împărțirea ambelor părți ale ecuației la un număr diferit de zero, dă o ecuație echivalentă. Prin urmare, putem efectua următoarele transformări echivalente ecuație pătratică incompletă a x 2 +c=0 :

• mutați c în partea dreaptă, ceea ce dă ecuația a x 2 =−c,
• și împărțim ambele părți cu a, obținem .

Ecuația rezultată ne permite să tragem concluzii despre rădăcinile sale. În funcție de valorile lui a și c, valoarea expresiei poate fi negativă (de exemplu, dacă a=1 și c=2, atunci) sau pozitivă (de exemplu, dacă a=−2 și c=6, atunci ), nu este zero , deoarece prin condiția c≠0. Să ne uităm la cazuri separat.

Dacă , atunci ecuația nu are rădăcini. Această afirmație rezultă din faptul că pătratul oricărui număr este un număr nenegativ. De aici rezultă că atunci când , atunci pentru orice număr p egalitatea nu poate fi adevărată.

Dacă , atunci situația cu rădăcinile ecuației este diferită. În acest caz, dacă ne amintim despre , atunci rădăcina ecuației devine imediat evidentă; este numărul, deoarece . Este ușor de ghicit că numărul este și rădăcina ecuației, într-adevăr, . Această ecuație nu are alte rădăcini, care pot fi arătate, de exemplu, prin contradicție. Hai să o facem.

Să notăm rădăcinile ecuației tocmai anunțate ca x 1 și −x 1 . Să presupunem că ecuația are încă o rădăcină x 2, diferită de rădăcinile indicate x 1 și −x 1. Se știe că înlocuirea rădăcinilor sale într-o ecuație în loc de x transformă ecuația într-o egalitate numerică corectă. Pentru x 1 și −x 1 avem , iar pentru x 2 avem . Proprietățile egalităților numerice ne permit să efectuăm scăderea termen cu termen a egalităților numerice corecte, astfel încât scăderea părților corespunzătoare ale egalităților dă x 1 2 −x 2 2 =0. Proprietățile operațiilor cu numere ne permit să rescriem egalitatea rezultată ca (x 1 −x 2)·(x 1 +x 2)=0. Știm că produsul a două numere este egal cu zero dacă și numai dacă cel puțin unul dintre ele este egal cu zero. Prin urmare, din egalitatea rezultată rezultă că x 1 −x 2 =0 și/sau x 1 +x 2 =0, care este același, x 2 =x 1 și/sau x 2 =−x 1. Deci am ajuns la o contradicție, deoarece la început am spus că rădăcina ecuației x 2 este diferită de x 1 și −x 1. Aceasta demonstrează că ecuația nu are alte rădăcini decât și .

Să rezumam informațiile din acest paragraf. Ecuația pătratică incompletă a x 2 +c=0 este echivalentă cu ecuația care

• nu are rădăcini dacă,
• are două rădăcini și , dacă .

Să luăm în considerare exemple de rezolvare a ecuațiilor pătratice incomplete de forma a·x 2 +c=0.

Să începem cu ecuația pătratică 9 x 2 +7=0. După mutarea termenului liber în partea dreaptă a ecuației, acesta va lua forma 9 x 2 =−7. Împărțind ambele părți ale ecuației rezultate la 9, ajungem la . Deoarece partea dreaptă are un număr negativ, această ecuație nu are rădăcini, prin urmare, ecuația pătratică incompletă inițială 9 x 2 +7 = 0 nu are rădăcini.

Să rezolvăm o altă ecuație pătratică incompletă −x 2 +9=0. Mutăm cele nouă în partea dreaptă: −x 2 =−9. Acum împărțim ambele părți la −1, obținem x 2 =9. În partea dreaptă există un număr pozitiv, din care concluzionăm că sau . Apoi notăm răspunsul final: ecuația pătratică incompletă −x 2 +9=0 are două rădăcini x=3 sau x=−3.

a x 2 +b x=0

Rămâne să ne ocupăm de soluția ultimului tip de ecuații pătratice incomplete pentru c=0. Ecuațiile pătratice incomplete de forma a x 2 + b x = 0 vă permit să rezolvați metoda factorizării. Evident, putem, situat în partea stângă a ecuației, pentru care este suficient să scoatem factorul comun x din paranteze. Acest lucru ne permite să trecem de la ecuația pătratică incompletă inițială la o ecuație echivalentă de forma x·(a·x+b)=0. Și această ecuație este echivalentă cu o mulțime de două ecuații x=0 și a·x+b=0, cea din urmă fiind liniară și având rădăcina x=−b/a.

Deci, ecuația pătratică incompletă a·x 2 +b·x=0 are două rădăcini x=0 și x=−b/a.

Pentru a consolida materialul, vom analiza soluția la un exemplu concret.

Exemplu.

Rezolvați ecuația.

Soluţie.

Scotând x din paranteze rezultă ecuația . Este echivalentă cu două ecuații x=0 și . Rezolvăm ecuația liniară rezultată: , și împărțim numărul mixt la fracție comună, găsim . Prin urmare, rădăcinile ecuației originale sunt x=0 și .

După dobândirea practicii necesare, soluțiile la astfel de ecuații pot fi scrise pe scurt:

Răspuns:

x=0, .

Discriminant, formulă pentru rădăcinile unei ecuații pătratice

Pentru a rezolva ecuații pătratice, există o formulă rădăcină. Să-l notăm formula pentru rădăcinile unei ecuații pătratice: , Unde D=b 2 −4 a c- așa-zisul discriminant al unei ecuații pătratice. Intrarea înseamnă în esență că .

Este util să știm cum a fost obținută formula rădăcinii și cum este utilizată în găsirea rădăcinilor ecuațiilor pătratice. Să ne dăm seama.

Derivarea formulei pentru rădăcinile unei ecuații pătratice

Trebuie să rezolvăm ecuația pătratică a·x 2 +b·x+c=0. Să efectuăm câteva transformări echivalente:

• Putem împărți ambele părți ale acestei ecuații la un număr diferit de zero a, rezultând următoarea ecuație pătratică.
• Acum selectați un pătrat complet pe partea stângă: . După aceasta, ecuația va lua forma .
• În această etapă, este posibil să transferăm ultimii doi termeni în partea dreaptă cu semnul opus, avem .
• Și să transformăm și expresia din partea dreaptă: .

Ca rezultat, ajungem la o ecuație care este echivalentă cu ecuația pătratică inițială a·x 2 +b·x+c=0.

Am rezolvat deja ecuații similare ca formă în paragrafele precedente, când am examinat. Acest lucru ne permite să tragem următoarele concluzii cu privire la rădăcinile ecuației:

• dacă , atunci ecuația nu are soluții reale;
• dacă , atunci ecuația are forma , prin urmare, , din care este vizibilă singura sa rădăcină;
• dacă , atunci sau , care este același cu sau , adică ecuația are două rădăcini.

Astfel, prezența sau absența rădăcinilor ecuației și, prin urmare, a ecuației pătratice originale, depinde de semnul expresiei din partea dreaptă. La rândul său, semnul acestei expresii este determinat de semnul numărătorului, întrucât numitorul 4·a 2 este întotdeauna pozitiv, adică de semnul expresiei b 2 −4·a·c. Această expresie b 2 −4 a c a fost numită discriminant al unei ecuații pătraticeși desemnat prin scrisoare D. De aici, esența discriminantului este clară - pe baza valorii și semnului său, ei ajung la concluzia dacă ecuația pătratică are rădăcini reale și, dacă da, care este numărul lor - unul sau doi.

Să revenim la ecuație și să o rescriem folosind notația discriminantă: . Și tragem concluzii:

• daca D<0 , то это уравнение не имеет действительных корней;
• dacă D=0, atunci această ecuație are o singură rădăcină;
• în sfârșit, dacă D>0, atunci ecuația are două rădăcini sau, care pot fi rescrise sub forma sau, iar după extinderea și aducerea fracțiilor la un numitor comun obținem.

Deci am derivat formulele pentru rădăcinile ecuației pătratice, ele arată ca , unde discriminantul D este calculat prin formula D=b 2 −4·a·c.

Cu ajutorul lor, cu un discriminant pozitiv, puteți calcula ambele rădăcini reale ale unei ecuații pătratice. Când discriminantul este egal cu zero, ambele formule dau aceeași valoare a rădăcinii, corespunzătoare singura solutie ecuație pătratică. Și cu un discriminant negativ, atunci când încercăm să folosim formula pentru rădăcinile unei ecuații pătratice, ne confruntăm cu extragerea rădăcinii pătrate a unui număr negativ, ceea ce ne duce dincolo de sfera programului școlar. Cu un discriminant negativ, ecuația pătratică nu are rădăcini reale, ci are o pereche conjugare complexa rădăcini, care pot fi găsite folosind aceleași formule de rădăcină pe care le-am obținut.

Algoritm pentru rezolvarea ecuațiilor pătratice cu ajutorul formulelor rădăcinilor

În practică, atunci când rezolvați ecuații pătratice, puteți utiliza imediat formula rădăcinii pentru a calcula valorile acestora. Dar acest lucru este mai mult legat de găsirea rădăcinilor complexe.

Cu toate acestea, într-un curs de algebră școlară vorbim de obicei nu despre complex, ci despre rădăcinile reale ale unei ecuații pătratice. În acest caz, este recomandabil, înainte de a folosi formulele pentru rădăcinile unei ecuații pătratice, să găsiți mai întâi discriminantul, să vă asigurați că acesta este nenegativ (în caz contrar, putem concluziona că ecuația nu are rădăcini reale), și abia apoi calculați valorile rădăcinilor.

Raționamentul de mai sus ne permite să scriem algoritm pentru rezolvarea unei ecuații pătratice. Pentru a rezolva ecuația pătratică a x 2 +b x+c=0, trebuie să:

• folosind formula discriminantă D=b 2 −4·a·c, calculați valoarea acesteia;
• concluzionați că o ecuație pătratică nu are rădăcini reale dacă discriminantul este negativ;
• calculați singura rădăcină a ecuației folosind formula dacă D=0;
• găsiți două rădăcini reale ale unei ecuații pătratice folosind formula rădăcinii dacă discriminantul este pozitiv.

Aici observăm doar că, dacă discriminantul este egal cu zero, puteți folosi și formula; aceasta va da aceeași valoare ca .

Puteți trece la exemple de utilizare a algoritmului pentru rezolvarea ecuațiilor pătratice.

Exemple de rezolvare a ecuațiilor pătratice

Să considerăm soluții la trei ecuații pătratice cu discriminant pozitiv, negativ și zero. După ce s-a ocupat de soluția lor, prin analogie va fi posibil să se rezolve orice altă ecuație pătratică. Sa incepem.

Exemplu.

Aflați rădăcinile ecuației x 2 +2·x−6=0.

Soluţie.

În acest caz, avem următorii coeficienți ai ecuației pătratice: a=1, b=2 și c=−6. Conform algoritmului, mai întâi trebuie să calculați discriminantul; pentru a face acest lucru, înlocuim a, b și c indicate în formula discriminantă, avem D=b 2 −4·a·c=2 2 −4·1·(−6)=4+24=28. Din moment ce 28>0, adică discriminantul Peste zero, atunci ecuația pătratică are două rădăcini reale. Să le găsim folosind formula rădăcină, obținem , aici puteți simplifica expresiile rezultate făcând deplasarea multiplicatorului dincolo de semnul rădăcinii urmată de reducerea fracției:

Răspuns:

Să trecem la următorul exemplu tipic.

Exemplu.

Rezolvați ecuația pătratică −4 x 2 +28 x−49=0 .

Soluţie.

Începem prin a găsi discriminantul: D=28 2 −4·(−4)·(−49)=784−784=0. Prin urmare, această ecuație pătratică are o singură rădăcină, pe care o găsim ca , adică

Răspuns:

x=3,5.

Rămâne de luat în considerare rezolvarea ecuațiilor pătratice cu un discriminant negativ.

Exemplu.

Rezolvați ecuația 5·y 2 +6·y+2=0.

Soluţie.

Iată coeficienții ecuației pătratice: a=5, b=6 și c=2. Substituim aceste valori în formula discriminantă, avem D=b 2 −4·a·c=6 2 −4·5·2=36−40=−4. Discriminantul este negativ, prin urmare, această ecuație pătratică nu are rădăcini reale.

Dacă trebuie să indicați rădăcini complexe, apoi aplicăm formula binecunoscută pentru rădăcinile unei ecuații pătratice și efectuăm actiuni cu numere complexe :

Răspuns:

nu există rădăcini reale, rădăcini complexe sunt: ​​.

Să remarcăm încă o dată că, dacă discriminantul unei ecuații pătratice este negativ, atunci la școală de obicei notează imediat un răspuns în care indică că nu există rădăcini reale și nu se găsesc rădăcini complexe.

Formula rădăcină pentru chiar al doilea coeficienți

Formula pentru rădăcinile unei ecuații pătratice, unde D=b 2 −4·a·c vă permite să obțineți o formulă de formă mai compactă, permițându-vă să rezolvați ecuații pătratice cu un coeficient par pentru x (sau pur și simplu cu o coeficient având forma 2·n, de exemplu, sau 14·ln5=2·7·ln5). Hai să o scoatem afară.

Să presupunem că trebuie să rezolvăm o ecuație pătratică de forma a x 2 +2 n x+c=0. Să-i găsim rădăcinile folosind formula pe care o cunoaștem. Pentru a face acest lucru, calculăm discriminantul D=(2 n) 2 −4 a c=4 n 2 −4 a c=4 (n 2 −a c), și apoi folosim formula rădăcină:

Să notăm expresia n 2 −a · c ca D 1 (uneori se notează D”). Atunci formula pentru rădăcinile ecuației pătratice luate în considerare cu al doilea coeficient 2 n ia forma , unde D 1 =n 2 −a·c.

Este ușor de observat că D=4·D 1, sau D 1 =D/4. Cu alte cuvinte, D 1 este a patra parte a discriminantului. Este clar că semnul lui D 1 este același cu semnul lui D . Adică, semnul D 1 este, de asemenea, un indicator al prezenței sau absenței rădăcinilor unei ecuații pătratice.

Deci, pentru a rezolva o ecuație pătratică cu un al doilea coeficient 2·n, aveți nevoie

• Calculați D 1 =n 2 −a·c ;
• Dacă D 1<0 , то сделать вывод, что действительных корней нет;
• Dacă D 1 =0, atunci calculați singura rădăcină a ecuației folosind formula;
• Dacă D 1 >0, atunci găsiți două rădăcini reale folosind formula.

Să luăm în considerare rezolvarea exemplului folosind formula rădăcină obținută în acest paragraf.

Exemplu.

Rezolvați ecuația pătratică 5 x 2 −6 x −32=0 .

Soluţie.

Al doilea coeficient al acestei ecuații poate fi reprezentat ca 2·(−3) . Adică, puteți rescrie ecuația pătratică inițială sub forma 5 x 2 +2 (−3) x−32=0, aici a=5, n=−3 și c=−32 și calculați a patra parte a discriminant: D 1 =n 2 −a·c=(−3) 2 −5·(−32)=9+160=169. Deoarece valoarea sa este pozitivă, ecuația are două rădăcini reale. Să le găsim folosind formula rădăcină adecvată:

Rețineți că a fost posibil să se folosească formula obișnuită pentru rădăcinile unei ecuații pătratice, dar în acest caz ar trebui efectuată mai multă muncă de calcul.

Răspuns:

Simplificarea formei ecuațiilor pătratice

Uneori, înainte de a începe să calculați rădăcinile unei ecuații pătratice folosind formule, nu strică să puneți întrebarea: „Este posibil să simplificați forma acestei ecuații?” De acord că din punct de vedere al calculelor va fi mai ușor de rezolvat ecuația pătratică 11 x 2 −4 x−6=0 decât 1100 x 2 −400 x−600=0.

De obicei, simplificarea formei unei ecuații pătratice se realizează prin înmulțirea sau împărțirea ambelor părți cu un anumit număr. De exemplu, în paragraful anterior a fost posibilă simplificarea ecuației 1100 x 2 −400 x −600=0 împărțind ambele părți la 100.

O transformare similară este efectuată cu ecuații pătratice, ai căror coeficienți nu sunt . În acest caz, împărțim de obicei ambele părți ale ecuației cu valori absolute coeficienții săi. De exemplu, să luăm ecuația pătratică 12 x 2 −42 x+48=0. valorile absolute ale coeficienților săi: GCD(12, 42, 48)= GCD(GCD(12, 42), 48)= GCD(6, 48)=6. Împărțind ambele părți ale ecuației pătratice originale la 6, ajungem la ecuația pătratică echivalentă 2 x 2 −7 x+8=0.

Și înmulțirea ambelor părți ale unei ecuații pătratice se face de obicei pentru a scăpa de coeficienții fracționali. În acest caz, înmulțirea se realizează prin numitorii coeficienților săi. De exemplu, dacă ambele părți ale ecuației pătratice sunt înmulțite cu LCM(6, 3, 1)=6, atunci aceasta va lua forma mai simplă x 2 +4·x−18=0.

În concluzia acestui punct, observăm că ei scapă aproape întotdeauna de minus la cel mai mare coeficient al unei ecuații pătratice prin schimbarea semnelor tuturor termenilor, ceea ce corespunde înmulțirii (sau împărțirii) ambelor părți cu −1. De exemplu, de obicei se trece de la ecuația pătratică −2 x 2 −3 x+7=0 la soluția 2 x 2 +3 x−7=0 .

Relația dintre rădăcini și coeficienți ai unei ecuații pătratice

Formula pentru rădăcinile unei ecuații pătratice exprimă rădăcinile ecuației prin coeficienții săi. Pe baza formulei rădăcinii, puteți obține alte relații între rădăcini și coeficienți.

Cele mai cunoscute și aplicabile formule din teorema lui Vieta sunt de forma și . În special, pentru ecuația pătratică dată, suma rădăcinilor este egală cu al doilea coeficient cu semnul opus, iar produsul rădăcinilor este egal cu termenul liber. De exemplu, privind forma ecuației pătratice 3 x 2 −7 x + 22 = 0, putem spune imediat că suma rădăcinilor sale este egală cu 7/3, iar produsul rădăcinilor este egal cu 22 /3.

Folosind formulele deja scrise, puteți obține o serie de alte conexiuni între rădăcinile și coeficienții ecuației pătratice. De exemplu, puteți exprima suma pătratelor rădăcinilor unei ecuații pătratice prin coeficienții ei: .

Bibliografie.

• Algebră: manual pentru clasa a VIII-a. educatie generala instituții / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; editat de S. A. Teliakovsky. - Ed. a XVI-a. - M.: Educație, 2008. - 271 p. : bolnav. - ISBN 978-5-09-019243-9.
• Mordkovich A.G. Algebră. clasa a 8-a. În 2 ore.Partea 1. Manual pentru studenții instituțiilor de învățământ general / A. G. Mordkovich. - Ed. a XI-a, șters. - M.: Mnemosyne, 2009. - 215 p.: ill. ISBN 978-5-346-01155-2.