Équation quadratique et théorème de Pythagore. Histoire du théorème de Pythagore

Selon van der Waerden, il est très probable que le ratio en vue généraleétait connue à Babylone déjà vers le 18ème siècle avant JC. e.

Environ 400 av. e., selon Proclus, Platon a donné une méthode pour trouver des triplets de Pythagore, combinant l'algèbre et la géométrie. Vers 300 av. e. dans les « Éléments » d'Euclide apparaît la plus ancienne preuve axiomatique du théorème de Pythagore.

Formulation

La formulation principale contient des opérations algébriques - dans un triangle rectangle, dont les longueurs des jambes sont égales un (\displaystyle un) et b (\ displaystyle b), et la longueur de l'hypoténuse est c (\ displaystyle c), la relation est satisfaite :

Une formulation géométrique équivalente est également possible, recourant à la notion d'aire figure : dans un triangle rectangle, l'aire du carré construit sur l'hypoténuse est égale à la somme des aires des carrés construits sur les jambes. Sous cette forme, le théorème est formulé dans les Principia d'Euclide.

Théorème de Pythagore inverse- la déclaration sur la rectangulaire de tout triangle dont les longueurs des côtés sont liées par la relation une 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). Par conséquent, pour tout triplet de nombres positifs un (\displaystyle un), b (\ displaystyle b) et c (\ displaystyle c), tel que une 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), il y a un triangle rectangle avec des jambes un (\displaystyle un) et b (\ displaystyle b) et hypoténuse c (\ displaystyle c).

Preuve de

Au moins 400 preuves du théorème de Pythagore ont été enregistrées dans la littérature scientifique, ce qui s'explique à la fois par la valeur fondamentale de la géométrie et par le caractère élémentaire du résultat. Les principales directions de preuves sont : l'utilisation algébrique des rapports éléments triangle (telle, par exemple, la méthode de similarité populaire), la méthode des aires, il existe également diverses preuves exotiques (par exemple, en utilisant équations différentielles).

A travers des triangles semblables

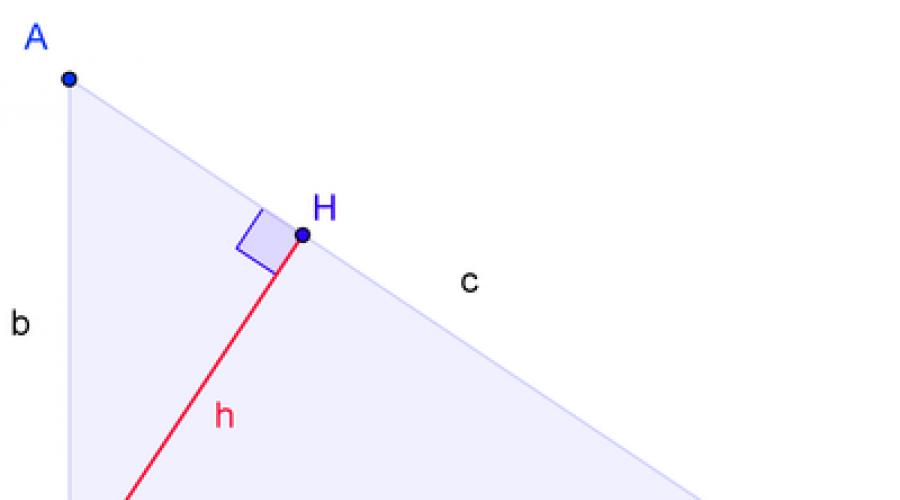
La preuve classique d'Euclide vise à établir l'égalité des aires entre les rectangles formés en disséquant le carré au-dessus de l'hypoténuse avec la hauteur à partir de l'angle droit avec les carrés au-dessus des jambes.

La construction utilisée pour la preuve est la suivante : pour un triangle rectangle avec un angle droit C (\displaystyle C), carrés sur les jambes et et carrés sur l'hypoténuse A B I K (\displaystyle ABIK) la hauteur est en cours de construction CH (\displaystyle CH) et le faisceau qui le prolonge s (\ displaystyle s), divisant le carré au-dessus de l'hypoténuse en deux rectangles et . La preuve vise à établir l'égalité des aires du rectangle A H J K (\displaystyle AHJK) avec un carré sur la jambe A C (\displaystyle AC); l'égalité des aires du deuxième rectangle, qui est un carré au-dessus de l'hypoténuse, et du rectangle au-dessus de l'autre jambe s'établit de la même manière.

Egalité des aires d'un rectangle A H J K (\displaystyle AHJK) et A C E D (\displaystyle ACED)établi par la congruence des triangles △ A C K ​​​​(\ displaystyle \ triangle ACK) et △ A B D (\displaystyle\triangle ABD), dont l'aire de chacun est égale à la moitié de l'aire des carrés A H J K (\displaystyle AHJK) et A C E D (\displaystyle ACED) respectivement, en relation avec la propriété suivante : l'aire d'un triangle est égale à la moitié de l'aire d'un rectangle si les figures ont un côté commun, et la hauteur du triangle au côté commun est l'autre côté de le rectangle. La congruence des triangles découle de l'égalité de deux côtés (côtés des carrés) et de l'angle entre eux (composé d'un angle droit et d'un angle à A (\displaystyle A).

Ainsi, la preuve établit que l'aire du carré au-dessus de l'hypoténuse, composé de rectangles A H J K (\displaystyle AHJK) et B H J I (\displaystyle BHJI), est égal à la somme des aires des carrés au-dessus des jambes.

Preuve de Léonard de Vinci

La méthode des aires comprend également la preuve trouvée par Léonard de Vinci. Qu'il y ait un triangle rectangle △ A B C (\displaystyle\triangle ABC) angle droit C (\displaystyle C) et carrés A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG) et A B H J (\displaystyle ABHJ)(voir l'image). Dans cette preuve à côté HJ (\displaystyle HJ) le dernier à l'extérieur un triangle est construit, congruent △ A B C (\displaystyle\triangle ABC), de plus, réfléchi à la fois par rapport à l'hypoténuse et par rapport à sa hauteur (c'est-à-dire J I = B C (\displaystyle JI=BC) et H je = A C (\displaystyle HI=AC)). Droit C I (\displaystyle CI) divise le carré construit sur l'hypoténuse en deux parties égales, puisque les triangles △ A B C (\displaystyle\triangle ABC) et △ J H I (\displaystyle\triangle JHI) sont égaux en construction. La preuve établit la congruence des quadrilatères C A J I (\displaystyle CAJI) et D A B G (\displaystyle DABG), dont l'aire de chacun, d'une part, est égale à la somme de la moitié des aires des carrés sur les jambes et l'aire du triangle d'origine, d'autre part, à la moitié de l'aire de le carré sur l'hypoténuse plus l'aire du triangle d'origine. Au total, la moitié de la somme des aires des carrés sur les jambes est égale à la moitié de l'aire du carré sur l'hypoténuse, ce qui équivaut à la formulation géométrique du théorème de Pythagore.

Preuve par la méthode infinitésimale

Il existe plusieurs preuves utilisant la technique des équations différentielles. En particulier, Hardy est crédité d'une preuve utilisant des incréments de jambe infinitésimaux un (\displaystyle un) et b (\ displaystyle b) et hypoténuse c (\ displaystyle c), et en préservant la similitude avec le rectangle d'origine, c'est-à-dire en assurant la réalisation des relations différentielles suivantes :

Par la méthode de séparation des variables, une équation différentielle en est dérivée c ré c = une ré une + b ré b (\displaystyle c\ dc=a\,da+b\,db), dont l'intégration donne la relation c 2 = une 2 + b 2 + C o n s t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). Application des conditions initiales une = b = c = 0 (\displaystyle a=b=c=0) définit une constante comme 0, ce qui aboutit à l'assertion du théorème.

La dépendance quadratique dans la formule finale apparaît en raison de la proportionnalité linéaire entre les côtés du triangle et les incréments, tandis que la somme est due aux contributions indépendantes de l'incrément des différentes jambes.

Variations et généralisations

Formes géométriques similaires sur trois côtés

Une généralisation géométrique importante du théorème de Pythagore a été donnée par Euclide dans les Éléments, passant des aires de carrés sur les côtés aux aires de semblables arbitraires. formes géométriques: la somme des aires de telles figures construites sur les jambes sera égale à l'aire d'une figure similaire à celles-ci, construite sur l'hypoténuse.

L'idée principale de cette généralisation est que l'aire d'une telle figure géométrique est proportionnelle au carré de n'importe laquelle de ses dimensions linéaires et, en particulier, au carré de la longueur de n'importe quel côté. Par conséquent, pour des figures similaires avec des aires A (\displaystyle A), B (\displaystyle B) et C (\displaystyle C) construit sur des jambes avec des longueurs un (\displaystyle un) et b (\ displaystyle b) et hypoténuse c (\ displaystyle c) il existe donc une relation :

Puisque d'après le théorème de Pythagore une 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), alors c'est fait.

De plus, s'il est possible de prouver sans utiliser le théorème de Pythagore que pour Trois figures géométriques similaires sur les côtés d'un triangle rectangle A + B = C (\displaystyle A+B=C), puis en utilisant l'inverse de la preuve de la généralisation d'Euclide, nous pouvons dériver la preuve du théorème de Pythagore. Par exemple, si sur l'hypoténuse on construit un triangle rectangle congru au premier d'aire C (\displaystyle C), et sur les jambes - deux semblables à lui triangle rectangle avec des zones A (\displaystyle A) et B (\displaystyle B), alors il s'avère que les triangles sur les jambes sont formés en divisant le triangle initial par sa hauteur, c'est-à-dire que la somme de deux aires plus petites des triangles est égale à l'aire du troisième, donc A + B = C (\displaystyle A+B=C) et, en appliquant la relation pour des figures similaires, le théorème de Pythagore est dérivé.

Théorème du cosinus

Le théorème de Pythagore est un cas particulier du théorème cosinus plus général qui relie les longueurs des côtés dans un triangle arbitraire :

où est l'angle entre les côtés un (\displaystyle un) et b (\ displaystyle b). Si l'angle est de 90°, alors cos ⁡ θ = 0 (\displaystyle \cos \theta =0), et la formule se simplifie au théorème de Pythagore habituel.

Triangle arbitraire

Il y a une généralisation du théorème de Pythagore à un triangle arbitraire, fonctionnant uniquement sur le rapport des longueurs des côtés, on pense qu'il a été établi pour la première fois par l'astronome sabien Sabit ibn Kurra. Dans celui-ci, pour un triangle arbitraire avec des côtés, un triangle isocèle avec une base sur le côté c (\ displaystyle c), le sommet coïncidant avec le sommet du triangle d'origine, opposé au côté c (\ displaystyle c) et coins à la base, égal à l'angle θ (\displaystyle \theta ) le côté opposé c (\ displaystyle c). En conséquence, deux triangles sont formés, semblables à celui d'origine : le premier avec des côtés un (\displaystyle un), le côté latéral du triangle isocèle inscrit éloigné de lui, et r (\ displaystyle r)- parties latérales c (\ displaystyle c); le second lui est symétrique du côté b (\ displaystyle b) avec une fête s (\ displaystyle s)- la partie pertinente du côté c (\ displaystyle c). Il en résulte que la relation est satisfaite :

qui dégénère en théorème de Pythagore à θ = π / 2 (\displaystyle \theta =\pi /2). Le rapport est une conséquence de la similitude des triangles formés :

Théorème de l'aire de Pappus

Géométrie non euclidienne

Le théorème de Pythagore est dérivé des axiomes de la géométrie euclidienne et n'est pas valide pour la géométrie non euclidienne - l'accomplissement du théorème de Pythagore équivaut au postulat du parallélisme euclidien.

En géométrie non euclidienne, la relation entre les côtés d'un triangle rectangle sera nécessairement sous une forme différente du théorème de Pythagore. Par exemple, en géométrie sphérique, les trois côtés d'un triangle rectangle, qui délimitent l'octant de la sphère unité, ont une longueur π / 2 (\displaystyle \pi /2), ce qui contredit le théorème de Pythagore.

De plus, le théorème de Pythagore est valable en géométrie hyperbolique et elliptique, si l'exigence que le triangle soit rectangulaire est remplacée par la condition que la somme de deux angles du triangle doit être égale au troisième.

géométrie sphérique

Pour tout triangle rectangle sur une sphère de rayon R (\displaystyle R)(par exemple, si l'angle dans le triangle est droit) avec des côtés une , b , c (\displaystyle a,b,c) la relation entre les côtés est :

Cette égalité peut être dérivée comme un cas particulier du théorème du cosinus sphérique, qui est valable pour tous les triangles sphériques :

où ch (\displaystyle\nomopérateur(ch) )- cosinus hyperbolique. Cette formule est un cas particulier du théorème du cosinus hyperbolique, valable pour tous les triangles :

où γ (\displaystyle\gamma )- un angle dont le sommet est opposé à un côté c (\ displaystyle c).

En utilisant la série de Taylor pour le cosinus hyperbolique ( ch ⁡ X ≈ 1 + X 2 / 2 (\displaystyle\operatorname (ch) x\approx 1+x^(2)/2)) on peut montrer que si le triangle hyperbolique diminue (c'est-à-dire lorsque un (\displaystyle un), b (\ displaystyle b) et c (\ displaystyle c) tendent vers zéro), alors les relations hyperboliques dans un triangle rectangle se rapprochent de la relation du théorème de Pythagore classique.

Application

Distance dans les systèmes rectangulaires bidimensionnels

L'application la plus importante du théorème de Pythagore est de déterminer la distance entre deux points dans un système de coordonnées rectangulaire : distance s (\ displaystyle s) entre des points avec des coordonnées (a , b) (\displaystyle (a,b)) et (c , ré) (\displaystyle (c,d))équivaut à:

Pour nombres complexes le théorème de Pythagore donne une formule naturelle pour trouver le nombre module complexe  - pour z = x + y je (\displaystyle z=x+yi) elle est égale à la longueur

théorème de Pythagore: La somme des aires des carrés supportés par les jambes ( un et b), est égal à l'aire du carré construit sur l'hypoténuse ( c).

Formulation géométrique :

Le théorème a été initialement formulé de la manière suivante:

Formulation algébrique :

Autrement dit, indiquant la longueur de l'hypoténuse du triangle passant par c, et les longueurs des jambes à travers un et b :

Les deux formulations du théorème sont équivalentes, mais la deuxième formulation est plus élémentaire, elle ne nécessite pas la notion d'aire. Autrement dit, la deuxième affirmation peut être vérifiée sans rien savoir de l'aire et en mesurant uniquement les longueurs des côtés d'un triangle rectangle.

Théorème de Pythagore inverse :

Preuve de

Sur le ce moment 367 preuves de ce théorème sont enregistrées dans la littérature scientifique. Probablement, le théorème de Pythagore est le seul théorème avec un nombre aussi impressionnant de preuves. Une telle variété ne peut s'expliquer que par la signification fondamentale du théorème pour la géométrie.

Bien sûr, conceptuellement, tous peuvent être divisés en un petit nombre de classes. Les plus célèbres d'entre elles : les preuves par la méthode des aires, les preuves axiomatiques et exotiques (par exemple, en utilisant des équations différentielles).

A travers des triangles semblables

La preuve suivante de la formulation algébrique est la plus simple des preuves construites directement à partir des axiomes. En particulier, il n'utilise pas la notion d'aire de figure.

Laisser abc il y a un triangle rectangle C. Tirons une hauteur de C et notons sa base par H. Triangle ACH semblable à un triangle abcà deux coins. De même, le triangle CBH similaire abc. Présentation de la notation

on a

Ce qui est équivalent

En ajoutant, on obtient

Preuves de zone

Les preuves suivantes, malgré leur simplicité apparente, ne sont pas si simples du tout. Tous utilisent les propriétés de l'aire, dont la preuve est plus compliquée que la preuve du théorème de Pythagore lui-même.

Preuve par équivalence

1. Disposez quatre triangles rectangles égaux comme illustré à la figure 1.
2. Quadrilatère avec côtés c est un carré car la somme de deux coins pointus 90° et l'angle droit est de 180°.
3. L'aire de la figure entière est égale, d'une part, à l'aire d'un carré de côté (a + b), et d'autre part, à la somme des aires de quatre triangles et de deux intérieurs carrés.

Q.E.D.

Preuve par équivalence

Une preuve de permutation élégante

Un exemple d'une de ces preuves est montré dans le dessin de droite, où le carré construit sur l'hypoténuse est converti par permutation en deux carrés construits sur les jambes.

Preuve d'Euclide

Dessin pour la preuve d'Euclide

Illustration pour la preuve d'Euclide

L'idée de la preuve d'Euclide est la suivante : essayons de prouver que la moitié de l'aire du carré construit sur l'hypoténuse est égale à la somme des demi-aires des carrés construits sur les jambes, puis les aires de le grand et les deux petits carrés sont égaux.

Considérez le dessin à gauche. Nous avons construit des carrés sur les côtés d'un triangle rectangle dessus et avons tracé un rayon s du sommet de l'angle droit C perpendiculaire à l'hypoténuse AB, il coupe le carré ABIK, construit sur l'hypoténuse, en deux rectangles - BHJI et HAKJ , respectivement. Il s'avère que les aires de ces rectangles sont exactement égales aux aires des carrés construits sur les jambes correspondantes.

Essayons de prouver que l'aire du carré DECA est égale à l'aire du rectangle AHJK Pour ce faire, nous utilisons une observation auxiliaire : L'aire d'un triangle de même hauteur et base que le donné rectangle est égal à la moitié de l'aire du rectangle donné. Ceci est une conséquence de la définition de l'aire d'un triangle comme la moitié du produit de la base et de la hauteur. De cette observation, il résulte que l'aire du triangle ACK est égale à l'aire du triangle AHK (non représenté), qui, à son tour, est égale à la moitié de l'aire du rectangle AHJK.

Prouvons maintenant que l'aire du triangle ACK est également égale à la moitié de l'aire du carré DECA. La seule chose à faire pour cela est de prouver l'égalité des triangles ACK et BDA (puisque l'aire du triangle BDA est égale à la moitié de l'aire du carré par la propriété ci-dessus). Cette égalité est évidente, les triangles sont égaux en deux côtés et l'angle entre eux. A savoir - AB=AK,AD=AC - l'égalité des angles CAK et BAD est facile à prouver par la méthode du mouvement : faisons tourner le triangle CAK de 90° dans le sens inverse des aiguilles d'une montre, alors il est évident que les côtés correspondants des deux triangles considérés vont coïncider (du fait que l'angle au sommet du carré est de 90°).

L'argument sur l'égalité des aires du carré BCFG et du rectangle BHJI est tout à fait analogue.

Ainsi, nous avons prouvé que l'aire du carré construit sur l'hypoténuse est la somme des aires des carrés construits sur les jambes. L'idée derrière cette preuve est encore illustrée avec l'animation ci-dessus.

Preuve de Léonard de Vinci

Preuve de Léonard de Vinci

Les principaux éléments de la preuve sont la symétrie et le mouvement.

Considérez le dessin, comme on peut le voir à partir de la symétrie, le segment Cje décortique le carré UNBHJ en deux parties identiques (puisque les triangles UNBC et JHje sont égaux dans la construction). En utilisant une rotation de 90 degrés dans le sens antihoraire, nous voyons l'égalité des chiffres ombrés CUNJje et gréUNB . Maintenant, il est clair que l'aire de la figure ombrée par nous est égale à la somme de la moitié des aires des carrés construits sur les jambes et de l'aire du triangle d'origine. D'autre part, il est égal à la moitié de l'aire du carré construit sur l'hypoténuse, plus l'aire du triangle d'origine. La dernière étape de la démonstration est laissée au lecteur.

Preuve par la méthode infinitésimale

La preuve suivante utilisant des équations différentielles est souvent attribuée au célèbre mathématicien anglais Hardy, qui a vécu dans la première moitié du XXe siècle.

En considérant le dessin montré sur la figure et en observant le changement de côté un, on peut écrire la relation suivante pour des incréments latéraux infinitésimaux Avec et un(en utilisant des triangles semblables) :

Preuve par la méthode infinitésimale

En utilisant la méthode de séparation des variables, on trouve

Une expression plus générale pour changer l'hypoténuse dans le cas d'incréments des deux jambes

En intégrant équation donnée et en utilisant les conditions initiales, on obtient

Ainsi, nous arrivons à la réponse souhaitée

Comme il est facile de le voir, la dépendance quadratique dans la formule finale apparaît en raison de la proportionnalité linéaire entre les côtés du triangle et les incréments, tandis que la somme est due aux contributions indépendantes de l'incrément des différentes jambes.

Une preuve plus simple peut être obtenue si l'on suppose que l'une des jambes ne subit pas d'incrément (dans ce cas, la jambe b). Alors pour la constante d'intégration on obtient

Variations et généralisations

• Si, au lieu de carrés, d'autres figures similaires sont construites sur les jambes, alors la généralisation suivante du théorème de Pythagore est vraie : Dans un triangle rectangle, la somme des aires de figures similaires construites sur les jambes est égale à l'aire de la figure construite sur l'hypoténuse. En particulier:
  • La somme des aires des triangles réguliers construits sur les jambes est égale à l'aire d'un triangle régulier construit sur l'hypoténuse.
  • La somme des aires des demi-cercles construits sur les jambes (comme sur le diamètre) est égale à l'aire du demi-cercle construit sur l'hypoténuse. Cet exemple sert à prouver les propriétés des figures délimitées par des arcs de deux cercles et portant le nom de lunule hippocratique.

Histoire

Chu-pei 500–200 av. A gauche se trouve l'inscription : la somme des carrés des longueurs de la hauteur et de la base est le carré de la longueur de l'hypoténuse.

L'ancien livre chinois Chu-pei parle de Triangle de Pythagore avec les côtés 3, 4 et 5 : Dans le même livre, un dessin est proposé qui coïncide avec l'un des dessins de la géométrie hindoue de Bashara.

Kantor (le plus grand historien allemand des mathématiques) estime que l'égalité 3 ² + 4 ² = 5² était déjà connue des Égyptiens vers 2300 av. e., à l'époque du roi Amenemhet Ier (selon le papyrus 6619 du Musée de Berlin). Selon Cantor, les harpedonapts, ou "stringers", construisaient des angles droits à l'aide de triangles rectangles de côtés 3, 4 et 5.

Il est très facile de reproduire leur méthode de construction. Prenez une corde de 12 m de long et attachez-la le long d'une bande colorée à une distance de 3 m. d'un bout et à 4 mètres de l'autre. Un angle droit sera enserré entre des côtés de 3 et 4 mètres de long. On pourrait objecter aux Harpédonaptes que leur mode de construction devient superflu si l'on utilise, par exemple, l'équerre de bois utilisée par tous les charpentiers. En effet, on connaît des dessins égyptiens dans lesquels on retrouve un tel outil, par exemple des dessins représentant un atelier de menuiserie.

On en sait un peu plus sur le théorème de Pythagore chez les Babyloniens. Dans un texte datant de l'époque d'Hammourabi, c'est-à-dire de 2000 av. e., un calcul approximatif de l'hypoténuse d'un triangle rectangle est donné. De cela, nous pouvons conclure qu'en Mésopotamie, ils ont pu effectuer des calculs avec des triangles rectangles, au moins dans certains cas. Se fondant, d'une part, sur le niveau actuel des connaissances des mathématiques égyptiennes et babyloniennes, et d'autre part, sur une étude critique des sources grecques, Van der Waerden (un mathématicien hollandais) a conclu ce qui suit :

Littérature

En russe

• Skopets Z.A. Miniatures géométriques. M., 1990
• Yelenski Sh. Sur les traces de Pythagore. M., 1961
• Van der Waerden B.L. Sciences de l'éveil. Mathématiques l'Egypte ancienne, Babylone et la Grèce. M., 1959
• Glazer GI Histoire des mathématiques à l'école. M., 1982
• W. Litzman, "Le théorème de Pythagore" M., 1960.
  • Un site sur le théorème de Pythagore avec un grand nombre de preuves, le matériel est tiré du livre de V. Litzman, grand nombre les dessins sont présentés sous forme de fichiers graphiques séparés.
• Le théorème de Pythagore et le chapitre des triplets de Pythagore du livre de D. V. Anosov "Un regard sur les mathématiques et quelque chose qui en découle"
• Sur le théorème de Pythagore et les méthodes de sa preuve G. Glaser, académicien de l'Académie russe de l'éducation, Moscou

En anglais

• Le théorème de Pythagore à WolframMathWorld
• Cut-The-Knot, section sur le théorème de Pythagore, environ 70 preuves et de nombreuses informations supplémentaires (eng.)

Fondation Wikimédia. 2010 .

Pythagore est un scientifique grec qui a vécu il y a environ 2500 ans (564-473 avant JC).

Soit un triangle rectangle dont les côtés un, b et Avec(Fig. 267).

Construisons des carrés sur ses côtés. Les aires de ces carrés sont respectivement un 2 , b 2 et Avec 2. Prouvons que Avec 2 = un 2 +b 2 .

Construisons deux carrés MKOR et M'K'O'R' (Fig. 268, 269), en prenant pour côté de chacun d'eux un segment égal à la somme des côtés du triangle rectangle ABC.

Après avoir terminé les constructions illustrées aux figures 268 et 269 dans ces carrés, nous verrons que le carré MKOR est divisé en deux carrés avec des aires un 2 et b 2 et quatre triangles rectangles égaux, dont chacun est égal au triangle rectangle ABC. Le carré M'K'O'R' est divisé en un quadrilatère (il est grisé sur la figure 269) et en quatre triangles rectangles, chacun étant également égal au triangle ABC. Le quadrilatère grisé est un carré, puisque ses côtés sont égaux (chacun est égal à l'hypoténuse du triangle ABC, c'est-à-dire Avec), et les angles sont des droites ∠1 + ∠2 = 90°, d'où ∠3 = 90°).

Ainsi, la somme des aires des carrés construits sur les jambes (sur la figure 268 ces carrés sont ombrés) est égale à l'aire du carré MKOR sans la somme des aires de quatre triangles égaux, et l'aire de ​​le carré construit sur l'hypoténuse (sur la Figure 269 ce carré est également grisé) est égal à l'aire du carré M'K'O'R', égale au carré de MKOR, sans la somme des aires de quatre triangles semblables. Par conséquent, l'aire du carré construit sur l'hypoténuse d'un triangle rectangle est égale à la somme des aires des carrés construits sur les jambes.

On obtient la formule Avec 2 = un 2 +b 2 , où Avec- hypoténuse, un et b- jambes d'un triangle rectangle.

Le théorème de Pythagore peut être résumé comme suit :

Le carré de l'hypoténuse d'un triangle rectangle est égal à la somme des carrés des jambes.

De la formule Avec 2 = un 2 +b 2 vous pouvez obtenir les formules suivantes :

un 2 = Avec 2 - b 2 ;

b 2 = Avec 2 - un 2 .

Ces formules peuvent être utilisées pour trouver le côté inconnu d'un triangle rectangle étant donné deux de ses côtés.

Par exemple:

a) si les jambes sont données un= 4cm, b\u003d 3 cm, alors vous pouvez trouver l'hypoténuse ( Avec):

Avec 2 = un 2 +b 2, c'est-à-dire Avec 2 = 4 2 + 3 2 ; avec 2 = 25, d'où Avec= √25 = 5(cm);

b) si l'hypoténuse est donnée Avec= 17 cm et jambe un= 8 cm, alors vous pouvez trouver une autre jambe ( b):

b 2 = Avec 2 - un 2, c'est-à-dire b 2 = 17 2 - 8 2 ; b 2 = 225, d'où b= √225 = 15 (cm).

Corollaire : Si dans deux triangles rectangles ABC et A 1 B 1 C 1 hypoténuse Avec et Avec 1 sont égaux, et la jambe b le triangle ABC est plus grand que la jambe b 1 triangle A 1 B 1 C 1,

puis la jambe un le triangle ABC est plus petit que la jambe un 1 triangle A 1 B 1 C 1 .

En effet, d'après le théorème de Pythagore, on obtient :

un 2 = Avec 2 - b 2 ,

un 1 2 = Avec 1 2 - b 1 2

Dans les formules écrites, les diminutifs sont égaux et le sous-traitant dans la première formule est supérieur au sous-traitant dans la deuxième formule, par conséquent, la première différence moins d'une seconde,

c'est à dire. un 2 à 1 2 . Où un un 1 .

Le texte de l'œuvre est placé sans images ni formules.
La version complète de l'ouvrage est disponible dans l'onglet "Job Files" au format PDF

Introduction

Dans le cours de géométrie de l'école, en utilisant le théorème de Pythagore, seuls les problèmes mathématiques sont résolus. Malheureusement, la question de l'application pratique du théorème de Pythagore n'est pas envisagée.

À cet égard, le but de mon travail était de découvrir la portée du théorème de Pythagore.

À l'heure actuelle, il est généralement reconnu que le succès du développement de nombreux domaines de la science et de la technologie dépend du développement de divers domaines des mathématiques. Une condition importante améliorer l'efficacité de la production est l'introduction généralisée méthodes mathématiques dans la technologie et économie nationale qui implique la création de nouveaux méthodes efficaces des recherches qualitatives et quantitatives, qui permettent de résoudre les problèmes posés par la pratique.

Je vais considérer des exemples d'application pratique du théorème de Pythagore. Je n'essaierai pas de donner tous les exemples d'utilisation du théorème - ce ne serait guère possible. Le domaine d'application du théorème est assez étendu et ne peut généralement pas être indiqué avec suffisamment d'exhaustivité.

Hypothèse:

En utilisant le théorème de Pythagore, vous pouvez résoudre non seulement des problèmes mathématiques.

Selon ce travail de recherche l'objectif suivant est défini :

Découvrez la portée du théorème de Pythagore.

Sur la base de l'objectif ci-dessus, les tâches suivantes ont été identifiées :

Recueillir des informations sur l'application pratique du théorème de Pythagore dans différentes sources et déterminer la portée du théorème.

Apprenez quelques informations historiques sur Pythagore et son théorème.

Montrez l'application du théorème à la résolution de problèmes historiques.

Traiter les données collectées sur le sujet.

J'étais engagé dans la recherche et la collecte d'informations - j'ai étudié des documents imprimés, travaillé avec des documents sur Internet et traité les données collectées.

Méthodologie de recherche :

L'étude du matériel théorique.

L'étude des méthodes de recherche.

Mise en œuvre pratique rechercher.

Communicatif (méthode de mesure, questionnement).

Type de projet: recherche d'informations. Le travail a été fait sur mon temps libre.

À propos de Pythagore.

Pythagore est un ancien philosophe, mathématicien et astronome grec. Fondé de nombreuses propriétés des formes géométriques, développé théorie mathématique nombres et leurs proportions. Il a apporté une contribution significative au développement de l'astronomie et de l'acoustique. Auteur des "Versets d'or", fondateur de l'école pythagoricienne de Crotone.

Selon la légende, Pythagore serait né vers 580 av. e. sur l'île de Samos dans une riche famille de marchands. Sa mère, Pythasis, a obtenu son nom en l'honneur de la Pythie, la prêtresse d'Apollon. La Pythie a prédit à Mnesarchus et à sa femme la naissance d'un fils, le fils a également été nommé d'après la Pythie. Selon de nombreux témoignages anciens, le garçon était fabuleusement beau et a rapidement montré ses capacités exceptionnelles. Il a reçu ses premières connaissances de son père Mnesarchus, un bijoutier, sculpteur pierres précieuses qui rêvait que son fils deviendrait le successeur de son œuvre. Mais la vie en a jugé autrement. Le futur philosophe a montré une grande aptitude pour les sciences. Parmi les maîtres de Pythagore se trouvaient Pherekides de Syros et l'aîné Germodamant. Le premier a inculqué au garçon un amour pour la science, et le second pour la musique, la peinture et la poésie. Par la suite, Pythagore rencontra célèbre philosophe- mathématicien Thales de Milet et, sur ses conseils, se rendit en Egypte - le centre de l'époque scientifique et activités de recherche. Après avoir vécu 22 ans en Égypte et 12 ans à Babylone, il retourne sur l'île de Samos, puis la quitte pour des raisons inconnues et s'installe dans la ville de Crotone, dans le sud de l'Italie. Ici, il a créé l'école pythagoricienne (union), qui a étudié diverses questions de philosophie et de mathématiques. Vers l'âge d'environ 60 ans, Pythagore épouse Théano, l'un de ses élèves. Ils ont trois enfants et ils deviennent tous des disciples de leur père. Les conditions historiques de cette époque sont caractérisées par un large mouvement du démos contre le pouvoir des aristocrates. Fuyant les vagues de colère populaire, Pythagore et ses élèves s'installent dans la ville de Tarente. Selon une version: Kilon, un homme riche et méchant, est venu vers lui, voulant rejoindre la confrérie en état d'ébriété. Ayant été refusé, Cylon a commencé un combat avec Pythagore. Pendant l'incendie, les étudiants à leurs dépens ont sauvé la vie de l'enseignant. Pythagore a eu le mal du pays et s'est rapidement suicidé.

Il convient de noter que c'est l'une des variantes de sa biographie. Les dates exactes de sa naissance et de sa mort n'ont pas été établies, de nombreux faits de sa vie sont contradictoires. Mais une chose est claire : cet homme a vécu, et a laissé à ses descendants un grand héritage philosophique et mathématique.

Théorème de Pythagore.

Le théorème de Pythagore est l'énoncé le plus important de la géométrie. Le théorème est formulé comme suit : l'aire d'un carré construit sur l'hypoténuse d'un triangle rectangle est égale à la somme des aires des carrés construits sur ses jambes.

La découverte de ce relevé est attribuée à Pythagore de Samos (XIIe siècle av. J.-C.)

L'étude des tablettes cunéiformes babyloniennes et des anciens manuscrits chinois (copies de manuscrits encore plus anciens) a montré que le célèbre théorème était connu bien avant Pythagore, peut-être plusieurs millénaires avant lui.

(Mais il y a une hypothèse que Pythagore lui a donné une preuve complète)

Mais il y a une autre opinion : dans l'école pythagoricienne, c'était une merveilleuse coutume d'attribuer tous les mérites à Pythagore et de ne pas s'approprier quelque peu la gloire des découvreurs, sauf peut-être dans quelques cas.

(Écrivain de langue grecque Iamblique-syriaque, auteur du traité "La vie de Pythagore." (IIe siècle après JC)

Ainsi l'historien allemand des mathématiques Kantor pense que l'égalité 3 2 + 4 2= 5 2 était

connu des Égyptiens vers 2300 av. e. à l'époque du roi Amenechmet (d'après le papyrus 6619 du Musée de Berlin). Certains pensent que Pythagore a donné au théorème une preuve complète, tandis que d'autres lui refusent ce mérite.

Certains attribuent à Pythagore la preuve donnée par Euclide dans ses Éléments. D'autre part, Proclus (mathématicien, 5ème siècle) prétend que la preuve dans les "Principes" appartenait à Euclide lui-même, c'est-à-dire que l'histoire des mathématiques n'a presque aucune donnée fiable sur l'activité mathématique de Pythagore. En mathématiques, peut-être, il n'y a pas d'autre théorème qui mérite toutes sortes de comparaisons.

Dans certaines listes des "Débuts" d'Euclide, ce théorème s'appelait le "théorème de la nymphe" pour la similitude du dessin avec une abeille, un papillon ("théorème du papillon"), qui en grec s'appelait une nymphe. Les Grecs appelaient également ce mot d'autres déesses, ainsi que des jeunes femmes et des mariées. Le traducteur arabe n'a pas prêté attention au dessin et a traduit le mot "nymphe" par "mariée". C'est ainsi qu'est apparu le nom affectueux "le théorème de la mariée". Selon une légende, lorsque Pythagore de Samos a prouvé son théorème, il a remercié les dieux en sacrifiant 100 taureaux. D'où un autre nom - "théorème d'une centaine de taureaux".

Dans les pays anglophones, cela s'appelait : " Moulin à vent", "queue de paon", "chaise de la mariée", "pont d'âne" (si l'étudiant ne pouvait pas "passer" à travers, alors il était un vrai "âne")

Dans la Russie pré-révolutionnaire, le dessin du théorème de Pythagore pour le cas d'un triangle isocèle s'appelait "pantalon de Pythagore".

Ces "pantalons" apparaissent lorsque, de chaque côté d'un triangle rectangle, construisez des carrés vers l'extérieur.

Combien y a-t-il de preuves différentes du théorème de Pythagore ?

Depuis l'époque de Pythagore, plus de 350 d'entre eux sont apparus.Le théorème a été inclus dans le livre Guinness des records. Si nous analysons les preuves du théorème, alors en principe diverses idées peu est utilisé en eux.

Domaines d'application du théorème.

Il est largement utilisé pour résoudre géométrique Tâches.

C'est avec son aide que vous pouvez trouver géométriquement les valeurs des racines carrées des nombres entiers:

Pour ce faire, on construit un triangle rectangle AOB (l'angle A est de 90°) avec des jambes unitaires. Alors son hypoténuse est √2. On construit alors un seul segment BC, BC est perpendiculaire à OB, la longueur de l'hypoténuse OS=√3, etc.

(cette méthode se retrouve chez Euclid et F. Kirensky).

Tâches dans le cours la physique lycée exigent la connaissance du théorème de Pythagore.

Ce sont des tâches liées à l'addition des vitesses.

Faites attention à la diapositive : une tâche d'un manuel de physique de 9e année. À sens pratique il peut être formulé comme suit : à quel angle par rapport au débit du fleuve un bateau transportant des passagers entre les quais doit-il se déplacer pour respecter l'horaire ? (les quais sont situés sur des rives opposées du fleuve)

Lorsqu'un biathlète tire sur une cible, il effectue une "correction de vent". Si le vent souffle de la droite et que l'athlète tire en ligne droite, la balle ira vers la gauche. Pour atteindre la cible, vous devez déplacer le viseur vers la droite de la distance de déplacement de la balle. Des tableaux spéciaux ont été compilés pour eux (basés sur les conséquences du camarade Pythagore). Le biathlète sait sous quel angle déplacer le viseur à une vitesse de vent connue.

Astronomie -également un large domaine d'application du théorème trajet du faisceau lumineux. La figure montre le trajet d'un faisceau lumineux depuis UNà B et retour. Le trajet du faisceau est représenté par une flèche incurvée pour plus de clarté, en fait, le faisceau lumineux est droit.

Quel est le chemin du faisceau? La lumière va et vient de la même manière. Quelle est la moitié du chemin parcouru par le rayon ? Si nous marquons le segment UN B symbole je, la moitié du temps comme t, et désignant également la vitesse de la lumière par la lettre c, alors notre équation prendra la forme

c*t=l

C'est le produit du temps passé sur la vitesse !

Essayons maintenant d'examiner le même phénomène à partir d'un autre référentiel, par exemple, à partir d'un vaisseau spatial passant devant un faisceau progressif avec une vitesse v. Avec une telle observation, les vitesses de tous les corps changeront, et les corps stationnaires commenceront à se déplacer avec une vitesse v dans la direction opposée. Supposons que le navire se déplace vers la gauche. Ensuite, les deux points entre lesquels le lapin court se déplaceront vers la droite avec la même vitesse. De plus, pendant que le lapin court son chemin, le point de départ UN se déplace et le faisceau revient à un nouveau point C.

Question : combien de temps le point va-t-il se déplacer (pour devenir le point C) pendant que le faisceau lumineux se déplace ? Plus précisément : à quoi correspond la moitié de ce décalage ? Si l'on note la moitié du temps de parcours du faisceau par la lettre t", et la moitié de la distance CA lettre ré, alors nous obtenons notre équation sous la forme :

v * t" = ré

lettre v indique la vitesse du vaisseau spatial.

Autre question : quel chemin va parcourir le rayon lumineux dans ce cas ?(Plus précisément, quelle est la moitié de ce chemin ? Quelle est la distance à l'objet inconnu ?)

Si nous désignons la moitié de la longueur du trajet de la lumière par la lettre s, alors nous obtenons l'équation :

c * t" = s

Ici c est la vitesse de la lumière, et t" est le même temps que décrit ci-dessus.

Considérons maintenant le triangle abc. C'est un triangle isocèle dont la hauteur est je, que nous avons introduit en considérant le processus d'un point de vue fixe. Puisque le mouvement est perpendiculaire je, alors cela ne pouvait pas l'affecter.

Triangle abc composé de deux moitiés - triangles rectangles identiques, dont les hypoténuses UN B et avant JC doit être connecté avec les jambes d'après le théorème de Pythagore. L'une des jambes est ré, que nous venons de calculer, et la deuxième jambe est s, que la lumière traverse, et que nous avons également calculée. Nous obtenons l'équation :

s 2 = l 2 +d 2

C'est théorème de Pythagore!

Phénomène aberration stellaire, découvert en 1729, réside dans le fait que toutes les étoiles sphère céleste décrire des ellipses. Le demi-grand axe de ces ellipses est observé depuis la Terre sous un angle de 20,5 degrés. Cet angle est associé au mouvement de la Terre autour du Soleil à une vitesse de 29,8 km/h. Pour observer une étoile depuis une Terre en mouvement, il est nécessaire d'incliner le tube du télescope vers l'avant le long du mouvement de l'étoile, car pendant que la lumière parcourt la longueur du télescope, l'oculaire avance avec la Terre. L'addition des vitesses de la lumière et de la Terre se fait de manière vectorielle, en utilisant le soi-disant.

Pythagoras. U 2 \u003d C 2 + V 2

C est la vitesse de la lumière

Vitesse au sol en V

tube de télescope

À la fin du XIXe siècle, diverses hypothèses ont été émises sur l'existence d'habitants de Mars similaires aux humains, ce fut le résultat des découvertes de l'astronome italien Schiaparelli (il a ouvert des canaux sur Mars qui ont longtemps été considérés comme artificiels) . Naturellement, la question de savoir s'il est possible de communiquer avec ces créatures hypothétiques à l'aide de signaux lumineux a suscité une discussion animée. L'Académie des sciences de Paris a même institué un prix de 100 000 francs pour la première personne à entrer en contact avec un habitant d'un autre corps céleste ; ce prix attend toujours l'heureux élu. Par plaisanterie, bien que pas complètement déraisonnable, il a été décidé d'envoyer un signal aux habitants de Mars sous la forme du théorème de Pythagore.

On ne sait pas comment faire cela; mais il est évident pour tout le monde que le fait mathématique exprimé par le théorème de Pythagore se produit partout, et donc les habitants d'un autre monde comme nous devraient comprendre un tel signal.

connexion mobile

Qui dans le monde d'aujourd'hui n'utilise pas de téléphone portable ? Chaque abonné mobile est intéressé par sa qualité. Et la qualité, à son tour, dépend de la hauteur de l'antenne de l'opérateur mobile. Pour calculer dans quel rayon une transmission peut être reçue, nous utilisons le théorème de Pythagore.

Quoi altitude la plus élevée doit avoir une antenne d'opérateur mobile pour que la transmission puisse être reçue dans un rayon de R = 200 km ? (Le rayon de la Terre est de 6380 km.)

La solution:

Laisser AB=x , CB=R=200 km , OC = r = 6380 km.

OB=OA+ABOB=r+x.

En utilisant le théorème de Pythagore, on obtient Réponse : 2,3 km.

Lors de la construction de maisons et de chalets, la question se pose souvent de la longueur des chevrons du toit, si les poutres ont déjà été faites. Par exemple: il est prévu de construire un toit à pignon dans une maison (forme en coupe). Quelle doit être la longueur des chevrons si les poutres sont faites AC=8 m., et AB=BF.

La solution:

Le triangle ADC est isocèle AB = BC = 4 m., BF = 4 m. Si nous supposons que FD = 1,5 m., alors :

A) A partir du triangle DBC : DB=2,5 m.

B) Du triangle ABF :

Fenêtre

Dans les bâtiments Style gothique et roman les parties supérieures des fenêtres sont divisées par des nervures en pierre, qui non seulement jouent le rôle d'ornement, mais contribuent également à la solidité des fenêtres. La figure montre un exemple simple d'une telle fenêtre de style gothique. La méthode de construction est très simple : à partir de la figure, il est facile de trouver les centres de six arcs de cercles dont les rayons sont égaux à

largeur de fenêtre (b) pour les arcs extérieurs

demi-largeur, (b/2) pour les arcs internes

Il y a encore un cercle complet touchant les quatre arcs. Puisqu'il est enfermé entre deux cercles concentriques, son diamètre est égal à la distance entre ces cercles, soit b/2 et, par conséquent, le rayon est égal à b/4. Et puis ça devient clair

la position de son centre.

À Architecture romane le motif représenté sur la figure se retrouve souvent. Si b désigne toujours la largeur de la fenêtre, les rayons des demi-cercles seront égaux à R = b / 2 et r = b / 4. Le rayon p du cercle intérieur peut être calculé à partir du triangle rectangle illustré à la fig. ligne pointillée. L'hypoténuse de ce triangle, passant par le point tangent des cercles, est égale à b/4+p, une jambe est égale à b/4 et l'autre à b/2-p. D'après le théorème de Pythagore, nous avons :

(b/4+p) 2 =(b/4) 2 +(b/4-p) 2

b 2 /16+ pb / 2 + p 2 \u003d b 2 / 16 + b 2 / 4 - pb / 2 + p 2,

En divisant par b et en rapprochant les mêmes termes, on obtient :

(3/2)p=b/4, p=b/6.

Dans l'industrie forestière: pour les besoins de la construction, les grumes sont sciées en bois, tandis que la tâche principale est d'obtenir le moins de déchets possible. La plus petite quantité de déchets sera lorsque le faisceau a le plus grand volume. Que devrait-il y avoir dans la section ? Comme on peut le voir à partir de la solution, la section transversale doit être carrée, et théorème de Pythagore et d'autres considérations permettent de tirer une telle conclusion.

Barre du plus grand volume

Une tâche

À partir d'une bûche cylindrique, il est nécessaire de couper une poutre rectangulaire du plus grand volume. Quelle doit être la forme de sa section transversale (Fig. 23) ?

La solution

Si les côtés d'une section rectangulaire sont x et y, alors par le théorème de Pythagore

x 2 + y 2 \u003d d 2,

où d est le diamètre du rondin. Le volume du bois est le plus grand lorsque sa section transversale est la plus grande, c'est-à-dire lorsque xy atteint sa plus grande valeur. Mais si xy est le plus grand, alors le produit x 2 y 2 sera aussi le plus grand. Puisque la somme x 2 + y 2 est inchangée, alors, selon ce qui a été prouvé précédemment, le produit x 2 y 2 est le plus grand lorsque

x 2 \u003d y 2 ou x \u003d y.

Ainsi, la section transversale de la poutre doit être carrée.

Tâches de transport(les tâches dites d'optimisation ; tâches dont la solution permet de répondre à la question : comment disposer des fonds pour obtenir de grands avantages)

A première vue, rien de spécial : mesurez la hauteur du sol au plafond en plusieurs points, soustrayez quelques centimètres pour que le meuble ne repose pas contre le plafond. Cela fait, lors du processus d'assemblage des meubles, des difficultés peuvent survenir. Après tout, les fabricants de meubles assemblent le cadre en plaçant le meuble en position horizontale, et lorsque le cadre est assemblé, ils le soulèvent en position verticale. Considérez la paroi latérale de l'armoire. La hauteur de l'armoire doit être inférieure de 10 cm à la distance entre le sol et le plafond, à condition que cette distance ne dépasse pas 2500 mm. Et la profondeur de l'armoire est de 700 mm. Pourquoi 10 cm, et non 5 cm ou 7, et qu'est-ce que le théorème de Pythagore a à voir là-dedans ?

Donc : paroi latérale 2500-100=2400(mm) - la hauteur maximale de la structure.

La paroi latérale en train de soulever le cadre doit passer librement en hauteur et en diagonale. Par le théorème de Pythagore

CA \u003d √ AB 2 + BC 2

AC= √ 2400 2 + 700 2 = 2500 (mm)

Que se passe-t-il si la hauteur de l'armoire est réduite de 50 mm ?

AC= √ 2450 2 + 700 2 = 2548 (mm)

Diagonale 2548 mm. Donc, vous ne pouvez pas mettre de placard (vous pouvez ruiner le plafond).

Paratonnerre.

On sait qu'un paratonnerre protège de la foudre tous les objets dont la distance à sa base ne dépasse pas sa hauteur doublée. Il est nécessaire de déterminer la position optimale du paratonnerre sur un toit à pignon, en fournissant sa hauteur disponible la plus basse.

D'après le théorème de Pythagore h 2 ≥ un 2 +b 2 signifie h≥(un 2 +b 2) 1/2

d'urgence pour zone suburbaine besoin de faire une serre pour les semis.

Des planches renversées un carré de 1m1m. Il y a des restes d'un film mesurant 1.5m1.5m. A quelle hauteur au centre du carré faut-il fixer le rail pour que le film le recouvre complètement ?

1) Diagonale de la serre d == 1,4 ; 0,7

2) Diagonale du film d 1= 2,12 1,06

3) Hauteur des rails x= 0,7

Conclusion

À la suite de la recherche, j'ai découvert certains domaines d'application du théorème de Pythagore. J'ai collecté et traité beaucoup de matériel provenant de sources littéraires et d'Internet sur ce sujet. J'ai étudié quelques informations historiques sur Pythagore et son théorème. Oui, en effet, en utilisant le théorème de Pythagore, vous pouvez résoudre non seulement des problèmes mathématiques. Le théorème de Pythagore a trouvé son application dans la construction et l'architecture, les communications mobiles et la littérature.

Étude et analyse des sources d'information sur le théorème de Pythagore

ont montré que:

un) l'attention exclusive des mathématiciens et des mathématiciens au théorème est basée sur sa simplicité, sa beauté et sa signification;

b) le théorème de Pythagore pendant de nombreux siècles sert d'impulsion à des découvertes mathématiques intéressantes et importantes (théorème de Fermat, théorie de la relativité d'Einstein);

dans) le théorème de Pythagore - est l'incarnation du langage universel des mathématiques, valable dans le monde entier;

g) la portée du théorème est assez étendue et ne peut généralement pas être indiquée de manière suffisamment complète ;

ré) les secrets du théorème de Pythagore continuent d'exciter l'humanité et chacun de nous a donc la possibilité d'être impliqué dans leur révélation.

Bibliographie

Uspekhi matematicheskikh nauk, 1962, volume 17, n° 6 (108).

Alexander Danilovich Alexandrov (à l'occasion du cinquantième anniversaire de date d'anniversaire),

Alexandrov A.D., Werner A.L., Ryzhik V.I. Géométrie, 10 - 11 cellules. - M. : Lumières, 1992.

Atanasyan L.S. etc. Géométrie, 10 - 11 cellules. - M. : Lumières, 1992.

Vladimirov Yu.S. Espace - temps : dimensions explicites et cachées. - M. : "Nauka", 1989.

Volochine A.V. Pythagoras. - M. : Lumières, 1993.

Journal "Mathématiques", n° 21, 2006.

Journal "Mathématiques", n° 28, 1995.

Géométrie : Proc. Pour 7 - 11 cellules. collège / G.P. Bevz, V.G. Bevz, N.G. Vladimirova. - M. : Lumières, 1992.

Géométrie : manuel pour 7 à 9 cellules. enseignement général Institutions/ L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev et autres - 6e éd. - M. : Lumières, 1996.

Glazer GI Histoire des mathématiques à l'école : IX - Xcl. Un guide pour les enseignants. - M. : Lumières, 1983.

Chapitres supplémentaires au manuel scolaire 8e année: Manuel pour les élèves. et des cours avec approfondissement. étude mathématiques /L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev et autres - M.: Education, 1996.

Yelensky Sh. Sur les traces de Pythagore. M., 1961.

Kiselev A.P., Rybkin N.A. Géométrie : Planimétrie : 7 - 9 cellules : Manuel et cahier de problèmes. - M. : Outarde, 1995.

Kline M. Mathématiques. Recherche de la vérité : traduction de l'anglais. / Éd. et avant-propos. DANS ET. Arshinova, Yu.V. Satchkov. - M. : Mir, 1998.

Liturman V. Le théorème de Pythagore. - M., 1960.

Mathématiques : Manuel des écoliers et des étudiants / B. Frank et autres ; Traduction de lui. - 3e éd., stéréotype. - M. : Outarde, 2003.

Peltwer A. Qui es-tu Pythagore ? - M. : Savoir c'est pouvoir, n°12, 1994.

Perelman Ya. I. Mathématiques ludiques. - M. : "Sciences", 1976.

Ponomareva TD De grands scientifiques. - M. : LLC Maison d'édition Astrel, 2002.

Sveshnikova A. Voyage dans l'histoire des mathématiques. - M., 1995.

Semionov E.E. Nous étudions la géométrie : Livre. Pour les étudiants 6 - 8 cellules. école intermédiaire - M. : Lumières, 1987.

Smyshliaev V.K. À propos des mathématiques et des mathématiciens. - Maison d'édition Mari, 1977.

Tuchnin N.P. Comment poser une question. - M. : Lumières, 1993.

Cherkasov O.Yu. Planimétrie à l'examen d'entrée. - M. : Lycée de Moscou, 1996.

Dictionnaire encyclopédique jeune mathématicien. Comp. A.P. Sauvin. - M. : Pédagogie, 1985.

Encyclopédie pour enfants. T. 11. Mathématiques. /Ch. Éd. MARYLAND. Aksénova. - M. : Avanta+, 2001.

En une chose, vous pouvez être sûr à cent pour cent que lorsqu'on lui demande quel est le carré de l'hypoténuse, tout adulte répondra hardiment : "La somme des carrés des jambes". Cette théorie est fermement ancrée dans l'esprit de chacun. personne instruite, mais il suffit de demander à quelqu'un de le prouver, et des difficultés peuvent survenir. Par conséquent, rappelons-nous et considérons différentes manières de prouver le théorème de Pythagore.

Bref aperçu de la biographie

Le théorème de Pythagore est familier à presque tout le monde, mais pour une raison quelconque, la biographie de la personne qui l'a produit n'est pas si populaire. Nous allons le réparer. Par conséquent, avant d'étudier les différentes manières de prouver le théorème de Pythagore, vous devez vous familiariser brièvement avec sa personnalité.

Pythagore - philosophe, mathématicien, penseur, originaire de Aujourd'hui, il est très difficile de distinguer sa biographie des légendes qui se sont développées à la mémoire de ce grand homme. Mais comme il ressort des écrits de ses disciples, Pythagore de Samos est né sur l'île de Samos. Son père était un tailleur de pierre ordinaire, mais sa mère venait d'une famille noble.

Selon la légende, la naissance de Pythagore a été prédite par une femme nommée Pythia, en l'honneur de laquelle le garçon a été nommé. Selon sa prédiction, un garçon né devait apporter de nombreux avantages et bien à l'humanité. C'est ce qu'il a fait en réalité.

La naissance d'un théorème

Dans sa jeunesse, Pythagore a déménagé en Égypte pour y rencontrer les célèbres sages égyptiens. Après les avoir rencontrés, il a été admis à étudier, où il a appris toutes les grandes réalisations de la philosophie, des mathématiques et de la médecine égyptiennes.

C'est probablement en Égypte que Pythagore s'est inspiré de la majesté et de la beauté des pyramides et a créé sa grande théorie. Cela peut choquer les lecteurs, mais les historiens modernes pensent que Pythagore n'a pas prouvé sa théorie. Mais il n'a transmis ses connaissances qu'à ses disciples, qui ont ensuite effectué tous les calculs mathématiques nécessaires.

Quoi qu'il en soit, aujourd'hui on ne connaît pas une technique pour prouver ce théorème, mais plusieurs à la fois. Aujourd'hui, nous ne pouvons que deviner comment exactement les anciens Grecs effectuaient leurs calculs, nous allons donc examiner ici différentes manières de prouver le théorème de Pythagore.

théorème de Pythagore

Avant de commencer les calculs, vous devez déterminer quelle théorie prouver. Le théorème de Pythagore ressemble à ceci : "Dans un triangle dont l'un des angles mesure 90°, la somme des carrés des jambes est égale au carré de l'hypoténuse."

Il existe 15 façons différentes de prouver le théorème de Pythagore au total. C'est un nombre assez important, alors faisons attention aux plus populaires d'entre eux.

Première méthode

Définissons d'abord ce que nous avons. Ces données s'appliqueront également à d'autres façons de prouver le théorème de Pythagore, vous devez donc vous souvenir immédiatement de toutes les notations disponibles.

Supposons qu'un triangle rectangle soit donné, avec des jambes a, b et une hypoténuse égale à c. La première méthode de preuve est basée sur le fait qu'un carré doit être tiré d'un triangle rectangle.

Pour ce faire, vous devez dessiner un segment égal à la jambe dans la longueur de la jambe a, et vice versa. Il devrait donc s'avérer que deux côtés égaux du carré. Il ne reste plus qu'à tracer deux lignes parallèles, et le carré est prêt.

À l'intérieur de la figure résultante, vous devez dessiner un autre carré avec un côté égale à l'hypoténuse triangle d'origine. Pour ce faire, à partir des sommets ac et sv, vous devez tracer deux segments parallèles égaux à c. Ainsi, nous obtenons trois côtés du carré, dont l'un est l'hypoténuse du triangle rectangle d'origine. Il ne reste plus qu'à dessiner le quatrième segment.

Sur la base de la figure résultante, nous pouvons conclure que l'aire du carré extérieur est (a + b) 2. Si vous regardez à l'intérieur de la figure, vous pouvez voir qu'en plus du carré intérieur, il y a quatre triangles rectangles. La superficie de chacune est de 0,5 av.

Par conséquent, la zone est: 4 * 0,5av + s 2 \u003d 2av + s 2

D'où (a + c) 2 \u003d 2av + c 2

Et, par conséquent, avec 2 \u003d un 2 + en 2

Le théorème a été démontré.

Deuxième méthode : triangles similaires

Cette formule pour la preuve du théorème de Pythagore a été dérivée sur la base d'une déclaration de la section de géométrie sur triangles semblables. Il dit que la jambe d'un triangle rectangle est la moyenne proportionnelle à son hypoténuse et au segment d'hypoténuse émanant du sommet d'un angle de 90 o.

Les données initiales restent les mêmes, alors commençons tout de suite par la preuve. Traçons un segment CD perpendiculaire au côté AB. Sur la base de la déclaration ci-dessus, les jambes des triangles sont égales :

AC=√AB*AD, SW=√AB*DV.

Pour répondre à la question de savoir comment prouver le théorème de Pythagore, la preuve doit être établie en mettant au carré les deux inégalités.

AC 2 \u003d AB * ENFER et SV 2 \u003d AB * DV

Maintenant, nous devons ajouter les inégalités résultantes.

AC 2 + SV 2 \u003d AB * (AD * DV), où AD + DV \u003d AB

Il se trouve que:

AC 2 + CB 2 \u003d AB * AB

Et donc:

AC 2 + CB 2 \u003d AB 2

Preuve du théorème de Pythagore et différentes manières ses solutions nécessitent une approche multidimensionnelle de ce problème. Cependant, cette option est l'une des plus simples.

Une autre méthode de calcul

La description des différentes façons de prouver le théorème de Pythagore peut ne rien dire, jusqu'à ce que vous commenciez à pratiquer par vous-même. De nombreuses méthodes impliquent non seulement des calculs mathématiques, mais également la construction de nouvelles figures à partir du triangle d'origine.

Dans ce cas, il est nécessaire de compléter un autre triangle rectangle VSD depuis la jambe de l'avion. Ainsi, il y a maintenant deux triangles avec une jambe commune BC.

Sachant que les aires de figures semblables ont un rapport égal aux carrés de leurs dimensions linéaires semblables, alors :

S avs * s 2 - S avd * en 2 \u003d S avd * a 2 - S vd * a 2

S avs * (de 2 à 2) \u003d a 2 * (S avd -S vvd)

de 2 à 2 \u003d un 2

c 2 \u003d un 2 + en 2

Étant donné que cette option ne convient guère aux différentes méthodes de démonstration du théorème de Pythagore pour la 8e année, vous pouvez utiliser la technique suivante.

Le moyen le plus simple de prouver le théorème de Pythagore. Commentaires

Les historiens pensent que cette méthode a été utilisée pour la première fois pour prouver le théorème en la Grèce ancienne. C'est le plus simple, puisqu'il ne nécessite absolument aucun calcul. Si vous dessinez correctement une image, la preuve de l'affirmation selon laquelle a 2 + b 2 \u003d c 2 sera clairement visible.

Conditions pour cette méthode sera légèrement différent du précédent. Pour prouver le théorème, supposons que le triangle rectangle ABC soit isocèle.

Nous prenons l'hypoténuse AC comme côté du carré et dessinons ses trois côtés. De plus, il est nécessaire de tracer deux lignes diagonales dans le carré résultant. Ainsi, à l'intérieur, vous obtenez quatre triangles isocèles.

Pour les jambes AB et CB, vous devez également dessiner un carré et tracer une ligne diagonale dans chacune d'elles. Nous dessinons la première ligne du sommet A, la seconde - de C.

Maintenant, vous devez regarder attentivement l'image résultante. Puisqu'il y a quatre triangles sur l'hypoténuse AC, égaux à celui d'origine, et deux sur les jambes, cela indique la véracité de ce théorème.

Au fait, grâce à cette méthode de démonstration du théorème de Pythagore, la célèbre phrase est née: "Les pantalons de Pythagore sont égaux dans toutes les directions."

Preuve par J. Garfield

James Garfield est le 20e président des États-Unis d'Amérique. En plus d'avoir laissé sa marque dans l'histoire en tant que dirigeant des États-Unis, il était également un autodidacte doué.

Au début de sa carrière, il était enseignant ordinaire dans une école populaire, mais est rapidement devenu directeur de l'un des établissements d'enseignement supérieur. Le désir d'auto-développement et lui a permis d'offrir une nouvelle théorie de la preuve du théorème de Pythagore. Le théorème et un exemple de sa solution sont les suivants.

Vous devez d'abord dessiner deux triangles rectangles sur une feuille de papier afin que la jambe de l'un d'eux soit une continuation de la seconde. Les sommets de ces triangles doivent être reliés pour former un trapèze.

Comme vous le savez, l'aire d'un trapèze est égale au produit de la moitié de la somme de ses bases et de la hauteur.

S=a+b/2 * (a+b)

Si nous considérons le trapèze résultant comme une figure composée de trois triangles, son aire peut être trouvée comme suit :

S \u003d av / 2 * 2 + s 2 / 2

Maintenant, nous devons égaliser les deux expressions originales

2av / 2 + s / 2 \u003d (a + c) 2 / 2

c 2 \u003d un 2 + en 2

Plus d'un volume peut être écrit sur le théorème de Pythagore et comment le prouver guide d'étude. Mais cela a-t-il un sens lorsque ces connaissances ne peuvent pas être mises en pratique ?

Application pratique du théorème de Pythagore

Malheureusement, les programmes scolaires modernes ne prévoient l'utilisation de ce théorème que dans les problèmes géométriques. Les diplômés partiront bientôt murs de l'école sans savoir comment ils peuvent appliquer leurs connaissances et leurs compétences dans la pratique.

En fait, utilisez le théorème de Pythagore dans votre Vie courante tout le monde peut. Et pas seulement dans les activités professionnelles, mais aussi dans les tâches ménagères ordinaires. Considérons plusieurs cas où le théorème de Pythagore et les méthodes de sa preuve peuvent être extrêmement nécessaires.

Connexion du théorème et de l'astronomie

Il semblerait que les étoiles et les triangles puissent être connectés sur papier. En fait, l'astronomie est un domaine scientifique dans lequel le théorème de Pythagore est largement utilisé.

Par exemple, considérons le mouvement d'un faisceau lumineux dans l'espace. Nous savons que la lumière voyage dans les deux sens à la même vitesse. On appelle la trajectoire AB le long de laquelle se déplace le rayon lumineux je. Et la moitié du temps qu'il faut à la lumière pour aller d'un point A à un point B, appelons t. Et la vitesse du faisceau - c. Il se trouve que: c*t=l

Si vous regardez ce même faisceau depuis un autre avion, par exemple depuis un vaisseau spatial qui se déplace à une vitesse v, alors avec une telle observation des corps, leur vitesse changera. Dans ce cas, même les éléments stationnaires se déplaceront à une vitesse v dans la direction opposée.

Disons que le paquebot comique navigue vers la droite. Ensuite, les points A et B, entre lesquels le rayon se précipite, se déplaceront vers la gauche. De plus, lorsque le faisceau se déplace du point A au point B, le point A a le temps de se déplacer et, par conséquent, la lumière arrivera déjà à un nouveau point C. Pour trouver la moitié de la distance sur laquelle le point A s'est déplacé, vous devez multiplier la vitesse du liner par la moitié du temps de parcours du faisceau (t").

Et pour trouver la distance parcourue par un rayon de lumière pendant ce temps, vous devez désigner la moitié du chemin des nouveaux hêtres et obtenir l'expression suivante :

Si nous imaginons que les points de lumière C et B, ainsi que la doublure de l'espace, sont les sommets d'un triangle isocèle, alors le segment du point A à la doublure le divisera en deux triangles rectangles. Par conséquent, grâce au théorème de Pythagore, vous pouvez trouver la distance que pourrait parcourir un rayon de lumière.

Cet exemple, bien sûr, n'est pas le plus réussi, car seuls quelques-uns peuvent avoir la chance de l'essayer dans la pratique. Par conséquent, nous considérons des applications plus banales de ce théorème.

Portée de transmission du signal mobile

La vie moderne ne peut plus être imaginée sans l'existence des smartphones. Mais à quoi serviraient-ils s'ils ne pouvaient pas connecter les abonnés via les communications mobiles ? !

La qualité des communications mobiles dépend directement de la hauteur à laquelle se trouve l'antenne de l'opérateur mobile. Afin de calculer à quelle distance d'une tour mobile un téléphone peut recevoir un signal, vous pouvez appliquer le théorème de Pythagore.

Disons que vous devez trouver la hauteur approximative d'une tour fixe afin qu'elle puisse propager un signal dans un rayon de 200 kilomètres.

AB (hauteur de la tour) = x ;

BC (rayon de transmission du signal) = 200 km ;

OS (rayon du globe) = 6380 km ;

OB=OA+ABOB=r+x

En appliquant le théorème de Pythagore, nous constatons que la hauteur minimale de la tour doit être de 2,3 kilomètres.

Théorème de Pythagore dans la vie quotidienne

Curieusement, le théorème de Pythagore peut être utile même dans les affaires courantes, comme déterminer la hauteur d'un placard, par exemple. À première vue, il n'est pas nécessaire d'utiliser des calculs aussi complexes, car vous pouvez simplement prendre des mesures avec un ruban à mesurer. Mais beaucoup sont surpris de savoir pourquoi certains problèmes surviennent lors du processus d'assemblage si toutes les mesures ont été prises avec plus de précision.

Le fait est que la garde-robe est assemblée en position horizontale et seulement ensuite se lève et est installée contre le mur. Par conséquent, la paroi latérale de l'armoire en train de soulever la structure doit passer librement à la fois le long de la hauteur et en diagonale de la pièce.

Supposons qu'il y ait une armoire d'une profondeur de 800 mm. Distance du sol au plafond - 2600 mm. Un fabricant de meubles expérimenté dira que la hauteur du meuble doit être inférieure de 126 mm à la hauteur de la pièce. Mais pourquoi exactement 126 mm ? Prenons un exemple.

Avec les dimensions idéales de l'armoire, vérifions le fonctionnement du théorème de Pythagore :

CA \u003d √AB 2 + √BC 2

AC \u003d √ 2474 2 +800 2 \u003d 2600 mm - tout converge.

Disons que la hauteur du meuble n'est pas de 2474 mm, mais de 2505 mm. Alors:

CA \u003d √2505 2 + √800 2 \u003d 2629 mm.

Par conséquent, cette armoire n'est pas adaptée à une installation dans cette pièce. Depuis lors, en le soulevant en position verticale, des dommages à son corps peuvent être causés.

Peut-être, après avoir examiné différentes manières de prouver le théorème de Pythagore par différents scientifiques, pouvons-nous conclure que c'est plus que vrai. Vous pouvez maintenant utiliser les informations reçues dans votre vie quotidienne et être totalement sûr que tous les calculs seront non seulement utiles, mais également corrects.