Benachbarte Flächen eines Parallelepipeds sind parallel. Rechteckiges Parallelepiped – Wissens-Hypermarkt

In dieser Lektion kann sich jeder mit dem Thema „Rechteckiges Parallelepiped“ befassen. Zu Beginn der Lektion werden wir wiederholen, was beliebige und gerade Parallelepipede sind, und uns an die Eigenschaften ihrer gegenüberliegenden Flächen und Diagonalen des Parallelepipeds erinnern. Dann schauen wir uns an, was ein Quader ist und besprechen seine grundlegenden Eigenschaften.

Thema: Rechtwinkligkeit von Linien und Ebenen

Lektion: Quader

Eine Fläche bestehend aus zwei gleichen Parallelogrammen ABCD und A 1 B 1 C 1 D 1 und vier Parallelogrammen ABV 1 A 1, BCC 1 B 1, CDD 1 C 1, DAA 1 D 1 heißt Parallelepiped(Abb. 1).

Reis. 1 Parallelepiped

Das heißt: Wir haben zwei gleiche Parallelogramme ABCD und A 1 B 1 C 1 D 1 (Basen), sie liegen also in parallelen Ebenen seitliche Rippen AA 1, BB 1, DD 1, CC 1 sind parallel. So nennt man eine aus Parallelogrammen zusammengesetzte Fläche Parallelepiped.

Somit ist die Oberfläche eines Parallelepipeds die Summe aller Parallelogramme, aus denen das Parallelepiped besteht.

1. Die gegenüberliegenden Flächen eines Parallelepipeds sind parallel und gleich.

(die Formen sind gleich, d. h. sie können durch Überlappung kombiniert werden)

Zum Beispiel:

ABCD = A 1 B 1 C 1 D 1 (per Definition gleiche Parallelogramme),

AA 1 B 1 B = DD 1 C 1 C (da AA 1 B 1 B und DD 1 C 1 C gegenüberliegende Flächen des Parallelepipeds sind),

AA 1 D 1 D = BB 1 C 1 C (da AA 1 D 1 D und BB 1 C 1 C gegenüberliegende Flächen des Parallelepipeds sind).

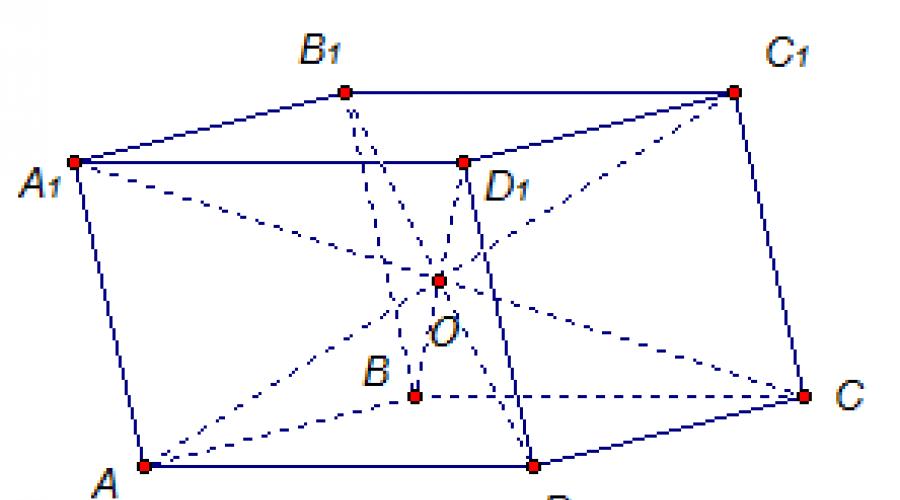
2. Die Diagonalen eines Parallelepipeds schneiden sich in einem Punkt und werden durch diesen Punkt halbiert.

Die Diagonalen des Parallelepipeds AC 1, B 1 D, A 1 C, D 1 B schneiden sich in einem Punkt O, und jede Diagonale wird durch diesen Punkt in zwei Hälften geteilt (Abb. 2).

Reis. 2 Die Diagonalen eines Parallelepipeds schneiden sich und werden durch den Schnittpunkt in zwei Hälften geteilt.

3. Es gibt drei Quadrupel gleicher und paralleler Kanten eines Parallelepipeds: 1 - AB, A 1 B 1, D 1 C 1, DC, 2 - AD, A 1 D 1, B 1 C 1, BC, 3 - AA 1, BB 1, CC 1, DD 1.

Definition. Ein Parallelepiped heißt gerade, wenn seine Seitenkanten senkrecht zu den Grundflächen stehen.

Die Seitenkante AA 1 sei senkrecht zur Basis (Abb. 3). Dies bedeutet, dass die Gerade AA 1 senkrecht zu den Geraden AD und AB steht, die in der Ebene der Grundfläche liegen. Das bedeutet, dass die Seitenflächen Rechtecke enthalten. Und die Basen enthalten beliebige Parallelogramme. Bezeichnen wir ∠BAD = φ, der Winkel φ kann beliebig sein.

Reis. 3 Rechter Parallelepiped

Ein rechtwinkliges Parallelepiped ist also ein Parallelepiped, bei dem die Seitenkanten senkrecht zu den Grundflächen des Parallelepipeds stehen.

Definition. Das Parallelepiped heißt rechteckig, wenn seine Seitenkanten senkrecht zur Basis stehen. Die Grundflächen sind Rechtecke.

Das Parallelepiped ABCDA 1 B 1 C 1 D 1 ist rechteckig (Abb. 4), wenn:

1. AA 1 ⊥ ABCD (Seitenkante senkrecht zur Grundebene, also ein gerades Parallelepiped).

2. ∠BAD = 90°, d. h. die Grundfläche ist ein Rechteck.

Reis. 4 Rechteckiges Parallelepiped

Ein rechteckiges Parallelepiped hat alle Eigenschaften eines beliebigen Parallelepipeds. Es gibt aber noch weitere Eigenschaften, die sich aus der Definition eines Quaders ableiten.

Also, Quader ist ein Parallelepiped, dessen Seitenkanten senkrecht zur Grundfläche stehen. Die Grundfläche eines Quaders ist ein Rechteck.

1. Bei einem rechteckigen Parallelepiped sind alle sechs Flächen Rechtecke.

ABCD und A 1 B 1 C 1 D 1 sind per Definition Rechtecke.

2. Die seitlichen Rippen stehen senkrecht zur Basis. Dies bedeutet, dass alle Seitenflächen eines rechteckigen Parallelepipeds Rechtecke sind.

3. Alle Diederwinkel rechteckige parallelepipedische gerade Linien.

Betrachten wir zum Beispiel den Diederwinkel eines rechteckigen Parallelepipeds mit der Kante AB, also den Diederwinkel zwischen den Ebenen ABC 1 und ABC.

AB ist eine Kante, Punkt A 1 liegt in einer Ebene – in der Ebene ABB 1 und Punkt D in der anderen – in der Ebene A 1 B 1 C 1 D 1. Dann kann auch der betrachtete Diederwinkel angegeben werden auf die folgende Weise: ∠A 1 ABD.

Nehmen wir Punkt A auf der Kante AB. AA 1 ist senkrecht zur Kante AB in der Ebene АВВ-1, AD ist senkrecht zur Kante AB in der Ebene ABC. Dies bedeutet, dass ∠A 1 AD der lineare Winkel eines gegebenen Diederwinkels ist. ∠A 1 AD = 90°, was bedeutet, dass der Diederwinkel an der Kante AB 90° beträgt.

∠(ABB 1, ABC) = ∠(AB) = ∠A 1 ABD= ∠A 1 AD = 90°.

Ebenso wird bewiesen, dass alle Diederwinkel eines rechteckigen Parallelepipeds richtig sind.

Das Quadrat der Diagonale eines rechteckigen Parallelepipeds ist gleich der Summe der Quadrate seiner drei Dimensionen.

Notiz. Die Längen der drei Kanten, die von einer Ecke eines Quaders ausgehen, sind die Maße des Quaders. Sie werden manchmal als Länge, Breite und Höhe bezeichnet.

Gegeben: ABCDA 1 B 1 C 1 D 1 - rechteckiges Parallelepiped (Abb. 5).

Beweisen: .

Reis. 5 Rechteckiges Parallelepiped

Nachweisen:

Die Gerade CC 1 steht senkrecht zur Ebene ABC und damit zur Geraden AC. Das bedeutet, dass das Dreieck CC 1 A rechtwinklig ist. Nach dem Satz des Pythagoras:

Lassen Sie uns überlegen rechtwinkliges Dreieck ABC. Nach dem Satz des Pythagoras:

Aber BC und AD sind gegenüberliegende Seiten des Rechtecks. Also BC = AD. Dann:

Als , A , Das. Da CC 1 = AA 1, musste dies bewiesen werden.

Die Diagonalen eines rechteckigen Parallelepipeds sind gleich.

Bezeichnen wir die Abmessungen des Parallelepipeds ABC als a, b, c (siehe Abb. 6), dann AC 1 = CA 1 = B 1 D = DB 1 =

Ein Parallelepiped ist geometrische Figur, alle 6 Flächen davon sind Parallelogramme.

Abhängig von der Art dieser Parallelogramme werden folgende Arten von Parallelepipeden unterschieden:

• gerade;
• geneigt;
• rechteckig.

Ein Quader ist ein viereckiges Prisma, dessen Kanten mit der Grundebene einen Winkel von 90° bilden.

Ein rechteckiges Parallelepiped ist ein viereckiges Prisma, dessen Flächen alle Rechtecke sind. Ein Würfel ist eine Art viereckiges Prisma, bei dem alle Flächen und Kanten einander gleich sind.

Die Merkmale einer Figur bestimmen ihre Eigenschaften. Dazu gehören die folgenden 4 Aussagen:

Alle oben genannten Eigenschaften sind leicht zu merken, leicht zu verstehen und logisch aus der Art und den Eigenschaften des geometrischen Körpers abzuleiten. Einfache Anweisungen können jedoch bei der Lösung typischer USE-Aufgaben unglaublich nützlich sein und die Zeit sparen, die zum Bestehen des Tests erforderlich ist.

Parallelepiped-Formeln

Um Antworten auf das Problem zu finden, reicht es nicht aus, nur die Eigenschaften der Figur zu kennen. Möglicherweise benötigen Sie auch einige Formeln, um die Fläche und das Volumen eines geometrischen Körpers zu ermitteln.

Die Fläche der Basen wird auf die gleiche Weise ermittelt wie der entsprechende Indikator eines Parallelogramms oder Rechtecks. Die Basis des Parallelogramms können Sie selbst wählen. Bei der Lösung von Problemen ist es in der Regel einfacher, mit einem Prisma zu arbeiten, dessen Grundfläche ein Rechteck ist.

Die Formel zum Ermitteln der Seitenfläche eines Parallelepipeds kann auch für Testaufgaben benötigt werden.

Beispiele für die Lösung typischer Aufgaben des Einheitlichen Staatsexamens

Übung 1.

Gegeben: ein rechteckiges Parallelepiped mit den Abmessungen 3, 4 und 12 cm.
Notwendig Finden Sie die Länge einer der Hauptdiagonalen der Figur.
Lösung: Jede Lösung eines geometrischen Problems muss mit der Erstellung einer korrekten und klaren Zeichnung beginnen, auf der „vorgegeben“ und der gewünschte Wert angegeben sind. Das Bild unten zeigt ein Beispiel richtiges Design Aufgabenbedingungen.

Nachdem wir die erstellte Zeichnung untersucht und uns alle Eigenschaften des geometrischen Körpers gemerkt haben, kommen wir zur einzig richtigen Lösungsmethode. Wenn wir die vierte Eigenschaft eines Parallelepipeds anwenden, erhalten wir den folgenden Ausdruck:

Nach einfachen Berechnungen erhalten wir den Ausdruck b2=169, also b=13. Die Antwort auf die Aufgabe wurde gefunden, Sie müssen nicht mehr als 5 Minuten damit verbringen, danach zu suchen und sie zu zeichnen.

Es gibt verschiedene Arten von Parallelepipeden:

· Rechteckiges Parallelepiped- ist ein Parallelepiped, dessen Flächen alle sind - Rechtecke;

· Ein rechtwinkliges Parallelepiped ist ein Parallelepiped mit 4 Seitenflächen – Parallelogrammen;

· Ein geneigtes Parallelepiped ist ein Parallelepiped, dessen Seitenflächen nicht senkrecht zu den Grundflächen stehen.

Wesentliche Elemente

Zwei Flächen eines Parallelepipeds, die keine gemeinsame Kante haben, werden als gegenüberliegend bezeichnet, und diejenigen, die eine gemeinsame Kante haben, werden als benachbart bezeichnet. Zwei Eckpunkte eines Parallelepipeds, die nicht zur gleichen Fläche gehören, werden als gegenüberliegend bezeichnet. Liniensegment, Das Verbinden gegenüberliegender Eckpunkte heißt schräg Parallelepiped. Die Längen von drei Kanten eines rechteckigen Parallelepipeds mit einem gemeinsamen Scheitelpunkt werden aufgerufen Messungen.

Eigenschaften

· Das Parallelepiped ist symmetrisch zur Mitte seiner Diagonale.

· Jedes Segment, dessen Enden zur Oberfläche des Parallelepipeds gehören und durch die Mitte seiner Diagonale verlaufen, wird durch dieses in zwei Hälften geteilt; Insbesondere schneiden sich alle Diagonalen eines Parallelepipeds in einem Punkt und werden von diesem halbiert.

· Gegenüberliegende Flächen eines Parallelepipeds sind parallel und gleich.

· Das Quadrat der Diagonallänge eines rechteckigen Parallelepipeds ist gleich der Summe der Quadrate seiner drei Dimensionen

Grundformeln

Rechter Parallelepiped

· Seitenfläche S b =P o *h, wobei P o der Umfang der Basis und h die Höhe ist

· Gesamtfläche S p =S b +2S o, wobei S o die Grundfläche ist

· Volumen V=S o *h

Rechteckiges Parallelepiped

· Seitenfläche S b =2c(a+b), wobei a, b die Seiten der Basis und c die Seitenkante des rechteckigen Parallelepipeds sind

· Gesamtfläche S p =2(ab+bc+ac)

· Volumen V=abc, wobei a, b, c die Abmessungen eines rechteckigen Parallelepipeds sind.

· Seitenfläche S=6*h 2, wobei h die Höhe der Würfelkante ist

34. Tetraeder- regelmäßiges Polyeder, hat 4 Flächen, die regelmäßige Dreiecke sind. Eckpunkte eines Tetraeders 4 , konvergiert zu jedem Scheitelpunkt 3 Rippen und Gesamtrippen 6 . Außerdem ist ein Tetraeder eine Pyramide.

Die Dreiecke, aus denen ein Tetraeder besteht, heißen Gesichter (AOS, OSV, ACB, AOB), ihre Seiten --- Rippen (AO, OC, OB), und die Eckpunkte --- Eckpunkte (A, B, C, O) Tetraeder. Man nennt zwei Kanten eines Tetraeders, die keine gemeinsamen Eckpunkte haben Gegenteil... Manchmal wird eine der Flächen des Tetraeders isoliert und benannt Basis, und die anderen drei --- Seitenflächen.

Der Tetraeder heißt richtig, wenn alle seine Flächen gleichseitige Dreiecke sind. In diesem Fall ein regelmäßiges Tetraeder und ein reguläres Dreieckige Pyramide– Das ist nicht dasselbe.

U regelmäßiges Tetraeder Alle Diederwinkel an den Kanten und alle Dreieckswinkel an den Eckpunkten sind gleich.

35. Richtiges Prisma

Ein Prisma ist ein Polyeder, dessen zwei Flächen (Grundflächen) in parallelen Ebenen liegen und alle Kanten außerhalb dieser Flächen parallel zueinander sind. Die Flächen außer den Basen werden Seitenflächen genannt, und ihre Kanten werden Seitenkanten genannt. Alle Seitenkanten sind einander gleich als parallele Segmente, die durch zwei parallele Ebenen begrenzt werden. Alle Seitenflächen des Prismas sind Parallelogramme. Relevante Parteien Die Grundflächen des Prismas sind gleich und parallel. Ein Prisma, dessen Seitenkante senkrecht zur Grundebene steht, wird als gerades Prisma bezeichnet; andere Prismen werden als geneigte Prismen bezeichnet. An der Wurzel richtiges Prisma Lügen regelmäßiges Vieleck. Alle Flächen eines solchen Prismas sind gleiche Rechtecke.

Die Oberfläche des Prismas besteht aus zwei Grundflächen und einer Seitenfläche. Die Höhe eines Prismas ist ein Segment, das eine gemeinsame Senkrechte zu den Ebenen ist, in denen die Grundflächen des Prismas liegen. Die Höhe des Prismas ist der Abstand H zwischen den Ebenen der Basen.

Seitenfläche S b eines Prismas ist die Summe der Flächen seiner Seitenflächen. Gesamtfläche S n eines Prismas ist die Summe der Flächen aller seiner Flächen. S n = S b + 2 S,Wo S– Fläche der Basis des Prismas, S b – Seitenfläche.

36. Ein Polyeder mit einer Fläche, genannt Basis, – Polygon,
und die anderen Flächen sind Dreiecke mit einem gemeinsamen Scheitelpunkt, genannt Pyramide .

Andere Flächen als die Basis werden aufgerufen seitlich.
Der gemeinsame Scheitelpunkt der Seitenflächen wird aufgerufen die Spitze der Pyramide.
Die Kanten, die die Spitze der Pyramide mit den Spitzen der Basis verbinden, werden genannt seitlich.
Pyramidenhöhe wird als Senkrechte bezeichnet, die von der Spitze der Pyramide zu ihrer Basis verläuft.

Die Pyramide heißt richtig, wenn seine Basis ein regelmäßiges Vieleck ist und seine Höhe durch die Mitte der Basis verläuft.

Apothem Seitenkante regelmäßige Pyramide Die Höhe dieser Fläche, die von der Spitze der Pyramide ausgeht, wird aufgerufen.

Eine Ebene parallel zur Basis der Pyramide schneidet sie in eine ähnliche Pyramide und Pyramidenstumpf.

Eigenschaften regelmäßiger Pyramiden

• Die Seitenkanten einer regelmäßigen Pyramide sind gleich.
• Die Seitenflächen einer regelmäßigen Pyramide sind gleichschenklige Dreiecke, die untereinander gleich sind.

Wenn alle Seitenkanten gleich sind, dann

·Höhe wird auf die Mitte des umschriebenen Kreises projiziert;

Die Seitenrippen bilden mit der Ebene der Basis gleiche Winkel.

Wenn die Seitenflächen im gleichen Winkel zur Grundebene geneigt sind, dann

·Höhe wird auf die Mitte des eingeschriebenen Kreises projiziert;

· die Höhen der Seitenflächen sind gleich;

·Die Fläche der Seitenfläche ist gleich der Hälfte des Produkts aus dem Umfang der Basis und der Höhe der Seitenfläche

37. Funktion y=f(x), wobei x zur Menge gehört natürliche Zahlen, heißt die Funktion des natürlichen Arguments oder Zahlenfolge. Es wird mit y=f(n) oder (y n) bezeichnet.

Es können Sequenzen angegeben werden verschiedene Wege, verbal, so wird die Reihenfolge festgelegt Primzahlen:

2, 3, 5, 7, 11 usw.

Eine Folge gilt als analytisch gegeben, wenn die Formel für ihren n-ten Term gegeben ist:

1, 4, 9, 16, …, n 2, …

2) y n = C. Eine solche Folge heißt konstant oder stationär. Zum Beispiel:

2, 2, 2, 2, …, 2, …

3) y n =2 n . Zum Beispiel,

2, 2 2, 2 3, 2 4, …, 2 n, …

Eine Folge heißt obenbeschränkt, wenn alle ihre Glieder nicht größer als eine bestimmte Zahl sind. Mit anderen Worten, eine Folge kann als beschränkt bezeichnet werden, wenn es eine Zahl M gibt, so dass die Ungleichung y n kleiner oder gleich M ist. Die Zahl M wird als Obergrenze der Folge bezeichnet. Zum Beispiel die Sequenz: -1, -4, -9, -16, ..., - n 2 ; von oben begrenzt.

Ebenso kann eine Folge als nach unten beschränkt bezeichnet werden, wenn alle ihre Glieder größer als eine bestimmte Zahl sind. Wenn eine Folge sowohl nach oben als auch nach unten beschränkt ist, heißt sie beschränkt.

Eine Folge heißt aufsteigend, wenn jeder nachfolgende Term größer als der vorherige ist.

Eine Folge heißt abnehmend, wenn jedes nachfolgende Mitglied kleiner als das vorherige ist. Zunehmende und fallende Folgen werden durch einen Begriff definiert – monotone Folgen.

Betrachten Sie zwei Sequenzen:

1) y n: 1, 3, 5, 7, 9, …, 2n-1, …

2) x n: 1, ½, 1/3, 1/ 4, …, 1/n, …

Wenn wir die Glieder dieser Folge auf dem Zahlenstrahl darstellen, werden wir feststellen, dass im zweiten Fall die Glieder der Folge um einen Punkt verdichtet sind, im ersten Fall ist dies jedoch nicht der Fall. IN ähnliche Fälle Die Folge y n soll divergieren und die Folge x n konvergieren.

Die Zahl b heißt Grenzwert der Folge y n, wenn eine vorab ausgewählte Umgebung des Punktes b alle Mitglieder der Folge enthält, beginnend mit einer bestimmten Zahl.

In diesem Fall können wir schreiben:

Wenn der Quotient einer Folge kleiner als eins im Modul ist, dann ist der Grenzwert dieser Folge, da x gegen Unendlich geht, gleich Null.

Wenn die Folge konvergiert, dann nur zu einem Grenzwert

Wenn die Folge konvergiert, ist sie beschränkt.

Satz von Weierstrass: Wenn eine Folge monoton konvergiert, dann ist sie beschränkt.

Der Grenzwert einer stationären Folge ist gleich jedem Term der Folge.

Eigenschaften:

1) Die Betragsgrenze entspricht der Summe der Grenzen

2) Der Grenzwert eines Produkts ist gleich dem Produkt der Grenzwerte

3) Der Grenzwert des Quotienten ist gleich dem Quotienten der Grenzwerte

4) Der konstante Faktor kann über das Grenzzeichen hinaus angenommen werden

Frage 38
Summe der unendlichen geometrischen Progression

Geometrischer Verlauf- eine Folge von Zahlen b 1, b 2, b 3,.. (Mitglieder der Folge), bei der jede nachfolgende Zahl, beginnend mit der zweiten, aus der vorherigen durch Multiplikation mit einer bestimmten Zahl q (Nenner) erhalten wird der Progression), wobei b 1 ≠0, q ≠0.

Summe einer unendlichen geometrischen Folge ist die Grenzzahl, gegen die die Folge der Progression konvergiert.

Mit anderen Worten, egal wie lange geometrischer Verlauf, die Summe seiner Mitglieder ist nicht größer als eine bestimmte Zahl und ist praktisch gleich dieser Zahl. Dies wird als Summe einer geometrischen Folge bezeichnet.

Nicht jede geometrische Folge hat eine solche Grenzsumme. Dies kann nur für eine Folge gelten, deren Nenner eine Bruchzahl kleiner als 1 ist.

Oder (äquivalent) ein Polyeder, das sechs Flächen hat und jede davon – Parallelogramm.

Arten von Parallelepipeden

Es gibt verschiedene Arten von Parallelepipeden:

• Ein Quader ist ein Parallelepiped, dessen Flächen alle Rechtecke sind.
• Ein Parallelepiped ist ein Parallelepiped mit 4 Seitenflächen, die Rechtecke sind.
• Ein geneigtes Parallelepiped ist ein Parallelepiped, dessen Seitenflächen nicht senkrecht zu den Grundflächen stehen.

Wesentliche Elemente

Zwei Flächen eines Parallelepipeds, die keine gemeinsame Kante haben, werden als gegenüberliegend bezeichnet, und diejenigen, die eine gemeinsame Kante haben, werden als benachbart bezeichnet. Zwei Eckpunkte eines Parallelepipeds, die nicht zur gleichen Fläche gehören, werden als gegenüberliegend bezeichnet. Das Segment, das gegenüberliegende Eckpunkte verbindet, wird Diagonale des Parallelepipeds genannt. Die Längen von drei Kanten eines rechteckigen Parallelepipeds, die einen gemeinsamen Scheitelpunkt haben, werden als Abmessungen bezeichnet.

Eigenschaften

• Das Parallelepiped ist ungefähr in der Mitte seiner Diagonale symmetrisch.
• Jedes Segment, dessen Enden zur Oberfläche des Parallelepipeds gehören und durch die Mitte seiner Diagonale verlaufen, wird durch dieses in zwei Hälften geteilt; Insbesondere schneiden sich alle Diagonalen eines Parallelepipeds in einem Punkt und werden von diesem halbiert.
• Die gegenüberliegenden Flächen eines Parallelepipeds sind parallel und gleich.
• Das Quadrat der Diagonalenlänge eines rechteckigen Parallelepipeds ist gleich der Summe der Quadrate seiner drei Dimensionen.

Grundformeln

Rechter Parallelepiped

Seitenfläche S b =P o *h, wobei P o der Umfang der Basis und h die Höhe ist

Gesamtfläche S p =S b +2S o, wobei S o die Grundfläche ist

Volumen V=S o *h

Rechteckiges Parallelepiped

Seitenfläche S b =2c(a+b), wobei a, b die Seiten der Basis und c die Seitenkante des rechteckigen Parallelepipeds sind

Gesamtfläche S p =2(ab+bc+ac)

Volumen V=abc, wobei a, b, c die Abmessungen eines rechteckigen Parallelepipeds sind.

Würfel

Oberfläche: $S=6a^2$
Volumen: $V=a^3$, Wo $A$- Rand eines Würfels.

Irgendein Parallelepiped

Das Volumen und die Verhältnisse in einem geneigten Parallelepiped werden häufig mithilfe der Vektoralgebra bestimmt. Das Volumen eines Parallelepipeds ist gleich dem Absolutwert des gemischten Produkts dreier Vektoren, die durch die drei Seiten des Parallelepipeds bestimmt werden, die von einem Scheitelpunkt ausgehen. Die Beziehung zwischen den Längen der Seiten des Parallelepipeds und den Winkeln zwischen ihnen ergibt die Aussage, dass die Gram-Determinante der angegebenen drei Vektoren gleich dem Quadrat ihres gemischten Produkts ist: 215.

In der mathematischen Analyse

IN mathematische Analyse unter einem n-dimensionalen Quader $B$ viele Punkte verstehen $x\; =\; (x\_1,\backslash ldots,x\_n)$ Art $B\; =\; \backslash (x|a\_1\backslash leqslant\; x\_1\backslash leqslant\; b\_1,\backslash ldots,a\_n\backslash leqslant\; x\_n\backslash leqslant\; b\_n\backslash )$

Schreiben Sie eine Rezension zum Artikel „Parallelepiped“

Anmerkungen

Links

Richtig Richtig nicht konvex Konvex Formeln, Sätze, Theorien Andere

Ein Auszug, der das Parallelepiped charakterisiert

- On dit que les rivaux se sont versöhnt Grace a l "angine... [Man sagt, dass sich die Rivalen dank dieser Krankheit versöhnt haben.]
Das Wort Angine wurde mit großer Freude wiederholt.
– Le vieux comte est touchant a ce qu"on dit. Il a pleure comme un enfant quand le medecin lui a dit que le cas etait hazardeux. [Der alte Graf ist sehr rührend, sagt man. Er weinte wie ein Kind, als der Arzt kam sagte dieser gefährliche Fall.]
- Oh, das ist wirklich schrecklich. C'est une femme ravissante. [Oh, das wäre ein großer Verlust. So eine schöne Frau.]
„Vous parlez de la pauvre comtesse“, sagte Anna Pawlowna, als sie näherkam. „Ich bin ein Gesandter, der sich mit diesen neuen Dingen auskennt. Ich habe gesagt, dass sie mir vielleicht ein bisschen sagen wird. Oh, ohne Zweifel, das ist die charmanteste Frau der Welt“, sagte Anna Pawlowna mit einem Lächeln über ihre Begeisterung. – Wir wohnen in verschiedenen Lagern, aber ich muss sie nicht schätzen, weil ich sie verdient habe. Elle est bien malheureuse, [Sie sprechen von der armen Gräfin... die ich geschickt habe, um mich nach ihrem Gesundheitszustand zu erkundigen. Sie sagten mir, dass es ihr etwas besser ginge. Oh, ohne Zweifel, das ist die schönste Frau der Welt. Wir gehören verschiedenen Lagern an, aber das hindert mich nicht daran, sie aufgrund ihrer Verdienste zu respektieren. Sie ist so unglücklich.] – fügte Anna Pawlowna hinzu.
Ein nachlässiger junger Mann glaubte, dass Anna Pawlowna mit diesen Worten den Schleier der Geheimhaltung über die Krankheit der Gräfin ein wenig lüftete, und erlaubte sich, seine Überraschung darüber zum Ausdruck zu bringen, dass keine berühmten Ärzte hinzugezogen wurden, sondern dass die Gräfin von einem Scharlatan behandelt wurde, der gefährlich sein konnte Heilmittel.
„Vos information peuvent etre meilleures que les miennes“, attackierte Anna Pawlowna plötzlich den unerfahrenen Mann mit Gift. junger Mann. – Ich glaube aber auch, dass dieser Mediziner ein Mann ist, der sehr begabt und begabt ist. Es ist der Intime-Mediziner von Reine d'Espagne. [Ihre Nachrichten mögen genauer sein als meine ... aber ich weiß aus guten Quellen, dass dieser Arzt eine sehr gebildete und geschickte Person ist. Dies ist der Lebensarzt der Königin von Spanien.] - Und so zerstörte Anna Pawlowna den jungen Mann und wandte sich an Bilibin, der in einem anderen Kreis die Haut aufhob und offenbar gerade dabei war, sie zu lösen, um un mot zu sagen, und sprach Über die Österreicher.
„Je trouve que c"est charmant! [Ich finde es bezaubernd!]“, sagte er über das diplomatische Papier, mit dem die von Wittgenstein erbeuteten österreichischen Banner nach Wien geschickt wurden, le heros de Petropol [der Held von Petropol] (wie er wurde in Petersburg gerufen).
- Wie, wie ist das? - Anna Pawlowna drehte sich zu ihm um und erweckte Stille, um das Motiv zu hören, das sie bereits kannte.
Und Bilibin wiederholte die folgenden ursprünglichen Worte der von ihm verfassten diplomatischen Depesche:
„L"Empereur renvoie les drapeaux Autrichiens“, sagte Bilibin, „drapeaux amis et gares qu"il a trouve hors de la route, [Der Kaiser schickt den österreichischen Bannern, freundliche und verlorene Banner, die er außerhalb der echten Straße gefunden hat.], „Bilibin beendete den Vorgang und lockerte die Haut.
„Charmant, charmant, [lieblich, charmant“, sagte Prinz Wassili.
„C“est la route de Varsovie peut être, [Das ist vielleicht die Warschauer Straße.]“, sagte Prinz Hippolyte laut und unerwartet. Alle blickten ihn an, ohne zu verstehen, was er damit sagen wollte. Auch Prinz Hippolyte blickte zurück Mit fröhlicher Überraschung um ihn herum. Er verstand wie andere nicht, was die Worte bedeuteten, die er sagte. Während seiner diplomatischen Karriere bemerkte er mehr als einmal, dass sich die auf diese Weise gesprochenen Worte plötzlich als sehr witzig herausstellten, und er sagte diese Worte für alle Fälle, die ersten, die ihm in den Sinn kamen. „Vielleicht wird es ganz gut klappen“, dachte er, „und wenn es nicht klappt, können sie es dort arrangieren.“ In der Tat, während Es herrschte eine peinliche Stille, Anna Pawlowna trat in dieses nicht genügend patriotische Gesicht, und sie lud Prinz Wassili lächelnd und mit dem Finger zu Ippolit schüttelnd an den Tisch, schenkte ihm zwei Kerzen und ein Manuskript und forderte ihn auf, zu beginnen. Alles verstummte .