Welche Methoden zur Festlegung von Sequenzen kennen Sie? Zahlenfolgen

Die Definition einer Zahlenfolge ist gegeben. Es werden Beispiele für unendlich wachsende, konvergente und divergente Folgen betrachtet. Es wird eine Folge betrachtet, die alle rationalen Zahlen enthält.

Definition.
Numerische Reihenfolge (xn) ist ein Gesetz (Regel), nach dem für jede natürliche Zahl n = 1, 2, 3, . . . eine bestimmte Anzahl x n wird zugewiesen.
Das Element x n heißt n. Semester oder ein Element einer Sequenz.

Die Folge wird als n-ter Term in geschweiften Klammern bezeichnet: . Folgende Bezeichnungen sind ebenfalls möglich: . Sie geben explizit an, dass Index n zur Menge gehört natürliche Zahlen und die Folge selbst hat unendlich viele Terme. Hier einige Beispielsequenzen:
, , .

Mit anderen Worten: Eine Zahlenfolge ist eine Funktion, deren Definitionsbereich die Menge der natürlichen Zahlen ist. Die Anzahl der Elemente der Folge ist unendlich. Unter den Elementen können auch Elemente mit gleicher Bedeutung vorhanden sein. Eine Folge kann auch als eine nummerierte Zahlenmenge betrachtet werden, die aus einer unendlichen Anzahl von Mitgliedern besteht.

Uns wird vor allem die Frage interessieren, wie sich Folgen verhalten, wenn n gegen Unendlich geht: . Dieses Material wird im Abschnitt Grenzwert einer Folge – Grundsätze und Eigenschaften vorgestellt. Hier sehen wir uns einige Beispiele für Sequenzen an.

Sequenzbeispiele

Beispiele für unendlich steigende Folgen

Betrachten Sie die Reihenfolge. Das gemeinsame Mitglied dieser Sequenz ist . Schreiben wir die ersten paar Begriffe auf:
.
Es ist ersichtlich, dass mit zunehmender Zahl n die Elemente in Richtung unendlich zunehmen positive Werte. Wir können sagen, dass diese Sequenz dazu tendiert: für .

Betrachten Sie nun eine Folge mit einem gemeinsamen Term. Hier sind die ersten Mitglieder:
.
Mit zunehmender Zahl n nehmen die Elemente dieser Folge ins Unendliche zu Absolutwert, haben aber kein konstantes Vorzeichen. Das heißt, diese Sequenz neigt dazu: bei .

Beispiele für Folgen, die gegen eine endliche Zahl konvergieren

Betrachten Sie die Reihenfolge. Ihr gemeinsames Mitglied. Die ersten Terme haben die folgende Form:
.
Es ist ersichtlich, dass sich die Elemente dieser Folge mit zunehmender Zahl n ihrem Grenzwert a nähern = 0 : bei . Jeder nachfolgende Term liegt also näher bei Null als der vorherige. In gewissem Sinne können wir davon ausgehen, dass es einen Näherungswert für die Zahl a gibt = 0 mit Fehler. Es ist klar, dass dieser Fehler mit zunehmendem n gegen Null tendiert, das heißt, durch die Wahl von n kann der Fehler so klein wie gewünscht gemacht werden. Darüber hinaus gilt für jeden gegebenen Fehler ε > 0 Sie können eine Zahl N angeben, sodass für alle Elemente mit Zahlen größer als N: die Abweichung der Zahl von Grenzwert a wird den Fehler ε: nicht überschreiten.

Betrachten Sie als nächstes die Reihenfolge. Ihr gemeinsames Mitglied. Hier sind einige seiner ersten Mitglieder:
.
In dieser Sequenz sind gerade Terme gleich Null. Terme mit ungeradem n sind gleich. Daher nähern sich ihre Werte mit zunehmendem n dem Grenzwert a = 0 . Dies ergibt sich auch aus der Tatsache, dass
.
Genau wie im vorherigen Beispiel können wir einen beliebig kleinen Fehler ε angeben > 0 , für die es möglich ist, eine Zahl N zu finden, so dass Elemente mit Zahlen größer als N vom Grenzwert a abweichen = 0 um einen Betrag, der den angegebenen Fehler nicht überschreitet. Daher konvergiert diese Folge gegen den Wert a = 0 : bei .

Beispiele für divergente Sequenzen

Betrachten Sie eine Sequenz mit dem folgenden allgemeinen Begriff:

Hier sind seine ersten Mitglieder:


.
Es ist ersichtlich, dass Terme mit geraden Zahlen:
,
gegen den Wert a konvergieren 1 = 0 . Mitglieder mit ungerader Nummer:
,
gegen den Wert a konvergieren 2 = 2 . Die Folge selbst konvergiert mit zunehmendem n gegen keinen Wert.

Folge mit im Intervall (0;1) verteilten Termen

Schauen wir uns nun eine interessantere Sequenz an. Nehmen wir ein Segment auf der Zahlengeraden. Teilen wir es in zwei Hälften. Wir erhalten zwei Segmente. Lassen
.
Teilen wir jedes der Segmente noch einmal in zwei Hälften. Wir erhalten vier Segmente. Lassen
.
Teilen wir jedes Segment noch einmal in zwei Hälften. Lass uns nehmen


.
Usw.

Als Ergebnis erhalten wir eine Folge, deren Elemente in einem offenen Intervall verteilt sind (0; 1) . Welchen Punkt wir auch immer aus dem geschlossenen Intervall nehmen können wir immer Elemente der Folge finden, die beliebig nahe an diesem Punkt liegen oder mit ihm zusammenfallen.

Dann kann man aus der ursprünglichen Folge eine Teilfolge auswählen, die zu einem beliebigen Punkt aus dem Intervall konvergiert . Das heißt, mit zunehmender Zahl n kommen die Mitglieder der Teilfolge immer näher an den vorgewählten Punkt heran.

Zum Beispiel für Punkt a = 0 Sie können die folgende Teilsequenz wählen:
.
= 0 .

Für Punkt a = 1 Wählen wir die folgende Teilsequenz:
.
Die Terme dieser Teilfolge konvergieren zum Wert a = 1 .

Da es Teilfolgen gibt, die gegen konvergieren unterschiedliche Bedeutungen, dann konvergiert die ursprüngliche Folge selbst gegen keine Zahl.

Folge, die alle rationalen Zahlen enthält

Konstruieren wir nun eine Folge, die alle rationalen Zahlen enthält. Darüber hinaus kommt jede rationale Zahl in einer solchen Folge unendlich oft vor.

Die rationale Zahl r lässt sich wie folgt darstellen:
,
wo ist eine ganze Zahl; - natürlich.
Wir müssen jede natürliche Zahl n einem Zahlenpaar p und q zuordnen, sodass jedes Paar p und q in unserer Folge enthalten ist.

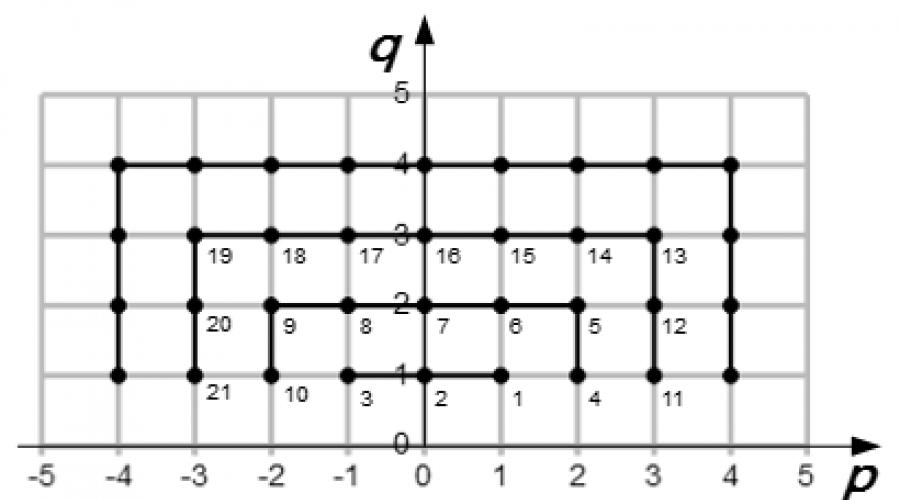
Zeichnen Sie dazu die p- und q-Achsen in die Ebene ein. Wir zeichnen Gitterlinien durch die ganzzahligen Werte von p und q. Dann entspricht jeder Knoten dieses Gitters Rationale Zahl. Die gesamte Menge rationaler Zahlen wird durch eine Menge von Knoten dargestellt. Wir müssen einen Weg finden, alle Knoten zu nummerieren, damit wir keinen Knoten übersehen. Das geht ganz einfach, wenn man die Knoten durch Quadrate nummeriert, deren Mittelpunkte im Punkt liegen (0; 0) (siehe Bild). In diesem Fall sind die unteren Teile der Quadrate mit q < 1 wir brauchen es nicht. Daher sind sie in der Abbildung nicht dargestellt.

Für die Oberseite des ersten Quadrats gilt also:
.
Als nächstes nummerieren wir den oberen Teil des nächsten Quadrats:

.
Wir nummerieren den oberen Teil des folgenden Quadrats:

.
Usw.

Auf diese Weise erhalten wir eine Folge, die alle rationalen Zahlen enthält. Sie können feststellen, dass jede rationale Zahl in dieser Reihenfolge unendlich oft vorkommt. Tatsächlich enthält diese Sequenz neben dem Knoten auch den Knoten , bei dem es sich um eine natürliche Zahl handelt. Aber alle diese Knoten entsprechen derselben rationalen Zahl.

Dann können wir aus der von uns konstruierten Folge eine Teilfolge (mit unendlich vielen Elementen) auswählen, deren Elemente alle einer vorgegebenen rationalen Zahl entsprechen. Da die von uns konstruierte Folge Teilfolgen hat, die gegen verschiedene Zahlen konvergieren, konvergiert die Folge gegen keine Zahl.

Abschluss

Hier haben wir eine genaue Definition der Zahlenfolge gegeben. Wir haben auch die Frage seiner Konvergenz aufgeworfen, basierend auf intuitiven Ideen. Die genaue Definition der Konvergenz wird auf der Seite Den Grenzwert einer Folge definieren besprochen. Verwandte Eigenschaften und Theoreme sind auf der Seite angegeben

2. Definieren Arithmetische Operation, mit deren Hilfe der Durchschnitt aus zwei Extremzahlen ermittelt wird, und fügen Sie anstelle des *-Zeichens die fehlende Zahl ein: ,3104.62.51043.60.94 1,7*4,43,1*37,2*0,8

3. Die Schüler lösten eine Aufgabe, bei der sie fehlende Zahlen finden mussten. Sie bekamen unterschiedliche Antworten. Finden Sie die Regeln, nach denen die Jungs die Zellen ausgefüllt haben. Aufgabe Antwort 1Antwort

Definition einer Zahlenfolge Man sagt, dass eine Zahlenfolge gegeben ist, wenn nach einem Gesetz jede natürliche Zahl (Ortszahl) einer bestimmten Zahl (Teil der Folge) eindeutig zugeordnet ist. IN Gesamtansicht Die angegebene Entsprechung lässt sich wie folgt darstellen: y 1, y 2, y 3, y 4, y 5, ..., y n, ... ... n ... Die Zahl n ist der n-te Term der Folge . Die gesamte Sequenz wird normalerweise mit (y n) bezeichnet.

Analytische Methode zur Angabe numerischer Folgen Eine Folge wird analytisch angegeben, wenn die Formel des n-ten Termes angegeben wird. Zum Beispiel 1) y n= n 2 – analytische Aufgabe der Sequenz 1, 4, 9, 16, … 2) y n= С – konstante (stationäre) Sequenz 2) y n= 2 n – analytische Aufgabe der Sequenz 2, 4 , 8, 16, ... Lösen Sie 585

Rekurrente Methode zur Angabe numerischer Folgen Die wiederkehrende Methode zur Angabe einer Folge besteht darin, eine Regel anzugeben, mit der Sie den n-ten Term berechnen können, wenn seine vorherigen Mitglieder bekannt sind. 1) Eine arithmetische Folge ist durch wiederkehrende Beziehungen a 1 =a, a n+ gegeben 1 =a n + d 2 ) geometrischer Verlauf– b 1 =b, b n+1 =b n * q

Befestigung 591, 592 (a, b) 594, – 614 (a)

Von oben beschränkt Eine Folge (y n) heißt von oben beschränkt, wenn alle ihre Glieder nicht größer als eine bestimmte Zahl sind. Mit anderen Worten, die Folge (y n) ist nach oben beschränkt, wenn es eine Zahl M gibt, so dass für jedes n die Ungleichung y n M gilt. M ist die obere Grenze der Folge. Zum Beispiel -1, -4, -9, - 16, ..., -n 2, ...

Nach unten beschränkt Eine Folge (y n) heißt nach unten beschränkt, wenn alle ihre Glieder mindestens eine bestimmte Zahl haben. Mit anderen Worten: Die Folge (y n) ist nach oben beschränkt, wenn es eine Zahl m gibt, so dass für jedes n die Ungleichung y n m gilt. m – untere Grenze der Folge. Zum Beispiel 1, 4, 9, 16, …, n 2, …

Beschränktheit einer Folge Eine Folge (y n) heißt beschränkt, wenn zwei Zahlen A und B angegeben werden können, zwischen denen alle Glieder der Folge liegen. Die Ungleichung Ay n B A ist die untere Grenze, B ist die obere Grenze. Beispielsweise ist 1 die obere Grenze, 0 die untere Grenze

Absteigende Folge Eine Folge heißt abnehmend, wenn jedes Mitglied kleiner als das vorherige ist: y 1 > y 2 > y 3 > y 4 > y 5 > … > y n > … Zum Beispiel: y 2 > y 3 > y 4 > y 5 > … > y n > … Zum Beispiel: „> y 2 > y 3 > y 4 > y 5 > … > y n > … Zum Beispiel:“> y 2 > y 3 > y 4 > y 5 > … > y n > … Zum Beispiel:" title="Abnehmende Sequenz Eine Sequenz wird als absteigend bezeichnet, wenn jedes Mitglied kleiner als das vorherige ist: y 1 > y 2 > y 3 > y 4 > y 5 > … > y n >...Zum Beispiel:"> title="Absteigende Folge Eine Folge heißt abnehmend, wenn jedes Mitglied kleiner als das vorherige ist: y 1 > y 2 > y 3 > y 4 > y 5 > … > y n > … Zum Beispiel:"> !} 23

Testarbeit Option 1Option 2 1. Die Zahlenfolge ergibt sich aus der Formel a) Berechnen Sie die ersten vier Glieder dieser Folge. b) Ist eine Zahl ein Mitglied der Folge? b) Ist die Zahl 12,25 ein Mitglied der Folge? 2. Erstellen Sie eine Formel für den dritten Term der Folge 2, 5, 10, 17, 26,…1, 2, 4, 8, 16,…

Eine Zahlenfolge ist ein Sonderfall einer Zahlenfunktion, daher werden auch für Folgen eine Reihe von Eigenschaften von Funktionen berücksichtigt.

1. Definition . Folge ( y n} heißt steigend, wenn jeder seiner Terme (außer dem ersten) größer als der vorherige ist:

j 1 < j 2 < j 3 < … < y n < y n+1 < ….

2. Definition.Sequenz ( y n} heißt abnehmend, wenn jeder seiner Terme (außer dem ersten) kleiner als der vorherige ist:

j 1 > j 2 > j 3 > … > y n> y n+1 > … .

3. Zunehmende und abnehmende Folgen werden durch einen gemeinsamen Begriff vereint – monotone Folgen.

Zum Beispiel: j 1 = 1; y n= N 2… ist eine aufsteigende Folge. j 1 = 1; – absteigende Reihenfolge. j 1 = 1; – Diese Folge ist weder nicht steigend noch fallend.

4. Definition. Eine Folge heißt periodisch, wenn es eine natürliche Zahl T gibt, für die ausgehend von einem n die Gleichung yn = yn+T gilt. Die Zahl T wird Periodenlänge genannt.

5. Eine Folge heißt unten beschränkt, wenn alle ihre Glieder mindestens eine bestimmte Zahl sind.

6. Eine Folge heißt obenbeschränkt, wenn alle ihre Glieder nicht größer als eine bestimmte Zahl sind.

7. Eine Folge heißt beschränkt, wenn sie sowohl nach oben als auch nach unten beschränkt ist, d. h. Es gibt eine positive Zahl, sodass alle Terme einer gegebenen Folge diese Zahl im absoluten Wert nicht überschreiten. (Aber seine Begrenzung auf zwei Seiten bedeutet nicht notwendigerweise, dass es endlich ist.)

8. Eine Folge kann nur einen Grenzwert haben.

9. Jede nicht abnehmende und nach oben begrenzte Folge hat einen Grenzwert (lim).

10. Jede nach unten begrenzte, nicht zunehmende Folge hat einen Grenzwert.

Der Grenzwert einer Folge ist ein Punkt (Anzahl), in dessen Nähe sich die meisten Glieder der Folge befinden; sie kommen diesem Grenzwert sehr nahe, erreichen ihn aber nicht.

Geometrisch und arithmetische Folge sind Sonderfälle der Folge.

Methoden zum Festlegen der Reihenfolge:

Sequenzen können auf verschiedene Arten spezifiziert werden, von denen drei besonders wichtig sind: analytisch, deskriptiv und wiederkehrend.

1. Eine Folge ist analytisch gegeben, wenn die Formel ihres n-ten Termes gegeben ist:

Beispiel. yn = 2n – 1 – Folge ungerader Zahlen: 1, 3, 5, 7, 9, …

2. Die beschreibende Art, eine numerische Folge anzugeben, besteht darin, dass erklärt wird, aus welchen Elementen die Folge aufgebaut ist.

Beispiel 1. „Alle Terme der Folge sind gleich 1.“ Es handelt sich also um eine stationäre Folge 1, 1, 1, …, 1, ….

Beispiel 2. „Eine Sequenz besteht aus allem.“ Primzahlen in aufsteigender Reihenfolge". Somit ist die gegebene Reihenfolge 2, 3, 5, 7, 11, …. Mit dieser Methode zur Angabe der Reihenfolge in in diesem Beispiel Es ist schwierig zu beantworten, was beispielsweise das 1000. Element der Folge ist.

3. Die wiederkehrende Methode zum Angeben einer Sequenz besteht darin, eine Regel anzugeben, die eine Berechnung ermöglicht n. Semester Sequenz, wenn ihre vorherigen Mitglieder bekannt sind. Der Name der wiederkehrenden Methode kommt vom lateinischen Wort recurrere – zurückkommen. Am häufigsten wird in solchen Fällen eine Formel angegeben, die es ermöglicht, das n-te Glied der Folge durch die vorherigen auszudrücken, und es werden 1–2 Anfangsglieder der Folge angegeben.

Beispiel 1. y1 = 3; yn = yn–1 + 4, wenn n = 2, 3, 4,….

Hier ist y1 = 3; y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….

Sie sehen, dass die in diesem Beispiel erhaltene Folge auch analytisch angegeben werden kann: yn = 4n – 1.

Beispiel 2. j 1 = 1; j 2 = 1; y n = y n–2 + y n–1 wenn N = 3, 4,….

Hier: j 1 = 1; j 2 = 1; j 3 = 1 + 1 = 2; j 4 = 1 + 2 = 3; j 5 = 2 + 3 = 5; j 6 = 3 + 5 = 8;

Die Folge in diesem Beispiel wird besonders in der Mathematik untersucht, da sie eine Reihe interessanter Eigenschaften und Anwendungen aufweist. Sie wird Fibonacci-Folge genannt, benannt nach dem italienischen Mathematiker aus dem 13. Jahrhundert. Es ist sehr einfach, die Fibonacci-Folge wiederkehrend zu definieren, aber analytisch sehr schwierig. N Die Fibonacci-Zahl wird durch ausgedrückt Ordnungsnummer die folgende Formel.

Auf den ersten Blick ist die Formel für N Die Fibonacci-Zahl scheint unplausibel, da die Formel, die die Folge natürlicher Zahlen angibt, allein enthält Quadratwurzeln, aber Sie können die Gültigkeit dieser Formel für die ersten paar „manuell“ überprüfen N.

Fibonacci-Geschichte:

Fibonacci (Leonardo von Pisa), ca. 1175–1250

Italienischer Mathematiker. Er wurde in Pisa geboren und wurde im Spätmittelalter der erste große Mathematiker Europas. Die praktische Notwendigkeit, Geschäftskontakte zu knüpfen, faszinierte ihn zur Mathematik. Er veröffentlichte seine Bücher über Arithmetik, Algebra und andere mathematische Disziplinen. Von muslimischen Mathematikern lernte er das in Indien erfundene und bereits in der arabischen Welt übernommene Zahlensystem kennen und war von dessen Überlegenheit überzeugt (diese Zahlen waren die Vorläufer der modernen arabischen Zahlen).

Leonardo von Pisa, bekannt als Fibonacci, war der erste der großen Mathematiker Europas im Spätmittelalter. Er wurde in Pisa als Sohn einer wohlhabenden Kaufmannsfamilie geboren und kam aus dem rein praktischen Bedürfnis heraus, Geschäftskontakte zu knüpfen, zur Mathematik. In seiner Jugend reiste Leonardo viel und begleitete seinen Vater auf Geschäftsreisen. Wir wissen beispielsweise von seinem langen Aufenthalt in Byzanz und Sizilien. Während solcher Reisen kommunizierte er viel mit lokalen Wissenschaftlern.

Die Zahlenreihe, die heute seinen Namen trägt, entstand aus dem Hasenproblem, das Fibonacci in seinem 1202 verfassten Buch Liber abacci beschrieb:

Ein Mann setzte ein Kaninchenpaar in einen Pferch, der auf allen Seiten von einer Mauer umgeben war. Wie viele Kaninchenpaare kann dieses Paar in einem Jahr hervorbringen, wenn bekannt ist, dass jedes Kaninchenpaar ab dem zweiten Monat jeden Monat ein Paar hervorbringt?

Sie können sicher sein, dass die Anzahl der Paare in jedem der zwölf Folgemonate 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... beträgt.

Mit anderen Worten: Die Anzahl der Kaninchenpaare bildet eine Reihe, in der jeder Term die Summe der beiden vorherigen darstellt. Sie ist als Fibonacci-Reihe bekannt, und die Zahlen selbst werden als Fibonacci-Zahlen bezeichnet. Es stellt sich heraus, dass diese Sequenz aus mathematischer Sicht viele interessante Eigenschaften hat. Hier ein Beispiel: Sie können eine Linie in zwei Segmente unterteilen, sodass das Verhältnis zwischen dem größeren und dem kleineren Segment proportional zum Verhältnis zwischen der gesamten Linie und dem größeren Segment ist. Dieser Proportionalitätsfaktor, etwa 1,618, wird als Goldener Schnitt bezeichnet. Während der Renaissance glaubte man, dass genau dieses Verhältnis in beobachtet wurde architektonische Strukturen, am angenehmsten für das Auge. Wenn Sie aufeinanderfolgende Paare aus der Fibonacci-Reihe nehmen und die größere Zahl jedes Paars durch die kleinere Zahl dividieren, nähert sich Ihr Ergebnis allmählich dem Goldenen Schnitt an.

Seit Fibonacci seine Sequenz entdeckte, wurden sogar Naturphänomene gefunden, bei denen diese Sequenz eine wichtige Rolle zu spielen scheint. Eine davon ist die Phyllotaxis (Blattanordnung) – die Regel, nach der beispielsweise Samen in einem Sonnenblumenblütenstand angeordnet werden. Sonnenblumenkerne sind in zwei Spiralen angeordnet. Die Zahlen, die die Anzahl der Samen in jeder Spirale angeben, sind Mitglieder einer erstaunlichen mathematischen Folge. Die Samen sind in zwei Spiralreihen angeordnet, von denen eine im Uhrzeigersinn und die andere gegen den Uhrzeigersinn verläuft. Und wie viele Samen gibt es jeweils? 34 und 55.

Aufgabe Nr. 1:

Schreiben Sie die ersten fünf Terme der Sequenz.

1. a n =2 n +1/2 n

und n =2 n +1/2 n

Aufgabe Nr. 2:

Schreiben Sie eine Formel für den allgemeinen Term einer Folge natürlicher Zahlen, die ein Vielfaches von 3 sind.

Antwort: 0,3,6,9,12,15,.... 3n und n =3n

Aufgabe Nr. 3:

Schreiben Sie eine Formel für den allgemeinen Term einer Folge natürlicher Zahlen, deren Division durch 4 einen Rest von 1 ergibt.

Antwort:5,9,13,17,21....... 4 n +1 und n =4n+1

Nr. 19. Funktion.

Funktion (Karte, Operator, Transformation) ist ein mathematisches Konzept, das die Beziehung zwischen Elementen von Mengen widerspiegelt. Wir können sagen, dass eine Funktion ein „Gesetz“ ist, nach dem jedes Element einer Menge (Definitionsbereich genannt) mit einem Element einer anderen Menge (Wertebereich genannt) verknüpft ist.

Eine Funktion ist eine Abhängigkeit von Eins variable Größe von einem anderen. Mit anderen Worten, die Beziehung zwischen Mengen.

Das mathematische Konzept einer Funktion drückt die intuitive Vorstellung davon aus, wie eine Größe den Wert einer anderen Größe vollständig bestimmt. Somit bestimmt der Wert der Variablen x eindeutig den Wert des Ausdrucks und der Wert des Monats bestimmt eindeutig den Wert des darauf folgenden Monats; außerdem kann jede Person mit einer anderen Person verglichen werden – ihrem Vater. In ähnlicher Weise erzeugt ein vorgefertigter Algorithmus bestimmte Ausgabedaten basierend auf variierenden Eingabedaten.

Oftmals bezieht sich der Begriff „Funktion“ auf eine numerische Funktion; das heißt, eine Funktion, die einige Zahlen mit anderen in Übereinstimmung bringt. Diese Funktionen werden praktischerweise in Form von Diagrammen in Zahlen dargestellt.

Es kann eine andere Definition gegeben werden. Eine Funktion ist eine bestimmte Aktionüber die Variable.

Das bedeutet, dass wir einen Wert nehmen, eine bestimmte Aktion damit ausführen (zum Beispiel quadrieren oder seinen Logarithmus berechnen) – und den Wert erhalten.

Lassen Sie uns noch eine Definition einer Funktion geben – diejenige, die am häufigsten in Lehrbüchern zu finden ist.

Eine Funktion ist eine Entsprechung zwischen zwei Mengen, wobei jedes Element der ersten Menge genau einem Element der zweiten Menge entspricht.

Beispielsweise weist die Funktion jeder reellen Zahl eine Zahl zu, die doppelt so groß ist wie .

Die Menge der Elemente einer bestimmten Funktion, die x ersetzt, wird als Definitionsbereich bezeichnet, und die Menge der Elemente einer bestimmten Funktion wird als Bereich ihrer Werte bezeichnet.

Geschichte des Begriffs:

Der Begriff „Funktion“ (im engeren Sinne) wurde erstmals von Leibniz (1692) verwendet. Johann Bernoulli wiederum verwendete diesen Begriff in einem Brief an Leibniz in einem Sinne, der dem modernen näher kam. Der Begriff einer Funktion war zunächst nicht vom Begriff einer analytischen Darstellung zu unterscheiden. Anschließend erschien die Definition einer Funktion, gegeben von Euler (1751), dann von Lacroix (1806) – fast moderne Form. Endlich, allgemeine Definition Funktionen (in moderne Form, aber für numerische Funktionen) wurde von Lobatschewski (1834) und Dirichlet (1837) gegeben. ZU Ende des 19. Jahrhunderts Jahrhundert ist der Funktionsbegriff über den Rahmen numerischer Systeme hinausgewachsen. Vektorfunktionen waren die ersten, die dies taten, bald führte Frege logische Funktionen ein (1879) und nach dem Aufkommen der Mengenlehre formulierten Dedekind (1887) und Peano (1911) die moderne universelle Definition.

Nr. 20. Methoden zur Angabe einer Funktion.

Es gibt 4 Möglichkeiten, eine Funktion anzugeben:

1. tabellarisch Eine ziemlich häufige Möglichkeit besteht darin, eine Tabelle mit einzelnen Personen anzugeben

Argumentwerte und ihre entsprechenden Funktionswerte. Diese Methode zum Definieren einer Funktion wird verwendet, wenn der Definitionsbereich der Funktion eine diskrete endliche Menge ist.

Praktisch, wenn f eine endliche Menge ist, aber wenn f unendlich ist, werden nur ausgewählte Paare (x, y) angezeigt.

Mit der tabellarischen Methode zur Angabe einer Funktion ist es möglich, die Werte der Funktion, die nicht in der Tabelle enthalten sind und Zwischenwerten des Arguments entsprechen, näherungsweise zu berechnen. Verwenden Sie dazu die Interpolationsmethode.

Vorteile: Genauigkeit, Geschwindigkeit, leicht aus der Wertetabelle zu ermitteln gewünschter Wert Funktionen. Die Vorteile der tabellarischen Methode zur Angabe einer Funktion bestehen darin, dass sie die Bestimmung der einen oder anderen Funktion ermöglicht spezifische Werte sofort, ohne zusätzliche Messungen oder Berechnungen.

Mängel: Unvollständigkeit, Unklarheit. In einigen Fällen definiert die Tabelle die Funktion nicht vollständig, sondern nur für einige Werte des Arguments und bietet keine visuelle Darstellung der Art der Funktionsänderung in Abhängigkeit von der Argumentänderung.

2. analytisch(Formeln). Am häufigsten stellt das Gesetz den Zusammenhang zwischen her

Argument und Funktion, spezifiziert durch Formeln. Diese Methode zur Angabe einer Funktion wird als analytisch bezeichnet. Dies ist vor allem für MA (mathematische Analysis) wichtig, da MA-Methoden (Differential-, Integralrechnung) diese Zuordnungsmethode erfordern. Die gleiche Funktion kann angegeben werden verschiedene Formeln: j=∣sin( X)∣j=√1−cos2( X) Manchmal kann die definierte Funktion in verschiedenen Teilen ihres Bereichs durch unterschiedliche Formeln angegeben werden F(X)={F 1(X),X∈D 1 fn(X),X∈Dn ∪nk=1Dk=D(F). Bei dieser Methode zur Angabe einer Funktion wird häufig der Definitionsbereich nicht angegeben, dann wird unter dem Definitionsbereich der natürliche Definitionsbereich verstanden, d.h. die Menge aller Werte von x, für die die Funktion einen reellen Wert annimmt.

Diese Methode ermöglicht es, für jeden numerischen Wert des Arguments x den entsprechenden numerischen Wert der Funktion y genau oder mit einiger Genauigkeit zu finden.

Ein Sonderfall der analytischen Methode zur Spezifikation einer Funktion besteht darin, die Funktion durch eine Gleichung der Form F(x,y)=0 (1) zu spezifizieren. Wenn diese Gleichung die Eigenschaft hat, dass ∀ X∈D ist auf das Einzige abgestimmt j, so dass F(X,j)=0, dann sagen sie, dass Gleichung (1) auf D implizit die Funktion definiert. Ein weiterer Sonderfall der Angabe einer Funktion ist parametrisch, wobei jedes Paar ( X,j)∈F wird mithilfe eines Funktionspaars angegeben X=ϕ( T),j=ψ( T) Wo T∈M.

NUMERISCHE SEQUENZEN VI

§ 127. Zahlenfolgen und Möglichkeiten, sie festzulegen. Endliche und unendliche Folgen.

Betrachten Sie die folgenden drei Zahlenreihen:

Es liegt nahe, anzunehmen, dass jeder Zahl in einer dieser Sammlungen eine Nummer zugewiesen wird, die dem Platz entspricht, den sie in dieser Sammlung einnimmt. Im zweiten Satz ist beispielsweise die Zahl 1 die Zahl 1, die Zahl 1/2 die Zahl 2, die Zahl 1/3 die Zahl 3 usw.

Im Gegenteil, egal welche Nummer wir angeben, in jeder dieser Sammlungen gibt es eine Nummer, die mit dieser Nummer ausgestattet ist. Zum Beispiel hat Nummer 2 in der ersten Sequenz die Nummer 2, in der zweiten - die Nummer - 1/2, in der dritten - die Nummer sin 2. Ebenso hat Nummer 10: in der ersten Sequenz - die Nummer 10, in die zweite - die Zahl - 1/10, die dritte - die Zahl sin 10 usw. Somit hat in den obigen Aggregaten jede Zahl eine ganz bestimmte Zahl und wird vollständig durch diese Zahl bestimmt.

Eine Sammlung von Zahlen, jede mit ihrer eigenen Nummer P (P = 1, 2, 3, ...) heißt Zahlenfolge.

Die einzelnen Zahlen einer Folge heißen ihre Terme und werden üblicherweise wie folgt bezeichnet: erster Term A 1 Sekunde A 2 , .... P Mitglied A N usw. Die gesamte Zahlenfolge wird bezeichnet

A 1 , A 2 , A 3 , ... , A N, ... oder ( A N }.

Eine Zahlenfolge anzugeben bedeutet, anzugeben, wie das eine oder andere ihrer Mitglieder gefunden wird, wenn die Nummer der Stelle bekannt ist, die es einnimmt. Es gibt viele verschiedene Möglichkeiten, Zahlenfolgen anzugeben. Im Folgenden werden wir einige davon betrachten.

1. Normalerweise wird eine Zahlenfolge mithilfe einer Formel angegeben, mit der Sie dieses Mitglied anhand der Nummer des Folgemitglieds bestimmen können. Zum Beispiel, wenn das für irgendjemanden bekannt ist P

A N = n 2 ,

A 1 = 1, A 2 = 4, A 3 = 9

usw. Wann A N= Sünde π / 2 P wir bekommen: A 1 = Sünde π / 2 = 1, A 2 = Sünde π = 0, A 3 = Sünde 3 π / 2 = - 1, A 4 = Sünde 2 π = 0 usw.

Eine Formel, mit der Sie jedes Mitglied einer Zahlenfolge anhand seiner Nummer finden können, wird als Formel für ein allgemeines Mitglied einer Zahlenfolge bezeichnet.

2. Es gibt Fälle, in denen eine Sequenz durch die Beschreibung ihrer Mitglieder spezifiziert wird. Sie sagen zum Beispiel, dass die Reihenfolge

1,4; 1,41; 1,414; 1,4142; ...

bestehend aus Näherungswerten von √2 mit einer Abweichung von 0,1; 0,01; 0,001; 0,0001 usw. B ähnliche Fälle manchmal ist es überhaupt unmöglich, die Formel des allgemeinen Begriffs festzulegen; Dennoch scheint die Reihenfolge vollständig definiert zu sein.

3. Manchmal werden die ersten paar Terme einer Folge angegeben und alle anderen Terme werden durch diese gegebenen Terme nach der einen oder anderen Regel bestimmt. Lassen Sie zum Beispiel

A 1 = 1, A 2 = 1,

und jeder nachfolgende Term ist als Summe der beiden vorherigen definiert. Mit anderen Worten, für jeden P > 3

A N = A N- 1 + A N- 2

So wird die Zahlenfolge 1, 1, 2, 3, 5, 8, 13, 21, 34, ... definiert, deren Glieder „Fibonacci-Zahlen“ genannt werden [nach dem italienischen Mathematiker Leonard von Pisa (ca 1170-1250), der auch Fibonacci genannt wurde, was „Sohn von Bonaccio“ bedeutet. Sie haben viele interessante Eigenschaften, deren Betrachtung jedoch den Rahmen unseres Programms sprengen würde.

Eine Folge kann entweder eine endliche oder eine unendliche Anzahl von Termen enthalten.

Eine Folge, die aus endlich vielen Gliedern besteht, heißt endlich, und eine Folge, die aus unendlich vielen Gliedern besteht, heißt unendliche Folge.

Beispielsweise ist die Folge aller geraden positiven Zahlen 2, 4, 6, 8, 10, 12, ... unendlich, aber die Folge der einstelligen geraden positiven Zahlen 2, 4, 6, 8 ist endlich.

Übungen

932. Schreiben Sie die ersten 4 Zahlen der Folge mit einem gemeinsamen Begriff:

933. Finden Sie die Formel für den gemeinsamen Term für jede der angegebenen Folgen:

a) 1, 3, 5, 7, 9, ... ; . e) TG 45°, TG 22°30", TG 11°15", ... ;

b) 2, 4, 6, 8, 10, ... ; f) 1, - 1/2, 1/4, - 1/8, 1/16, ...;

c) 3, -3, 3, -3, 3, ... ; g) 1, 9, 25, 49, 81.....

d) 1/3, 1/9, 1/27, 1/81, ....;

934. Ist die Folge aller positiven Wurzeln der Gleichung endlich:

wie in x = x - 1; b) tg X = X ; c) Sünde x = Axt + B ?

Lektion Nr. 32 Datum ____________

Algebra

Klasse: 9 „B“

Thema: „Numerische Reihenfolge und Methoden zu ihrer Zuordnung.“

Der Zweck der Lektion: Die Schüler sollten wissen, was eine Zahlenfolge ist; Methoden zur Angabe einer Zahlenfolge; unterscheiden können verschiedene Wege Zuordnungen von Zahlenfolgen.

Didaktische Materialien: Handouts, Begleitnotizen.

Technische Schulungshilfen: Vortrag zum Thema „Zahlenfolgen“.

Während des Unterrichts.

1. Organisatorischer Moment.

2. Unterrichtsziele festlegen.

Heute werdet ihr im Unterricht lernen:

Was ist eine Sequenz?

Welche Arten von Sequenzen gibt es?

Wie wird die Zahlenfolge angegeben?

Lernen Sie, eine Sequenz mithilfe einer Formel und ihren vielen Elementen zu schreiben.

Lernen Sie, Mitglieder einer Sequenz zu finden.

3. Arbeiten Sie an dem zu untersuchenden Material.

3.1. Vorbereitungsphase.

Leute, lasst uns eure logischen Fähigkeiten testen. Ich nenne ein paar Worte, und Sie müssen fortfahren:

-Montag Dienstag,…..

- Januar Februar März…;

– Glebova L, Ganovichev E, Dryakhlov V, Ibraeva G,…..(Klassenliste);

–10,11,12,…99;

Aus den Antworten der Jungs wird geschlossen, dass es sich bei den oben genannten Aufgaben um Folgen handelt, also um eine Art geordnete Reihe von Zahlen oder Konzepten, bei denen jede Zahl oder jedes Konzept genau an ihrem Platz ist und die Folge vertauscht wird, wenn die Mitglieder vertauscht werden gebrochen sein (Dienstag, Donnerstag, Montag ist einfach eine Liste von Wochentagen). Das Thema der Lektion ist also die Zahlenfolge.

3.1. Erläuterung des neuen Materials. (Demomaterial)

Analysieren Sie die Antworten der Schüler, geben Sie eine Definition einer Zahlenfolge und zeigen Sie Möglichkeiten zur Zuweisung von Zahlenfolgen auf.

(Arbeiten mit dem Lehrbuch S. 66 – 67)

Definition 1. Die Funktion y = f(x), xN heißt Funktion eines natürlichen Arguments oder einer Zahlenfolge und wird bezeichnet: y = f(n) oder y 1, y 2, y 3, ..., y n, .. . oder (y n).

In diesem Fall ist die unabhängige Variable eine natürliche Zahl.

Am häufigsten bezeichnen wir Folgen wie folgt: ( A N), (B N), (Mit N) usw.

Definition 2. Sequenzmitglieder.

Die Elemente, die eine Sequenz bilden, werden Sequenzmitglieder genannt.

Neue Konzepte: vorheriges und nachfolgendes Mitglied einer Sequenz,

A 1 …A P. (1. und n-ter Term der Folge)

Methoden zur Angabe einer Zahlenfolge.

Analytische Methode.

Beliebig n-tes Element Sequenzen können anhand einer Formel ermittelt werden. (Demonstrationsmaterial)

Entdecken Sie Beispiele

Beispiel 1. Folge gerader Zahlen: y = 2n.

Beispiel 2. Folge des Quadrats der natürlichen Zahlen: y = n 2 ;

1, 4, 9, 16, 25, ..., n 2, ... .

Beispiel 3. Stationäre Folge: y = C;

C, C, C, ..., C, ... .

Sonderfall: y = 5; 5, 5, 5, ..., 5, ... .

Beispiel 4. Folge y = 2 n ;

2, 2 2, 2 3, 2 4, ..., 2 n, ... .

Verbale Methode.

Die Regeln zur Angabe einer Sequenz werden in Worten beschrieben, ohne Angabe von Formeln oder wenn zwischen den Elementen der Sequenz kein Muster vorhanden ist.

Beispiel 1: Zahlennäherungenπ.

Beispiel 2. Folge der Primzahlen: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... .

Beispiel 3. Durch 5 teilbare Zahlenfolge.

Beispiel 2. Beliebige Zahlenmenge: 1, 4, 12, 25, 26, 33, 39, ... .

Beispiel 3. Folge der geraden Zahlen 2, 4, 6, 8, 10, 12, 14, 16, ... .

Wiederkehrende Methode.

Die wiederkehrende Methode besteht darin, eine Regel anzugeben, die es ermöglicht, das n-te Mitglied einer Folge zu berechnen, wenn ihre ersten paar Mitglieder angegeben sind (mindestens ein erstes Mitglied), und eine Formel anzugeben, die es ermöglicht, ihr nächstes Mitglied unter Verwendung der vorherigen Mitglieder zu berechnen. Begriff wiederkehrend kommt vom lateinischen Wort wiederkehrend , was bedeutet Komm zurück . Wenn wir die Terme einer Folge mit dieser Regel berechnen, scheinen wir ständig zurückzugehen und den nächsten Term auf der Grundlage des vorherigen zu berechnen. Die Besonderheit dieser Methode besteht darin, dass zur Bestimmung beispielsweise des 100. Gliedes der Folge zunächst alle vorherigen 99 Glieder ermittelt werden müssen.

Beispiel 1 . a 1 =a, a n+1 =a n +0,7. Sei a 1 =5, dann sieht die Sequenz wie folgt aus: 5; 5,7; 6,4; 7,1; 7,8; 8,5; ... .

Beispiel 2. b 1 = b, b n +1 = ½ b n. Sei b 1 =23, dann sieht die Sequenz wie folgt aus: 23; 11,5; 5,75; 2,875; ... .

Beispiel 3. Fibonacci-Folge. Diese Sequenz lässt sich leicht rekursiv spezifizieren: y 1 =1, y 2 =1,y n -2 +y n -1 wenn n=3, 4, 5, 6, ... . Es wird so aussehen:

1, 1,2, 3, 5, 8, 13, 21, 34, 55, ... . (P Der te Term dieser Folge ist gleich der Summe der beiden vorherigen Terme)

Es ist schwierig, die Fibonacci-Folge analytisch zu definieren, aber es ist möglich. Die Formel, nach der jedes Element dieser Sequenz bestimmt wird, sieht folgendermaßen aus:

Weitere Informationen:

Der italienische Kaufmann Leonardo von Pisa (1180–1240), besser bekannt unter seinem Spitznamen Fibonacci, war ein bedeutender Mathematiker des Mittelalters. Mit dieser Folge ermittelte Fibonacci die Zahl φ (fi); φ=1,618033989.

Grafische Methode

Mitglieder der Folge können durch Punkte auf der Koordinatenebene dargestellt werden. Dazu wird die Zahl entlang der horizontalen Achse und der Wert des entsprechenden Elements der Folge entlang der vertikalen Achse aufgetragen.

Um die Zuordnungsmethoden zu festigen, geben Sie bitte einige Beispiele für Sequenzen an, die entweder verbal, analytisch oder wiederkehrend spezifiziert werden.

Arten von Zahlenfolgen

(Anhand der unten aufgeführten Sequenzen werden Sequenztypen geübt).

Arbeiten mit dem Lehrbuch S. 69-70

1) Zunehmend – wenn jeder Term kleiner als der nächste ist, d. h. A N A N +1.

2) Abnehmend – wenn jeder Term größer als der nächste ist, d. h. A N A N +1 .

3) Unendlich.

4) Endgültig.

5) Wechselzeichen.

6) Konstant (stationär).

Eine steigende oder fallende Folge nennt man monoton.

3; 6; 9; 12; 15; 18;…

1. –1; 2; –3; 4; –5; …

   1, 4, 9, 16 ,…

   –1; 2; –3; 4; –5; 6; …

   3; 3; 3; 3; …; 3; … .

Arbeiten mit dem Lehrbuch: Machen wir es mündlich Nr. 150, 159 S. 71, 72

3.2. Konsolidierung von neuem Material. Probleme lösen.

Zur Festigung des Wissens werden je nach Vorbereitungsstand der Studierenden Beispiele ausgewählt.

Beispiel 1. Erstellen Sie eine mögliche Formel für das n-te Element der Sequenz (y n):

a) 1, 3, 5, 7, 9, 11, ...;

b) 4, 8, 12, 16, 20, ...;

Lösung.

a) Dies ist eine Folge ungerader Zahlen. Analytisch kann diese Folge durch die Formel y = 2n+1 angegeben werden.

b) Dies ist eine numerische Folge, in der das nachfolgende Element um 4 größer als das vorherige ist. Analytisch kann diese Folge durch die Formel y = 4n angegeben werden.

Beispiel 2. Schreiben Sie die ersten zehn Elemente der wiederkehrenden Folge auf: y 1 =1, y 2 =2, y n = y n -2 +y n -1, wenn n = 3, 4, 5, 6, ....

Lösung.

Jedes nachfolgende Element dieser Sequenz ist gleich der Summe der beiden vorherigen Elemente.

Beispiel 3. Die Folge (y n) ist wiederkehrend gegeben: y 1 =1, y 2 =2,y n =5y n -1 - 6y n -2. Definieren Sie diese Reihenfolge analytisch.

Lösung.

Lassen Sie uns die ersten paar Elemente der Sequenz finden.

y 3 =5y 2 -6y 1 =10-6=4;

y 4 =5y 3 -6y 2 =20-12=8;

y 5 =5y 4 -6y 3 =40-24=16;

y 6 =5y 5 -6y 4 =80-48=32;

y 7 =5y 6 -6y 5 =160-96=64.

Wir erhalten die Reihenfolge: 1; 2; 4; 8; 16; 32; 64; ..., was dargestellt werden kann als

2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 ... .

n = 1; 2; 3; 4; 5; 6; 7... .

Wenn wir die Sequenz analysieren, erhalten wir das folgende Muster: y = 2 n -1 .

Beispiel 4. Gegeben sei die Folge y n =24n+36-5n 2 .

a) Wie viele positive Mitglieder hat es?

b) Finden Sie das größte Element der Folge.

c) Gibt es in dieser Folge ein kleinstes Element?

Diese Zahlenfolge ist eine Funktion der Form y = -5x 2 +24x+36, wobei x

a) Finden Sie die Werte der Funktion, bei denen -5x 2 +24x+360 gilt. Lösen wir die Gleichung -5x 2 +24x+36=0.

D = b 2 -4ac = 1296, X 1 = 6, X 2 = -1,2.

Die Gleichung für die Symmetrieachse der Parabel y = -5x 2 +24x+36 kann mit der Formel x= ermittelt werden, wir erhalten: x=2,4.

Für -1,2 gilt die Ungleichung -5x 2 +24x+360. In diesem Intervall gibt es fünf natürliche Zahlen (1, 2, 3, 4, 5). Dies bedeutet, dass es in einer bestimmten Sequenz fünf positive Elemente der Sequenz gibt.

b) Das größte Element der Sequenz wird durch die Auswahlmethode bestimmt und ist gleich y 2 =64.

V) Kleinstes Element Nein.

3.4.Aufgaben für selbstständiges Arbeiten