So ermitteln Sie den Sinus eines Winkels in der Trigonometrie. Trigonometrische Funktionen des Winkel- und Zahlenarguments
Lesen Sie auch
In diesem Artikel zeigen wir, wie man gibt Definitionen von Sinus, Cosinus, Tangens und Kotangens eines Winkels und einer Zahl in der Trigonometrie. Hier werden wir über Notationen sprechen, Beispiele für Einträge geben und grafische Illustrationen geben. Lassen Sie uns abschließend eine Parallele zwischen den Definitionen von Sinus, Cosinus, Tangens und Kotangens in der Trigonometrie und Geometrie ziehen.
Seitennavigation.
Definition von Sinus, Cosinus, Tangens und Kotangens
Sehen wir uns an, wie in einem Schulmathematikkurs die Vorstellung von Sinus, Cosinus, Tangens und Kotangens entsteht. Im Geometrieunterricht wird die Definition von Sinus, Cosinus, Tangens und Kotangens gegeben spitzer Winkel in einem rechtwinkligen Dreieck. Und später wird die Trigonometrie untersucht, die sich mit Sinus, Cosinus, Tangens und Kotangens des Drehwinkels und der Zahl befasst. Lassen Sie uns alle diese Definitionen vorstellen, Beispiele nennen und die notwendigen Kommentare abgeben.
Spitzer Winkel in einem rechtwinkligen Dreieck
Aus dem Geometriekurs kennen wir die Definitionen von Sinus, Cosinus, Tangens und Kotangens eines spitzen Winkels in einem rechtwinkligen Dreieck. Sie werden als Verhältnis der Seiten angegeben rechtwinkliges Dreieck. Geben wir ihre Formulierungen.
Definition.
Sinus eines spitzen Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Gegenkathete zur Hypotenuse.
Definition.
Kosinus eines spitzen Winkels in einem rechtwinkligen Dreieck ist das Verhältnis des Nachbarschenkels zur Hypotenuse.
Definition.
Tangente eines spitzen Winkels in einem rechtwinkligen Dreieck– das ist das Verhältnis der Gegenseite zur Nachbarseite.
Definition.
Kotangens eines spitzen Winkels in einem rechtwinkligen Dreieck- Dies ist das Verhältnis der Anliegerseite zur Gegenseite.
Dort werden auch die Bezeichnungen für Sinus, Cosinus, Tangens und Kotangens eingeführt – sin, cos, tg bzw. ctg.
Wenn ABC beispielsweise ein rechtwinkliges Dreieck mit dem rechten Winkel C ist, dann ist der Sinus des spitzen Winkels A gleich dem Verhältnis der gegenüberliegenden Seite BC zur Hypotenuse AB, d. h. sin∠A=BC/AB.
Mit diesen Definitionen können Sie die Werte von Sinus, Cosinus, Tangens und Kotangens eines spitzen Winkels aus den bekannten Längen der Seiten eines rechtwinkligen Dreiecks sowie aus den bekannten Werten von Sinus, Cosinus, Tangens berechnen. Kotangens und die Länge einer der Seiten, um die Längen der anderen Seiten zu ermitteln. Wenn wir beispielsweise wüssten, dass in einem rechtwinkligen Dreieck der Schenkel AC gleich 3 und die Hypotenuse AB gleich 7 ist, könnten wir den Wert des Kosinus des spitzen Winkels A per Definition berechnen: cos∠A=AC/ AB=3/7.
Drehwinkel
In der Trigonometrie beginnen sie, den Winkel umfassender zu betrachten – sie führen das Konzept des Drehwinkels ein. Die Größe des Drehwinkels ist im Gegensatz zu einem spitzen Winkel nicht auf 0 bis 90 Grad beschränkt; der Drehwinkel in Grad (und im Bogenmaß) kann durch jede reelle Zahl von −∞ bis +∞ ausgedrückt werden.
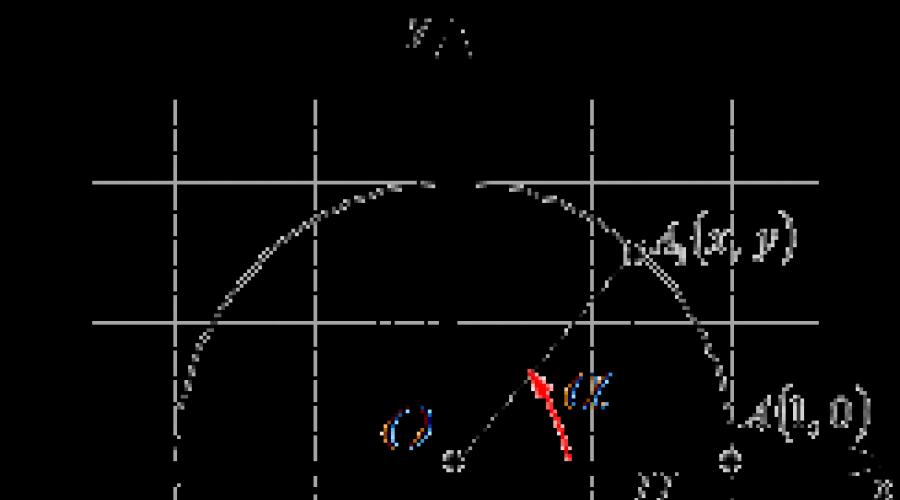
Vor diesem Hintergrund beziehen sich die Definitionen von Sinus, Cosinus, Tangens und Kotangens nicht auf einen spitzen Winkel, sondern auf einen Winkel beliebiger Größe – den Drehwinkel. Sie sind durch die x- und y-Koordinaten des Punktes A 1 gegeben, zu dem der sogenannte Startpunkt A(1, 0) nach seiner Drehung um einen Winkel α um den Punkt O – den Beginn des rechtwinkligen kartesischen Koordinatensystems – geht und der Mittelpunkt des Einheitskreises.
Definition.
Sinus des Drehwinkelsα ist die Ordinate des Punktes A 1, also sinα=y.
Definition.
Kosinus des Drehwinkelsα heißt Abszisse des Punktes A 1, also cosα=x.
Definition.
Tangente des Drehwinkelsα ist das Verhältnis der Ordinate des Punktes A 1 zu seiner Abszisse, also tanα=y/x.
Definition.
Kotangens des Drehwinkelsα ist das Verhältnis der Abszisse des Punktes A 1 zu seiner Ordinate, d. h. ctgα=x/y.
Sinus und Cosinus sind für jeden Winkel α definiert, da wir immer die Abszisse und Ordinate des Punktes bestimmen können, der durch Drehen des Startpunkts um den Winkel α entsteht. Aber Tangens und Kotangens sind für keinen Winkel definiert. Die Tangente ist für Winkel α nicht definiert, bei denen der Startpunkt zu einem Punkt mit der Abszisse Null (0, 1) oder (0, −1) geht, und dies geschieht bei Winkeln 90°+180° k, k∈Z (π /2+π·k rad). Tatsächlich ergibt bei solchen Drehwinkeln der Ausdruck tgα=y/x keinen Sinn, da er eine Division durch Null enthält. Der Kotangens ist nicht für Winkel α definiert, bei denen der Startpunkt zum Punkt mit der Null-Ordinate (1, 0) oder (−1, 0) geht, und dies gilt für Winkel 180° k, k ∈Z (π·k rad).
Sinus und Kosinus sind also für alle Drehwinkel definiert, der Tangens ist für alle Winkel außer 90°+180°k, k∈Z (π/2+πk rad) definiert und der Kotangens ist für alle Winkel außer 180° ·k definiert , k∈Z (π·k rad).
Die Definitionen umfassen die uns bereits bekannten Bezeichnungen sin, cos, tg und ctg, sie werden auch zur Bezeichnung von Sinus, Cosinus, Tangens und Kotangens des Drehwinkels verwendet (manchmal findet man die Bezeichnungen tan und cotentsprechend Tangens und Kotangens) . So kann der Sinus eines Drehwinkels von 30 Grad als sin30° geschrieben werden, die Einträge tg(−24°17′) und ctgα entsprechen dem Tangens des Drehwinkels −24 Grad 17 Minuten und dem Kotangens des Drehwinkels α . Denken Sie daran, dass beim Schreiben des Bogenmaßes eines Winkels die Bezeichnung „rad“ oft weggelassen wird. Beispielsweise wird der Kosinus eines Drehwinkels von drei pi rad üblicherweise mit cos3·π bezeichnet.
Abschließend ist es erwähnenswert, dass bei Sinus, Cosinus, Tangens und Kotangens des Drehwinkels häufig der Ausdruck „Drehwinkel“ oder das Wort „Rotation“ weggelassen wird. Das heißt, anstelle der Formulierung „Sinus des Drehwinkels Alpha“ wird üblicherweise die Formulierung „Sinus des Alpha-Winkels“ oder noch kürzer „Sinus Alpha“ verwendet. Das Gleiche gilt für Kosinus, Tangens und Kotangens.
Wir werden auch sagen, dass die Definitionen von Sinus, Cosinus, Tangens und Kotangens eines spitzen Winkels in einem rechtwinkligen Dreieck mit den Definitionen übereinstimmen, die gerade für Sinus, Cosinus, Tangens und Kotangens eines Drehwinkels im Bereich von 0 bis 90 Grad gegeben wurden. Wir werden dies begründen.
Zahlen
Definition.
Sinus, Cosinus, Tangens und Kotangens einer Zahl t ist eine Zahl, die jeweils dem Sinus, Cosinus, Tangens und Kotangens des Drehwinkels im Bogenmaß t entspricht.
Beispielsweise ist der Kosinus der Zahl 8·π per Definition eine Zahl, die gleich dem Kosinus des Winkels 8·π rad ist. Und der Kosinus eines Winkels von 8·π rad ist gleich eins, daher ist der Kosinus der Zahl 8·π gleich 1.
Es gibt einen anderen Ansatz zur Bestimmung von Sinus, Cosinus, Tangens und Kotangens einer Zahl. Sie besteht darin, dass jeder reellen Zahl t ein Punkt auf dem Einheitskreis mit dem Mittelpunkt im Ursprung des rechtwinkligen Koordinatensystems zugeordnet ist und Sinus, Cosinus, Tangens und Kotangens durch die Koordinaten dieses Punktes bestimmt werden. Schauen wir uns das genauer an.
Lassen Sie uns zeigen, wie eine Entsprechung zwischen reellen Zahlen und Punkten auf einem Kreis hergestellt wird:
- der Zahl 0 wird der Startpunkt A(1, 0) zugewiesen;
- die positive Zahl t ist mit einem Punkt auf dem Einheitskreis verbunden, zu dem wir gelangen, wenn wir uns vom Startpunkt aus entgegen dem Uhrzeigersinn entlang des Kreises bewegen und einen Weg der Länge t zurücklegen;
- Die negative Zahl t ist mit einem Punkt auf dem Einheitskreis verbunden, zu dem wir gelangen, wenn wir uns vom Startpunkt aus im Uhrzeigersinn entlang des Kreises bewegen und einen Weg der Länge |t| zurücklegen .
Nun kommen wir zu den Definitionen von Sinus, Cosinus, Tangens und Kotangens der Zahl t. Nehmen wir an, dass die Zahl t einem Punkt auf dem Kreis A 1 (x, y) entspricht (zum Beispiel entspricht die Zahl &pi/2; dem Punkt A 1 (0, 1)).
Definition.
Sinus der Zahl t ist die Ordinate des Punktes auf dem Einheitskreis, der der Zahl t entspricht, also sint=y.
Definition.
Kosinus der Zahl t wird als Abszisse des Punktes des Einheitskreises bezeichnet, der der Zahl t entspricht, dh Kosten = x.
Definition.
Tangens der Zahl t ist das Verhältnis der Ordinate zur Abszisse eines Punktes auf dem Einheitskreis, der der Zahl t entspricht, d. h. tgt=y/x. In einer anderen äquivalenten Formulierung ist der Tangens einer Zahl t das Verhältnis des Sinus dieser Zahl zum Kosinus, also tgt=sint/cost.
Definition.
Kotangens der Zahl t ist das Verhältnis der Abszisse zur Ordinate eines Punktes auf dem Einheitskreis, der der Zahl t entspricht, d. h. ctgt=x/y. Eine andere Formulierung lautet: Der Tangens der Zahl t ist das Verhältnis des Kosinus der Zahl t zum Sinus der Zahl t: ctgt=cost/sint.
Hier stellen wir fest, dass die soeben gegebenen Definitionen mit der Definition am Anfang dieses Absatzes übereinstimmen. Tatsächlich stimmt der Punkt auf dem Einheitskreis, der der Zahl t entspricht, mit dem Punkt überein, den man durch Drehen des Startpunkts um einen Winkel von t im Bogenmaß erhält.
Es lohnt sich dennoch, diesen Punkt zu klären. Nehmen wir an, wir haben den Eintrag sin3. Wie können wir verstehen, ob wir über den Sinus der Zahl 3 oder den Sinus des Drehwinkels von 3 Bogenmaß sprechen? Dies geht in der Regel aus dem Kontext hervor, andernfalls ist es wahrscheinlich nicht von grundlegender Bedeutung.
Trigonometrische Funktionen des Winkel- und Zahlenarguments
Gemäß den Definitionen im vorherigen Absatz entspricht jeder Drehwinkel α einem ganz bestimmten Wert sinα sowie dem Wert cosα. Darüber hinaus entsprechen alle anderen Rotationswinkel als 90°+180°k, k∈Z (π/2+πk rad) tgα-Werten und andere Werte als 180°k, k∈Z (πk rad) – Werten von ctgα . Daher sind sinα, cosα, tanα und ctgα Funktionen des Winkels α. Mit anderen Worten, dies sind Funktionen des Winkelarguments.
Ähnlich können wir über die Funktionen Sinus, Cosinus, Tangens und Kotangens eines numerischen Arguments sprechen. Tatsächlich entspricht jede reelle Zahl t einem ganz bestimmten Wert sint sowie Kosten. Darüber hinaus entsprechen alle Zahlen außer π/2+π·k, k∈Z den Werten tgt und die Zahlen π·k, k∈Z den Werten ctgt.
Es werden die Funktionen Sinus, Cosinus, Tangens und Kotangens aufgerufen grundlegende trigonometrische Funktionen.
Aus dem Kontext geht meist klar hervor, ob es sich um trigonometrische Funktionen eines Winkelarguments oder eines numerischen Arguments handelt. Ansonsten können wir uns die unabhängige Variable sowohl als Maß für den Winkel (Winkelargument) als auch als numerisches Argument vorstellen.
In der Schule beschäftigen wir uns jedoch hauptsächlich mit numerischen Funktionen, also Funktionen, deren Argumente sowie die entsprechenden Funktionswerte Zahlen sind. Wenn wir also speziell über Funktionen sprechen, ist es ratsam, trigonometrische Funktionen als Funktionen numerischer Argumente zu betrachten.
Zusammenhang zwischen Definitionen aus Geometrie und Trigonometrie
Wenn wir den Drehwinkel α im Bereich von 0 bis 90 Grad betrachten, dann stimmen die Definitionen von Sinus, Cosinus, Tangens und Kotangens des Drehwinkels im Kontext der Trigonometrie vollständig mit den Definitionen von Sinus, Cosinus, Tangens und Kotangens von an überein Spitze Winkel in einem rechtwinkligen Dreieck, die im Geometriekurs angegeben werden. Begründen wir das.
Stellen wir den Einheitskreis im rechtwinkligen kartesischen Koordinatensystem Oxy dar. Markieren wir den Startpunkt A(1, 0) . Drehen wir es um einen Winkel α im Bereich von 0 bis 90 Grad, wir erhalten Punkt A 1 (x, y). Lassen Sie uns die Senkrechte A 1 H vom Punkt A 1 zur Ox-Achse fallen lassen.

Es ist leicht zu erkennen, dass in einem rechtwinkligen Dreieck der Winkel A 1 OH gleich dem Drehwinkel α ist, die Länge des an diesen Winkel angrenzenden Schenkels OH gleich der Abszisse des Punktes A 1 ist, also |OH |=x, die Länge des Schenkels A 1 H gegenüber dem Winkel ist gleich der Ordinate des Punktes A 1, d. h. |A 1 H|=y, und die Länge der Hypotenuse OA 1 ist gleich eins, da es sich um den Radius des Einheitskreises handelt. Dann ist per Definition aus der Geometrie der Sinus eines spitzen Winkels α in einem rechtwinkligen Dreieck A 1 OH gleich dem Verhältnis des gegenüberliegenden Schenkels zur Hypotenuse, d. h. sinα=|A 1 H|/|OA 1 |= y/1=y. Und per Definition aus der Trigonometrie ist der Sinus des Drehwinkels α gleich der Ordinate des Punktes A 1, also sinα=y. Dies zeigt, dass die Bestimmung des Sinus eines spitzen Winkels in einem rechtwinkligen Dreieck der Bestimmung des Sinus des Drehwinkels α entspricht, wenn α zwischen 0 und 90 Grad liegt.
Ebenso kann gezeigt werden, dass die Definitionen von Kosinus, Tangens und Kotangens eines spitzen Winkels α mit den Definitionen von Kosinus, Tangens und Kotangens des Drehwinkels α übereinstimmen.
Referenzliste.
- Geometrie. 7-9 Klassen: Lehrbuch für die Allgemeinbildung Institutionen / [L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev usw.]. - 20. Aufl. M.: Bildung, 2010. - 384 S.: Abb. - ISBN 978-5-09-023915-8.
- Pogorelov A.V. Geometrie: Lehrbuch. für die Klassenstufen 7-9. Allgemeinbildung Institutionen / A. V. Pogorelov. - 2. Aufl. - M.: Education, 2001. - 224 S.: Abb. - ISBN 5-09-010803-X.
- Algebra und Elementarfunktionen : Lernprogramm für Schüler der 9. Klasse weiterführende Schule/ E. S. Kochetkov, E. S. Kochetkova; Herausgegeben vom Doktor der Physikalischen und Mathematischen Wissenschaften O. N. Golovin. – 4. Auflage. M.: Bildung, 1969.
- Algebra: Lehrbuch für die 9. Klasse. Durchschn. Schule/Ju. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky. - M.: Education, 1990. - 272 Seiten: Abb. - ISBN 5-09-002727-7
- Algebra und der Beginn der Analyse: Proc. für 10-11 Klassen. Allgemeinbildung Institutionen / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn und andere; Ed. A. N. Kolmogorov. – 14. Auflage – M.: Education, 2004. – 384 Seiten: Abb. – ISBN 5-09-013651-3.
- Mordkovich A. G. Algebra und die Anfänge der Analysis. 10. Klasse. Um 14 Uhr Teil 1: Lehrbuch für Bildungseinrichtungen ( Profilebene)/ A. G. Mordkovich, P. V. Semenov. - 4. Aufl., hinzufügen. - M.: Mnemosyne, 2007. - 424 S.: Abb. ISBN 978-5-346-00792-0.
- Algebra und begann mathematische Analyse. 10. Klasse: Lehrbuch. für die Allgemeinbildung Institutionen: Basis und Profil. Ebenen /[Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; bearbeitet von A. B. Schizhchenko. - 3. Aufl. - I.: Education, 2010.- 368 S.: Abb.- ISBN 978-5-09-022771-1.
- Baschmakow M. I. Algebra und die Anfänge der Analysis: Lehrbuch. für 10-11 Klassen. Durchschn. Schule - 3. Aufl. - M.: Bildung, 1993. - 351 S.: Abb. - ISBN 5-09-004617-4.
- Gusev V. A., Mordkovich A. G. Mathematik (ein Handbuch für diejenigen, die technische Schulen besuchen): Proc. Zulage.- M.; Höher Schule, 1984.-351 S., mit Abb.
Sinus Der spitze Winkel α eines rechtwinkligen Dreiecks ist das Verhältnis Gegenteil Bein zur Hypotenuse.
Es wird wie folgt bezeichnet: sin α.
Kosinus Der spitze Winkel α eines rechtwinkligen Dreiecks ist das Verhältnis des benachbarten Schenkels zur Hypotenuse.
Er wird wie folgt bezeichnet: cos α.
Tangente Der spitze Winkel α ist das Verhältnis der Gegenseite zur Nachbarseite.
Es wird wie folgt bezeichnet: tg α.
Kotangens Der spitze Winkel α ist das Verhältnis der Anliegerseite zur Gegenseite.
Es wird wie folgt bezeichnet: ctg α.
Sinus, Cosinus, Tangens und Kotangens eines Winkels hängen nur von der Größe des Winkels ab.
Regeln:
Grundlegende trigonometrische Identitäten in einem rechtwinkligen Dreieck:
(α – spitzer Winkel gegenüber dem Bein B und neben dem Bein A . Seite Mit – Hypotenuse. β – zweiter spitzer Winkel).
B | sin 2 α + cos 2 α = 1 | |
A | 1 | |
B | 1 | |
A | 1 1 | |
Sünde α |
Mit zunehmendem spitzen Winkelsin α undtan α-Erhöhung undcos α nimmt ab.
Für jeden spitzen Winkel α:
sin (90° – α) = cos α
cos (90° – α) = sin α
Beispiel-Erklärung:
Lassen Sie ein rechtwinkliges Dreieck ABC ein
AB = 6,
BC = 3,
Winkel A = 30º.
Lassen Sie uns den Sinus von Winkel A und den Kosinus von Winkel B herausfinden.

Lösung .
1) Zuerst ermitteln wir den Wert des Winkels B. Hier ist alles einfach: Da in einem rechtwinkligen Dreieck die Summe der spitzen Winkel 90° beträgt, ist Winkel B = 60°:
B = 90º – 30º = 60º.
2) Berechnen wir Sin A. Wir wissen, dass der Sinus gleich dem Verhältnis der Gegenkathete zur Hypotenuse ist. Für Winkel A ist die gegenüberliegende Seite die Seite BC. Also:
Chr. 3 1
Sünde A = -- = - = -
AB 6 2
3) Berechnen wir nun den Kosinus B. Wir wissen, dass der Kosinus gleich dem Verhältnis des benachbarten Schenkels zur Hypotenuse ist. Für Winkel B ist der benachbarte Schenkel dieselbe Seite BC. Das bedeutet, dass wir BC erneut durch AB dividieren müssen – also die gleichen Aktionen ausführen wie bei der Berechnung des Sinus des Winkels A:
Chr. 3 1
cos B = -- = - = -
AB 6 2
Das Ergebnis ist:
sin A = cos B = 1/2.
sin 30º = cos 60º = 1/2.
Daraus folgt, dass in einem rechtwinkligen Dreieck der Sinus eines spitzen Winkels ist gleich Kosinus ein weiterer spitzer Winkel - und umgekehrt. Genau das bedeuten unsere beiden Formeln:
sin (90° – α) = cos α
cos (90° – α) = sin α
Stellen wir das noch einmal sicher:
1) Sei α = 60º. Wenn wir den Wert von α in die Sinusformel einsetzen, erhalten wir:
sin (90º – 60º) = cos 60º.
sin 30º = cos 60º.
2) Sei α = 30º. Wenn wir den Wert von α in die Kosinusformel einsetzen, erhalten wir:
cos (90° – 30º) = sin 30º.
cos 60° = sin 30°.
(Weitere Informationen zur Trigonometrie finden Sie im Abschnitt Algebra.)
Einer der Bereiche der Mathematik, mit denen Schüler am meisten zu kämpfen haben, ist die Trigonometrie. Es ist nicht verwunderlich: Um dieses Wissensgebiet frei zu beherrschen, braucht man räumliches Denken, die Fähigkeit, Sinus, Cosinus, Tangens, Kotangens mithilfe von Formeln zu finden, Ausdrücke zu vereinfachen und die Zahl Pi in verwenden zu können Berechnungen. Darüber hinaus müssen Sie beim Beweisen von Theoremen in der Lage sein, die Trigonometrie anzuwenden, und dies erfordert entweder ein ausgeprägtes mathematisches Gedächtnis oder die Fähigkeit, komplexe logische Ketten abzuleiten.
Ursprünge der Trigonometrie
Wenn Sie sich mit dieser Wissenschaft vertraut machen, sollten Sie mit der Definition von Sinus, Cosinus und Tangens eines Winkels beginnen. Zunächst müssen Sie jedoch verstehen, was die Trigonometrie im Allgemeinen bewirkt.
Historisch gesehen waren rechtwinklige Dreiecke das Hauptforschungsobjekt in diesem Zweig der Mathematik. Das Vorhandensein eines Winkels von 90 Grad ermöglicht die Durchführung verschiedener Operationen, die es ermöglichen, die Werte aller Parameter der betreffenden Figur anhand von zwei Seiten und einem Winkel oder zwei Winkeln und einer Seite zu bestimmen. In der Vergangenheit bemerkten die Menschen dieses Muster und begannen, es aktiv beim Bau von Gebäuden, in der Navigation, in der Astronomie und sogar in der Kunst zu nutzen.
Erste Stufe
Über den Zusammenhang zwischen Winkeln und Seiten wurde zunächst ausschließlich am Beispiel rechtwinkliger Dreiecke gesprochen. Dann wurden spezielle Formeln entdeckt, die es ermöglichten, die Anwendungsgrenzen zu erweitern Alltagsleben Dieser Zweig der Mathematik.
Das Studium der Trigonometrie in der Schule beginnt heute mit rechtwinkligen Dreiecken, danach nutzen die Schüler die erworbenen Kenntnisse in Physik und lösen abstrakte trigonometrische Gleichungen, die in der High School beginnen.
Sphärische Trigonometrie
Später, als die Wissenschaft die nächste Entwicklungsstufe erreichte, wurden Formeln mit Sinus, Cosinus, Tangens und Kotangens in der Kugelgeometrie verwendet, wo andere Regeln gelten und die Winkelsumme in einem Dreieck immer mehr als 180 Grad beträgt. Dieser Abschnitt wird in der Schule nicht studiert, aber es ist notwendig, über seine Existenz Bescheid zu wissen, zumindest weil die Erdoberfläche und die Oberfläche jedes anderen Planeten konvex ist, was bedeutet, dass jede Oberflächenmarkierung „bogenförmig“ ist dreidimensionaler Raum.

Nimm den Globus und den Faden. Befestigen Sie den Faden an zwei beliebigen Punkten des Globus, sodass er gespannt ist. Bitte beachten Sie, dass es die Form eines Bogens angenommen hat. Mit solchen Formen beschäftigt sich die Kugelgeometrie, die in der Geodäsie, Astronomie und anderen theoretischen und angewandten Bereichen Anwendung findet.
Rechtwinkliges Dreieck
Nachdem wir ein wenig über die Verwendungsmöglichkeiten der Trigonometrie gelernt haben, kehren wir zur grundlegenden Trigonometrie zurück, um besser zu verstehen, was Sinus, Cosinus und Tangens sind, welche Berechnungen mit ihrer Hilfe durchgeführt werden können und welche Formeln zu verwenden sind.
Der erste Schritt besteht darin, die Konzepte im Zusammenhang mit einem rechtwinkligen Dreieck zu verstehen. Erstens ist die Hypotenuse die Seite gegenüber dem 90-Grad-Winkel. Es ist das längste. Wir erinnern uns, dass nach dem Satz des Pythagoras sein numerischer Wert gleich der Wurzel der Summe der Quadrate der beiden anderen Seiten ist.
Wenn die beiden Seiten beispielsweise 3 bzw. 4 Zentimeter lang sind, beträgt die Länge der Hypotenuse 5 Zentimeter. Das wussten übrigens schon die alten Ägypter vor etwa viereinhalbtausend Jahren.
Die beiden verbleibenden Seiten, die einen rechten Winkel bilden, werden Beine genannt. Darüber hinaus müssen wir bedenken, dass die Summe der Winkel in einem Dreieck in einem rechtwinkligen Koordinatensystem 180 Grad beträgt.
Definition
Mit einem guten Verständnis der geometrischen Grundlagen kann man sich schließlich der Definition von Sinus, Cosinus und Tangens eines Winkels zuwenden.
Der Sinus eines Winkels ist das Verhältnis des gegenüberliegenden Schenkels (d. h. der dem gewünschten Winkel gegenüberliegenden Seite) zur Hypotenuse. Der Kosinus eines Winkels ist das Verhältnis der Ankathete zur Hypotenuse.

Denken Sie daran, dass weder Sinus noch Cosinus größer als eins sein können! Warum? Weil die Hypotenuse standardmäßig die längste ist. Egal wie lang das Bein ist, es wird kürzer als die Hypotenuse sein, was bedeutet, dass ihr Verhältnis immer kleiner als eins ist. Wenn Sie also in Ihrer Antwort auf eine Aufgabe einen Sinus- oder Kosinuswert mit einem Wert größer als 1 erhalten, suchen Sie nach einem Fehler in den Berechnungen oder der Argumentation. Diese Antwort ist eindeutig falsch.
Schließlich ist der Tangens eines Winkels das Verhältnis der gegenüberliegenden Seite zur benachbarten Seite. Die Division des Sinus durch den Cosinus führt zum gleichen Ergebnis. Schauen Sie: Gemäß der Formel teilen wir die Länge der Seite durch die Hypotenuse, dividieren dann durch die Länge der zweiten Seite und multiplizieren mit der Hypotenuse. Somit erhalten wir die gleiche Beziehung wie bei der Definition der Tangente.
Der Kotangens ist dementsprechend das Verhältnis der an die Ecke angrenzenden Seite zur gegenüberliegenden Seite. Das gleiche Ergebnis erhalten wir, wenn wir eins durch die Tangente dividieren.
Wir haben uns also die Definitionen von Sinus, Cosinus, Tangens und Kotangens angesehen und können nun mit den Formeln fortfahren.
Die einfachsten Formeln
In der Trigonometrie kommt man ohne Formeln nicht aus – wie findet man Sinus, Cosinus, Tangens, Kotangens ohne sie? Aber genau das ist bei der Lösung von Problemen erforderlich.
Die erste Formel, die Sie kennen müssen, wenn Sie mit dem Studium der Trigonometrie beginnen, besagt, dass die Summe der Quadrate von Sinus und Cosinus eines Winkels gleich eins ist. Diese Formel ist eine direkte Folge des Satzes des Pythagoras, spart jedoch Zeit, wenn Sie die Größe des Winkels und nicht die Seite kennen müssen.
Viele Schüler können sich nicht an die zweite Formel erinnern, die auch bei der Lösung von Schulaufgaben sehr beliebt ist: Die Summe aus eins und dem Quadrat des Tangens eines Winkels ist gleich eins geteilt durch das Quadrat des Kosinus des Winkels. Schauen Sie genauer hin: Dies ist die gleiche Aussage wie in der ersten Formel, nur dass beide Seiten der Identität durch das Quadrat des Kosinus geteilt wurden. Es stellt sich heraus, dass eine einfache mathematische Operation die trigonometrische Formel völlig unkenntlich macht. Denken Sie daran: Wenn Sie Sinus, Cosinus, Tangens und Kotangens, Transformationsregeln und einige Grundformeln kennen, können Sie jederzeit die erforderlichen komplexeren Formeln auf einem Blatt Papier ableiten.
Formeln für Doppelwinkel und Addition von Argumenten
Zwei weitere Formeln, die Sie lernen müssen, beziehen sich auf die Werte von Sinus und Cosinus für die Summe und Differenz von Winkeln. Sie sind in der folgenden Abbildung dargestellt. Bitte beachten Sie, dass im ersten Fall Sinus und Cosinus beide Male multipliziert werden und im zweiten Fall das paarweise Produkt aus Sinus und Cosinus addiert wird.

Es gibt auch Formeln, die mit Doppelwinkelargumenten verknüpft sind. Sie sind vollständig von den vorherigen abgeleitet – versuchen Sie als Training, sie selbst zu erhalten, indem Sie den Alpha-Winkel einnehmen gleich dem Winkel Beta.
Beachten Sie abschließend, dass Doppelwinkelformeln neu angeordnet werden können, um die Potenz von Sinus, Cosinus und Tangens Alpha zu reduzieren.
Theoreme
Die beiden Hauptsätze der grundlegenden Trigonometrie sind der Sinussatz und der Kosinussatz. Mit Hilfe dieser Theoreme können Sie leicht verstehen, wie Sie Sinus, Cosinus und Tangens und damit die Fläche der Figur und die Größe jeder Seite usw. ermitteln.
Der Sinussatz besagt, dass wir erhalten, wenn wir die Länge jeder Seite eines Dreiecks durch den entgegengesetzten Winkel dividieren selbe Nummer. Darüber hinaus entspricht diese Zahl zwei Radien des umschriebenen Kreises, also des Kreises, der alle Punkte eines gegebenen Dreiecks enthält.

Der Kosinussatz verallgemeinert den Satz des Pythagoras und projiziert ihn auf beliebige Dreiecke. Es stellt sich heraus, dass man von der Summe der Quadrate der beiden Seiten deren Produkt multipliziert mit dem doppelten Kosinus des angrenzenden Winkels subtrahiert – der resultierende Wert ist gleich dem Quadrat der dritten Seite. Somit erweist sich der Satz des Pythagoras als Sonderfall des Kosinussatzes.
Flüchtigkeitsfehler
Selbst wenn man weiß, was Sinus, Cosinus und Tangens sind, kann man aufgrund von Geistesabwesenheit oder einem Fehler bei den einfachsten Berechnungen leicht einen Fehler machen. Um solche Fehler zu vermeiden, werfen wir einen Blick auf die beliebtesten.
Erstens sollten Sie Brüche nicht in Dezimalzahlen umwandeln, bis Sie das Endergebnis erhalten – Sie können die Antwort so belassen gemeinsamer Bruch, sofern in den Bedingungen nichts anderes angegeben ist. Eine solche Transformation kann nicht als Fehler bezeichnet werden, es sollte jedoch beachtet werden, dass in jeder Phase des Problems neue Wurzeln entstehen können, die nach Ansicht des Autors reduziert werden sollten. In diesem Fall verschwenden Sie Ihre Zeit mit unnötigen mathematischen Operationen. Dies gilt insbesondere für Werte wie die Wurzel aus drei oder die Wurzel aus zwei, da sie bei jedem Schritt in Problemen vorkommen. Das Gleiche gilt für das Runden „hässlicher“ Zahlen.

Beachten Sie außerdem, dass der Kosinussatz auf jedes Dreieck anwendbar ist, nicht jedoch der Satz des Pythagoras! Wenn Sie versehentlich vergessen, das Doppelte des Produkts aus den Seiten multipliziert mit dem Kosinus des Winkels zwischen ihnen zu subtrahieren, erhalten Sie nicht nur ein völlig falsches Ergebnis, sondern demonstrieren auch ein völliges Unverständnis für das Thema. Das ist schlimmer als ein Flüchtigkeitsfehler.
Drittens verwechseln Sie nicht die Werte für Winkel von 30 und 60 Grad für Sinus, Cosinus, Tangens, Kotangens. Merken Sie sich diese Werte, denn der Sinus von 30 Grad ist gleich dem Kosinus von 60 und umgekehrt. Es ist leicht, sie zu verwechseln, was unweigerlich zu einem falschen Ergebnis führt.
Anwendung
Viele Studierende haben es nicht eilig, mit dem Studium der Trigonometrie zu beginnen, weil sie deren praktische Bedeutung nicht verstehen. Was ist Sinus, Cosinus, Tangens für einen Ingenieur oder Astronomen? Das sind Konzepte, mit denen man die Entfernung zu entfernten Sternen berechnen, den Fall eines Meteoriten vorhersagen oder eine Forschungssonde zu einem anderen Planeten schicken kann. Ohne sie ist es unmöglich, ein Gebäude zu bauen, ein Auto zu entwerfen, die Belastung einer Oberfläche oder die Flugbahn eines Objekts zu berechnen. Und das sind nur die offensichtlichsten Beispiele! Schließlich wird Trigonometrie in der einen oder anderen Form überall verwendet, von der Musik bis zur Medizin.
Abschließend
Sie sind also Sinus, Cosinus, Tangens. Sie können sie in Berechnungen verwenden und Schulprobleme erfolgreich lösen.

Der Sinn der Trigonometrie besteht darin, dass man mithilfe der bekannten Parameter eines Dreiecks die Unbekannten berechnen muss. Insgesamt gibt es sechs Parameter: Länge drei Seiten und die Größen der drei Winkel. Der einzige Unterschied bei den Aufgaben besteht darin, dass unterschiedliche Eingabedaten angegeben werden.
Sie wissen jetzt, wie Sie Sinus, Cosinus und Tangens anhand der bekannten Längen der Beine oder der Hypotenuse ermitteln. Da diese Begriffe nichts anderes als ein Verhältnis bedeuten und ein Verhältnis ein Bruch ist, Hauptziel Das trigonometrische Problem besteht darin, die Wurzeln einer gewöhnlichen Gleichung oder eines Gleichungssystems zu finden. Und hier hilft Ihnen die reguläre Schulmathematik.
Die Konzepte Sinus, Cosinus, Tangens und Kotangens sind die Hauptkategorien der Trigonometrie, einem Teilgebiet der Mathematik, und untrennbar mit der Definition des Winkels verbunden. Die Beherrschung dieser mathematischen Wissenschaft erfordert das Auswendiglernen und Verstehen von Formeln und Theoremen sowie ein ausgeprägtes räumliches Denken. Aus diesem Grund bereiten trigonometrische Berechnungen Schülern und Studenten oft Schwierigkeiten. Um sie zu überwinden, sollten Sie sich mit trigonometrischen Funktionen und Formeln vertraut machen.
Konzepte in der Trigonometrie
Um die Grundkonzepte der Trigonometrie zu verstehen, müssen Sie zunächst verstehen, was ein rechtwinkliges Dreieck und ein Winkel in einem Kreis sind und warum alle grundlegenden trigonometrischen Berechnungen damit verbunden sind. Ein Dreieck, bei dem einer der Winkel 90 Grad beträgt, ist rechteckig. Historisch gesehen wurde diese Figur häufig von Menschen in der Architektur, Navigation, Kunst und Astronomie verwendet. Durch das Studium und die Analyse der Eigenschaften dieser Figur gelangten die Menschen dazu, die entsprechenden Verhältnisse ihrer Parameter zu berechnen.
Die mit rechtwinkligen Dreiecken verbundenen Hauptkategorien sind die Hypotenuse und die Beine. Hypotenuse – die gegenüberliegende Seite eines Dreiecks rechter Winkel. Die Beine sind jeweils die anderen beiden Seiten. Die Winkelsumme aller Dreiecke beträgt immer 180 Grad.
Die sphärische Trigonometrie ist ein Teilbereich der Trigonometrie, der in der Schule nicht studiert wird, aber in angewandten Wissenschaften wie Astronomie und Geodäsie von Wissenschaftlern verwendet wird. Die Besonderheit eines Dreiecks in der sphärischen Trigonometrie besteht darin, dass es immer eine Winkelsumme von mehr als 180 Grad aufweist.
Winkel eines Dreiecks
 In einem rechtwinkligen Dreieck ist der Sinus eines Winkels das Verhältnis des Schenkels gegenüber dem gewünschten Winkel zur Hypotenuse des Dreiecks. Demnach ist der Kosinus das Verhältnis von Ankathete und Hypotenuse. Beide Werte haben immer einen Betrag kleiner als eins, da die Hypotenuse immer länger als das Bein ist.
In einem rechtwinkligen Dreieck ist der Sinus eines Winkels das Verhältnis des Schenkels gegenüber dem gewünschten Winkel zur Hypotenuse des Dreiecks. Demnach ist der Kosinus das Verhältnis von Ankathete und Hypotenuse. Beide Werte haben immer einen Betrag kleiner als eins, da die Hypotenuse immer länger als das Bein ist.
Der Tangens eines Winkels ist ein Wert, der dem Verhältnis der Gegenseite zur Nachbarseite des gewünschten Winkels oder Sinus zu Kosinus entspricht. Der Kotangens wiederum ist das Verhältnis der angrenzenden Seite des gewünschten Winkels zur gegenüberliegenden Seite. Der Kotangens eines Winkels kann auch durch Division von eins durch den Tangenswert ermittelt werden.
Einheitskreis
Ein Einheitskreis ist in der Geometrie ein Kreis, dessen Radius gleich eins ist. Ein solcher Kreis wird in einem kartesischen Koordinatensystem konstruiert, wobei der Mittelpunkt des Kreises mit dem Ursprungspunkt zusammenfällt und die Anfangsposition des Radiusvektors entlang der positiven Richtung der X-Achse (Abszissenachse) bestimmt wird. Jeder Punkt auf dem Kreis hat zwei Koordinaten: XX und YY, also die Koordinaten der Abszisse und der Ordinate. Indem wir einen beliebigen Punkt auf dem Kreis in der XX-Ebene auswählen und von dort aus eine Senkrechte zur Abszissenachse ziehen, erhalten wir ein rechtwinkliges Dreieck, das durch den Radius zum ausgewählten Punkt (bezeichnet mit dem Buchstaben C), der zur X-Achse gezogenen Senkrechten, gebildet wird (Der Schnittpunkt wird mit dem Buchstaben G bezeichnet) und das Segment der Abszissenachse zwischen dem Ursprung (der Punkt wird mit dem Buchstaben A bezeichnet) und dem Schnittpunkt G. Das resultierende Dreieck ACG ist ein rechtwinkliges Dreieck, das in einen Kreis eingeschrieben ist. wobei AG die Hypotenuse und AC und GC die Beine sind. Der Winkel zwischen dem Radius des Kreises AC und dem Segment der Abszissenachse mit der Bezeichnung AG wird als α (Alpha) definiert. Also, cos α = AG/AC. Wenn man bedenkt, dass AC der Radius des Einheitskreises ist und gleich eins ist, ergibt sich, dass cos α=AG. Ebenso ist sin α=CG.
Wenn Sie diese Daten kennen, können Sie außerdem die Koordinate von Punkt C auf dem Kreis bestimmen, da cos α=AG und sin α=CG, was bedeutet, dass Punkt C die angegebenen Koordinaten (cos α;sin α) hat. Da wir wissen, dass der Tangens dem Verhältnis von Sinus zu Kosinus entspricht, können wir bestimmen, dass tan α = y/x und cot α = x/y. Durch die Betrachtung von Winkeln in einem negativen Koordinatensystem können Sie berechnen, dass die Sinus- und Cosinuswerte einiger Winkel negativ sein können.
Berechnungen und Grundformeln
Trigonometrische Funktionswerte
Nachdem wir das Wesen trigonometrischer Funktionen durch den Einheitskreis betrachtet haben, können wir die Werte dieser Funktionen für einige Winkel ableiten. Die Werte sind in der folgenden Tabelle aufgeführt.
Die einfachsten trigonometrischen Identitäten
Gleichungen, in denen das Vorzeichen der trigonometrischen Funktion enthalten ist unbekannter Wert, werden trigonometrisch genannt. Identitäten mit dem Wert sin x = α, k – jede ganze Zahl:
- sin x = 0, x = πk.
- 2. sin x = 1, x = π/2 + 2πk.
- sin x = -1, x = -π/2 + 2πk.
- sin x = a, |a| > 1, keine Lösungen.
- sin x = a, |a| ≦ 1, x = (-1)^k * arcsin α + πk.
Identitäten mit dem Wert cos x = a, wobei k eine beliebige ganze Zahl ist:
- cos x = 0, x = π/2 + πk.
- cos x = 1, x = 2πk.
- cos x = -1, x = π + 2πk.
- cos x = a, |a| > 1, keine Lösungen.
- cos x = a, |a| ≦ 1, x = ±arccos α + 2πk.
Identitäten mit dem Wert tg x = a, wobei k eine beliebige ganze Zahl ist:
- tan x = 0, x = π/2 + πk.
- tan x = a, x = arctan α + πk.
Identitäten mit dem Wert ctg x = a, wobei k eine beliebige ganze Zahl ist:
- cot x = 0, x = π/2 + πk.
- ctg x = a, x = arcctg α + πk.
Reduktionsformeln
Diese Kategorie konstanter Formeln bezeichnet Methoden, mit denen Sie von trigonometrischen Funktionen der Form zu Funktionen eines Arguments wechseln können, d das Intervall von 0 bis 90 Grad für eine einfachere Berechnung.
Formeln für Reduktionsfunktionen für den Sinus eines Winkels sehen wie folgt aus:
- sin(900 - α) = α;
- sin(900 + α) = cos α;
- sin(1800 - α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 - α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 - α) = -sin α;
- sin(3600 + α) = sin α.
Für den Winkelkosinus:
- cos(900 - α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 - α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 - α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 - α) = cos α;
- cos(3600 + α) = cos α.
Die Verwendung der oben genannten Formeln ist unter zwei Regeln möglich. Erstens: Wenn der Winkel als Wert (π/2 ± a) oder (3π/2 ± a) dargestellt werden kann, ändert sich der Wert der Funktion:
- von der Sünde zur Sünde;
- von cos zu sin;
- von tg bis ctg;
- von ctg bis tg.
Der Wert der Funktion bleibt unverändert, wenn der Winkel als (π ± a) oder (2π ± a) dargestellt werden kann.
Zweitens ändert sich das Vorzeichen der reduzierten Funktion nicht: War sie zunächst positiv, bleibt sie es auch. Das Gleiche gilt für negative Funktionen.
Additionsformeln
Diese Formeln drücken die Werte von Sinus, Cosinus, Tangens und Kotangens der Summe und Differenz zweier Drehwinkel durch ihre trigonometrischen Funktionen aus. Typischerweise werden die Winkel als α und β bezeichnet.
Die Formeln sehen so aus:
- sin(α ± β) = sin α * cos β ± cos α * sin.
- cos(α ± β) = cos α * cos β ∓ sin α * sin.
- tan(α ± β) = (tg α ± tan β) / (1 ∓ tan α * tan β).
- ctg(α ± β) = (-1 ± ctg α * ctg β) / (ctg α ± ctg β).
Diese Formeln gelten für alle Winkel α und β.
Doppel- und Dreifachwinkelformeln
Die trigonometrischen Formeln für den Doppel- und Dreifachwinkel sind Formeln, die die Funktionen der Winkel 2α bzw. 3α mit den trigonometrischen Funktionen des Winkels α in Beziehung setzen. Abgeleitet aus Additionsformeln:
- sin2α = 2sinα*cosα.
- cos2α = 1 - 2sin^2 α.
- tan2α = 2tgα / (1 - tan^2 α).
- sin3α = 3sinα - 4sin^3 α.
- cos3α = 4cos^3 α - 3cosα.
- tg3α = (3tgα - tg^3 α) / (1-tg^2 α).
Übergang von der Summe zum Produkt
Unter Berücksichtigung von 2sinx*cosy = sin(x+y) + sin(x-y) erhalten wir durch Vereinfachung dieser Formel die Identität sinα + sinβ = 2sin(α + β)/2 * cos(α − β)/2. Ähnlich sinα - sinβ = 2sin(α - β)/2 * cos(α + β)/2; cosα + cosβ = 2cos(α + β)/2 * cos(α − β)/2; cosα — cosβ = 2sin(α + β)/2 * sin(α − β)/2; tanα + tanβ = sin(α + β) / cosα * cosβ; tgα – tgβ = sin(α – β) / cosα * cosβ; cosα + sinα = √2sin(π/4 ∓ α) = √2cos(π/4 ± α).
Übergang vom Produkt zur Summe
Diese Formeln ergeben sich aus den Identitäten des Übergangs einer Summe zu einem Produkt:
- sinα * sinβ = 1/2*;
- cosα * cosβ = 1/2*;
- sinα * cosβ = 1/2*.
Formeln zur Gradreduzierung
In diesen Identitäten können die quadratischen und kubischen Potenzen von Sinus und Cosinus als Sinus und Cosinus der ersten Potenz eines Mehrfachwinkels ausgedrückt werden:
- sin^2 α = (1 - cos2α)/2;
- cos^2 α = (1 + cos2α)/2;
- sin^3 α = (3 * sinα - sin3α)/4;
- cos^3 α = (3 * cosα + cos3α)/4;
- sin^4 α = (3 - 4cos2α + cos4α)/8;
- cos^4 α = (3 + 4cos2α + cos4α)/8.
Universeller Ersatz
Formeln für die universelle trigonometrische Substitution drücken trigonometrische Funktionen als Tangens eines halben Winkels aus.
- sin x = (2tgx/2) * (1 + tan^2 x/2), mit x = π + 2πn;
- cos x = (1 - tan^2 x/2) / (1 + tan^2 x/2), wobei x = π + 2πn;
- tg x = (2tgx/2) / (1 - tg^2 x/2), wobei x = π + 2πn;
- cot x = (1 - tg^2 x/2) / (2tgx/2), mit x = π + 2πn.
Sonderfälle
Sonderfälle der einfachsten trigonometrischen Gleichungen sind unten aufgeführt (k ist eine beliebige ganze Zahl).
Quotienten für Sinus:
| Sin x-Wert | x-Wert |
|---|---|
| 0 | πk |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk oder 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk oder -5π/6 + 2πk |
| √2/2 | π/4 + 2πk oder 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk oder -3π/4 + 2πk |
| √3/2 | π/3 + 2πk oder 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk oder -2π/3 + 2πk |
Quotienten für Kosinus:
| cos x-Wert | x-Wert |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Quotienten für Tangens:
| tg x-Wert | x-Wert |
|---|---|
| 0 | πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Quotienten für Kotangens:
| ctg x-Wert | x-Wert |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Theoreme
Satz der Sinus
Es gibt zwei Versionen des Theorems – eine einfache und eine erweiterte. Einfacher Sinussatz: a/sin α = b/sin β = c/sin γ. In diesem Fall sind a, b, c die Seiten des Dreiecks und α, β, γ die entgegengesetzten Winkel.
Erweiterter Sinussatz für ein beliebiges Dreieck: a/sin α = b/sin β = c/sin γ = 2R. In dieser Identität bezeichnet R den Radius des Kreises, in den das gegebene Dreieck eingeschrieben ist.
Kosinussatz
Die Identität wird wie folgt angezeigt: a^2 = b^2 + c^2 - 2*b*c*cos α. In der Formel sind a, b, c die Seiten des Dreiecks und α ist der Winkel gegenüber der Seite a.
Tangentensatz
Die Formel drückt die Beziehung zwischen den Tangenten zweier Winkel und der Länge der ihnen gegenüberliegenden Seiten aus. Die Seiten sind mit a, b, c bezeichnet und die entsprechenden entgegengesetzten Winkel sind α, β, γ. Formel des Tangentensatzes: (a - b) / (a+b) = tan((α - β)/2) / tan((α + β)/2).
Kotangenssatz
Verbindet den Radius eines in ein Dreieck eingeschriebenen Kreises mit der Länge seiner Seiten. Wenn a, b, c die Seiten des Dreiecks und A, B, C jeweils die ihnen gegenüberliegenden Winkel sind, r der Radius des eingeschriebenen Kreises und p der Halbumfang des Dreiecks ist, ergibt sich Folgendes Identitäten sind gültig:
- Kinderbett A/2 = (p-a)/r;
- Kinderbett B/2 = (p-b)/r;
- Kinderbett C/2 = (p-c)/r.
Anwendung

Trigonometrie ist nicht nur eine theoretische Wissenschaft, die mit mathematischen Formeln verbunden ist. Seine Eigenschaften, Theoreme und Regeln werden in der Praxis von verschiedenen Bereichen der menschlichen Tätigkeit genutzt – Astronomie, Luft- und Seeschifffahrt, Musiktheorie, Geodäsie, Chemie, Akustik, Optik, Elektronik, Architektur, Wirtschaftswissenschaften, Maschinenbau, Messarbeiten, Computergrafik, Kartographie, Ozeanographie und viele andere.
Sinus, Cosinus, Tangens und Kotangens sind die Grundbegriffe der Trigonometrie, mit deren Hilfe man die Beziehungen zwischen den Winkeln und Längen der Seiten eines Dreiecks mathematisch ausdrücken und durch Identitäten, Theoreme und Regeln die benötigten Größen ermitteln kann.
Wie findet man Sinus?



Das Studium der Geometrie hilft, das Denken zu entwickeln. Dieses Fach ist unbedingt in die Schulvorbereitung einzubeziehen. Im Alltag können Kenntnisse zu diesem Thema nützlich sein – zum Beispiel bei der Planung einer Wohnung.
Aus der Geschichte
Der Geometriekurs umfasst auch die Trigonometrie, die trigonometrische Funktionen untersucht. In der Trigonometrie untersuchen wir Sinus, Cosinus, Tangens und Kotangens von Winkeln.
Aber weiter dieser Moment Beginnen wir mit dem Einfachsten – dem Sinus. Schauen wir uns das allererste Konzept genauer an – den Sinus eines Winkels in der Geometrie. Was ist Sinus und wie findet man ihn?
Das Konzept des „Sinuswinkels“ und der Sinuskurven
Der Sinus eines Winkels ist das Verhältnis der Werte der Gegenkathete und der Hypotenuse eines rechtwinkligen Dreiecks. Dies ist eine direkte trigonometrische Funktion, die als „sin (x)“ geschrieben wird, wobei (x) der Winkel des Dreiecks ist.
In der Grafik wird der Sinus eines Winkels durch eine Sinuswelle mit eigenen Eigenschaften dargestellt. Eine Sinuswelle sieht aus wie eine durchgehende Wellenlinie, die innerhalb bestimmter Grenzen auf der Koordinatenebene liegt. Die Funktion ist ungerade, also symmetrisch um 0 auf der Koordinatenebene (sie geht vom Koordinatenursprung aus).
Der Definitionsbereich dieser Funktion liegt im Bereich von -1 bis +1 im kartesischen Koordinatensystem. Die Periode der Sinuswinkelfunktion beträgt 2 Pi. Das bedeutet, dass sich das Muster alle 2 Pi wiederholt und die Sinuswelle einen vollständigen Zyklus durchläuft.
Sinuswellengleichung
- sin x = a/c
- wobei a der dem Winkel des Dreiecks entgegengesetzte Schenkel ist
- c - Hypotenuse eines rechtwinkligen Dreiecks
Eigenschaften des Sinus eines Winkels
- sin(x) = - sin(x). Dieses Merkmal zeigt, dass die Funktion symmetrisch ist und wenn die Werte x und (-x) in beiden Richtungen im Koordinatensystem aufgetragen werden, sind die Ordinaten dieser Punkte entgegengesetzt. Sie werden den gleichen Abstand voneinander haben.
- Ein weiteres Merkmal dieser Funktion besteht darin, dass der Graph der Funktion auf dem Segment [- P/2 + 2 Pn] zunimmt; [P/2 + 2Pn], wobei n eine beliebige ganze Zahl ist. Auf dem Segment wird eine Abnahme des Diagramms des Sinus des Winkels beobachtet: [P/2 + 2Pn]; [3P/2 + 2Pn].
- sin(x) > 0, wenn x im Bereich (2Пn, П + 2Пn) liegt
- (X)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)
Die Werte der Sinuswerte des Winkels werden anhand spezieller Tabellen ermittelt. Solche Tabellen wurden erstellt, um den Zählvorgang zu erleichtern komplexe Formeln und Gleichungen. Es ist einfach zu verwenden und enthält nicht nur die Werte der sin(x)-Funktion, sondern auch die Werte anderer Funktionen.
Darüber hinaus ist im obligatorischen Gedächtnisstudium eine Tabelle mit Standardwerten dieser Funktionen enthalten, ähnlich einer Multiplikationstabelle. Dies gilt insbesondere für Kurse mit physikalischem und mathematischem Schwerpunkt. In der Tabelle sehen Sie die Werte der in der Trigonometrie verwendeten Hauptwinkel: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 und 360 Grad.
Es gibt auch eine Tabelle, die die Werte trigonometrischer Funktionen nicht standardmäßiger Winkel definiert. Mithilfe verschiedener Tabellen können Sie Sinus, Cosinus, Tangens und Kotangens einiger Winkel einfach berechnen.
Gleichungen werden mit trigonometrischen Funktionen erstellt. Das Lösen dieser Gleichungen ist einfach, wenn Sie einfache trigonometrische Identitäten und Reduktionen von Funktionen kennen, beispielsweise sin (P/2 + x) = cos (x) und andere. Auch für solche Kürzungen wurde eine eigene Tabelle erstellt.
So finden Sie den Sinus eines Winkels
Wenn die Aufgabe darin besteht, den Sinus eines Winkels zu finden, und je nach Bedingung haben wir nur den Kosinus, Tangens oder Kotangens des Winkels, können wir mithilfe trigonometrischer Identitäten leicht berechnen, was wir brauchen.
- sin 2 x + cos 2 x = 1
Aus dieser Gleichung können wir sowohl Sinus als auch Cosinus ermitteln, je nachdem, welcher Wert unbekannt ist. Wir können es schaffen trigonometrische Gleichung mit einer Unbekannten:
- Sünde 2 x = 1 - cos 2 x
- sin x = ± √ 1 - cos 2 x
- Kinderbett 2 x + 1 = 1 / Sünde 2 x
Aus dieser Gleichung können Sie den Wert des Sinus ermitteln, indem Sie den Wert des Kotangens des Winkels kennen. Ersetzen Sie zur Vereinfachung sin 2 x = y und Sie haben eine einfache Gleichung. Der Kotangenswert ist beispielsweise 1, dann gilt:
- 1 + 1 = 1/Jahr
- 2 = 1/Jahr
- 2у = 1
- y = 1/2
Jetzt führen wir den umgekehrten Austausch des Players durch:
- Sünde 2 x = ½
- Sünde x = 1 / √2
Da wir den Kotangenswert für den Standardwinkel (45 0) genommen haben, können die erhaltenen Werte in der Tabelle überprüft werden.
Wenn Sie einen Tangenswert erhalten und den Sinus ermitteln müssen, hilft eine andere trigonometrische Identität:
- tg x * ctg x = 1
Es folgt dem:
- Kinderbett x = 1 / tan x
Um den Sinus eines nicht standardmäßigen Winkels, beispielsweise 240 0, zu ermitteln, müssen Sie Winkelreduktionsformeln verwenden. Wir wissen, dass π 180 0 entspricht. Somit drücken wir unsere Gleichheit unter Verwendung von Standardwinkeln durch Erweiterung aus.
- 240 0 = 180 0 + 60 0
Wir müssen Folgendes finden: sin (180 0 + 60 0). Die Trigonometrie verfügt über Reduktionsformeln, die in diesem Fall nützlich sind. Dies ist die Formel:
- sin (π + x) = - sin (x)
Somit ist der Sinus eines Winkels von 240 Grad gleich:
- Sünde (180 0 + 60 0) = - Sünde (60 0) = - √3/2
In unserem Fall ist x = 60 bzw. P 180 Grad. Den Wert (-√3/2) haben wir aus der Wertetabelle der Funktionen von Standardwinkeln gefunden.
Auf diese Weise können nicht standardmäßige Winkel erweitert werden, zum Beispiel: 210 = 180 + 30.
