Im schulischen Lehrplan für einen Stereometriekurs beginnt das Studium dreidimensionaler Figuren meist mit einem einfachen geometrischen Körper – dem Polyeder eines Prismas. Die Rolle seiner Basen übernehmen zwei gleiche Polygone, die in parallelen Ebenen liegen. Ein Sonderfall ist ein regelmäßiges viereckiges Prisma. Seine Grundflächen sind zwei identische regelmäßige Vierecke, zu denen die Seiten senkrecht stehen und die Form von Parallelogrammen (oder Rechtecken, wenn das Prisma nicht geneigt ist) haben.

Wie sieht ein Prisma aus?

Ein regelmäßiges viereckiges Prisma ist ein Sechseck, dessen Grundflächen zwei Quadrate sind und dessen Seitenflächen durch Rechtecke dargestellt werden. Ein anderer Name dafür geometrische Figur- gerades Parallelepiped.

Unten ist eine Zeichnung dargestellt, die ein viereckiges Prisma zeigt.

Kann man auch auf dem Bild sehen wesentliche Elemente, aus dem der geometrische Körper besteht. Diese beinhalten:

Bei Geometrieproblemen kann man manchmal auf das Konzept eines Abschnitts stoßen. Die Definition wird so klingen: Ein Abschnitt sind alle Punkte eines volumetrischen Körpers, die zu einer Schnittebene gehören. Der Schnitt kann senkrecht sein (schneidet die Kanten der Figur in einem Winkel von 90 Grad). Für ein rechteckiges Prisma wird auch ein diagonaler Abschnitt berücksichtigt (die maximale Anzahl der konstruierbaren Abschnitte beträgt 2), der durch 2 Kanten und die Diagonalen der Basis verläuft.

Wird der Schnitt so gezeichnet, dass die Schnittebene weder zu den Grundflächen noch zu den Seitenflächen parallel ist, entsteht ein Prismenstumpf.

Um die reduzierten prismatischen Elemente zu finden, werden verschiedene Beziehungen und Formeln verwendet. Einige davon sind aus dem Planimetriekurs bekannt (um beispielsweise die Grundfläche eines Prismas zu ermitteln, genügt es, sich an die Formel für die Fläche eines Quadrats zu erinnern).

Oberfläche und Volumen

Um das Volumen eines Prismas anhand der Formel zu bestimmen, müssen Sie die Fläche seiner Grundfläche und Höhe kennen:

V = Sbas h

Da die Grundfläche eines regelmäßigen tetraedrischen Prismas ein Quadrat mit einer Seite ist A, Sie können die Formel detaillierter schreiben:

V = a²·h

Wenn es sich um einen Würfel handelt – ein regelmäßiges Prisma mit gleicher Länge, Breite und Höhe – berechnet sich das Volumen wie folgt:

Um zu verstehen, wie man die Mantelfläche eines Prismas ermittelt, muss man sich dessen Entwicklung vorstellen.

Aus der Zeichnung ist ersichtlich, dass die Seitenfläche aus 4 gleichen Rechtecken besteht. Seine Fläche wird als Produkt aus dem Umfang der Basis und der Höhe der Figur berechnet:

Sside = Posn h

Berücksichtigen Sie, dass der Umfang des Quadrats gleich ist P = 4a, Die Formel hat die Form:

Sside = 4a h

Für Würfel:

Sseite = 4a²

Fläche berechnen Vollflächig eines Prismas müssen Sie zur Seitenfläche zwei Grundflächen hinzufügen:

Sfull = Sside + 2Smain

Bezogen auf ein viereckiges regelmäßiges Prisma sieht die Formel wie folgt aus:

Gesamt = 4a h + 2a²

Für die Oberfläche eines Würfels:

Sfull = 6a²

Wenn Sie das Volumen oder die Oberfläche kennen, können Sie die einzelnen Elemente eines geometrischen Körpers berechnen.

Finden von Prismenelementen

Oft gibt es Probleme, bei denen das Volumen angegeben ist oder der Wert der Mantelfläche bekannt ist, bei denen es notwendig ist, die Seitenlänge der Basis oder die Höhe zu bestimmen. In solchen Fällen können die Formeln abgeleitet werden:

• Basisseitenlänge: a = Sside / 4h = √(V / h);
• Höhe bzw. Seitenrippenlänge: h = Sside / 4a = V / a²;
• Grundfläche: Sbas = V/h;
• Seitenfläche: Seite gr = Seite / 4.

Um zu bestimmen, wie groß die Fläche des Diagonalabschnitts ist, müssen Sie die Länge der Diagonale und die Höhe der Figur kennen. Für ein Quadrat d = a√2. Daher:

Sdiag = ah√2

Um die Diagonale eines Prismas zu berechnen, verwenden Sie die Formel:

dprize = √(2a² + h²)

Um zu verstehen, wie man die gegebenen Zusammenhänge anwendet, können Sie einige einfache Aufgaben üben und lösen.

Beispiele für Probleme mit Lösungen

Hier finden Sie einige Aufgaben aus staatlichen Abschlussprüfungen in Mathematik.

Übung 1.

In einer Box, die die richtige Form hat viereckiges Prisma, Sand wird gegossen. Die Höhe des Sandspiegels beträgt 10 cm. Wie hoch wird der Sandpegel sein, wenn Sie ihn in einen Behälter derselben Form, aber mit doppelt so langem Boden, umfüllen?

Man sollte argumentieren auf die folgende Weise. Die Sandmenge im ersten und zweiten Behälter hat sich nicht verändert, d. h. das Volumen darin ist gleich. Sie können die Länge der Basis mit bezeichnen A. In diesem Fall beträgt das Volumen des Stoffes für das erste Kästchen:

V₁ = ha² = 10a²

Für die zweite Box beträgt die Länge der Basis 2a, aber die Höhe des Sandspiegels ist unbekannt:

V₂ = h (2a)² = 4ha²

Weil das V₁ = V₂, wir können die Ausdrücke gleichsetzen:

10a² = 4ha²

Nachdem wir beide Seiten der Gleichung um a² reduziert haben, erhalten wir:

Dadurch entsteht ein neuer Sandspiegel h = 10 / 4 = 2,5 cm.

Aufgabe 2.

ABCDA₁B₁C₁D₁ ist ein korrektes Prisma. Es ist bekannt, dass BD = AB₁ = 6√2. Finden Sie die Gesamtoberfläche des Körpers.

Um leichter zu verstehen, welche Elemente bekannt sind, können Sie eine Figur zeichnen.

Da es sich um ein regelmäßiges Prisma handelt, können wir daraus schließen, dass sich an der Basis ein Quadrat mit einer Diagonale von 6√2 befindet. Die Diagonale der Seitenfläche ist gleich groß, daher hat die Seitenfläche auch die Form eines Quadrats gleich der Grundfläche. Es stellt sich heraus, dass alle drei Dimensionen – Länge, Breite und Höhe – gleich sind. Wir können daraus schließen, dass ABCDA₁B₁C₁D₁ ein Würfel ist.

Die Länge einer beliebigen Kante wird durch eine bekannte Diagonale bestimmt:

a = d / √2 = 6√2 / √2 = 6

Die Gesamtoberfläche wird mit der Formel für einen Würfel ermittelt:

Sfull = 6a² = 6 6² = 216

Aufgabe 3.

Das Zimmer wird renoviert. Es ist bekannt, dass sein Boden die Form eines Quadrats mit einer Fläche von 9 m² hat. Die Raumhöhe beträgt 2,5 m. Wie hoch sind die geringsten Kosten für das Tapezieren eines Raumes, wenn 1 m² 50 Rubel kostet?

Da Boden und Decke Quadrate, also regelmäßige Vierecke, sind und seine Wände senkrecht zu horizontalen Flächen stehen, können wir daraus schließen, dass es sich um ein regelmäßiges Prisma handelt. Es ist notwendig, die Fläche seiner Seitenfläche zu bestimmen.

Die Länge des Raumes beträgt a = √9 = 3 M.

Der Bereich wird mit Tapeten abgedeckt Seitenteil = 4 3 2,5 = 30 m².

Die niedrigsten Tapetenkosten für diesen Raum betragen 50·30 = 1500 Rubel

Um Probleme mit einem rechteckigen Prisma zu lösen, reicht es daher aus, die Fläche und den Umfang eines Quadrats und eines Rechtecks ​​berechnen zu können sowie die Formeln zur Ermittlung des Volumens und der Oberfläche zu kennen.

So finden Sie die Fläche eines Würfels

Ein Zweig der Mathematik, der sich mit der Untersuchung der Eigenschaften verschiedener Figuren (Punkte, Linien, Winkel, zweidimensionale und dreidimensionale Objekte), ihrer Größe und befasst relative Position. Um den Unterricht zu erleichtern, wird die Geometrie in Planimetrie und Stereometrie unterteilt. IN… … Colliers Enzyklopädie

Geometrie von Räumen mit Dimensionen größer als drei; Der Begriff wird auf solche Räume angewendet, deren Geometrie ursprünglich für den Fall von drei Dimensionen entwickelt und dann erst auf die Anzahl der Dimensionen n>3 verallgemeinert wurde, hauptsächlich der euklidische Raum, ... ... Mathematische Enzyklopädie

Die N-dimensionale euklidische Geometrie ist eine Verallgemeinerung der euklidischen Geometrie auf einen Raum mit mehr Dimensionen. Obwohl der physische Raum dreidimensional ist und die menschlichen Sinne darauf ausgelegt sind, drei Dimensionen wahrzunehmen, ist N dimensional... ... Wikipedia

Dieser Begriff hat andere Bedeutungen, siehe Pyramidatsu (Bedeutungen). Die Zuverlässigkeit dieses Abschnitts des Artikels wurde in Frage gestellt. Sie müssen die Richtigkeit der in diesem Abschnitt genannten Fakten überprüfen. Möglicherweise gibt es Erklärungen auf der Diskussionsseite ... Wikipedia

- (Constructive Solid Geometry, CSG) Technologie zur Modellierung fester Körper. Konstruktive Blockgeometrie ist oft, aber nicht immer, die Methode zur Modellierung in 3D-Grafiken und CAD. Es ermöglicht Ihnen, eine komplexe Szene zu erstellen oder... Wikipedia

Constructive Solid Geometry (CSG) ist eine Technologie, die bei der Volumenmodellierung verwendet wird. Konstruktive Blockgeometrie ist oft, aber nicht immer, die Methode zur Modellierung in 3D-Grafiken und CAD. Sie... ... Wikipedia

Dieser Begriff hat andere Bedeutungen, siehe Volumen (Bedeutungen). Das Volumen ist eine additive Funktion einer Menge (eines Maßes), die die Kapazität des Raumbereichs charakterisiert, den sie einnimmt. Ursprünglich entstand und wurde ohne strenge... ... Wikipedia angewendet

Würfeltyp Regelmäßiges Polyeder Fläche Quadrat Eckpunkte Kanten Flächen ... Wikipedia

Das Volumen ist eine additive Funktion einer Menge (eines Maßes), die die Kapazität des Raumbereichs charakterisiert, den sie einnimmt. Ursprünglich entstand und wurde es ohne strenge Definition in Bezug auf dreidimensionale Körper des dreidimensionalen euklidischen Raums angewendet.... ... Wikipedia

Ein Teil des Raums, der durch eine Ansammlung einer endlichen Anzahl planarer Polygone (siehe GEOMETRIE) begrenzt wird, die so verbunden sind, dass jede Seite eines beliebigen Polygons eine Seite genau eines anderen Polygons ist (genannt... ... Colliers Enzyklopädie

Bücher

• Satz Tische. Geometrie. 10. Klasse. 14 Tabellen + Methodik, . Die Tabellen sind auf dickem bedrucktem Karton mit den Maßen 680 x 980 mm gedruckt. Das Kit enthält eine Broschüre mit methodische Empfehlungen für den Lehrer. Lehralbum mit 14 Blättern.…

Definition 1. Prismatische Oberfläche
Satz 1. Auf parallelen Abschnitten einer prismatischen Oberfläche
Definition 2. Senkrechter Abschnitt einer prismatischen Oberfläche
Definition 3. Prisma
Definition 4. Prismenhöhe
Definition 5. Rechtes Prisma
Satz 2. Die Fläche der Seitenfläche des Prismas

Parallelepiped:
Definition 6. Parallelepiped
Satz 3. Über den Schnittpunkt der Diagonalen eines Parallelepipeds
Definition 7. Rechter Parallelepiped
Definition 8. Rechteckiges Parallelepiped
Definition 9. Maße eines Parallelepipeds
Definition 10. Würfel
Definition 11. Rhomboeder
Satz 4. Auf den Diagonalen eines rechteckigen Parallelepipeds
Satz 5. Volumen eines Prismas
Satz 6. Volumen eines geraden Prismas
Satz 7. Volumen eines rechteckigen Parallelepipeds

Prisma ist ein Polyeder, dessen zwei Flächen (Grundflächen) in parallelen Ebenen liegen und dessen Kanten, die nicht in diesen Flächen liegen, parallel zueinander sind.
Andere Flächen als die Basen werden aufgerufen seitlich.
Die Seiten der Seitenflächen und Basen werden aufgerufen Prismenrippen, die Enden der Kanten heißen die Spitzen des Prismas. Seitliche Rippen Kanten, die nicht zu den Basen gehören, werden aufgerufen. Die Vereinigung von Seitenflächen heißt Seitenfläche des Prismas, und die Vereinigung aller Gesichter wird genannt die gesamte Oberfläche des Prismas. Prismenhöhe nennt man die Senkrechte, die vom Punkt der oberen Basis zur Ebene der unteren Basis fällt, oder die Länge dieser Senkrechten. Direktes Prisma ein Prisma genannt, in dem seitliche Rippen senkrecht zu den Ebenen der Basen. Richtig ein gerades Prisma genannt (Abb. 3), an dessen Basis liegt regelmäßiges Vieleck.

Bezeichnungen:
l - Seitenrippe;
P – Basisumfang;
S o - Grundfläche;
H - Höhe;
P^ - Umfang des senkrechten Abschnitts;
S b – seitliche Oberfläche;
V – Volumen;
S p ist die Fläche der Gesamtoberfläche des Prismas.

V=SH S p = S b + 2S o S b = P ^ l

Definition 1 . Eine prismatische Fläche ist eine Figur, die aus Teilen mehrerer Ebenen besteht, die parallel zu einer Geraden verlaufen und durch die Geraden begrenzt werden, entlang derer sich diese Ebenen nacheinander schneiden*; Diese Linien sind parallel zueinander und werden aufgerufen Kanten der prismatischen Oberfläche.
*Es wird angenommen, dass sich jeweils zwei aufeinanderfolgende Ebenen schneiden und dass die letzte Ebene die erste schneidet

Satz 1 . Abschnitte einer prismatischen Oberfläche durch zueinander parallele Ebenen (aber nicht parallel zu ihren Kanten) sind gleiche Polygone.
Seien ABCDE und A"B"C"D"E" Schnitte einer prismatischen Fläche durch zwei parallele Ebenen. Um sicherzustellen, dass diese beiden Polygone gleich sind, genügt es zu zeigen, dass die Dreiecke ABC und A"B"C" gleich sind gleich sind und die gleiche Drehrichtung haben und dass das Gleiche auch für die Dreiecke ABD und A"B"D", ABE und A"B"E" gilt. Aber die entsprechenden Seiten dieser Dreiecke sind parallel (zum Beispiel ist AC parallel zu AC), wie die Schnittlinie einer bestimmten Ebene mit zwei parallelen Ebenen; Daraus folgt, dass diese Seiten gleich sind (zum Beispiel ist AC gleich A"C"), wie gegenüberliegende Seiten eines Parallelogramms, und dass die von diesen Seiten gebildeten Winkel gleich sind und die gleiche Richtung haben.

Definition 2 . Ein senkrechter Abschnitt einer prismatischen Oberfläche ist ein Abschnitt dieser Oberfläche durch eine Ebene senkrecht zu ihren Kanten. Basierend auf dem vorherigen Satz sind alle senkrechten Abschnitte derselben prismatischen Oberfläche gleiche Polygone.

Definition 3 . Ein Prisma ist ein Polyeder, das durch eine prismatische Oberfläche und zwei zueinander parallele Ebenen (jedoch nicht parallel zu den Kanten der prismatischen Oberfläche) begrenzt wird.
Die in diesen letzten Ebenen liegenden Gesichter werden aufgerufen Prismenbasen; Flächen, die zur prismatischen Oberfläche gehören - Seitenflächen; Kanten der prismatischen Oberfläche - Seitenrippen des Prismas. Aufgrund des vorherigen Satzes ist die Basis des Prismas gleiche Polygone. Alle Seitenflächen des Prismas - Parallelogramme; alle Seitenrippen sind einander gleich.
Wenn die Basis des Prismas ABCDE und eine der Kanten AA" in Größe und Richtung angegeben sind, ist es natürlich möglich, ein Prisma zu konstruieren, indem die Kanten BB", CC", ... gleich und parallel zur Kante AA" gezeichnet werden. .

Definition 4 . Die Höhe eines Prismas ist der Abstand zwischen den Ebenen seiner Grundflächen (HH").

Definition 5 . Ein Prisma heißt gerade, wenn seine Grundflächen senkrechte Abschnitte der Prismenfläche sind. In diesem Fall ist die Höhe des Prismas natürlich gleich seitliche Rippe; Die Seitenkanten werden sein Rechtecke.
Prismen können nach der Anzahl der Seitenflächen klassifiziert werden. gleiche Anzahl Seiten des Polygons, das als Basis dient. Somit können Prismen dreieckig, viereckig, fünfeckig usw. sein.

Satz 2 . Die Fläche der Seitenfläche des Prismas ist gleich dem Produkt aus Seitenkante und Umfang des senkrechten Abschnitts.
Sei ABCDEA"B"C"D"E" ein gegebenes Prisma und abcde seinen senkrechten Abschnitt, so dass die Segmente ab, bc, .. senkrecht zu seinen Seitenkanten stehen. Die Fläche ABA"B" ist ein Parallelogramm; ihre Fläche ist gleich dem Produkt der Basis AA " zu einer Höhe, die mit ab übereinstimmt; die Fläche der Fläche ВСВ „С“ ist gleich dem Produkt der Grundfläche ВВ“ mit der Höhe bc usw. Folglich ist die Seitenfläche (d. h. die Summe der Flächen der Seitenflächen) gleich dem Produkt der Seitenkante, also die Gesamtlänge der Segmente AA", ВВ", .., für den Betrag ab+bc+cd+de+ea.

Die Basis des Prismas kann ein beliebiges Polygon sein – Dreieck, Viereck usw. Beide Basen sind absolut identisch und dementsprechend auch die Winkel parallele Flächen sind miteinander verbunden und verlaufen immer parallel. An der Basis eines regelmäßigen Prismas liegt ein regelmäßiges Vieleck, also eines, bei dem alle Seiten gleich sind. Bei einem geraden Prisma stehen die Rippen zwischen den Seitenflächen senkrecht zur Grundfläche. In diesem Fall kann die Basis eines geraden Prismas ein Polygon mit beliebig vielen Winkeln enthalten. Ein Prisma, dessen Basis ein Parallelogramm ist, wird Parallelepiped genannt. Ein Rechteck ist ein Sonderfall eines Parallelogramms. Wenn diese Figur an der Basis liegt und die Seitenflächen im rechten Winkel zur Basis stehen, heißt das Parallelepiped rechteckig. Der zweite Name für diesen geometrischen Körper ist rechteckig.

Wie sieht sie aus

Rechteckige Prismen umgeben moderner Mann ziemlich viel. Dies ist beispielsweise gewöhnlicher Karton für Schuhe, Computerkomponenten usw. Umschauen. Selbst in einem Raum werden Sie wahrscheinlich viele rechteckige Prismen sehen. Dazu gehören ein Computergehäuse, ein Bücherregal, ein Kühlschrank, ein Kleiderschrank und viele andere Gegenstände. Die Form ist vor allem deshalb äußerst beliebt, weil Sie damit Ihren Raum optimal nutzen können, egal ob Sie Ihr Interieur dekorieren oder Dinge vor dem Umzug in Pappe verpacken.

Eigenschaften eines rechteckigen Prismas

Ein rechteckiges Prisma hat eine Reihe spezifischer Eigenschaften. Als Flächenpaar kann jedes beliebige Flächenpaar dienen, da alle angrenzenden Flächen im gleichen Winkel zueinander stehen und dieser Winkel 90° beträgt. Das Volumen und die Oberfläche eines rechteckigen Prismas sind einfacher zu berechnen als bei jedem anderen. Nehmen Sie einen beliebigen Gegenstand, der die Form eines rechteckigen Prismas hat. Messen Sie seine Länge, Breite und Höhe. Um das Volumen zu ermitteln, multiplizieren Sie einfach diese Maße. Das heißt, die Formel sieht so aus: V=a*b*h, wobei V das Volumen ist, a und b die Seiten der Basis sind, h die Höhe ist, die mit der Seitenkante dieses geometrischen Körpers zusammenfällt. Die Grundfläche wird nach der Formel S1=a*b berechnet. Für die Seitenfläche müssen Sie zunächst den Umfang der Basis mit der Formel P=2(a+b) berechnen und diesen dann mit der Höhe multiplizieren. Die resultierende Formel lautet S2=P*h=2(a+b)*h. Um die Gesamtoberfläche eines rechteckigen Prismas zu berechnen, addieren Sie das Doppelte der Grundfläche und der Seitenfläche. Die Formel lautet S=2S1+S2=2*a*b+2*(a+b)*h=2

Definition.

Dies ist ein Sechseck, dessen Grundflächen zwei gleiche Quadrate und dessen Seitenflächen gleiche Rechtecke sind

Seitliche Rippe- ist die gemeinsame Seite zweier benachbarter Seitenflächen

Prismenhöhe- Dies ist ein Segment senkrecht zur Basis des Prismas

Prismendiagonale- ein Segment, das zwei Eckpunkte der Basen verbindet, die nicht zur gleichen Fläche gehören

Diagonale Ebene- eine Ebene, die durch die Diagonale des Prismas und seine Seitenkanten verläuft

Diagonaler Abschnitt- die Grenzen des Schnittpunkts des Prismas und der Diagonalebene. Der diagonale Querschnitt eines regelmäßigen viereckigen Prismas ist ein Rechteck

Senkrechter Schnitt (orthogonaler Schnitt)- Dies ist der Schnittpunkt eines Prismas und einer Ebene, die senkrecht zu seinen Seitenkanten verläuft

Elemente eines regelmäßigen viereckigen Prismas

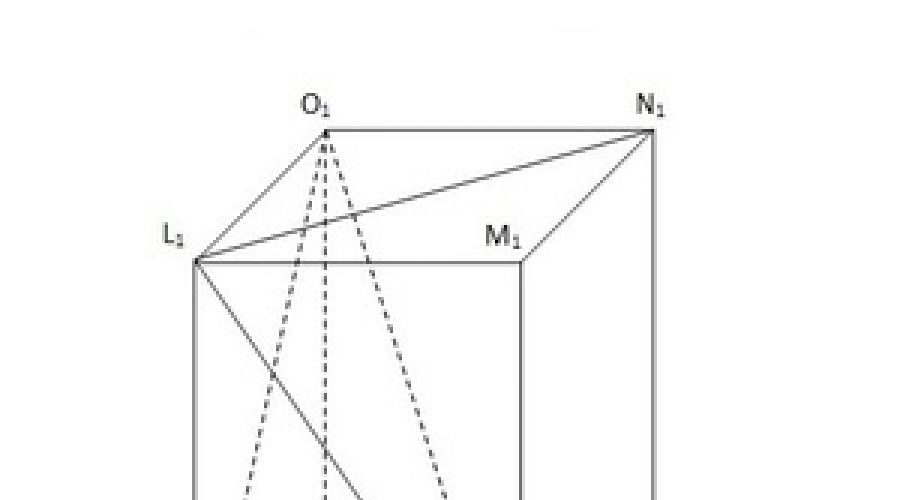
Die Abbildung zeigt zwei regelmäßige viereckige Prismen, die durch die entsprechenden Buchstaben gekennzeichnet sind:

• Die Basen ABCD und A 1 B 1 C 1 D 1 sind gleich und parallel zueinander
• Seitenflächen AA 1 D 1 D, AA 1 B 1 B, BB 1 C 1 C und CC 1 D 1 D, die jeweils ein Rechteck sind
• Seitenfläche- die Summe der Flächen aller Seitenflächen des Prismas
• Gesamtfläche – die Summe der Flächen aller Grundflächen und Seitenflächen (Summe der Fläche der Seitenfläche und Grundflächen)
• Seitenrippen AA 1, BB 1, CC 1 und DD 1.
• Diagonale B 1 D
• Basisdiagonale BD
• Diagonalschnitt BB 1 D 1 D
• Senkrechter Abschnitt A 2 B 2 C 2 D 2.

Eigenschaften eines regelmäßigen viereckigen Prismas

• Die Grundflächen sind zwei gleiche Quadrate
• Die Basen sind parallel zueinander
• Die Seitenflächen sind Rechtecke
• Die Seitenkanten sind einander gleich
• Seitenflächen stehen senkrecht zu den Basen
• Die seitlichen Rippen sind parallel zueinander und gleich
• Senkrechter Schnitt senkrecht zu allen Seitenrippen und parallel zu den Basen
• Winkel des senkrechten Abschnitts - gerade
• Der diagonale Querschnitt eines regelmäßigen viereckigen Prismas ist ein Rechteck
• Senkrecht (orthogonaler Schnitt) parallel zu den Basen

Formeln für ein regelmäßiges viereckiges Prisma

Anleitung zur Problemlösung

Bei der Lösung von Problemen zum Thema „ regelmäßiges viereckiges Prisma" bedeutet, dass:

Richtiges Prisma- ein Prisma, an dessen Basis ein regelmäßiges Vieleck liegt und dessen Seitenkanten senkrecht zu den Ebenen der Basis stehen. Das heißt, ein regelmäßiges viereckiges Prisma enthält an seiner Basis Quadrat. (siehe Eigenschaften eines regelmäßigen viereckigen Prismas oben) Notiz. Dies ist Teil einer Lektion mit Geometrieproblemen (Abschnitt Stereometrie – Prisma). Hier gibt es Probleme, die schwer zu lösen sind. Wenn Sie ein Geometrieproblem lösen müssen, das hier nicht aufgeführt ist, schreiben Sie im Forum darüber. Um die Aktion des Abrufens anzuzeigen Quadratwurzel Das Symbol wird zur Lösung von Problemen verwendet√ .

Aufgabe.

Bei einem regelmäßigen viereckigen Prisma beträgt die Grundfläche 144 cm 2 und die Höhe 14 cm. Ermitteln Sie die Diagonale des Prismas und die Gesamtoberfläche.

Lösung.
Ein regelmäßiges Viereck ist ein Quadrat.
Dementsprechend ist die Seite der Basis gleich

√144 = 12 cm.
Von dort aus ist die Diagonale der Basis eines regelmäßigen rechteckigen Prismas gleich
√(12 2 + 12 2 ) = √288 = 12√2

Die Diagonale eines regelmäßigen Prismas bildet sich aus der Diagonale der Grundfläche und der Höhe des Prismas rechtwinkliges Dreieck. Dementsprechend ist nach dem Satz des Pythagoras die Diagonale eines gegebenen regelmäßigen viereckigen Prismas gleich:
√((12√2) 2 + 14 2 ) = 22 cm

Antwort: 22 cm

Aufgabe

Bestimmen Sie die Gesamtoberfläche eines regelmäßigen viereckigen Prismas, wenn seine Diagonale 5 cm und die Diagonale seiner Seitenfläche 4 cm beträgt.

Lösung.
Da die Grundfläche eines regelmäßigen viereckigen Prismas ein Quadrat ist, ermitteln wir die Seite der Grundfläche (bezeichnet als a) mithilfe des Satzes des Pythagoras:

A 2 + a 2 = 5 2
2a 2 = 25
a = √12,5

Die Höhe der Seitenfläche (bezeichnet als h) ist dann gleich:

H 2 + 12,5 = 4 2
h 2 + 12,5 = 16
h2 = 3,5
h = √3,5

Die Gesamtoberfläche entspricht der Summe aus der Seitenoberfläche und dem Doppelten der Grundfläche

S = 2a 2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 cm 2.

Antwort: 25 + 10√7 ≈ 51,46 cm 2.