So lösen Sie die Multiplikation gemischter Brüche. Fraktion

Im Rahmen der Sekundar- und weiterführende Schule Die Studierenden beschäftigten sich mit dem Thema „Brüche“. Dieses Konzept ist jedoch viel umfassender als das, was im Lernprozess vermittelt wird. Heutzutage ist das Konzept eines Bruchs recht häufig anzutreffen, und nicht jeder kann einen beliebigen Ausdruck berechnen, beispielsweise durch Multiplizieren von Brüchen.

Was ist ein Bruch?

Historisch gesehen entstanden Bruchzahlen aus der Notwendigkeit des Messens. Wie die Praxis zeigt, gibt es oft Beispiele für die Bestimmung der Länge eines Segments und des Volumens eines rechteckigen Rechtecks.

Zunächst werden die Studierenden mit dem Konzept einer Aktie vertraut gemacht. Wenn Sie beispielsweise eine Wassermelone in 8 Teile teilen, erhält jede Person ein Achtel der Wassermelone. Dieser eine Teil von acht wird als Anteil bezeichnet.

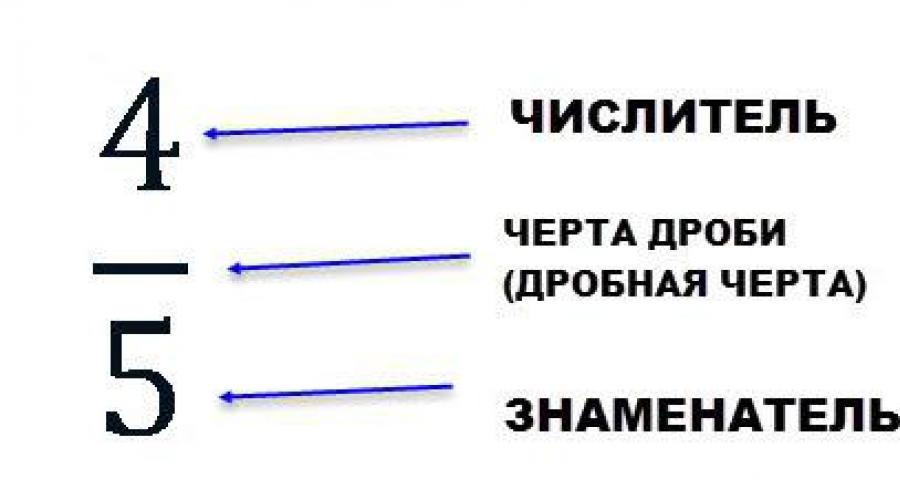
Ein Anteil, der der Hälfte eines beliebigen Wertes entspricht, wird als Hälfte bezeichnet; ⅓ - Drittel; ¼ - ein Viertel. Datensätze der Form 5/8, 4/5, 2/4 werden als gewöhnliche Brüche bezeichnet. Ein gewöhnlicher Bruch wird in einen Zähler und einen Nenner unterteilt. Dazwischen befindet sich der Bruchstrich oder Bruchstrich. Die Bruchlinie kann entweder als horizontale oder schräge Linie gezeichnet werden. In diesem Fall bezeichnet es das Divisionszeichen.

Der Nenner gibt an, in wie viele gleiche Teile die Menge oder das Objekt geteilt wird; und der Zähler gibt an, wie viele identische Aktien übernommen werden. Der Zähler steht über dem Bruchstrich, der Nenner steht darunter.

Am bequemsten ist es, gewöhnliche Brüche auf einem Koordinatenstrahl darzustellen. Wenn ein einzelnes Segment in 4 gleiche Teile unterteilt wird und jeder Teil mit einem lateinischen Buchstaben gekennzeichnet wird, kann das Ergebnis eine hervorragende visuelle Hilfe sein. Punkt A zeigt also einen Anteil von 1/4 des gesamten Einheitssegments und Punkt B markiert 2/8 eines bestimmten Segments.

Arten von Brüchen

Brüche können gewöhnliche, dezimale und gemischte Zahlen sein. Darüber hinaus können Brüche in echte und unechte Brüche unterteilt werden. Diese Klassifizierung eignet sich besser für gewöhnliche Brüche.

Ein echter Bruch ist eine Zahl, deren Zähler kleiner als ihr Nenner ist. Demnach ist ein unechter Bruch eine Zahl, deren Zähler größer als ihr Nenner ist. Der zweite Typ wird normalerweise als gemischte Zahl geschrieben. Dieser Ausdruck besteht aus einem ganzzahligen und einem gebrochenen Teil. Zum Beispiel 1½. 1 ist ein ganzzahliger Teil, ½ ist ein Bruchteil. Wenn Sie jedoch einige Manipulationen am Ausdruck vornehmen müssen (Brüche dividieren oder multiplizieren, reduzieren oder umwandeln), wird die gemischte Zahl in einen unechten Bruch umgewandelt.

Ein korrekter Bruchausdruck ist immer kleiner als eins und ein falscher immer größer oder gleich 1.

Mit diesem Ausdruck meinen wir einen Datensatz, in dem eine beliebige Zahl dargestellt wird, deren Nenner des Bruchausdrucks als Eins mit mehreren Nullen ausgedrückt werden kann. Wenn der Bruch richtig ist, ist der ganzzahlige Teil in der Dezimalschreibweise gleich Null.

Um einen Dezimalbruch zu schreiben, müssen Sie zuerst den ganzen Teil schreiben, ihn durch ein Komma vom Bruch trennen und dann den Bruchausdruck schreiben. Es ist zu beachten, dass der Zähler nach dem Dezimalpunkt genauso viele digitale Zeichen enthalten muss, wie Nullen im Nenner vorhanden sind.

Beispiel. Drücken Sie den Bruch 7 21 / 1000 in Dezimalschreibweise aus.

Algorithmus zur Umwandlung eines unechten Bruchs in eine gemischte Zahl und umgekehrt

Es ist falsch, in der Antwort auf eine Aufgabe einen unechten Bruch zu schreiben, daher muss er in eine gemischte Zahl umgewandelt werden:

• Teilen Sie den Zähler durch den vorhandenen Nenner.
• V konkretes Beispiel unvollständiger Quotient – ​​ganz;
• und der Rest ist der Zähler des Bruchteils, wobei der Nenner unverändert bleibt.

Beispiel. Wandeln Sie einen unechten Bruch in eine gemischte Zahl um: 47 / 5.

Lösung. 47: 5. Der Teilquotient ist 9, der Rest = 2. Also 47 / 5 = 9 2 / 5.

Manchmal müssen Sie eine gemischte Zahl als unechten Bruch darstellen. Dann müssen Sie den folgenden Algorithmus verwenden:

• der ganzzahlige Teil wird mit dem Nenner des Bruchausdrucks multipliziert;
• das resultierende Produkt wird zum Zähler addiert;
• das Ergebnis wird in den Zähler geschrieben, der Nenner bleibt unverändert.

Beispiel. Stellen Sie die Zahl in gemischter Form als unechten Bruch dar: 9 8 / 10.

Lösung. 9 x 10 + 8 = 90 + 8 = 98 ist der Zähler.

Antwort: 98 / 10.

Brüche multiplizieren

Mit gewöhnlichen Brüchen können verschiedene algebraische Operationen durchgeführt werden. Um zwei Zahlen zu multiplizieren, müssen Sie den Zähler mit dem Zähler und den Nenner mit dem Nenner multiplizieren. Darüber hinaus unterscheidet sich die Multiplikation von Brüchen mit unterschiedlichen Nennern nicht von der Multiplikation von Brüchen mit demselben Nenner.

Es kommt vor, dass Sie den Bruch reduzieren müssen, nachdem Sie das Ergebnis gefunden haben. Es ist unbedingt erforderlich, den resultierenden Ausdruck so weit wie möglich zu vereinfachen. Natürlich kann man nicht sagen, dass ein unechter Bruch in einer Antwort ein Fehler ist, aber es ist auch schwierig, ihn als richtige Antwort zu bezeichnen.

Beispiel. Finden Sie das Produkt zweier gewöhnlicher Brüche: ½ und 20/18.

Wie aus dem Beispiel ersichtlich ist, erhält man nach dem Finden des Produkts eine reduzierbare Bruchschreibweise. Sowohl der Zähler als auch der Nenner werden in diesem Fall durch 4 geteilt und das Ergebnis ist die Antwort 5 / 9.

Dezimalbrüche multiplizieren

Das Produkt von Dezimalbrüchen unterscheidet sich in seinem Prinzip deutlich vom Produkt gewöhnlicher Brüche. Die Multiplikation von Brüchen ist also wie folgt:

• zwei Dezimalbrüche müssen untereinander geschrieben werden, sodass die Ziffern ganz rechts untereinander liegen;
• Sie müssen die geschriebenen Zahlen trotz der Kommas multiplizieren, also als natürliche Zahlen;
• Zählen Sie die Anzahl der Nachkommastellen in jeder Zahl.
• in dem nach der Multiplikation erhaltenen Ergebnis müssen Sie von rechts so viele digitale Symbole zählen, wie in der Summe in beiden Faktoren nach dem Komma enthalten sind, und ein Trennzeichen setzen;
• Wenn das Produkt weniger Zahlen enthält, müssen Sie so viele Nullen davor schreiben, dass diese Zahl abgedeckt ist, ein Komma setzen und den ganzen Teil addieren, der Null ist.

Beispiel. Berechnen Sie das Produkt zweier Dezimalbrüche: 2,25 und 3,6.

Lösung.

Gemischte Brüche multiplizieren

Um das Produkt zweier gemischter Brüche zu berechnen, müssen Sie die Regel zum Multiplizieren von Brüchen verwenden:

• gemischte Zahlen in unechte Brüche umwandeln;
• Finden Sie das Produkt der Zähler.
• Finden Sie das Produkt der Nenner;
• schreibe das Ergebnis auf;
• Vereinfachen Sie den Ausdruck so weit wie möglich.

Beispiel. Finden Sie das Produkt aus 4½ und 6 2/5.

Eine Zahl mit einem Bruch multiplizieren (Brüche mit einer Zahl)

Neben der Bestimmung des Produkts zweier Brüche und gemischter Zahlen gibt es Aufgaben, bei denen Sie mit einem Bruch multiplizieren müssen.

Also, um das Produkt zu finden Dezimal und eine natürliche Zahl, Sie benötigen:

• Schreiben Sie die Zahl so unter den Bruch, dass die Ziffern ganz rechts übereinander liegen.
• das Produkt trotz Komma finden;
• Trennen Sie im resultierenden Ergebnis den ganzzahligen Teil vom Bruchteil durch ein Komma und zählen Sie von rechts die Anzahl der Ziffern, die sich nach dem Dezimalpunkt im Bruch befinden.

Um einen gewöhnlichen Bruch mit einer Zahl zu multiplizieren, müssen Sie das Produkt aus Zähler und natürlichem Faktor ermitteln. Ergibt die Antwort einen Bruch, der reduziert werden kann, muss dieser umgerechnet werden.

Beispiel. Berechnen Sie das Produkt aus 5 / 8 und 12.

Lösung. 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Antwort: 7 1 / 2.

Wie Sie dem vorherigen Beispiel entnehmen können, war es notwendig, das resultierende Ergebnis zu reduzieren und den falschen Bruchausdruck in eine gemischte Zahl umzuwandeln.

Bei der Multiplikation von Brüchen geht es auch darum, das Produkt einer Zahl in gemischter Form und eines natürlichen Faktors zu finden. Um diese beiden Zahlen zu multiplizieren, müssen Sie den ganzen Teil des gemischten Faktors mit der Zahl multiplizieren, den Zähler mit demselben Wert multiplizieren und den Nenner unverändert lassen. Bei Bedarf müssen Sie das resultierende Ergebnis so weit wie möglich vereinfachen.

Beispiel. Finden Sie das Produkt aus 9 5 / 6 und 9.

Lösung. 9 5 / 6 x 9 = 9 x 9 + (5 x 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.

Antwort: 88 1 / 2.

Multiplikation mit den Faktoren 10, 100, 1000 oder 0,1; 0,01; 0,001

Die folgende Regel ergibt sich aus dem vorherigen Absatz. Um einen Dezimalbruch mit 10, 100, 1000, 10000 usw. zu multiplizieren, müssen Sie den Dezimalpunkt um so viele Stellen nach rechts verschieben, wie im Faktor nach der Eins Nullen stehen.

Beispiel 1. Finden Sie das Produkt aus 0,065 und 1000.

Lösung. 0,065 x 1000 = 0065 = 65.

Antwort: 65.

Beispiel 2. Finden Sie das Produkt aus 3,9 und 1000.

Lösung. 3,9 x 1000 = 3,900 x 1000 = 3900.

Antwort: 3900.

Wenn Sie multiplizieren müssen natürliche Zahl und 0,1; 0,01; 0,001; B. 0,0001 usw., sollten Sie das Komma im resultierenden Produkt um so viele Ziffern nach links verschieben, wie Nullen vor der Eins stehen. Bei Bedarf werden ausreichend viele Nullen vor die natürliche Zahl geschrieben.

Beispiel 1. Finden Sie das Produkt aus 56 und 0,01.

Lösung. 56 x 0,01 = 0056 = 0,56.

Antwort: 0,56.

Beispiel 2. Finden Sie das Produkt aus 4 und 0,001.

Lösung. 4 x 0,001 = 0004 = 0,004.

Antwort: 0,004.

Das Finden des Produkts verschiedener Brüche sollte also keine Schwierigkeiten bereiten, außer vielleicht die Berechnung des Ergebnisses; In diesem Fall können Sie auf einen Taschenrechner einfach nicht verzichten.

Um einen Bruch mit einem Bruch oder einen Bruch mit einer Zahl richtig zu multiplizieren, müssen Sie es wissen einfache Regeln. Wir werden diese Regeln nun im Detail analysieren.

Einen gewöhnlichen Bruch mit einem Bruch multiplizieren.

Um einen Bruch mit einem Bruch zu multiplizieren, müssen Sie das Produkt der Zähler und das Produkt der Nenner dieser Brüche berechnen.

\(\bf \frac(a)(b) \times \frac(c)(d) = \frac(a \times c)(b \times d)\\\)

Schauen wir uns ein Beispiel an:
Wir multiplizieren den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs und multiplizieren außerdem den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs.

\(\frac(6)(7) \times \frac(2)(3) = \frac(6 \times 2)(7 \times 3) = \frac(12)(21) = \frac(4 \ mal 3)(7 \times 3) = \frac(4)(7)\\\)

Der Bruch \(\frac(12)(21) = \frac(4 \times 3)(7 \times 3) = \frac(4)(7)\\\) wurde um 3 reduziert.

Einen Bruch mit einer Zahl multiplizieren.

Erinnern wir uns zunächst an die Regel: Jede Zahl kann als Bruch \(\bf n = \frac(n)(1)\) dargestellt werden.

Lassen Sie uns diese Regel beim Multiplizieren verwenden.

\(5 \times \frac(4)(7) = \frac(5)(1) \times \frac(4)(7) = \frac(5 \times 4)(1 \times 7) = \frac (20)(7) = 2\frac(6)(7)\\\)

Unechter Bruch \(\frac(20)(7) = \frac(14 + 6)(7) = \frac(14)(7) + \frac(6)(7) = 2 + \frac(6)( 7)= 2\frac(6)(7)\\\) in einen gemischten Bruch umgewandelt.

Mit anderen Worten, Wenn wir eine Zahl mit einem Bruch multiplizieren, multiplizieren wir die Zahl mit dem Zähler und lassen den Nenner unverändert. Beispiel:

\(\frac(2)(5) \times 3 = \frac(2 \times 3)(5) = \frac(6)(5) = 1\frac(1)(5)\\\\\) \(\bf \frac(a)(b) \times c = \frac(a \times c)(b)\\\)

Gemischte Brüche multiplizieren.

Um gemischte Brüche zu multiplizieren, müssen Sie zunächst jeden gemischten Bruch als unechten Bruch darstellen und dann die Multiplikationsregel anwenden. Wir multiplizieren den Zähler mit dem Zähler und den Nenner mit dem Nenner.

Beispiel:
\(2\frac(1)(4) \times 3\frac(5)(6) = \frac(9)(4) \times \frac(23)(6) = \frac(9 \times 23) (4 \times 6) = \frac(3 \times \color(rot) (3) \times 23)(4 \times 2 \times \color(rot) (3)) = \frac(69)(8) = 8\frac(5)(8)\\\)

Multiplikation reziproker Brüche und Zahlen.

Der Bruch \(\bf \frac(a)(b)\) ist die Umkehrung des Bruchs \(\bf \frac(b)(a)\), vorausgesetzt a≠0,b≠0.
Die Brüche \(\bf \frac(a)(b)\) und \(\bf \frac(b)(a)\) heißen reziproke Brüche. Das Produkt der reziproken Brüche ist gleich 1.
\(\bf \frac(a)(b) \times \frac(b)(a) = 1 \\\)

Beispiel:
\(\frac(5)(9) \times \frac(9)(5) = \frac(45)(45) = 1\\\)

Verwandte Fragen:
Wie multipliziert man einen Bruch mit einem Bruch?
Antwort: Das Produkt gewöhnlicher Brüche ist die Multiplikation eines Zählers mit einem Zähler, eines Nenners mit einem Nenner. Um das Produkt gemischter Brüche zu erhalten, müssen Sie diese in einen unechten Bruch umwandeln und gemäß den Regeln multiplizieren.

Wie multipliziert man Brüche mit unterschiedlichen Nennern?
Antwort: Es spielt keine Rolle, ob Brüche den gleichen oder unterschiedliche Nenner haben, die Multiplikation erfolgt nach der Regel, das Produkt eines Zählers mit einem Zähler, eines Nenners mit einem Nenner zu finden.

Wie multipliziert man gemischte Brüche?
Antwort: Zuerst müssen Sie den gemischten Bruch in einen unechten Bruch umwandeln und dann das Produkt mithilfe der Multiplikationsregeln ermitteln.

Wie multipliziert man eine Zahl mit einem Bruch?
Antwort: Wir multiplizieren die Zahl mit dem Zähler, lassen aber den Nenner gleich.

Beispiel 1:
Berechnen Sie das Produkt: a) \(\frac(8)(9) \times \frac(7)(11)\) b) \(\frac(2)(15) \times \frac(10)(13) \ )

Lösung:
a) \(\frac(8)(9) \times \frac(7)(11) = \frac(8 \times 7)(9 \times 11) = \frac(56)(99)\\\\ \)
b) \(\frac(2)(15) \times \frac(10)(13) = \frac(2 \times 10)(15 \times 13) = \frac(2 \times 2 \times \color( rot) (5))(3 \times \color(rot) (5) \times 13) = \frac(4)(39)\)

Beispiel #2:
Berechnen Sie die Produkte einer Zahl und eines Bruchs: a) \(3 \times \frac(17)(23)\) b) \(\frac(2)(3) \times 11\)

Lösung:
a) \(3 \times \frac(17)(23) = \frac(3)(1) \times \frac(17)(23) = \frac(3 \times 17)(1 \times 23) = \frac(51)(23) = 2\frac(5)(23)\\\\\)
b) \(\frac(2)(3) \times 11 = \frac(2)(3) \times \frac(11)(1) = \frac(2 \times 11)(3 \times 1) = \frac(22)(3) = 7\frac(1)(3)\)

Beispiel #3:
Schreiben Sie den Kehrwert des Bruchs \(\frac(1)(3)\)?
Antwort: \(\frac(3)(1) = 3\)

Beispiel #4:
Berechnen Sie das Produkt zweier zueinander inverser Brüche: a) \(\frac(104)(215) \times \frac(215)(104)\)

Lösung:
a) \(\frac(104)(215) \times \frac(215)(104) = 1\)

Beispiel #5:
Können reziproke Brüche sein:
a) gleichzeitig mit echten Brüchen;
b) gleichzeitig unechte Brüche;
c) gleichzeitig natürliche Zahlen?

Lösung:
a) Um die erste Frage zu beantworten, geben wir ein Beispiel. Der Bruch \(\frac(2)(3)\) ist echt, sein Umkehrbruch ist gleich \(\frac(3)(2)\) – ein unechter Bruch. Antwort: Nein.

b) In fast allen Aufzählungen von Brüchen ist diese Bedingung nicht erfüllt, aber es gibt einige Zahlen, die die Bedingung erfüllen, gleichzeitig ein unechter Bruch zu sein. Der unechte Bruch ist beispielsweise \(\frac(3)(3)\), sein Umkehrbruch ist gleich \(\frac(3)(3)\). Wir erhalten zwei unechte Brüche. Antwort: Nicht immer unter bestimmten Bedingungen, wenn Zähler und Nenner gleich sind.

c) Natürliche Zahlen sind Zahlen, die wir beim Zählen verwenden, zum Beispiel 1, 2, 3, …. Wenn wir die Zahl \(3 = \frac(3)(1)\) nehmen, dann ist ihr Umkehrbruch \(\frac(1)(3)\). Der Bruch \(\frac(1)(3)\) ist keine natürliche Zahl. Wenn wir alle Zahlen durchgehen, ist der Kehrwert der Zahl immer ein Bruch, außer 1. Wenn wir die Zahl 1 nehmen, dann ist ihr Kehrwert \(\frac(1)(1) = \frac(1 )(1) = 1\). Nummer 1 ist eine natürliche Zahl. Antwort: Sie können nur in einem Fall gleichzeitig natürliche Zahlen sein, wenn es sich um die Zahl 1 handelt.

Beispiel #6:
Bilden Sie das Produkt gemischter Brüche: a) \(4 \times 2\frac(4)(5)\) b) \(1\frac(1)(4) \times 3\frac(2)(7)\ )

Lösung:
a) \(4 \times 2\frac(4)(5) = \frac(4)(1) \times \frac(14)(5) = \frac(56)(5) = 11\frac(1 )(5)\\\\ \)
b) \(1\frac(1)(4) \times 3\frac(2)(7) = \frac(5)(4) \times \frac(23)(7) = \frac(115)( 28) = 4\frac(3)(7)\)

Beispiel #7:
Können zwei Kehrwerte gleichzeitig gemischte Zahlen sein?

Schauen wir uns ein Beispiel an. Nehmen wir einen gemischten Bruch \(1\frac(1)(2)\, finden seinen Umkehrbruch und wandeln ihn dazu in einen unechten Bruch \(1\frac(1)(2) = \frac(3) um )(2) \) . Sein Umkehrbruch ist gleich \(\frac(2)(3)\) . Der Bruch \(\frac(2)(3)\) ist ein echter Bruch. Antwort: Zwei zueinander inverse Brüche können nicht gleichzeitig gemischte Zahlen sein.

Gewöhnliche Bruchzahlen begegnen Schulkindern erstmals in der 5. Klasse und begleiten sie ein Leben lang, da es im Alltag oft notwendig ist, einen Gegenstand nicht als Ganzes, sondern in Einzelteilen zu betrachten oder zu nutzen. Beginnen Sie mit dem Studium dieses Themas - Aktien. Aktien sind gleiche Teile, in die dieses oder jenes Objekt unterteilt ist. Schließlich ist es nicht immer möglich, beispielsweise die Länge oder den Preis eines Produkts als ganze Zahl auszudrücken; es sollten Teile oder Bruchteile eines Maßes berücksichtigt werden. Das Wort „Fraktion“ selbst entstand aus dem Verb „spalten“ – in Teile teilen und hat arabische Wurzeln. Es entstand im 8. Jahrhundert in der russischen Sprache.

Bruchausdrücke galten lange Zeit als der schwierigste Zweig der Mathematik. Als im 17. Jahrhundert die ersten Lehrbücher zur Mathematik erschienen, wurden sie „gebrochene Zahlen“ genannt, was für die Menschen sehr schwer zu verstehen war.

Moderner Look Einfache gebrochene Reste, deren Teile durch eine horizontale Linie getrennt sind, wurden zuerst von Fibonacci – Leonardo von Pisa – gefördert. Seine Werke werden auf das Jahr 1202 datiert. Der Zweck dieses Artikels besteht jedoch darin, dem Leser einfach und anschaulich zu erklären, wie gemischte Brüche mit unterschiedlichen Nennern multipliziert werden.

Brüche mit unterschiedlichen Nennern multiplizieren

Zunächst lohnt es sich zu bestimmen Arten von Brüchen:

• richtig;
• falsch;
• gemischt.

Als nächstes müssen Sie sich daran erinnern, wie Bruchzahlen mit demselben Nenner multipliziert werden. Die eigentliche Regel dieses Prozesses ist nicht schwer unabhängig zu formulieren: Das Ergebnis der Multiplikation einfacher Brüche mit identischen Nennern ist ein Bruchausdruck, dessen Zähler das Produkt der Zähler und der Nenner das Produkt der Nenner dieser Brüche ist . Das heißt, der neue Nenner ist tatsächlich das Quadrat eines der ursprünglich vorhandenen.

Beim Multiplizieren einfache Brüche mit unterschiedlichen Nennern Für zwei oder mehr Faktoren ändert sich die Regel nicht:

A/B * C/D = a*c / b*d.

Der einzige Unterschied besteht darin gebildete Zahl Unter der Bruchlinie befindet sich das Produkt verschiedener Zahlen und natürlich das Quadrat von Eins numerischer Ausdruck es ist unmöglich, es zu benennen.

Es lohnt sich, die Multiplikation von Brüchen mit unterschiedlichen Nennern anhand von Beispielen zu betrachten:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 <> 2*3 / 3*7 = 6/ 21 .

In den Beispielen werden Methoden zum Reduzieren gebrochener Ausdrücke verwendet. Sie können Zählerzahlen nur mit Nennerzahlen reduzieren; benachbarte Faktoren oberhalb oder unterhalb der Bruchlinie können nicht reduziert werden.

Neben einfachen Brüchen gibt es das Konzept der gemischten Brüche. Eine gemischte Zahl besteht aus einem ganzzahligen und einem gebrochenen Teil, ist also die Summe dieser Zahlen:

1 4/ 11 =1 + 4/ 11.

Wie funktioniert die Multiplikation?

Zur Betrachtung werden mehrere Beispiele bereitgestellt.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

Das Beispiel verwendet die Multiplikation einer Zahl mit gewöhnlicher Bruchteil, die Regel für diese Aktion kann wie folgt geschrieben werden:

A* B/C = a*b /C.

Tatsächlich ist ein solches Produkt die Summe identischer gebrochener Reste, und die Anzahl der Terme gibt diese natürliche Zahl an. Besonderer Fall:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Es gibt eine andere Lösung zum Multiplizieren einer Zahl mit einem gebrochenen Rest. Sie müssen nur den Nenner durch diese Zahl dividieren:

D* e/F = e/f: d.

Diese Technik ist nützlich, wenn der Nenner durch eine natürliche Zahl ohne Rest oder, wie man sagt, durch eine ganze Zahl dividiert wird.

Wandeln Sie gemischte Zahlen in unechte Brüche um und erhalten Sie das Produkt auf die zuvor beschriebene Weise:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

In diesem Beispiel geht es um die Darstellung eines gemischten Bruchs als unechten Bruch; er kann auch als dargestellt werden allgemeine Formel:

A BC = a*b+ c / c, wobei der Nenner des neuen Bruchs durch Multiplikation des ganzen Teils mit dem Nenner und Addition mit dem Zähler des ursprünglichen Bruchrests gebildet wird und der Nenner derselbe bleibt.

Dieser Vorgang funktioniert auch in Rückseite. Um den ganzen Teil und den gebrochenen Rest zu trennen, müssen Sie den Zähler eines unechten Bruchs durch seinen Nenner dividieren, indem Sie eine „Ecke“ verwenden.

Unechte Brüche multiplizieren in allgemein anerkannter Weise hergestellt werden. Wenn Sie unter eine einzelne Bruchlinie schreiben, müssen Sie die Brüche nach Bedarf kürzen, um die Zahlen mit dieser Methode zu reduzieren und die Berechnung des Ergebnisses zu erleichtern.

Im Internet gibt es viele Helfer, um auch komplexe mathematische Probleme in verschiedenen Programmvarianten zu lösen. Eine ausreichende Anzahl solcher Dienste bietet ihre Hilfe bei der Berechnung der Multiplikation von Brüchen mit unterschiedlichen Zahlen im Nenner an – sogenannte Online-Rechner zur Bruchrechnung. Sie können nicht nur multiplizieren, sondern auch alle anderen einfachen Rechenoperationen mit gewöhnlichen Brüchen und gemischten Zahlen ausführen. Es ist nicht schwierig, damit zu arbeiten: Sie füllen die entsprechenden Felder auf der Website-Seite aus, wählen das Vorzeichen der mathematischen Operation aus und klicken auf „Berechnen“. Das Programm rechnet automatisch.

Thema Rechenoperationen mit Bruchzahlen ist für die gesamte Ausbildung von Mittel- und Oberstufenschülern relevant. In der High School betrachten sie nicht mehr die einfachsten Arten, sondern ganzzahlige Bruchausdrücke, aber die zuvor erworbenen Kenntnisse der Transformations- und Berechnungsregeln werden in ihrer ursprünglichen Form angewendet. Gut beherrschtes Grundwissen gibt volle Sicherheit erfolgreiche Entscheidung am meisten komplexe Aufgaben.

Abschließend ist es sinnvoll, die Worte von Lew Nikolajewitsch Tolstoi zu zitieren, der schrieb: „Der Mensch ist ein Bruchteil. Es liegt nicht in der Macht eines Menschen, seinen Zähler – seine Verdienste – zu vergrößern, aber jeder kann seinen Nenner – seine Meinung über sich selbst – verkleinern und mit dieser Verkleinerung seiner Vollkommenheit näher kommen.

) und Nenner für Nenner (wir erhalten den Nenner des Produkts).

Formel zur Multiplikation von Brüchen:

Zum Beispiel:

Bevor Sie mit der Multiplikation von Zählern und Nennern beginnen, müssen Sie prüfen, ob der Bruch reduziert werden kann. Wenn Sie den Bruch reduzieren können, können Sie weitere Berechnungen einfacher durchführen.

Einen gemeinsamen Bruch durch einen Bruch dividieren.

Division von Brüchen mit natürlichen Zahlen.

Es ist nicht so beängstigend, wie es scheint. Wie bei der Addition wandeln wir die ganze Zahl in einen Bruch mit Eins im Nenner um. Zum Beispiel:

Gemischte Brüche multiplizieren.

Regeln zum Multiplizieren von Brüchen (gemischt):

• gemischte Brüche in unechte Brüche umwandeln;
• Multiplizieren der Zähler und Nenner von Brüchen;
• Reduziere den Bruch;
• Wenn Sie einen unechten Bruch erhalten, wandeln wir den unechten Bruch in einen gemischten Bruch um.

Beachten Sie! Um einen gemischten Bruch mit einem anderen gemischten Bruch zu multiplizieren, müssen Sie ihn zunächst in die Form unechter Brüche umwandeln und dann gemäß der Regel zur Multiplikation gewöhnlicher Brüche multiplizieren.

Die zweite Möglichkeit, einen Bruch mit einer natürlichen Zahl zu multiplizieren.

Möglicherweise ist es bequemer, die zweite Multiplikationsmethode zu verwenden gemeinsamer Bruch pro Nummer.

Beachten Sie! Um einen Bruch mit einer natürlichen Zahl zu multiplizieren, müssen Sie den Nenner des Bruchs durch diese Zahl dividieren und den Zähler unverändert lassen.

Aus dem obigen Beispiel wird deutlich, dass diese Option bequemer zu verwenden ist, wenn der Nenner eines Bruchs ohne Rest durch eine natürliche Zahl dividiert wird.

Mehrstöckige Brüche.

In der Oberstufe trifft man häufig auf dreistöckige (oder mehrstöckige) Brüche. Beispiel:

Um einen solchen Bruch in seine übliche Form zu bringen, verwenden Sie die Division durch 2 Punkte:

Beachten Sie! Bei der Division von Brüchen ist die Reihenfolge der Division sehr wichtig. Seien Sie vorsichtig, hier kann man leicht verwirrt werden.

Beachten Sie, Zum Beispiel:

Wenn man eins durch einen beliebigen Bruch dividiert, ist das Ergebnis derselbe Bruch, nur invertiert:

Praktische Tipps zum Multiplizieren und Dividieren von Brüchen:

1. Das Wichtigste bei der Arbeit mit gebrochenen Ausdrücken ist Genauigkeit und Aufmerksamkeit. Führen Sie alle Berechnungen sorgfältig und genau, konzentriert und klar durch. Es ist besser, ein paar zusätzliche Zeilen in Ihren Entwurf zu schreiben, als sich in gedanklichen Berechnungen zu verlieren.

2. Bei Aufgaben mit verschiedene Typen Brüche – gehen Sie zur Form gewöhnlicher Brüche über.

3. Wir reduzieren alle Brüche, bis eine Reduzierung nicht mehr möglich ist.

4. Wir wandeln mehrstufige Bruchausdrücke durch Division durch 2 Punkte in gewöhnliche um.

5. Teilen Sie im Kopf eine Einheit durch einen Bruch, indem Sie den Bruch einfach umdrehen.