Ce metode de setare a secvențe cunoașteți. Secvențe de numere

Este dată definiția unei secvențe numerice. Sunt luate în considerare exemple de secvențe infinit crescătoare, convergente și divergente. Se consideră o succesiune care conține toate numerele raționale.

Definiție .
Succesiunea numerică ( x n ) numită legea (regula), conform căreia, pentru fiecare număr natural n = 1, 2, 3, . . . i se atribuie un număr x n.
Elementul x n este numit al-lea membru sau un element al unei secvențe.

Secvența este notată ca al n-lea membru cuprins între paranteze: . Sunt posibile și următoarele denumiri: . Ele indică în mod explicit că indicele n aparține mulțimii numere naturale iar succesiunea în sine are un număr infinit de membri. Iată câteva exemple de secvențe:
, , .

Cu alte cuvinte, o secvență numerică este o funcție al cărei domeniu este mulțimea numerelor naturale. Numărul de elemente din succesiune este infinit. Printre elemente, pot fi și membri care au aceeași valoare. De asemenea, succesiunea poate fi considerată ca un set numerotat de numere, format dintr-un număr infinit de membri.

Ne va interesa în principal întrebarea - cum se comportă secvențele când n tinde spre infinit: . Acest material este prezentat în secțiunea Limită secvență - teoreme de bază și proprietăți. Și aici ne vom uita la câteva exemple de secvențe.

Exemple de secvențe

Exemple de secvențe infinit crescătoare

Să luăm în considerare o secvență. Termenul general al acestei secvențe este . Să scriem primii termeni:
.
Se poate observa că pe măsură ce numărul n crește, elementele cresc la nesfârșit spre valori pozitive. Putem spune că această secvență tinde spre : la .

Acum luați în considerare o secvență cu un termen comun. Iată câțiva dintre primii săi membri:
.
Pe măsură ce numărul n crește, elementele acestei secvențe cresc la nesfârșit în valoare absolută, dar nu au un semn constant. Adică această secvență tinde să : la .

Exemple de secvențe care converg către un număr finit

Să luăm în considerare o secvență. Membrul său comun Primii termeni sunt după cum urmează:
.
Se poate observa că pe măsură ce numărul n crește, elementele acestei secvențe se apropie de valoarea limită a = 0 : la . Deci, fiecare termen ulterior este mai aproape de zero decât cel anterior. Într-un fel, putem presupune că există o valoare aproximativă pentru numărul a = 0 cu o eroare. Este clar că pe măsură ce n crește, această eroare tinde spre zero, adică alegând n, eroarea poate fi făcută arbitrar mică. Mai mult, pentru orice eroare dată ε > 0 puteți specifica un număr N astfel încât pentru toate elementele cu numere mai mari decât N : , abaterea numărului de la valoare limită a nu va depăşi eroarea ε : .

Apoi, luați în considerare succesiunea. Membrul său comun Iată câțiva dintre primii săi membri:
.
În această secvență, termenii pari sunt zero. Membrii cu n impar sunt . Prin urmare, pe măsură ce n crește, valorile lor se apropie de valoarea limită a = 0 . Acest lucru rezultă și din faptul că
.
Ca și în exemplul anterior, putem specifica o eroare ε arbitrar mică > 0 , pentru care este posibil să se găsească un astfel de număr N încât elementele cu numere mai mari decât N se vor abate de la valoarea limită a = 0 cu o valoare care nu depăşeşte eroarea specificată. Prin urmare, această secvență converge către valoarea a = 0 : la .

Exemple de secvențe divergente

Luați în considerare o succesiune cu următorul termen comun:

Iată primii săi membri:


.
Se poate observa că termenii cu numere pare:
,
converg spre valoarea a 1 = 0 . Membrii cu numere impare:
,
converg spre valoarea a 2 = 2 . Secvența în sine, pe măsură ce n crește, nu converge către nicio valoare.

Secvență cu termeni distribuiți în intervalul (0;1)

Acum luați în considerare o secvență mai interesantă. Luați un segment pe linia numerică. Să o împărțim în jumătate. Obținem două segmente. Lăsa
.
Fiecare dintre segmente este din nou împărțit în jumătate. Obținem patru segmente. Lăsa
.
Împărțiți din nou fiecare segment în jumătate. Hai sa luam


.
Și așa mai departe.

Ca rezultat, obținem o succesiune ale cărei elemente sunt distribuite într-un interval deschis (0; 1) . Indiferent de punctul pe care îl luăm din intervalul închis , putem găsi întotdeauna membri ai secvenței care sunt în mod arbitrar aproape de acest punct sau care coincid cu acesta.

Apoi, din secvența originală se poate evidenția o subsecvență care va converge către un punct arbitrar din interval . Adică, pe măsură ce numărul n crește, membrii subsecvenței se vor apropia din ce în ce mai mult de punctul preselectat.

De exemplu, pentru punctul a = 0 puteți alege următoarea secvență:
.
= 0 .

Pentru punctul a = 1 alege urmatoarea urmarire:
.
Membrii acestei subsecvențe converg către valoarea a = 1 .

Întrucât există subsecvențe care converg către sensuri diferite, atunci secvența originală în sine nu converge către niciun număr.

Secvență care conține toate numerele raționale

Acum să construim o secvență care conține toate numerele raționale. Mai mult, fiecare număr rațional va fi inclus într-o astfel de secvență de un număr infinit de ori.

Numărul rațional r poate fi reprezentat astfel:
,
unde este un număr întreg; - naturală.
Trebuie să atribuim fiecărui număr natural n o pereche de numere p și q, astfel încât orice pereche de p și q să fie inclusă în succesiunea noastră.

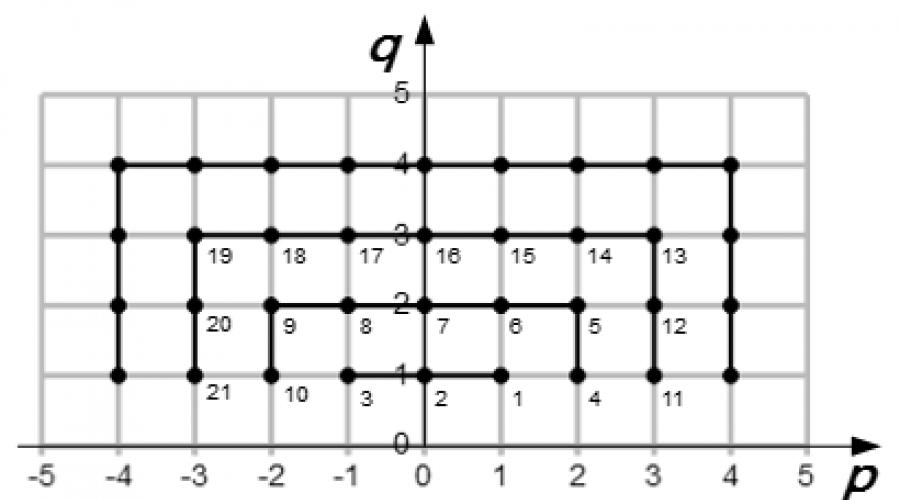
Pentru a face acest lucru, desenați axele p și q pe plan. Desenăm linii de grilă prin valori întregi p și q. Apoi fiecare nod al acestei grile va corespunde cu Numar rational. Întregul set de numere raționale va fi reprezentat printr-un set de noduri. Trebuie să găsim o modalitate de a numerota toate nodurile, astfel încât să nu pierdem niciun nod. Acest lucru este ușor de făcut dacă numerotăm nodurile în funcție de pătratele ale căror centre sunt situate în punct (0; 0) (Vezi poza). În acest caz, părțile inferioare ale pătratelor cu q < 1 nu avem nevoie. Prin urmare, ele nu sunt prezentate în figură.

Deci, pentru partea superioară a primului pătrat avem:
.
În continuare, numerotăm partea superioară a următorului pătrat:

.
Numerotăm partea superioară a pătratului următor:

.
Și așa mai departe.

În acest fel obținem o succesiune care conține toate numerele raționale. Se poate observa că orice număr rațional apare în această succesiune de un număr infinit de ori. Într-adevăr, împreună cu nodul , această secvență va include și noduri , unde este un număr natural. Dar toate aceste noduri corespund aceluiași număr rațional.

Apoi, din șirul pe care am construit-o, putem selecta o subsecvență (având un număr infinit de elemente), toate elementele care sunt egale cu un număr rațional predeterminat. Deoarece șirul pe care am construit-o are subsecvențe care converg către numere diferite, șirul nu converge către niciun număr.

Concluzie

Aici am dat o definiție precisă a secvenței numerice. Am atins și problema convergenței sale, bazată pe idei intuitive. Definiția exactă a convergenței este discutată la pagina Determinarea limitei unei secvențe. Proprietățile și teoremele înrudite sunt prezentate pe pagină

2. Determinați operație aritmetică, cu ajutorul căruia s-a obținut media din cele două numere extreme, iar în locul semnului * se introduce numărul care lipsește: ,3104.62.51043.60.94

3. Elevii au rezolvat sarcina în care se cere găsirea numerelor lipsă. Au primit răspunsuri diferite. Găsiți regulile după care băieții au completat celulele. Sarcină Răspuns 1 Răspuns

Definiţia unei secvenţe numerice Se spune că o secvenţă numerică este dată dacă, conform unei legi, unui anumit număr (un membru al şirului) este atribuit în mod unic oricărui număr natural (număr de loc). ÎN vedere generala corespondența indicată poate fi reprezentată astfel: y 1, y 2, y 3, y 4, y 5, …, y n, … … n … Numărul n este al n-lea membru al secvenței. Întreaga secvență este de obicei notă (y n).

Mod analitic de specificare a secvenţelor numerice O secvenţă este specificată analitic dacă se specifică formula celui de-al n-lea membru. De exemplu, 1) y n= n 2 - alocarea analitică a secvenței 1, 4, 9, 16, ... 2) y n= С - secvența constantă (staționară) 2) y n= 2 n - alocarea analitică a secvenței 2 , 4, 8, 16, … Rezolvați 585

Metoda recurentă de specificare a secvențelor numerice Metoda recurentă de specificare a unei secvențe este că acestea indică o regulă care vă permite să calculați al n-lea termen dacă membrii săi anteriori sunt cunoscuți 1) o progresie aritmetică este dată de relații recursive ) progresie geometrică– b 1 \u003d b, b n + 1 \u003d b n * q

Ancorare 591, 592 (a, b) 594, – 614 (a)

Delimitat superior Se spune că o secvență (y n) este mărginită de sus dacă toți membrii săi sunt cel mult un anumit număr. Cu alte cuvinte, o secvență (y n) este mărginită de sus dacă există un număr M astfel încât pentru orice n să fie valabilă inegalitatea y n M. M este limita superioară a șirului De exemplu, -1, -4, -9, -16, …, -n 2, …

Mărginită de jos O secvență (y n) se numește mărginită de jos dacă toți membrii ei sunt cel puțin un număr. Cu alte cuvinte, șirul (y n) este mărginit de sus dacă există un număr m astfel încât pentru orice n inegalitatea y n m să fie valabilă. m este limita inferioară a secvenței De exemplu, 1, 4, 9, 16, …, n 2, …

Mărginirea unei secvențe O secvență (y n) se numește mărginită dacă este posibil să se specifice două numere A și B între care se află toți membrii șirului. Inegalitatea Ay n B A este limita inferioară, B este limita superioară De exemplu, 1 este limita superioară, 0 este limita inferioară

Secvență descrescătoare O secvență se numește descrescătoare dacă fiecare membru este mai mic decât cel precedent: y 1 > y 2 > y 3 > y 4 > y 5 > ... > y n > ... De exemplu, y 2 > y 3 > y 4 > y 5 > … > y n > … De exemplu, „> y 2 > y 3 > y 4 > y 5 > … > y n > … De exemplu,”> y 2 > y 3 > y 4 > y 5 > … > y n > … De exemplu," title="Secvență descendentă O secvență se numește descrescătoare dacă fiecare dintre membrii săi este mai mic decât cel anterior: y 1 > y 2 > y 3 > y 4 > y 5 > … > y n > … De exemplu,"> title="Secvență descrescătoare O secvență se numește descrescătoare dacă fiecare membru este mai mic decât cel precedent: y 1 > y 2 > y 3 > y 4 > y 5 > ... > y n > ... De exemplu,"> !} 23

Lucrare de verificare Opțiunea 1Opțiunea 2 1. Succesul numeric este dat de formula a) Calculați primii patru termeni ai acestei secvențe b) Numărul este membru al șirului? b) Este numărul 12,25 un membru al succesiunii? 2. Formulați al treilea termen al șirului 2, 5, 10, 17, 26,…1, 2, 4, 8, 16,…

O secvență numerică este un caz special al unei funcții numerice, astfel încât o serie de proprietăți ale funcțiilor sunt de asemenea luate în considerare pentru secvențe.

1. Definiție . Urmărire ( y n} se numește crescător dacă fiecare dintre termenii săi (cu excepția primului) este mai mare decât cel anterior:

y 1 < y 2 < y 3 < … < y n < y n+1 < ….

2. Definiție.Secvență ( y n} se numește descrescător dacă fiecare dintre termenii săi (cu excepția primului) este mai mic decât cel anterior:

y 1 > y 2 > y 3 > … > y n> y n+1 > … .

3. Secvențele crescătoare și descrescătoare sunt unite printr-un termen comun - secvențe monotone.

De exemplu: y 1 = 1; y n= n 2... este o secvență crescătoare. y 1 = 1; este o secvență descendentă. y 1 = 1; – această secvență nu este necrescătoare nedescrescătoare.

4. Definiție. O secvență se numește periodică dacă există un număr natural T astfel încât, pornind de la un n, să fie valabilă egalitatea yn = yn+T. Numărul T se numește lungimea perioadei.

5. O secvență se numește mărginită de jos dacă toți membrii ei sunt cel puțin un număr.

6. Se spune că o secvență este mărginită de sus dacă toți membrii ei sunt cel mult un anumit număr.

7. O secvență se numește mărginită dacă este mărginită atât deasupra cât și dedesubt, adică. există un număr pozitiv astfel încât toți termenii secvenței date nu depășesc acest număr în valoare absolută. (Dar a fi limitat de ambele părți nu înseamnă neapărat că este finit.)

8. O secvență poate avea doar o limită.

9. Orice succesiune nedescrescătoare mărginită mai sus are o limită (lim).

10. Orice succesiune necrescătoare mărginită mai jos are o limită.

Limita secvenței este un punct (număr) în vecinătatea căruia se află majoritatea membrilor secvenței, se apropie foarte mult de această limită, dar nu o ating.

Geometric și progresie aritmetică sunt cazuri speciale ale secvenței.

Metode de secvențiere:

Secvențele pot fi specificate în diferite moduri, dintre care trei sunt deosebit de importante: analitice, descriptive și recurente.

1. Secvența este dată analitic dacă este dată formula celui de-al n-lea membru al său:

Exemplu. yn \u003d 2n - 1 - o succesiune de numere impare: 1, 3, 5, 7, 9, ...

2. O modalitate descriptivă de a seta o secvență numerică este aceea că explică din ce elemente este construită secvența.

Exemplul 1. „Toți membrii secvenței sunt egali cu 1”. Aceasta înseamnă că vorbim despre o secvență staționară 1, 1, 1, …, 1, ….

Exemplul 2. „Succesiunea constă din toate numere primeîn ordine crescătoare”. Astfel, este dată șirul 2, 3, 5, 7, 11, …. Cu această metodă de specificare a secvenței în acest exemplu este greu de răspuns cu ce este, să zicem, al 1000-lea element al secvenței.

3. Modul recurent de a specifica o secvență este că este indicată o regulă care permite calcularea al-lea membru secvența dacă membrii săi anteriori sunt cunoscuți. Denumirea de metodă recurentă provine din cuvântul latin recurrere - a reveni. Cel mai adesea, în astfel de cazuri, este indicată o formulă care permite exprimarea celui de-al n-lea membru al secvenței în termenii celor anterioare și sunt specificate 1–2 membri inițiali ai secvenței.

Exemplul 1. y1 = 3; yn = yn–1 + 4 dacă n = 2, 3, 4,….

Aici y1 = 3; y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….

Se poate observa că secvența obținută în acest exemplu poate fi specificată și analitic: yn = 4n – 1.

Exemplul 2 y 1 = 1; y 2 = 1; y n = y n–2 + y n-1 dacă n = 3, 4,….

Aici: y 1 = 1; y 2 = 1; y 3 = 1 + 1 = 2; y 4 = 1 + 2 = 3; y 5 = 2 + 3 = 5; y 6 = 3 + 5 = 8;

Secvența compusă în acest exemplu este studiată special în matematică deoarece are o serie de proprietăți și aplicații interesante. Se numește șirul Fibonacci - după matematicianul italian din secolul al XIII-lea. Definirea secvenței Fibonacci recursiv este foarte ușoară, dar analitic este foarte dificilă. n-al-lea număr Fibonacci este exprimat prin intermediul său număr de serie următoarea formulă.

La prima vedere, formula pentru n al-lea număr Fibonacci pare neplauzibil, deoarece formula care specifică succesiunea numerelor naturale conține numai rădăcini pătrate, dar puteți verifica „manual” validitatea acestei formule pentru primele câteva n.

Istoria lui Fibonacci:

Fibonacci (Leonardo din Pisa), c. 1175–1250

matematician italian. Născut la Pisa, a devenit primul mare matematician al Europei la sfârșitul Evului Mediu. Nevoia practică de a stabili contacte de afaceri a fost cea care l-a condus la matematică. Și-a publicat cărțile despre aritmetică, algebră și alte discipline matematice. De la matematicienii musulmani, a aflat despre sistemul de numere inventat în India și adoptat deja în lumea arabă și a fost convins de superioritatea acestuia (aceste numere au fost precursorii cifrelor arabe moderne).

Leonardo din Pisa, cunoscut sub numele de Fibonacci, a fost primul dintre marii matematicieni europeni ai Evului Mediu târziu. Născut la Pisa într-o familie de comercianți bogată, a intrat în matematică printr-o nevoie pur practică de a stabili contacte de afaceri. În tinerețe, Leonardo a călătorit mult, însoțindu-și tatăl în călătoriile de afaceri. De exemplu, știm despre șederea lui îndelungată în Bizanț și Sicilia. În astfel de călătorii, el a interacționat foarte mult cu oamenii de știință locali.

Secvența de numere care îi poartă astăzi numele a apărut din problema cu iepurii pe care Fibonacci a subliniat-o în Liber abacci, scris în 1202:

Un bărbat a pus o pereche de iepuri într-un tarc, înconjurat din toate părțile de un zid. Câte perechi de iepuri poate naște această pereche într-un an, dacă se știe că în fiecare lună, începând din a doua, fiecare pereche de iepuri produce câte o pereche?

Vă puteți asigura că numărul de cupluri din fiecare dintre următoarele douăsprezece luni ale lunilor va fi respectiv 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Cu alte cuvinte, numărul de perechi de iepuri creează o serie, fiecare termen în care este suma celor doi anteriori. Este cunoscut sub numele de seria Fibonacci și numerele în sine sunt numerele Fibonacci. Se pare că această secvență are multe proprietăți interesante din punct de vedere matematic. Iată un exemplu: puteți împărți o linie în două segmente, astfel încât raportul dintre segmentul mai mare și cel mai mic să fie proporțional cu raportul dintre întreaga linie și segmentul mai mare. Acest factor de proporționalitate, aproximativ egal cu 1,618, este cunoscut sub numele de raportul de aur. În Renaștere, se credea că aceasta era această proporție, observată în structuri arhitecturale cel mai plăcut ochiului. Dacă luați perechi Fibonacci consecutive și împărțiți numărul mai mare al fiecărei perechi la cel mai mic, rezultatul dvs. se va apropia treptat de raportul de aur.

De când Fibonacci și-a descoperit secvența, s-au găsit chiar și fenomene naturale în care această secvență pare să joace un rol important. Una dintre ele este filotaxia (aranjarea frunzelor) - regula conform căreia, de exemplu, semințele sunt situate într-o inflorescență de floarea soarelui. Semințele de floarea soarelui sunt aranjate în două spirale. Numerele care indică numărul de semințe din fiecare dintre spirale sunt membrii unei secvențe matematice uimitoare. Semințele sunt dispuse în două rânduri de spirale, dintre care unul merge în sensul acelor de ceasornic, celălalt împotriva. Și care este numărul de semințe în fiecare caz? 34 și 55.

Sarcina 1:

Scrieți primii cinci termeni ai șirului.

1. a n \u003d 2 n + 1/2 n

și n \u003d 2 n + 1/2 n

Sarcina numărul 2:

Scrieți formula termenului comun al unei șiruri de numere naturale care sunt multipli ai lui 3.

Răspuns: 0,3,6,9,12,15,.... 3n și n = 3n

Sarcina numărul 3:

Scrieți formula termenului comun al unei șiruri de numere naturale care, atunci când sunt împărțite la 4, au restul de 1.

Raspuns: 5,9,13,17,21....... 4 n +1 si n = 4n+1

nr. 19. Funcţie.

Funcția (afișare, operator, transformare) este un concept matematic care reflectă relația dintre elementele mulțimilor. Putem spune că o funcție este o „lege” conform căreia fiecărui element dintr-o mulțime (numit domeniul definiției) i se atribuie un element al altei mulțimi (numit domeniul valorilor).

O funcție este o dependență de una variabil din alta. Cu alte cuvinte, relația dintre cantități.

Conceptul matematic al unei funcții exprimă o idee intuitivă a modului în care o cantitate determină complet valoarea unei alte mărimi. Deci valoarea variabilei x determină în mod unic valoarea expresiei, iar valoarea lunii determină în mod unic valoarea lunii care o urmează, iar orice persoană poate fi comparată cu o altă persoană - tatăl său. În mod similar, un algoritm preconceput, având în vedere diferite date de intrare, produce anumite date de ieșire.

Adesea, termenul „funcție” se referă la o funcție numerică; adică o funcție care pune unele numere în corespondență cu altele. Aceste funcții sunt reprezentate convenabil în figuri sub formă de grafice.

Se poate da o altă definiție. O funcție este un specific acțiune peste o variabilă.

Aceasta înseamnă că luăm valoarea , facem o acțiune cu ea (de exemplu, o pătram sau îi calculăm logaritmul) - și obținem valoarea .

Să dăm o altă definiție a unei funcții - cea care se găsește cel mai des în manuale.

O funcție este o corespondență între două mulțimi, fiecare element din primul set corespunzând unuia și doar unui element al celui de-al doilea set.

De exemplu, funcția atribuie fiecărui număr real un număr de două ori mai mare decât .

Mulțimea elementelor unor F. substituite cu x se numește domeniul său de definiție, iar mulțimea elementelor y a unor F. se numește domeniul său de valori.

Istoricul termenului:

Termenul „funcție” (într-un sens oarecum mai restrâns) a fost folosit pentru prima dată de Leibniz (1692). La rândul său, Johann Bernoulli, într-o scrisoare către același Leibniz, a folosit acest termen într-un sens mai apropiat de cel modern. Inițial, conceptul de funcție nu se distingea de conceptul de reprezentare analitică. Ulterior, a apărut definiția funcției dată de Euler (1751), apoi - de Lacroix (1806) - aproape în formă modernă. In cele din urma, definiție generală funcții (în formă modernă, dar pentru funcții numerice) a fost dat de Lobaciovski (1834) și Dirichlet (1837). LA sfârşitul XIX-lea secolul, conceptul de funcție a depășit cadrul sistemelor numerice. Funcțiile vectoriale au fost primele care au făcut acest lucru, Frege a introdus curând funcțiile logice (1879), iar după apariția teoriei mulțimilor, Dedekind (1887) și Peano (1911) au formulat definiția universală modernă.

nr. 20. Modalități de a seta o funcție.

Există 4 moduri de a defini o funcție:

1. tabulară Destul de comun, este de a stabili o masă de individ

valorile argumentelor și valorile funcției corespunzătoare ale acestora. Această metodă de definire a unei funcții este utilizată atunci când domeniul funcției este o mulțime finită discretă.

Este convenabil când f este o mulțime finită, dar când f este infinită, sunt indicate doar perechile selectate (x, y).

Cu metoda tabelară de specificare a unei funcții, este posibil să se calculeze aproximativ valorile funcției care nu sunt conținute în tabel, corespunzătoare valorilor intermediare ale argumentului. Pentru a face acest lucru, utilizați metoda de interpolare.

Avantaje: precizie, viteza, usor de gasit in tabelul de valori valoarea dorită funcții. Avantajele modului tabelar de specificare a unei funcții sunt că face posibilă determinarea anumitor valori specifice imediat, fără măsurători sau calcule suplimentare.

Defecte: incompletitudine, lipsă de claritate. În unele cazuri, tabelul nu definește complet funcția, ci numai pentru unele valori ale argumentului și nu oferă o reprezentare vizuală a naturii modificării funcției în funcție de modificarea argumentului.

2. analitice(formule). Cel mai adesea, o lege care stabilește o legătură între

argument și funcție, este specificat prin intermediul formulelor. Acest mod de a defini o funcție se numește analitic. Este cea mai importantă pentru MA (analiza matematică), întrucât metodele MA (calcul diferențial, integral) sugerează acest mod de setare. Aceeași funcție poate fi dată diverse formule: y=∣sin( X)∣y=√1−cos2( X) Uneori, în diferite părți ale domeniilor lor, funcția în curs de definire poate fi dată prin diferite formule f(X)={f 1(X),X∈D 1 fn(X),X∈Dn ∪nk=1Dk=D(f). Adesea, cu această metodă de definire a unei funcții, domeniul definiției nu este indicat, atunci domeniul definiției este înțeles ca domeniul natural al definiției, adică. mulțimea tuturor valorilor x pentru care funcția ia o valoare reală.

Această metodă face posibil ca fiecare valoare numerică a argumentului x să găsească valoarea numerică corespunzătoare a funcției y exact sau cu o oarecare precizie.

Un caz special al modului analitic de definire a unei funcții este definirea unei funcții printr-o ecuație de forma F(x,y)=0 (1) Dacă această ecuație are proprietatea că ∀ X∈D se potrivește numai y, astfel încât F(X,y)=0, atunci spunem că ecuația (1) de pe D definește implicit o funcție. Un alt caz particular de definire a unei funcții este parametric, cu fiecare pereche ( X,y)∈f setați folosind o pereche de funcții X=ϕ( t),y=ψ( t) Unde t∈M.

SECVENȚE NUMERICE VI

§ 127. Secvențe de numereși cum să le setați. Secvențe finite și infinite.

Luați în considerare următoarele trei seturi de numere:

Este firesc să considerăm că fiecare număr din oricare dintre aceste colecții este prevăzut cu un număr în conformitate cu locul pe care îl ocupă în această colecție. De exemplu, în al doilea set, numărul 1 are numărul 1, numărul 1/2 are numărul 2, numărul 1/3 are numărul 3 și așa mai departe.

Dimpotrivă, indiferent de numărul am indicat, în fiecare dintre aceste colecții există un număr dotat cu acest număr. De exemplu, numărul 2 din prima secvență are numărul 2, în a doua - numărul - 1/2, în a treia - numărul sin 2. În mod similar, numărul 10 are: în prima secvență - numărul 10, în al doilea - numărul - 1/10, în al treilea - numărul păcatul 10 etc. Astfel, în seturile de mai sus, fiecare număr are un număr bine definit și este complet determinat de acest număr.

O colecție de numere, fiecare cu propriul său număr P (P = 1, 2, 3, ...) se numește șir de numere.

Numerele individuale ale unei secvențe se numesc membrii acesteia și sunt de obicei notate astfel: primul membru A 1 secunda A 2 , .... P al-lea membru A n etc.Se notează întreaga succesiune numerică

A 1 , A 2 , A 3 , ... , A n, ... sau ( A n }.

Specificați o succesiune numerică - aceasta înseamnă să indicați cum se găsește unul sau altul dintre membrii săi, dacă se cunoaște numărul locului ocupat de acesta. Există multe moduri diferite de a specifica secvențe numerice. Mai jos ne vom concentra asupra unora dintre ele.

1. De obicei, o secvență numerică este specificată folosind o formulă care vă permite să determinați acest membru după numărul unui membru al secvenței. De exemplu, dacă se știe că pentru oricare P

A n =n 2 ,

A 1 = 1, A 2 = 4, A 3 = 9

etc Când A n= păcat π / 2 P vom obține: A 1 = păcat π / 2 = 1, A 2 = păcat π = 0, A 3 = păcatul 3 π / 2 = - 1, A 4 = păcatul 2 π = 0 etc.

O formulă care vă permite să găsiți orice membru al unei secvențe numerice după numărul său se numește formula unui membru comun al unei secvențe numerice.

2. Există cazuri când o secvență este specificată prin descrierea membrilor săi. De exemplu, spuneți că secvența

1,4; 1,41; 1,414; 1,4142; ...

este compus din valori aproximative de √2 cu o deficiență cu o precizie de 0,1; 0,01; 0,001; 0,0001 etc. B cazuri similare uneori este imposibil să se stabilească formula generală a termenului; cu toate acestea, succesiunea se dovedește a fi complet determinată.

3. Uneori sunt indicați primii câțiva membri ai secvenței, iar toți ceilalți membri sunt determinați de acești membri dați în conformitate cu o regulă sau alta. Să, de exemplu,

A 1 = 1, A 2 = 1,

iar fiecare termen ulterior este definit ca suma celor doi anteriori. Cu alte cuvinte, pentru orice P > 3

A n = A n- 1 + A n- 2

Așa se determină șirul numeric 1, 1, 2, 3, 5, 8, 13, 21, 34, .... ai cărui membri se numesc „numere Fibonacci” [după matematicianul italian Leonard de Pisa ( circa 1170-1250), care a fost numit și Fibonacci, ceea ce înseamnă „fiul lui Bonaccio”]. Au multe proprietăți interesante, a căror considerare însă depășește sfera programului nostru.

O secvență poate conține fie un număr finit, fie un număr infinit de membri.

O secvență formată dintr-un număr finit de membri se numește o secvență finită, iar o secvență formată dintr-un număr infinit de membri este numită o secvență infinită.

De exemplu, succesiunea tuturor numerelor pozitive pare 2, 4, 6, 8, 10, 12, ... este infinită, în timp ce succesiunea numerelor pozitive pare cu o singură cifră 2, 4, 6, 8 este finită.

Exerciții

932. Scrieți primele 4 numere ale șirului cu un membru comun:

933. Găsiți formula generală a termenului pentru fiecare dintre secvențele date:

a) 1, 3, 5, 7, 9, ...; . e) tg 45°, tg 22°30", tg 11°15", ... ;

b) 2, 4, 6, 8, 10, ...; e) 1, - 1/2, 1/4, - 1/8, 1/16, ...;

c) 3, -3, 3, -3, 3, ...; g) 1, 9, 25, 49, 81.....

d) 1/3, 1/9, 1/27, 1/81, ....;

934. Secvența tuturor rădăcinilor pozitive ale ecuației este finită?

ca în x = x - 1; b) tg X = X ; c) păcatul x = ax + b ?

Lecția #32 Data ____________

Algebră

Clasa: 9 "B"

Subiect: „Secvență numerică și modalități de setare”.

Scopul lecției: elevii ar trebui să știe ce este o secvență de numere; modalități de a seta o secvență numerică; să poată distinge diferite căi atribuiri de secvente numerice.

Materiale didactice: fișe, note de referință.

Ajutoare tehnice de instruire: prezentare pe tema „Secvențe numerice”.

În timpul orelor.

1. Moment organizatoric.

2. Stabilirea scopurilor lecției.

Astăzi, în lecția pe care o veți învăța:

Ce este o secvență?

Ce fel de secvențe există?

Cum este specificată secvența de numere?

Aflați cum să scrieți o secvență folosind o formulă și numeroasele ei elemente.

Învață să găsești membrii unei secvențe.

3. Lucrați asupra materialului studiat.

3.1. Etapa pregătitoare.

Băieți, să vă testăm abilitățile de logică. Voi enumera câteva cuvinte și ar trebui să continuați:

-Luni Marți,…..

- Ianuarie februarie Martie…;

- Glebova L, Ganovichev E, Dryahlov V, Ibraeva G, ... .. (lista clasei);

–10,11,12,…99;

Din răspunsurile băieților, se ajunge la concluzia că sarcinile de mai sus sunt secvențe, adică un fel de serii ordonate de numere sau concepte, când fiecare număr sau concept este strict în locul lui, iar dacă membrii sunt schimbați, succesiunea va fi încălcat (marți, joi, luni este doar o listă a zilelor săptămânii). Deci, subiectul lecției este o succesiune numerică.

3.1. Explicarea noului material. (Material demonstrativ)

Analizând răspunsurile elevilor, definiți secvența de numere și arătați cum să setați secvențele de numere.

(Lucrul cu manualul pp. 66 - 67)

Definiția 1. Funcția y = f(x), xN se numește o funcție a unui argument natural sau a unei secvențe numerice și se notează: y = f(n) sau y 1 , y 2 , y 3 , ..., y n , ... sau (y n).

În acest caz, variabila independentă este un număr natural.

Cel mai adesea, secvențele vor fi notate după cum urmează: ( A n), (b n), (Cu n) etc.

Definiția 2. Membrii secvenței.

Elementele care formează o secvență se numesc membri ai secvenței.

Concepte noi: membrul anterior și ulterior al secvenței,

A 1 …A P. (primul și al n-lea membru al secvenței)

Metode de setare a unei secvențe numerice.

mod analitic.

Orice al n-lea element secvențele pot fi determinate folosind o formulă. (demo)

Analizați exemple

Exemplul 1 Sirul numerelor pare: y = 2n.

Exemplul 2 Sirul pătratului numerelor naturale: y = n 2 ;

1, 4, 9, 16, 25, ..., n 2 , ... .

Exemplul 3 Secvență staționară: y = C;

C, C, C, ..., C, ... .

Caz special: y = 5; 5, 5, 5, ..., 5, ... .

Exemplul 4. Secvența y = 2 n ;

2, 2 2 , 2 3 , 2 4 , ..., 2 n , ... .

mod verbal.

Regulile de stabilire a secvenței sunt descrise în cuvinte, fără a specifica formule sau când nu există modele între elementele secvenței.

Exemplul 1. Aproximații numericeπ.

Exemplul 2 Succesiunea numerelor prime: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... .

Exemplul 3 O succesiune de numere divizibile cu 5.

Exemplul 2 Set aleatoriu de numere: 1, 4, 12, 25, 26, 33, 39, ... .

Exemplul 3 Secvența numerelor pare 2, 4, 6, 8, 10, 12, 14, 16, ... .

mod recursiv.

Metoda recurentă constă în specificarea unei reguli care vă permite să calculați al n-lea membru al secvenței dacă sunt specificati primii câțiva membri ai acestuia (cel puțin un prim membru) și o formulă care vă permite să calculați următorul său membru din membrii anteriori. Termen recurent derivat din cuvântul latin se repetă , care înseamnă întoarce-te . Când calculăm membrii secvenței conform acestei reguli, ne cam întoarcem tot timpul, calculând următorul membru pe baza celui precedent. O caracteristică a acestei metode este că pentru a determina, de exemplu, al 100-lea membru al secvenței, trebuie mai întâi să determinați toți cei 99 de membri anteriori.

Exemplu 1 . a 1 \u003d a, a n + 1 \u003d a n +0,7. Fie a 1 =5, atunci secvența va arăta astfel: 5; 5,7; 6,4; 7,1; 7,8; 8,5; ... .

Exemplul 2 b 1 \u003d b, b n +1 \u003d ½ b n. Fie b 1 =23, atunci șirul va arăta astfel: 23; 11,5; 5,75; 2,875; ... .

Exemplul 3 Secvența Fibonacci. Această secvență este ușor de definit recursiv: y 1 =1, y 2 =1,y n -2 +y n -1 dacă n=3, 4, 5, 6, ... . Va arata ca:

1, 1,2, 3, 5, 8, 13, 21, 34, 55, ... . (P al treilea termen al acestei secvențe este egal cu suma celor doi termeni anteriori)

Este dificil de definit analitic șirul lui Fibonacci, dar este posibil. Formula prin care este determinat orice element al acestei secvențe arată astfel:

Informații suplimentare:

Negustorul italian Leonardo din Pisa (1180-1240), mai cunoscut sub porecla Fibonacci, a fost un important matematician medieval. Cu ajutorul acestei secvențe, Fibonacci a determinat numărul φ (phi); φ=1,618033989.

Mod grafic

Membrii unei secvențe pot fi reprezentați ca puncte pe planul de coordonate. Pentru a face acest lucru, numărul este reprezentat de-a lungul axei orizontale, iar valoarea membrului corespunzător al secvenței este reprezentată de-a lungul axei verticale.

Pentru a consolida metodele de atribuire, vă rog să oferiți mai multe exemple de secvențe care sunt specificate fie verbal, fie analitic, fie în mod recurent.

Tipuri de secvențe de numere

(Pe secvențele enumerate mai jos, sunt elaborate tipuri de secvențe).

Lucrul cu manualul p.69-70

1) Crescator - daca fiecare termen este mai mic decat urmatorul, i.e. A n A n +1.

2) Descrescator - daca fiecare termen este mai mare decat urmatorul, i.e. A n A n +1 .

3) Nesfârșit.

4) Ultima.

5) Alternand.

6) Constant (staționar).

O secvență crescătoare sau descrescătoare se numește monotonă.

3; 6; 9; 12; 15; 18;…

1. –1; 2; –3; 4; –5; …

   1, 4, 9, 16 ,…

   –1; 2; –3; 4; –5; 6; …

   3; 3; 3; 3; …; 3; … .

Lucrează cu manualul: fă-o oral nr. 150, 159 p. 71, 72

3.2. Consolidarea materialului nou. Rezolvarea problemelor.

Pentru consolidarea cunoștințelor se selectează exemple în funcție de nivelul de pregătire al elevilor.

Exemplul 1 Scrieți o formulă posibilă pentru al n-lea element al șirului (y n):

a) 1, 3, 5, 7, 9, 11, ...;

b) 4, 8, 12, 16, 20, ...;

Soluţie.

a) Este o succesiune de numere impare. Analitic, această secvență poate fi dată prin formula y = 2n+1.

b) Aceasta este o succesiune numerică în care elementul următor este mai mare decât precedentul cu 4. Analitic, această succesiune poate fi specificată prin formula y = 4n.

Exemplul 2. Scrieți primele zece elemente ale șirului dat în mod recurent: y 1 =1, y 2 =2, y n = y n -2 +y n -1 dacă n = 3, 4, 5, 6, ... .

Soluţie.

Fiecare element ulterior al acestei secvențe este egal cu suma celor două elemente anterioare.

Exemplul 3 Secvența (y n) este dată recurent: y 1 =1, y 2 =2,y n =5y n -1 - 6y n -2 . Specificați această secvență analitic.

Soluţie.

Găsiți primele câteva elemente ale secvenței.

y3 =5y2 -6y1 =10-6=4;

y 4 \u003d 5y 3 -6y 2 \u003d 20-12 \u003d 8;

y 5 \u003d 5y 4 -6y 3 \u003d 40-24 \u003d 16;

y 6 \u003d 5y 5 -6y 4 \u003d 80-48 \u003d 32;

y 7 \u003d 5y 6 -6y 5 \u003d 160-96 \u003d 64.

Obținem succesiunea: 1; 2; 4; 8; 16; 32; 64; ... care poate fi reprezentat ca

2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 ... .

n = 1; 2; 3; 4; 5; 6; 7... .

Analizând șirul, obținem următoarea regularitate: y = 2 n -1 .

Exemplul 4 Având în vedere o secvență y n =24n+36-5n 2 .

a) Câți termeni pozitivi are?

b) Aflați cel mai mare element al șirului.

c) Există un element cel mai mic în această secvență?

Această succesiune numerică este o funcție de forma y = -5x 2 +24x+36, unde x

a) Aflați valorile funcției pentru care -5x 2 +24x+360. Să rezolvăm ecuația -5x 2 +24x+36=0.

D \u003d b 2 -4ac \u003d 1296, X 1 \u003d 6, X 2 \u003d -1,2.

Ecuația axei de simetrie a parabolei y \u003d -5x 2 + 24x + 36 poate fi găsită prin formula x \u003d, obținem: x \u003d 2.4.

Inegalitatea -5x 2 +24x+360 este valabilă pentru -1,2 Acest interval conține cinci numere naturale (1, 2, 3, 4, 5). Deci există cinci elemente pozitive ale secvenței în secvența dată.

b) Cel mai mare element al secvenței este determinat prin metoda de selecție și este egal cu y 2 =64.

V) cel mai mic element Nu.

3.4.Sarcini pentru munca independentă