Semn de progresie. Progresii aritmetice și geometrice
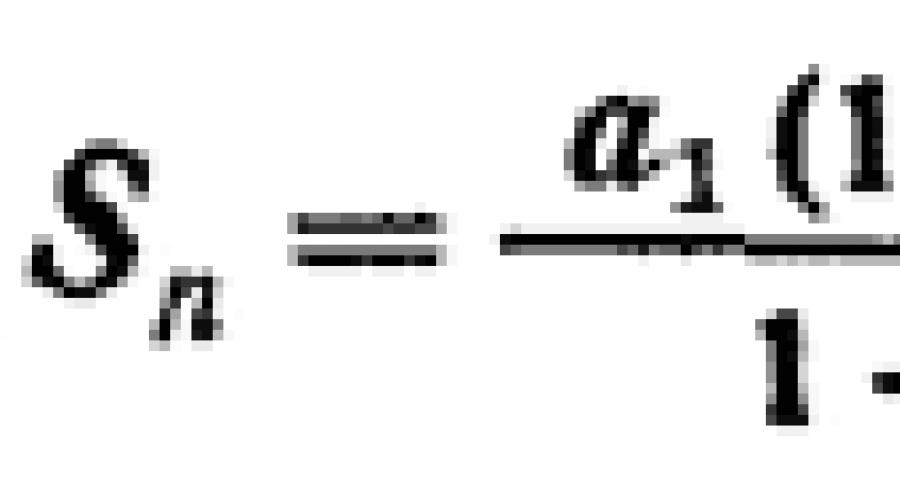
Citeste si
SECVENȚE NUMERICE VI
§ l48. Suma unei progresii geometrice infinit descrescătoare
Până acum, vorbind de sume, am presupus întotdeauna că numărul de termeni din aceste sume este finit (de exemplu, 2, 15, 1000 etc.). Dar atunci când rezolvi unele probleme (în special matematica superioară), trebuie să te ocupi de sumele unui număr infinit de termeni
S= A 1 + A 2 + ... + A n + ... . (1)
Care sunt aceste sume? A-prioriu suma unui număr infinit de termeni A 1 , A 2 , ..., A n , ... se numește limita sumei S n primul P numere când P -> ∞ :
S=S n = (A 1 + A 2 + ... + A n ). (2)
Limita (2), desigur, poate exista sau nu. În consecință, se spune că suma (1) există sau nu există.
Cum să aflăm dacă suma (1) există în fiecare caz particular? Decizie comună Această întrebare depășește cu mult scopul programului nostru. Cu toate acestea, există un caz special important pe care trebuie să îl luăm în considerare acum. Vom vorbi despre însumarea termenilor unei progresii geometrice infinit descrescătoare.
Lăsa A 1 , A 1 q , A 1 q 2 , ... este o progresie geometrică infinit descrescătoare. Aceasta înseamnă că | q |< 1. Сумма первых P membrii acestei progresii este egal cu
![]()
Din principalele teoreme limită variabile(vezi § 136) obținem:

Dar 1 = 1, a q n = 0. Prin urmare

Deci, suma unei progresii geometrice infinit descrescătoare este egală cu primul termen al acestui progres împărțit la unu minus numitorul acestei progresii.
1) Suma progresiei geometrice 1, 1/3, 1/9, 1/27, ... este

iar suma unei progresii geometrice este 12; -6; 3; - 3 / 2 , ... egal

2) O fracție periodică simplă 0,454545 ... se transformă într-una obișnuită.
Pentru a rezolva această problemă, reprezentăm această fracție ca o sumă infinită:
Partea dreaptă a acestei egalități este suma unei progresii geometrice infinit descrescătoare, al cărei prim termen este 45/100, iar numitorul este 1/100. De aceea

În modul descris, se poate obține regula generala conversia fracțiilor periodice simple în fracții obișnuite (vezi cap. II, § 38):
Pentru a converti o fracție periodică simplă într-una obișnuită, trebuie să faceți în felul următor: la numărător puneți perioada fracției zecimale, iar la numitor - un număr format din nouă luate de câte ori există cifre în perioada fracției zecimale.
3) Fracția periodică mixtă 0,58333 .... se transformă într-o fracție obișnuită.
Să reprezentăm această fracție ca o sumă infinită:
În partea dreaptă a acestei egalități, toți termenii, începând de la 3/1000, formează o progresie geometrică infinit descrescătoare, al cărei prim termen este 3/1000, iar numitorul este 1/10. De aceea

În modul descris, se poate obține și regula generală pentru conversia fracțiilor periodice mixte în fracții obișnuite (vezi Capitolul II, § 38). În mod deliberat, nu îl includem aici. Nu este nevoie să memorezi această regulă greoaie. Este mult mai util să știm că orice fracție periodică mixtă poate fi reprezentată ca suma unei progresii geometrice infinit descrescătoare și a unui număr. Și formula
pentru suma unei progresii geometrice infinit descrescătoare, trebuie, desigur, să ne amintim.
Ca exercițiu, vă invităm, pe lângă problemele nr. 995-1000 de mai jos, să apelați din nou la problema nr. 301 § 38.
Exerciții
995. Ce se numește suma unei progresii geometrice infinit descrescătoare?
996. Găsiți sume ale progresiilor geometrice infinit descrescătoare:

997. Pentru ce valori X progresie
![]()
scade la infinit? Găsiți suma unei astfel de progresii.
998. Într-un triunghi echilateral cu o latură A un nou triunghi este înscris prin conectarea punctelor medii ale laturilor sale; un nou triunghi este înscris în acest triunghi în același mod și așa mai departe la infinit.
a) suma perimetrelor tuturor acestor triunghiuri;
b) suma suprafețelor acestora.
999. Într-un pătrat cu o latură A un pătrat nou este înscris prin conectarea punctelor medii ale laturilor sale; un pătrat este înscris în acest pătrat în același mod și așa mai departe la infinit. Aflați suma perimetrelor tuturor acestor pătrate și suma ariilor lor.
1000. Faceți o progresie geometrică infinit descrescătoare, astfel încât suma ei să fie egală cu 25 / 4, iar suma pătratelor termenilor săi să fie egală cu 625 / 24.
Scopul lecției: introducerea elevilor într-un nou tip de succesiune - o progresie geometrică infinit descrescătoare.
Sarcini:
formularea ideii inițiale a limitei succesiunii numerice;
cunoașterea unui alt mod de conversie a fracțiilor periodice infinite în fracții obișnuite folosind formula pentru suma unei progresii geometrice infinit descrescătoare;
dezvoltarea calităților intelectuale ale personalității școlarilor, cum ar fi gândirea logică, capacitatea de acțiuni evaluative, generalizare;
educarea activității, asistență reciprocă, colectivism, interes pentru subiect.
Descarca:
Previzualizare:
Lecție aferentă „Progresie geometrică în scădere infinită” (algebră, clasa a 10-a)
Scopul lecției: introducerea elevilor într-un nou tip de succesiune – o progresie geometrică în scădere infinită.
Sarcini:
formularea ideii inițiale a limitei succesiunii numerice; cunoașterea unui alt mod de conversie a fracțiilor periodice infinite în fracții obișnuite folosind formula pentru suma unei progresii geometrice infinit descrescătoare;
dezvoltarea calităților intelectuale ale personalității școlarilor, cum ar fi gândirea logică, capacitatea de acțiuni evaluative, generalizare;
educarea activității, asistență reciprocă, colectivism, interes pentru subiect.
Echipament: clasa de calculatoare, proiector, ecran.
Tip de lecție: Lecție - stăpânirea unui subiect nou.
În timpul orelor
I. Org. moment. Mesaj despre subiectul și scopul lecției.
II. Actualizarea cunoștințelor elevilor.
În clasa a IX-a ai studiat progresiile aritmetice și geometrice.
Întrebări
1. Definiție progresie aritmetică.
(O progresie aritmetică este o succesiune în care fiecare membru,
Începând cu al doilea, este egal cu termenul anterior, adăugat cu același număr).
2. Formula n -al-lea membru al unei progresii aritmetice
3. Formula pentru suma primelor n membrii unei progresii aritmetice.
( sau )
4. Definirea unei progresii geometrice.
(O progresie geometrică este o succesiune de numere diferite de zero,
Fiecare termen al căruia, începând cu al doilea, este egal cu termenul anterior, înmulțit cu
același număr).
5. Formula n al treilea termen al unei progresii geometrice
6. Formula pentru suma primelor n membrii unei progresii geometrice.
7. Ce formule mai știi?
(, Unde ; ;
; , )
Sarcini
1. Progresia aritmetică este dată de formula a n = 7 - 4n. Găsiți un 10. (-33)
2. Progresie aritmetică a 3 = 7 și a 5 = 1 . Găsiți un 4. (4)
3. Progresie aritmetică a 3 = 7 și a 5 = 1 . Găsiți un 17. (-35)
4. Progresie aritmetică a 3 = 7 și a 5 = 1 . Găsiți S 17 . (-187)
5. Pentru o progresie geometricăgăsiți al cincilea termen.
6. Pentru o progresie geometrică găsiți al n-lea termen.
7. Exponenţial b 3 = 8 și b 5 = 2 . Găsiți b 4 . (4)
8. Exponenţial b 3 = 8 și b 5 = 2 . Găsiți b 1 și q .
9. Exponenţial b 3 = 8 și b 5 = 2 . Găsiți S 5 . (62)
III. Explorarea unui subiect nou(prezentare demonstrativă).
Să considerăm un pătrat cu latura egală cu 1. Să desenăm un alt pătrat, a cărui latură este jumătate din primul pătrat, apoi altul, a cărui latură este jumătate din al doilea, apoi următorul și așa mai departe. De fiecare dată când latura noului pătrat este jumătate din cea precedentă.
Ca rezultat, am obținut o succesiune de laturi ale pătratelorformând o progresie geometrică cu un numitor.
Și, ceea ce este foarte important, cu cât construim mai multe astfel de pătrate, cu atât latura pătratului va fi mai mică. De exemplu ,
Acestea. pe măsură ce numărul n crește, termenii progresiei se apropie de zero.
Cu ajutorul acestei figuri, mai poate fi luată în considerare o secvență.
De exemplu, succesiunea ariilor pătratelor:
Și, din nou, dacă n crește la nesfârșit, apoi zona se apropie de zero în mod arbitrar aproape.
Să luăm în considerare încă un exemplu. Un triunghi echilateral cu latura de 1 cm. Să construim următorul triunghi cu vârfuri în punctele mijlocii ale laturilor primului triunghi, conform teoremei liniei mediane a triunghiului - latura celui de-al 2-lea este egală cu jumătatea laturii primului, latura celui de-al 3-lea este jumătatea laturii lui. al 2-lea etc. Din nou obținem o succesiune de lungimi ale laturilor triunghiurilor.
La .
Dacă luăm în considerare o progresie geometrică cu numitor negativ.
Apoi, din nou, cu un număr tot mai mare n termenii progresiei se apropie de zero.
Să fim atenți la numitorii acestor secvențe. Peste tot numitorii au fost mai mici de 1 modulo.
Putem concluziona: o progresie geometrică va fi infinit descrescătoare dacă modulul numitorului său este mai mic de 1.
Lucru din față.
Definiție:
Progresie geometrică se numește infinit descrescătoare dacă modulul numitorului său este mai mic de unu..
Cu ajutorul definiției, este posibil să se rezolve întrebarea dacă o progresie geometrică este în scădere infinit sau nu.
Sarcină
Este succesiunea o progresie geometrică infinit descrescătoare dacă este dată de formula:
Soluţie:
Să găsim q.
; ; ; .
această progresie geometrică este infinit în scădere.
b) această succesiune nu este o progresie geometrică infinit descrescătoare.
Luați în considerare un pătrat cu latura egală cu 1. Împărțiți-l în jumătate, iar una dintre jumătăți în jumătate și așa mai departe. ariile tuturor dreptunghiurilor rezultate formează o progresie geometrică infinit descrescătoare:
Suma ariilor tuturor dreptunghiurilor obținute în acest fel va fi egală cu aria primului pătrat și egală cu 1.
Dar în partea stângă a acestei egalități se află suma unui număr infinit de termeni.
Luați în considerare suma primilor n termeni.
Conform formulei pentru suma primilor n termeni ai unei progresii geometrice, este egal cu.
Dacă n crește la nesfârșit, atunci
sau . Prin urmare, i.e. .
Suma unei progresii geometrice infinit descrescătoareexistă o limită de secvență S 1 , S 2 , S 3 , …, Sn , … .
De exemplu, pentru o progresie,
avem
Deoarece
Suma unei progresii geometrice infinit descrescătoarepoate fi găsit folosind formula.
III. Reflecție și consolidare(finalizarea sarcinilor).
№13; №14; №15(1,3); №16(1,3); №18(1,3); №19; №20.
IV. Rezumând.
Ce secvență v-ați întâlnit astăzi?
Definiți o progresie geometrică infinit descrescătoare.
Cum se demonstrează că o progresie geometrică este în scădere infinită?
Dați formula pentru suma unei progresii geometrice infinit descrescătoare.
V. Tema pentru acasă.
2. № 15(2,4); №16(2,4); 18(2,4).
Previzualizare:
Pentru a utiliza previzualizarea prezentărilor, creați un cont Google (cont) și conectați-vă: https://accounts.google.com
Subtitrările slide-urilor:
Toată lumea ar trebui să fie capabilă să gândească consecvent, să judece în mod concludent și să respingă concluziile greșite: un fizician și un poet, un tractorist și un chimist. E.Kolman În matematică, ar trebui să ne amintim nu formulele, ci procesele gândirii. VP Ermakov Este mai ușor să găsești pătratul unui cerc decât să depășești un matematician. Augustus de Morgan Ce știință ar putea fi mai nobilă, mai admirabilă, mai utilă omenirii decât matematica? Franklin
Progresie geometrică în scădere infinită Clasa 10
eu. Progresii aritmetice și geometrice. Întrebări 1. Definirea unei progresii aritmetice. O progresie aritmetică este o succesiune în care fiecare termen, începând cu al doilea, este egal cu termenul anterior adăugat aceluiași număr. 2. Formula celui de-al n-lea membru al unei progresii aritmetice. 3. Formula pentru suma primilor n membri ai unei progresii aritmetice. 4. Definirea unei progresii geometrice. O progresie geometrică este o succesiune de numere nenule, fiecare membru al cărora, începând cu al doilea, este egal cu membrul anterior înmulțit cu același număr 5. Formula celui de-al n-lea membru al unei progresii geometrice. 6. Formula pentru suma primilor n membri ai unei progresii geometrice.
II. Progresie aritmetică. Atribuții O progresie aritmetică este dată de formula a n = 7 – 4 n Aflați a 10 . (-33) 2. În progresia aritmetică a 3 = 7 și a 5 = 1 . Găsiți un 4. (4) 3. În progresia aritmetică a 3 = 7 și a 5 = 1 . Găsiți un 17. (-35) 4. În progresia aritmetică a 3 = 7 și a 5 = 1 . Găsiți S 17 . (-187)
II. Progresie geometrică. Sarcini 5. Pentru o progresie geometrică, găsiți al cincilea termen 6. Pentru o progresie geometrică, găsiți al n-lea termen. 7. Exponențial b 3 = 8 și b 5 = 2. Găsiți b 4 . (4) 8. În progresie geometrică b 3 = 8 și b 5 = 2 . Găsiți b 1 și q . 9. În progresie geometrică b 3 = 8 și b 5 = 2. Găsiți S 5 . (62)
definiție: Se spune că o progresie geometrică este infinit descrescătoare dacă modulul numitorului său este mai mic de unu.
Problema №1 Este succesiunea o progresie geometrică infinit descrescătoare, dacă este dată de formula: Rezolvare: a) această progresie geometrică este infinit descrescătoare. b) această succesiune nu este o progresie geometrică infinit descrescătoare.
Suma unei progresii geometrice infinit descrescătoare este limita șirului S 1 , S 2 , S 3 , …, S n , … . De exemplu, pentru o progresie, avem Deoarece suma unei progresii geometrice infinit descrescătoare poate fi găsită prin formula
Finalizarea sarcinilor Aflați suma unei progresii geometrice infinit descrescătoare cu primul termen 3, al doilea 0,3. 2. Nr. 13; nr. 14; manual, p. 138 3. Nr. 15 (1; 3); #16(1;3) #18(1;3); 4. Nr. 19; nr. 20.
Ce secvență v-ați întâlnit astăzi? Definiți o progresie geometrică infinit descrescătoare. Cum se demonstrează că o progresie geometrică este în scădere infinită? Dați formula pentru suma unei progresii geometrice infinit descrescătoare. Întrebări
Celebrul matematician polonez Hugo Steinghaus susține în glumă că există o lege care este formulată astfel: un matematician o va face mai bine. Și anume, dacă încredințezi două persoane, dintre care unul matematician, să facă orice lucrare pe care nu o cunosc, atunci rezultatul va fi întotdeauna următorul: matematicianul o va face mai bine. Hugo Steinghaus 14.01.1887-25.02.1972
Lecție și prezentare pe tema: „Secvențe de numere. Progresie geometrică”
Materiale suplimentare
Dragi utilizatori, nu uitați să lăsați comentariile, feedback-ul, sugestiile voastre! Toate materialele sunt verificate de un program antivirus.
Mijloace și simulatoare didactice în magazinul online „Integral” pentru clasa a 9-a
Puteri și rădăcini Funcții și grafice
Băieți, astăzi ne vom familiariza cu un alt tip de progresie.
Tema lecției de astăzi este progresia geometrică.
Progresie geometrică
Definiție. O succesiune numerică în care fiecare termen, începând de la al doilea, este egal cu produsul celui precedent și un număr fix, se numește progresie geometrică.Să definim secvența noastră recursiv: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
unde b și q sunt anumite numere date. Numărul q se numește numitorul progresiei.
Exemplu. 1,2,4,8,16… Progresie geometrică, în care primul membru este egal cu unu și $q=2$.
Exemplu. 8,8,8,8... O progresie geometrică al cărei prim termen este opt,
și $q=1$.
Exemplu. 3,-3,3,-3,3... O progresie geometrică al cărei prim termen este trei,
și $q=-1$.
Progresia geometrică are proprietățile monotonității.
Dacă $b_(1)>0$, $q>1$,
atunci secvența crește.
Dacă $b_(1)>0$, $0 Secvența este de obicei notă ca: $b_(1), b_(2), b_(3), ..., b_(n), ...$.
La fel ca într-o progresie aritmetică, dacă numărul de elemente dintr-o progresie geometrică este finit, atunci progresia se numește progresie geometrică finită.
$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Rețineți că dacă șirul este o progresie geometrică, atunci șirul de termeni pătrați este, de asemenea, o progresie geometrică. A doua secvență are primul termen $b_(1)^2$ și numitorul $q^2$.
Formula celui de-al n-lea membru al unei progresii geometrice
Progresia geometrică poate fi specificată și sub formă analitică. Să vedem cum se face:$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
Putem vedea cu ușurință modelul: $b_(n)=b_(1)*q^(n-1)$.
Formula noastră se numește „formula celui de-al n-lea membru al unei progresii geometrice”.
Să revenim la exemplele noastre.
Exemplu. 1,2,4,8,16... O progresie geometrică al cărei prim termen este egal cu unu,
și $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.
Exemplu. 16,8,4,2,1,1/2… O progresie geometrică al cărei prim termen este șaisprezece și $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.
Exemplu. 8,8,8,8... O progresie geometrică în care primul termen este opt și $q=1$.
$b_(n)=8*1^(n-1)=8$.
Exemplu. 3,-3,3,-3,3... O progresie geometrică al cărei prim termen este trei și $q=-1$.
$b_(n)=3*(-1)^(n-1)$.
Exemplu. Având în vedere o progresie geometrică $b_(1), b_(2), …, b_(n), … $.
a) Se știe că $b_(1)=6, q=3$. Găsiți $b_(5)$.
b) Se știe că $b_(1)=6, q=2, b_(n)=768$. Găsiți n.
c) Se știe că $q=-2, b_(6)=96$. Găsiți $b_(1)$.
d) Se știe că $b_(1)=-2, b_(12)=4096$. Găsiți q.
Soluţie.
a) $b_(5)=b_(1)*q^4=6*3^4=486$.
b) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$ deoarece $2^7=128 => n-1=7; n=8$.
c) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
d) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.
Exemplu. Diferența dintre al șaptelea și al cincilea membru al progresiei geometrice este 192, suma celui de-al cincilea și al șaselea membru al progresiei este 192. Aflați al zecelea membru al acestei progresii.
Soluţie.
Știm că: $b_(7)-b_(5)=192$ și $b_(5)+b_(6)=192$.
Mai știm: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Apoi:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
Avem un sistem de ecuații:
$\begin(cases)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(cases)$.
Echivalând, ecuațiile noastre obțin:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
Avem două soluții q: $q_(1)=2, q_(2)=-1$.
Înlocuiți succesiv în a doua ecuație:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ nicio soluție.
Am obținut că: $b_(1)=4, q=2$.
Să găsim al zecelea termen: $b_(10)=b_(1)*q^9=4*2^9=2048$.
Suma unei progresii geometrice finite
Să presupunem că avem o progresie geometrică finită. Să calculăm, ca și pentru o progresie aritmetică, suma membrilor săi.Să fie dată o progresie geometrică finită: $b_(1),b_(2),…,b_(n-1),b_(n)$.
Să introducem notația pentru suma membrilor săi: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
În cazul în care $q=1$. Toți membrii progresiei geometrice sunt egali cu primul membru, atunci este evident că $S_(n)=n*b_(1)$.
Luați în considerare acum cazul $q≠1$.
Înmulțiți suma de mai sus cu q.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Notă:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.
$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2) )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.
$S_(n)(q-1)=b_(n)*q-b_(1)$.
$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.
$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.
Am obținut formula pentru suma unei progresii geometrice finite.
Exemplu.
Aflați suma primilor șapte termeni ai unei progresii geometrice al cărei prim termen este 4 și numitorul este 3.
Soluţie.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.
Exemplu.
Aflați al cincilea membru al progresiei geometrice, care este cunoscut: $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$.
Soluţie.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.
$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
$-4095(q-1)=-3*(q^(n)-1)$.
$-4095(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
341$ q=1364$.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.
Proprietatea caracteristică a unei progresii geometrice
Băieți, având în vedere o progresie geometrică. Să luăm în considerare cei trei membri consecutivi ai săi: $b_(n-1),b_(n),b_(n+1)$.Noi stim aia:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Apoi:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
Dacă progresia este finită, atunci această egalitate este valabilă pentru toți termenii, cu excepția primului și ultimului.
Dacă nu se știe dinainte ce fel de succesiune are șirul, dar se știe că: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Apoi putem spune cu siguranță că aceasta este o progresie geometrică.
O secvență de numere este o progresie geometrică numai atunci când pătratul fiecăruia dintre termenii săi este egal cu produsul celor doi termeni vecini ai progresiei. Nu uitați că pentru o progresie finită această condiție nu este îndeplinită pentru primul și ultimul termen.
Să ne uităm la această identitate: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$ se numește medie numere geometrice a și b.
Modulul oricărui membru al unei progresii geometrice este egal cu media geometrică a celor două elemente adiacente acestuia.
Exemplu.
Găsiți x astfel încât $x+2; 2x+2; 3x+3$ au fost trei membri consecutivi ai unei progresii geometrice.
Soluţie.
Să folosim proprietatea caracteristică:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ și $x_(2)=-1$.
Înlocuiți secvențial în expresia originală, soluțiile noastre:
Cu $x=2$, am obținut succesiunea: 4;6;9 este o progresie geometrică cu $q=1.5$.
Cu $x=-1$, avem succesiunea: 1;0;0.
Răspuns: $x=2.$
Sarcini pentru soluție independentă
1. Aflați al optulea prim membru al progresiei geometrice 16; -8; 4; -2 ....2. Aflați al zecelea membru al progresiei geometrice 11,22,44….
3. Se știe că $b_(1)=5, q=3$. Găsiți $b_(7)$.
4. Se știe că $b_(1)=8, q=-2, b_(n)=512$. Găsiți n.
5. Aflați suma primilor 11 membri ai progresiei geometrice 3;12;48….
6. Găsiți x astfel încât $3x+4; 2x+4; x+5$ sunt trei membri consecutivi ai unei progresii geometrice.
Progresia geometrică este succesiune numerică, al cărui prim termen este diferit de zero, iar fiecare termen următor este egal cu termenul anterior înmulțit cu același număr diferit de zero.
Conceptul de progresie geometrică
Progresia geometrică se notează cu b1,b2,b3, …, bn, … .
Raportul dintre orice termen al erorii geometrice și termenul său anterior este egal cu același număr, adică b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Aceasta rezultă direct din definiția unei progresii aritmetice. Acest număr se numește numitorul unei progresii geometrice. De obicei, numitorul unei progresii geometrice este notat cu litera q.
Suma unei progresii geometrice infinite pentru |q|<1
O modalitate de a seta o progresie geometrică este de a stabili primul său termen b1 și numitorul erorii geometrice q. De exemplu, b1=4, q=-2. Aceste două condiții dau o progresie geometrică de 4, -8, 16, -32, … .
Dacă q>0 (q nu este egal cu 1), atunci progresia este o secvență monotonă. De exemplu, secvența, 2, 4,8,16,32, ... este o secvență crescătoare monoton (b1=2, q=2).
Dacă numitorul q=1 în eroarea geometrică, atunci toți membrii progresiei geometrice vor fi egali între ei. În astfel de cazuri, se spune că progresia este o secvență constantă.
Pentru ca șirul numeric (bn) să fie o progresie geometrică este necesar ca fiecare dintre membrii săi, începând de la al doilea, să fie media geometrică a membrilor învecinați. Adică, este necesar să se îndeplinească următoarea ecuație
(b(n+1))^2 = bn * b(n+2), pentru orice n>0, unde n aparține mulțimii numerelor naturale N.
Acum să punem (Xn) - o progresie geometrică. Numitorul progresiei geometrice q, cu |q|∞).
Dacă notăm acum cu S suma unei progresii geometrice infinite, atunci următoarea formulă va fi valabilă:
S=x1/(1-q).
Luați în considerare un exemplu simplu:
Aflați suma unei progresii geometrice infinite 2, -2/3, 2/9, - 2/27, ... .
Pentru a găsi S, folosim formula pentru suma unei progresii infinit aritmetice. |-1/3|< 1. x1 = 2. S=2/(1-(-1/3)) = 3/2.
Primul nivel
Progresie geometrică. Ghid cuprinzător cu exemple (2019)
Secvență numerică
Așa că hai să ne așezăm și să începem să scriem câteva numere. De exemplu:
Puteți scrie orice numere și pot fi câte doriți (în cazul nostru, ele). Indiferent câte numere am scrie, putem spune întotdeauna care dintre ele este primul, care este al doilea și tot așa până la ultimul, adică le putem numerota. Acesta este un exemplu de succesiune de numere:
Secvență numerică este un set de numere, fiecăruia cărora li se poate atribui un număr unic.
De exemplu, pentru secvența noastră:
Numărul atribuit este specific unui singur număr de secvență. Cu alte cuvinte, nu există trei numere secunde în succesiune. Al doilea număr (ca și al-lea număr) este întotdeauna același.
Numărul cu numărul se numește --lea membru al secvenței.
De obicei, numim întreaga secvență o literă (de exemplu,) și fiecare membru al acestei secvențe - aceeași literă cu un index, egală cu numărul acest membru: .
În cazul nostru:

Cele mai comune tipuri de progresie sunt aritmetice și geometrice. În acest subiect, vom vorbi despre al doilea tip - progresie geometrică.
De ce avem nevoie de o progresie geometrică și de istoria ei.
Chiar și în cele mai vechi timpuri, matematicianul italian, călugărul Leonardo din Pisa (mai bine cunoscut sub numele de Fibonacci), s-a ocupat de nevoile practice ale comerțului. Călugărul s-a confruntat cu sarcina de a determina cu ce cea mai mica cantitate greutățile pot cântări mărfurile? În scrierile sale, Fibonacci demonstrează că un astfel de sistem de ponderi este optim: Aceasta este una dintre primele situații în care oamenii au avut de-a face cu o progresie geometrică, despre care probabil ați auzit și despre care aveți cel puțin concept general. Odată ce ați înțeles pe deplin subiectul, gândiți-vă de ce un astfel de sistem este optim?
În prezent, în practica de viață, o progresie geometrică se manifestă la investirea fondurilor într-o bancă, când se percepe suma dobânzii la suma acumulată în cont pentru perioada anterioară. Cu alte cuvinte, dacă puneți bani pe un depozit la termen într-o bancă de economii, atunci într-un an depozitul va crește cu de la suma inițială, adică. noua sumă va fi egală cu contribuția înmulțită cu. Într-un alt an, această sumă va crește cu, i.е. suma obţinută în acel moment se înmulţeşte din nou cu şi aşa mai departe. O situație similară este descrisă în problemele de calcul așa-numitele interes compus- procentul se ia de fiecare data din suma care se afla in cont, tinand cont de dobanda anterioara. Despre aceste sarcini vom vorbi puțin mai târziu.
Există multe mai multe cazuri simple în care se aplică o progresie geometrică. De exemplu, răspândirea gripei: o persoană a infectat o persoană, ea, la rândul său, a infectat o altă persoană și, prin urmare, al doilea val de infecție - o persoană și ei, la rândul lor, au infectat o alta ... și așa mai departe. .
Apropo, o piramidă financiară, același MMM, este un calcul simplu și uscat în funcție de proprietățile unei progresii geometrice. Interesant? Să ne dăm seama.
Progresie geometrică.
Să presupunem că avem o secvență de numere:
Veți răspunde imediat că este ușor și numele unei astfel de secvențe este o progresie aritmetică cu diferența dintre membrii ei. Ce zici de asa ceva:

Dacă scadeți numărul anterior din următorul număr, atunci veți vedea că de fiecare dată când obțineți o nouă diferență (etc.), dar succesiunea există cu siguranță și este ușor de observat - fiecare număr următor este de ori mai mare decât precedentul!

Acest tip de secvență se numește progresie geometrică si este marcat.
O progresie geometrică ( ) este o succesiune numerică, al cărei prim termen este diferit de zero, iar fiecare termen, începând cu al doilea, este egal cu cel precedent, înmulțit cu același număr. Acest număr se numește numitorul unei progresii geometrice.
Constrângerile conform cărora primul termen ( ) nu este egal și nu sunt aleatorii. Să spunem că nu există, iar primul termen este încă egal, iar q este, hmm .. să, atunci rezultă:
De acord că aceasta nu este o progresie.
După cum înțelegeți, vom obține aceleași rezultate dacă este orice număr, altul decât zero, dar. În aceste cazuri, pur și simplu nu va exista o progresie, deoarece întreaga serie de numere va fi fie toate zerourile, fie un număr și toate restul zerouri.
Acum să vorbim mai detaliat despre numitorul unei progresii geometrice, adică despre.
Să repetăm: - acesta este un număr, de câte ori se schimbă fiecare termen ulterior progresie geometrică.
Ce crezi că ar putea fi? Așa este, pozitiv și negativ, dar nu zero (am vorbit despre asta puțin mai sus).
Să spunem că avem un pozitiv. Să fie în cazul nostru, a. Care este al doilea termen și? Puteți răspunde cu ușurință:
În regulă. În consecință, dacă, atunci toți membrii următori ai progresiei au același semn - ei pozitiv.
Dacă este negativ? De exemplu, a. Care este al doilea termen și?
Este o cu totul altă poveste
Încercați să numărați termenul acestei progresii. Cât ai primit? Eu am. Astfel, dacă, atunci alternează semnele termenilor progresiei geometrice. Adică, dacă vedeți o progresie cu semne alternante în membrii săi, atunci numitorul ei este negativ. Aceste cunoștințe vă pot ajuta să vă testați atunci când rezolvați probleme pe această temă.
Acum să exersăm puțin: încercați să determinați care secvențe numerice sunt o progresie geometrică și care sunt una aritmetică:
Am înţeles? Comparați răspunsurile noastre:
- Progresie geometrică - 3, 6.
- Progresie aritmetică - 2, 4.
- Nu este nici o progresie aritmetică, nici geometrică - 1, 5, 7.
Să revenim la ultima noastră progresie și să încercăm să-i găsim termenul în același mod ca în aritmetică. După cum probabil ați ghicit, există două moduri de a-l găsi.
Înmulțim succesiv fiecare termen cu.
Deci, al-lea membru al progresiei geometrice descrise este egal cu.
După cum ghiciți deja, acum voi înșivă veți obține o formulă care vă va ajuta să găsiți orice membru al unei progresii geometrice. Sau l-ai scos deja pentru tine, descriind cum să-l găsești pe al treilea membru în etape? Dacă da, atunci verificați corectitudinea raționamentului dvs.
Să ilustrăm acest lucru prin exemplul găsirii celui de-al-lea membru al acestei progresii:

Cu alte cuvinte:
Găsiți-vă valoarea unui membru al unei progresii geometrice date.
S-a întâmplat? Comparați răspunsurile noastre:
Atenție că ați obținut exact același număr ca în metoda anterioară, când am înmulțit succesiv cu fiecare membru anterior al progresiei geometrice.
Să încercăm să „depersonalizăm” această formulă - o aducem într-o formă generală și obținem:
Formula derivată este valabilă pentru toate valorile - atât pozitive, cât și negative. Verificați-l singur calculând termenii unei progresii geometrice cu următoarele condiții: , a.
ai numarat? Să comparăm rezultatele:
Sunteți de acord că ar fi posibil să găsiți un membru al progresiei în același mod ca un membru, cu toate acestea, există posibilitatea de a calcula greșit. Și dacă am găsit deja al treilea termen al unei progresii geometrice, a, atunci ce ar putea fi mai ușor decât să folosim partea „trunchiată” a formulei.
O progresie geometrică infinit descrescătoare.
Mai recent, am vorbit despre ceea ce poate fi fie mai mare, fie mai mic decât zero, cu toate acestea, există valori speciale pentru care se numește progresia geometrică în scădere infinit.
De ce crezi că are un astfel de nume?
Pentru început, să scriem o progresie geometrică formată din membri.
Sa zicem, atunci:
Vedem că fiecare termen următor este mai mic decât cel anterior în timp, dar va fi vreun număr? Răspunzi imediat - „nu”. De aceea, infinit descrescătoare - scade, scade, dar nu devine niciodată zero.
Pentru a înțelege clar cum arată acest lucru vizual, să încercăm să desenăm un grafic al progresiei noastre. Deci, pentru cazul nostru, formula ia următoarea formă:
Pe grafice, suntem obișnuiți să construim dependență de:
Esența expresiei nu s-a schimbat: în prima intrare, am arătat dependența valorii unui membru de progresie geometrică de numărul său ordinal, iar în a doua intrare, am luat pur și simplu valoarea unui membru de progresie geometrică pentru, și numărul ordinal a fost desemnat nu ca, ci ca. Tot ce mai rămâne de făcut este să trasezi graficul.
Să vedem ce ai. Iată graficul pe care l-am primit:

Vedea? Funcția scade, tinde spre zero, dar nu o traversează niciodată, deci este în scădere infinit. Să ne marchem punctele pe grafic și, în același timp, ce înseamnă și coordonatele:

Încercați să descrieți schematic un grafic al unei progresii geometrice dacă primul său termen este, de asemenea, egal. Analizați care este diferența cu graficul nostru anterior?
Ai reușit? Iată graficul pe care l-am primit:

Acum că ați înțeles pe deplin elementele de bază ale subiectului progresiei geometrice: știți ce este, știți cum să-i găsiți termenul și, de asemenea, știți ce este o progresie geometrică infinit descrescătoare, să trecem la proprietatea sa principală.
proprietatea unei progresii geometrice.
Vă amintiți proprietatea membrilor unei progresii aritmetice? Da, da, cum să găsiți valoarea unui anumit număr al unei progresii atunci când există valori anterioare și ulterioare ale membrilor acestei progresii. Amintit? Acest:
Acum ne confruntăm cu exact aceeași întrebare pentru termenii unei progresii geometrice. Pentru a obține o astfel de formulă, să începem să desenăm și să raționăm. Vei vedea, este foarte ușor, iar dacă uiți, îl poți scoate singur.
Să luăm o altă progresie geometrică simplă, în care știm și. Cum să găsești? Cu o progresie aritmetică, acest lucru este ușor și simplu, dar cum este aici? De fapt, nici în geometrie nu este nimic complicat - trebuie doar să pictezi fiecare valoare dată nouă conform formulei.
Tu intrebi, si acum ce facem cu ea? Da, foarte simplu. Pentru început, să descriem aceste formule în figură și să încercăm să facem diverse manipulări cu ele pentru a ajunge la o valoare.
Facem abstracție de numerele pe care ni le sunt date, ne vom concentra doar pe exprimarea lor printr-o formulă. Trebuie să găsim valoarea evidențiată portocale, cunoscând termenii adiacente acestuia. Să încercăm să producem cu ei diverse activitati, în urma căruia putem obține.
Plus.
Să încercăm să adăugăm două expresii și obținem:
Din această expresie, după cum puteți vedea, nu vom putea exprima în niciun fel, prin urmare, vom încerca o altă opțiune - scăderea.
Scădere.
După cum puteți vedea, nici din aceasta nu putem exprima, prin urmare, vom încerca să înmulțim aceste expresii unele cu altele.
Multiplicare.
Acum priviți cu atenție ce avem, înmulțind termenii unei progresii geometrice date nouă în comparație cu ceea ce trebuie găsit:
Ghici despre ce vorbesc? Bine, pentru a găsi trebuie să luăm Rădăcină pătrată din numerele de progresie geometrică adiacente numărului dorit înmulțite între ele:
Poftim. Tu însuți ai dedus proprietatea unei progresii geometrice. Încercați să scrieți această formulă vedere generala. S-a întâmplat?
Ați uitat starea când? Gândiți-vă de ce este important, de exemplu, încercați să îl calculați singur, la. Ce se întâmplă în acest caz? Așa e, prostie completă, deoarece formula arată așa:
În consecință, nu uitați de această limitare.
Acum să calculăm ce este
Răspuns corect - ! Dacă nu ai uitat a doua valoare posibilă la calcul, atunci ești un om grozav și poți trece imediat la antrenament, iar dacă ai uitat, citește ce este analizat mai jos și fii atent la motivul pentru care ambele rădăcini trebuie să fie scrise în răspuns .
Să desenăm ambele progresii geometrice - una cu o valoare, iar cealaltă cu o valoare și să verificăm dacă ambele au dreptul de a exista:

Pentru a verifica dacă o astfel de progresie geometrică există sau nu, este necesar să vedem dacă este aceeași între toți membrii ei dați? Calculați q pentru primul și al doilea caz.
Vedeți de ce trebuie să scriem două răspunsuri? Pentru că semnul termenului cerut depinde dacă este pozitiv sau negativ! Și din moment ce nu știm ce este, trebuie să scriem ambele răspunsuri cu un plus și un minus.
Acum că ați stăpânit punctele principale și ați dedus formula proprietății unei progresii geometrice, găsiți, știind și
Comparați răspunsurile dvs. cu cele corecte:
Ce credeți, dacă ni s-ar da nu valorile membrilor progresiei geometrice adiacente numărului dorit, ci echidistante de acesta. De exemplu, trebuie să găsim, și dat și. Putem folosi formula pe care am derivat-o în acest caz? Încercați să confirmați sau să infirmați această posibilitate în același mod, descriind în ce constă fiecare valoare, așa cum ați făcut atunci când ați derivat formula inițial.
Ce ai primit?
Acum uită-te din nou cu atenție.
si corespunzator:
De aici putem concluziona că formula funcționează nu numai cu vecinii cu termenii doriti ai unei progresii geometrice, dar si cu echidistant din ceea ce caută membrii.
Astfel, formula noastră originală devine:
Adică dacă în primul caz am spus asta, acum spunem că poate fi egal cu oricare numar natural, care este mai puțin. Principalul lucru este să fie același pentru ambele numere date.
Practica pentru exemple concrete doar fii extrem de atent!
- , . Găsi.
- , . Găsi.
- , . Găsi.
Hotărât? Sper că ați fost extrem de atenți și ați observat o mică captură.
Comparăm rezultatele.
În primele două cazuri, aplicăm cu calm formula de mai sus și obținem următoarele valori:
În al treilea caz, la o examinare mai atentă numere de serie numerele care ni s-au dat, înțelegem că nu sunt echidistante față de numărul pe care îl căutăm: este numărul anterior, dar scos în poziție, deci nu se poate aplica formula.
Cum să o rezolv? De fapt, nu este atât de dificil pe cât pare! Să scriem împreună cu tine în ce constă fiecare număr dat nouă și numărul dorit.
Deci avem și. Să vedem ce putem face cu ei. Sugerez despartirea. Primim:
Înlocuim datele noastre în formula:
Următorul pas îl putem găsi - pentru asta trebuie să-l facem rădăcină cubă de la numărul primit.
Acum să ne uităm din nou la ce avem. Avem, dar trebuie să găsim și, la rândul său, este egal cu:
Am găsit toate datele necesare pentru calcul. Inlocuieste in formula:
Raspunsul nostru: .
Încercați să rezolvați singur o altă problemă:
Dat: ,
Găsi:
Cât ai primit? Eu am - .
După cum puteți vedea, de fapt, aveți nevoie amintiți-vă doar o singură formulă- . Tot restul le puteți retrage fără nicio dificultate în orice moment. Pentru a face acest lucru, pur și simplu scrieți cea mai simplă progresie geometrică pe o bucată de hârtie și notați cu ce, conform formulei de mai sus, este egal cu fiecare dintre numerele sale.
Suma termenilor unei progresii geometrice.
Acum luați în considerare formulele care ne permit să calculăm rapid suma termenilor unei progresii geometrice într-un interval dat:
Pentru a obține formula pentru suma termenilor unei progresii geometrice finite, înmulțim toate părțile ecuației de mai sus cu. Primim:
Privește atent: ce au în comun ultimele două formule? Așa este, membri comuni, de exemplu și așa mai departe, cu excepția primului și ultimului membru. Să încercăm să scădem prima ecuație din a doua ecuație. Ce ai primit?
Acum exprimați prin formula unui membru al unei progresii geometrice și înlocuiți expresia rezultată în ultima noastră formulă:
Grupați expresia. Ar trebui să iei:
Tot ce rămâne de făcut este să exprime:
În consecință, în acest caz.
Și dacă? Ce formulă funcționează atunci? Imaginați-vă o progresie geometrică la. Cum este ea? Rândul corect aceleasi numere, deci formula va arăta astfel:
Ca și în cazul progresiei aritmetice și geometrice, există multe legende. Una dintre ele este legenda lui Seth, creatorul șahului.
Mulți oameni știu că jocul de șah a fost inventat în India. Când regele hindus a întâlnit-o, a fost încântat de inteligența ei și de varietatea de poziții posibile în ea. Aflând că a fost inventat de unul dintre supușii săi, regele a decis să-l recompenseze personal. L-a chemat pe inventator la el și a ordonat să-i ceară tot ce vrea, promițându-i că-i va îndeplini și cea mai pricepută dorință.
Seta a cerut timp să se gândească, iar când a doua zi Seta a apărut în fața regelui, acesta l-a surprins pe rege cu modestia fără egal a cererii sale. A cerut un bob de grâu pentru primul pătrat al tablei de șah, grâu pentru al doilea, pentru al treilea, pentru al patrulea și așa mai departe.
Regele s-a supărat și l-a alungat pe Set, spunând că cererea slujitorului este nedemnă de generozitatea regală, dar a promis că slujitorul își va primi boabele pentru toate celulele consiliului.
Și acum întrebarea este: folosind formula pentru suma membrilor unei progresii geometrice, calculați câte boabe ar trebui să primească Seth?
Să începem să discutăm. Întrucât, conform condiției, Seth a cerut un bob de grâu pentru prima celulă a tablei de șah, pentru a doua, pentru a treia, pentru a patra etc., vedem că problema este despre o progresie geometrică. Ce este egal în acest caz?
Dreapta.
Total celule ale tablei de șah. Respectiv, . Avem toate datele, rămâne doar să înlocuim în formulă și să calculăm.
Pentru a reprezenta cel puțin aproximativ „scalele” unui număr dat, transformăm folosind proprietățile gradului:
Desigur, dacă vrei, poți să iei un calculator și să calculezi cu ce fel de număr ajungi, iar dacă nu, va trebui să mă crezi pe cuvânt: valoarea finală a expresiei va fi.
Acesta este:
quintilioane cvadrilioane trilioane miliarde de milioane de mii.
Fuh) Dacă doriți să vă imaginați enormitatea acestui număr, atunci estimați ce dimensiune ar fi hambară necesară pentru a găzdui întreaga cantitate de cereale.
Cu o înălțime de hambar de m și o lățime de m, lungimea sa ar trebui să se extindă la km, adică. de două ori mai departe decât de la Pământ la Soare.
Dacă regele ar fi puternic la matematică, i-ar putea oferi însuși savantului să numere boabele, pentru că pentru a număra un milion de boabe, ar avea nevoie de cel puțin o zi de numărare neobosită și, având în vedere că este necesar să numere chintilioanele, boabele ar trebui să fie numărate toată viața.
Și acum vom rezolva o problemă simplă pe suma termenilor unei progresii geometrice.
Vasia, elev în clasa a V-a, s-a îmbolnăvit de gripă, dar continuă să meargă la școală. În fiecare zi, Vasya infectează două persoane care, la rândul lor, infectează încă două persoane și așa mai departe. Doar o singură persoană în clasă. În câte zile toată clasa se va îmbolnăvi de gripă?
Deci, primul membru al unei progresii geometrice este Vasya, adică o persoană. Al-lea membru al progresiei geometrice, acestea sunt cele două persoane pe care le-a infectat în prima zi de la sosire. Suma totală a membrilor progresiei este egală cu numărul de elevi 5A. În consecință, vorbim despre o progresie în care:
Să substituim datele noastre în formula pentru suma termenilor unei progresii geometrice:
Întreaga clasă se va îmbolnăvi în câteva zile. Nu crezi în formule și numere? Încercați să înfățișați singur „infecția” elevilor. S-a întâmplat? Vezi cum arată pentru mine:

Calculați singur în câte zile ar lua studenții gripa dacă toată lumea ar infecta o persoană și ar fi o persoană în clasă.
Ce valoare ai primit? S-a dovedit că toată lumea a început să se îmbolnăvească după o zi.
După cum puteți vedea, o astfel de sarcină și desenul pentru ea seamănă cu o piramidă, în care fiecare „aduce” ulterior oameni noi. Totuși, mai devreme sau mai târziu vine un moment în care acesta din urmă nu poate atrage pe nimeni. În cazul nostru, dacă ne imaginăm că clasa este izolată, persoana din închide lanțul (). Astfel, dacă o persoană ar fi implicată într-o piramidă financiară în care s-au dat bani dacă ai aduce alți doi participanți, atunci persoana respectivă (sau în cazul general) nu ar aduce pe nimeni, respectiv, ar pierde tot ce a investit în această înșelătorie financiară. .
Tot ceea ce s-a spus mai sus se referă la o progresie geometrică în scădere sau în creștere, dar, după cum vă amintiți, avem un tip special - o progresie geometrică în scădere infinit. Cum se calculează suma membrilor săi? Și de ce acest tip de progresie are anumite caracteristici? Să ne dăm seama împreună.
Deci, pentru început, să ne uităm din nou la această imagine a unei progresii geometrice în scădere infinită din exemplul nostru:

Și acum să ne uităm la formula pentru suma unei progresii geometrice, derivată puțin mai devreme:
sau
Pentru ce ne străduim? Așa este, graficul arată că tinde spre zero. Adică când, va fi aproape egală, respectiv, la calcularea expresiei, vom obține aproape. În acest sens, credem că atunci când se calculează suma unei progresii geometrice infinit descrescătoare, această paranteză poate fi neglijată, deoarece va fi egală.
- formula este suma termenilor unei progresii geometrice infinit descrescătoare.
IMPORTANT! Folosim formula pentru suma termenilor unei progresii geometrice infinit descrescătoare numai dacă condiția afirmă în mod explicit că trebuie să găsim suma fără sfârşit numarul de membri.
Dacă este indicat un anumit număr n, atunci folosim formula pentru suma n termeni, chiar dacă sau.
Și acum să exersăm.
- Aflați suma primilor termeni ai unei progresii geometrice cu și.
- Aflați suma termenilor unei progresii geometrice infinit descrescătoare cu și.
Sper că ai fost foarte atent. Comparați răspunsurile noastre:
Acum știi totul despre progresia geometrică și este timpul să treci de la teorie la practică. Cele mai frecvente probleme exponențiale găsite la examen sunt problemele de interes compus. Despre ei vom vorbi.
Probleme pentru calcularea dobânzii compuse.
Trebuie să fi auzit de așa-numita formulă a dobânzii compuse. Înțelegi ce vrea să spună? Dacă nu, să ne dăm seama, pentru că, după ce ați realizat procesul în sine, veți înțelege imediat ce are de-a face progresia geometrică cu el.
Mergem cu toții la bancă și știm că există conditii diferite asupra depozitelor: acesta este atât un termen, cât și întreținere suplimentară și un procent cu doi căi diferite calculul său - simplu și complex.
CU interes simplu totul este mai mult sau mai puțin clar: dobânda se percepe o singură dată la sfârșitul termenului de depozit. Adică, dacă vorbim despre punerea sub 100 de ruble pe an, atunci acestea vor fi creditate abia la sfârșitul anului. În consecință, până la sfârșitul depozitului, vom primi ruble.
Interes compus este o opţiune în care capitalizarea dobânzii, adică adăugarea acestora la suma depozitului și calculul ulterior al venitului nu din suma inițială, ci din suma acumulată a depozitului. Capitalizarea nu are loc constant, ci cu o oarecare periodicitate. De regulă, astfel de perioade sunt egale și cel mai adesea băncile folosesc o lună, un trimestru sau un an.
Să presupunem că punem toate aceleași ruble pe an, dar cu o capitalizare lunară a depozitului. Ce primim?
Înțelegi totul aici? Dacă nu, hai să o luăm pas cu pas.
Am adus ruble la bancă. Până la sfârșitul lunii, ar trebui să avem o sumă în cont constând din rublele noastre plus dobânda pentru ele, adică:
De acord?
O putem scoate din paranteză și apoi obținem:
De acord, această formulă este deja mai asemănătoare cu cea pe care am scris-o la început. Rămâne să ne ocupăm de procente
În starea problemei, ni se spune despre anual. După cum știți, nu înmulțim cu - convertim procentele în zecimale, acesta este:
Dreapta? Acum te întrebi, de unde a venit numărul? Foarte simplu!
Repet: starea problemei spune despre ANUAL dobânda acumulată LUNAR. După cum știți, într-un an de luni, respectiv, banca ne va percepe o parte din dobânda anuală pe lună:
Realizat? Acum încercați să scrieți cum ar arăta această parte a formulei dacă aș spune că dobânda se calculează zilnic.
Ai reușit? Să comparăm rezultatele:

Bine făcut! Să revenim la sarcina noastră: notați cât va fi creditat în contul nostru pentru a doua lună, ținând cont că se percepe dobândă la suma acumulată a depozitului.
Iată ce mi s-a întâmplat:
Sau, cu alte cuvinte:

Cred că ați observat deja un model și ați văzut o progresie geometrică în toate acestea. Scrieți cu ce va fi membrul său, sau, cu alte cuvinte, câți bani vom primi la sfârșitul lunii.
Făcut? Control!
După cum puteți vedea, dacă puneți bani într-o bancă timp de un an la o dobândă simplă, atunci veți primi ruble, iar dacă le puneți la o rată compusă, veți primi ruble. Beneficiul este mic, dar acest lucru se întâmplă doar în timpul celui de-al treilea an, dar pentru o perioadă mai lungă, capitalizarea este mult mai profitabilă:

Luați în considerare un alt tip de probleme ale dobânzii compuse. După ce ți-ai dat seama, va fi elementar pentru tine. Deci sarcina este:
Zvezda a început să investească în industrie în 2000 cu un capital în dolari. În fiecare an, din 2001, a realizat un profit egal cu capitalul din anul precedent. Cât profit va primi compania Zvezda la sfârșitul anului 2003, dacă profitul nu a fost retras din circulație?
Capitalul companiei Zvezda în 2000.
- capitalul companiei Zvezda în 2001.
- capitalul companiei Zvezda în 2002.
- capitalul companiei Zvezda în 2003.
Sau putem scrie pe scurt:
Pentru cazul nostru:
2000, 2001, 2002 și 2003.
Respectiv:
ruble
Rețineți că în această problemă nu avem o împărțire nici prin sau după, deoarece procentul este dat ANUAL și se calculează ANUAL. Adică, atunci când citiți problema pentru dobânda compusă, acordați atenție la ce procent este dat și în ce perioadă este percepută și abia apoi treceți la calcule.
Acum știi totul despre progresia geometrică.
Instruire.
- Găsiți un termen al unei progresii geometrice dacă se știe că și
- Aflați suma primilor termeni ai unei progresii geometrice, dacă se știe că și
- MDM Capital a început să investească în industrie în 2003 cu un capital în dolari. În fiecare an, din 2004, ea a realizat un profit egal cu capitalul din anul precedent. Compania „MSK” flux de fonduri” a început să investească în industrie în 2005 în valoare de 10.000 de dolari, începând să facă profit din 2006 în valoare de. Cu câți dolari îl depășește capitalul unei companii pe cel al alteia la sfârșitul anului 2007, dacă profiturile nu au fost retrase din circulație?
Raspunsuri:
- Deoarece condiția problemei nu spune că progresia este infinită și este necesară găsirea sumei unui anumit număr de membri ai săi, calculul se efectuează conform formulei:
Compania „MDM Capital”:2003, 2004, 2005, 2006, 2007.
- crește cu 100%, adică de 2 ori.
Respectiv:
ruble
Fluxuri de numerar MSK:2005, 2006, 2007.
- crește cu, adică ori.
Respectiv:
ruble
ruble
Să rezumam.
1) O progresie geometrică ( ) este o succesiune numerică, al cărei prim termen este diferit de zero, iar fiecare termen, începând cu al doilea, este egal cu cel precedent, înmulțit cu același număr. Acest număr se numește numitorul unei progresii geometrice.
2) Ecuația membrilor unei progresii geometrice -.
3) poate lua orice valoare, cu excepția și.
- dacă, atunci toți membrii următori ai progresiei au același semn - ei pozitiv;
- dacă, atunci toți membrii următori ai progresiei semne alternative;
- când - progresia se numește infinit descrescătoare.
4) , at - proprietatea unei progresii geometrice (termeni învecinați)
sau
, la (termeni echidistanti)
Când îl găsiți, nu uitați asta ar trebui să existe două răspunsuri..
De exemplu,
5) Suma membrilor unei progresii geometrice se calculează prin formula:
sau
Dacă progresia este în scădere infinită, atunci:
sau
IMPORTANT! Folosim formula pentru suma termenilor unei progresii geometrice infinit descrescătoare numai dacă condiția afirmă în mod explicit că trebuie să găsim suma unui număr infinit de termeni.
6) Sarcinile pentru dobânda compusă se calculează și prin formula celui de-al treilea membru al unei progresii geometrice, cu condiția ca bani gheata neretras din circulatie:
PROGRESIA GEOMETRICA. SCURT DESPRE PRINCIPALA
Progresie geometrică( ) este o succesiune numerică, al cărei prim termen este diferit de zero, iar fiecare termen, începând cu al doilea, este egal cu cel precedent, înmulțit cu același număr. Acest număr este numit numitorul unei progresii geometrice.
Numitorul unei progresii geometrice poate lua orice valoare cu excepția și.
- Dacă, atunci toți membrii următori ai progresiei au același semn - sunt pozitivi;
- dacă, atunci toți membrii următori ai progresiei semnează alternativ;
- când - progresia se numește infinit descrescătoare.
Ecuația membrilor unei progresii geometrice - .
Suma termenilor unei progresii geometrice calculat prin formula:
sau