Solution d'équations exponentielles en ligne avec une solution détaillée. Équations en ligne
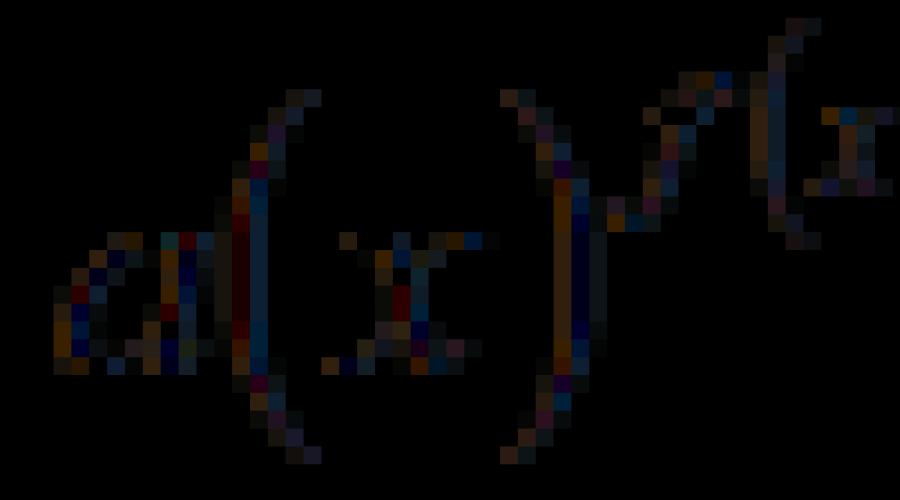
Lire aussi
Les équations dites de la forme, où l'inconnue est à la fois dans l'exposant et dans la base du degré.
Vous pouvez spécifier un algorithme complètement clair pour résoudre une équation de la forme. Pour cela, il faut être attentif au fait que Oh) non égal à zéro, un et moins un, l'égalité des degrés avec les mêmes bases (qu'elles soient positives ou négatives) n'est possible que si les indicateurs sont égaux C'est-à-dire que toutes les racines de l'équation seront les racines de l'équation f(x) = g(x) L'énoncé inverse n'est pas vrai si Oh)< 0 et valeurs fractionnaires f(x) et g(x) expressions Oh) f(x) et
Oh) g(x) perdre leur sens. c'est-à-dire en partant de f(x) = g(x)(pour et des racines étrangères peuvent apparaître, qui doivent être exclues en vérifiant selon l'équation d'origine. Et les cas une = 0, une = 1, une = -1 doivent être considérés séparément.
Donc pour solution complète les équations considèrent les cas:
un(x) = 0 f(x) et g(x) sont des nombres positifs, alors c'est la solution. Sinon, non
a(x) = 1. Les racines de cette équation sont aussi les racines de l'équation d'origine.
a(x) = -1. Si, pour une valeur de x qui satisfait cette équation, f(x) et g(x) sont des entiers de même parité (soit les deux sont pairs, soit les deux sont impairs), alors c'est la solution. Sinon, non
Pour et on résout l'équation f(x)=g(x) et en substituant les résultats obtenus dans l'équation originale, nous supprimons les racines étrangères.
Exemples de résolution d'équations à puissance exponentielle.
Exemple 1.
1) x - 3 = 0, x = 3. car 3 > 0, et 3 2 > 0, alors x 1 = 3 est la solution.
2) x - 3 \u003d 1, x 2 \u003d 4.
3) x - 3 \u003d -1, x \u003d 2. Les deux indicateurs sont pairs. C'est la solution x 3 = 1.
4) x - 3 ? 0 et x ? ± 1. x \u003d x 2, x \u003d 0 ou x \u003d 1. Pour x \u003d 0, (-3) 0 \u003d (-3) 0, cette solution est x 4 \u003d 0. Pour x \ u003d 1, (-2) 1 = (-2) 1 - cette solution est correcte x 5 = 1.
Réponse : 0, 1, 2, 3, 4.
Exemple #2.

Par la définition de l'arithmétique racine carrée: x - 1 ? 0,x ? une.
1) x - 1 = 0 ou x = 1, = 0, 0 0 n'est pas une solution.
2) X - 1 = 1 X 1 = 2.
3) x - 1 \u003d -1 x 2 \u003d 0 ne rentre pas dans l'ODZ.
D \u003d (-2) - 4 * 1 * 5 \u003d 4 - 20 \u003d -16 - il n'y a pas de racines.
Les équations sont dites exponentielles si l'inconnue est contenue dans l'exposant. L'équation exponentielle la plus simple a la forme: a x \u003d a b, où a> 0 et 1, x est une inconnue.
Les principales propriétés des degrés, à l'aide desquelles les équations exponentielles sont transformées : a>0, b>0.
Au moment de décider équations exponentielles ils utilisent également les propriétés suivantes de la fonction exponentielle : y = a x , a > 0, a1 :
Pour représenter un nombre sous forme de puissance, l'identité logarithmique de base est utilisée : b = , a > 0, a1, b > 0.
Tâches et tests sur le thème "Équations exponentielles"
- équations exponentielles
Leçons : 4 Devoirs : 21 Tests : 1
- équations exponentielles - Sujets importants pour répéter l'examen en mathématiques
Tâches : 14
- Systèmes d'équations exponentielles et logarithmiques - Fonctions exponentielles et logarithmiques 11e année
Leçons : 1 Devoirs : 15 Tests : 1
- §2.1. Solution d'équations exponentielles
Leçons : 1 Devoirs : 27
- §7 Équations et inégalités exponentielles et logarithmiques - Section 5. Fonctions exponentielles et logarithmiques 10e année
Leçons : 1 Devoirs : 17
Pour solution réussieéquations exponentielles Vous devez connaître les propriétés de base des puissances, les propriétés de la fonction exponentielle, l'identité logarithmique de base.
Lors de la résolution d'équations exponentielles, deux méthodes principales sont utilisées :
- passage de l'équation a f(x) = a g(x) à l'équation f(x) = g(x);
- introduction de nouvelles lignes.
Exemples.
1. Équations se réduisant au plus simple. Ils sont résolus en ramenant les deux côtés de l'équation à une puissance de même base.
3x \u003d 9x - 2.
La solution:
3 x \u003d (3 2) x - 2;
3x = 3 2x - 4 ;
x = 2x -4 ;
x=4.
Réponse: 4.
2. Équations résolues en mettant entre parenthèses le facteur commun.
La solution:
3x - 3x - 2 = 24
3 x - 2 (3 2 - 1) = 24
3 x - 2 x 8 = 24
3 x - 2 = 3
x - 2 = 1
x=3.
Réponse: 3.
3. Équations résolues par changement de variable.
La solution:
2 2x + 2x - 12 = 0
Nous notons 2 x \u003d y.
y 2 + y - 12 = 0
y 1 = - 4 ; y 2 = 3.
a) 2 x = - 4. L'équation n'a pas de solution, car 2 x > 0.
b) 2x = 3 ; 2 x = 2 log 2 3 ; x = log 2 3.
Réponse: journal 2 3.
4. Équations contenant des puissances de deux bases différentes (non réductibles l'une à l'autre).
3 × 2 X + 1 - 2 × 5 X - 2 \u003d 5 X + 2 X - 2.
3 x 2 x + 1 - 2 x - 2 = 5 x - 2 x 5 x - 2
2 x - 2 × 23 = 5 x - 2
×23
2 x - 2 = 5 x - 2
(5/2) x– 2 = 1
x - 2 = 0
x = 2.
Réponse: 2.
5. Équations homogènes par rapport à a x et b x .
Forme générale: .
9 x + 4 x = 2,5 x 6 x .
La solution:
3 2x – 2,5 × 2x × 3x +2 2x = 0 |: 2 2x > 0
(3/2) 2x - 2,5 × (3/2) x + 1 = 0.
Notons (3/2) x = y.
y 2 - 2,5y + 1 \u003d 0,
y 1 = 2; y2 = ½. 
Réponse: bûche 3/2 2 ; - bûche 3/2 2.
À la chaîne youtube de notre site site pour être au courant de toutes les nouvelles leçons vidéo.
Rappelons d'abord les formules de base des degrés et leurs propriétés.
Produit d'un nombre un se produit n fois sur lui-même, on peut écrire cette expression sous la forme a a … a=a n
1. un 0 = 1 (un ≠ 0)
3. une n une m = une n + m
4. (un n) m = un nm
5. une n b n = (ab) n
7. un n / un m \u003d un n - m
Équations de puissance ou exponentielles- ce sont des équations dans lesquelles les variables sont en puissances (ou exposants), et la base est un nombre.
Exemples d'équations exponentielles :
Dans cet exemple, le nombre 6 est la base, il est toujours en bas, et la variable X degré ou mesure.
Donnons d'autres exemples d'équations exponentielles.
2 × *5=10
16x-4x-6=0
Voyons maintenant comment les équations exponentielles sont résolues ?
Prenons une équation simple :
2 x = 2 3
Un tel exemple peut être résolu même dans l'esprit. On voit que x=3. Après tout, pour que les côtés gauche et droit soient égaux, vous devez mettre le chiffre 3 au lieu de x.
Voyons maintenant comment cette décision doit être prise :
2 x = 2 3
x = 3
Pour résoudre cette équation, nous avons supprimé mêmes motifs(c'est-à-dire deux) et a écrit ce qui restait, ce sont des degrés. Nous avons eu la réponse que nous cherchions.
Résumons maintenant notre solution.
Algorithme de résolution de l'équation exponentielle :
1. Besoin de vérifier le même si les bases de l'équation à droite et à gauche. Si les motifs ne sont pas les mêmes, nous recherchons des options pour résoudre cet exemple.
2. Une fois que les bases sont les mêmes, assimiler degré et résoudre la nouvelle équation résultante.
Résolvons maintenant quelques exemples :
Commençons simple.
Les bases des côtés gauche et droit sont égales au nombre 2, ce qui signifie que nous pouvons rejeter la base et égaliser leurs degrés.
x+2=4 L'équation la plus simple s'est avérée.
x=4 - 2
x=2
Réponse : x=2
Dans l'exemple suivant, vous pouvez voir que les bases sont différentes, ce sont 3 et 9.
3 3x - 9x + 8 = 0
Pour commencer, nous transférons le neuf sur le côté droit, nous obtenons:
Maintenant, vous devez faire les mêmes bases. On sait que 9=3 2 . Utilisons la formule de puissance (a n) m = a nm .
3 3x \u003d (3 2) x + 8
Nous obtenons 9 x + 8 \u003d (3 2) x + 8 \u003d 3 2 x + 16
3 3x \u003d 3 2x + 16 maintenant vous pouvez voir que dans la gauche et côté droit les bases sont les mêmes et égales à trois, ce qui signifie que nous pouvons les éliminer et égaliser les degrés.
3x=2x+16 a obtenu l'équation la plus simple
3x-2x=16
x=16
Réponse : x=16.
Regardons l'exemple suivant :
2 2x + 4 - 10 4x \u003d 2 4
Tout d'abord, nous regardons les bases, les bases sont différentes deux et quatre. Et nous devons être les mêmes. On transforme le quadruple selon la formule (a n) m = a nm .
4 x = (2 2) x = 2 2x
Et nous utilisons également une formule a n a m = a n + m :
2 2x+4 = 2 2x 2 4
Ajouter à l'équation :
2 2x 2 4 - 10 2 2x = 24
Nous avons donné un exemple pour les mêmes raisons. Mais d'autres chiffres 10 et 24 interfèrent avec nous, que faire d'eux ? Si vous regardez attentivement, vous pouvez voir que sur le côté gauche, nous répétons 2 2x, voici la réponse - nous pouvons mettre 2 2x hors parenthèses :
2 2x (2 4 - 10) = 24
Calculons l'expression entre parenthèses :
2 4 — 10 = 16 — 10 = 6
On divise l'équation entière par 6 :
Imaginez 4=2 2 :
2 2x \u003d 2 2 bases sont les mêmes, jetez-les et égalisez les degrés.
2x \u003d 2 s'est avéré être l'équation la plus simple. On le divise par 2, on obtient
x = 1
Réponse : x = 1.
Résolvons l'équation :
9x - 12*3x +27= 0
Transformons :
9 x = (3 2) x = 3 2x
On obtient l'équation :
3 2x - 12 3x +27 = 0
Nos bases sont les mêmes, égales à 3. Dans cet exemple, il est clair que le premier triple a un degré deux fois (2x) que le second (juste x). Dans ce cas, vous pouvez décider méthode de substitution. Le nombre avec le plus petit degré est remplacé par :
Alors 3 2x \u003d (3 x) 2 \u003d t 2
Nous remplaçons tous les degrés par des x dans l'équation avec t :
t 2 - 12t + 27 \u003d 0
On a équation quadratique. On résout par le discriminant, on obtient :
D=144-108=36
t1 = 9
t2 = 3
Retour aux variables X.
On prend t 1 :
t 1 \u003d 9 \u003d 3 x
C'est-à-dire,
3 x = 9
3 x = 3 2
x 1 = 2
Une racine a été trouvée. Nous recherchons le second, à partir de t 2 :
t 2 \u003d 3 \u003d 3 x
3 x = 3 1
x 2 = 1
Réponse : x 1 \u003d 2 ; x2 = 1.
Sur le site, vous pouvez dans la section AIDE À DÉCIDER poser des questions d'intérêt, nous vous répondrons certainement.
Rejoindre un groupe
Université d'État de Belgorod
CHAISE algèbre, théorie des nombres et géométrie
Thème de travail : Équations et inégalités à puissance exponentielle.
Travail de fin d'étudesétudiant de la Faculté de Physique et Mathématiques
Conseiller scientifique:
______________________________
Réviseur : _______________________________
________________________
Belgorod. 2006
| Introduction | 3 | ||
| Sujet JE. | Analyse de la littérature sur le sujet de recherche. | ||
| Sujet II. | Fonctions et leurs propriétés utilisées pour résoudre des équations et des inégalités à puissance exponentielle. | ||
| I.1. | Fonction de puissance et ses propriétés. | ||
| I.2. | Fonction exponentielle et ses propriétés. | ||
| Sujet III. | Solution d'équations à puissance exponentielle, algorithme et exemples. | ||
| Sujet IV. | Résolution des inégalités de puissance exponentielle, plan de solution et exemples. | ||
| Sujet v. | Expérience dans la conduite de cours avec des écoliers sur le thème: "Solution d'équations de puissance exponentielles et d'inégalités". | ||
| v. 1. | Matériel d'apprentissage. | ||
| v. 2. | Tâches pour une solution indépendante. | ||
| Conclusion. | Conclusions et offres. | ||
| Bibliographie. | |||
| Applications | |||
Introduction.
"... la joie de voir et de comprendre..."
A.Einstein.
Dans cet ouvrage, j'ai essayé de transmettre mon expérience de professeur de mathématiques, de transmettre, au moins dans une certaine mesure, mon attitude face à l'enseignement des mathématiques - une matière humaine dans laquelle la science mathématique, la pédagogie, la didactique, la psychologie et même la philosophie sont étonnamment entrelacés.
Il m'est arrivé de travailler avec des enfants et des diplômés, avec des enfants debout sur les poteaux Développement intellectuel: ceux qui étaient inscrits chez un psychiatre et qui s'intéressaient vraiment aux mathématiques
J'ai dû résoudre de nombreux problèmes méthodologiques. Je vais essayer de parler de ceux que j'ai réussi à résoudre. Mais plus encore - ce n'était pas possible, et dans ceux qui semblent être résolus, de nouvelles questions apparaissent.
Mais plus importantes encore que l'expérience elle-même sont les réflexions et les doutes de l'enseignant : pourquoi est-ce exactement comme ça, cette expérience ?
Et l'été est différent maintenant, et le tournant de l'éducation est devenu plus intéressant. "Sous les Jupiters" aujourd'hui n'est pas la recherche d'un système optimal mythique d'enseignement de "tout et chacun", mais l'enfant lui-même. Mais alors - avec nécessité - et le professeur.
Dans le cours scolaire d'algèbre et a commencé l'analyse, de la 10e à la 11e année, lors de la réussite de l'examen du cours lycée et aux examens d'entrée aux universités, il y a des équations et des inégalités contenant l'inconnu à la base et des exposants - ce sont des équations et des inégalités à puissance exponentielle.
Peu d'attention leur est accordée à l'école, il n'y a pratiquement pas de tâches sur ce sujet dans les manuels. Cependant, maîtriser la technique pour les résoudre est, me semble-t-il, très utile : cela augmente les capacités mentales et Compétences créativesétudiants, de tout nouveaux horizons s'ouvrent devant nous. Lors de la résolution de problèmes, les élèves acquièrent les premières compétences travail de recherche, leur culture mathématique s'enrichit, leurs capacités de raisonnement logique se développent. Les écoliers développent des traits de personnalité tels que la détermination, l'établissement d'objectifs, l'indépendance, qui leur seront utiles plus tard dans la vie. Et il y a aussi une répétition, une expansion et une assimilation profonde du matériel pédagogique.
J'ai commencé à travailler sur ce sujet de ma recherche de thèse avec la rédaction d'un dissertation. Au cours de laquelle j'ai étudié et analysé plus en profondeur la littérature mathématique sur ce sujet, j'ai identifié la méthode la plus appropriée pour résoudre les équations et les inégalités à puissance exponentielle.
Elle réside dans le fait qu'en plus de l'approche généralement admise lors de la résolution d'équations à puissance exponentielle (la base est prise supérieure à 0) et lors de la résolution des mêmes inégalités (la base est prise supérieure à 1 ou supérieure à 0, mais inférieure à 1), les cas sont également considérés lorsque les bases sont négatives, sont 0 et 1.
L'analyse des épreuves écrites des étudiants montre que l'ignorance de la question de valeur négative l'argument d'une fonction puissance exponentielle dans les manuels scolaires, leur pose un certain nombre de difficultés et conduit à des erreurs. Et ils ont aussi des problèmes au stade de la systématisation des résultats obtenus, où, en raison du passage à une équation - une conséquence ou une inégalité - une conséquence, des racines étrangères peuvent apparaître. Afin d'éliminer les erreurs, nous utilisons une vérification par l'équation ou l'inégalité d'origine et un algorithme pour résoudre les équations à puissance exponentielle, ou un plan pour résoudre les inégalités à puissance exponentielle.
Pour que les étudiants puissent réussir les examens finaux et d'entrée, je pense qu'il est nécessaire d'accorder plus d'attention à la résolution des équations et des inégalités à puissance exponentielle en classe, ou en plus dans les cours facultatifs et les cercles.
De cette façon sujet , ma thèse est définie de la manière suivante: "Equations et inégalités à puissance exponentielle".
Buts travail présent sommes:
1. Analysez la littérature sur ce sujet.
2. Donnez analyse complète solutions d'équations et d'inéquations à puissance exponentielle.
3. Donnez un nombre suffisant d'exemples sur ce sujet de différents types.
4. Vérifier en classe, en classe optionnelle et en cercle comment seront perçues les méthodes proposées pour résoudre les équations à puissance exponentielle et les inégalités. Donner des recommandations appropriées pour l'étude de ce sujet.
Matière notre recherche consiste à développer une technique de résolution d'équations et d'inéquations à puissance exponentielle.
Le but et le sujet de l'étude ont nécessité la résolution des tâches suivantes :
1. Étudiez la littérature sur le sujet : "Équations et inégalités à puissance exponentielle".
2. Maîtriser les méthodes de résolution des équations et des inégalités à puissance exponentielle.
3. Sélectionner le matériel de formation et développer un système d'exercices différents niveaux sur le thème : « Solution d'équations et d'inégalités à puissance exponentielle ».
Au cours de la recherche de thèse, plus de 20 articles consacrés à l'application de diverses méthodes solutions d'équations et d'inéquations à puissance exponentielle. De là, nous obtenons.
Projet de thèse :
Introduction.
Chapitre I. Analyse de la littérature sur le sujet de recherche.
Chapitre II. Fonctions et leurs propriétés utilisées pour résoudre des équations et des inégalités à puissance exponentielle.
II.1. Fonction puissance et ses propriétés.
II.2. La fonction exponentielle et ses propriétés.
Chapitre III. Solution d'équations à puissance exponentielle, algorithme et exemples.
Chapitre IV. Résolution des inégalités de puissance exponentielle, plan de solution et exemples.
Chapitre V. Expérience dans la conduite de cours avec des écoliers sur ce sujet.
1. Matériel pédagogique.
2. Tâches pour une solution indépendante.
Conclusion. Conclusions et offres.
Liste de la littérature utilisée.
Littérature analysée au chapitre I
Premier niveau
équations exponentielles. Guide complet (2019)
Bonjour! Aujourd'hui, nous allons discuter avec vous de la façon de résoudre des équations qui peuvent être à la fois élémentaires (et j'espère qu'après avoir lu cet article, presque toutes le seront pour vous), et celles auxquelles on donne généralement un "remplissage". Apparemment, pour s'endormir complètement. Mais je vais essayer de faire de mon mieux pour que maintenant vous n'ayez pas d'ennuis face à ce type d'équation. Je ne tournerai plus autour du pot, mais je vais tout de suite révéler un petit secret : aujourd'hui nous allons étudier équations exponentielles.
Avant de procéder à une analyse des moyens de les résoudre, je vais immédiatement vous esquisser un cercle de questions (assez restreint) que vous devriez répéter avant de vous précipiter à l'assaut de ce sujet. Donc, pour de meilleurs résultats, veuillez répéter:
- propriétés et
- Solution et équations
Répété? Formidable! Il ne vous sera alors pas difficile de remarquer que la racine de l'équation est un nombre. Es-tu sûr de comprendre comment j'ai fait ? Vérité? Puis nous continuons. Maintenant, répondez-moi à la question, qu'est-ce qui est égal à la troisième puissance ? Vous avez absolument raison: . Huit est quelle puissance de deux ? C'est vrai - le troisième ! Car. Eh bien, essayons maintenant de résoudre le problème suivant : laissez-moi multiplier le nombre par lui-même une fois et obtenez le résultat. La question est, combien de fois ai-je multiplié par moi-même ? Vous pouvez bien sûr vérifier cela directement :
\begin(aligner) & 2=2 \\ & 2\cdot 2=4 \\ & 2\cdot 2\cdot 2=8 \\ & 2\cdot 2\cdot 2\cdot 2=16 \\ \end( aligner)
Ensuite, vous pouvez conclure que j'ai multiplié les temps par lui-même. Comment cela peut-il être vérifié autrement ? Et voici comment : directement par la définition du diplôme : . Mais, vous devez l'admettre, si je demandais combien de fois deux doivent être multipliés par lui-même pour obtenir, disons, vous me diriez : je ne vais pas me tromper et multiplier par moi-même jusqu'à ce que j'aie le visage bleu. Et il aurait parfaitement raison. Car comment peux-tu notez brièvement toutes les actions(et la concision est la soeur du talent)
où - c'est le très "fois" quand vous multipliez par lui-même.
Je pense que vous savez (et si vous ne savez pas, de toute urgence, de toute urgence, refaites les diplômes!) qu'alors mon problème sera écrit sous la forme:
Comment pouvez-vous raisonnablement conclure que :
Alors, tranquillement, j'ai écrit le plus simple équation exponentielle :
Et même trouvé racine. Ne pensez-vous pas que tout est assez trivial? C'est exactement ce que je pense aussi. Voici un autre exemple pour vous :
Mais que faire? Après tout, il ne peut pas être écrit comme un degré d'un nombre (raisonnable). Ne désespérons pas et notons que ces deux nombres sont parfaitement exprimés en termes de puissance du même nombre. Quoi? Droit: . Ensuite, l'équation d'origine est transformée sous la forme :
D'où, comme vous l'avez déjà compris, . Ne tirons plus et écrivons définition:
Dans notre cas avec vous : .
Ces équations sont résolues en les réduisant à la forme :
avec solution ultérieure de l'équation
En fait, nous l'avons fait dans l'exemple précédent : nous avons obtenu cela. Et nous avons résolu l'équation la plus simple avec vous.
Cela semble n'avoir rien de compliqué, n'est-ce pas ? Entraînons-nous d'abord sur le plus simple. exemples:
Nous voyons à nouveau que les côtés droit et gauche de l'équation doivent être représentés comme une puissance d'un nombre. Certes, cela a déjà été fait à gauche, mais à droite, il y a un numéro. Mais, ça va, après tout, et mon équation se transforme miraculeusement en ceci :
Qu'avais-je à faire ici ? Quelle règle ? Règle du pouvoir au pouvoir qui se lit :
Et qu'est-ce qui se passerait si:
Avant de répondre à cette question, remplissons avec vous le tableau suivant :
Il ne nous est pas difficile de remarquer que moins, plus moins de valeur, mais néanmoins, toutes ces valeurs Au dessus de zéro. ET CE SERA TOUJOURS AINSI !!! La même propriété est vraie POUR TOUTE BASE AVEC TOUT INDEX !! (pour tout et). Alors que pouvons-nous conclure sur l'équation? Et en voici une : elle n'a pas de racines! Comme toute équation n'a pas de racines. Maintenant pratiquons et Résolvons quelques exemples simples :
Allons vérifier:
1. Rien ne vous est demandé ici, si ce n'est de connaître les propriétés des puissances (que je vous ai d'ailleurs demandé de répéter !) En règle générale, tout aboutit à la plus petite base : , . Alors l'équation originale sera équivalente à la suivante : Tout ce dont j'ai besoin est d'utiliser les propriétés des puissances : lors de la multiplication de nombres avec la même base, les exposants sont ajoutés et lors de la division, ils sont soustraits. Alors j'obtiendrai : Eh bien, maintenant avec une conscience claire, je vais passer de l'équation exponentielle à l'équation linéaire : \begin(align)
& 2x+1+2(x+2)-3x=5 \\
& 2x+1+2x+4-3x=5 \\
&x=0. \\
\end(aligner)
2. Dans le deuxième exemple, il faut être plus prudent : le problème est que sur le côté gauche, on ne pourra pas représenter le même nombre comme une puissance. Dans ce cas, il est parfois utile représentent des nombres comme un produit de puissances avec des bases différentes, mais les mêmes exposants :
Le côté gauche de l'équation prendra la forme : Qu'est-ce que cela nous a donné ? Et voici quoi : Les nombres avec des bases différentes mais le même exposant peuvent être multipliés.Dans ce cas, les bases sont multipliées, mais l'exposant ne change pas :
Appliqué à ma situation, cela donnera :
\begin (aligner)
& 4\cdot ((64)^(x))((25)^(x))=6400, \\
& 4\cdot (((64\cdot 25))^(x))=6400, \\
& ((1600)^(x))=\frac(6400)(4), \\
& ((1600)^(x))=1600, \\
&x=1. \\
\end(aligner)
Pas mal, non ?
3. Je n'aime pas ça quand j'ai deux termes d'un côté de l'équation, et aucun de l'autre (parfois, bien sûr, c'est justifié, mais ce n'est plus le cas maintenant). Déplacez le terme moins vers la droite :
Maintenant, comme avant, j'écrirai tout par les puissances du triple :
J'additionne les puissances à gauche et j'obtiens une équation équivalente
Vous pouvez facilement trouver sa racine :
4. Comme dans l'exemple trois, le terme avec un moins - une place sur le côté droit !
A gauche, presque tout me va, sauf quoi ? Oui, le "mauvais degré" du diable me dérange. Mais je peux facilement résoudre ce problème en écrivant: . Eureka - à gauche, toutes les bases sont différentes, mais tous les diplômes sont les mêmes ! Nous multiplions rapidement!
Là encore, tout est clair: (si vous n'avez pas compris comment par magie j'ai obtenu la dernière égalité, faites une pause d'une minute, faites une pause et relisez très attentivement les propriétés du degré. Qui a dit que vous pouviez sauter le degré avec un exposant négatif ? Eh bien, ici, je suis à peu près comme personne). Maintenant j'obtiendrai :
\begin (aligner)
& ((2)^(4\left((x) -9 \right)))=((2)^(-1)) \\
&4((x) -9)=-1 \\
&x=\frac(35)(4). \\
\end(aligner)
Voici les tâches à pratiquer, auxquelles je ne donnerai que les réponses (mais sous une forme « mixte »). Résolvez-les, vérifiez, et nous continuerons nos recherches !
Prêt? Réponses comme ceux-ci :
- n'importe quel chiffre
Bon, d'accord, je plaisantais ! Voici les grandes lignes des solutions (certaines sont assez brèves !)
Ne pensez-vous pas que ce n'est pas un hasard si une fraction à gauche est une autre "inversée" ? Ce serait un péché de ne pas utiliser ceci :
Cette règle est très souvent utilisée lors de la résolution d'équations exponentielles, souvenez-vous-en bien !
Alors l'équation d'origine devient :
En résolvant cette équation quadratique, vous obtiendrez les racines suivantes :
2. Une autre solution : diviser les deux parties de l'équation par l'expression à gauche (ou à droite). Je vais diviser par ce qui est à droite, alors j'obtiendrai :
Où (pourquoi ?!)
3. Je ne veux même pas me répéter, tout a déjà été tellement "mâché".
4. équivalent à une équation quadratique, les racines
5. Vous devez utiliser la formule donnée dans la première tâche, puis vous obtiendrez cela :
L'équation s'est transformée en une identité triviale, ce qui est vrai pour tout. Alors la réponse est n'importe quel nombre réel.
Eh bien, vous êtes ici et pratiqué pour décider les équations exponentielles les plus simples. Maintenant, je veux vous donner quelques exemples de vie qui vous aideront à comprendre pourquoi ils sont nécessaires en principe. Ici, je vais donner deux exemples. L'un d'eux est assez courant, mais l'autre a plus d'intérêt scientifique que pratique.
Exemple 1 (marchand) Laissez-vous avoir des roubles, mais vous voulez le transformer en roubles. La banque vous propose de vous retirer cet argent à un taux d'intérêt annuel avec une capitalisation mensuelle des intérêts (mensual couru). La question est de savoir pendant combien de mois devez-vous ouvrir un dépôt afin de percevoir le montant final souhaité ? Une tâche assez banale, n'est-ce pas ? Néanmoins, sa solution est liée à la construction de l'équation exponentielle correspondante : Soit - le montant initial, - le montant final, - le taux d'intérêt de la période, - le nombre de périodes. Alors:
Dans notre cas (si le taux est annuel, alors il est calculé par mois). Pourquoi est-il divisé en ? Si vous ne connaissez pas la réponse à cette question, souvenez-vous du sujet "" ! On obtient alors l'équation suivante :
Cette équation exponentielle ne peut déjà être résolue qu'avec une calculatrice (sa apparence des allusions à cela, et cela nécessite une connaissance des logarithmes, que nous connaîtrons un peu plus tard), ce que je ferai: ... Ainsi, pour recevoir un million, nous devrons faire un dépôt pendant un mois ( pas très rapide, non ?).
Exemple 2 (plutôt scientifique). Malgré son, un certain "isolement", je vous recommande de faire attention à lui : il "se glisse régulièrement dans l'examen !! (la tâche est tirée de la version "réelle") Lors de la désintégration d'un isotope radioactif, sa masse diminue selon la loi, où (mg) est la masse initiale de l'isotope, (min.) est le temps écoulé depuis la moment initial, (min.) est la demi-vie. Au moment initial, la masse de l'isotope est de mg. Sa demi-vie est de min. Dans combien de minutes la masse de l'isotope sera-t-elle égale à mg ? C'est bon : on prend juste et on substitue toutes les données dans la formule qui nous est proposée :
Divisons les deux parties par, "dans l'espoir" qu'à gauche on obtienne quelque chose de digeste :
Eh bien, nous avons beaucoup de chance ! Il se tient à gauche, puis passons à l'équation équivalente :
Où min.
Comme vous pouvez le voir, les équations exponentielles ont une application très réelle dans la pratique. Maintenant, je veux discuter avec vous d'une autre façon (simple) de résoudre des équations exponentielles, qui consiste à retirer le facteur commun des parenthèses, puis à regrouper les termes. N'ayez pas peur de mes propos, vous avez déjà rencontré cette méthode en 7ème quand vous avez étudié les polynômes. Par exemple, si vous deviez factoriser l'expression :
Regroupons : les premier et troisième termes, ainsi que les deuxième et quatrième. Il est clair que le premier et le troisième sont la différence des carrés :
et les deuxième et quatrième ont un facteur commun de trois :
Alors l'expression originale est équivalente à ceci :
Où retirer le facteur commun n'est plus difficile:
Par conséquent,
Voici à peu près comment nous agirons lors de la résolution d'équations exponentielles : recherchez la "communauté" entre les termes et retirez-la des parenthèses, puis - quoi qu'il arrive, je crois que nous aurons de la chance =)) Par exemple :
À droite, c'est loin de la puissance sept (j'ai vérifié!) Et à gauche - un peu mieux, vous pouvez bien sûr "couper" le facteur a du premier terme et du second, puis traiter avec ce que vous avez reçu, mais faisons plus prudemment avec vous. Je ne veux pas m'occuper des fractions qui sont inévitablement produites par la "sélection", alors ne devrais-je pas mieux endurer ? Alors je n'aurai pas de fractions: comme on dit, les loups sont pleins et les moutons sont en sécurité:
Compter l'expression entre parenthèses. Comme par magie, comme par magie, il s'avère que (étonnamment, mais à quoi d'autre pouvons-nous nous attendre ?).
Ensuite, nous réduisons les deux côtés de l'équation par ce facteur. Nous obtenons: où.
Voici un exemple plus compliqué (un peu, vraiment):
Voici le problème! Nous n'avons aucun terrain d'entente ici ! Ce n'est pas tout à fait clair quoi faire maintenant. Et faisons ce que nous pouvons : dans un premier temps, nous allons déplacer les « quatre » dans un sens, et les « cinq » dans l'autre :
Retirons maintenant le "commun" à gauche et à droite :
Et maintenant ? Quel est l'intérêt d'un regroupement aussi stupide ? A première vue, ce n'est pas du tout visible, mais regardons plus en profondeur :
Eh bien, maintenant faisons en sorte qu'à gauche nous n'ayons que l'expression c, et à droite - tout le reste. Comment pouvons-nous le faire? Et voici comment : Divisez d'abord les deux côtés de l'équation par (pour nous débarrasser de l'exposant à droite), puis divisez les deux côtés par (pour vous débarrasser du facteur numérique à gauche). On obtient finalement :
Incroyable! À gauche, nous avons une expression et à droite - juste. Alors on en déduit immédiatement que
Voici un autre exemple pour renforcer:
je lui apporterai solution courte(pas vraiment la peine d'expliquer), essayez de comprendre vous-même toutes les "subtilités" de la solution.
Maintenant, la consolidation finale du matériel couvert. Essayez de résoudre les problèmes suivants par vous-même. Je ne donnerai que de brèves recommandations et astuces pour les résoudre :
- Prenons le facteur commun entre parenthèses :
- Nous représentons la première expression sous la forme : , divisons les deux parties par et obtenons que
- , puis l'équation d'origine est convertie sous la forme : Eh bien, maintenant un indice - cherchez où vous et moi avons déjà résolu cette équation !
- Imaginez comment, comment, ah, eh bien, puis divisez les deux parties par, pour obtenir l'équation exponentielle la plus simple.
- Sortez-le des crochets.
- Sortez-le des crochets.
ÉQUATIONS D'EXPOSITION. NIVEAU MOYEN
Je suppose qu'après avoir lu le premier article, qui racontait que sont les équations exponentielles et comment les résoudre tu as maîtrisé minimum nécessaire connaissances nécessaires pour résoudre des exemples simples.
Maintenant, je vais analyser une autre méthode pour résoudre des équations exponentielles, c'est
"méthode d'introduction d'une nouvelle variable" (ou substitution). Il résout la plupart des problèmes "difficiles", sur le thème des équations exponentielles (et pas seulement des équations). Cette méthode est l'une des plus utilisées en pratique. Tout d'abord, je vous recommande de vous familiariser avec le sujet.
Comme vous l'avez déjà compris d'après son nom, l'essence de cette méthode est d'introduire un tel changement de variable que votre équation exponentielle se transformera miraculeusement en une que vous pourrez déjà facilement résoudre. Il ne vous reste plus qu'après avoir résolu cette « équation très simplifiée » de faire un « remplacement inversé » : c'est-à-dire de revenir du remplacé au remplacé. Illustrons ce que nous venons de dire avec un exemple très simple :
Exemple 1:
Cette équation est résolue par une "simple substitution", comme l'appellent avec mépris les mathématiciens. En effet, la substitution est ici la plus évidente. Il suffit de voir que
Alors l'équation d'origine devient :
Si nous imaginons en plus comment, alors il est tout à fait clair ce qui doit être remplacé : bien sûr, . Que devient alors l'équation originale ? Et voici quoi :
Vous pouvez facilement trouver ses racines par vous-même :. Que devons-nous faire maintenant? Il est temps de revenir à la variable d'origine. Qu'est-ce que j'ai oublié d'inclure ? A savoir: lors du remplacement d'un certain degré par une nouvelle variable (c'est-à-dire lors du remplacement d'un type), je serai intéressé par que des racines positives ! Vous-même pouvez facilement répondre pourquoi. Ainsi, vous ne nous intéressez pas, mais la deuxième racine nous convient tout à fait :
Alors où.
Réponse:
Comme vous pouvez le voir, dans l'exemple précédent, le remplaçant demandait nos mains. Malheureusement, ce n'est pas toujours le cas. Cependant, n'allons pas directement au triste, mais pratiquons sur un autre exemple avec un remplacement assez simple
Exemple 2
Il est clair qu'il sera très probablement nécessaire de remplacer (c'est la plus petite des puissances incluses dans notre équation), cependant, avant d'introduire un remplacement, notre équation doit être "préparée" pour cela, à savoir : , . Ensuite, vous pouvez remplacer, en conséquence, j'obtiendrai l'expression suivante :
Oh horreur : une équation cubique avec des formules absolument terribles pour sa solution (enfin, parlant en vue générale). Mais ne désespérons pas tout de suite, mais réfléchissons à ce que nous devrions faire. Je suggérerai de tricher : nous savons que pour obtenir une "belle" réponse, nous devons obtenir une puissance de trois (pourquoi serait-ce le cas, hein ?). Et essayons de deviner au moins une racine de notre équation (je vais commencer à deviner à partir des puissances de trois).
Première supposition. N'est pas une racine. Hélas et euh...
.
Le côté gauche est égal.
Partie droite : !
Il y a! Deviné la première racine. Maintenant, les choses vont devenir plus faciles !
Connaissez-vous le schéma de division "corner" ? Bien sûr, vous le savez, vous l'utilisez lorsque vous divisez un nombre par un autre. Mais peu de gens savent que la même chose peut être faite avec des polynômes. Il y a un merveilleux théorème :
Applicable à ma situation, il me dit ce qui est divisible sans reste par. Comment s'effectue le partage ? C'est comme ça:
Je regarde sur quel monôme je dois multiplier pour obtenir Clear, puis :
Je soustrais l'expression résultante de, j'obtiens:
Maintenant, que dois-je multiplier pour obtenir ? Il est clair que sur, alors j'obtiendrai:
et soustrayez à nouveau l'expression résultante de celle qui reste :
Eh bien, la dernière étape, je multiplie par et soustrais de l'expression restante :
Hourra, la division est terminée ! Qu'avons-nous accumulé en privé ? Par lui-même: .
Ensuite, nous avons obtenu le développement suivant du polynôme original :
Résolvons la deuxième équation :
Il a des racines :
Puis l'équation d'origine :
a trois racines :
Bien sûr, nous écartons la dernière racine, car elle est inférieure à zéro. Et les deux premiers après le remplacement inverse nous donneront deux racines :
Réponse: ..
Par cet exemple, je ne voulais pas du tout vous effrayer, je me suis plutôt fixé comme objectif de montrer que bien que nous ayons eu un remplacement assez simple, il conduisait néanmoins à une équation assez complexe, dont la solution nécessitait des compétences particulières de la part de nous. Eh bien, personne n'est à l'abri de cela. Mais le changement dans ce cas était assez évident.
Voici un exemple avec une substitution un peu moins évidente :
Ce que nous devons faire n'est pas du tout clair : le problème est que dans notre équation, il y a deux bases différentes et qu'une base ne peut pas être obtenue à partir de l'autre en l'élevant à une puissance (raisonnable, naturellement). Cependant, que voyons-nous ? Les deux bases ne diffèrent que par le signe et leur produit est la différence de carrés égale à un :
Définition:
Ainsi, les nombres qui sont des bases dans notre exemple sont conjugués.
Dans ce cas, le geste intelligent serait multiplier les deux membres de l'équation par le nombre conjugué.
Par exemple, sur, alors le côté gauche de l'équation deviendra égal, et le côté droit. Si nous faisons un remplacement, alors notre équation originale avec vous deviendra comme ceci :
ses racines, alors, mais en se souvenant de cela, nous obtenons cela.
Réponse: , .
En règle générale, la méthode de remplacement suffit à résoudre la plupart des équations exponentielles "scolaires". Les tâches suivantes sont extraites du USE C1 ( niveau élevé des difficultés). Vous êtes déjà suffisamment alphabétisé pour résoudre ces exemples par vous-même. Je ne donnerai que le remplacement requis.
- Résous l'équation:
- Trouvez les racines de l'équation :
- Résous l'équation: . Trouvez toutes les racines de cette équation qui appartiennent au segment :
Maintenant, pour quelques explications et réponses rapides :
- Ici, il suffit de noter que et. Alors l'équation originale sera équivalente à ceci : Cette équation résolu par remplacement Effectuez d'autres calculs vous-même. Au final, votre tâche se réduira à résoudre le trigonométrique le plus simple (en fonction du sinus ou du cosinus). Nous discuterons de la solution de tels exemples dans d'autres sections.
- Ici, vous pouvez même vous passer d'un remplacement : déplacez simplement le sous-traitant vers la droite et représentez les deux bases par des puissances de deux : puis passez immédiatement à l'équation quadratique.
- La troisième équation est également résolue de manière assez classique : imaginez comment. Ensuite, en remplaçant, nous obtenons une équation quadratique : alors,
Savez-vous déjà ce qu'est un logarithme ? Pas? Alors lisez d'urgence le sujet!
La première racine, évidemment, n'appartient pas au segment, et la seconde est incompréhensible ! Mais nous le saurons très bientôt ! Puisque, alors (c'est une propriété du logarithme !) comparons :
Soustrayez des deux parties, alors nous obtenons:
Le côté gauche peut être représenté par :
multiplier les deux côtés par :
peut être multiplié par, alors
Alors comparons :
depuis:
Alors la deuxième racine appartient à l'intervalle désiré
Réponse:
Comme tu vois, la sélection des racines des équations exponentielles nécessite une connaissance assez approfondie des propriétés des logarithmes, je vous conseille donc d'être aussi prudent que possible lors de la résolution d'équations exponentielles. Comme vous le savez, en mathématiques tout est interconnecté ! Comme le disait mon professeur de maths : "On ne peut pas lire les maths comme l'histoire du jour au lendemain."
En règle générale, tous la difficulté à résoudre les problèmes C1 est précisément la sélection des racines de l'équation. Entraînons-nous avec un autre exemple :
Il est clair que l'équation elle-même est résolue assez simplement. Après avoir effectué la substitution, nous réduisons notre équation initiale à la suivante :
Regardons d'abord la première racine. Comparez et : depuis, alors. (propriété de la fonction logarithmique, at). Alors il est clair que la première racine n'appartient pas non plus à notre intervalle. Maintenant la deuxième racine : . Il est clair que (puisque la fonction est croissante). Il reste à comparer et
puisque, alors, en même temps. Ainsi, je peux "enfoncer une cheville" entre et. Cette cheville est un nombre. La première expression est inférieure à et la seconde est supérieure à. Alors la deuxième expression est supérieure à la première et la racine appartient à l'intervalle.
Réponse: .
En conclusion, regardons un autre exemple d'équation où le remplacement est plutôt non standard :
Commençons tout de suite par ce que vous pouvez faire et ce que - en principe, vous pouvez, mais il vaut mieux ne pas le faire. Il est possible - de tout représenter par les puissances de trois, deux et six. Où cela mène-t-il ? Oui, et n'aboutira à rien : un méli-mélo de diplômes, dont certains seront assez difficiles à éliminer. Que faut-il alors ? Notons qu'un Et que va-t-il nous donner ? Et le fait que l'on puisse réduire la solution de cet exemple à la solution d'une équation exponentielle assez simple ! Tout d'abord, réécrivons notre équation comme suit :
Maintenant, nous divisons les deux côtés de l'équation résultante en :
Eurêka ! Maintenant que nous pouvons remplacer, nous obtenons :
Eh bien, maintenant c'est à votre tour de résoudre des problèmes de démonstration, et je ne leur donnerai que de brefs commentaires afin que vous ne vous égariez pas le droit chemin! Bonne chance!
1. Le plus difficile ! Voir un remplaçant ici, c'est oh, comme c'est moche ! Néanmoins, cet exemple peut être complètement résolu en utilisant sélection d'un carré complet. Pour le résoudre, il suffit de noter que :
Alors voici votre remplaçant :
(Notez qu'ici, avec notre remplacement, nous ne pouvons pas éliminer la racine négative !!! Et pourquoi, qu'en pensez-vous ?)
Maintenant, pour résoudre l'exemple, vous devez résoudre deux équations :
Les deux sont résolus par le "remplacement standard" (mais le second dans un exemple !)
2. Remarquez cela et faites une substitution.
3. Développez le nombre en facteurs premiers entre eux et simplifiez l'expression résultante.
4. Divisez le numérateur et le dénominateur de la fraction par (ou si vous préférez) et effectuez la substitution ou.
5. Notez que les nombres et sont conjugués.
ÉQUATIONS D'EXPOSITION. NIVEAU AVANCÉ
De plus, regardons une autre façon - solution d'équations exponentielles par la méthode logarithmique. Je ne peux pas dire que la solution des équations exponentielles par cette méthode soit très populaire, mais dans certains cas seulement, elle peut nous conduire à la solution correcte de notre équation. Surtout souvent, il est utilisé pour résoudre le soi-disant " équations mixtes' : c'est-à-dire ceux où il existe des fonctions de différents types.
Par exemple, une équation comme :
dans le cas général, il ne peut être résolu qu'en prenant le logarithme des deux parties (par exemple, par base), dans lequel l'équation d'origine se transforme en la suivante :
Considérons l'exemple suivant :
Il est clair que nous ne nous intéressons qu'à l'ODZ de la fonction logarithmique. Cependant, cela découle non seulement de l'ODZ du logarithme, mais pour une autre raison. Je pense qu'il ne vous sera pas difficile de deviner lequel.
Prenons le logarithme des deux côtés de notre équation à la base :
Comme vous pouvez le voir, prendre le logarithme de notre équation originale nous a rapidement conduit à la bonne (et belle !) réponse. Entraînons-nous avec un autre exemple :
Là aussi, il n'y a pas lieu de s'inquiéter : on prend le logarithme des deux côtés de l'équation en fonction de la base, on obtient alors :
Faisons un remplacement :
Cependant, nous avons raté quelque chose! Avez-vous remarqué où j'ai fait une erreur? Après tout, alors :
qui ne satisfait pas à l'exigence (pensez d'où il vient !)
Réponse:
Essayez d'écrire la solution des équations exponentielles ci-dessous :
Maintenant, vérifiez votre solution avec ceci :
1. On logarithme les deux parties à la base, étant donné que :
(la deuxième racine ne nous convient pas à cause du remplacement)
2. Logarithme à la base :
Transformons l'expression résultante sous la forme suivante :
ÉQUATIONS D'EXPOSITION. BRÈVE DESCRIPTION ET FORMULE DE BASE
équation exponentielle
Tapez l'équation :
appelé l'équation exponentielle la plus simple.
Propriétés du diplôme
Approches de solutions
- Réduction à la même base
- Réduction au même exposant
- Substitution de variables
- Simplifiez l'expression et appliquez l'une des propositions ci-dessus.